Study on the Influence of Winding Height on the Short-Circuit Withstand Capability of 110 kV Transformers
Abstract
1. Introduction
2. Leakage Magnetic Field and Short-Circuit Forces in 110 kV Three-Phase Three-Limb Transformers
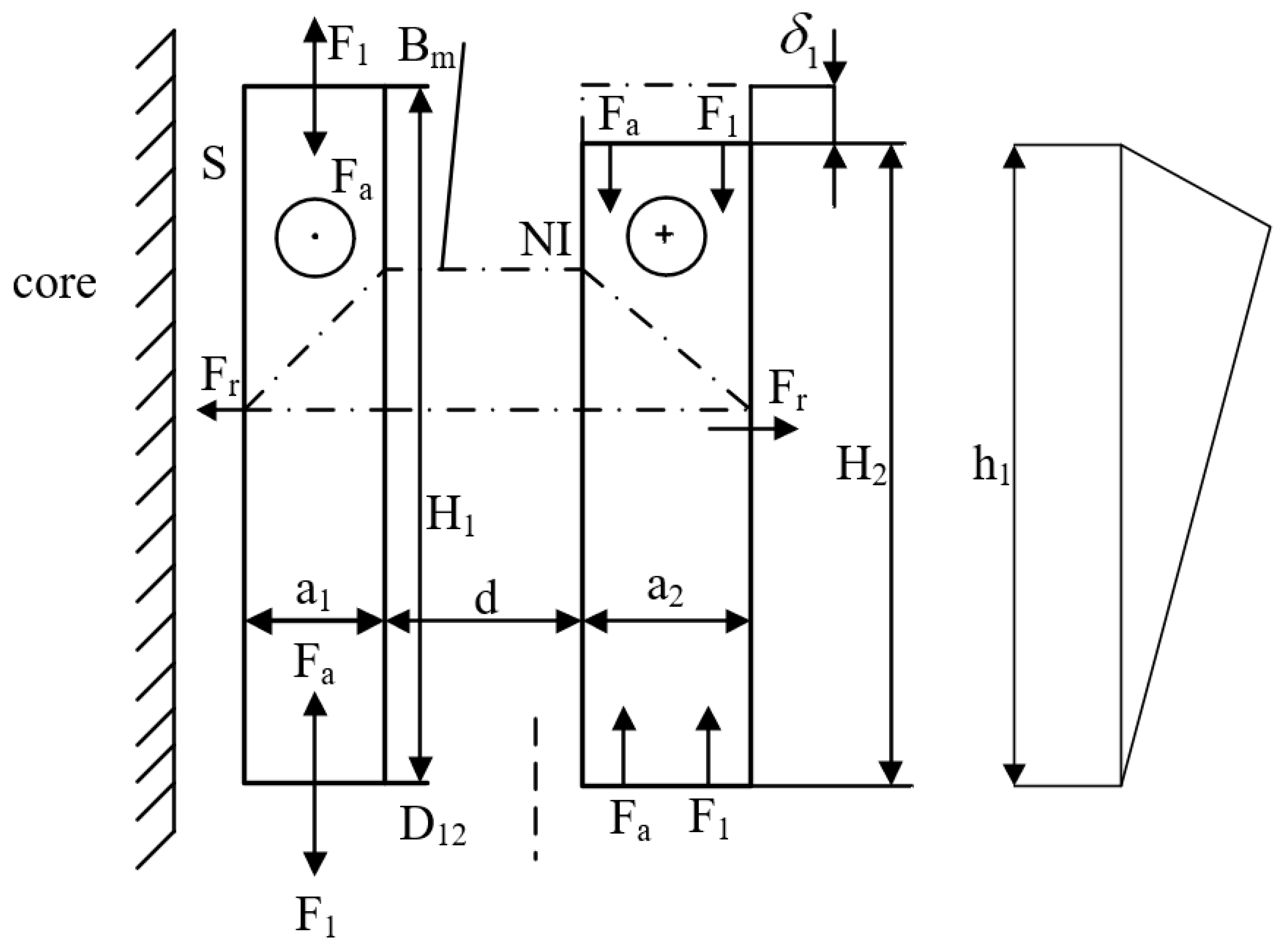
2.1. Analysis of Transformer Leakage Magnetic Field
2.2. Calculation of Axial Electromagnetic Forces in Transformers with Non-Equal Winding Heights
3. Simulation and Calculation of Transformer Leakage Magnetic Field and Short-Circuit Forces Based on the Finite Element Method
3.1. Model Construction
3.2. Comparison of Leakage Magnetic Field Simulation Results
3.3. Simulation Calculation Comparison of Electromagnetic Force for 110 kV Transformers
4. Field Testing and Algorithmic Prediction for 110 kV Three-Phase Three-Limb Transformers
4.1. Field Testing of 110 kV Transformers
4.2. Short-Circuit Experimental Diagnosis for 110 kV Transformers Based on Dual Convolutional Neural Network-Long Short-Term Memory Architecture
4.2.1. Model Principle
4.2.2. Diagnosis Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Z. Research on Cumulative Effects and Short-Circuit Strength of Transformers Under Repeated Short-Circuit Shocks. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2024. [Google Scholar]
- Li, P.; Sui, H.Z.; Xu, Z.Y.; Li, L.D.; Wang, K.; Wang, Z.X.; Zhang, S.Q.; Zhao, Z.G. Cumulative Effects on Transformer Windings Based on Equivalent Short-Circuit Tests. Proc. CSEE 2025, 45, 2411–2423. (In Chinese) [Google Scholar] [CrossRef]
- Wang, M.; Vandermaar, A.J.; Srivastava, K.D. Review of condition assessment of power transformers in service. IEEE Electr. Insul. Mag. 2002, 18, 12–25. [Google Scholar] [CrossRef]
- Cui, P.; Wu, M.K.; Lu, H.J.; An, Y.; Cao, Z.; Feng, X.; Feng, R. Fault Diagnosis of Converter Transformers Based on Time-Frequency Maps and Parallel CNN-LSTM. Ningxia Electr. Power 2025, 53–59+66. [Google Scholar]
- Guimarães, R.; Delaiba, A.C.; Rosentino, A.J., Jr.; Saraiva, E.; de Oliveira, J.C. Electromechanical stress intransformers caused by inrush and short circuit currents. J. Braz. Mech. Sci. Eng. 2015, 37, 243–253. [Google Scholar] [CrossRef]
- Li, Z.Y.; Meng, J.; Yang, X.D.; Ma, G.; Liu, S.J. Prediction of CO2 Concentration in Combustion Flue Gas Based on CNN-LSTM Model. J. Combust. Sci. Technol. 2025, 31, 406–414. [Google Scholar]
- Ahn, H.M.; Kim, S.Y.; Kim, J.K.; Oh, Y.H.; Hahn, S.C. Numerical investigation for transient electromagnetic force computation of power transformer during short-circuitcondition. Int. J. Appl. Electromagn. Mech. 2016, 52, 1141–1149. [Google Scholar] [CrossRef]
- Cheng, T.L.; Li, C.R.; Fu, Q.Q.; Jiang, Y.H.; Liu, J.J. Electric Vehicle Charging Load Prediction Based on CNN-LSTM-AM. Auto Electr. Parts 2025, 10, 62–64. (In Chinese) [Google Scholar] [CrossRef]
- Sinha, A.; Kaur, S. Analysis of short circuit electromagnetic forces in transformer with asymmetrically placed windings using Finite Element Method. In Proceedings of the 2016 Second International Innovative Applications of Computational Intelligence onPower, Energy and Controls with their Impact on Humanity (CIPECH), Ghaziabad, India, 18–19 November 2016; IEEE: New York, NY, USA, 2016; pp. 101–105. [Google Scholar]
- Gao, S.G.; Sun, L.; Liu, H.L. Calculation of Axial Electromagnetic Force in Transformers under Short-Circuit Conditions Based on COMSOL Multiphysics Simulation. Sci. Technol. Eng. 2022, 22, 5250–5256. [Google Scholar]
- Komurgoz, G.; Gundogdu, T. Effect of the tap winding configurations on the electromagnetic forces acting on the concentric transformer coils. In Proceedings of the 2013 3rd International Conference on Electric Power and Energy Conversion Systems, Istanbul, Turkey, 2–4 October 2013; IEEE: New York, NY, USA, 2013. [Google Scholar]
- Medeiros, L.H.; Maschio, G.; Oliveira, M.M.; Kaminski, A.M., Jr.; Bueno, D.M.; Bender, V.C.; Marchesan, T.B. Finite element analysis for calculation of total and distributed electromagnetic forces on power transformers windings arrangements. Electr. Eng. 2024, 106, 931–940. [Google Scholar] [CrossRef]
- Bakshi, A. An Investigation of Winding Curvature Effect on the Mechanical Strength of Transformer Windings. IEEE Trans. Power Deliv. 2015, 30, 1821–1826. [Google Scholar] [CrossRef]
- Liu, Y.R.; Chi, C.C. Transformer Fault Diagnosis Method Based on ChOA-CNN-LSTM. J. Shanghai Dianji Univ. 2025, 28, 142–147. [Google Scholar]
- Ahn, H.M.; Oh, Y.H.; Kim, J.K.; Song, J.S.; Hahn, S.C. Experimental Verification and Finite Element Analysis of Short-Circuit Electromagnetic Force for Dry-Type Transformer. IEEE Trans. Magn. 2012, 48, 819–822. [Google Scholar] [CrossRef]
- Qiu, S.X.; Wang, S.; Liu, Z.R.; Yu, Z.; Dong, W.; Liu, J. Research on Transformer Winding Fault Diagnosis Based on FRA Method and CNN. Large Electr. Mach. Hydraul. Turbine 2025, 108–116+122. [Google Scholar]
- Yadav, S.; Mehta, R.K. FEM Based Study of Short Circuit Forces on Power Transformer Windings. In Proceedings of the 2019 3rd International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 10–11 October 2019. [Google Scholar]
- Chen, Q.; Wang, S.; Lin, D.; Wang, S.; Wang, S.; Yuan, D.; Li, H. Analysis of mechanical characteristics of transformer windings undershort circuit fault. In Proceedings of the 2018 12th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Xi’an, China, 20–24 May 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Sun, P.; Liu, C.R.; Ma, J.M. Fault Diagnosis of Mining Transformers Based on Convolutional Neural Network and LSTM Network. Met. Mine 2025, 168–173. [Google Scholar] [CrossRef]
- Jiao, X.B.; Zhang, W.F.; Chang, F.H.; Li, Q.; Ge, Q. Application Research on Intelligent Fault Diagnosis of Substation Equipment Based on LSTM-CNN Model. Home Appl. Repair 2025, 128–130. [Google Scholar]
- Wang, F.; Cai, Q.N. Research on Transformer Oil Temperature Prediction Based on AIoT Cloud Platform and CNN-LSTM. Transformer 2025, 62, 21–26. [Google Scholar] [CrossRef]
- Liu, H.R.; Cheng, H.T.; Xiao, Y.J.; Zhou, B. Intelligent Evaluation Method for Power Transformer Operation Status Based on CNN-BiGRU Network. Electr. Eng. Econ. 2024, 226–228. [Google Scholar]
- Ni, X.Y. CNN Data-Driven Optimal Strategy for Active Distribution Network Under Multi-Source Uncertainties. Master’s Thesis, Guangxi University, Nanning, China, 2024. [Google Scholar] [CrossRef]
- Wu, M.D.; Zou, P.; Zhao, Z. Anomaly Detection Model for UAV Sensor Data Based on CNN-LSTM-BF. J. Chongqing Technol. Bus. Univ. (Nat. Sci. Ed.) 2025, 1–9. Available online: https://link.cnki.net/urlid/50.1155.n.20250818.1619.006 (accessed on 9 October 2025).
- Wang, H.J. Reservoir Landslide Displacement Prediction Based on GA-CNN-LSTM. Shaanxi Water Resour. 2025, 10, 18–21. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, P.N.; Li, P.Y.; Liu, Z.; Zhang, J.; Cao, Q.; Li, L. Dual Two-Dimensional Analytical Model for Leakage Inductance Calculation of High-Frequency Transformers with Round Litz Wires. High Volt. Eng. 2025, 51, 75–87. [Google Scholar] [CrossRef]
- Luo, W.B.; Li, L.; Zhang, Y.H.; Tong, L.; Wu, K. Time Series Prediction of Diaphragm Wall Deformation Based on GWO-LSTM-CNN. Ind. Constr. 2025, 1–10. Available online: https://link.cnki.net/urlid/11.2068.TU.20250813.1609.010 (accessed on 9 October 2025).
- Haack, R.W.; Girgis, S. Experimental verification of three-dimensional analysis ofleakage magnetic fields in large power transformers. IEEE Trans. Power Appar. Syst. 1983, 102, 3212–3217. [Google Scholar] [CrossRef]
- Wang, X.; Jing, Y.; Yu, Z.; Li, Y.; Meng, T. Evaluation Method for Anti-Short-Circuit Capacity of Power Transformers Based on Finite Element and Analytical Calculations. High Volt. Eng. 2025, 1–12. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.P. Research on Measures to Enhance the Short-Circuit Resistance of Dry-Type Transformer Windings. Mech. Electr. Inf. 2025, 06, 24–27. (In Chinese) [Google Scholar] [CrossRef]

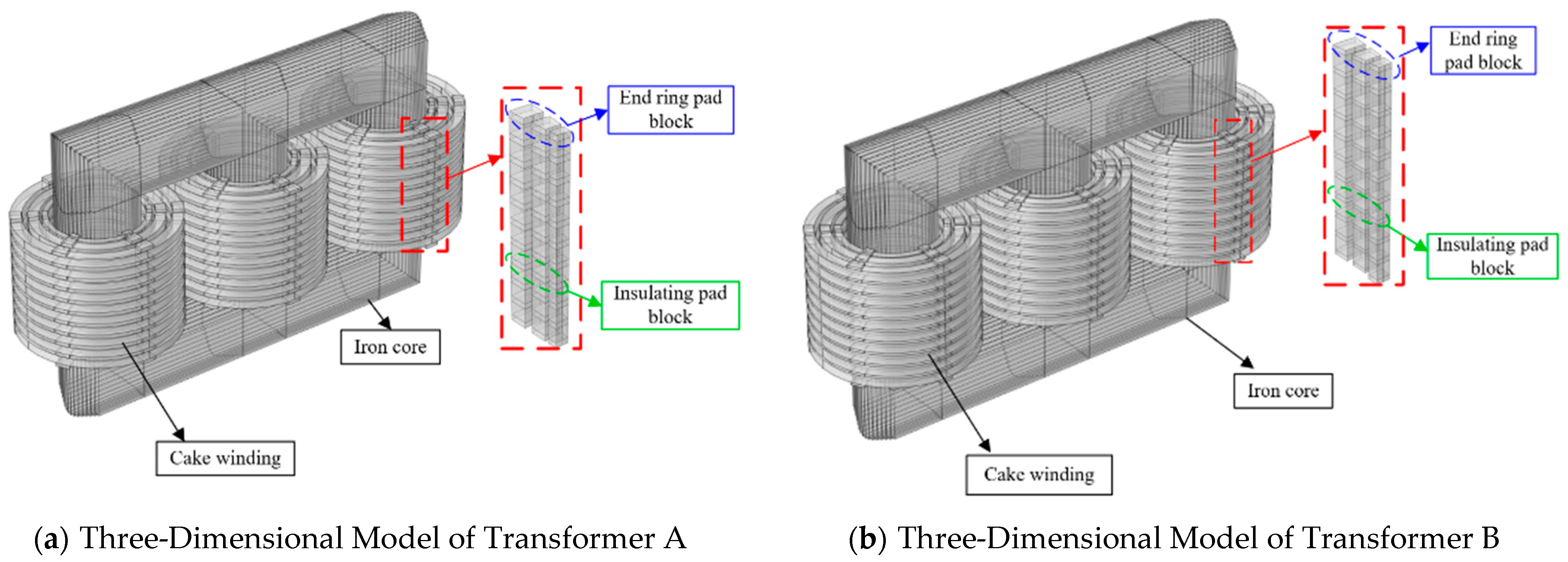
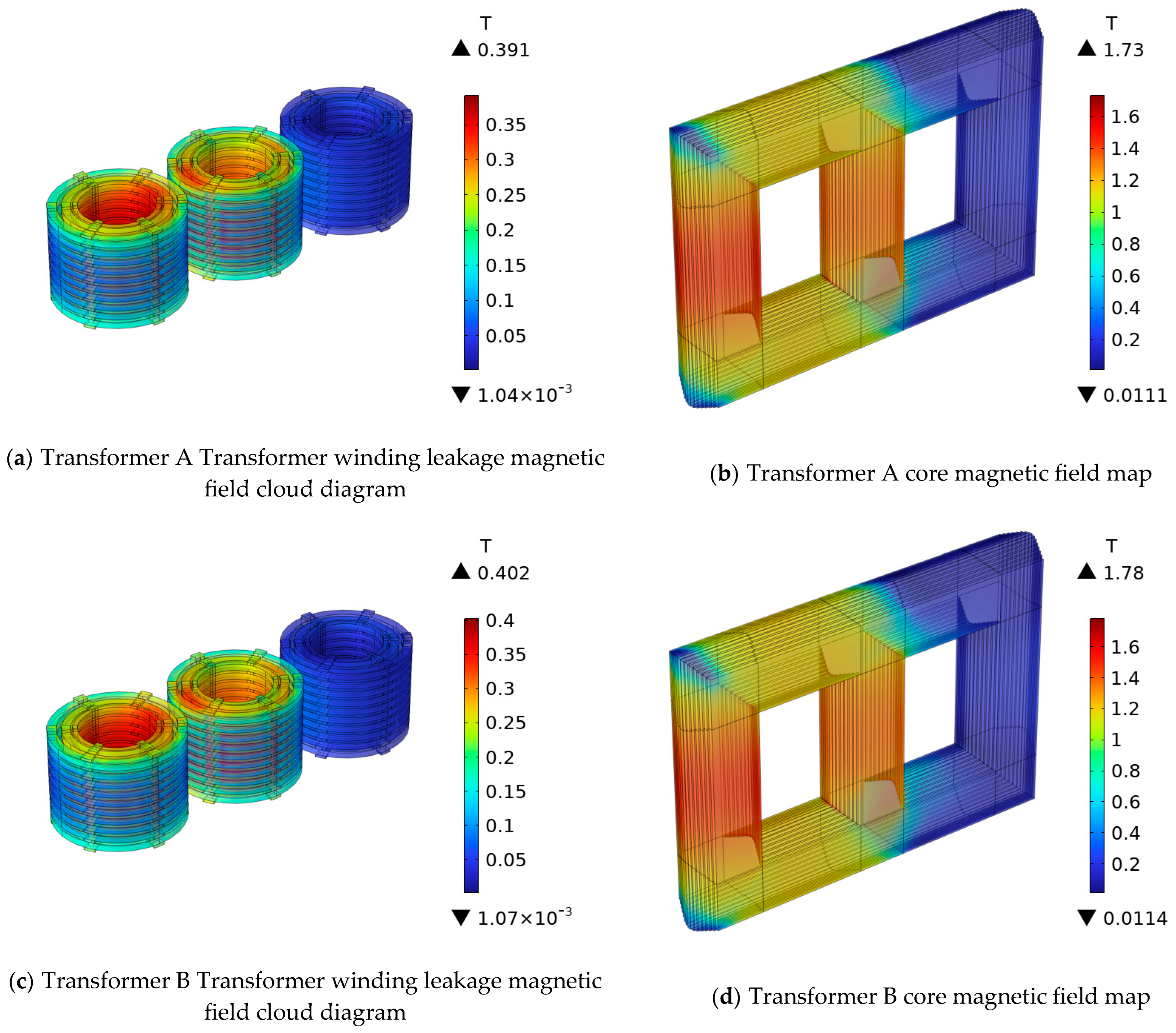
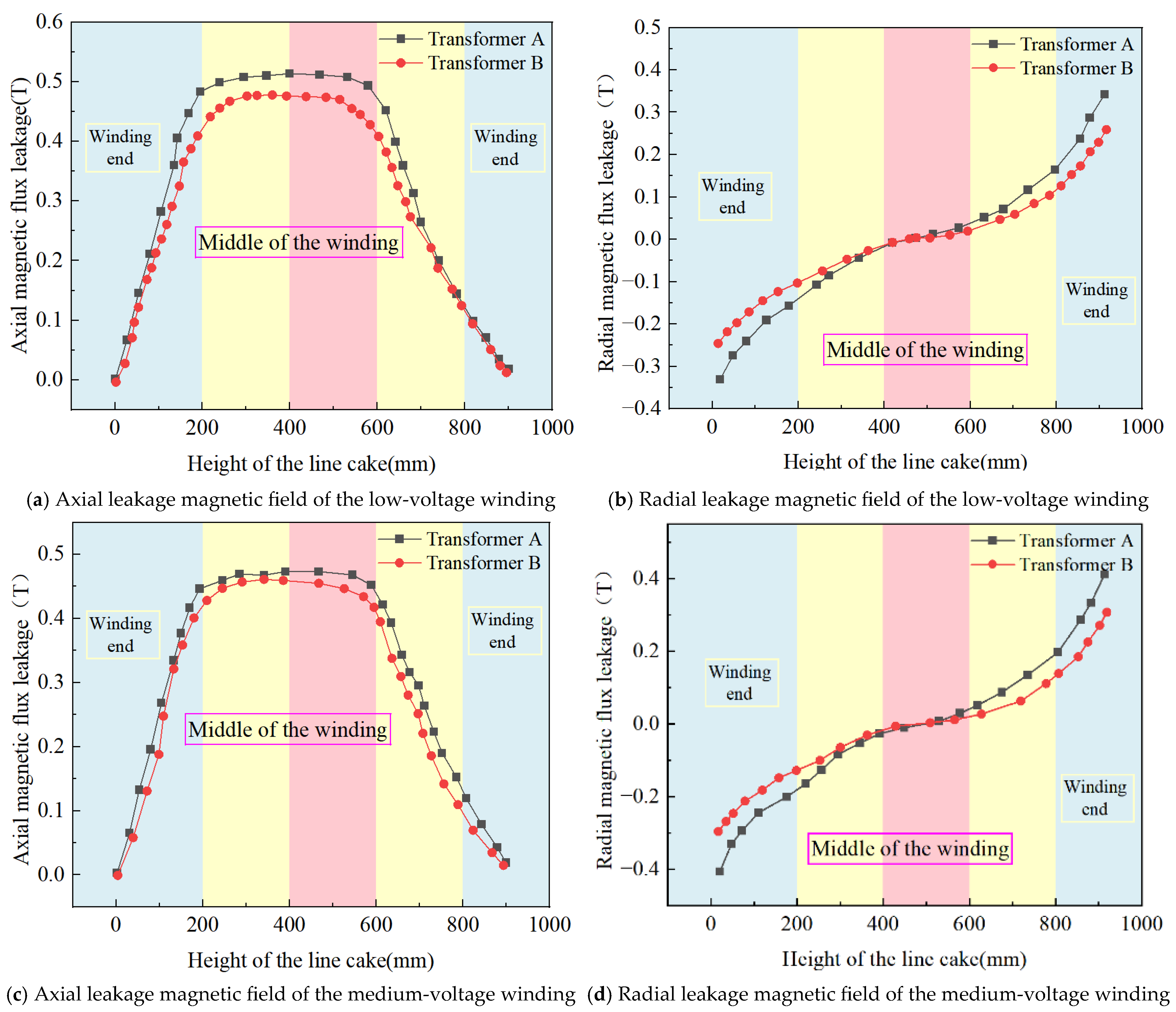
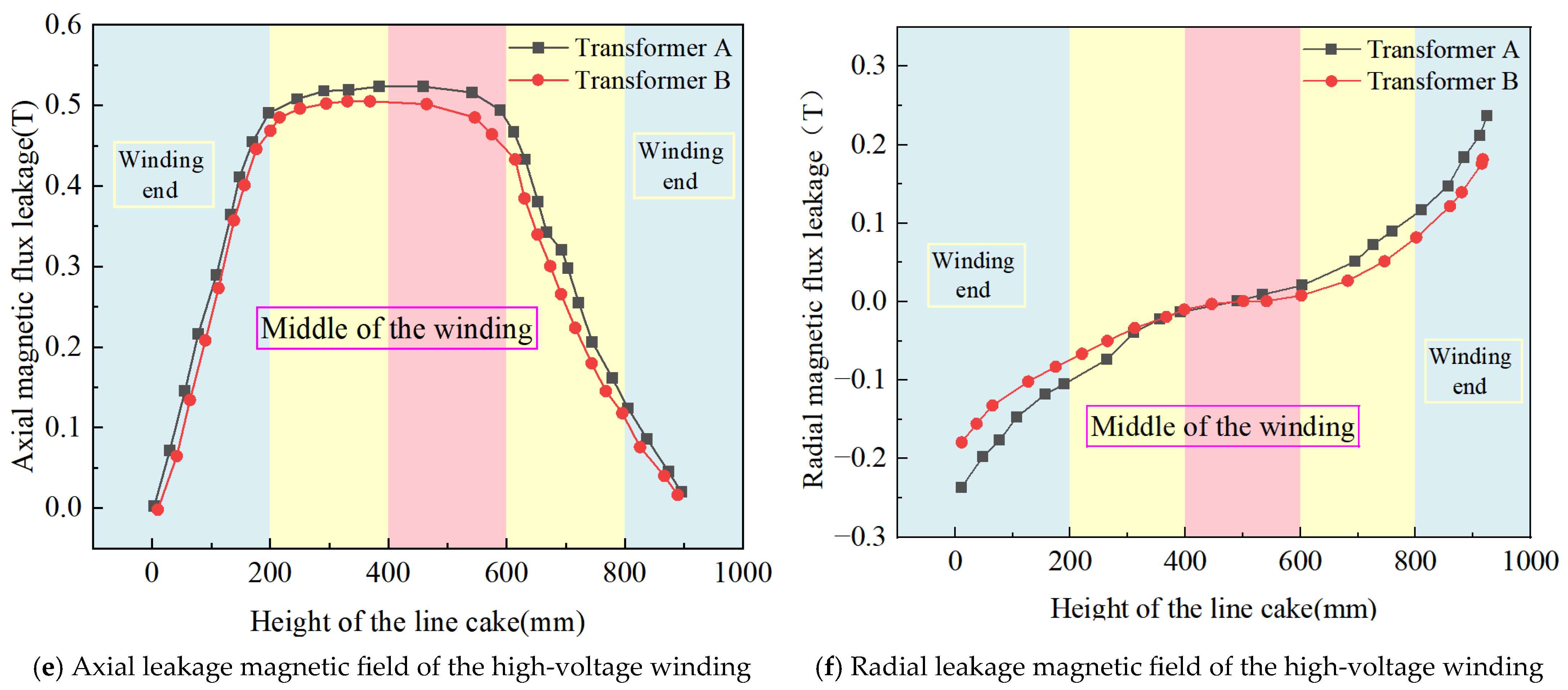
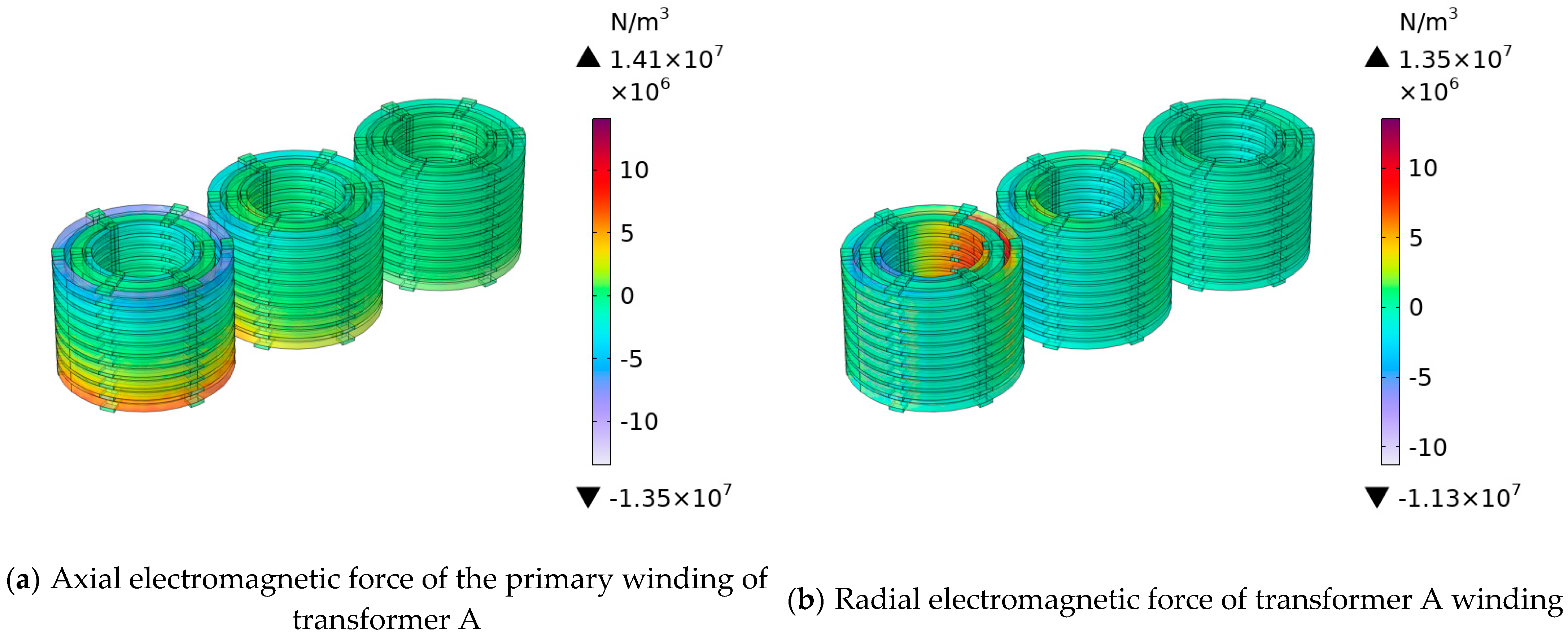
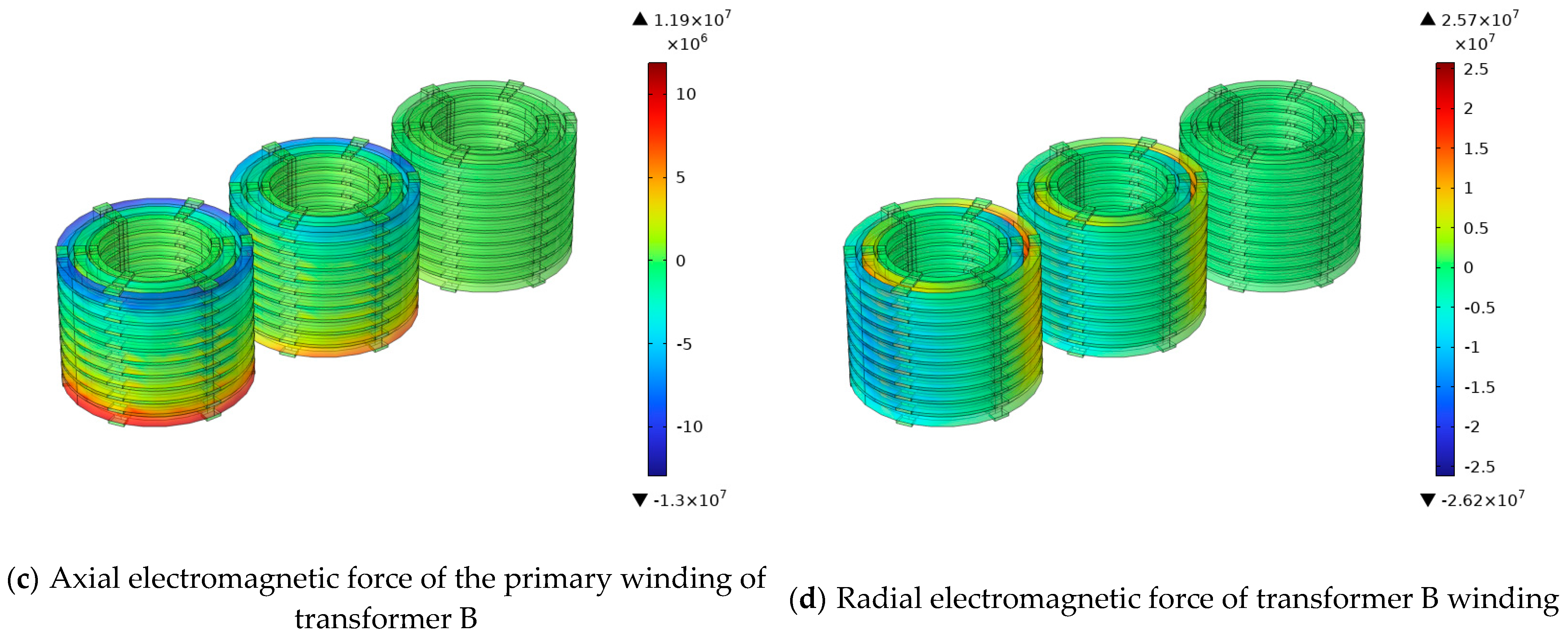

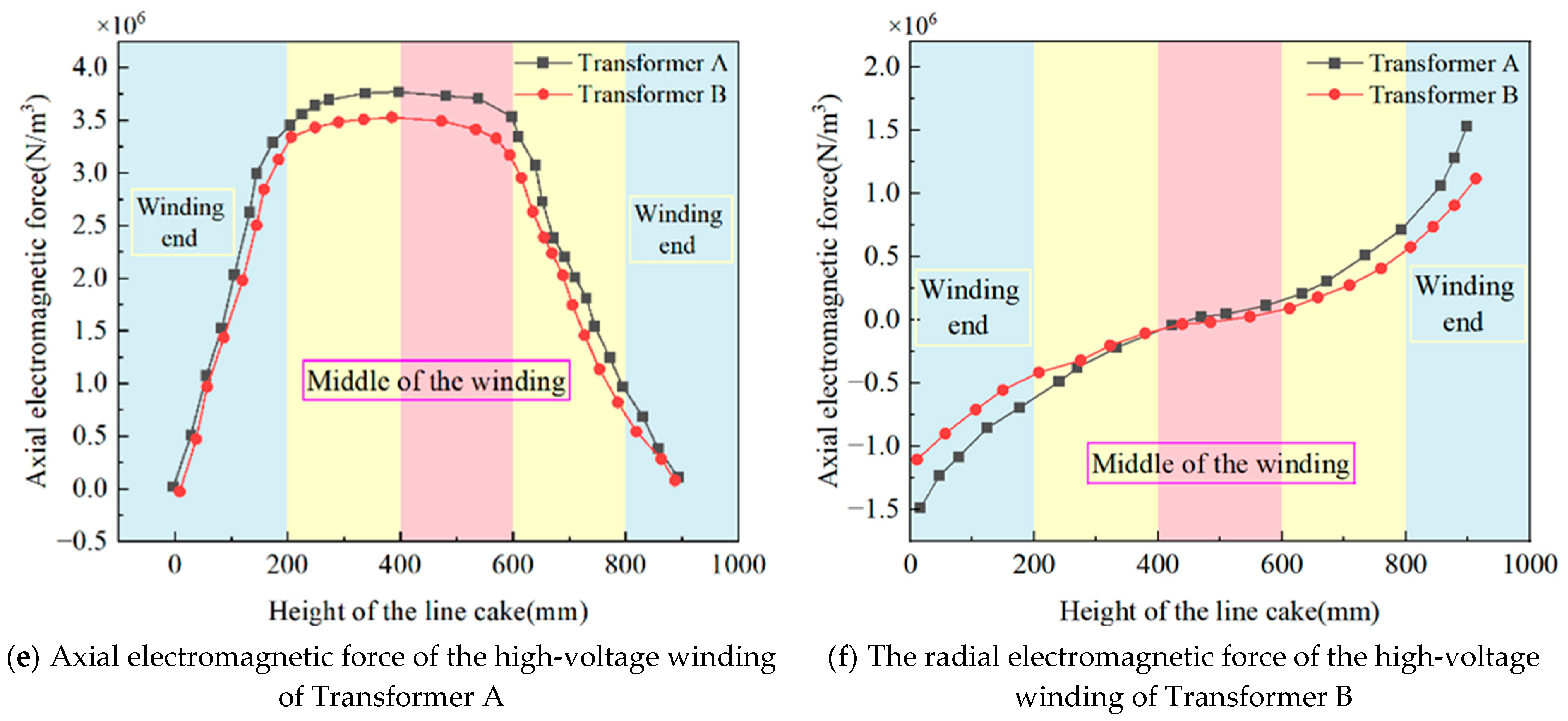
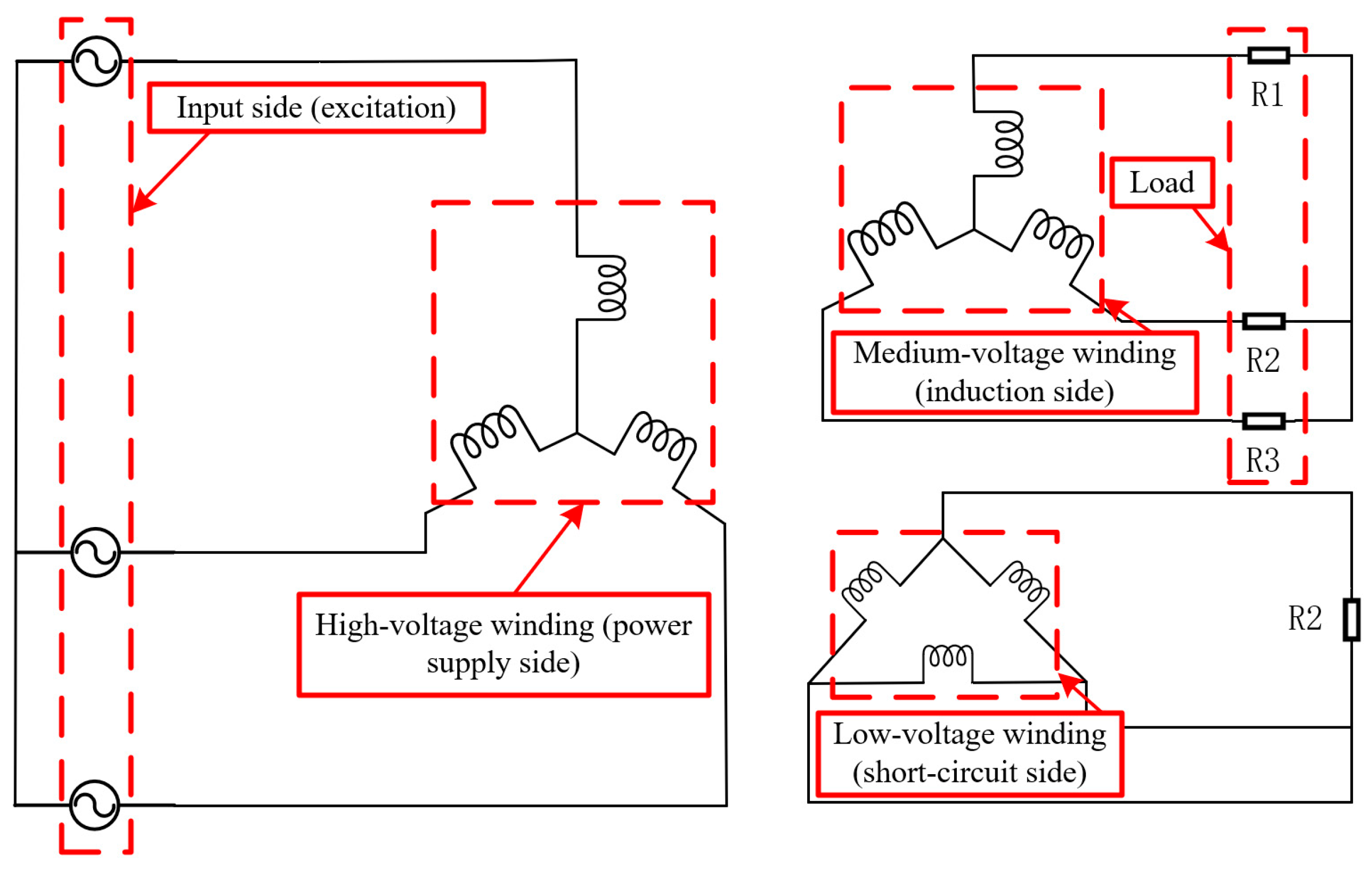

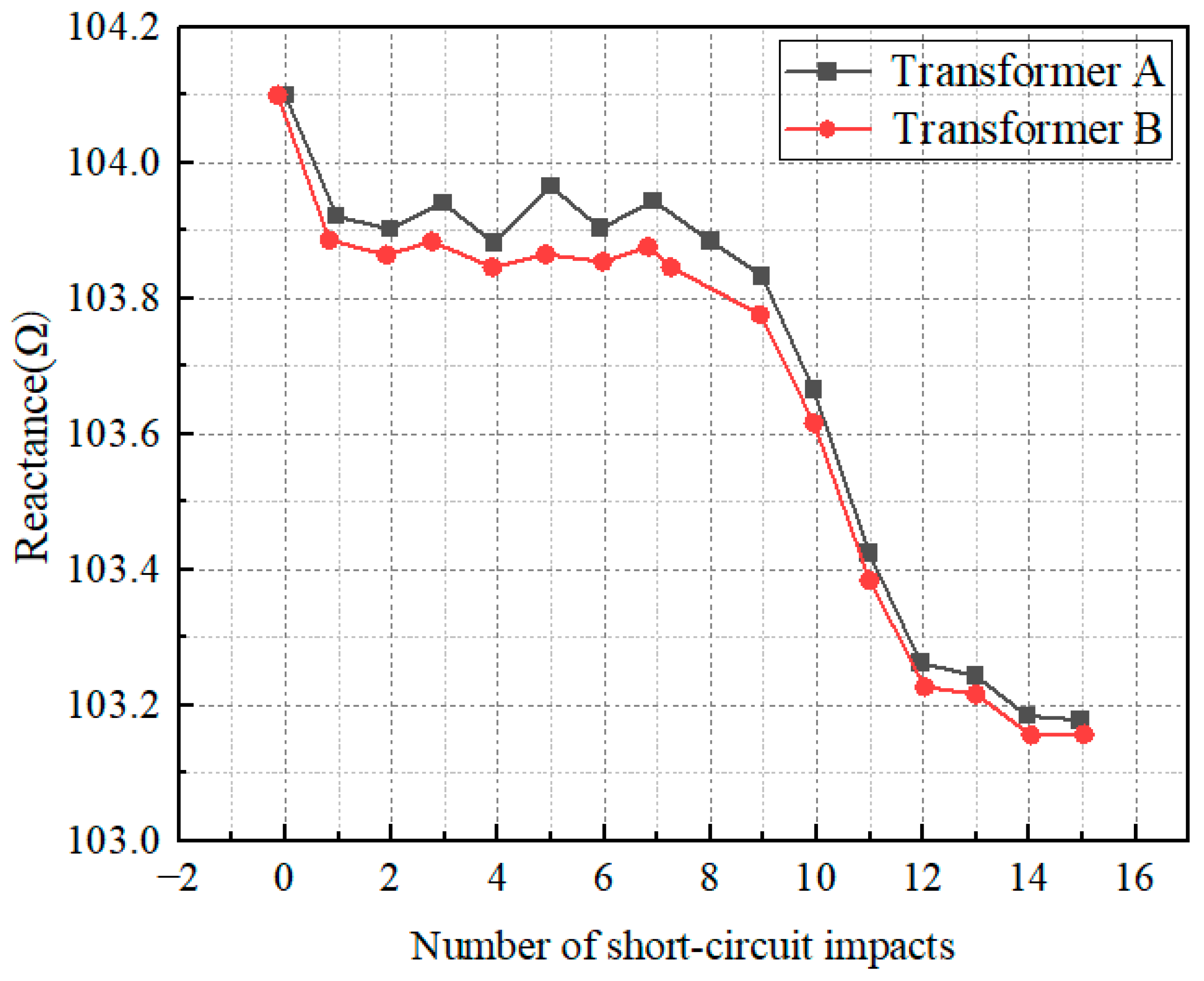



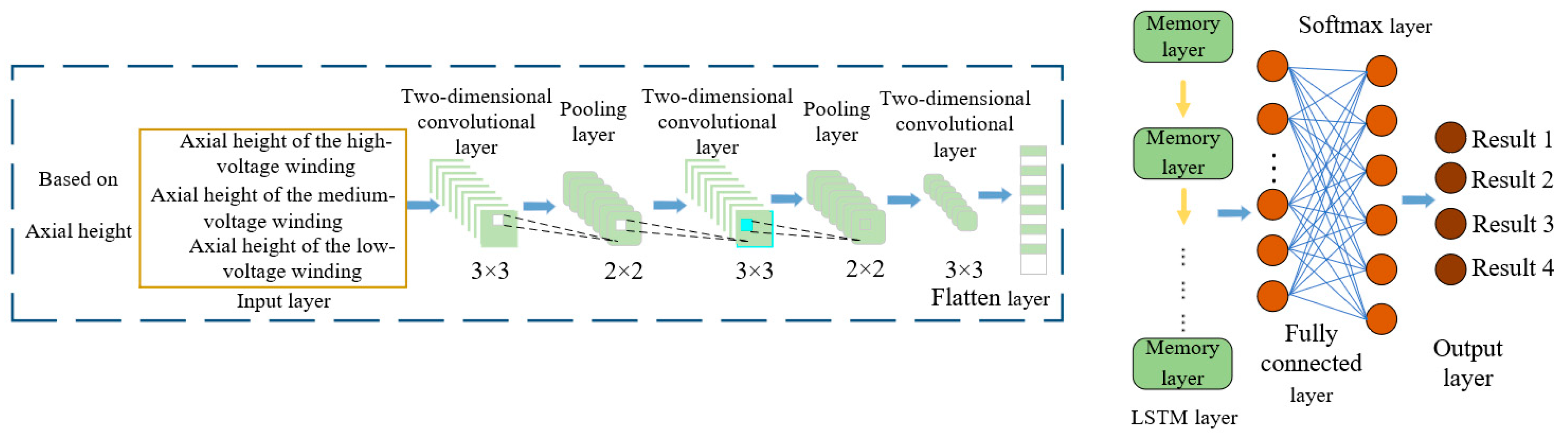



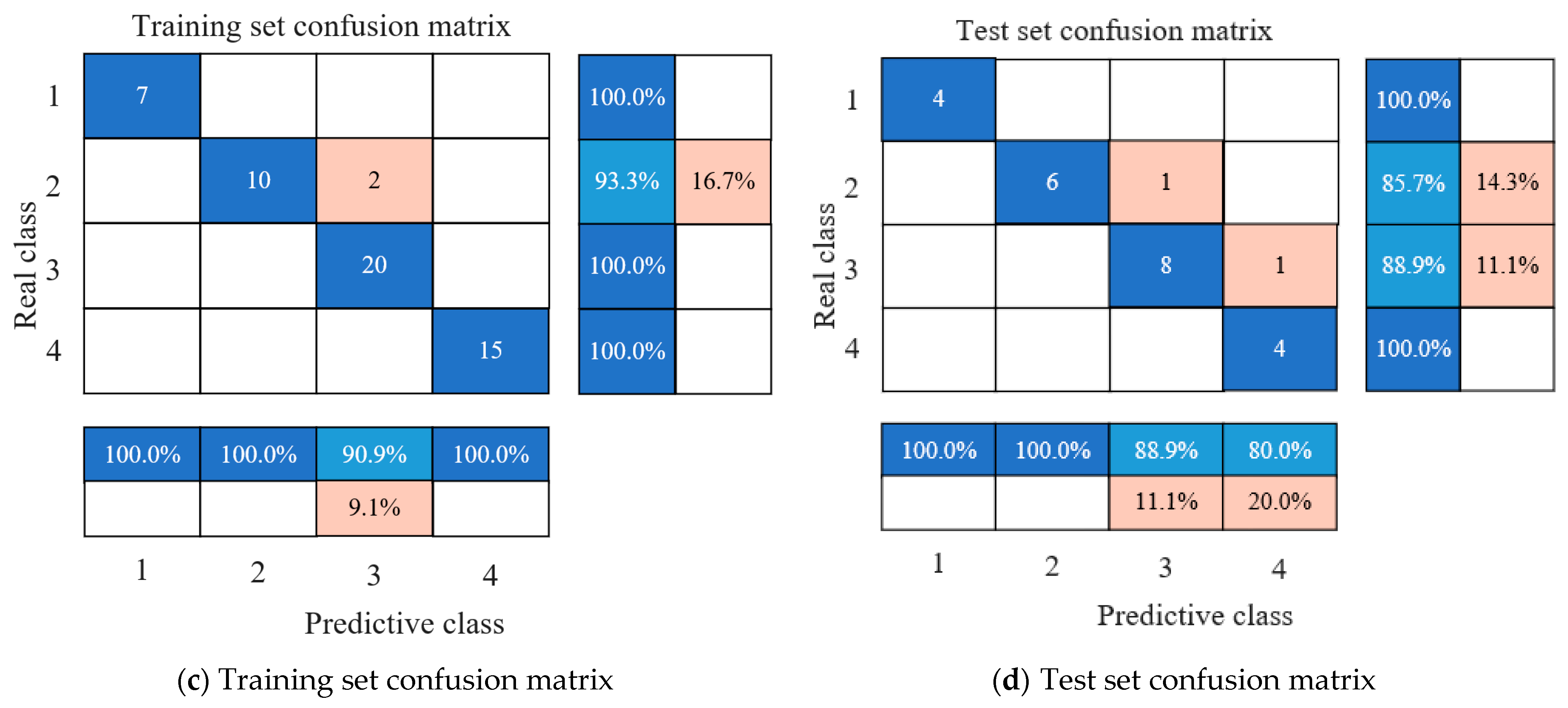
| Product Model | 110 kV Transformer | ||
|---|---|---|---|
| Rated Frequency/Hz | 50 | ||
| Core Structure | Three-phase three-limb | ||
| Winding Parameters | H-v winding | M-v winding | L-v winding |
| Rated Capacity/kVA | 50,000 | 50,000 | 50,000 |
| Rated Voltage/kV | 110 | 38.5 | 10.5 |
| Winding Inner Radius/mm | 557.5 | 430 | 363 |
| Winding Outer Radius/mm | 645 | 512.5 | 408 |
| Total Winding Height/mm | 995 | 995 | 1015 |
| Total Winding Turns | 478 | 167 | 79 |
| Spacer Dimensions (Length × Width)/mm | 87.5 × 19.18 | 82.5 × 22.9 | 45 × 27.45 |
| Product Model | 110 kV Transformer | ||
|---|---|---|---|
| Rated Frequency/Hz | 50 | ||
| Core Structure | Three-phase three-limb | ||
| Winding Parameters | H-v winding | M-v winding | L-v winding |
| Rated Capacity/kVA | 50,000 | 50,000 | 50,000 |
| Rated Voltage/kV | 110 | 38.5 | 10.5 |
| Winding Inner Radius/mm | 557.5 | 430 | 363 |
| Winding Outer Radius/mm | 645 | 512.5 | 408 |
| Total Winding Height/mm | 995 | 995 | 995 |
| Total Winding Turns | 478 | 167 | 79 |
| Spacer Dimensions (Length × Width)/mm | 87.5 × 19.18 | 82.5 × 22.9 | 45 × 27.45 |
| Transformer Model | Transformer A | Transformer B | ||||
|---|---|---|---|---|---|---|
| Winding Parameters | L-V winding | M-V winding | H-V winding | L-V winding | M-V winding | H-V winding |
| Axial magnetic flux leakage/(T) | 0.532 | 0.473 | 0.521 | 0.486 | 0.453 | 0.452 |
| Radial magnetic flux leakage/(T) | 0.251 | 0.425 | 0.395 | 0.187 | 0.296 | 0.256 |
| Axial electromagnetic force/(N/m3) | 3.97 × 106 | 3.98 × 106 | 3.76 × 106 | 3.66 × 106 | 3.73 × 106 | 3.52 × 106 |
| Radial electromagnetic force(N/m3) | 2.2 × 106 | 1.7 × 106 | 1.52 × 106 | 1.6 × 106 | 1.25 × 106 | 1.12 × 106 |
| Network Parameters | Numerical Value |
|---|---|
| Fill mode | Same mode |
| Activation function | ReLU |
| Weight | Random normal distribution |
| Number of neurons in the LSTM hidden layer | 100 |
| Optimize function | Adam |
| Learning rate | 1.45 × 10−3 |
| Learning rate decay factor | 0.09 |
| Learning rate decay period | 30 |
| L2 regularization parameter | 1.45 × 10−3 |
| Batch size | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Zhou, X.; Wang, X.; Tian, T.; Tai, C.; Chen, D.; Xin, Z.; Wang, S. Study on the Influence of Winding Height on the Short-Circuit Withstand Capability of 110 kV Transformers. Sensors 2025, 25, 6528. https://doi.org/10.3390/s25216528
Ma Y, Zhou X, Wang X, Tian T, Tai C, Chen D, Xin Z, Wang S. Study on the Influence of Winding Height on the Short-Circuit Withstand Capability of 110 kV Transformers. Sensors. 2025; 25(21):6528. https://doi.org/10.3390/s25216528
Chicago/Turabian StyleMa, Yukun, Xiu Zhou, Xiaokang Wang, Tian Tian, Chenfan Tai, Dezhi Chen, Ziyuan Xin, and Sijun Wang. 2025. "Study on the Influence of Winding Height on the Short-Circuit Withstand Capability of 110 kV Transformers" Sensors 25, no. 21: 6528. https://doi.org/10.3390/s25216528
APA StyleMa, Y., Zhou, X., Wang, X., Tian, T., Tai, C., Chen, D., Xin, Z., & Wang, S. (2025). Study on the Influence of Winding Height on the Short-Circuit Withstand Capability of 110 kV Transformers. Sensors, 25(21), 6528. https://doi.org/10.3390/s25216528





