“Speed”: A Dataset for Human Speed Estimation
Abstract
1. Introduction
- We present a medium-scale dataset, which contains IMU measurements from 33 healthy subjects, walking/running at speeds ranging from 4.0 km/h (1.11 m/s) to 9.5 km/h (2.64 m/s) in increments of 0.5 km/h (0.14 m/s) to suit the endurance level of the participants and most healthy (not necessarily athletic) people. We name it the “Speed” dataset. No other dataset is available in the literature with such a diverse and fine range of speed measurements for healthy subjects. We are making the dataset publicly available under a licensing agreement. This will be a great help for researchers working in the area.
- In addition, we employ deep learning in the form of a deep CNN, for speed estimation for baseline results. CNNs have the ability to extract features from raw data and are very powerful in image recognition. Researchers have also applied them for gait variable estimation and human activity recognition [16,17]. The resulting RMSE measures show that the proposed deep CNN beats the other methods for speed estimation from the literature. We call our baseline network SpeedNet. We leave other improvements in the model architecture, such as incorporating attention mechanisms [18], etc., for future researchers to build upon the baseline results.
2. Methodology
2.1. Data Collection
- Accelerometer range: ±2 g, ±4 g, ±8 g, ±16 g, 16-bit resolution.
- Gyroscope range: ±125°/s, ±250°/s, ±500°/s, ±1000°/s, ±2000°/s, 16-bit resolution.
- Static orientation error < 0.5°.
- Dynamic orientation error < 2°.
- Resolution of orientation < 0.05°.
2.2. Pre-Processing
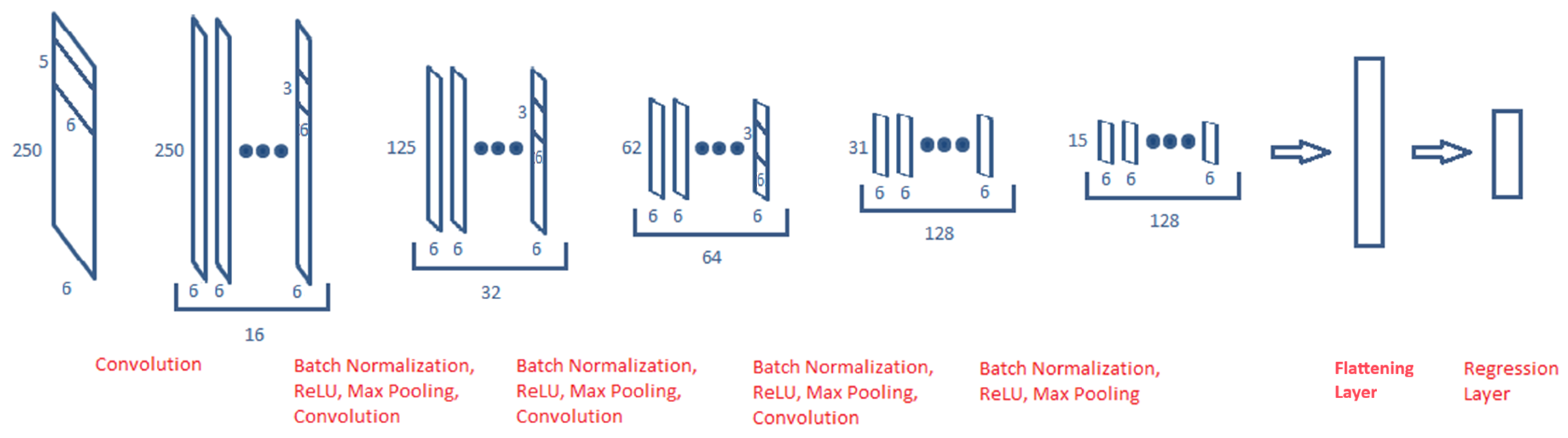
2.3. SpeedNet
2.4. Experimental Setup
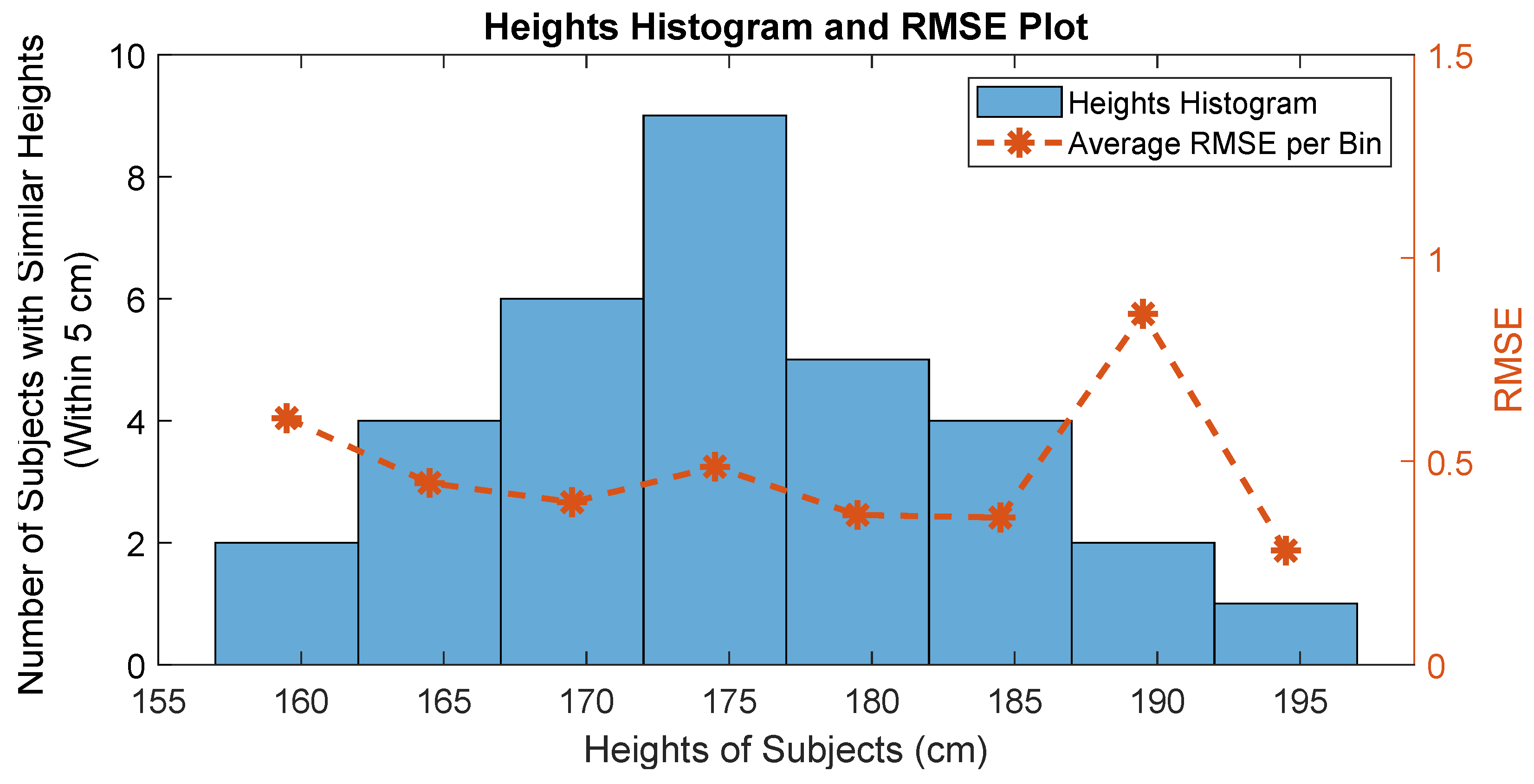
3. Results and Discussion
Subject-Dependent Approach
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Li, Q. Inertial sensor-based methods in walking speed estimation: A systematic review. Sensors 2012, 12, 6102–6116. [Google Scholar] [CrossRef] [PubMed]
- Malladi, A.; Srinu, V.; Srinu, V.; Chandrasekaran, V.; Meshram, P.; Taranath, T. Biomechanics Engineering Human Motion and Health; YAR TECH Publication: Chennai, India, 2024. [Google Scholar]
- Hu, J.S.; Sun, K.C.; Cheng, C.Y. A kinematic human-walking model for the normal-gait-speed estimation using tri-axial acceleration signals at waist location. IEEE Trans. Biomed. Eng. 2013, 60, 2271–2279. [Google Scholar] [PubMed]
- Bugané, F.; Benedetti, M.; Casadio, G.; Attala, S.; Biagi, F.; Manca, M.; Leardini, A. Estimation of spatial-temporal gait parameters in level walking based on a single accelerometer: Validation on normal subjects by standard gait analysis. Comput. Methods Programs Biomed. 2012, 108, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Mohr, C.; Li, Q. Ambulatory running speed estimation using an inertial sensor. Gait Posture 2011, 34, 462–466. [Google Scholar] [CrossRef] [PubMed]
- Chew, D.K.; Gouwanda, D.; Gopalai, A.A. Investigating running gait using a shoe-integrated wireless inertial sensor. In Proceedings of the TENCON 2015—2015 IEEE Region 10 Conference, Macao, China, 1–4 November 2015; IEEE: New York, NY, USA, 2015; pp. 1–6. [Google Scholar]
- McGinnis, R.S.; Mahadevan, N.; Moon, Y.; Seagers, K.; Sheth, N.; Wright, J.A., Jr.; DiCristofaro, S.; Silva, I.; Jortberg, E.; Ceruolo, M.; et al. A machine learning approach for gait speed estimation using skin-mounted wearable sensors: From healthy controls to individuals with multiple sclerosis. PLoS ONE 2017, 12, e0178366. [Google Scholar] [CrossRef] [PubMed]
- Vathsangam, H.; Emken, A.; Spruijt-Metz, D.; Sukhatme, G.S. Toward free-living walking speed estimation using Gaussian process-based regression with on-body accelerometers and gyroscopes. In Proceedings of the 2010 4th International Conference on Pervasive Computing Technologies for Healthcare, Munich, Germany, 22–25 March 2010; IEEE: New York, NY, USA, 2010; pp. 1–8. [Google Scholar]
- Zihajehzadeh, S.; Park, E.J. A Gaussian process regression model for walking speed estimation using a head-worn IMU. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; IEEE: New York, NY, USA, 2017; pp. 2345–2348. [Google Scholar]
- Zihajehzadeh, S.; Aziz, O.; Tae, C.G.; Park, E.J. Combined regression and classification models for accurate estimation of walking speed using a wrist-worn imu. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; IEEE: New York, NY, USA, 2018; pp. 3272–3275. [Google Scholar]
- Aminian, K.; Robert, P.; Jequier, E.; Schutz, Y. Estimation of speed and incline of walking using neural network. IEEE Trans. Instrum. Meas. 1995, 44, 743–746. [Google Scholar] [CrossRef]
- Song, Y.; Shin, S.; Kim, S.; Lee, D.; Lee, K.H. Speed estimation from a tri-axial accelerometer using neural networks. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; IEEE: New York, NY, USA, 2007; pp. 3224–3227. [Google Scholar]
- Lu, Z.; Zhou, H.; Wang, L.; Kong, D.; Lyu, H.; Wu, H.; Chen, B.; Chen, F.; Dong, N.; Yang, G. GaitFormer: Two-Stream Transformer Gait Recognition Using Wearable IMU Sensors in the Context of Industry 5.0. IEEE Sens. J. 2025, 25, 19947–19956. [Google Scholar] [CrossRef]
- Tan, Y.; He, X.; Liu, G.; Zhong, L.; Pan, H.; Zhu, K.; Shull, P. Transformer-Based Full-Body Pose Estimation for Rehabilitation via RGB Camera and IMU Fusion. In Proceedings of the IEEE-EMBS International Conference on Body Sensor Networks 2025, Los Angeles, CA, USA, 3 November 2025. [Google Scholar]
- Ahmadian, M.; Rahmani–Boldaji, S.; Shirian, A. Future Image Prediction of Plantar Pressure During Gait Using Spatio-temporal Transformer. In Proceedings of the 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Glasgow, UK, 11–15 July 2022; pp. 3039–3042. [Google Scholar] [CrossRef]
- Hannink, J.; Kautz, T.; Pasluosta, C.F.; Gaßmann, K.G.; Klucken, J.; Eskofier, B.M. Sensor-based gait parameter extraction with deep convolutional neural networks. IEEE J. Biomed. Health Inform. 2016, 21, 85–93. [Google Scholar] [CrossRef]
- Wagner, D.; Kalischewski, K.; Velten, J.; Kummert, A. Activity recognition using inertial sensors and a 2-D convolutional neural network. In Proceedings of the 2017 10th International Workshop on Multidimensional (nD) Systems (nDS), Zielona Gora, Poland, 13–15 September 2017; IEEE: New York, NY, USA, 2017; pp. 1–6. [Google Scholar]
- Huan, R.; Dong, G.; Cui, J.; Jiang, C.; Chen, P.; Liang, R. INSENGA: Inertial sensor gait recognition method using data imputation and channel attention weight redistribution. IEEE Sens. J. 2025. [Google Scholar] [CrossRef]
- AlHamaydeh, M.; Tellab, S.; Tariq, U. Deep-Learning-Based Strong Ground Motion Signal Prediction in Real Time. Buildings 2024, 14, 1267. [Google Scholar] [CrossRef]
- Zhou, J.T.; Zhang, H.; Jin, D.; Peng, X. Dual Adversarial Transfer for Sequence Labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 434–446. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, A.M.; Martelloni, C.; Scapellato, S.; Cavallo, F. Assessment of walking features from foot inertial sensing. IEEE Trans. Biomed. Eng. 2005, 52, 486–494. [Google Scholar] [CrossRef] [PubMed]
- MetaBase App. Available online: https://mbientlab.com/tutorials/MetaBaseApp.html (accessed on 2 October 2019).
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]


| Reference | Public Availability | Sensor | Sampling Frequency | # of Subjects | Healthy (H) / Patient (P) | Speeds (km/h) |
|---|---|---|---|---|---|---|
| Speed (Ours) | Publicly available | Acc + Gyro | 100 Hz | 33 | H | 4.0, 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0, 9.5 |
| Bugané et al. [4] | - | Acc + Gyro | 50 Hz | 22 | H | Preferred speed |
| Yang et al. [5] | - | Acc + Gyro | 100 Hz | 7 | H | 9, 9.9, 10.8, 11.7, 12.6 |
| Chew et al. [6] | - | Acc + Gyro | 128 Hz | 4 | H | 8, 9, 10, 11 |
| Hannink et al. [16] | Publicly available | Acc + Gyro | 102.4 Hz | 116 | Geriatric | Preferred speed |
| McGinnis et al. [7] | - | Acc | 50 Hz | A: 10 | H | A: 1.8, 2.7, 3.6, 4.5, 5.4 |
| B: 37 | H: 7 and MS P: 30 | B: comfortable and ±20% | ||||
| Vathsangam et al. [8] | - | Acc + Gyro | 100 Hz | 8 | H | 4, 4.5, 4.8, 5.3, 5.6, 6.1, 6.4 |
| Subject 9: 4, 4.16, 4.32, 4.48, 4.64, 4.8, 4.96, 5.12, 5.28, 5.44, 5.6, 5.76, 5.92, 6.08, 6.24, 6.4 | ||||||
| Zihajehzadeh et al. [9] | - | Acc | 100 Hz | 15 | H | Slow, Normal, Fast |
| Zihajehzadeh et al. [10] | Acc + Gyro + Mag | 100 Hz | 10 | H | 1.8, 2.7, 3.6, 4.5, 5.4, 6.3 | |
| Aminian et al. [11] | - | Acc | 40 Hz | 5 | H | Preferred speed |
| Song et al. [12] | - | Acc | 200 Hz | 17 | H | 4.8, 6.8, 7.8, 9, 10.2, 11.4, 12.6, 13.8, 15, 15.4 with different inclines |
| Summary of the “Speed” Dataset | |
|---|---|
| Number of subjects | 33 |
| Number of subject-independent sets | 22 |
| Examples per subject-independent set | 1775 |
| Length of each example | 250 samples |
| Number of speeds | 12 |
| Speeds (km/h) | 4.0, 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 7.5, 8.0, 8.5, 9.0, 9.5 |
| Sampling frequency | 100 Hz |
| Dimensionality—gyroscope data | 3 |
| Dimensionality—accelerometer data | 3 |
| Sets | SpeedNet RMSE | SVR RMSE | GPR RMSE | NN RMSE |
|---|---|---|---|---|
| 1 | 0.7546 | 0.8978 | 0.3334 | 0.8656 |
| 2 | 0.2326 | 1.0531 | 0.4825 | 0.7239 |
| 3 | 0.2097 | 0.4742 | 0.4929 | 0.8333 |
| 4 | 0.3671 | 1.1569 | 0.5923 | 2.5707 |
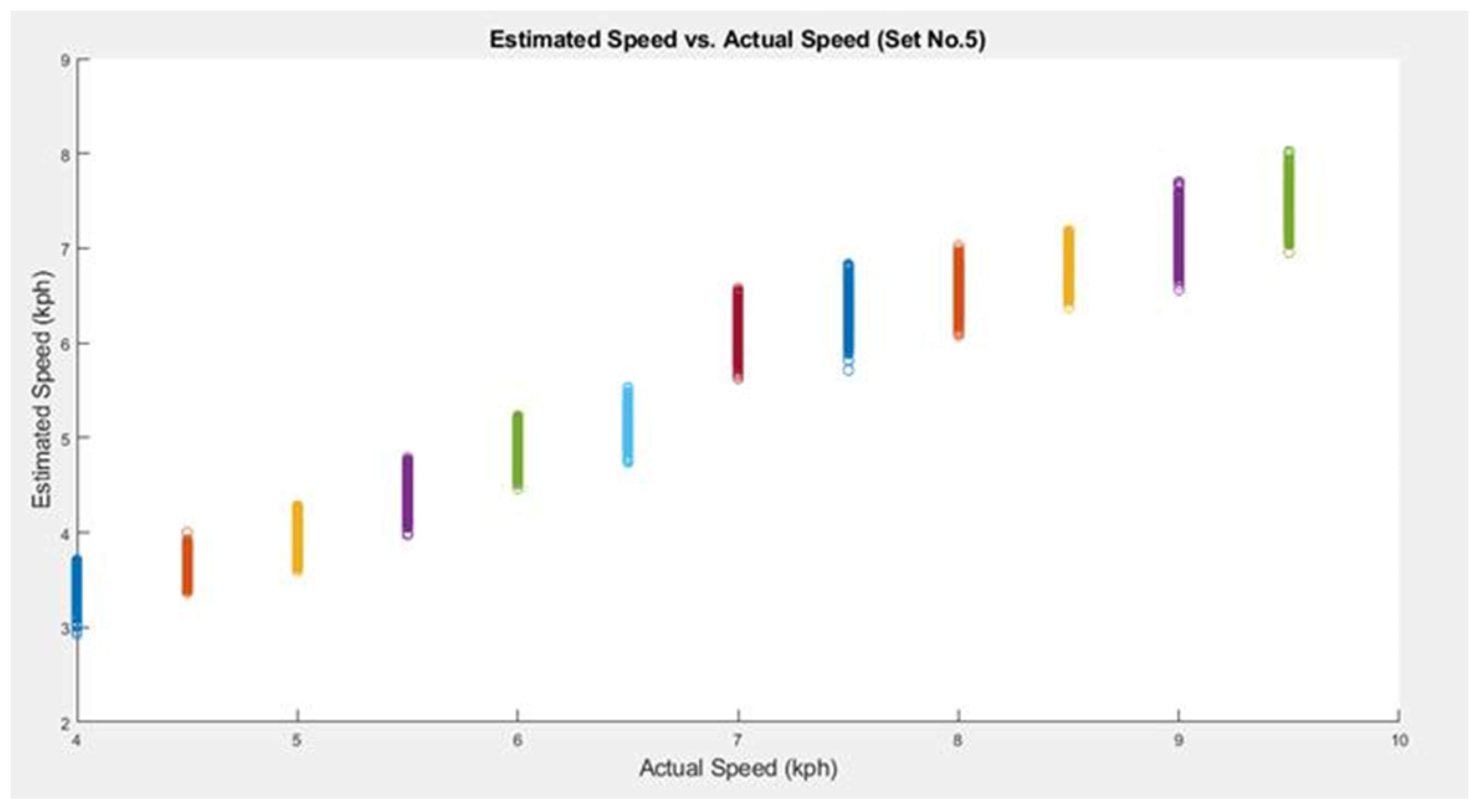
| 5 | 1.3399 | 1.7824 | 0.4166 | 1.8838 |
| 6 | 0.3085 | 0.7745 | 0.4989 | 0.9453 |
| 7 | 0.2669 | 1.6783 | 0.3318 | 0.8213 |
| 8 | 0.6732 | 0.9335 | 1.7265 | 0.6503 |
| 9 | 0.5721 | 0.9355 | 1.7262 | 1.0527 |
| 10 | 0.3097 | 1.6199 | 0.6005 | 1.1037 |
| 11 | 0.6521 | 1.8774 | 1.7263 | 1.206 |
| 12 | 0.657 | 0.9303 | 0.3397 | 0.918 |
| 13 | 0.3415 | 1.2703 | 0.4543 | 0.7662 |
| 14 | 0.4967 | 2.0762 | 0.4871 | 0.7508 |
| 15 | 0.2624 | 0.9382 | 0.4908 | 1.0484 |
| 16 | 0.4489 | 3.8393 | 0.4224 | 0.913 |
| 17 | 0.6249 | 2.6435 | 0.5142 | 1.0394 |
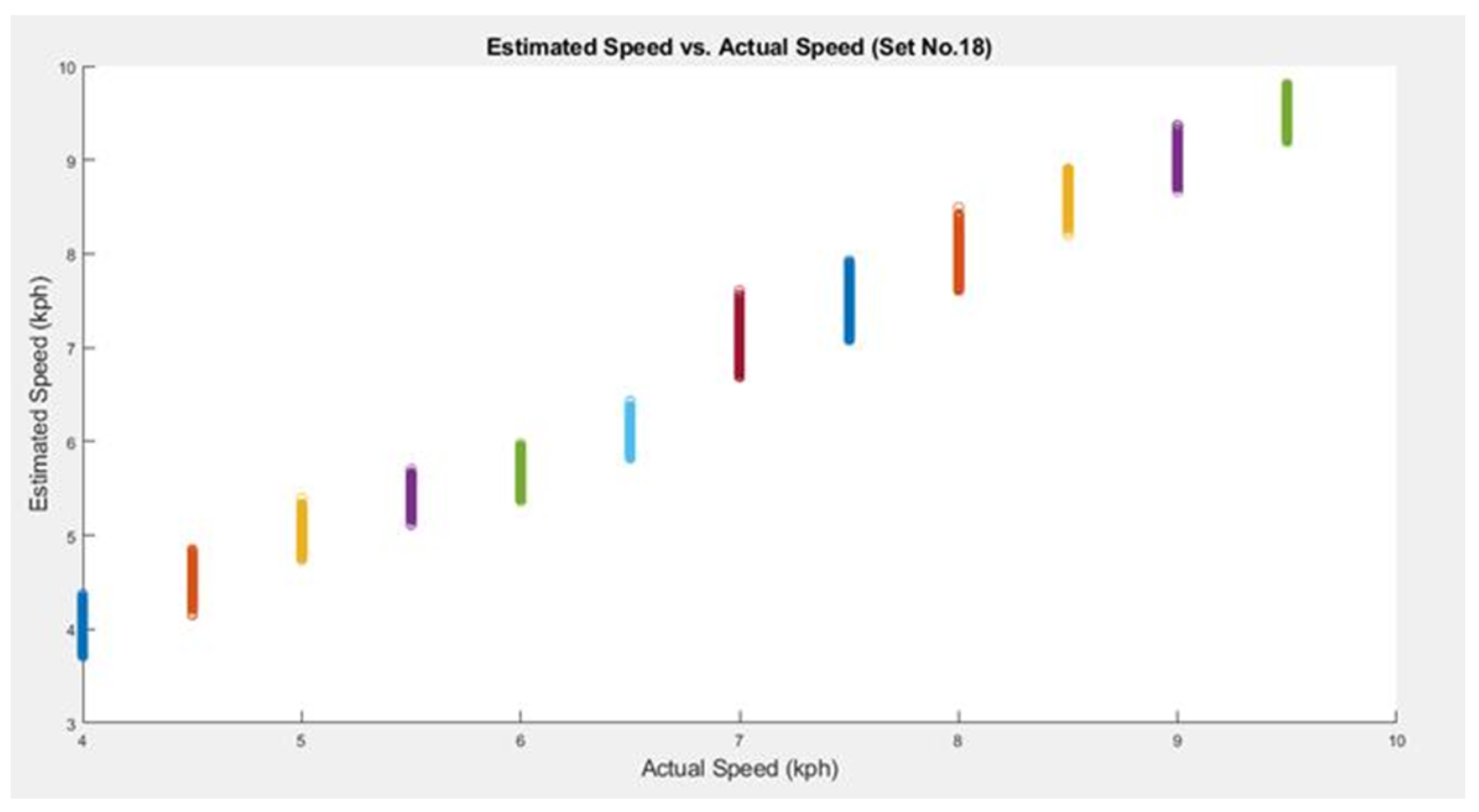
| 18 | 0.1963 | 0.739 | 0.3993 | 0.8137 |
| 19 | 0.8042 | 2.3644 | 1.727 | 0.8002 |
| 20 | 0.3379 | 0.7825 | 0.3443 | 0.934 |
| 21 | 0.2449 | 1.6502 | 0.6994 | 0.9793 |
| 22 | 0.4995 | 0.7577 | 0.4226 | 1.8615 |
| Average RMSE | 0.4819 | 1.4171 | 0.6922 | 1.0673 |
| Standard Deviation | 0.2693 | 0.7939 | 0.5071 | 0.4598 |
| CNN | SVR | GPR | NN |
|---|---|---|---|
| 0.0526 | 0.0393 | 0.18 | 0.0034 |
| Sets | RMSE | Sets | RMSE |
|---|---|---|---|
| 1 | 0.169 | 12 | 0.2205 |
| 2 | 0.1511 | 13 | 0.1873 |
| 3 | 0.1728 | 14 | 0.1493 |
| 4 | 0.18 | 15 | 0.178 |
| 5 | 0.1584 | 16 | 0.1762 |
| 6 | 0.1803 | 17 | 0.1521 |
| 7 | 0.202 | 18 | 0.1652 |
| 8 | 0.1701 | 19 | 0.2114 |
| 9 | 0.2241 | 20 | 0.1607 |
| 10 | 0.1539 | 21 | 0.1788 |
| 11 | 0.1571 | 22 | 0.1452 |
| Average RMSE | 0.1747 | ||
| Standard Deviation | 0.0227 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bachir, Z.R.; Tariq, U. “Speed”: A Dataset for Human Speed Estimation. Sensors 2025, 25, 6335. https://doi.org/10.3390/s25206335
Bachir ZR, Tariq U. “Speed”: A Dataset for Human Speed Estimation. Sensors. 2025; 25(20):6335. https://doi.org/10.3390/s25206335
Chicago/Turabian StyleBachir, Zainab R., and Usman Tariq. 2025. "“Speed”: A Dataset for Human Speed Estimation" Sensors 25, no. 20: 6335. https://doi.org/10.3390/s25206335
APA StyleBachir, Z. R., & Tariq, U. (2025). “Speed”: A Dataset for Human Speed Estimation. Sensors, 25(20), 6335. https://doi.org/10.3390/s25206335






