Joint Trajectory and IRS Phase Shift Optimization for Dual IRS-UAV-Assisted Uplink Data Collection in Wireless Sensor Networks
Abstract
Highlights
- This paper designed a completely new model of dual IRS-UAV-assisted communication.
- This paper presents a new trajectory optimization algorithm.
- Compared with the traditional single IRS-UAV-assisted communication model, the newly proposed model can significantly enhance the sum rate of the communication system.
- The proposed new algorithm can effectively address the non-convexity issue in optimization problems.
Abstract
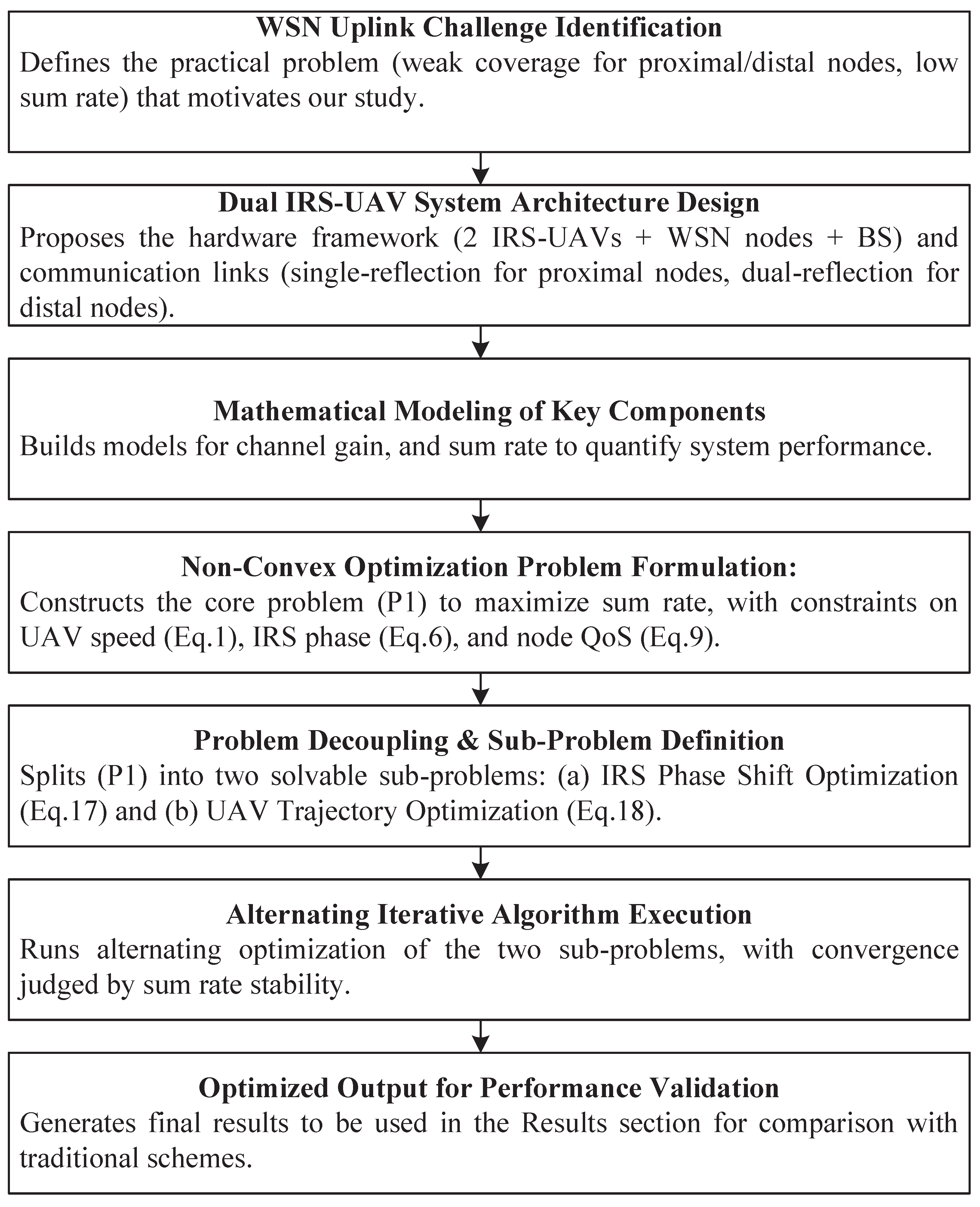
1. Introduction
2. Related Works
Key Contributions
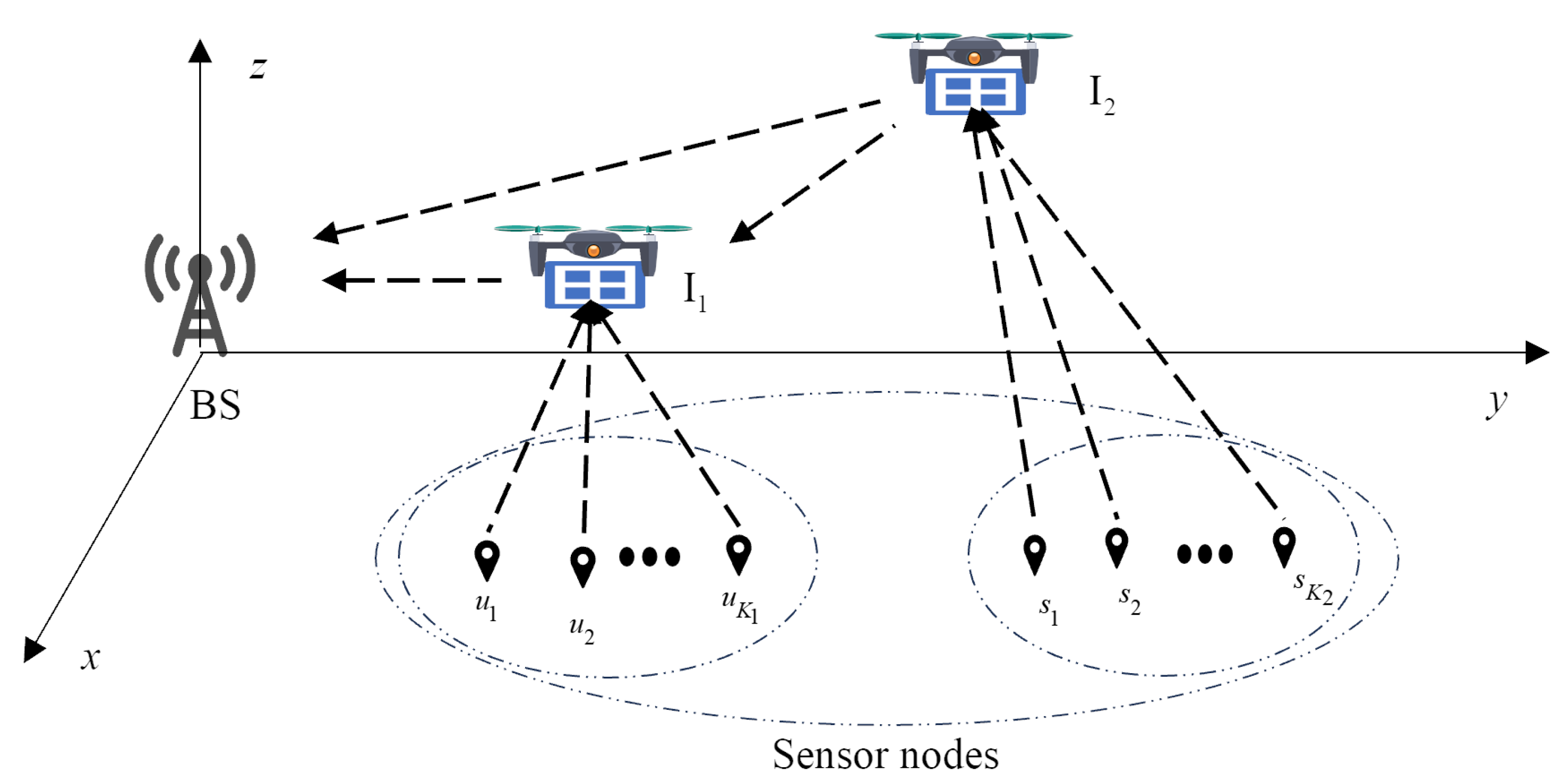
3. System Model and Problem Formulation
3.1. System Model
3.2. Problem Formulation
4. Proposed Algorithm
4.1. Phase Shift Optimization
4.2. Trajectory Optimization
4.3. Joint Optimization of Trajectory and Phase Shift Algorithm
| Algorithm 1 Proposed Solution for (P1) |
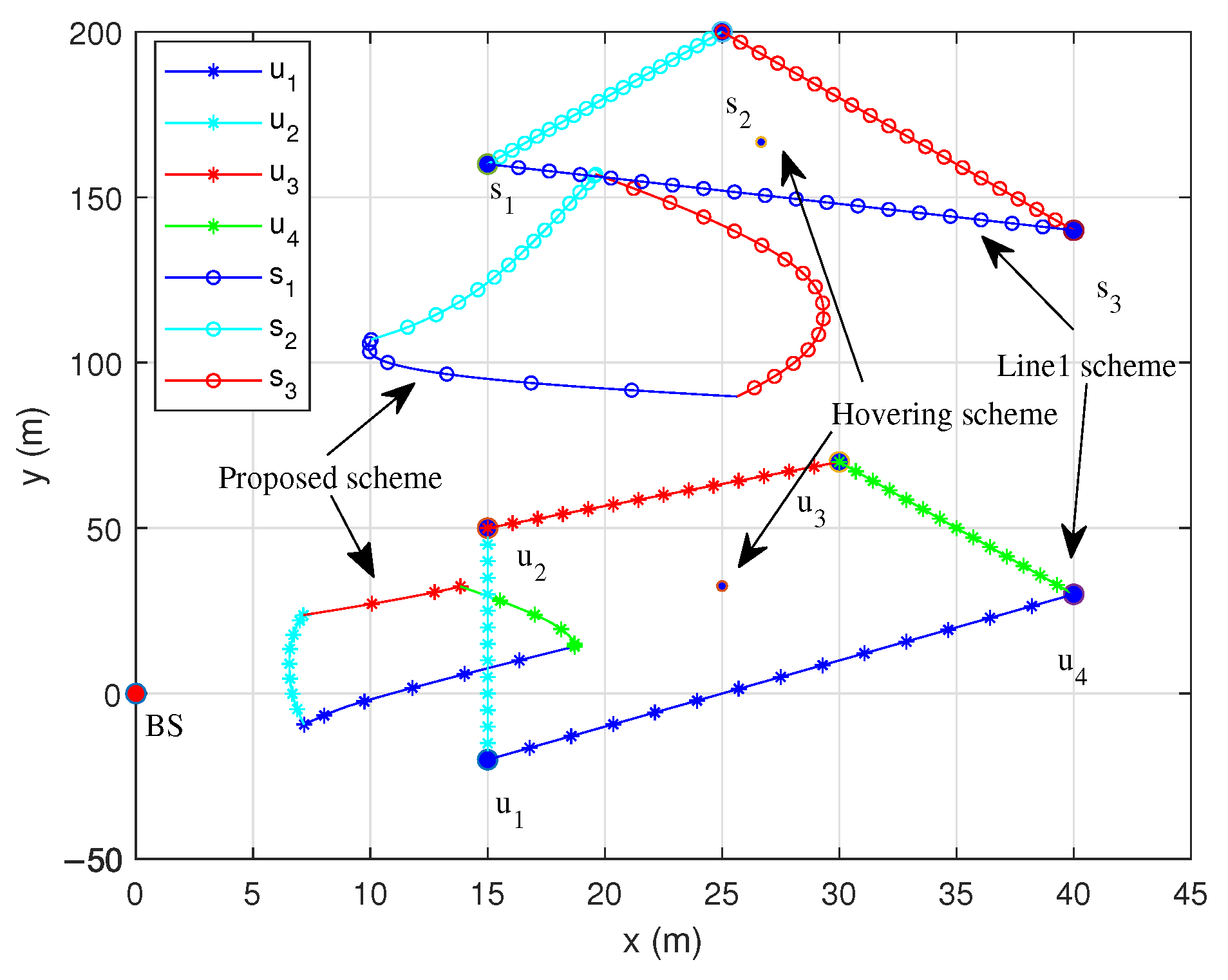
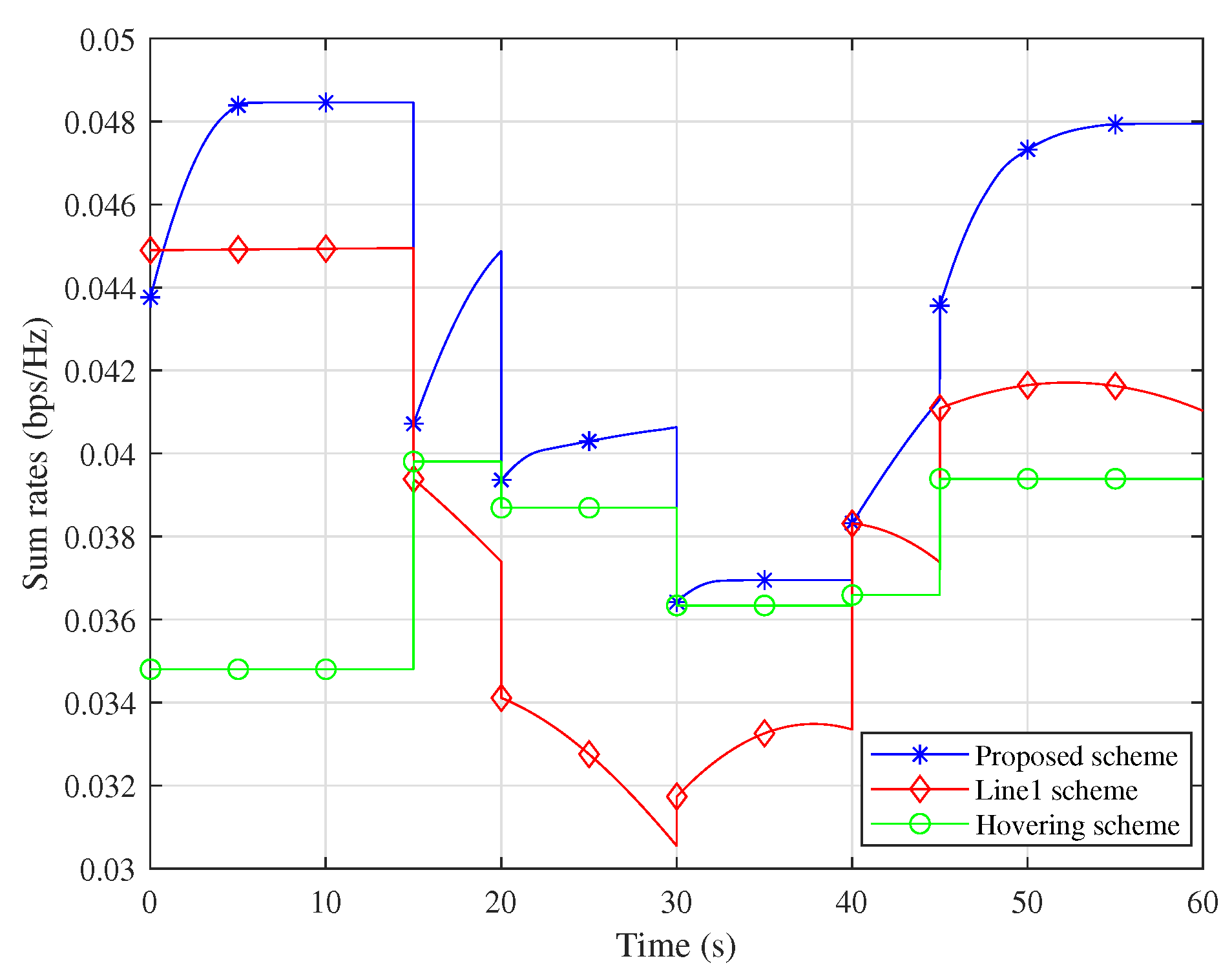
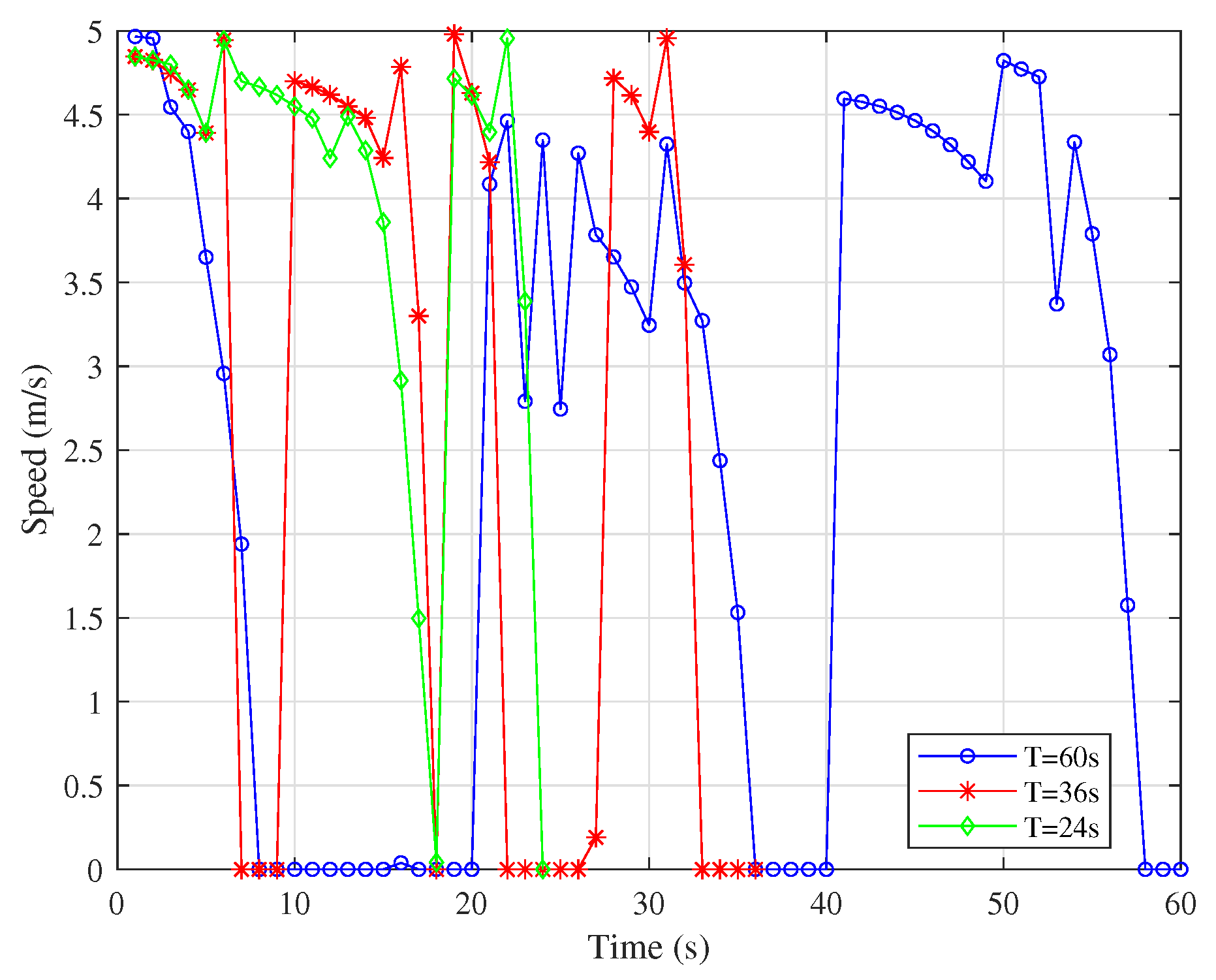
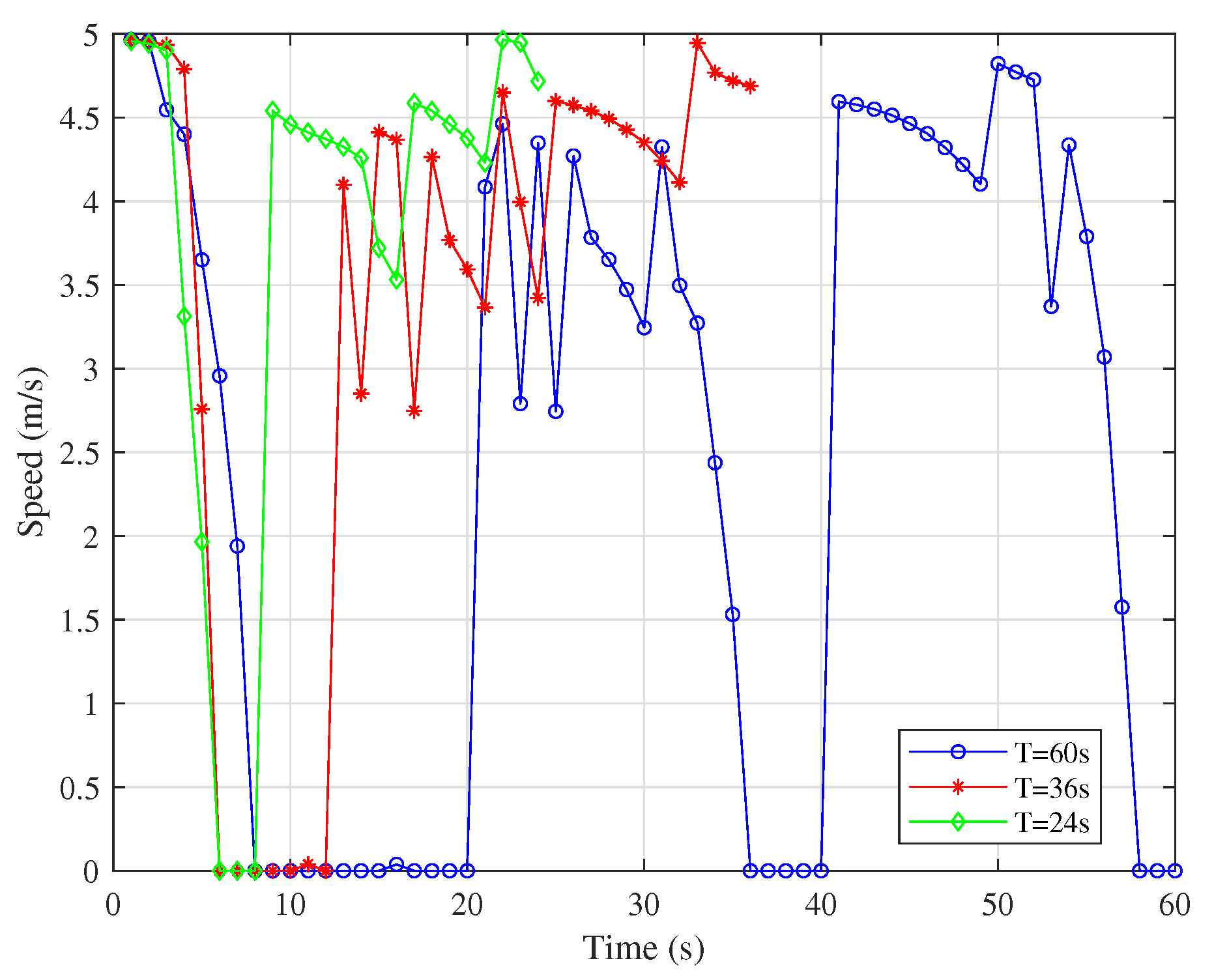
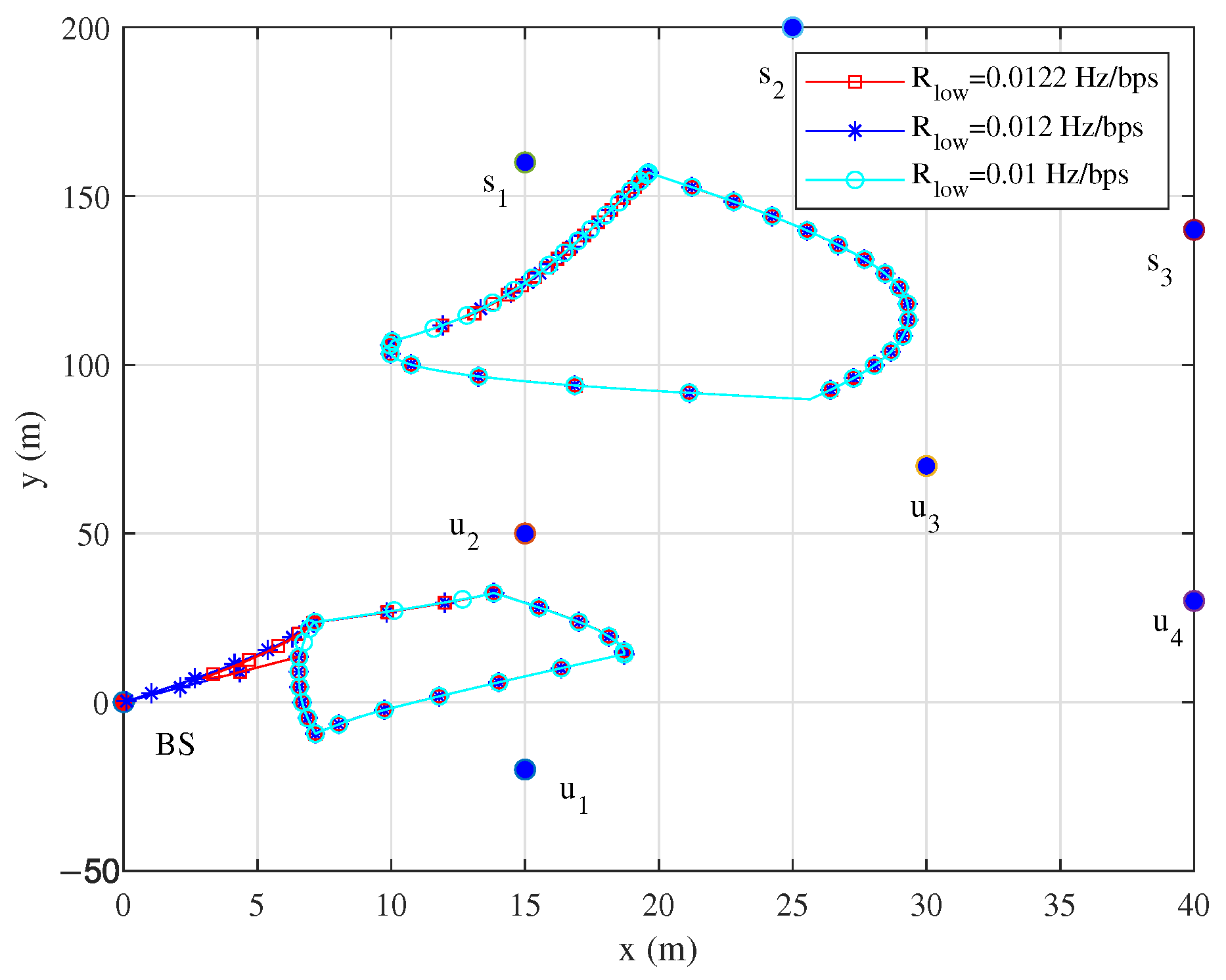
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Okogbaa, F.C. Design and Application of Intelligent Reflecting Surface (IRS) for Beyond 5G Wireless Networks: A Review. Sensors 2022, 22, 2436. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Zhang, S.; Zheng, B.; You, C.; Zhang, R. Intelligent reflecting surface-aided wireless communications: A tutorial. IEEE Trans. Commun. 2021, 69, 3313–3351. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 2020, 58, 106–112. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Alsharif, M.H.; Uthansakul, P.; Solyman, A.A.A. Intelligent Reflecting Surfaces Assisted UAV Communications for Massive Networks: Current Trends, Challenges, and Research Directions. Sensors 2022, 22, 5278. [Google Scholar] [CrossRef] [PubMed]
- Park, K.-W.; Kim, H.M.; Shin, O.-S. A Survey on Intelligent-Reflecting-Surface-Assisted UAV Communications. Energies 2022, 15, 5143. [Google Scholar] [CrossRef]
- Alsarayreh, S.A.; Radzi, N.A.M.; Alkahtani, A.A.; Azmi, K.H.M. Intelligent Reflecting Surface–UAV Systems in the Internet of Things Network: A Survey. IEEE Access 2023, 11, 85031–85049. [Google Scholar] [CrossRef]
- Shafique, T.; Tabassum, H.; Hossain, E. Optimization of Wireless Relaying With Flexible UAV-Borne Reflecting Surfaces. IEEE Trans. Commun. 2021, 69, 309–325. [Google Scholar] [CrossRef]
- Cai, Y.; Wei, Z.; Hu, S.; Liu, C.; Ng, D.W.K.; Yuan, J. Resource allocation and 3D trajectory design for power-efficient IRS-assisted UAVNOMA communications. IEEE Trans. Wirel. Commun. 2022, 21, 10315–10334. [Google Scholar] [CrossRef]
- Song, X.; Zhao, Y.; Wu, Z.; Yang, Z.; Tang, J. Joint trajectory and communication design for IRS-assisted UAV networks. IEEE Wirel. Commun. Lett. 2022, 11, 1538–1542. [Google Scholar] [CrossRef]
- Zhao, L.; Xu, H.; Qu, S.; Wei, Z.; Liu, Y. Joint Trajectory and Communication Design for UAV-Assisted Symbiotic Radio Networks. IEEE Trans. Veh. Technol. 2024, 73, 8367–8378. [Google Scholar] [CrossRef]
- Hou, Z. Joint IRS Selection and Passive Beamforming in Multiple IRS-UAV-Enhanced Anti-Jamming D2D Communication Networks. IEEE Internet Things J. 2023, 10, 19558–19569. [Google Scholar] [CrossRef]
- Al-Jarrah, M.; Al-Dweik, A.; Alsusa, E.; Iraqi, Y.; Alouini, M.-S. On the performance of IRS-Assisted multi-layer UAV communications with imperfect phase compensation. IEEE Trans. Commun. 2021, 69, 8551–8568. [Google Scholar] [CrossRef]
- Deng, Q.; Yu, G.; Liang, X.; Shu, F.; Wang, J. Joint Trajectory, Sensing, and Transmission Design for IRS-Assisted Cognitive UAV Systems. IEEE Wirel. Commun. Lett. 2024, 13, 233–237. [Google Scholar] [CrossRef]
- Hadi, M.; Ghazizadeh, R. UAV-mounted IRS assisted wireless powered mobile edge computing systems: Joint beamforming design, resource allocation and position optimization. Comput. Netws. 2024, 254, 110846. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, Z.; Yin, Z.; Yang, W.; Yang, Z. Trajectory and communication design for UAV-relayed wireless networks. IEEE Wirel. Commun. Lett. 2019, 8, 1600–1603. [Google Scholar] [CrossRef]
- Kang, Z.; You, C.; Zhang, R. IRS-Aided Wireless Relaying: Deployment Strategy and Capacity Scaling. IEEE Wirel. Commun. Lett. 2022, 11, 215–219. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]

| Compared to Line 1 Scheme | Compared to Hovering Scheme | |
|---|---|---|
| 300 | 11.91% | 16.36% |
| 400 | 13.56% | 17.65% |
| 500 | 14.11% | 18.35% |
| 600 | 14.63% | 18.77% |
| 1000 | 14.94% | 19.65% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, H.; Guo, H. Joint Trajectory and IRS Phase Shift Optimization for Dual IRS-UAV-Assisted Uplink Data Collection in Wireless Sensor Networks. Sensors 2025, 25, 6265. https://doi.org/10.3390/s25206265
Zou H, Guo H. Joint Trajectory and IRS Phase Shift Optimization for Dual IRS-UAV-Assisted Uplink Data Collection in Wireless Sensor Networks. Sensors. 2025; 25(20):6265. https://doi.org/10.3390/s25206265
Chicago/Turabian StyleZou, Heng, and Hui Guo. 2025. "Joint Trajectory and IRS Phase Shift Optimization for Dual IRS-UAV-Assisted Uplink Data Collection in Wireless Sensor Networks" Sensors 25, no. 20: 6265. https://doi.org/10.3390/s25206265
APA StyleZou, H., & Guo, H. (2025). Joint Trajectory and IRS Phase Shift Optimization for Dual IRS-UAV-Assisted Uplink Data Collection in Wireless Sensor Networks. Sensors, 25(20), 6265. https://doi.org/10.3390/s25206265





