Abnormal Vibration Identification of Metro Tunnels on the Basis of the Spatial Correlation of Dynamic Strain from Dense Measurement Points of Distributed Sensing Optical Fibers
Abstract
1. Introduction
2. Theory of the Proposed Method
2.1. Extraction of Multidimensional Dynamic Strain Features
2.2. Dynamic Strain Feature Update Method Based on the Spatial Correlation of Distributed Fiber-Optic Dense Measurement Points
2.2.1. Spatial Correlation Between the Dynamic Strain Features Obtained from the Dense Measurement Points of a Distributed Sensing Optical Fiber
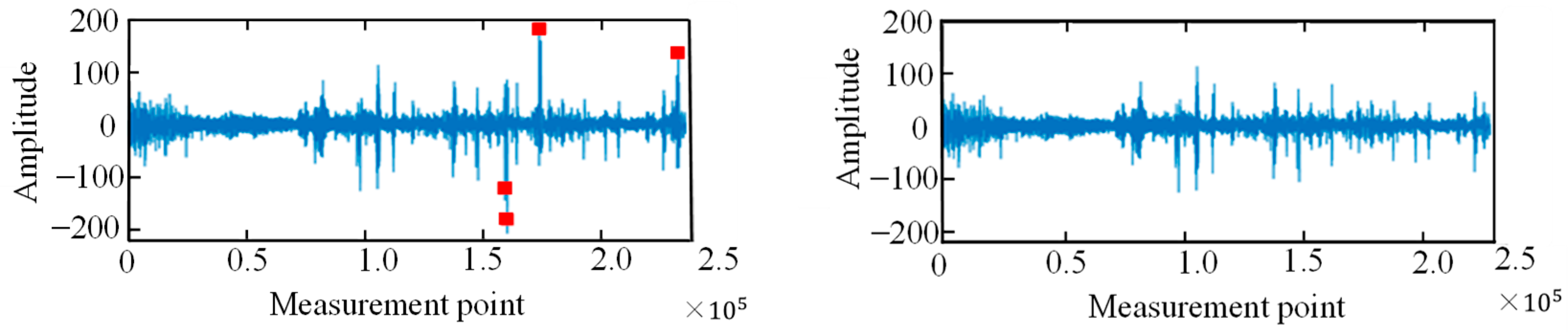
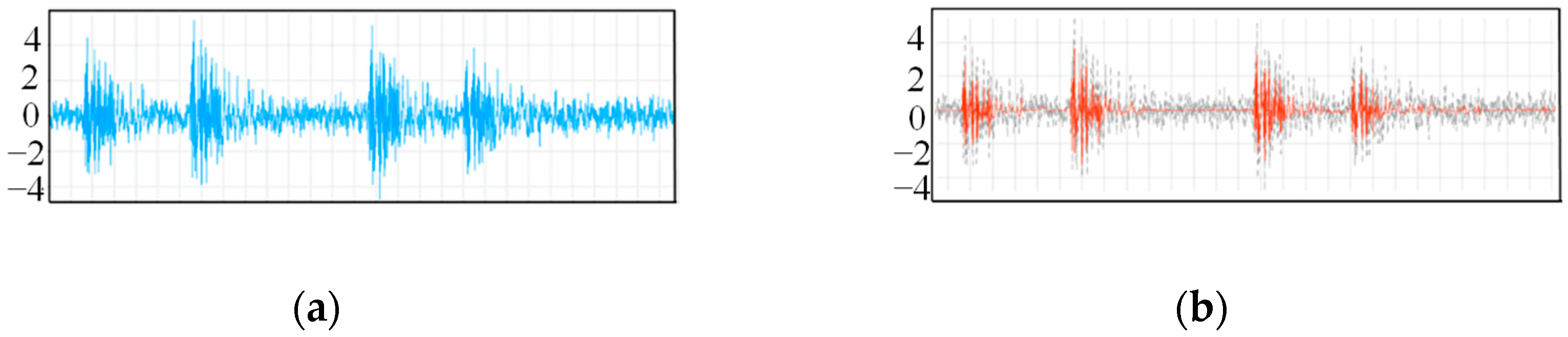
2.2.2. Updating the Dynamic Strain Features on the Basis of the Spatial Correlation Confidence Weight Assignment
2.3. SVM and BP Classification Model Eigenvalue Identification for Abnormal Vibrations
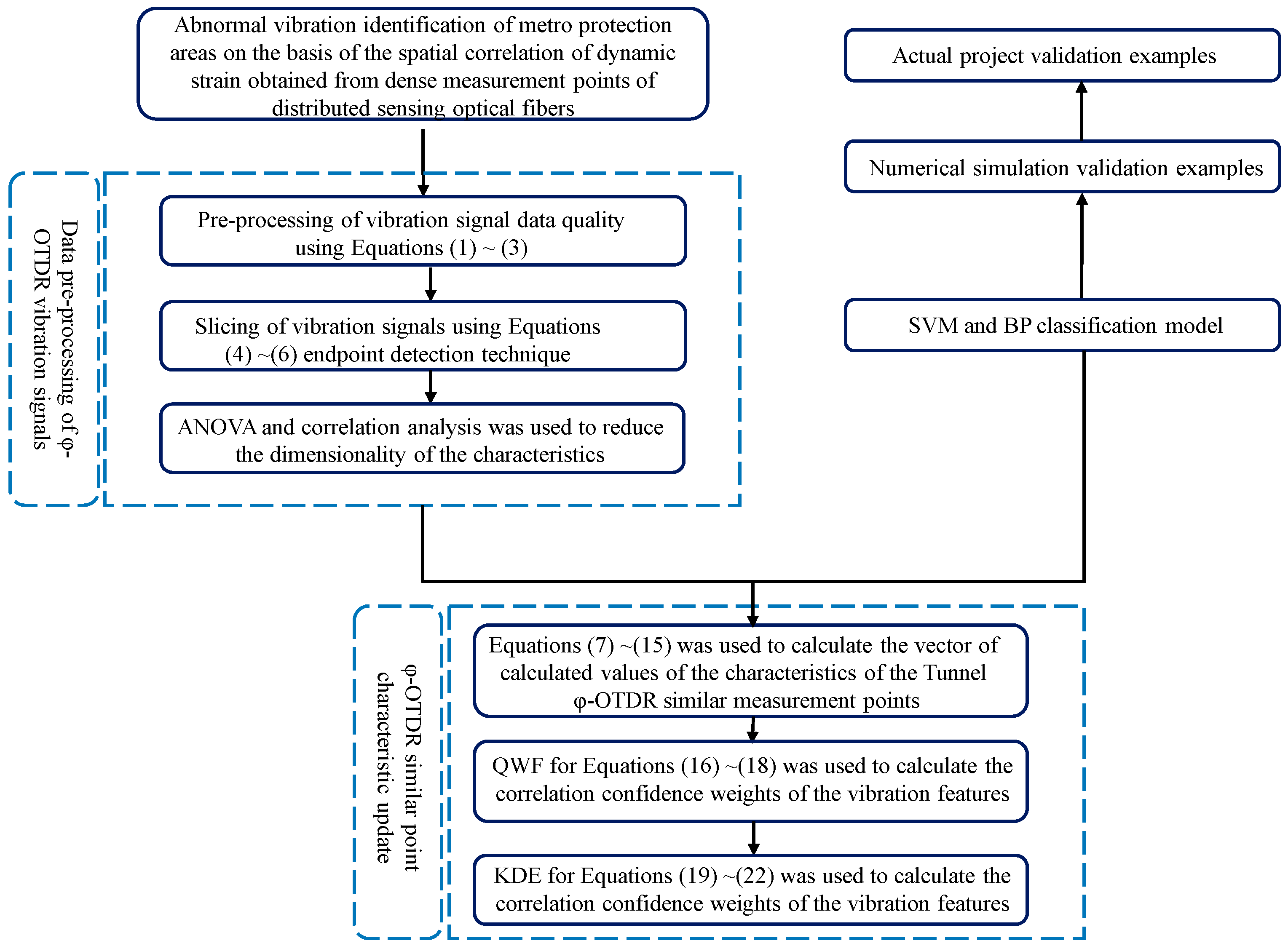
2.4. Procedure of the Proposed Method
3. Numerical Simulation Examples
3.1. Numerical Simulation of the Abnormal Vibration of the Metro Protection Area
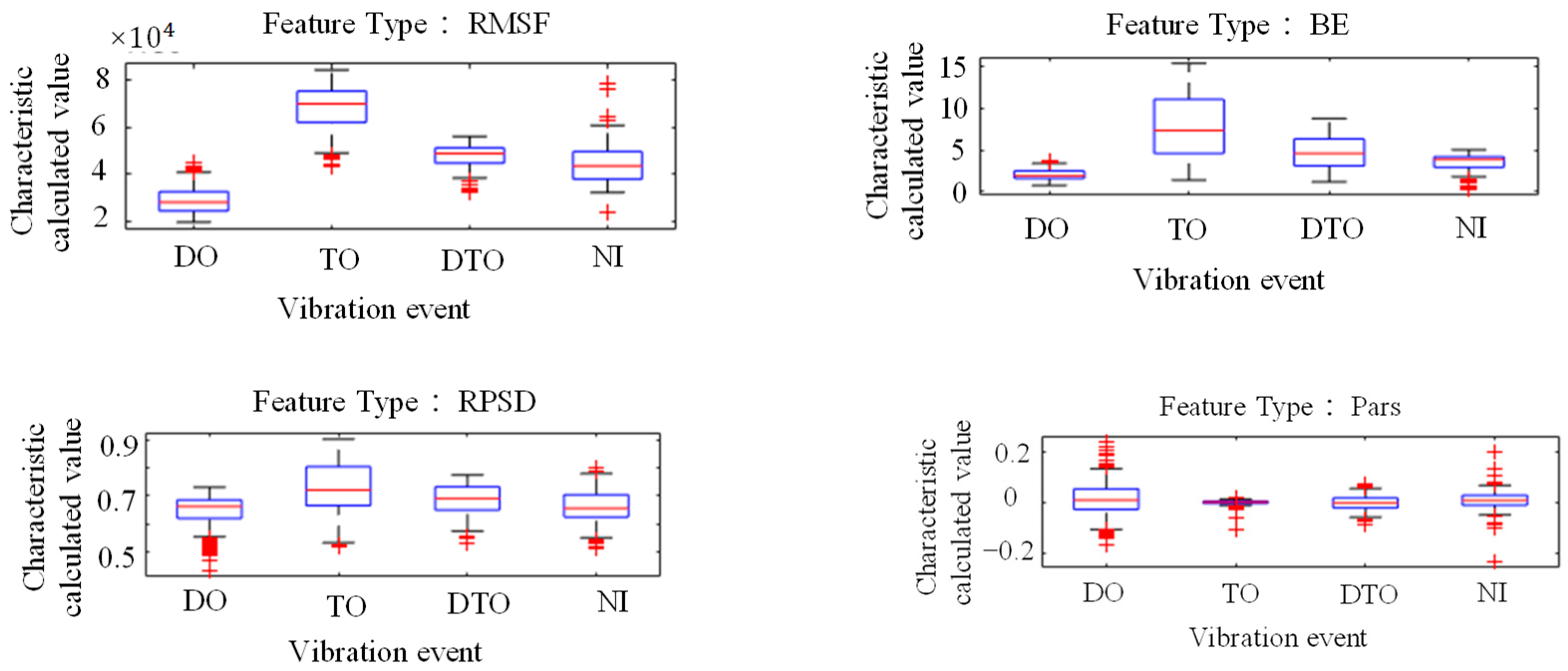
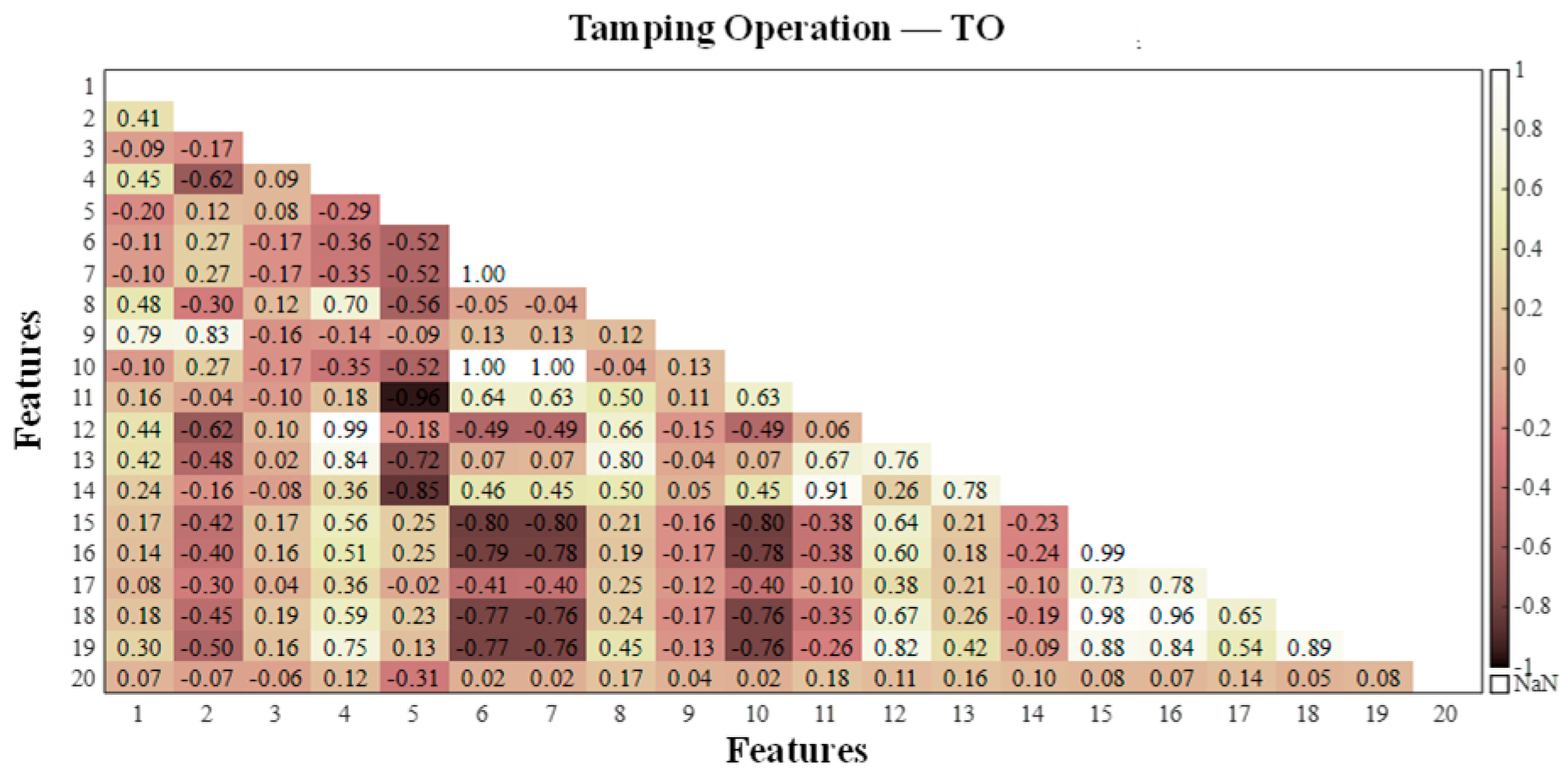
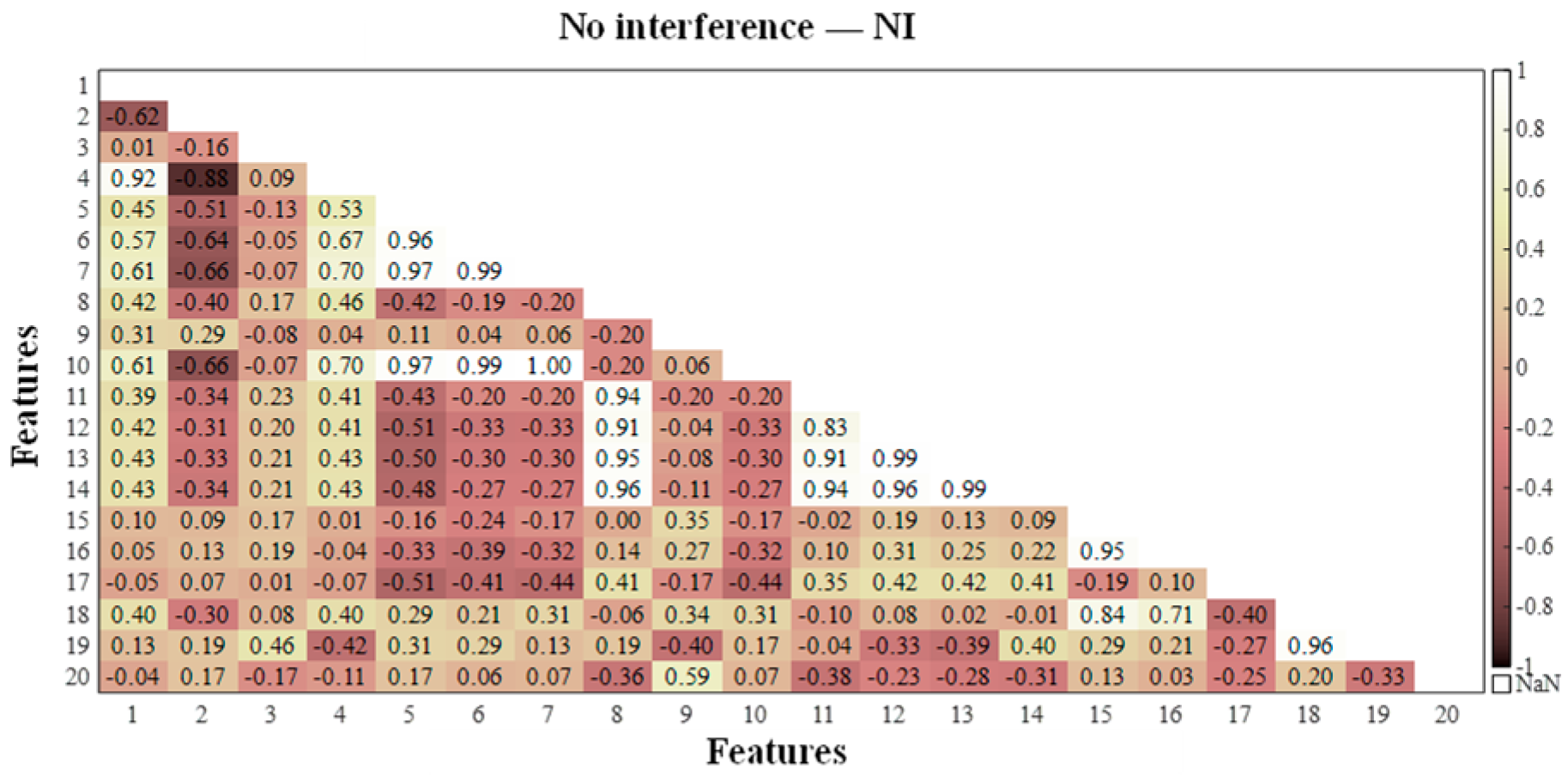
3.2. Reduction in the Dimensionality of the Dynamic Strain Characteristics Obtained from the Dense Measurement Points of the Distributed Sensing Optical Fiber
3.3. Results of Abnormal Vibrations in the Metro Protection Area
4. Example of an Actual Tunnel
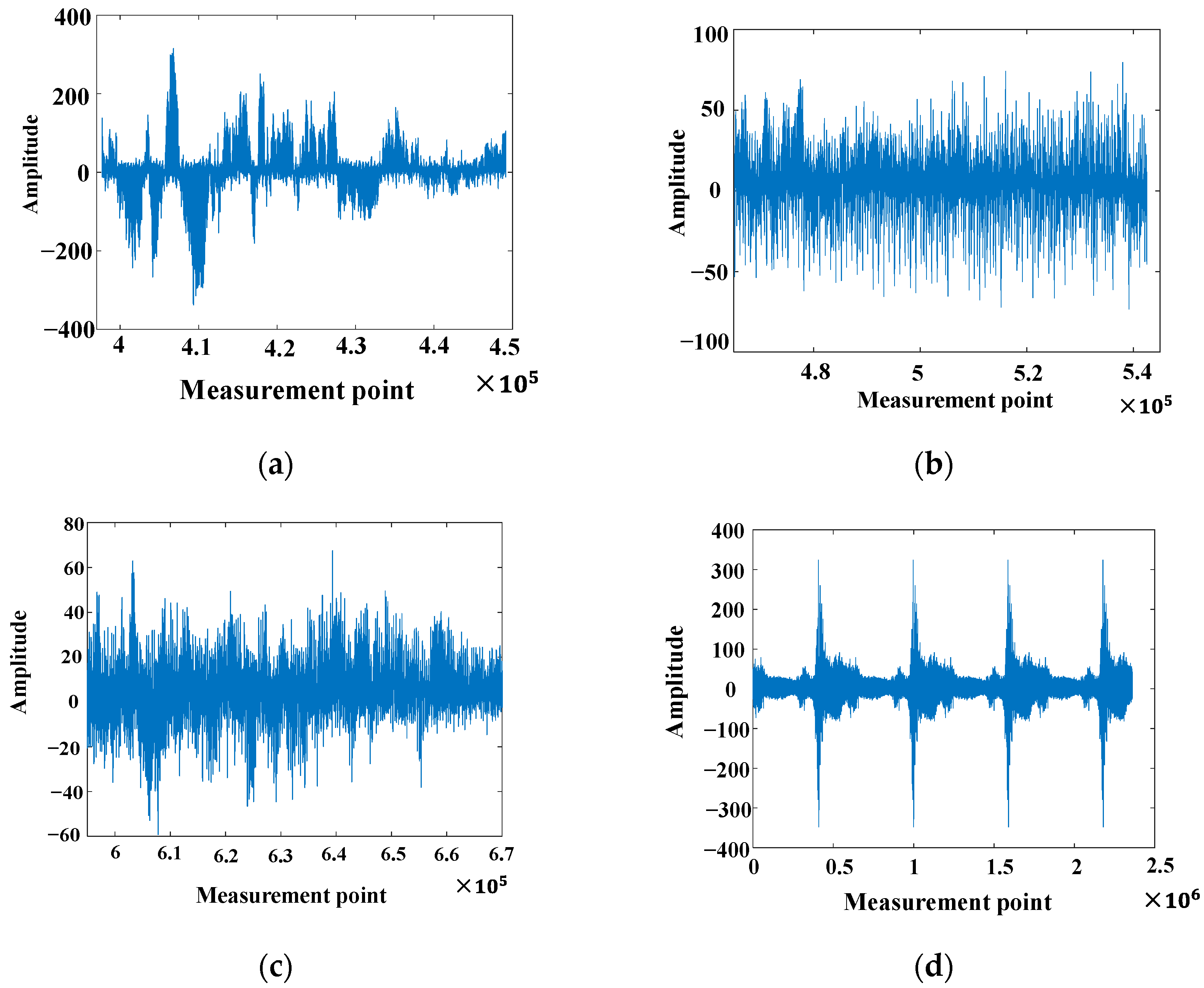
4.1. Extraction of the Dynamic Strain Features from Different Vibration Sources Generated in an Actual Metro Tunnel
4.2. Results of Abnormal Vibrations in an Actual Tunnel
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, H.; Liu, X.; Xiao, Y.; Rao, Y.-J. A Dynamic Time Sequence Identification and Knowledge Mining Method Based on the Hidden Markov Models (HMMs) for Pipeline Safety Monitoring with Φ-OTDR. J. Light. Technol. 2019, 37, 4991–5000. [Google Scholar] [CrossRef]
- Lin, T.H.; Wang, C.C. Deep learning of spatio-temporal features with geometric-based moving point detection for motion segmentation. In Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 3058–3065. [Google Scholar] [CrossRef]
- García, J.J.; Hernandez, A.; Urena, J.; Garcia, E. FPGA-based architecture for a multisensory barrier to enhance railway safety. IEEE Trans. Instrum. Meas. 2016, 65, 1352–1363. [Google Scholar] [CrossRef]
- Karaduman, M. Image processing based obstacle detection with laser measurement in railways. In Proceedings of the 10th International Conference on Electrical and Electronics Engineering, Bursa, Turkey, 30 November–2 December 2017; pp. 899–903. [Google Scholar]
- Barrias, A.; Casas, J.R.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef]
- Muanenda, Y. Recent advances in distributed acoustic sensing based on phase-sensitive optical time domain reflectometry. J. Sens. 2018, 2018, 3897873. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, Y.; Xie, Z.; Yang, T.; An, G. Intrusion detection for high-speed railway perimeter obstacle. In Proceedings of the International Conference on Electrical and Information Technologies for Rail Transportation, Changsha, China, 20–22 October 2017; Springer: Singapore, 2017; pp. 465–473. [Google Scholar] [CrossRef]
- Liu, D.; Sun, Q.; Lu, P.; Xia, L.; Sima, C. Research progress in the key device and technology for fiber optic sensor network. Photonic Sens. 2016, 6, 1–25. [Google Scholar] [CrossRef]
- He, Z.; Liu, Q.; Fan, X.; Chen, D.; Wang, S.; Yang, G. Fiber-optic distributed acoustic sensors (DAS) and applications in railway perimeter security. In Proceedings of the Advanced Sensor Systems and Applications VIII 2018, Beijing, China, 11–13 October 2018. [Google Scholar]
- Tu, G.J.; Zhang, X.P.; Zhang, Y.X.; Zhu, F.; Xia, L.; Nakarmi, B. The development of an Φ-OTDR system for quantitative vibration measurement. IEEE Photonics Technol. Lett. 2015, 27, 1349–1352. [Google Scholar] [CrossRef]
- Zhong, X.; Zhang, C.; Li, L.; Liang, S.; Li, H.; Sun, C. Influences of pulse on phase-sensitivity optical time domain reflectometer based distributed vibration sensor. Opt. Commun. 2016, 361, 1–5. [Google Scholar] [CrossRef]
- Hartog, A.H. An Introduction to Distributed Optical Fibre Sensors, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Chafiq, Y.; Tatin, M.; Postaspana, O.; Paris, J.; Maraval, D.; Lamour, V. Fiber optic sensing for monitoring structure and health of railway infrastructures. In Proceedings of the 26th International Conference on Optical Fiber Sensors, OSA Technical Digest, Lausanne, Switzerland, 24–28 September 2018. paper ThE97. [Google Scholar] [CrossRef]
- Lian, W.; Wang, G.; Liu, S.; Zhu, G. Real-Time Deformation Monitoring for Tunnels Using Distributed Millimeter Wave Radar. In Proceedings of the 2022 4th International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 9–11 December 2022; pp. 664–668. [Google Scholar] [CrossRef]
- Zhang, S.; Gadekallu, T.R. Digital interference signal filtering on laser interface for optical fiber communication. EAI Endorsed Scal Inf. Syst. 2022, 10, 14. [Google Scholar] [CrossRef]
- Wang, C.; Shang, Y.; Zhao, W.-A.; Liu, X.-H.; Wang, C.; Peng, G.-D. Investigation and Comparison of φ -OTDR and OTDR-Interferometry via Phase Demodulation. IEEE Sens. J. 2018, 18, 1501–1505. [Google Scholar] [CrossRef]
- Xu, Q.; Gao, Q.; Liu, Y. A method for suspenders tension identification of bridges based on the spatio-temporal correlation between the girder strain and suspenders tension. Comput. Aided Civ. Infrastruct. Eng. 2024, 39, 1641–1658. [Google Scholar] [CrossRef]
- Adeel, M.; Tejedor, J.; Iqbal, S.; Muaz, M.; Raza, A.; Macias-Guarasa, J. Differentiating trace-to-trace noise effects using novel signal characteristics in phase-sensitive OTDR systems. Opt. Quant. Electron. 2023, 55, 49. [Google Scholar] [CrossRef]
- Ashry, I.; Mao, Y.; Wang, B.W. A Review of Distributed Fiber-Optic Sensing in the Oil and Gas Industry. J. Light. Technol. 2022, 40, 1407–1431. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, F.; Pan, Z.; Ye, Q. Machine learning enhanced distributed acoustic sensing for pipeline third-party intrusion detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9562–9573. [Google Scholar]
- Masoudi, A.; Belal, M. Distributed optical fibre sensors for long-range perimeter security. Nat. Rev. Phys. 2020, 2, 610–623. [Google Scholar]
- Minardo, A.; Zeni, L.; Coscetta, A.; Catalano, E.; Zeni, G.; Damiano, E.; De Cristofaro, M.; Olivares, L. Distributed Optical Fiber Sensor Applications in Geotechnical Monitoring. Sensors 2021, 21, 7514. [Google Scholar] [CrossRef]
- Xu, C.J.; Guan, J.; Lu, G.; Ye, W. Pattern recognition based on time-frequency analysis and convolutional neural networks for vibrational events in φ- OTDR. Opt. Eng. 2018, 57, 016103. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, Y. A method for convergence monitoring considering the flattening effect in a shield tunnel with BOTDA sensors. Measurement 2023, 211, 112611. [Google Scholar] [CrossRef]
- An, X.; Hu, C.; Li, Z.; Lin, H.; Liu, G. Decentralized AdaBoost algorithm over sensor networks. Neurocomputing 2022, 479, 37–46. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Y.; Xin, C.; Yoo, C.; Liu, H. Kernel PLS with AdaBoost ensemble learning for particulate matters forecasting in subway environment. Measurement 2022, 204, 111974. [Google Scholar] [CrossRef]
- Soga, K.; Luo, L. Distributed fiber optics sensors for civil engineering infrastructure sensing. J. Struct. Integr. Maint. 2018, 3, 1–21. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Liu, Y. A method for monitoring the uneven settlement of shield tunnels considering the flattening effect using distributed strain data measured from BOTDA sensors. Struct. Health Monit. 2025, 24, 351–371. [Google Scholar] [CrossRef]
- Marie, T.F.B.; Han, D.; An, B.; Li, J. A Research on Fiber-optic Vibration Pattern Identification Based on Time-frequency Characteristics. Adv. Mech. Eng. 2018, 10, 1–10. [Google Scholar] [CrossRef]
- Wu, H.; Lu, M.; Xu, C.; Jiao, X.; Liao, H.; Wang, X.; Shu, X.; Liu, Y.; Wu, Y.; Rao, Y. Nonlinear Mixture Signal Separation With the Extended Slow Feature Analysis (xSFA) in Fiber-Optic Distributed Acoustic Sensor (DAS). J. Light. Technol. 2024, 42, 2580–2594. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, L.; Liu, Y.; Wang, S. Towards real-time multi-object tracking. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Volume 12356, pp. 107–122. [Google Scholar] [CrossRef]
- Lang, A.H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; Beijbom, O. Pointpillars: Fast encoders for object detection from point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Identification, Long Beach, CA, USA, 15–20 June 2019; pp. 12697–12705. [Google Scholar] [CrossRef]
- Yang, B.; Luo, W.; Urtasun, R. Pixor: Real-time 3d object detection from point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Identification, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7652–7660. [Google Scholar] [CrossRef]
- Liang, M.; Yang, B.; Wang, S.; Urtasun, R. Deep continuous fusion for multi-sensor 3d object detection. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 641–656. [Google Scholar] [CrossRef]
- Vora, S.; Lang, A.H.; Helou, B.; Beijbom, O. Pointpainting: Sequential fusion for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Identification, Seattle, WA, USA, 13–19 June 2020; pp. 4604–4612. [Google Scholar] [CrossRef]
- Chen, X.; Ma, H.; Wan, J.; Li, B.; Xia, T. Multi-view 3d object detection network for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Identification, Honolulu, HI, USA, 21–26 July 2017; pp. 1907–1915. [Google Scholar] [CrossRef]
- Qi, C.R.; Liu, W.; Wu, C.; Su, H.; Guibas, L.J. Frustum pointnets for 3d object detection from rgb-d data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Identification, Salt Lake City, UT, USA, 18–22 June 2018; pp. 918–927. [Google Scholar] [CrossRef]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. Dehazenet: An end-to-end system for single image haze removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef]
- Deshpande, S.; Hedaoo, N. Risk Assessment Study for Mega Tunnel in Fault Zone of the Lesser Himalayas Using Finite Element Analysis. In Proceedings of the ASCE International Conference on Transportation and Development, Atlanta, Georgia, 15–18 June 2024; pp. 181–191. [Google Scholar]
- Prakash, S.; Pandey, V.K. Associated Risk and Rectification during TBM Tunnelling. J. Rock Mech. Tunn. Technol. (JRMTT) 2020, 26, 93–108. [Google Scholar] [CrossRef]
- Peng, F.; Cao, X. A hybrid Φ/B-OTDR for simultaneous vibration and strain measurement. Photonics Sens. 2016, 6, 121–126. [Google Scholar] [CrossRef]
- Jiang, L.; Dai, B.; Wu, W.; Loy, C.C. Focal Frequency Loss for Image Reconstruction and Synthesis. In Proceedings of the 18th IEEE/CVF International Conference on Computer Vision (ICCV), New York, NY, USA, 11–17 October 2021; pp. 13899–13909. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Wang, Y.; Men, Y.; Xu, Q. Damage detection of tunnel based on the high-density cross-sectional curvature obtained using strain data from BOTDA sensors. Mech. Syst. Signal Process. 2021, 158, 107728. [Google Scholar] [CrossRef]
- Minaee, S.; Kalchbrenner, N. Deep Learning--based Text Classification: A Comprehensive Review. ACM J. 2021, 62, 1–40. [Google Scholar] [CrossRef]










| Ordinal Number | Feature Name | Feature Abbreviations | Ordinal Number | Feature Name | Feature Abbreviations |
|---|---|---|---|---|---|
| 1 | Maximum value | Max | 11 | Shape factor | Sh |
| 2 | Minimum value | Min | 12 | Crest factor | Cr |
| 3 | Mean | Me | 13 | Impulse factor | Im |
| 4 | Peak mean value | PM | 14 | Clearance factor | Cl |
| 5 | Average rectified value | Arv | 15 | Frequency of the center of gravity | CF |
| 6 | Variance | Var | 16 | Mean square frequency | MSF |
| 7 | Standard deviation | Std | 17 | Root mean square fluctuation | RMSF |
| 8 | Kurtosis | Kurt | 18 | Bandwidth energy | BE |
| 9 | Skewness | Skew | 19 | Relative power spectral entropy | RPSD |
| 10 | Root mean square | RMS | 20 | Peak average ratio | Pars |
| Soil Layer Type | Serious (KN/m3) | Lateral Pressure Coefficient | Elasticity Modulus (MPa) | Poisson’s Ratio | Cohesive Force (KPa) | Internal Friction Angle (°) | Damping Ratio |
|---|---|---|---|---|---|---|---|
| Silty clay | 19.6 | 0.42 | 9.8 | 0.40 | 12.0 | 35 | 4.2% |
| Sand | 19.0 | 0.38 | 16.5 | 0.30 | 3.0 | 28 | 3.8% |
| Pebbly soil | 21.5 | 0.28 | 45 | 0.21 | 0 | 35 | 1.5% |
| C50 | 24.5 | 0.25 | 3.45 × 104 | 0.20 | / | / | 2.5% |
| Various Location | 0 | 1/6π | 1/3π | 1/2π | 2/3π | 5/6π | π | 7/6π | 4/3π | 3/2π | 5/3π | 11/6π | Total Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5D | 20.56 | 24.77 | 24.85 | 18.09 | 15.5 | 11.56 | 8.02 | 6.32 | 8.21 | 9.77 | 12.89 | 13.76 | 174.3 |
| 1.5D | 22.54 | 25 | 21.82 | 17.33 | 12.8 | 12.34 | 7.57 | 5.86 | 8.15 | 11.36 | 12.87 | 16.69 | 174.33 |
| 3.0D | 22.23 | 19.29 | 18.21 | 16.61 | 11.58 | 8.11 | 6.67 | 7.17 | 8.57 | 13.47 | 14.78 | 18.02 | 164.71 |
| Feature Name | χ | Feature Name | χ | Feature Name | χ | Feature Name | χ |
|---|---|---|---|---|---|---|---|
| Max | 6.28 × 10−10 | Var | 5.31 × 10−10 | Sh | 8.41 × 10−14 | MSF | 7.77 × 10−8 |
| Min | 4.13 × 10−9 | Std | 2.34 × 10−10 | Cr | 6.22 × 10−9 | RMSF | 1.29 × 10−14 |
| Me | 9.10 × 10−3 | Kurt | 1.32 × 10−8 | Im | 6.34 × 10−18 | BE | 9.08 × 10−4 |
| PM | 4.60 × 10−11 | Skew | 2.61 × 10−13 | Cl | 2.28 × 10−20 | RPSD | 1.86 × 10−8 |
| Arv | 5.49 × 10−9 | RMS | 2.14 × 10−12 | CF | 6.37 × 10−9 | Pars | 6.81 × 10−3 |
| Loading Intensity | Classification Model | Identification Accuracy | |||||
|---|---|---|---|---|---|---|---|
| DO | TO | DTO | NI | Global Value | Global Value of Improvement | ||
| 50% | SVM-I | 73.44% | 83.46% | 74.12% | 89.43% | 80.9% | 14.63% |
| SVM-II | 92.16% | 98.23% | 95.69% | 96.02% | 95.53% | ||
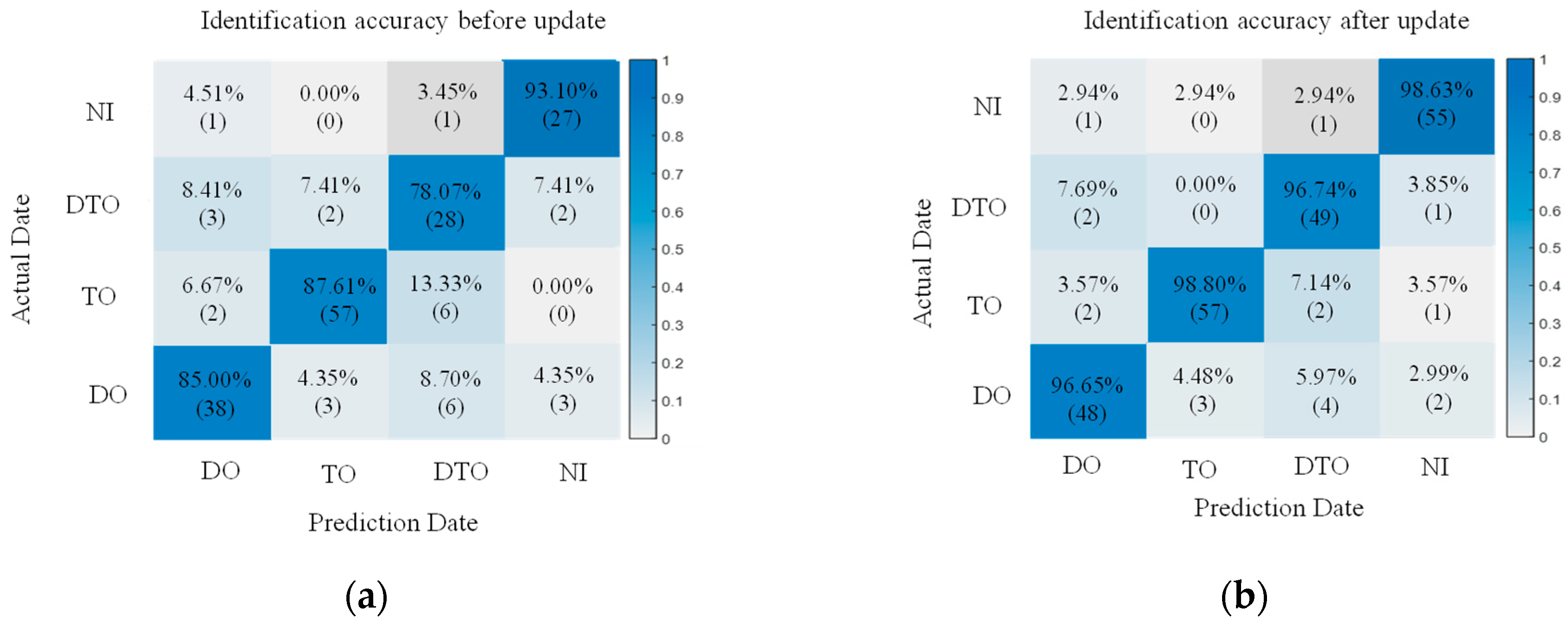
| 100% | SVM-I | 85.00% | 87.61% | 78.07% | 93.10% | 85.95% | 11.76% |
| SVM-II | 96.65% | 98.80% | 96.74% | 98.63% | 97.71% | ||
| 200% | SVM-I | 89.95% | 92.61% | 91.07% | 97.10% | 91.01% | 8.43% |
| SVM-II | 98.89% | 99.71% | 99.23% | 99.92% | 99.44% | ||
| 50% | BP-I | 71.68% | 82.59% | 75.33% | 90.04% | 79.91% | 14.82% |
| BP-II | 88.49% | 95.63% | 97.58% | 97.23% | 94.73% | ||
| 100% | BP-I | 84.36% | 88.43% | 78.86% | 92.68% | 86.08% | 11.09% |
| BP-II | 97.45% | 96.51% | 97.29% | 97.43% | 97.17% | ||
| 200% | BP-I | 90.12% | 92.33% | 92.41% | 96.82% | 92.92% | 6.00% |
| BP-II | 98.46% | 98.98% | 99.15% | 99.97% | 98.92% | ||
| Type of Vibration Signal | Metro Train Location Information | |||
|---|---|---|---|---|
| Number of signal clusters | 100 m | 50 m | 0 m | NI |
| 270 | 125 | 100 | 125 | |
| Type Classifier | Training Time (s) | Identification Accuracy of Different Vibration Sources | |||
|---|---|---|---|---|---|
| NI | 100 m | 50 m | 0 m | ||
| SVM (PF kernel function + no cross validation) | Identification accuracy before update | ||||
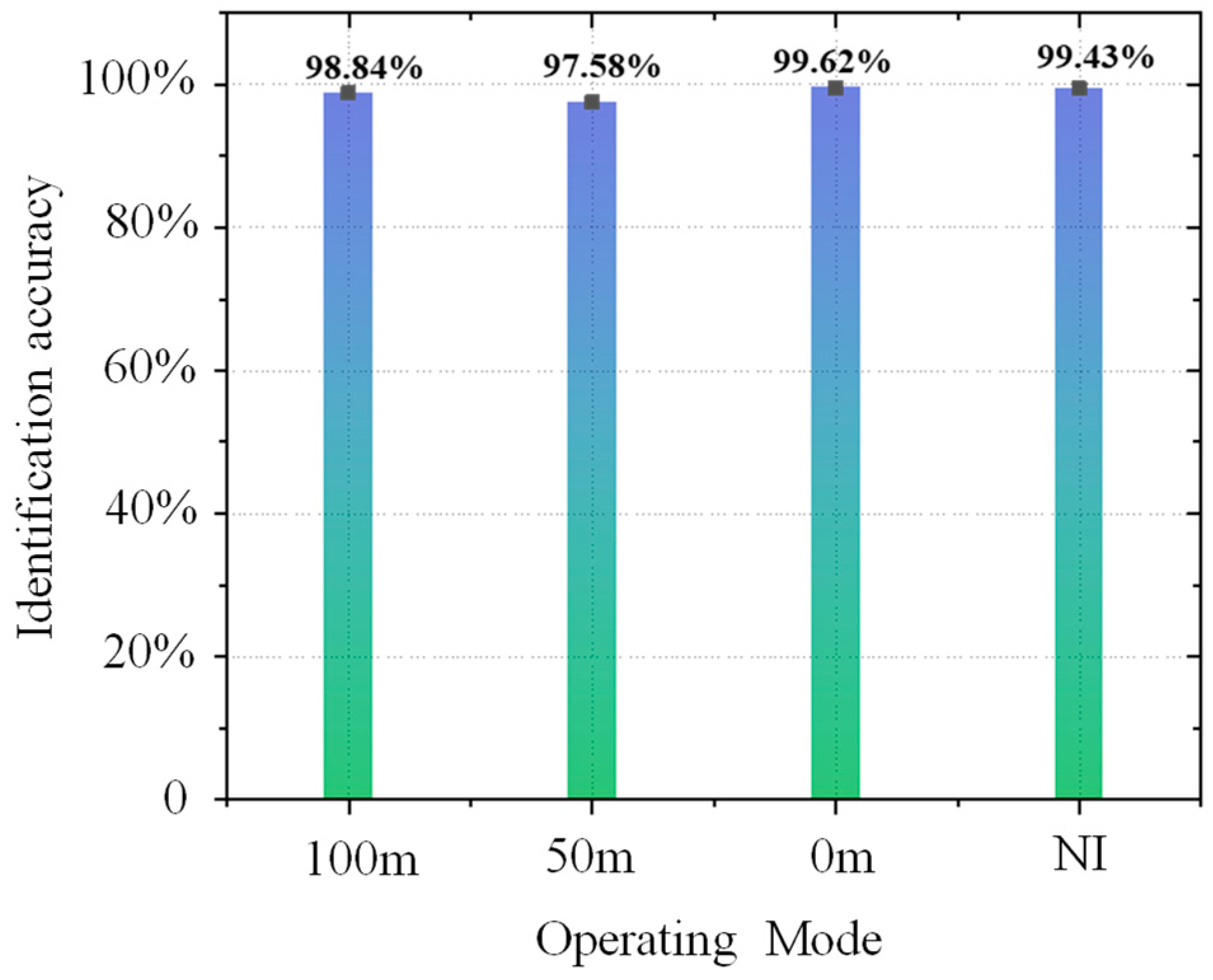
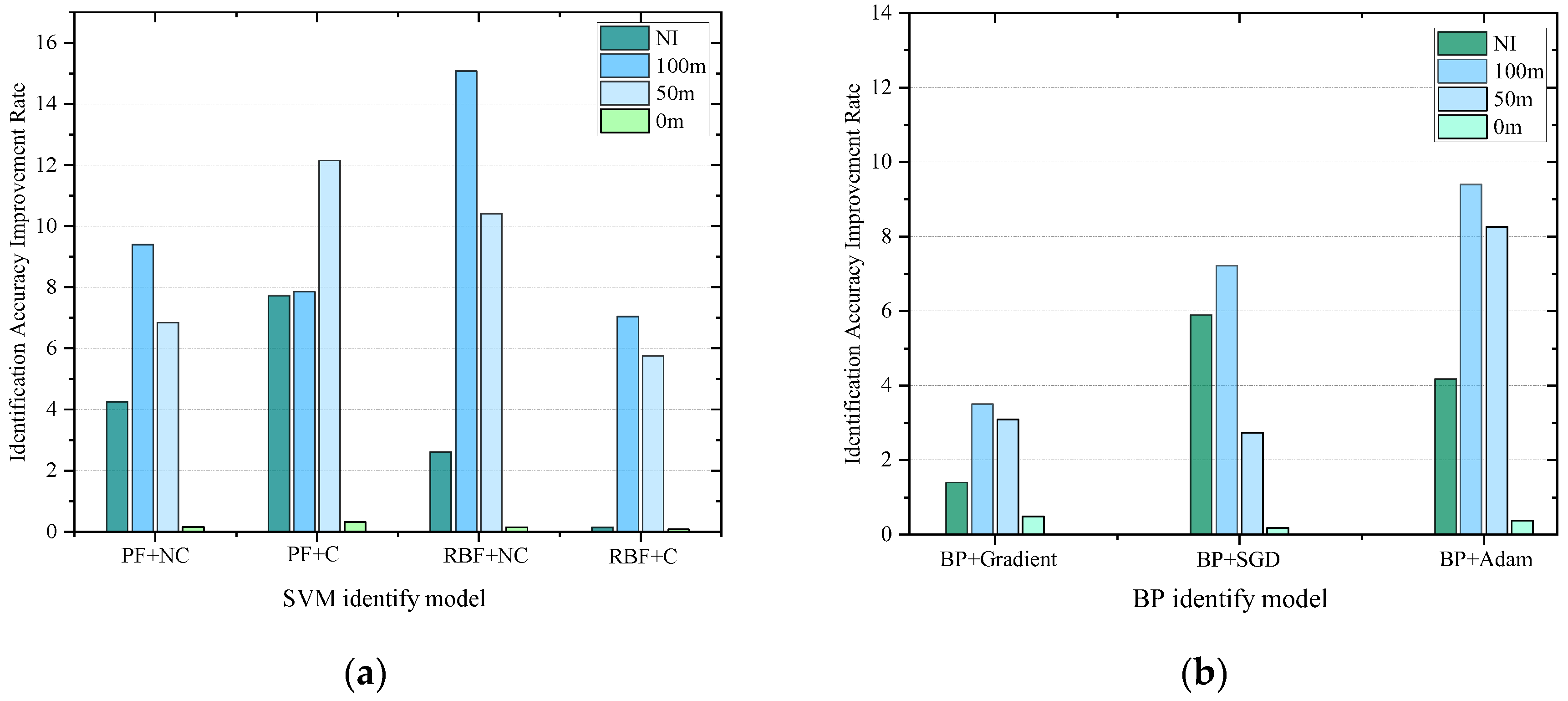
| 157.5 | 92.18% | 72.53% | 74.36% | 99.43% | |
| Identification accuracy after update | |||||
| 143.4 | 96.43% | 81.92% | 81.20% | 99.58% | |
| SVM (PF kernel function + cross validation) | Identification accuracy before update | ||||
| 277.2 | 89.96% | 77.61% | 72.48% | 98.68% | |
| Identification accuracy after update | |||||
| 261.5 | 97.68% | 85.46% | 84.62% | 98.98% | |
| SVM (RBF kernel function + no cross validation) | Identification accuracy before update | ||||
| 98.6 | 95.98% | 69.23% | 72.48% | 99.13% | |
| Identification accuracy after update | |||||
| 97.1 | 98.59% | 84.31% | 82.89% | 99.27% | |
| SVM (RBF kernel function) + cross-validation) | Identification accuracy before update | ||||
| 305.8 | 98.87% | 80.52% | 79.77% | 99.35% | |
| Identification accuracy after update | |||||
| 286.3 | 99.00% | 87.56% | 85.52% | 99.43% | |
| BP Neural Network (Gradient descent optimization) | Identification accuracy before update | ||||
| 189.4 | 98.42% | 93.45% | 92.34% | 99.33% | |
| Identification accuracy after update | |||||
| 165.5 | 99.83% | 96.95% | 95.43% | 99.82% | |
| BP Neural Network (SGD optimization) | Identification accuracy before update | ||||
| 143.2 | 92.89% | 90.34% | 92.44% | 99.06% | |
| Identification accuracy after update | |||||
| 118.9 | 98.78% | 97.55% | 95.17% | 99.24% | |
| BP Neural Network (Adam optimization) | Identification accuracy before update | ||||
| 157.4 | 94.46% | 89.41% | 88.39% | 99.15% | |
| Identification accuracy after update | |||||
| 124.2 | 98.63% | 98.80% | 96.65% | 99.52% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Cai, X.; Gao, L. Abnormal Vibration Identification of Metro Tunnels on the Basis of the Spatial Correlation of Dynamic Strain from Dense Measurement Points of Distributed Sensing Optical Fibers. Sensors 2025, 25, 6266. https://doi.org/10.3390/s25206266
Han H, Cai X, Gao L. Abnormal Vibration Identification of Metro Tunnels on the Basis of the Spatial Correlation of Dynamic Strain from Dense Measurement Points of Distributed Sensing Optical Fibers. Sensors. 2025; 25(20):6266. https://doi.org/10.3390/s25206266
Chicago/Turabian StyleHan, Hong, Xiaopei Cai, and Liang Gao. 2025. "Abnormal Vibration Identification of Metro Tunnels on the Basis of the Spatial Correlation of Dynamic Strain from Dense Measurement Points of Distributed Sensing Optical Fibers" Sensors 25, no. 20: 6266. https://doi.org/10.3390/s25206266
APA StyleHan, H., Cai, X., & Gao, L. (2025). Abnormal Vibration Identification of Metro Tunnels on the Basis of the Spatial Correlation of Dynamic Strain from Dense Measurement Points of Distributed Sensing Optical Fibers. Sensors, 25(20), 6266. https://doi.org/10.3390/s25206266







