Curvature-Aware Point-Pair Signatures for Robust Unbalanced Point Cloud Registration
Abstract
1. Introduction
2. Related Work
2.1. Balanced Point Cloud Registration
2.2. Unbalanced Point Cloud Registration
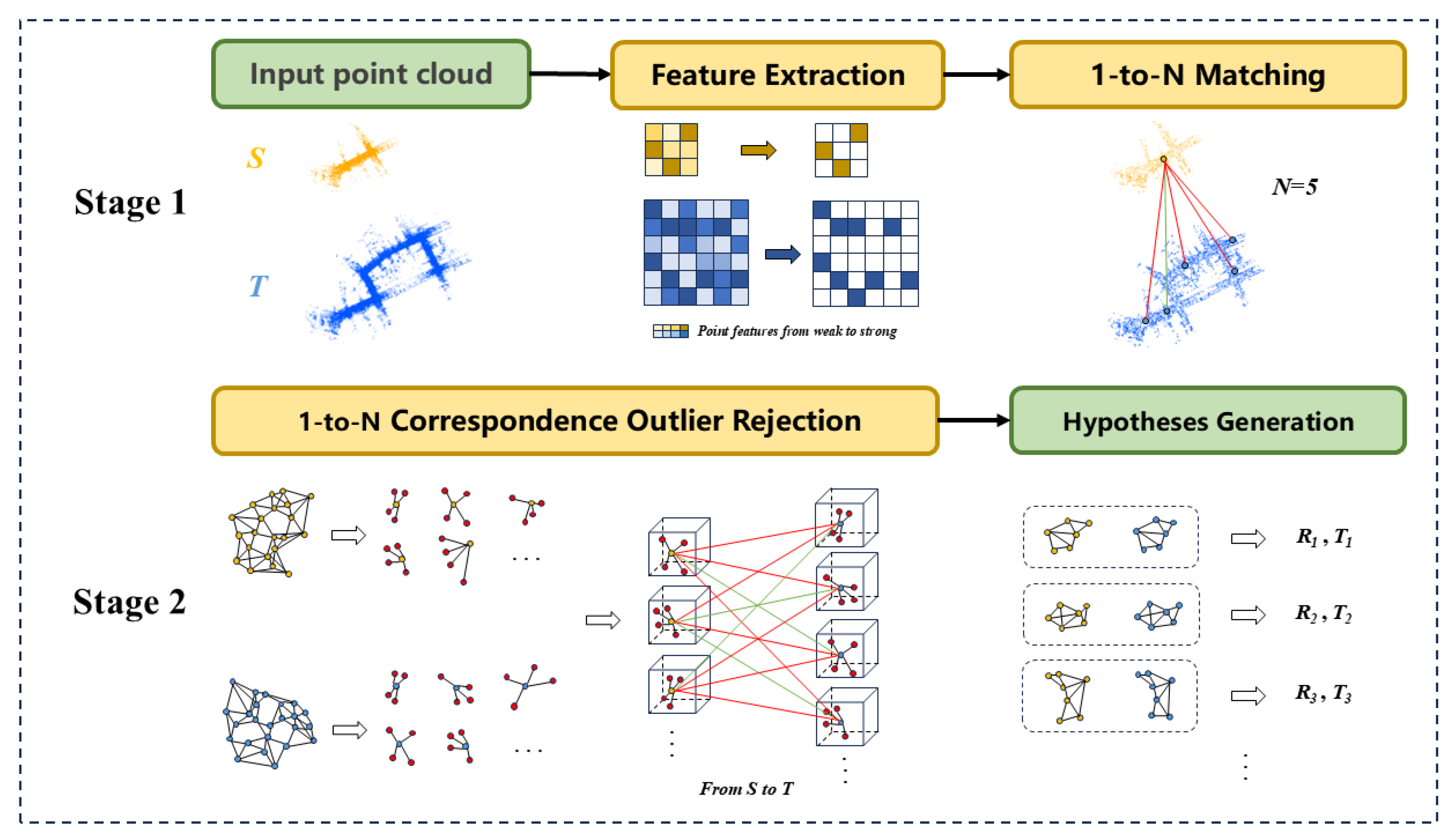
3. Method
3.1. Problem Formulation
3.2. Keypoint Detection
3.2.1. Voxel Downsampling
3.2.2. Local Curvature Estimation
3.2.3. Candidate Keypoint Selection
3.2.4. Non-Maximum Suppression
3.3. One-to-Many Correspondances
3.3.1. Feature Extraction
3.3.2. Similarity Metric
3.3.3. One-to-Many Correspondence Generation
3.4. Local Geometric Verification
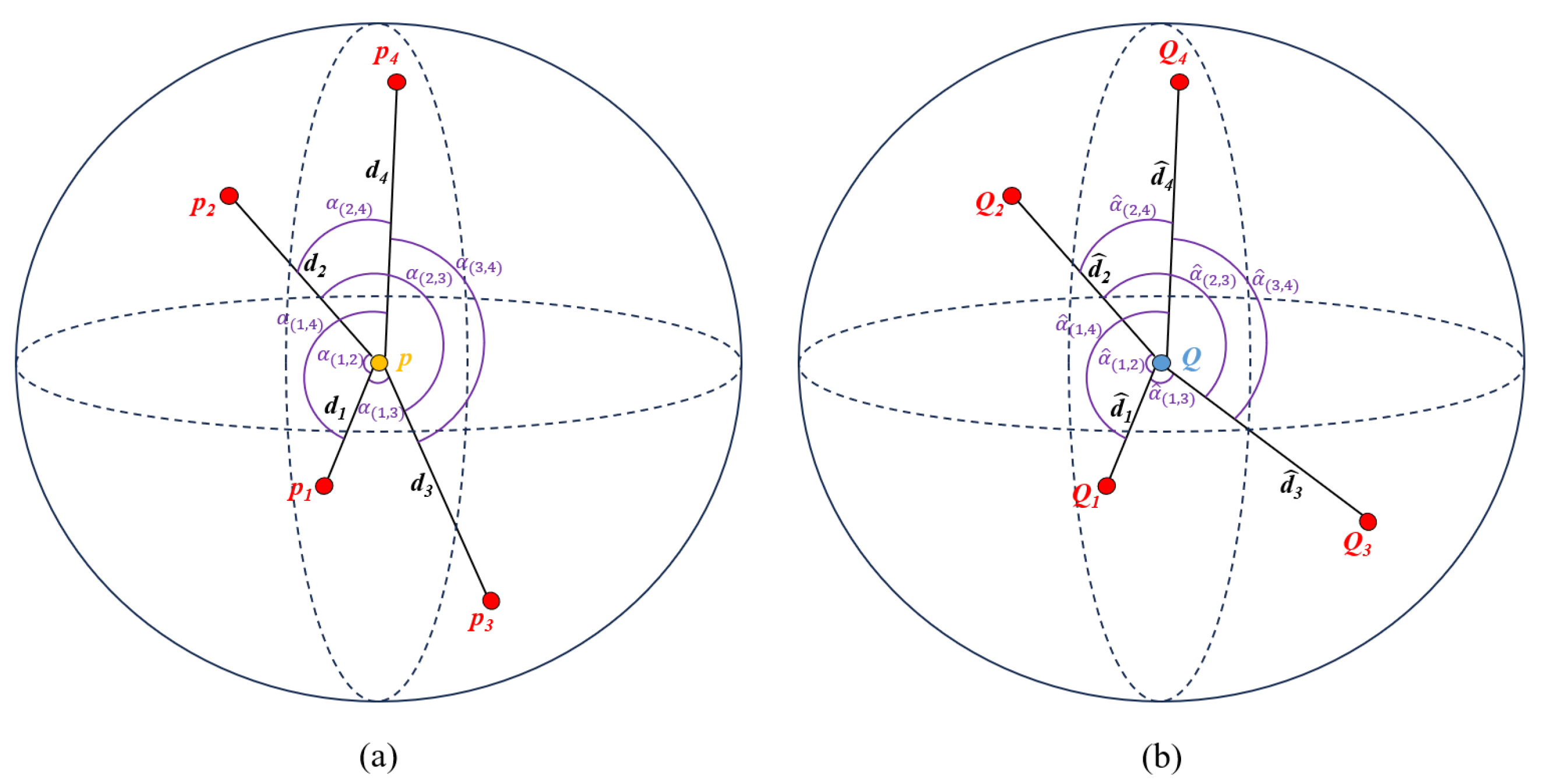
3.4.1. Local Structure Construction
3.4.2. Local Structure Similarity Matching
3.4.3. Matched Point Pairs Generation
3.5. Hypothesis Generation and Evaluation
4. Experiments
4.1. Experimental Setup
- Synthetic KITTI-UPP: Created from KITTI Odometry with fixed sampling interval (hop=10) to control unbalance ratios [44]:
- -
- Balanced (1:1): 150-frame query vs. 150-frame reference
- -
- Moderate Unbalance (1:4): 150-frame query vs. 600-frame reference
- -
- Severe Unbalance (1:10): 150-frame query vs. 1500-frame reference
Each group contains 108 registration pairs with query frames strictly excluded from reference point clouds. The unbalanced ratios (1:1, 1:4, 1:10) precisely define the relative scale between source and target point clouds based on frame aggregation ranges. For example, the 1:10 ratio configuration involves registration between a source point cloud aggregated from frames 0–150 and a target point cloud aggregated from frames 0–1500, ensuring the source is entirely contained within the target. Some samples are visualized in Figure 3. - Real-world TIESY dataset: Collected via mobile LiDAR scanning in diverse urban/rural environments by TIESY Survey Institute, featuring natural unbalance ratios of 1:4 to 1:6. This dataset comprises 95 registration pairs across 18 geographical areas, covering streets, buildings, vegetation, and infrastructure. Some samples of the dataset are visualized in Figure 4.
4.2. Results on KITTI-UPP Dataset
4.2.1. Evaluation on One-to-Many Correspondences
4.2.2. Experiments with Different Keypoint Modules
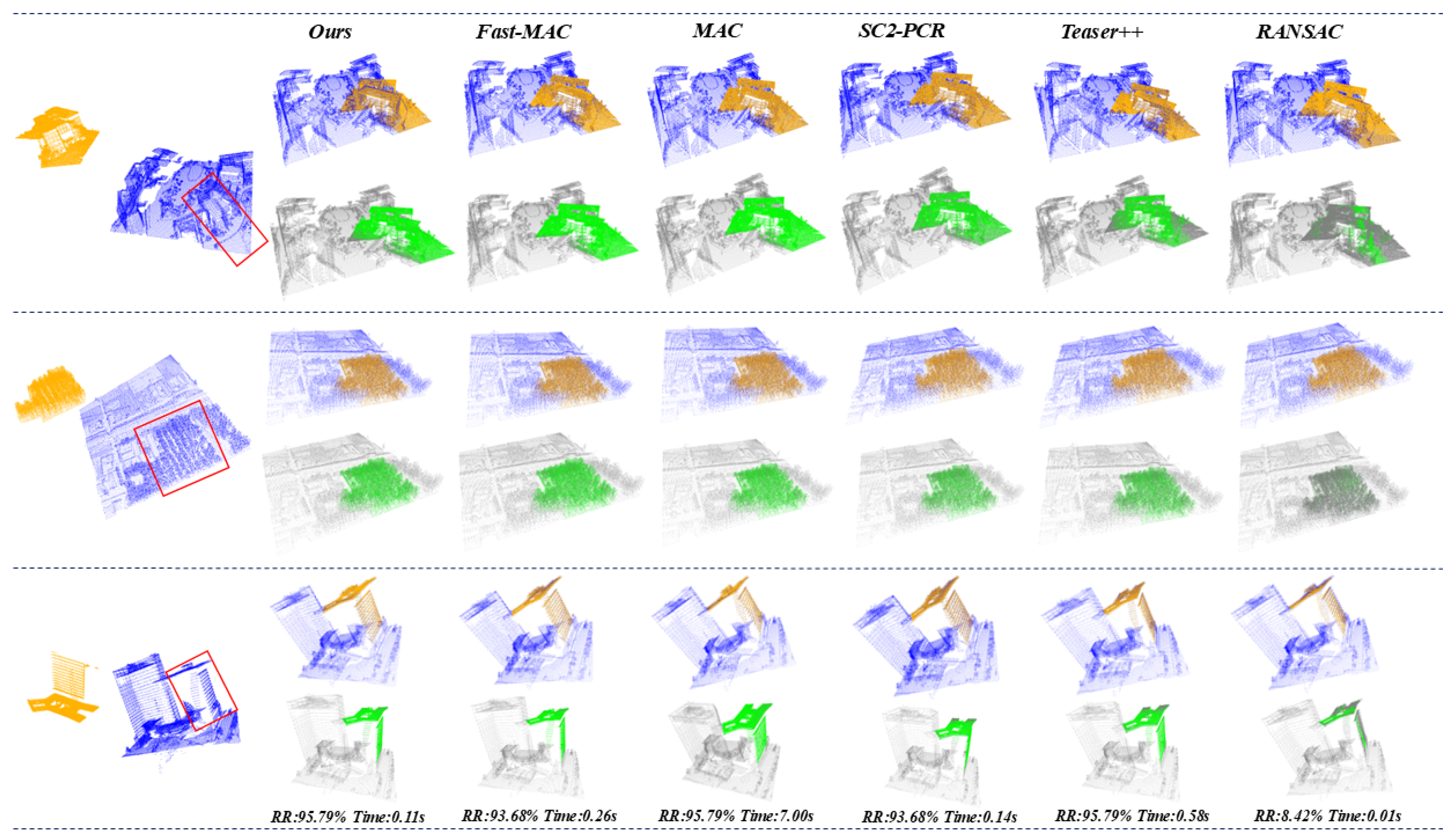
4.3. Results on TIESY Dataset
4.3.1. Evaluation on One-to-Many Correspondences
4.3.2. Robust Experiments
4.4. Ablation Study
4.4.1. Keypoint Detection Comparison
4.4.2. Parameter Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ao, S.; Hu, Q.; Yang, B.; Markham, A.; Guo, Y. Spinnet: Learning a general surface descriptor for 3d point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11753–11762. [Google Scholar]
- Wang, T.; Fu, Y.; Zhang, Z.; Cheng, X.; Li, L.; He, Z.; Wang, H.; Gong, K. Research on Ground Point Cloud Segmentation Algorithm Based on Local Density Plane Fitting in Road Scene. Sensors 2025, 25, 4781. [Google Scholar] [CrossRef] [PubMed]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & efficient point cloud registration using pointnet. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. 3D object recognition in cluttered scenes with local surface features: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2270–2287. [Google Scholar] [CrossRef] [PubMed]
- Mian, A.S.; Bennamoun, M.; Owens, R.A. Automatic correspondence for 3D modeling: An extensive review. Int. J. Shape Model. 2005, 11, 253–291. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Uy, M.A.; Lee, G.H. Pointnetvlad: Deep point cloud based retrieval for large-scale place recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4470–4479. [Google Scholar]
- Barath, D.; Matas, J. Graph-cut RANSAC. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6733–6741. [Google Scholar]
- Bustos, A.P.; Chin, T.J. Guaranteed outlier removal for point cloud registration with correspondences. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2868–2882. [Google Scholar] [CrossRef] [PubMed]
- Li, J. A Practical O(N2) Outlier Removal Method for Correspondence-Based Point Cloud Registration. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3926–3939. [Google Scholar]
- Bai, X.; Luo, Z.; Zhou, L.; Fu, H.; Quan, L.; Tai, C.L. D3feat: Joint learning of dense detection and description of 3d local features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6359–6367. [Google Scholar]
- Huang, S.; Gojcic, Z.; Usvyatsov, M.; Wieser, A.; Schindler, K. Predator: Registration of 3d point clouds with low overlap. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4267–4276. [Google Scholar]
- Yu, H.; Li, F.; Saleh, M.; Busam, B.; Ilic, S. Cofinet: Reliable coarse-to-fine correspondences for robust pointcloud registration. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS 2021), Online, 6–14 December 2021; Volume 34, pp. 23872–23884. [Google Scholar]
- Lee, J.; Kim, S.; Cho, M.; Park, J. Deep hough voting for robust global registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 15994–16003. [Google Scholar]
- Komorowski, J. Minkloc3d: Point cloud based large-scale place recognition. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual, 5–9 January 2021; pp. 1790–1799. [Google Scholar]
- Du, J.; Wang, R.; Cremers, D. Dh3d: Deep hierarchical 3d descriptors for robust large-scale 6dof relocalization. In Proceedings of the 16th European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 744–762. [Google Scholar]
- Choy, C.; Park, J.; Koltun, V. Fully convolutional geometric features. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8958–8966. [Google Scholar]
- Zhang, W.; Xiao, C. PCAN: 3D attention map learning using contextual information for point cloud based retrieval. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12436–12445. [Google Scholar]
- Liu, Z.; Zhou, S.; Suo, C.; Yin, P.; Chen, W.; Wang, H.; Li, H.; Liu, Y.H. Lpd-net: 3d point cloud learning for large-scale place recognition and environment analysis. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2831–2840. [Google Scholar]
- Quan, S.; Yang, J. Compatibility-guided sampling consensus for 3-d point cloud registration. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 7380–7392. [Google Scholar] [CrossRef]
- Yang, J.; Chen, J.; Quan, S.; Wang, W.; Zhang, Y. Correspondence selection with loose–tight geometric voting for 3-D point cloud registration. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhong, Y. Intrinsic shape signatures: A shape descriptor for 3D object recognition. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; IEEE: New York, NY, USA, 2009; pp. 689–696. [Google Scholar]
- Mian, A.; Bennamoun, M.; Owens, R. On the repeatability and quality of keypoints for local feature-based 3d object retrieval from cluttered scenes. Int. J. Comput. Vis. 2010, 89, 348–361. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Yang, J.; Huang, Z.; Quan, S.; Qi, Z.; Zhang, Y. SAC-COT: Sample consensus by sampling compatibility triangles in graphs for 3-D point cloud registration. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Z.; Quan, S.; Zhang, Q.; Zhang, Y.; Cao, Z. Toward efficient and robust metrics for RANSAC hypotheses and 3D rigid registration. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 893–906. [Google Scholar] [CrossRef]
- Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A globally optimal solution to 3D ICP point-set registration. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2241–2254. [Google Scholar] [CrossRef] [PubMed]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Yuan, H.; Li, G.; Wang, L.; Li, X. Research on the Improved ICP Algorithm for LiDAR Point Cloud Registration. Sensors 2025, 25, 4748. [Google Scholar] [CrossRef] [PubMed]
- Choy, C.; Gwak, J.; Savarese, S. 4d spatio-temporal convnets: Minkowski convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3075–3084. [Google Scholar]
- Pais, G.D.; Ramalingam, S.; Govindu, V.M.; Nascimento, J.C.; Chellappa, R.; Miraldo, P. 3dregnet: A deep neural network for 3d point registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7193–7203. [Google Scholar]
- Cai, P. Neural Network-Based Low-Level 3D Point Cloud Processing. Ph.D. Thesis, University of South Carolina, Columbia, SC, USA, 19 December 2024. [Google Scholar]
- Qin, Z.; Yu, H.; Wang, C.; Guo, Y.; Peng, Y.; Xu, K. Geometric transformer for fast and robust point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11143–11152. [Google Scholar]
- Došljak, V.; Jovančević, I.; Orteu, J.J.; Brault, R.; Belbacha, Z. Airplane panels inspection via 3D point cloud segmentation on low-volume training dataset. In Proceedings of the 17th International Conference on Quality Control by Artificial Vision, Yamanashi, Japan, 4–6 June 2025; SPIE: Bellingham, WA, USA, 2025; Volume 13737, pp. 13–20. [Google Scholar]
- Bai, X.; Luo, Z.; Zhou, L.; Chen, H.; Li, L.; Hu, Z.; Fu, H.; Tai, C.L. Pointdsc: Robust point cloud registration using deep spatial consistency. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15859–15869. [Google Scholar]
- Jirawattanasomkul, T.; Hang, L.; Srivaranun, S.; Likitlersuang, S.; Jongvivatsakul, P.; Yodsudjai, W.; Thammarak, P. Digital twin-based structural health monitoring and measurements of dynamic characteristics in balanced cantilever bridge. Resilient Cities Struct. 2025, 4, 48–66. [Google Scholar] [CrossRef]
- Ababsa, F.; Noureddine, M.; Bouali, M.; El Meouche, R.; Sammuneh, M.; De Martin, F.; Beaufils, M.; Viguier, F.; Salvati, B. Digital twins for predictive monitoring and anomaly detection: Application to seismic and railway infrastructures. In Proceedings of the 17th International Conference on Quality Control by Artificial Vision, Yamanashi, Japan, 4–6 June 2025; SPIE: Bellingham, WA, USA, 2025; Volume 13737, pp. 75–82. [Google Scholar]
- Yin, H.; Wang, Y.; Ding, X.; Tang, L.; Huang, S.; Xiong, R. 3d lidar-based global localization using siamese neural network. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1380–1392. [Google Scholar] [CrossRef]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. Scannet: Richly-annotated 3d reconstructions of indoor scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5828–5839. [Google Scholar]
- Choy, C.; Lee, J.; Ranftl, R.; Park, J.; Koltun, V. High-dimensional convolutional networks for geometric pattern recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11227–11236. [Google Scholar]
- Zhang, X.; Yang, J.; Zhang, S.; Zhang, Y. 3D registration with maximal cliques. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 17745–17754. [Google Scholar]
- Chen, Z.; Sun, K.; Yang, F.; Tao, W. Sc2-pcr: A second order spatial compatibility for efficient and robust point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13221–13231. [Google Scholar]
- Zhang, Y.; Zhao, H.; Li, H.; Chen, S. Fastmac: Stochastic spectral sampling of correspondence graph. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 17857–17867. [Google Scholar]
- Lee, K.; Lee, J.; Park, J. Learning to register unbalanced point pairs. arXiv 2022, arXiv:2207.04221. [Google Scholar] [CrossRef]
- Yang, H.; Shi, J.; Carlone, L. Teaser: Fast and certifiable point cloud registration. IEEE Trans. Robot. 2020, 37, 314–333. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Park, J.; Koltun, V. Fast global registration. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 766–782. [Google Scholar]
- Yao, R.; Du, S.; Cui, W.; Tang, C.; Yang, C. PARE-Net: Position-aware rotation-equivariant networks for robust point cloud registration. In Proceedings of the 18th European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 287–303. [Google Scholar]

| (a) Small-to-Large Scenario (Partial-to-Whole) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | N = 1 | N = 4 | N = 6 | N = 8 | ||||||||||||
| RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | |
| RANSAC [28] | 7.41 | 0.09 | 15.12 | 0.01 | 2.78 | 0.08 | 18.31 | 0.01 | 0.00 | / | / | / | 0.00 | / | / | / |
| FGR [46] | 39.81 | 2.25 | 42.35 | 0.34 | 41.67 | 1.81 | 45.56 | 1.28 | 41.67 | 2.24 | 47.58 | 2.13 | 42.59 | 2.39 | 55.21 | 2.88 |
| Teaser++ [45] | 57.41 | 9.03 | 36.21 | 0.07 | 82.41 | 0.02 | 9.56 | 0.32 | 87.04 | 0.01 | 4.11 | 0.87 | 92.59 | 0.03 | 5.63 | 1.49 |
| SC2-PCR [42] | 57.41 | 0.08 | 25.15 | 0.01 | 70.37 | 0.02 | 6.21 | 0.07 | 66.67 | 0.17 | 51.21 | 0.11 | 65.74 | 0.02 | 2.15 | 0.13 |
| MAC [41] | 52.78 | 0.01 | 44.12 | 0.10 | 82.41 | 0.01 | 14.52 | 2.30 | 87.96 | 0.02 | 13.25 | 5.10 | 94.44 | 0.01 | 25.69 | 10.65 |
| Fast-MAC [43] | 51.85 | 0.01 | 45.21 | 0.01 | 79.63 | 0.01 | 16.32 | 0.11 | 85.19 | 0.02 | 17.35 | 1.29 | 89.81 | 0.01 | 27.95 | 3.48 |
| Ours* | 35.19 | 0.11 | 34.44 | 0.10 | 62.04 | 0.06 | 19.12 | 0.10 | 78.70 | 0.02 | 0.82 | 0.10 | 88.88 | 0.02 | 4.82 | 0.10 |
| Ours | 70.37 | 0.01 | 2.85 | 0.09 | 95.37 | 0.01 | 0.25 | 0.10 | 99.07 | 0.01 | 0.13 | 0.10 | 99.07 | 0.01 | 0.17 | 0.10 |
| Method | N = 12 | N = 16 | N = 20 | N = 24 | ||||||||||||
| RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | |
| RANSAC [28] | 0.00 | / | / | / | 0.00 | / | / | / | 0.00 | / | / | / | 0.00 | / | / | / |
| FGR [46] | 37.96 | 2.23 | 54.47 | 4.15 | 30.81 | 2.48 | 40.60 | 5.08 | 34.26 | 2.08 | 41.66 | 6.30 | 37.96 | 2.64 | 56.32 | 7.60 |
| Teaser++ [45] | 96.30 | 0.02 | 5.01 | 2.72 | 98.15 | 0.01 | 3.69 | 5.09 | 100.00 | 0.01 | 4.52 | 8.77 | 61.11 | 0.01 | 3.24 | 15.83 |
| SC2-PCR [42] | 51.85 | 0.02 | 3.35 | 0.14 | 50.00 | 0.11 | 53.31 | 0.16 | 43.37 | 0.13 | 51.63 | 0.18 | 43.52 | 0.02 | 6.87 | 0.19 |
| MAC [41] | 97.22 | 0.01 | 18.56 | 44.26 | 87.04 | 0.01 | 31.32 | 68.25 | 51.85 | 0.01 | 31.85 | 79.05 | 26.85 | 0.02 | 30.21 | 95.14 |
| Fast-MAC [43] | 89.81 | 0.01 | 20.21 | 4.20 | 63.89 | 0.01 | 32.25 | 17.79 | 38.89 | 0.02 | 36.21 | 5.37 | 19.44 | 0.02 | 36.68 | 7.55 |
| Ours* | 97.22 | 0.01 | 3.58 | 0.11 | 97.22 | 0.01 | 4.02 | 0.11 | 98.15 | 0.05 | 6.52 | 0.11 | 99.07 | 0.01 | 3.54 | 0.11 |
| Ours | 99.07 | 0.01 | 0.14 | 0.10 | 100.00 | 0.01 | 0.08 | 0.11 | 100.00 | 0.01 | 0.09 | 0.11 | 100.00 | 0.01 | 0.06 | 0.11 |
| (b) Large-to-Small Scenario (Whole-to-Partial) | ||||||||||||||||
| Method | N = 1 | N = 2 | N = 4 | N = 6 | ||||||||||||
| RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | |
| RANSAC [28] | 0.93 | 0.02 | 10.36 | 0.01 | 0.93 | 0.09 | 15.36 | 0.02 | 0.00 | / | / | / | 0.00 | / | / | / |
| FGR [46] | 37.04 | 2.99 | 44.63 | 1.18 | 37.96 | 2.85 | 48.89 | 2.35 | 25.93 | 2.24 | 48.62 | 4.74 | 36.11 | 3.15 | 42.31 | 5.17 |
| Teaser++ [45] | 85.19 | 0.09 | 19.68 | 0.26 | 91.67 | 0.03 | 6.35 | 1.03 | 69.44 | 0.02 | 5.21 | 3.06 | 71.30 | 0.04 | 9.56 | 7.17 |
| SC2-PCR [42] | 65.74 | 0.10 | 27.58 | 0.06 | 59.26 | 0.05 | 6.84 | 0.12 | 44.44 | 0.12 | 25.01 | 0.15 | 48.15 | 0.04 | 10.25 | 0.18 |
| MAC [41] | 79.63 | 0.02 | 4.12 | 2.00 | 91.67 | 0.01 | 5.78 | 8.92 | 69.44 | 0.01 | 7.71 | 32.53 | 72.22 | 0.01 | 8.25 | 97.05 |
| Fast-MAC [43] | 75.00 | 0.02 | 4.69 | 0.10 | 85.19 | 0.01 | 17.86 | 6.94 | 64.81 | 0.02 | 8.96 | 4.39 | 62.96 | 0.01 | 8.63 | 8.47 |
| Ours* | 47.22 | 0.04 | 9.01 | 0.10 | 83.33 | 0.01 | 7.03 | 0.10 | 78.70 | 0.03 | 5.86 | 0.11 | 87.96 | 0.05 | 7.52 | 0.11 |
| Ours | 98.15 | 0.02 | 1.42 | 0.10 | 100.00 | 0.01 | 0.78 | 0.10 | 100.00 | 0.00 | 0.82 | 0.11 | 100.00 | 0.00 | 0.68 | 0.11 |
| Correspondence | Method | 1:10 Ratio | 1:4 Ratio | 1:1 Ratio | ||||
|---|---|---|---|---|---|---|---|---|
| RR (%) | Time (s) | RR (%) | Time (s) | RR (%) | Time (s) | |||
| (i) Deep learning | - | GeoTransformer [33] | 38.89 | 4.65 | 62.04 | 2.29 | 94.44 | 0.62 |
| PARENet [47] | 71.30 | 9.01 | 87.04 | 4.05 | 100.00 | 0.78 | ||
| (ii) Traditional | ISS+FPFH [22] | RANSAC [28] | 0.00 | 0.01 | 0.00 | 0.01 | 63.89 | 0.01 |
| FGR [46] | 43.52 | 1.19 | 37.96 | 4.15 | 94.44 | 1.06 | ||
| Teaser++ [45] | 81.48 | 0.45 | 96.30 | 2.72 | 95.37 | 0.90 | ||
| SC2-PCR [42] | 74.77 | 0.11 | 51.85 | 0.14 | 96.30 | 0.04 | ||
| MAC [41] | 88.66 | 9.90 | 97.22 | 44.26 | 94.44 | 2.02 | ||
| Fast-MAC [43] | 84.11 | 0.19 | 89.81 | 4.20 | 94.44 | 1.02 | ||
| H3D+FPFH [23] | RANSAC [28] | 0.00 | 0.01 | 0.00 | 0.01 | 47.22 | 0.01 | |
| FGR [46] | 50.00 | 5.60 | 64.81 | 2.87 | 100.00 | 0.62 | ||
| Teaser++ [45] | 83.33 | 1.98 | 89.81 | 1.16 | 100.00 | 2.33 | ||
| SC2-PCR [42] | 70.37 | 0.39 | 83.33 | 0.26 | 97.22 | 0.02 | ||
| MAC [41] | 93.51 | 26.52 | 94.44 | 11.47 | 100.00 | 3.44 | ||
| Fast-MAC [43] | 92.94 | 4.18 | 91.67 | 3.07 | 100.00 | 1.58 | ||
| CURV+FPFH | RANSAC [28] | 0.00 | 0.01 | 8.33 | 0.01 | 95.37 | 0.01 | |
| FGR [46] | 84.26 | 5.10 | 87.96 | 3.48 | 100.00 | 0.99 | ||
| Teaser++ [45] | 90.74 | 7.49 | 93.52 | 9.61 | 100.00 | 0.20 | ||
| SC2-PCR [42] | 94.44 | 0.14 | 99.07 | 0.11 | 100.00 | 0.30 | ||
| MAC [41] | 89.81 | 24.96 | 87.04 | 15.78 | 100.00 | 1.09 | ||
| Fast-MAC [43] | 87.96 | 6.46 | 87.04 | 2.78 | 100.00 | 0.15 | ||
| Ours | 95.37 | 0.10 | 99.07 | 0.10 | 100.00 | 0.11 | ||
| Method | RR (%) | Time (s) |
|---|---|---|
| TEASER++ [45] | 86.11 | 3.38 |
| SC2-PCR [42] | 91.67 | 0.16 |
| MAC [41] | 83.33 | 25.11 |
| Fast-MAC [43] | 79.63 | 4.15 |
| Ours | 94.44 | 0.11 |
| (a) Small-to-Large Scenario (Partial-to-Whole) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | N = 1 | N = 2 | N = 4 | N = 8 | ||||||||||||
| RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | |
| RANSAC [28] | 37.89 | 0.06 | 21.25 | 0.01 | 30.53 | 0.10 | 27.54 | 0.01 | 27.37 | 0.18 | 45.51 | 0.01 | 16.84 | 0.09 | 29.63 | 0.02 |
| FGR [46] | 47.37 | 0.72 | 45.85 | 0.53 | 46.32 | 0.63 | 41.44 | 0.75 | 42.11 | 0.75 | 46.35 | 0.67 | 41.05 | 0.88 | 41.01 | 2.26 |
| Teaser++ [45] | 69.47 | 0.01 | 1.36 | 0.03 | 75.79 | 0.00 | 0.98 | 0.08 | 84.21 | 0.00 | 1.55 | 0.26 | 84.21 | 0.02 | 6.36 | 1.01 |
| SC2-PCR [42] | 68.42 | 0.01 | 0.68 | 0.82 | 69.47 | 0.02 | 0.87 | 0.23 | 75.79 | 0.02 | 0.95 | 0.25 | 75.79 | 0.02 | 0.64 | 0.30 |
| MAC [41] | 68.42 | 0.01 | 5.21 | 0.46 | 72.63 | 0.01 | 8.62 | 1.35 | 83.16 | 0.01 | 18.54 | 2.59 | 85.26 | 0.01 | 18.75 | 11.71 |
| Fast-MAC [43] | 69.15 | 0.01 | 4.87 | 0.02 | 71.58 | 0.01 | 5.34 | 0.06 | 78.95 | 0.01 | 5.63 | 0.23 | 85.26 | 0.01 | 10.98 | 9.47 |
| Ours* | 63.82 | 0.01 | 0.89 | 0.09 | 67.02 | 0.01 | 1.02 | 0.09 | 74.47 | 0.00 | 0.45 | 0.10 | 84.21 | 0.02 | 0.82 | 0.10 |
| Ours | 72.34 | 0.01 | 0.47 | 0.09 | 79.79 | 0.01 | 0.65 | 0.10 | 86.17 | 0.01 | 0.82 | 0.10 | 92.55 | 0.02 | 0.77 | 0.10 |
| Method | N=12 | N=16 | N=22 | N=26 | ||||||||||||
| RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | |
| RANSAC [28] | 13.68 | 0.41 | 48.24 | 0.02 | 10.53 | 0.62 | 41.36 | 0.02 | 9.47 | 1.19 | 48.69 | 0.03 | 6.32 | 0.66 | 48.56 | 0.03 |
| FGR [46] | 38.95 | 1.46 | 40.08 | 3.30 | 33.68 | 1.09 | 39.62 | 4.36 | 30.53 | 1.18 | 41.14 | 5.94 | 30.53 | 1.24 | 40.05 | 6.98 |
| Teaser++ [45] | 86.32 | 0.00 | 1.08 | 2.32 | – | – | – | – | – | – | – | – | – | – | – | – |
| SC2-PCR [42] | 69.47 | 0.02 | 0.85 | 0.32 | 67.37 | 0.01 | 0.92 | 0.34 | 66.32 | 0.04 | 6.01 | 0.36 | 68.42 | 0.04 | 8.08 | 0.38 |
| MAC [41] | 86.32 | 0.01 | 16.52 | 29.84 | – | – | – | – | – | – | – | – | – | – | – | – |
| Fast-MAC [43] | 86.32 | 0.01 | 17.48 | 54.82 | – | – | – | – | – | – | – | – | – | – | – | – |
| Ours* | 86.32 | 0.01 | 0.95 | 0.10 | 87.23 | 0.01 | 0.68 | 0.10 | 89.36 | 0.01 | 1.20 | 0.10 | 90.43 | 0.01 | 1.04 | 0.10 |
| Ours | 92.55 | 0.01 | 0.65 | 0.10 | 94.68 | 0.06 | 0.68 | 0.10 | 96.81 | 0.02 | 0.59 | 0.10 | 96.81 | 0.01 | 0.49 | 0.10 |
| (b) Large-to-Small Scenario (Whole-to-Partial) | ||||||||||||||||
| Method | N = 1 | N = 2 | N = 3 | N = 4 | ||||||||||||
| RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | RR (%) | RE (°) | TE (cm) | Time (s) | |
| RANSAC [28] | 12.63 | 0.57 | 14.21 | 0.02 | 10.53 | 1.16 | 19.58 | 0.03 | 5.26 | 1.15 | 22.35 | 0.03 | 5.26 | 2.84 | 34.52 | 0.03 |
| FGR [46] | 35.79 | 0.90 | 52.01 | 1.92 | 33.68 | 1.18 | 54.45 | 3.72 | 34.74 | 1.17 | 49.86 | 5.56 | 31.58 | 1.13 | 48.78 | 7.27 |
| Teaser++ [45] | 81.05 | 0.01 | 0.87 | 0.97 | – | – | – | – | – | – | – | – | – | – | – | – |
| SC2-PCR [42] | 72.63 | 0.22 | 42.24 | 0.17 | 56.84 | 0.11 | 9.87 | 0.33 | 54.74 | 0.07 | 20.06 | 0.36 | 45.26 | 0.09 | 27.14 | 0.39 |
| MAC [41] | 81.05 | 0.01 | 0.45 | 12.22 | 91.49 | 0.01 | 0.86 | 26.23 | – | – | – | – | – | – | – | – |
| Fast-MAC [43] | 78.95 | 0.01 | 0.58 | 16.06 | 90.53 | 0.02 | 0.97 | 82.60 | – | – | – | – | – | – | – | – |
| Ours* | 73.40 | 0.01 | 1.29 | 0.10 | 85.11 | 0.02 | 1.05 | 0.11 | 88.29 | 0.01 | 3.58 | 0.10 | 92.55 | 0.01 | 2.25 | 0.10 |
| Ours | 90.43 | 0.01 | 1.01 | 0.10 | 92.55 | 0.01 | 0.85 | 0.10 | 93.62 | 0.01 | 0.82 | 0.10 | 93.62 | 0.01 | 0.55 | 0.10 |
| Method | RR (%) | Time (s) | |
|---|---|---|---|
| (i) Deep Learning | GeoTransformer [33] | 39.80 | 8.24 |
| PARENet [47] | 33.67 | 12.49 | |
| (ii) Traditional | RANSAC [28] | 8.42 | 0.02 |
| FGR [46] | 72.63 | 1.63 | |
| Teaser++ [45] | 95.79 | 0.58 | |
| SC2-PCR [42] | 93.68 | 0.14 | |
| MAC [41] | 95.79 | 7.00 | |
| Fast-MAC [43] | 93.68 | 0.26 | |
| Ours | 95.79 | 0.11 |
| Noise Level | RR (%) | Time (s) |
|---|---|---|
| 0.01 | 93.68 | 0.11 |
| 0.02 | 95.79 | 0.11 |
| 0.03 | 88.42 | 0.11 |
| Keypoint | Registration | Metric | N | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 8 | 12 | 24 | |||
| CURV | Small-to-Large | Correspondence Count | 1574.33 | 3148.66 | 6297.32 | 12,594.64 | 18,891.96 | 37,783.92 |
| Inlier Ratio (%) | 10.02 | 7.21 | 4.29 | 2.50 | 1.83 | 1.09 | ||
| Inlier Count | 161.13 | 230.87 | 274.63 | 320.36 | 348.62 | 389.35 | ||
| Large-to-Small | Correspondence Count | 5169.46 | 10,338.92 | 15,508.38 | 20,677.84 | 25,847.30 | 31,016.76 | |
| Inlier Ratio (%) | 3.83 | 2.78 | 2.09 | 1.70 | 1.44 | 1.26 | ||
| Inlier Count | 191.80 | 278.13 | 311.79 | 337.57 | 357.83 | 375.38 | ||
| H3D [23] | Small-to-Large | Correspondence Count | 1174.05 | 2348.10 | 4696.20 | 9392.40 | 14,088.60 | 28,177.20 |
| Inlier Ratio (%) | 2.20 | 1.49 | 1.02 | 0.68 | 0.55 | 0.37 | ||
| Inlier Count | 25.09 | 33.44 | 44.35 | 57.15 | 65.74 | 84.17 | ||
| Large-to-Small | Correspondence Count | 4810.85 | 9621.70 | 14,432.55 | 19,243.40 | 24,054.25 | 28,865.10 | |
| Inlier Ratio (%) | 0.85 | 0.60 | 0.49 | 0.42 | 0.37 | 0.33 | ||
| Inlier Count | 36.57 | 50.03 | 59.86 | 67.56 | 74.19 | 77.48 | ||
| ISS [22] | Small-to-Large | Correspondence Count | 1715.88 | 3431.76 | 6863.52 | 13,727.04 | 20,590.56 | 41,181.12 |
| Inlier Ratio (%) | 1.20 | 0.86 | 0.59 | 0.39 | 0.31 | 0.21 | ||
| Inlier Count | 21.56 | 30.86 | 41.75 | 54.93 | 65.29 | 88.81 | ||
| Large-to-Small | Correspondence Count | 5951.96 | 11,903.92 | 17,855.88 | 23,807.84 | 29,759.80 | 35,711.76 | |
| Inlier Ratio (%) | 0.56 | 0.40 | 0.33 | 0.28 | 0.25 | 0.23 | ||
| Inlier Count | 32.72 | 47.23 | 57.52 | 65.93 | 73.24 | 80.48 | ||
| Registration Mode | Metric | N | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 8 | 12 | 16 | 22 | 26 | ||
| Small-to-Large | Correspondence Count | 1540.93 | 3081.86 | 6163.72 | 12,327.44 | 18,491.16 | 24,654.88 | 33,900.46 | 40,064.18 |
| Inlier Ratio (%) | 10.15 | 6.37 | 3.99 | 2.51 | 1.93 | 1.60 | 1.30 | 1.16 | |
| Inlier Count | 141.23 | 176.86 | 219.87 | 273.60 | 313.26 | 344.47 | 383.58 | 405.41 | |
| Large-to-Small | Correspondence Count | 10,641.47 | 21,262.94 | 31,924.41 | 42,565.88 | – | – | – | – |
| Inlier Ratio (%) | 2.15 | 1.44 | 1.14 | 0.96 | – | – | – | – | |
| Inlier Count | 179.47 | 234.11 | 272.47 | 302.97 | – | – | – | – | |
| k | RR | RE | TE | Time |
|---|---|---|---|---|
| 3 | 95.37% | 0.0070 | 0.037 | 0.1491 |
| 4 | 100.00% | 0.0002 | 2.563 | 0.1488 |
| 5 | 100.00% | 0.0002 | 1.763 | 0.1487 |
| 6 | 99.07% | 0.0002 | 1.130 | 0.1487 |
| 7 | 99.07% | 0.0002 | 9.701 | 0.1487 |
| 8 | 98.15% | 0.0001 | 4.670 | 0.1488 |
| Descriptor | AC | DC | RR (%) | RE (°) | TE (cm) | Time (s) |
|---|---|---|---|---|---|---|
| FPFH [24] | ✓ | 92.59 | 0.0008 | 0.002 | 0.1144 | |
| ✓ | 25.00 | 0.0002 | 6.637 | 0.1153 | ||
| ✓ | ✓ | 100.00 | 0.0002 | 2.563 | 0.1488 | |
| PARENet [47] | ✓ | 77.78 | 0.0336 | 0.156 | 0.0967 | |
| ✓ | 85.19 | 0.0030 | 0.008 | 0.0949 | ||
| ✓ | ✓ | 93.52 | 0.0002 | 9.032 | 0.0975 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Zeng, Z.; Deng, J.; Wang, G.; Yang, J.; Quan, S. Curvature-Aware Point-Pair Signatures for Robust Unbalanced Point Cloud Registration. Sensors 2025, 25, 6267. https://doi.org/10.3390/s25206267
Hu X, Zeng Z, Deng J, Wang G, Yang J, Quan S. Curvature-Aware Point-Pair Signatures for Robust Unbalanced Point Cloud Registration. Sensors. 2025; 25(20):6267. https://doi.org/10.3390/s25206267
Chicago/Turabian StyleHu, Xinhang, Zhao Zeng, Jiwei Deng, Guangshuai Wang, Jiaqi Yang, and Siwen Quan. 2025. "Curvature-Aware Point-Pair Signatures for Robust Unbalanced Point Cloud Registration" Sensors 25, no. 20: 6267. https://doi.org/10.3390/s25206267
APA StyleHu, X., Zeng, Z., Deng, J., Wang, G., Yang, J., & Quan, S. (2025). Curvature-Aware Point-Pair Signatures for Robust Unbalanced Point Cloud Registration. Sensors, 25(20), 6267. https://doi.org/10.3390/s25206267







