Enhanced Neural Architecture for Real-Time Deep Learning Wavefront Sensing
Abstract
1. Introduction
2. Principle of the Method
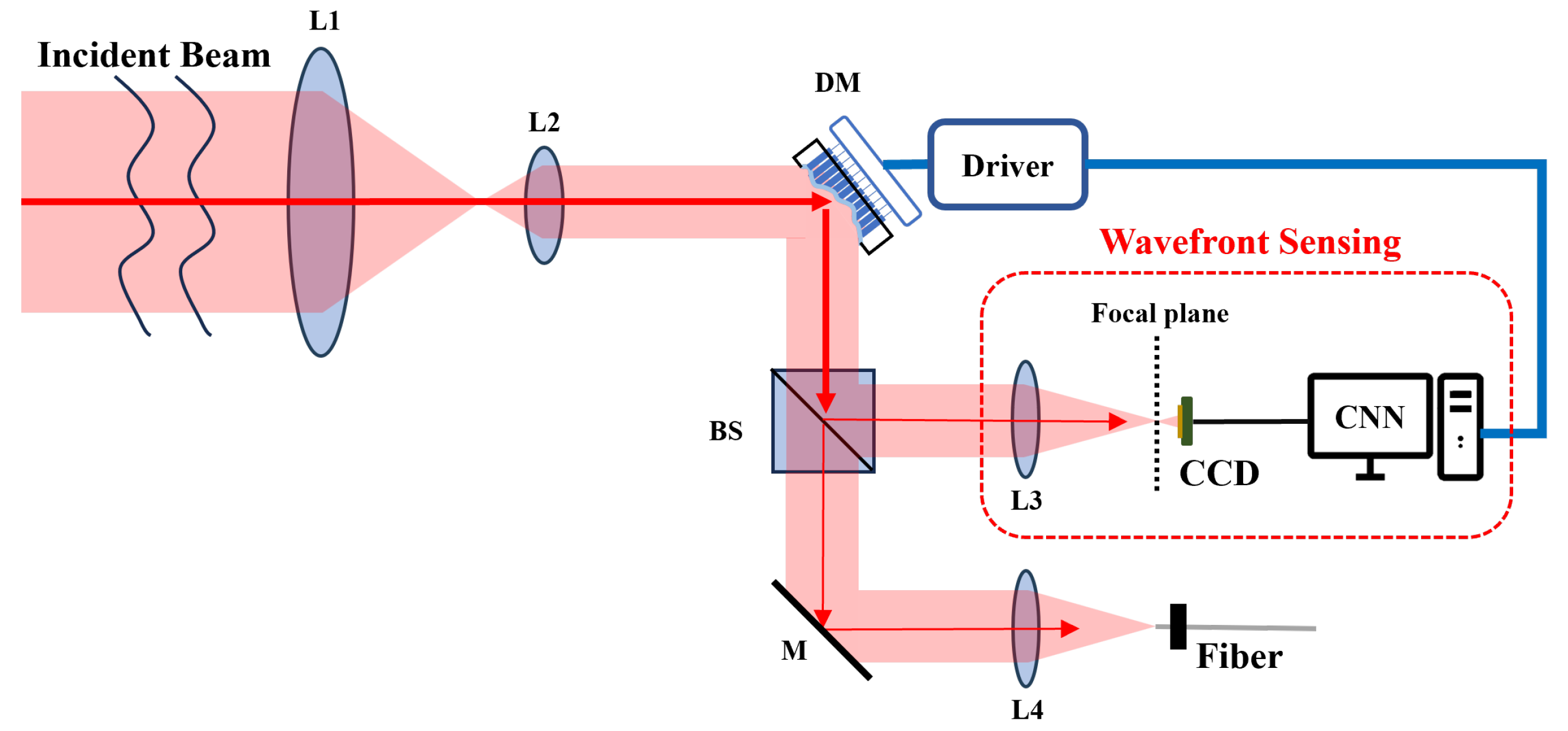
2.1. Configuration
2.2. Problem Modeling
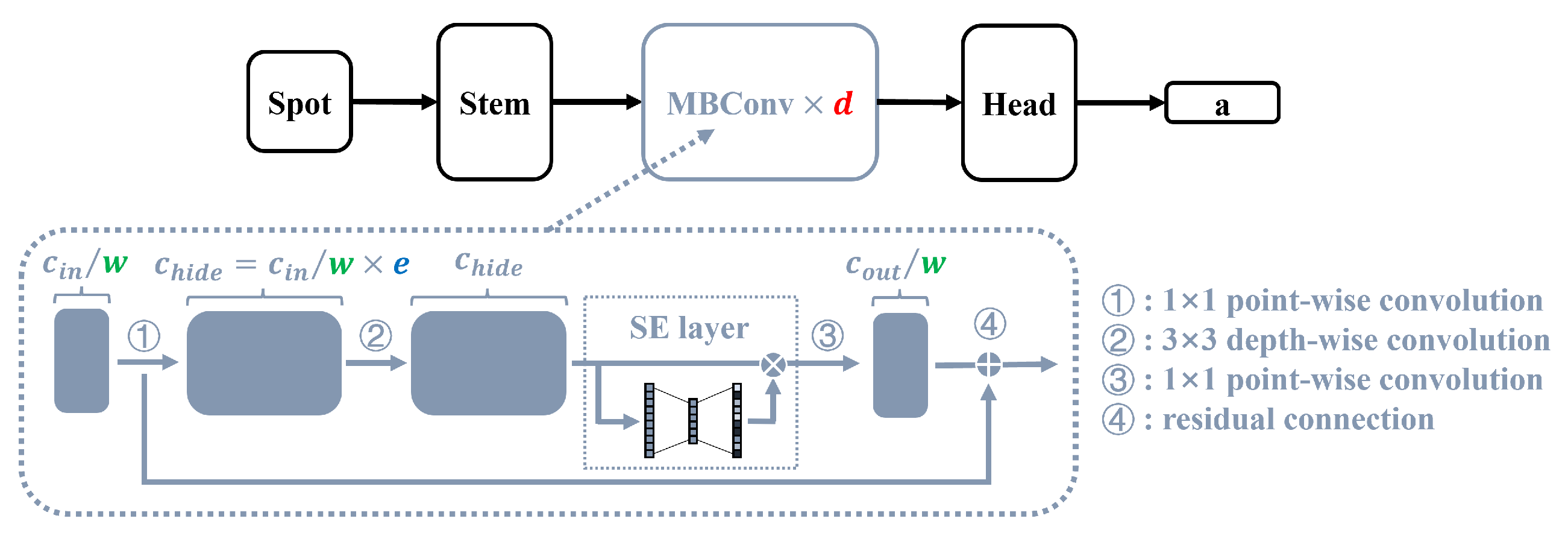
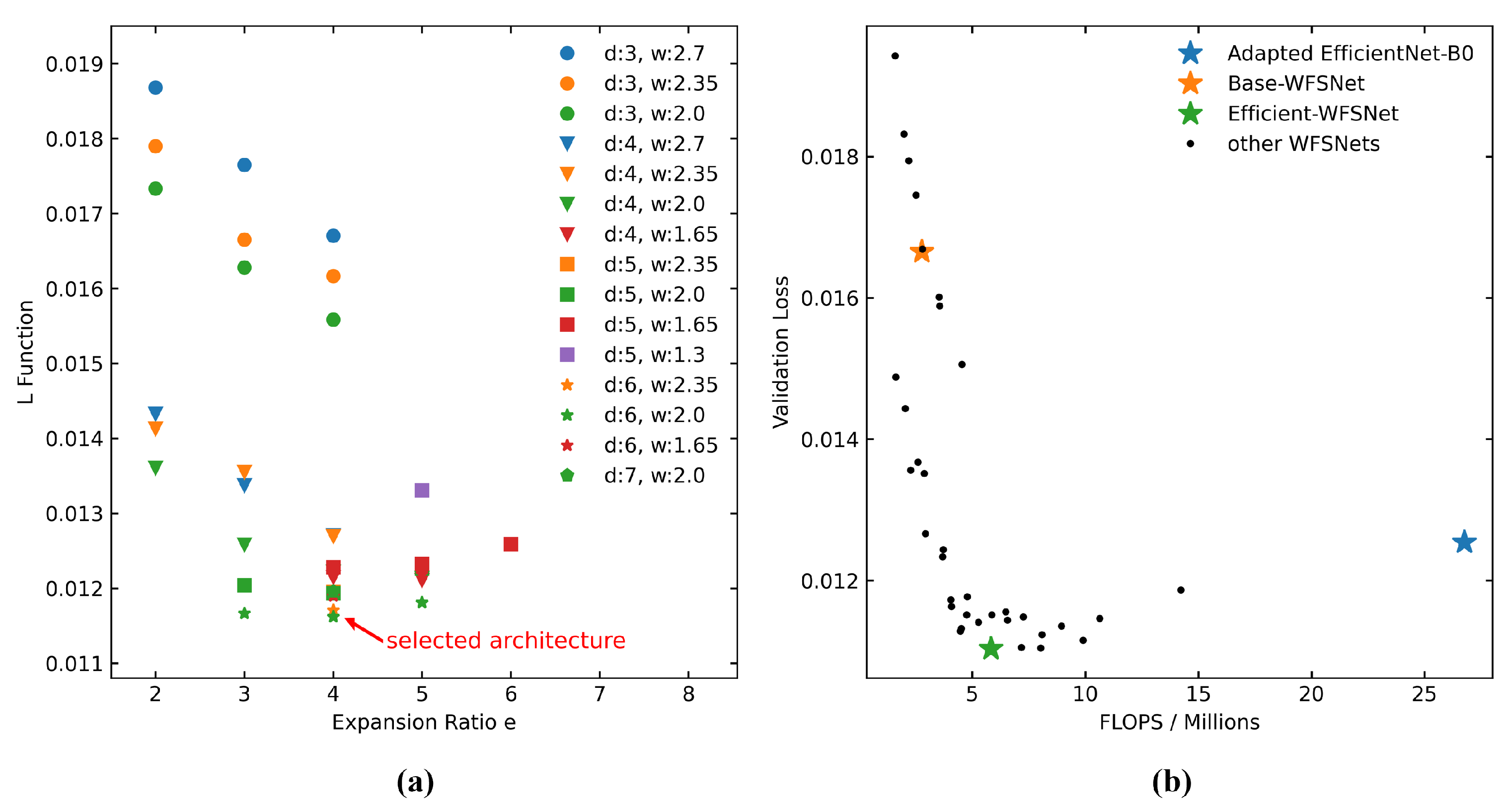
2.3. Model Structure Design and Optimization Method
| Algorithm 1: Gradient-assist grid search |
 |
3. Simulation Modeling
3.1. Sensor Noise
3.2. Wavefront Distortion
3.3. Simulation Setting
4. Validation of the Method
4.1. Model Optimization: EfficientNet Prototype
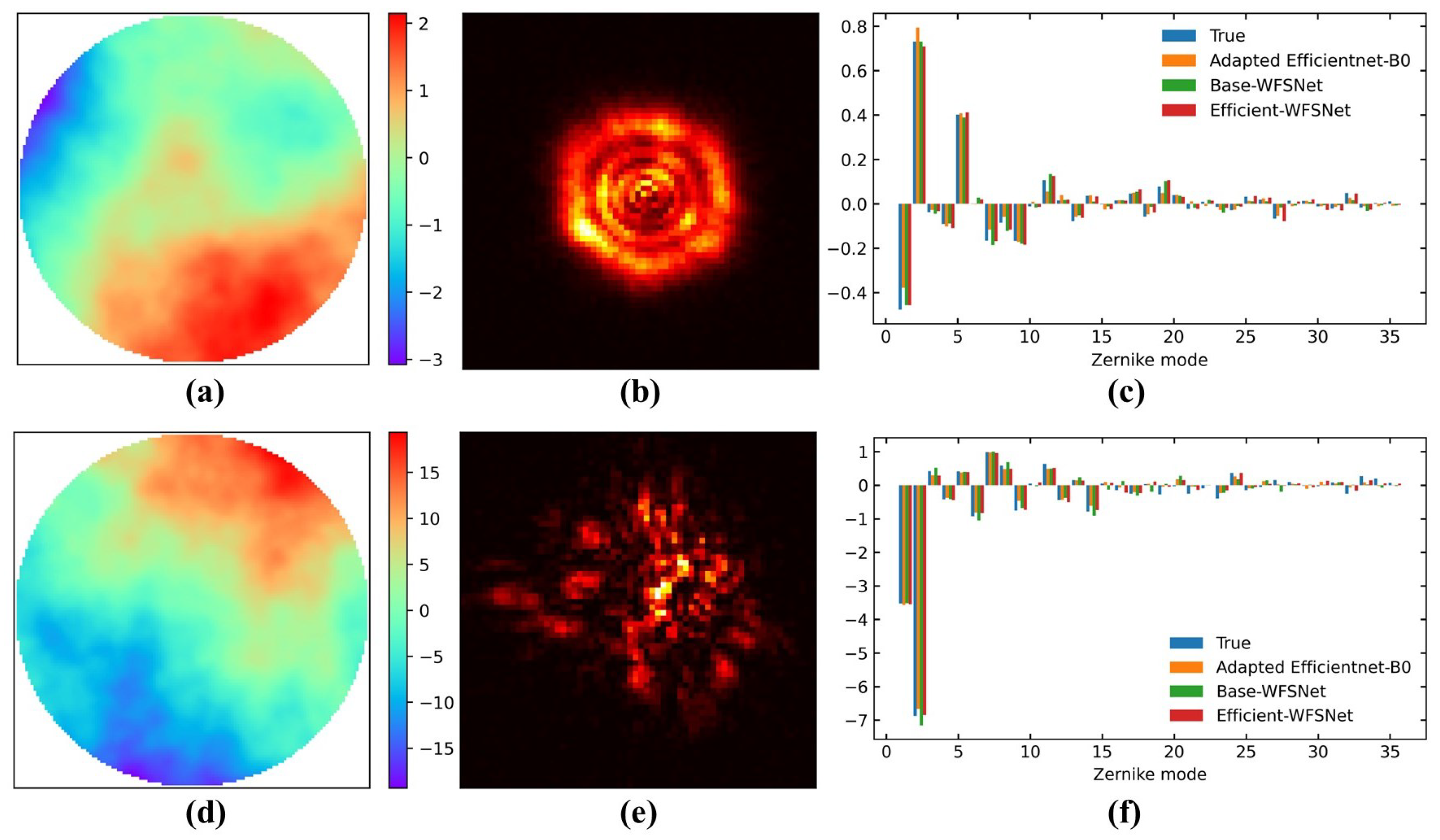
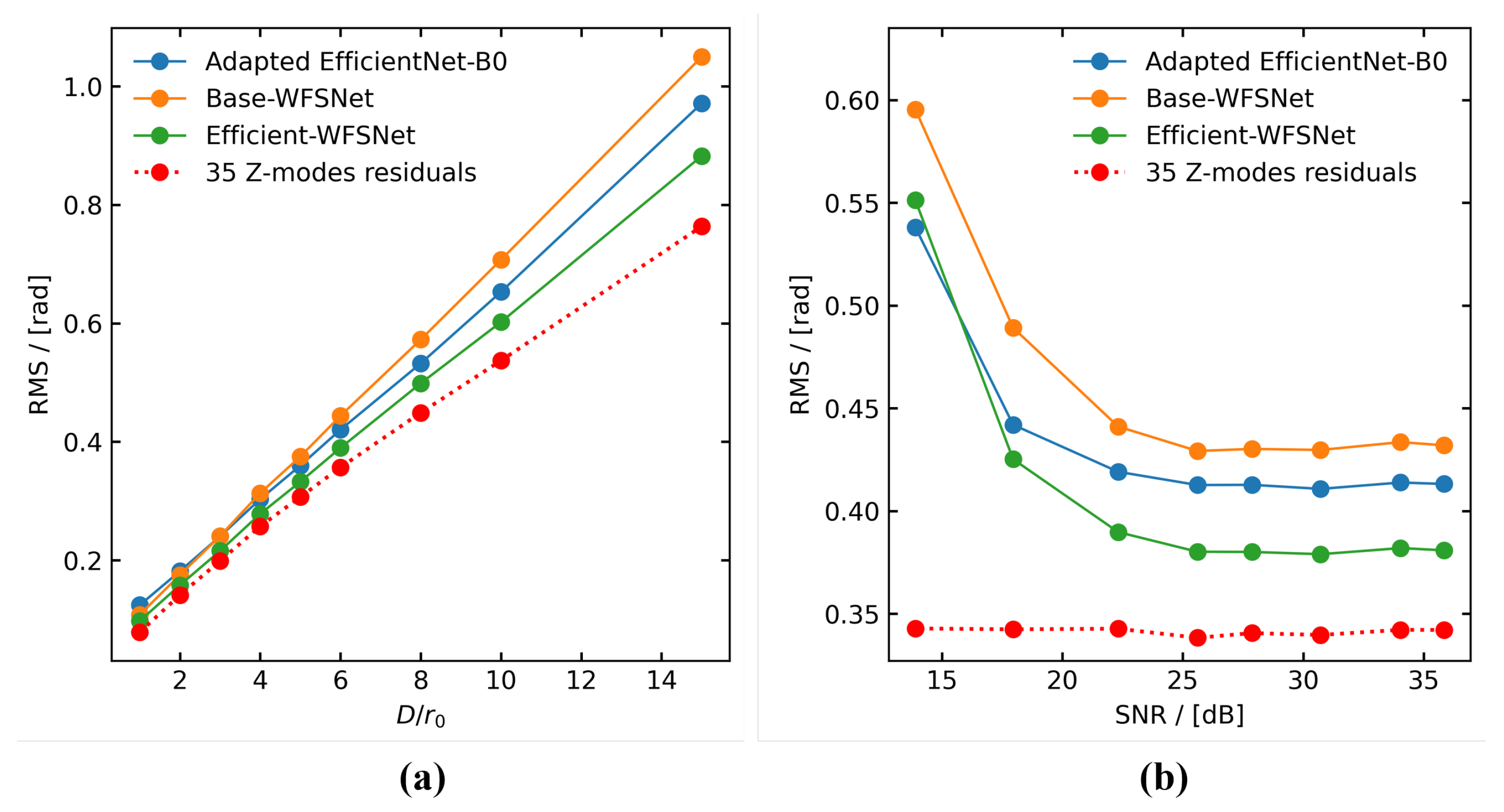
4.2. Robustness of the Method
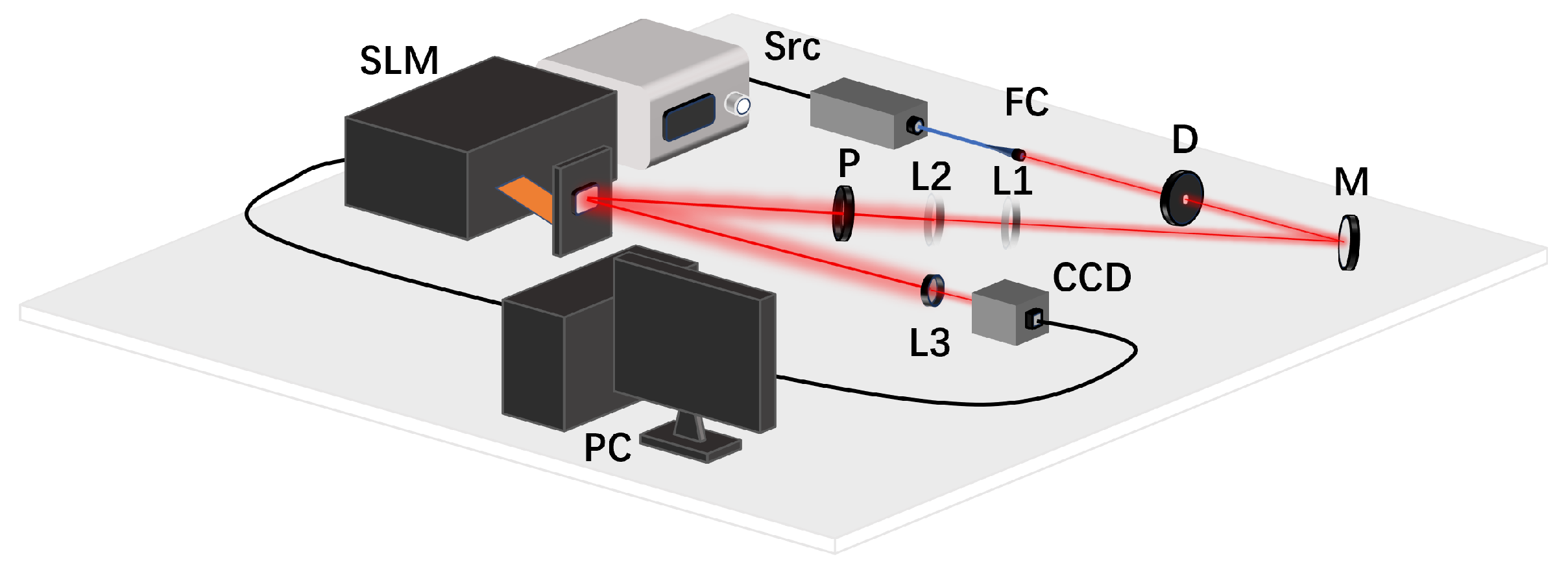
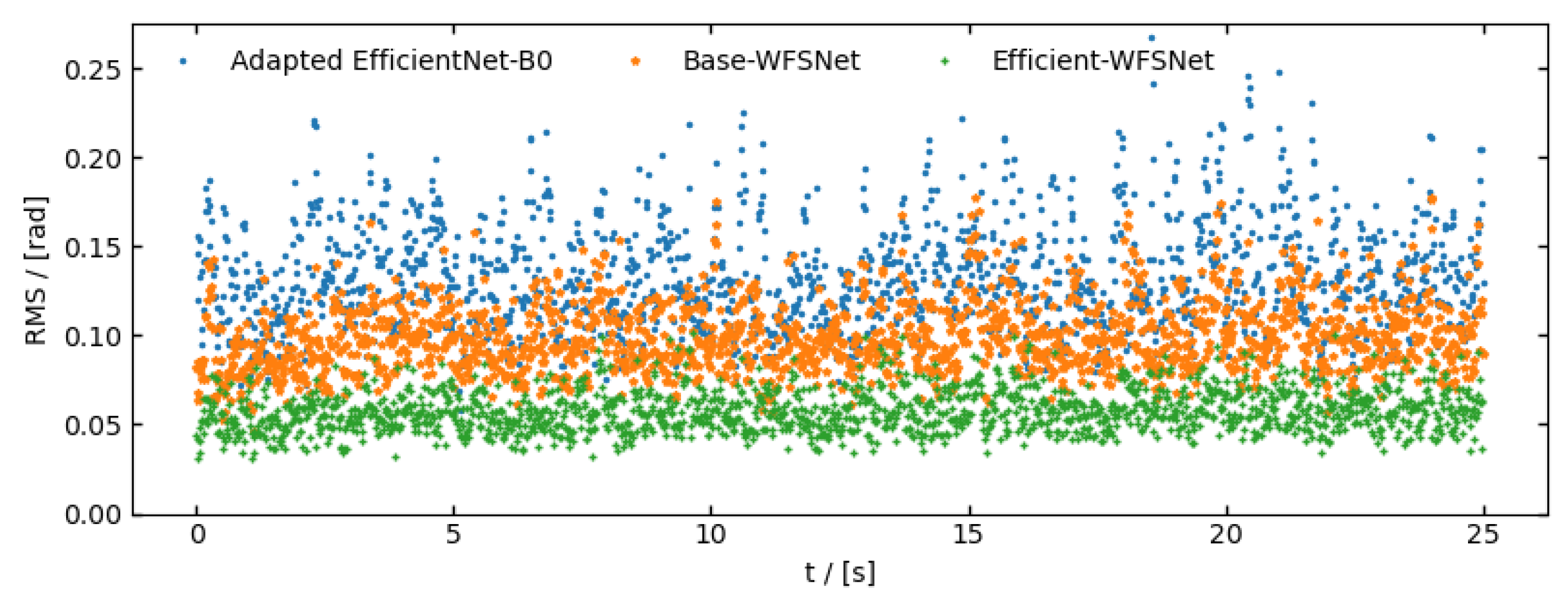
4.3. Experiment Validation
4.4. Disscusion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khalighi, M.A.; Uysal, M. Survey on Free Space Optical Communication: A Communication Theory Perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Flannigan, L.; Yoell, L.; Xu, C.-q. Mid-wave and long-wave infrared transmitters and detectors for optical satellite communications—A review. J. Opt. 2022, 24, 043002. [Google Scholar] [CrossRef]
- Tyson, R.K. Bit-error rate for free-space adaptive optics laser communications. J. Opt. Soc. Am. A 2002, 19, 753–758. [Google Scholar] [CrossRef]
- Huang, J.; Deng, K.; Liu, C.; Zhang, P.; Jiang, D.; Yao, Z. Effectiveness of adaptive optics system in satellite-to-ground coherent optical communication. Opt. Express 2014, 22, 16000–16007. [Google Scholar] [CrossRef]
- Levine, B.M.; Martinsen, E.A.; Wirth, A.; Jankevics, A.; Toledo-Quinones, M.; Landers, F.; Bruno, T.L. Horizontal line-of-sight turbulence over near-ground paths and implications for adaptive optics corrections in laser communications. Appl. Opt. 1998, 37, 4553–4560. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Li, D.; Wang, R.; Jin, C.; Yin, X.; Gao, S.; Mu, Q.; Xuan, L.; Cao, Z. Performance analysis of an adaptive optics system for free-space optics communication through atmospheric turbulence. Sci. Rep. 2018, 8, 1124. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, R.; Wang, Y.; Mao, H.; Xu, G.; Cao, Z.; Yang, X.; Hu, W.; Li, X.; Xuan, L. Extending the detection and correction abilities of an adaptive optics system for free-space optical communication. Opt. Commun. 2021, 482, 126571. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Gao, Z.; Jia, Q. Review of wavefront sensing technology in adaptive optics based on deep learning. High Power Laser Part. Beams 2021, 33, 081001. [Google Scholar] [CrossRef]
- Guo, Y.; Zhong, L.; Min, L.; Wang, J.; Wu, Y.; Chen, K.; Wei, K.; Rao, C. Adaptive optics based on machine learning: A review. Opto-Electron. Adv. 2022, 5, 200082. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Fu, Q.; Nie, Y. Phase-diversity wavefront sensing enhanced by a Fourier-based neural network. Opt. Express 2022, 30, 34396–34410. [Google Scholar] [CrossRef]
- Li, S.; Wang, B.; Wang, X. Untrained physics-driven aberration retrieval network. Opt. Lett. 2024, 49, 4545–4548. [Google Scholar] [CrossRef] [PubMed]
- Paine, S.W.; Fienup, J.R. Machine learning for improved image-based wavefront sensing. Opt. Lett. 2018, 43, 1235–1238. [Google Scholar] [CrossRef] [PubMed]
- Nishizaki, Y.; Valdivia, M.; Horisaki, R.; Kitaguchi, K.; Saito, M.; Tanida, J.; Vera, E. Deep learning wavefront sensing. Opt. Express 2019, 27, 240–251. [Google Scholar] [CrossRef]
- Guo, H.; Xu, Y.; Li, Q.; Du, S.; He, D.; Wang, Q.; Huang, Y. Improved Machine Learning Approach for Wavefront Sensing. Sensors 2019, 19, 3533. [Google Scholar] [CrossRef]
- Wang, M.; Guo, W.; Yuan, X. Single-shot wavefront sensing with deep neural networks for free-space optical communications. Opt. Express 2021, 29, 3465–3478. [Google Scholar] [CrossRef]
- You, J.; Gu, J.; Du, Y.; Wan, M.; Xie, C.; Xiang, Z. Atmospheric Turbulence Aberration Correction Based on Deep Learning Wavefront Sensing. Sensors 2023, 23, 9159. [Google Scholar] [CrossRef]
- Tan, M.; Chen, B.; Pang, R.; Vasudevan, V.; Sandler, M.; Howard, A.; Le, Q.V. MnasNet: Platform-Aware Neural Architecture Search for Mobile. arXiv 2019, arXiv:1807.11626. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2020, arXiv:1905.11946. [Google Scholar]
- Noll, R.J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 1976, 66, 207–211. [Google Scholar] [CrossRef]
- Ke, X. Spatial Optical-Fiber Coupling Technology in Optical-Wireless Communication; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; pp. 259–262. [Google Scholar]
- Faraji, H.; MacLean, W. CCD noise removal in digital images. IEEE Trans. Image Process. 2006, 15, 2676–2685. [Google Scholar] [CrossRef]
- Lane, R.G.; Glindemann, A.; Dainty, J.C. Simulation of a Kolmogorov phase screen. Waves Random Media 1992, 2, 209–224. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media; SPIE Press: Bellingham, WA, USA, 2005. [Google Scholar]
- Comeron, A.; Rubio, J.A.; Belmonte, A.M.; Garcia, E.; Prud’homme, T.; Sodnik, Z.; Connor, C. Propagation experiments in the near infrared along a 150-km path and from stars in the Canarian archipelago. Phys. Eng. Environ. Sci. 2002, 4678, 78–90. [Google Scholar] [CrossRef]
- Israel, D.J.; Edwards, B.L.; Staren, J.W. Laser Communications Relay Demonstration (LCRD) update and the path towards optical relay operations. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Townson, M.; Farley, O.; Orban de Xivry, G.; Osborn, J.; Reeves, A. AOtools: A Python package for adaptive optics modelling and analysis. Opt. Express 2019, 27, 31316. [Google Scholar] [CrossRef] [PubMed]
- Sandler, M.; Howard, A.G.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. arXiv 2019, arXiv:1709.0150. [Google Scholar]
- Assémat, F.; Wilson, R.W.; Gendron, E. Method for simulating infinitely long and non stationary phase screens with optimized memory storage. Opt. Express 2006, 14, 988–999. [Google Scholar] [CrossRef]

| Step | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Start point | |||||
| () | \ | −2.91 | −1.32 | 3.49 | 3.33 |
| () | \ | −33.6 | 2.17 | −2.91 | −3.10 |
| () | \ | 4.68 | −0.620 | 0.157 | 0.869 |
| () | \ | 0.763 | −9.82 | −3.49 | −2.74 |
| () | \ | −0.905 | 2.67 | 0.328 | 1.87 |
| () | \ | −3.56 | 0.410 | −1.09 | −0.435 |
| Adjacent best point | |||||
| Adjacent best L () | 1.223 | 1.193 | 1.211 | 1.162 | 1.162 |
| Params | Flops | Inference Time (ms) | Training Loss (rad) | Validation Loss (rad) | Test Loss (rad) | Test RMS (rad) | |
|---|---|---|---|---|---|---|---|
| Adapted EfficientNet-B0 | 324,644 | 26.75 m | 5.315 | 0.2261 | 0.2278 | 0.2307 | 0.4207 |
| Base-WFSNet | 13,869 | 2.77 m | 0.122 | 0.2681 | 0.2713 | 0.2733 | 0.4430 |
| Efficient-WFSNet | 67,766 | 5.83 m | 0.204 | 0.1756 | 0.1774 | 0.1793 | 0.3906 |
| Training Loss (rad) | Test Loss (rad) | Test RMS (rad) | |
|---|---|---|---|
| Adapted EfficientNet-B0 | 0.0510 | 0.1325 | 0.2179 |
| Base-WFSNet | 0.0651 | 0.0991 | 0.2032 |
| Efficient-WFSNet | 0.0399 | 0.0580 | 0.1918 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, Q.; Tan, L.; Ma, J.; Chen, N. Enhanced Neural Architecture for Real-Time Deep Learning Wavefront Sensing. Sensors 2025, 25, 480. https://doi.org/10.3390/s25020480
Li J, Liu Q, Tan L, Ma J, Chen N. Enhanced Neural Architecture for Real-Time Deep Learning Wavefront Sensing. Sensors. 2025; 25(2):480. https://doi.org/10.3390/s25020480
Chicago/Turabian StyleLi, Jianyi, Qingfeng Liu, Liying Tan, Jing Ma, and Nanxing Chen. 2025. "Enhanced Neural Architecture for Real-Time Deep Learning Wavefront Sensing" Sensors 25, no. 2: 480. https://doi.org/10.3390/s25020480
APA StyleLi, J., Liu, Q., Tan, L., Ma, J., & Chen, N. (2025). Enhanced Neural Architecture for Real-Time Deep Learning Wavefront Sensing. Sensors, 25(2), 480. https://doi.org/10.3390/s25020480






