Novel Fabry-Pérot Filter Structures for High-Performance Multispectral Imaging with a Broadband from the Visible to the Near-Infrared
Abstract
1. Introduction
2. Design and Principle
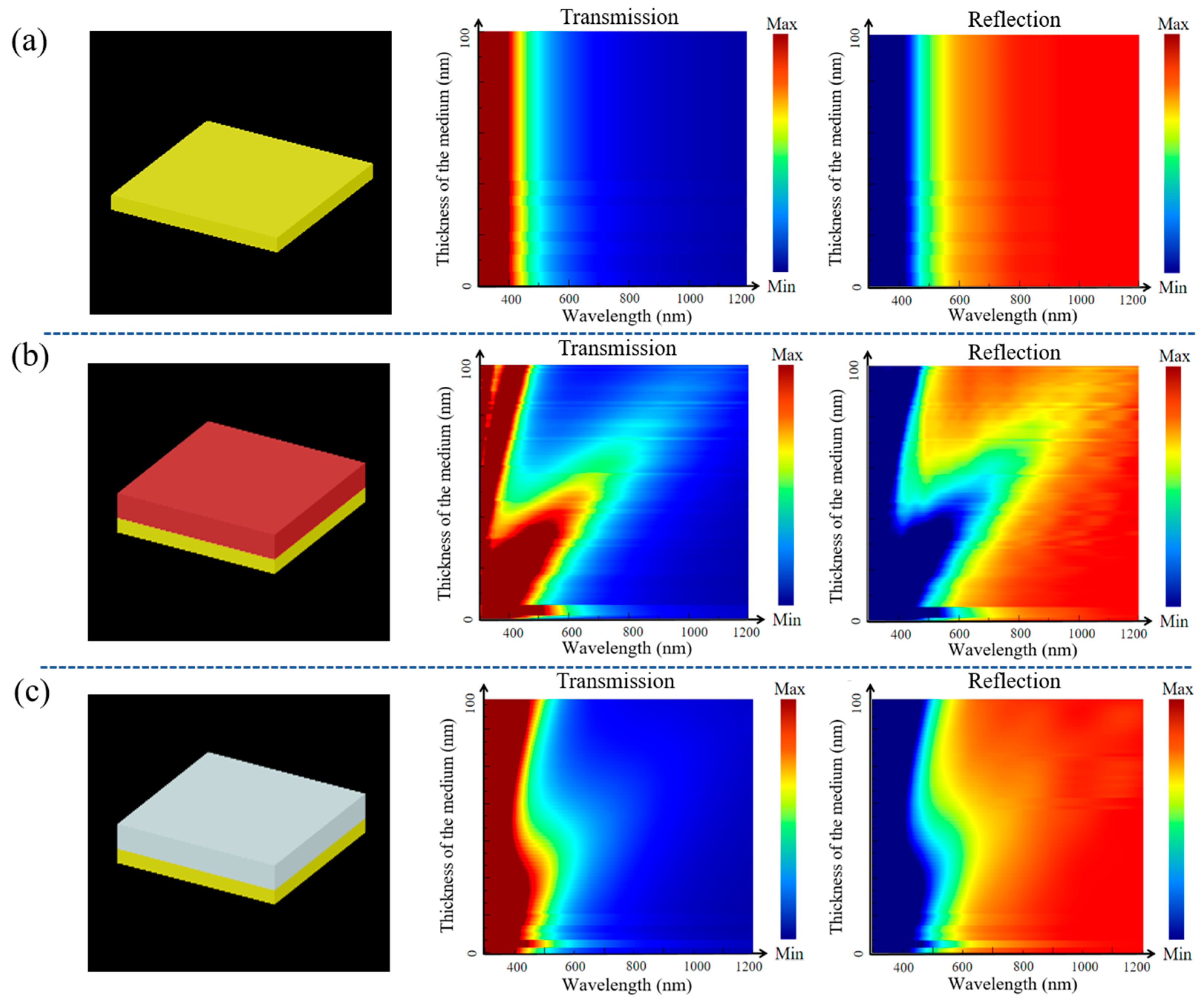
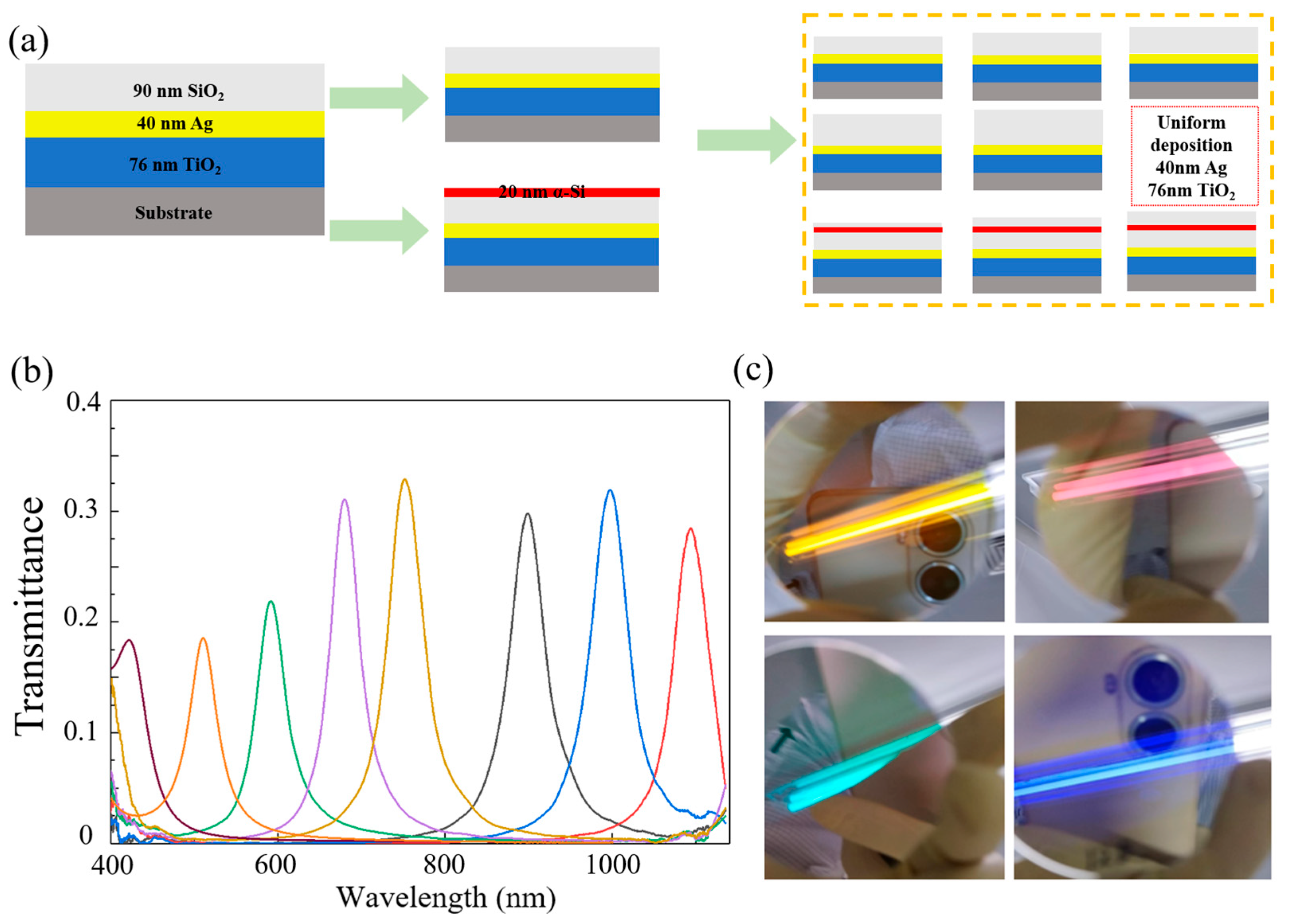
2.1. Construction of the Resonant Cavity
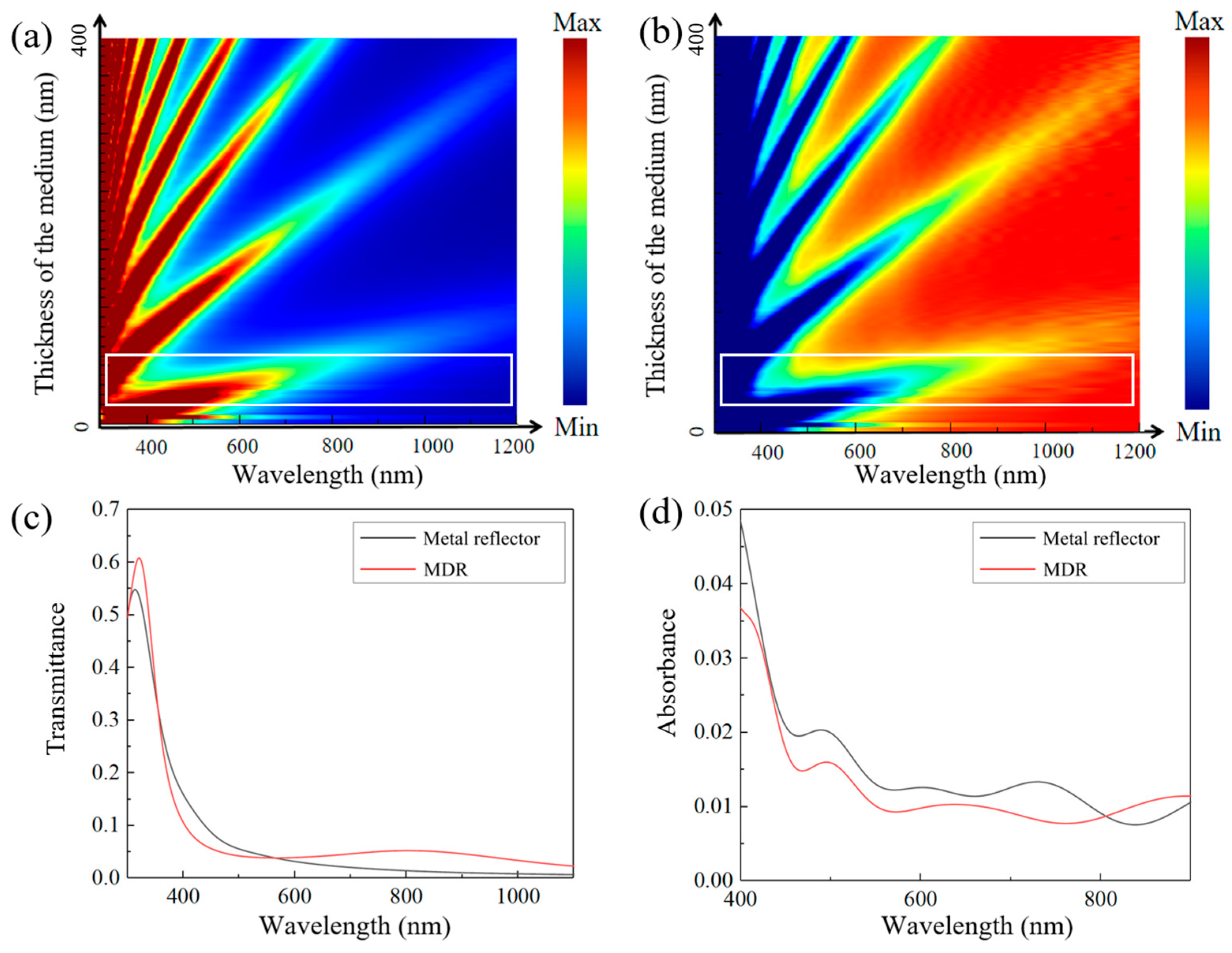
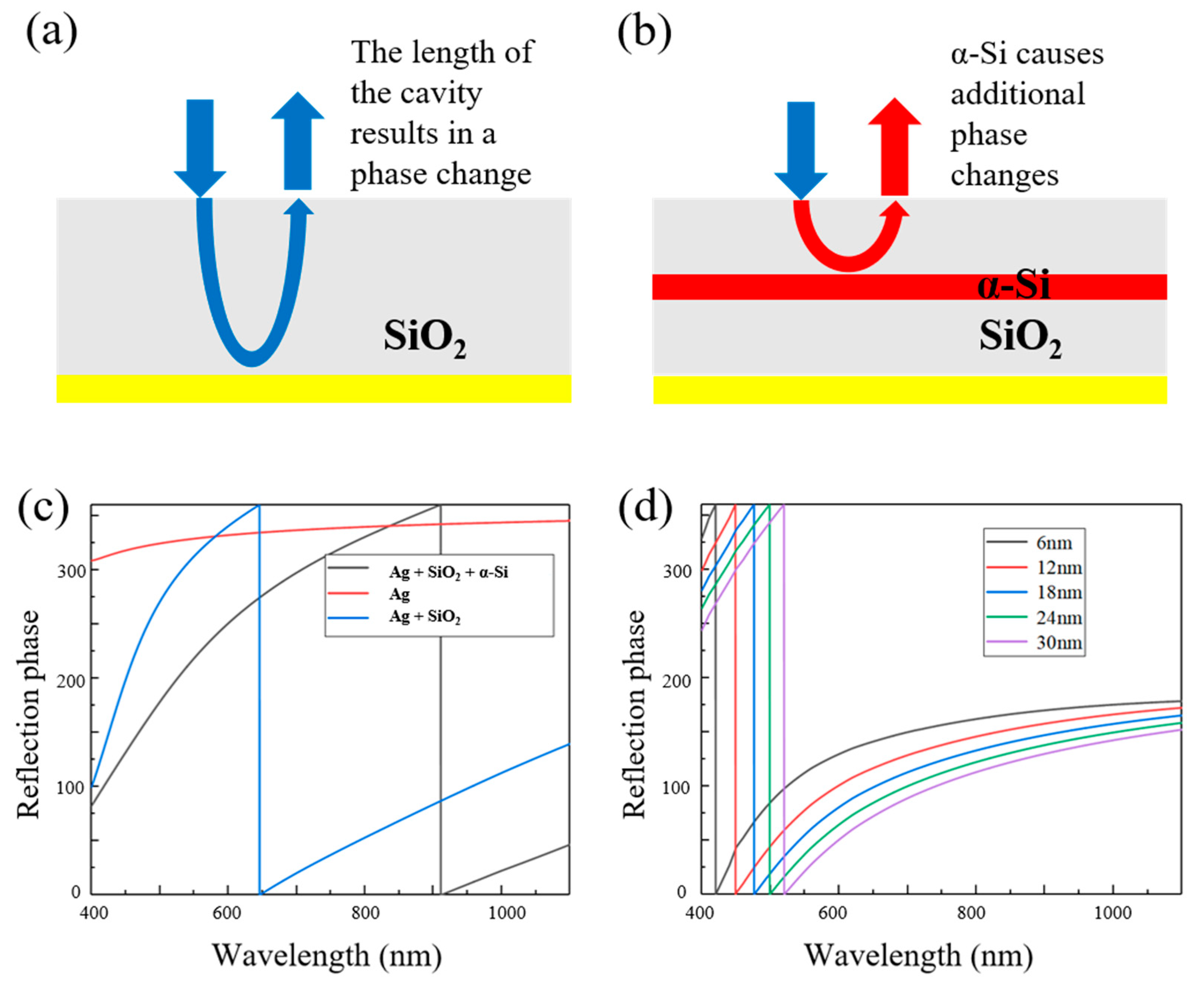
2.2. Elimination of the Influence of Secondary Transmission Peaks
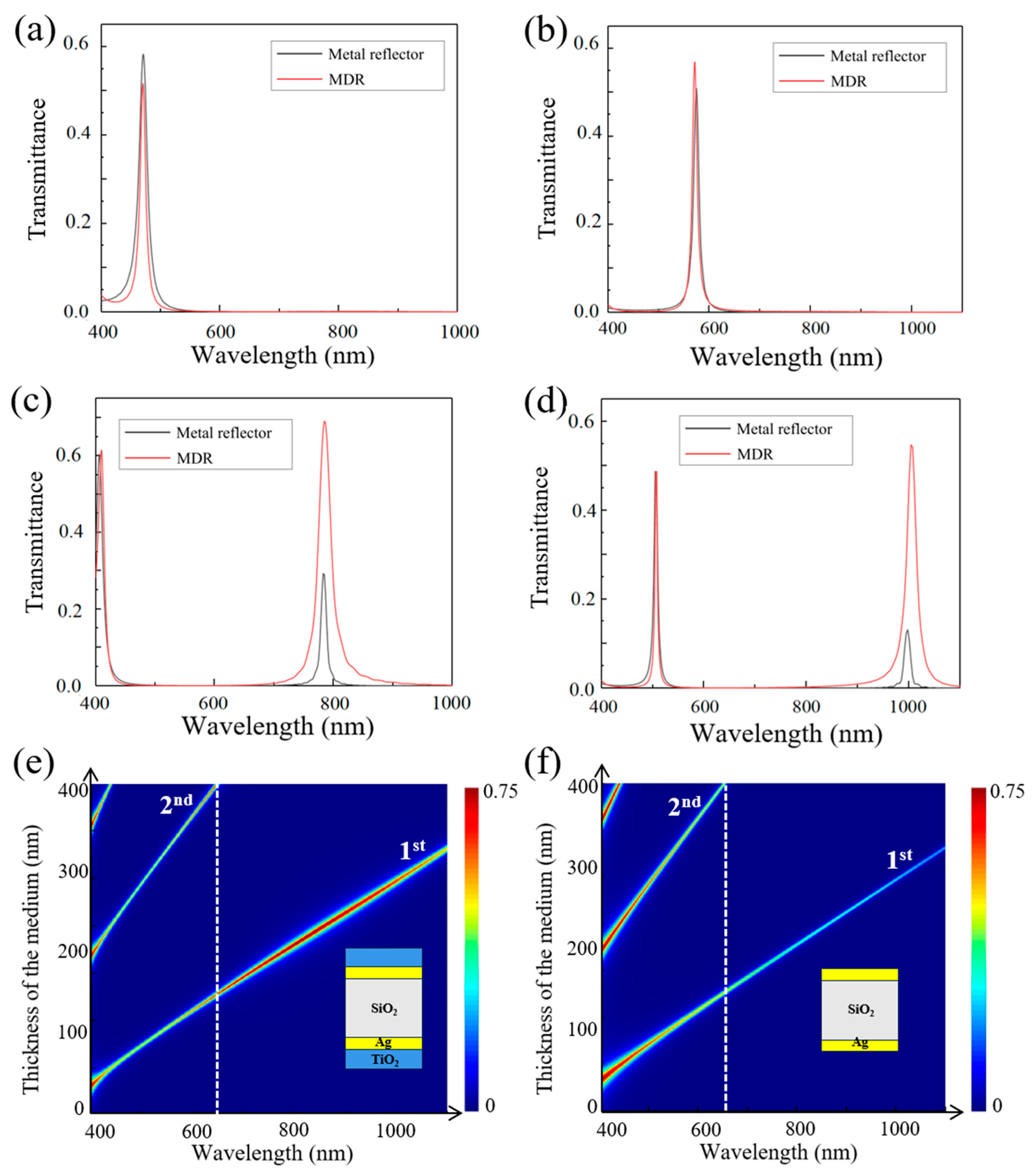
2.3. Design of Multi-Channel Filtering Structure
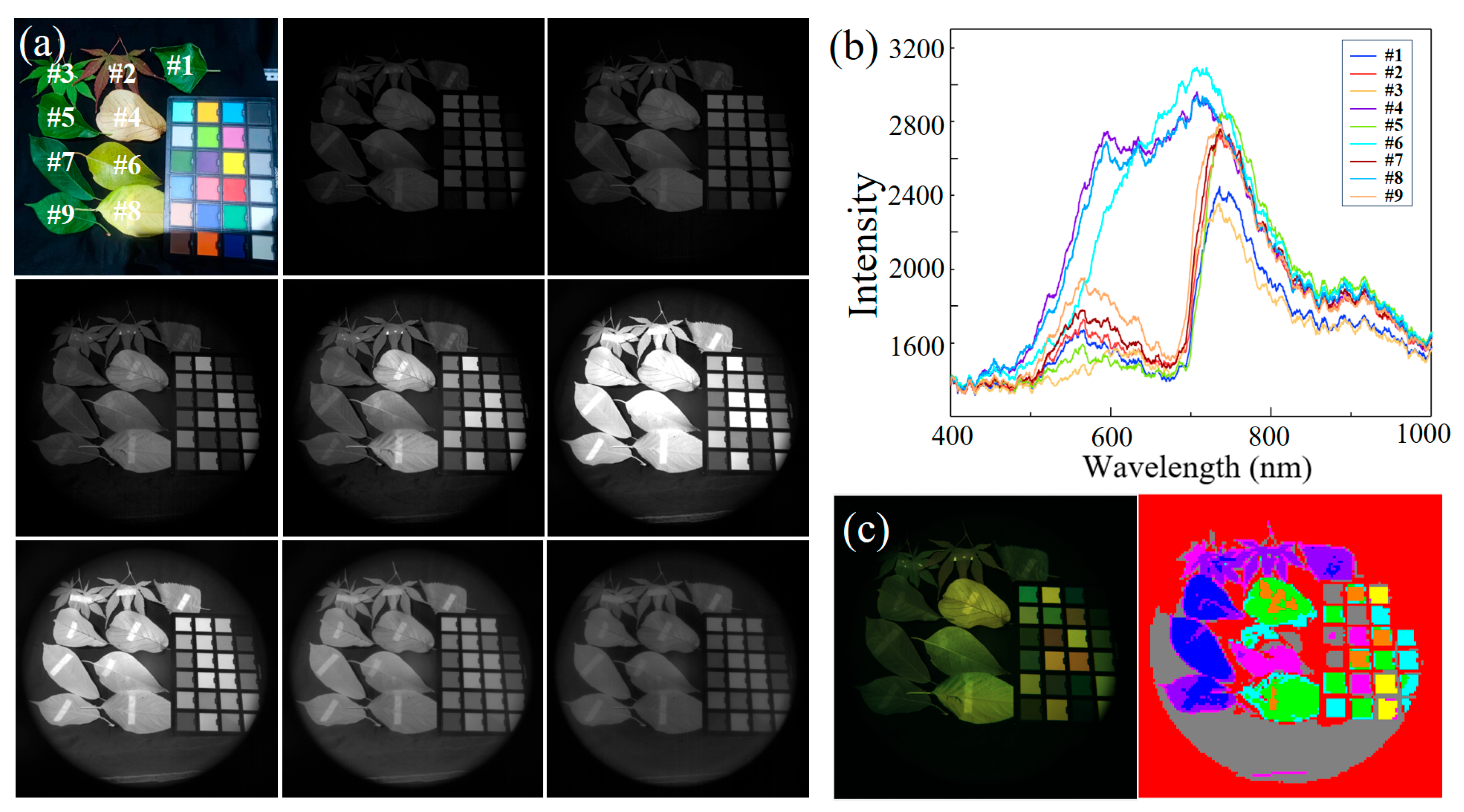
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, X.; Yue, T.; Lin, X.; Lin, S.; Yuan, X.; Dai, Q.H.; Carin, L.; Brady, D.J. Computational Snapshot Multispectral Cameras: Toward dynamic capture of the spectral world. IEEE Signal Process. Mag. 2016, 33, 95–108. [Google Scholar] [CrossRef]
- Dyer, J.; Verri, G.; Cupitt, J. Multispectral Imaging in Reflectance and Photo-induced Luminescence modes: A User Manual; The British Museum: London, UK, 2013. [Google Scholar]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Durini, D. High Performance Silicon Imaging: Fundamentals and Applications of CMOS and CCD sensors; Woodhead Publishing: Sawston, UK, 2014. [Google Scholar]
- Lapray, P.J.; Wang, X.B.; Thomas, J.B.; Gouton, P. Multispectral Filter Arrays: Recent Advances and Practical Implementation. Sensors 2014, 14, 21626–21659. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, B.; Wang, X. Strategies for high performance and scalable on-chip spectrometers. J. Phys. Photonics 2021, 3, 012006. [Google Scholar] [CrossRef]
- Sawyer, T.W.; Taylor-Williams, M.; Tao, R.; Xia, R.Q.; Williams, C.; Bohndiek, S.E. Opti-MSFA: A toolbox for generalized design and optimization of multispectral filter arrays. Opt. Express 2022, 30, 7591–7611. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H.R. The design and evaluation of a generic method for generating mosaicked multispectral filter arrays. IEEE Trans. Image Process. 2006, 15, 2780–2791. [Google Scholar] [CrossRef]
- Bigas, M.; Cabruja, E.; Forest, J.; Salvi, J. Review of CMOS image sensors. Microelectron. J. 2006, 37, 433–451. [Google Scholar] [CrossRef]
- Moser, N.; Lande, T.S.; Toumazou, C.; Georgiou, P. ISFETs in CMOS and Emergent Trends in Instrumentation: A Review. IEEE Sens. J. 2016, 16, 6496–6514. [Google Scholar] [CrossRef]
- Lee, T.; Lee, C.; Oh, D.K.; Badloe, T.; Ok, J.G.; Rho, J. Scalable and High-Throughput Top-Down Manufacturing of Optical Metasurfaces. Sensors 2020, 20, 4108. [Google Scholar] [CrossRef] [PubMed]
- Xiang, J.W.; Song, M.T.; Zhang, Y.; Kruschwitz, J.; Cardenas, J. Ultrabroadband, High Color Purity Multispectral Color Filter Arrays. ACS Photonics 2024, 11, 1163–1172. [Google Scholar] [CrossRef]
- Yu, X.C.; Su, Y.; Song, X.K.; Wang, F.; Gao, B.; Yu, Y.T. Batch fabrication and compact integration of customized multispectral filter arrays towards snapshot imaging. Opt. Express 2021, 29, 30655–30665. [Google Scholar] [CrossRef]
- Luo, X.G.; Tsai, D.P.; Gu, M.; Hong, M.H. Subwavelength interference of light on structured surfaces. Adv. Opt. Photonics 2018, 10, 757–842. [Google Scholar] [CrossRef]
- He, X.; Beckett, P.; Unnithan, R. Multispectral Image Sensors Using Metasurfaces; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Quaranta, G.; Basset, G.; Martin, O.J.F.; Gallinet, B. Recent Advances in Resonant Waveguide Gratings. Laser Photonics Rev. 2018, 12, 1800017. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, Z.H.; Zhou, W.J.; Li, S.; Liu, Z.R.; Zhao, X.Y.; Wu, X. High-Q guided mode resonance sensors based on shallow sub-wavelength grating structures. Nanotechnology 2020, 31, 325501. [Google Scholar] [CrossRef]
- Liu, Z. Design, fabrication, and characterization of guided-mode resonance filters and waveguide-grating couplers. Optik 2000, 124, 4805–4807. [Google Scholar]
- Fattal, D.; Li, J.J.; Peng, Z.; Fiorentino, M.; Beausoleil, R.G. Flat dielectric grating reflectors with focusing abilities. Nat. Photonics 2010, 4, 466–470. [Google Scholar] [CrossRef]
- Othonos, A. Fiber Bragg gratings. Rev. Sci. Instrum. 1997, 68, 4309–4341. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, C.G.; Park, Y.B.; Guo, L.J. Thin-Metal-Film-Based Transparent Conductors: Material Preparation, Optical Design, and Device Applications. Adv. Opt. Mater. 2021, 9, 2001298. [Google Scholar] [CrossRef]
- Williams, C.; Gordon, G.S.D.; Wilkinson, T.D.; Bohndiek, S.E. Grayscale-to-Color: Scalable Fabrication of Custom Multispectral Filter Arrays. ACS Photonics 2019, 6, 3132–3141. [Google Scholar] [CrossRef]
- Jung, I.; Kim, H.; Ju, S.; Kim, D.; Kwak, H.; Wang, H.; Jay Guo, L.; Park, H.J.; Ok, J.G.; Lee, K.T. Tailoring resonant modes in dual cavities for transmissive structural colors with high brightness and high purity. Opt. Express 2024, 32, 26136–26146. [Google Scholar] [CrossRef]
- Jung, I.; Kim, H.; Lim, D.; Kim, D.; Kang, C.; Ju, S.; Ok, J.G.; Lee, K.T.; Park, D.H. Flexible transmissive colors with enhanced purity and brightness through overlapping multi-cavity resonances. Opt. Lett 2024, 49, 7214–7217. [Google Scholar] [CrossRef]
- Yako, M.; Yamaoka, Y.; Kiyohara, T.; Hosokawa, C.; Noda, A.; Tack, K.; Spooren, N.; Hirasawa, T.; Ishikawa, A. Video-rate hyperspectral camera based on a CMOS-compatible random array of Fabry-Perot filters. Nat. Photonics 2023, 17, 218–223. [Google Scholar] [CrossRef]
- Caglar, M.; Caglar, Y.; Ilican, S. The determination of the thickness and optical constants of the ZnO crystalline thin film by using envelope method. J. Optoelectron. Adv. Mater. 2006, 8, 1410–1413. [Google Scholar]
- Kim, D.; Jung, I.; Ju, S.; Kang, C.; Lim, D.; Lee, M.; Ok, J.G.; Park, H.J.; Lee, K.T. Optical interference control for selectively suppressing higher-order modes in all-dielectric tri-layered structures for reflective RGB colors. Opt. Lett. 2025, 50, 1779–1782. [Google Scholar] [CrossRef]
- Macleod, H.A.; Macleod, H.A. Thin-Film Optical Filters; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Li, Z.Y.; Butun, S.; Aydin, K. Large-Area, Lithography-Free Super Absorbers and Color Filters at Visible Frequencies Using Ultrathin Metallic Films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
- Kats, M.A.; Capasso, F. Optical absorbers based on strong interference in ultra-thin films. Laser Photonics Rev. 2016, 10, 735–749. [Google Scholar] [CrossRef]
- Barrett, J.L.; Nyhof, M. Culture, Spreading Non-natural Concepts: The Role of Intuitive Conceptual Structures in Memory and Transmission of Cultural Materials. J. Cogn. Cult. 2001, 1, 69–100. [Google Scholar] [CrossRef]
- Berning, P.H.; Turner, A. Induced transmission in absorbing films applied to band pass filter design. J. Opt. Soc. Am. 1957, 47, 230–239. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, S.; Ning, Y.; Dun, X.; Dong, S.; Wang, Z.; Cheng, X. Grayscale-patterned integrated multilayer-metal-dielectric microcavities for on-chip multi/hyperspectral imaging in the extended visible bandwidth. Opt. Express 2023, 31, 14027–14036. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Mittra, R. FDTD Modeling of Metamaterials: Theory and Applications; Artech House: London, UK, 2008. [Google Scholar]
- Akgul, F.A.; Akgul, G.; Yildirim, N.; Unalan, H.E.; Turan, R. Influence of thermal annealing on microstructural, morphological, optical properties and surface electronic structure of copper oxide thin films. Mater. Chem. Phys. 2014, 147, 987–995. [Google Scholar] [CrossRef]
- Li, B.H.; Sanders, C.E.; McIlhargey, J.; Cheng, F.; Gu, C.; Zhang, G.; Wu, K.; Kim, J.; Mousavi, S.H.; Khanikaev, A.B.; et al. Contrast between surface plasmon polariton-mediated extraordinary optical transmission behavior in epitaxial and polycrystalline Ag films in the mid- and far-infrared regimes. Nano Lett. 2012, 12, 6187–6191. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhang, W.; Zhang, J.; Xu, L.; Yang, M.; Jiang, S.; Ma, D.; Jiao, Q.; Tan, X. Dual-Channel Electrostatically Actuated MEMS Fabry–Perot Filtering Module for Near-Infrared Spectroscopic Detection. Adv. Mater. Technol. 2024, 10, 2401503. [Google Scholar] [CrossRef]
- Straniero, N.; Degallaix, J.; Flaminio, R.; Pinard, L.; Cagnoli, G. Realistic loss estimation due to the mirror surfaces in a 10 meters-long high finesse Fabry-Perot filter-cavity. Opt. Express 2015, 23, 21455–21476. [Google Scholar] [CrossRef]
- Martinu, L.; Poitras, D. Plasma deposition of optical films and coatings: A review. J. Vac. Sci. Technol. A 2000, 18, 2619–2645. [Google Scholar] [CrossRef]
- Stokes, K.; Clark, K.; Odetade, D.; Hardy, M.; Oppenheimer, P.G. Advances in lithographic techniques for precision nanostructure fabrication in biomedical applications. Discov. Nano 2023, 18, 153. [Google Scholar] [CrossRef] [PubMed]




| Data Source | Data Type | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Simulation | Central Wavelength (nm) | 415 | 490 | 571 | 655 | 713 | 784 | 888 | 982 |
| Peak transmission (%) | 59 | 53 | 57 | 63 | 64 | 55 | 59 | 58 | |
| FWHM (nm) | 20 | 14 | 14 | 18 | 19 | 22 | 24 | 22 | |
| Experiment | Central Wavelength (nm) | 421 | 509 | 590 | 676 | 755 | 898 | 988 | 1094 |
| Peak transmission (%) | 18 | 18 | 22 | 31 | 33 | 28 | 31 | 28 | |
| FWHM (nm) | 47 | 41 | 40 | 40 | 46 | 45 | 45 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Wang, T.; Chen, L.; Wang, S.; Li, C.; Xiao, F.; Liu, Y.; Yu, W. Novel Fabry-Pérot Filter Structures for High-Performance Multispectral Imaging with a Broadband from the Visible to the Near-Infrared. Sensors 2025, 25, 6123. https://doi.org/10.3390/s25196123
Gao B, Wang T, Chen L, Wang S, Li C, Xiao F, Liu Y, Yu W. Novel Fabry-Pérot Filter Structures for High-Performance Multispectral Imaging with a Broadband from the Visible to the Near-Infrared. Sensors. 2025; 25(19):6123. https://doi.org/10.3390/s25196123
Chicago/Turabian StyleGao, Bo, Tianxin Wang, Lu Chen, Shuai Wang, Chenxi Li, Fajun Xiao, Yanyan Liu, and Weixing Yu. 2025. "Novel Fabry-Pérot Filter Structures for High-Performance Multispectral Imaging with a Broadband from the Visible to the Near-Infrared" Sensors 25, no. 19: 6123. https://doi.org/10.3390/s25196123
APA StyleGao, B., Wang, T., Chen, L., Wang, S., Li, C., Xiao, F., Liu, Y., & Yu, W. (2025). Novel Fabry-Pérot Filter Structures for High-Performance Multispectral Imaging with a Broadband from the Visible to the Near-Infrared. Sensors, 25(19), 6123. https://doi.org/10.3390/s25196123






