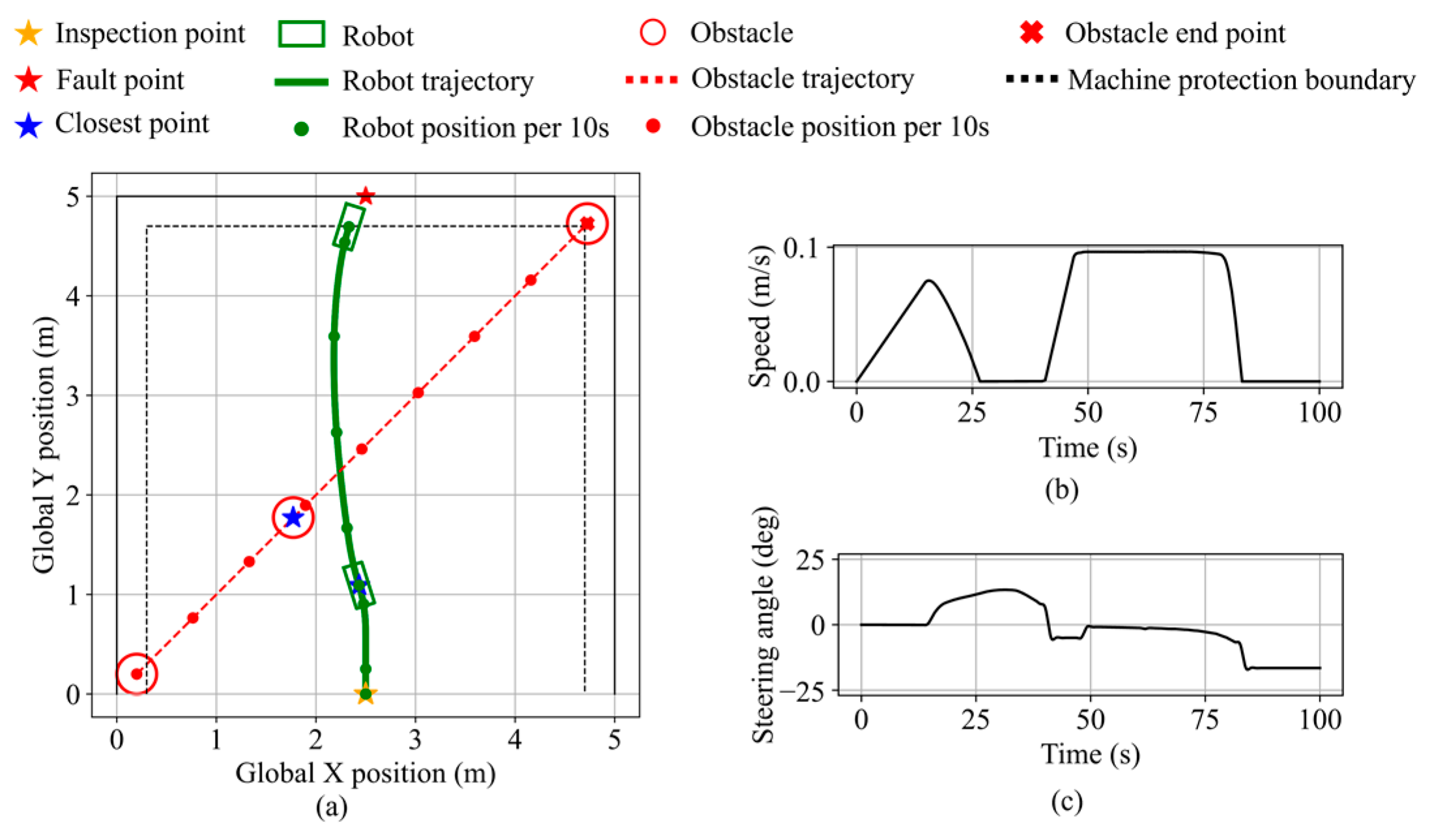
Figure 1.
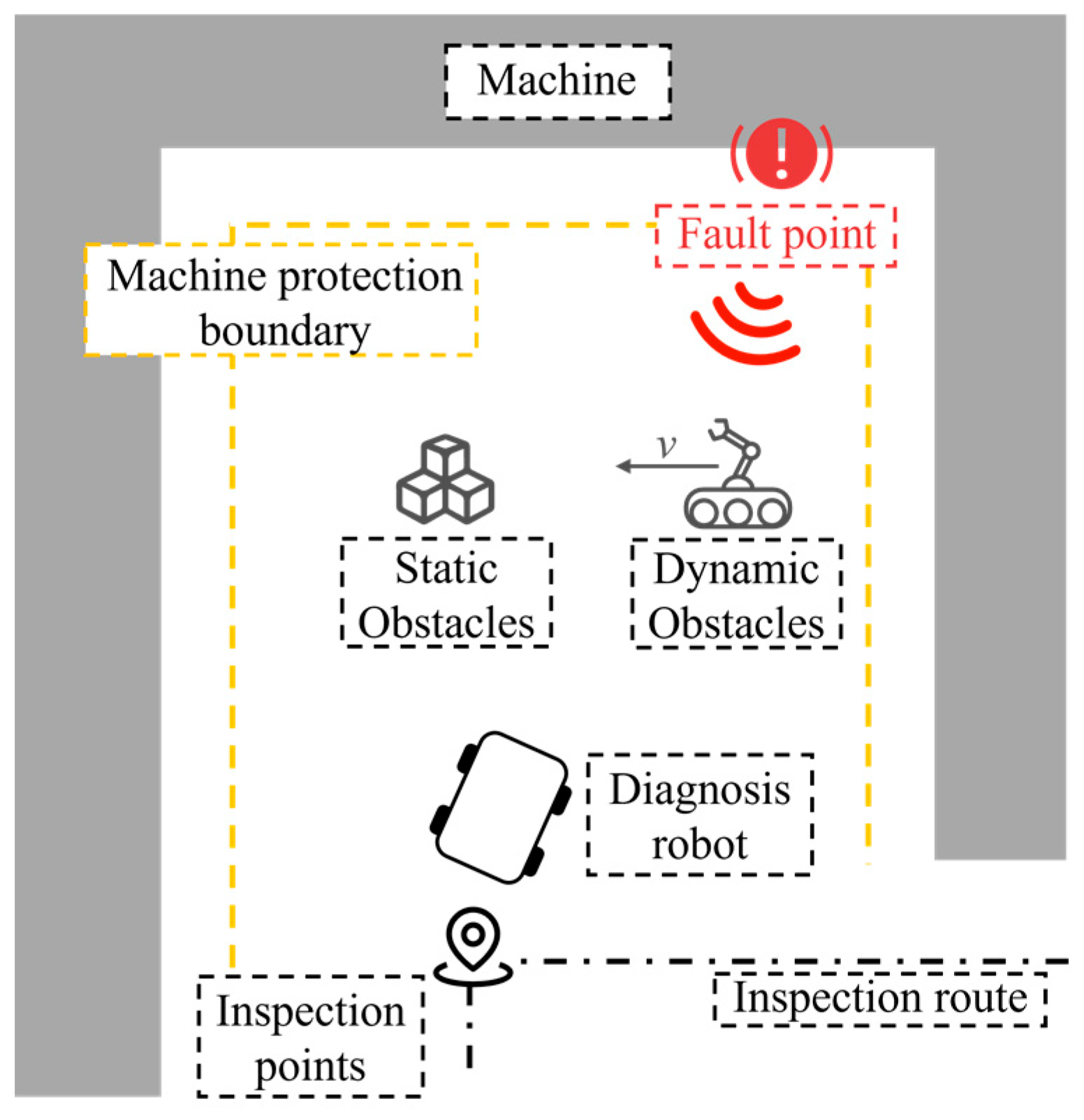
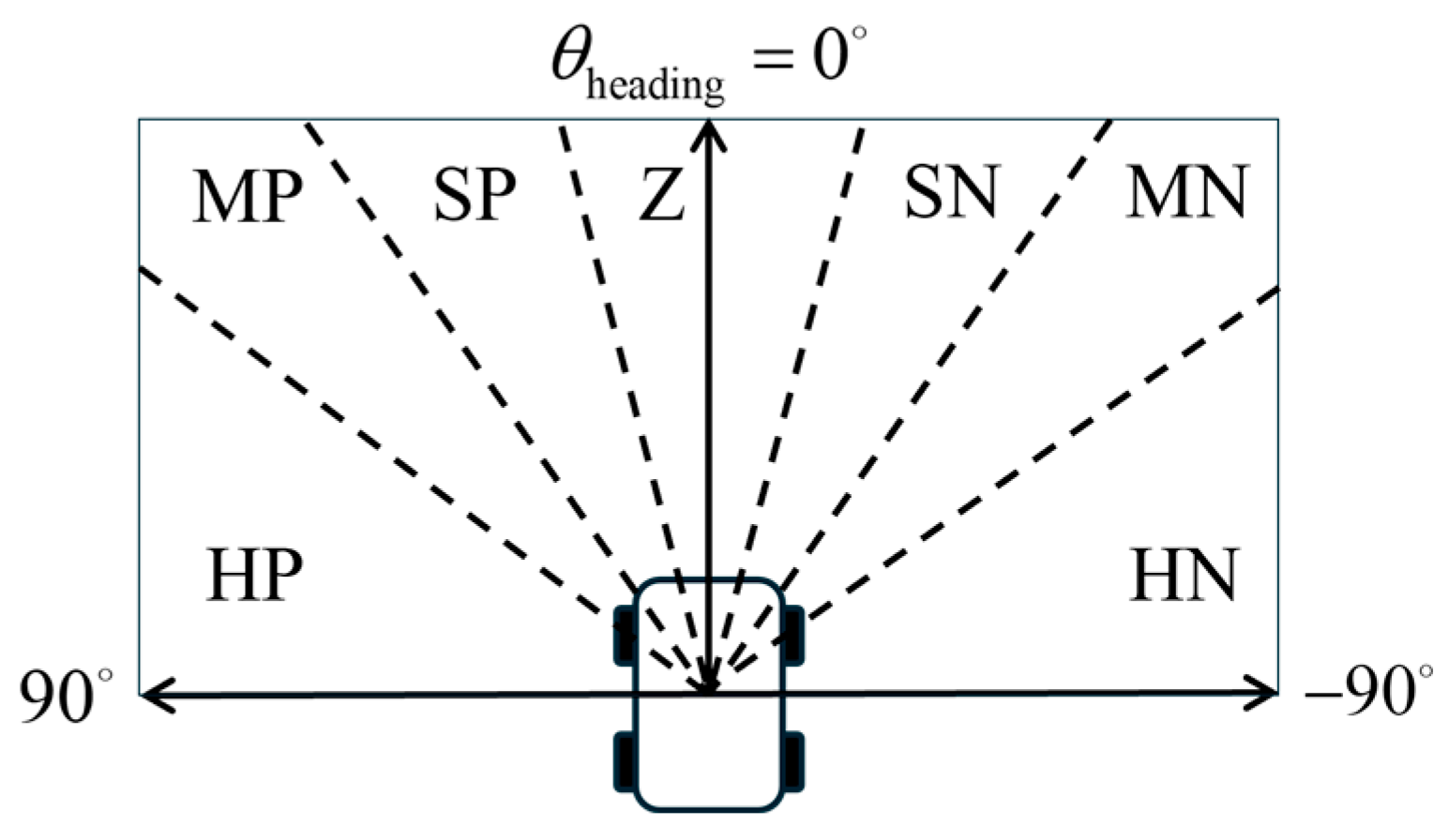
Fault point search scenario.
Figure 1.
Fault point search scenario.
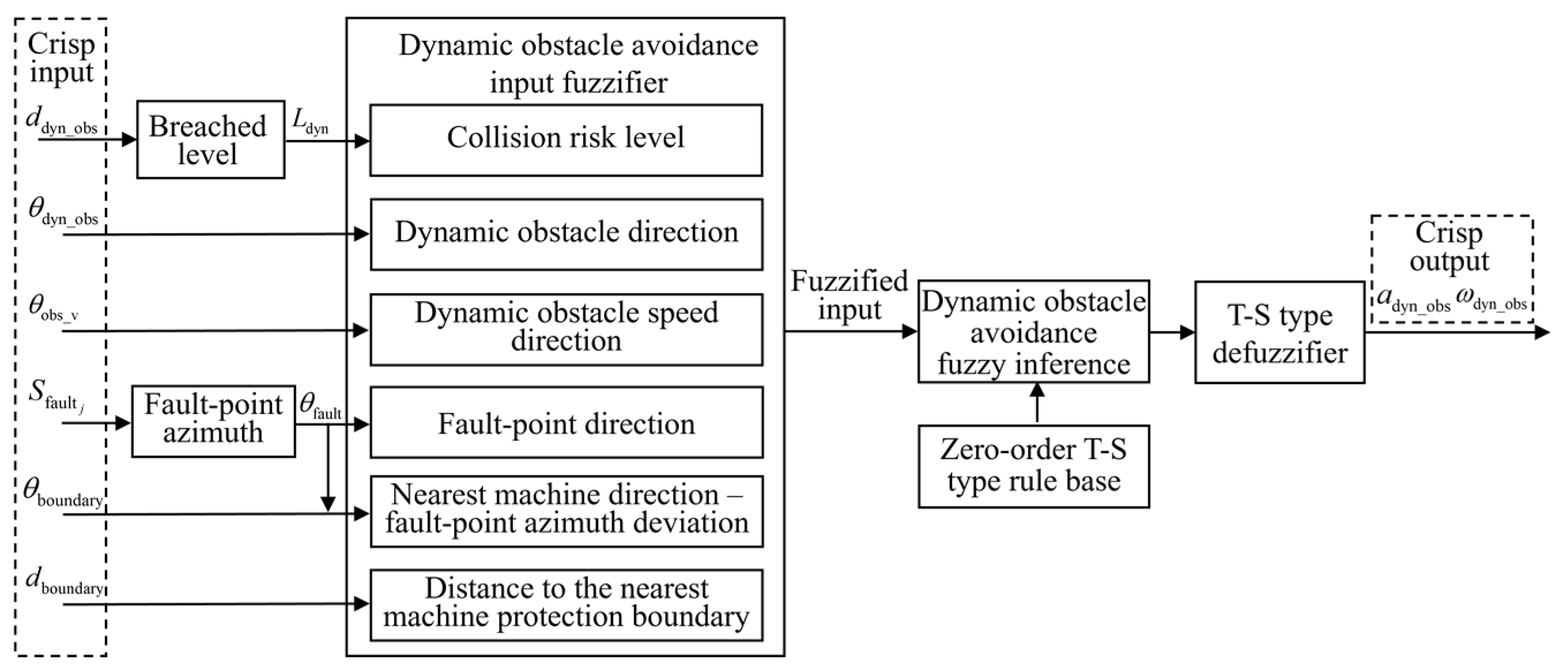
Figure 2.
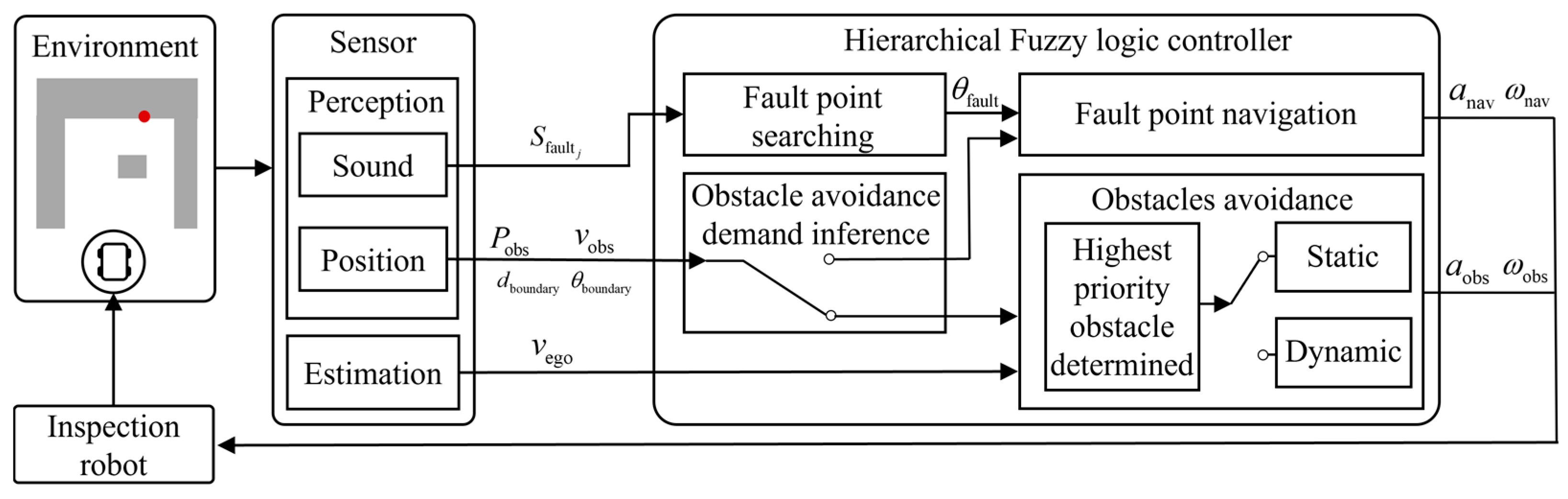
Hierarchical T–S FLC-based control framework.
Figure 2.
Hierarchical T–S FLC-based control framework.
Figure 3.
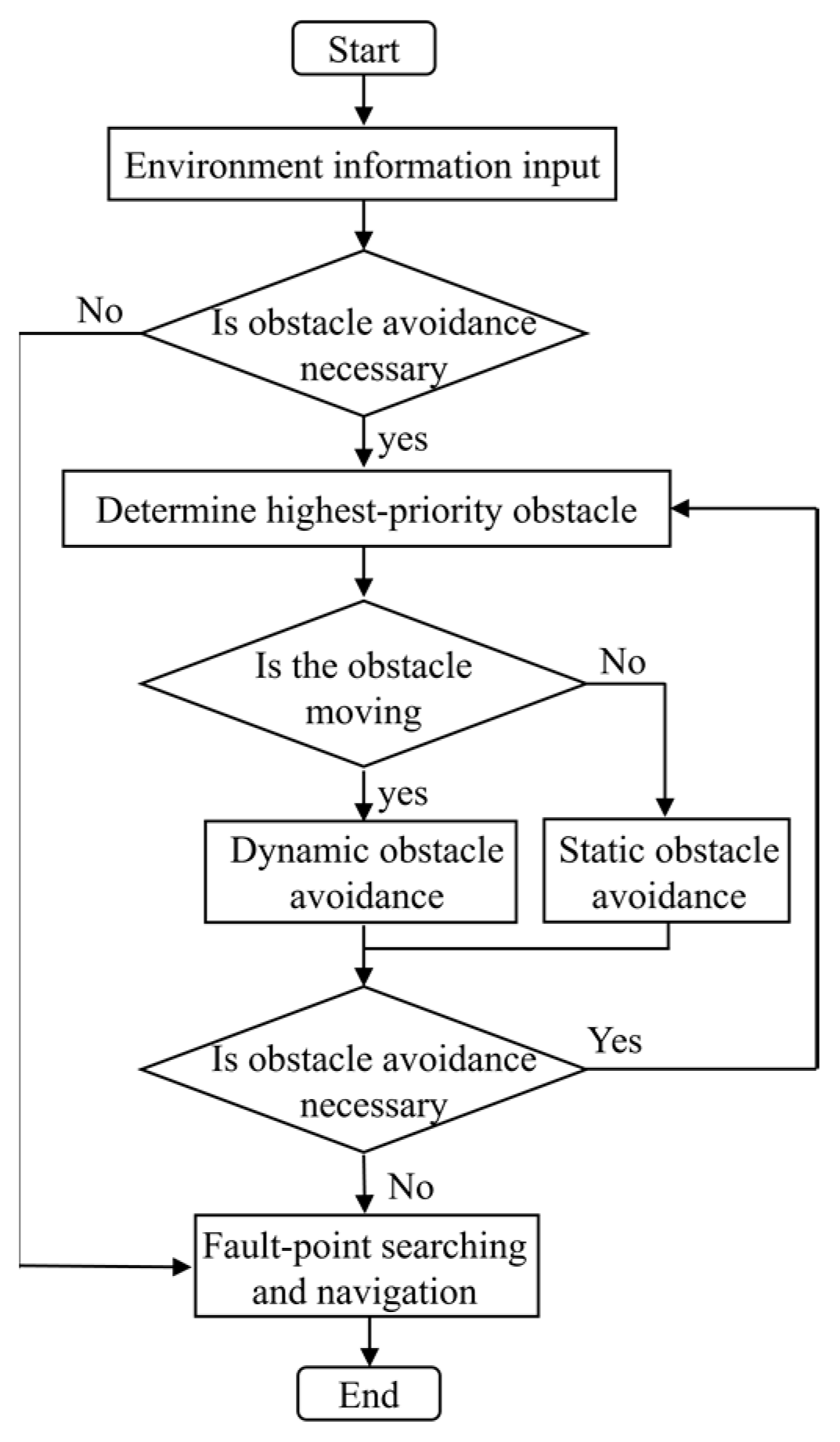
Control flow of navigation and obstacle avoidance in fault point search.
Figure 3.
Control flow of navigation and obstacle avoidance in fault point search.
Figure 4.
FLC process for navigation.
Figure 4.
FLC process for navigation.
Figure 5.
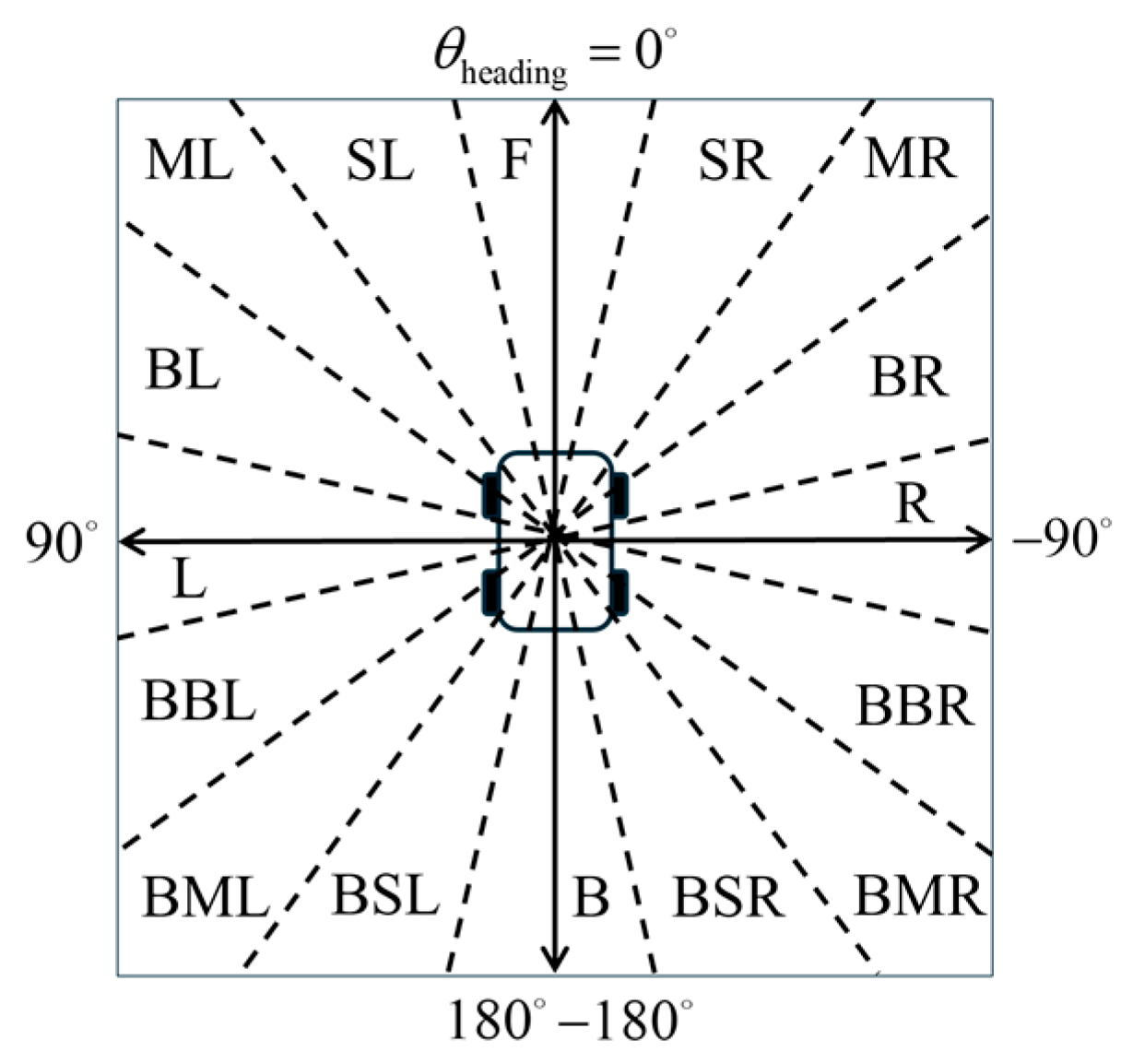
Semantic regions of fault point azimuth.
Figure 5.
Semantic regions of fault point azimuth.
Figure 6.
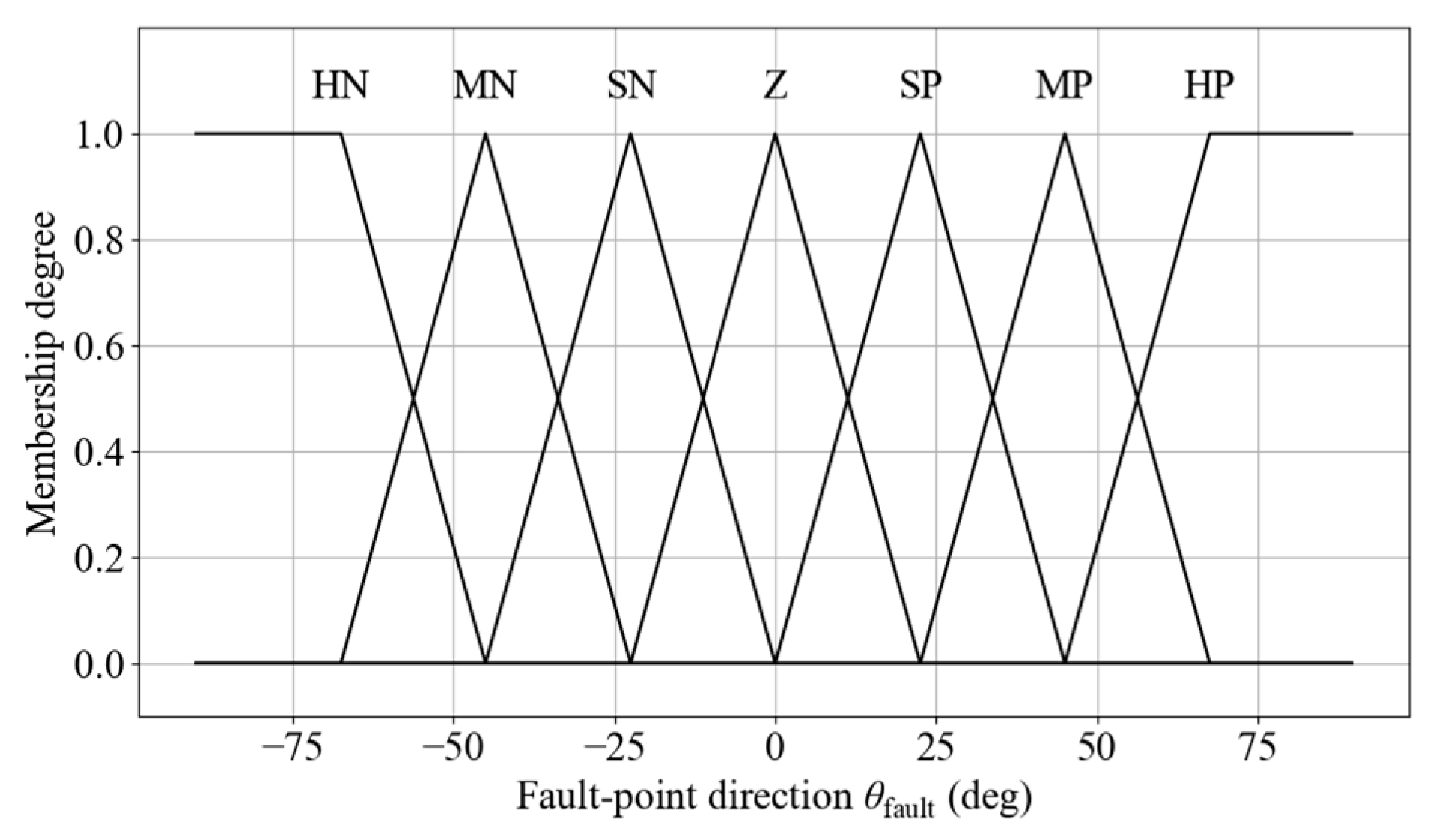
Semantic regions of fault point direction.
Figure 6.
Semantic regions of fault point direction.
Figure 7.
Membership functions for fault point direction.
Figure 7.
Membership functions for fault point direction.
Figure 8.
Membership functions for distance to the nearest equipment protection boundary.
Figure 8.
Membership functions for distance to the nearest equipment protection boundary.
Figure 9.
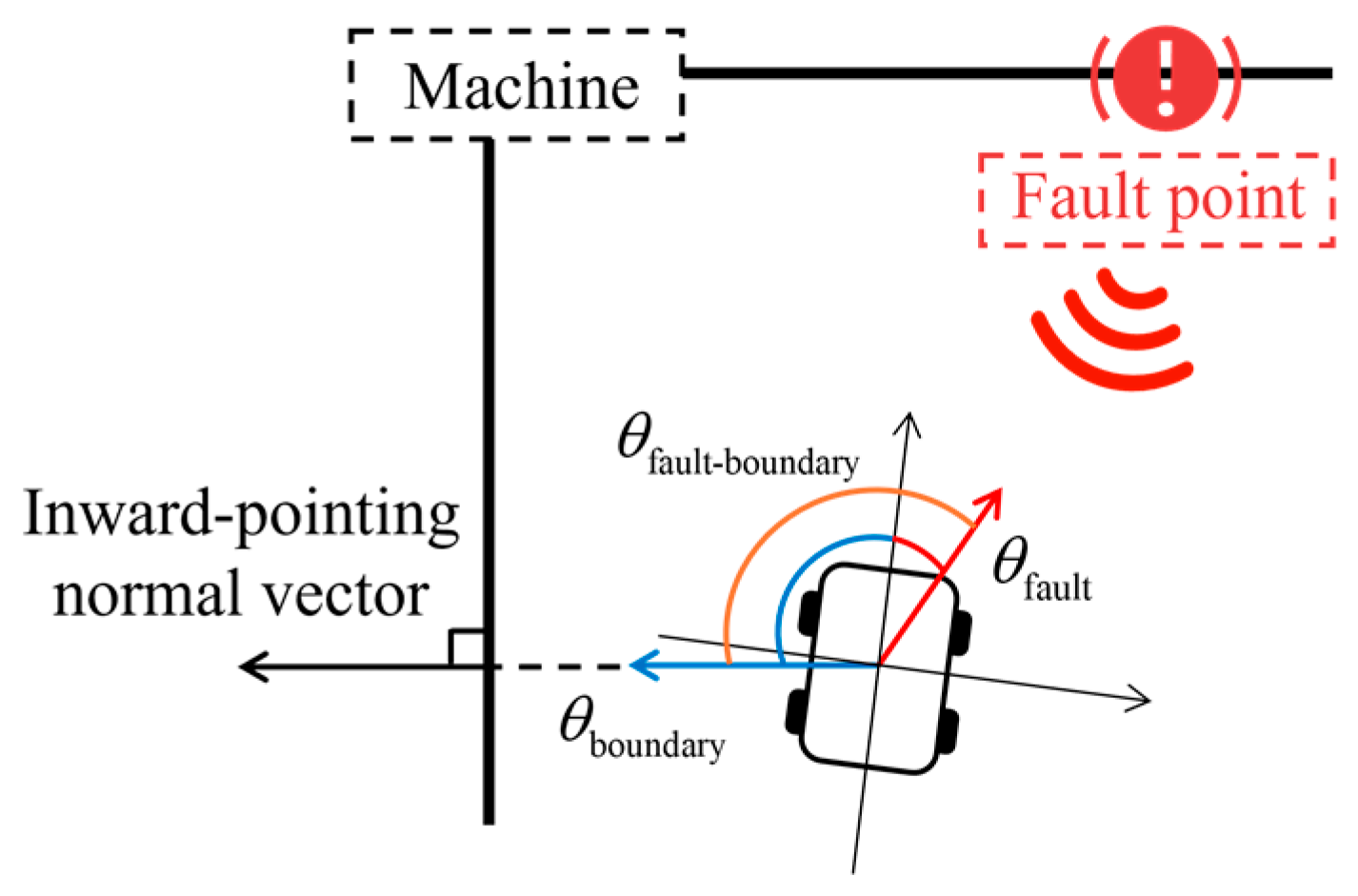
Azimuth difference between the nearest equipment and fault point.
Figure 9.
Azimuth difference between the nearest equipment and fault point.
Figure 10.
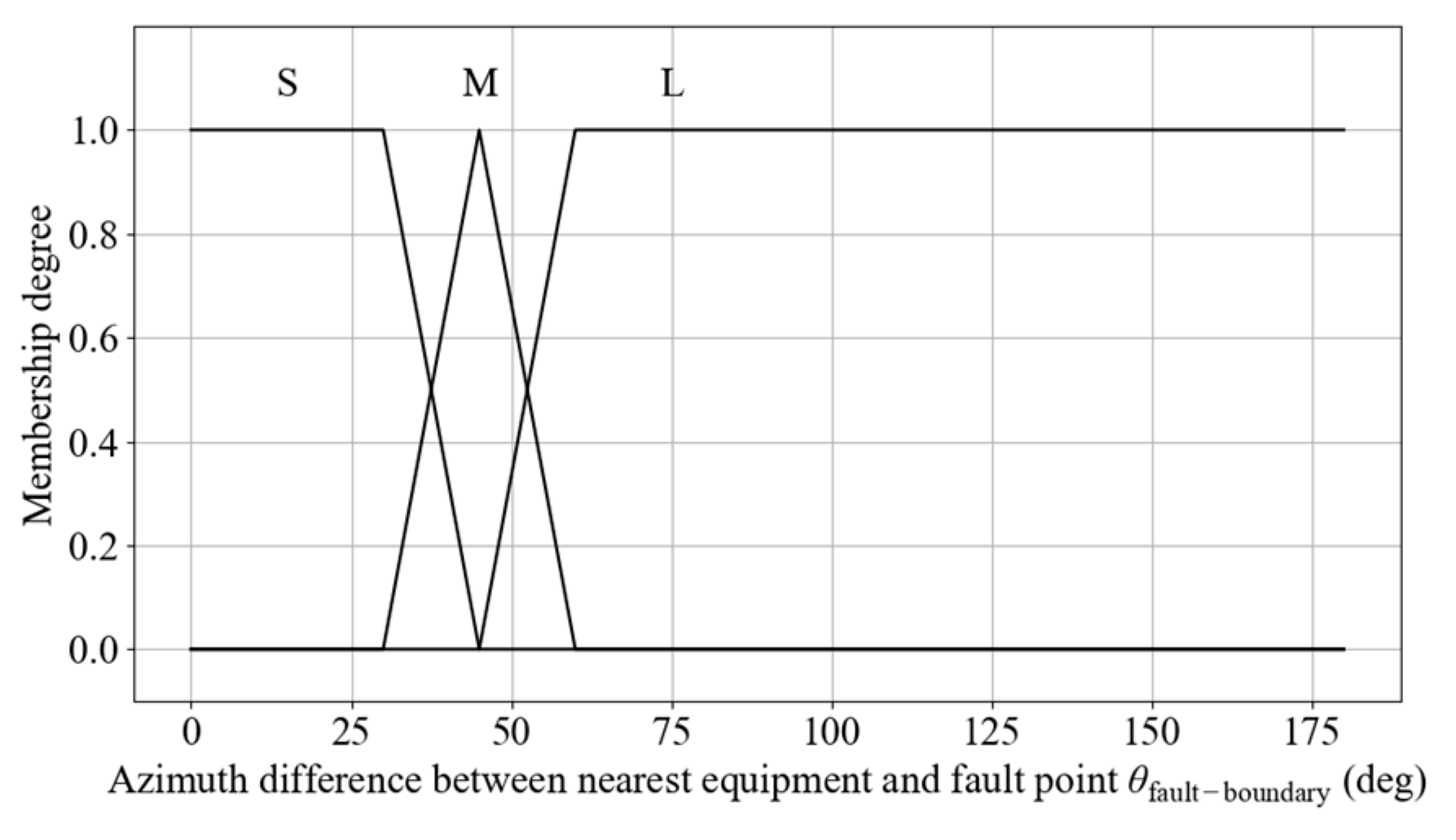
Membership functions for azimuth difference between the nearest equipment and fault point.
Figure 10.
Membership functions for azimuth difference between the nearest equipment and fault point.
Figure 11.
FLC process for static obstacle avoidance.
Figure 11.
FLC process for static obstacle avoidance.
Figure 12.
Membership functions for breached level.
Figure 12.
Membership functions for breached level.
Figure 13.
Membership functions for obstacle azimuth.
Figure 13.
Membership functions for obstacle azimuth.
Figure 14.
FLC process for dynamic obstacle avoidance.
Figure 14.
FLC process for dynamic obstacle avoidance.
Figure 15.
Semantic regions of the dynamic obstacle azimuth.
Figure 15.
Semantic regions of the dynamic obstacle azimuth.
Figure 16.
Membership functions for dynamic obstacle azimuth.
Figure 16.
Membership functions for dynamic obstacle azimuth.
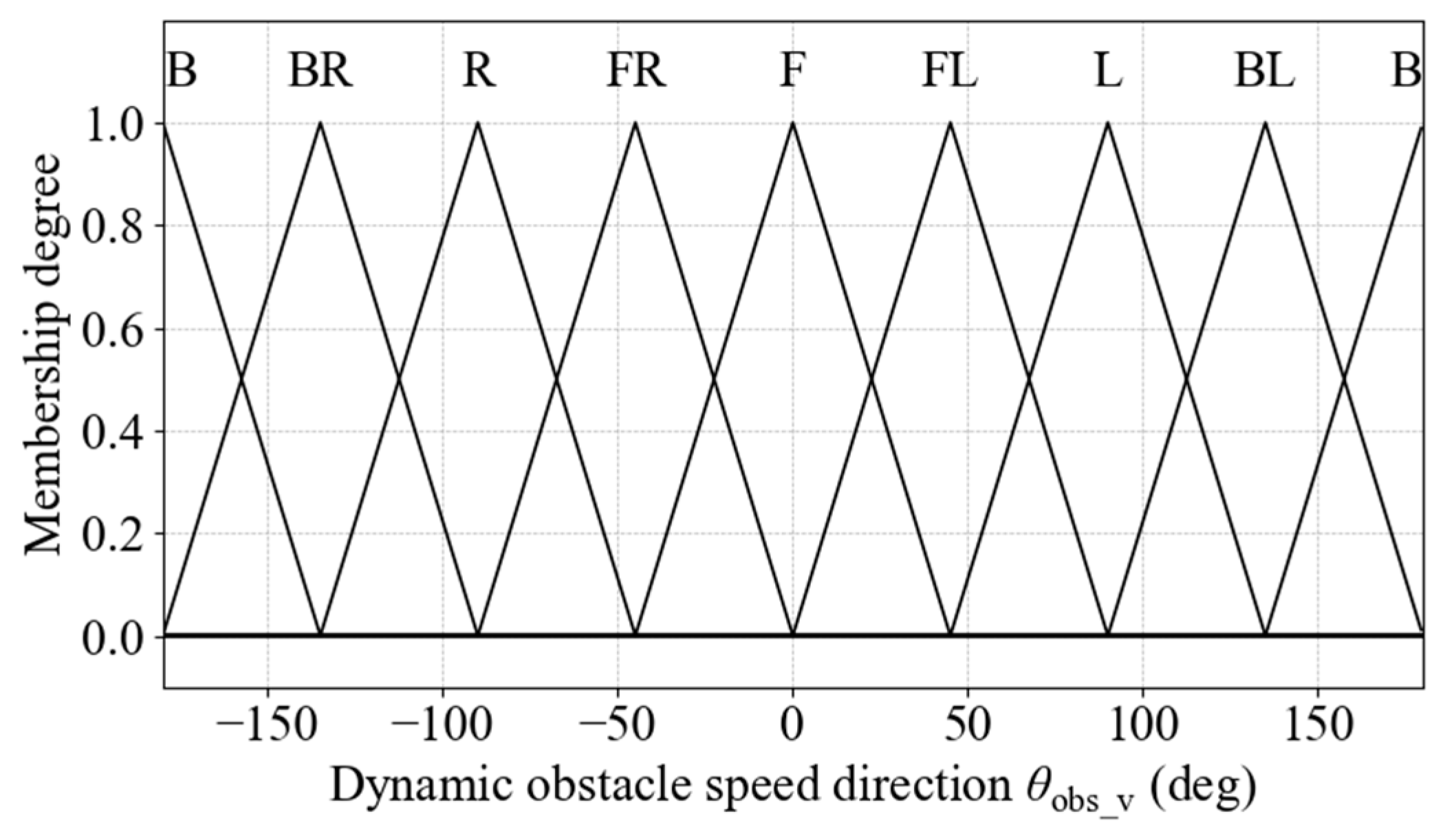
Figure 17.
Membership functions for dynamic obstacle speed direction.
Figure 17.
Membership functions for dynamic obstacle speed direction.
Figure 18.
FIS process for obstacle avoidance necessity.
Figure 18.
FIS process for obstacle avoidance necessity.
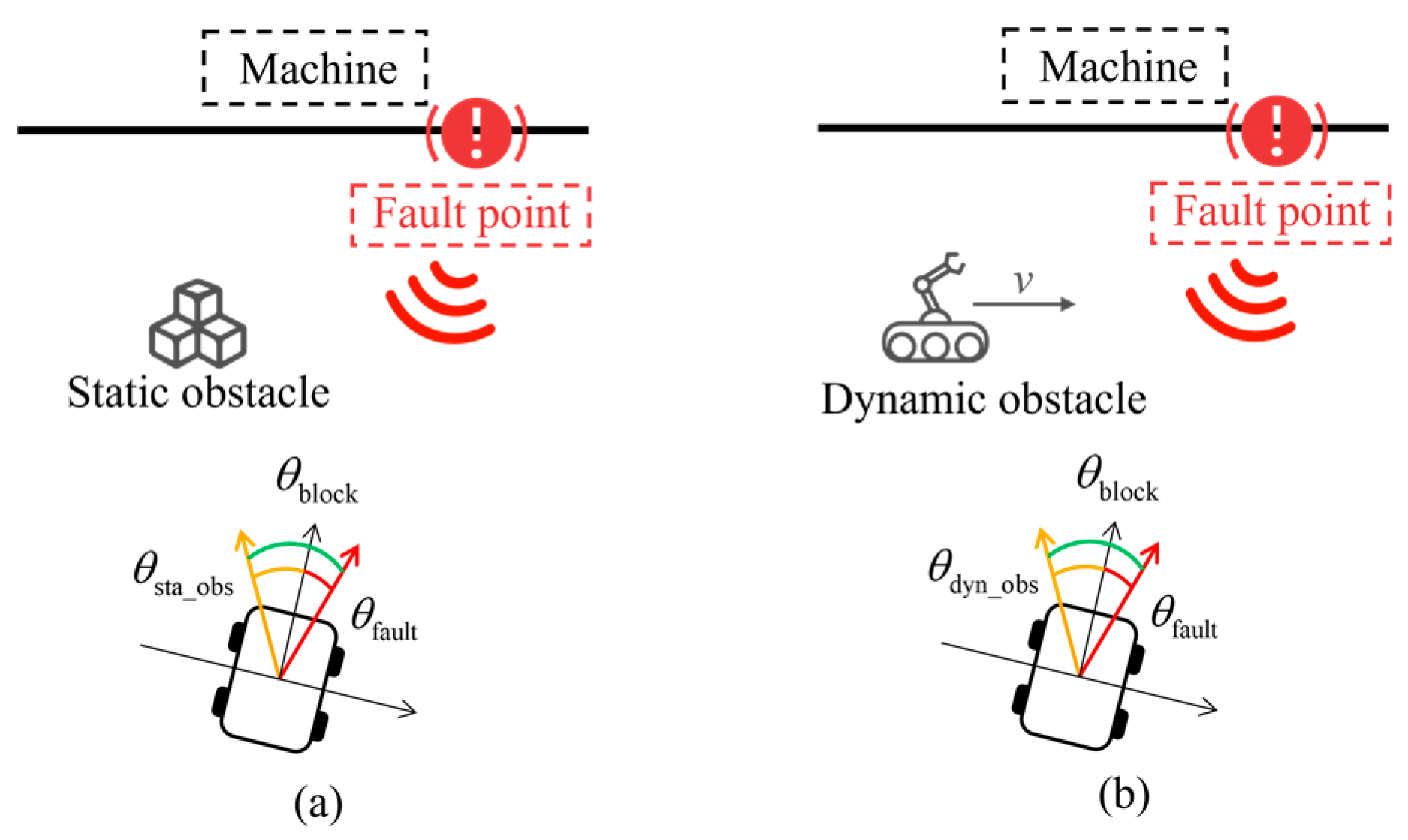
Figure 19.
Composition of blocking angle. (a) Angular configurations in static scenarios. (b) Angular configurations in dynamic scenarios.
Figure 19.
Composition of blocking angle. (a) Angular configurations in static scenarios. (b) Angular configurations in dynamic scenarios.
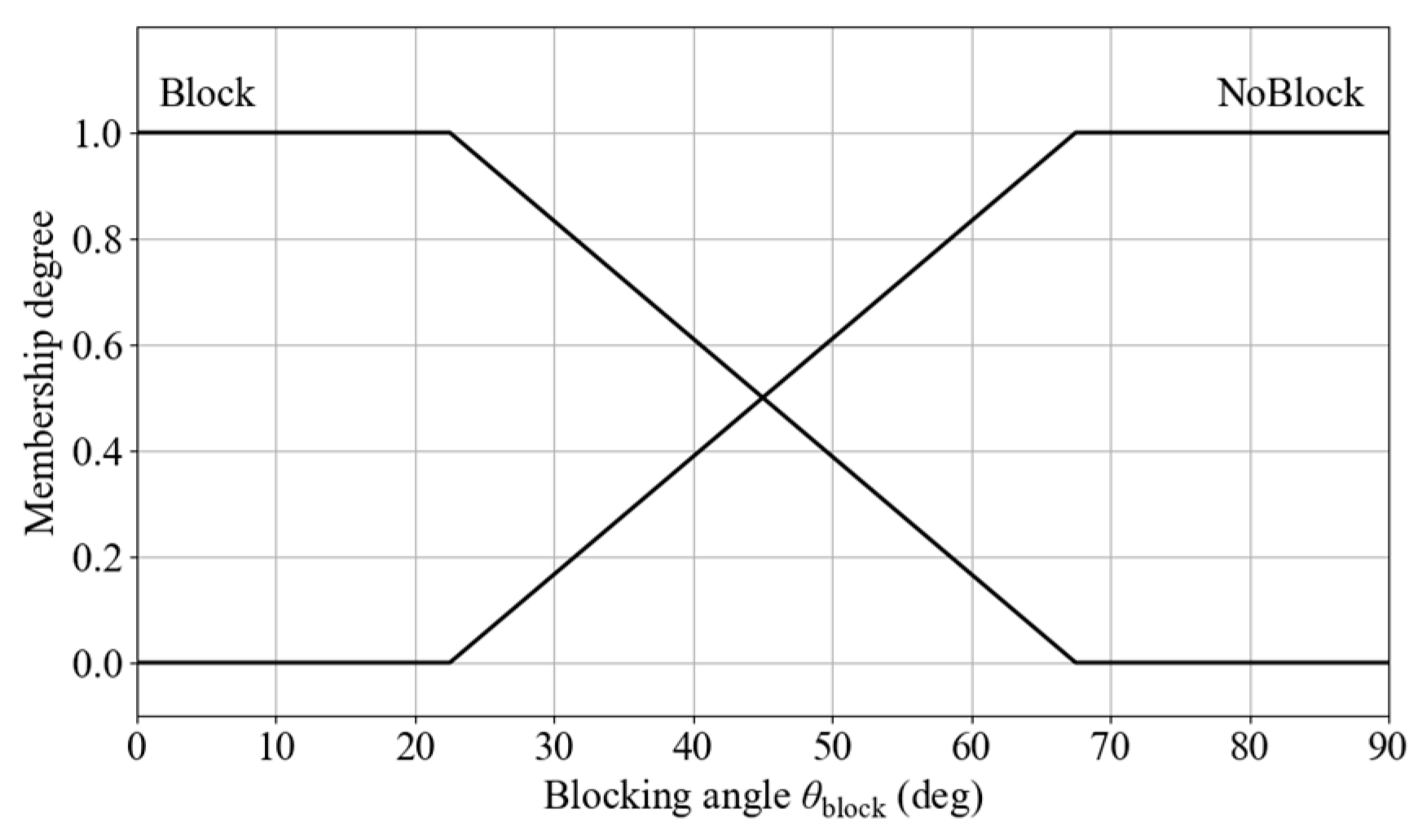
Figure 20.
Membership functions for blocking angle.
Figure 20.
Membership functions for blocking angle.
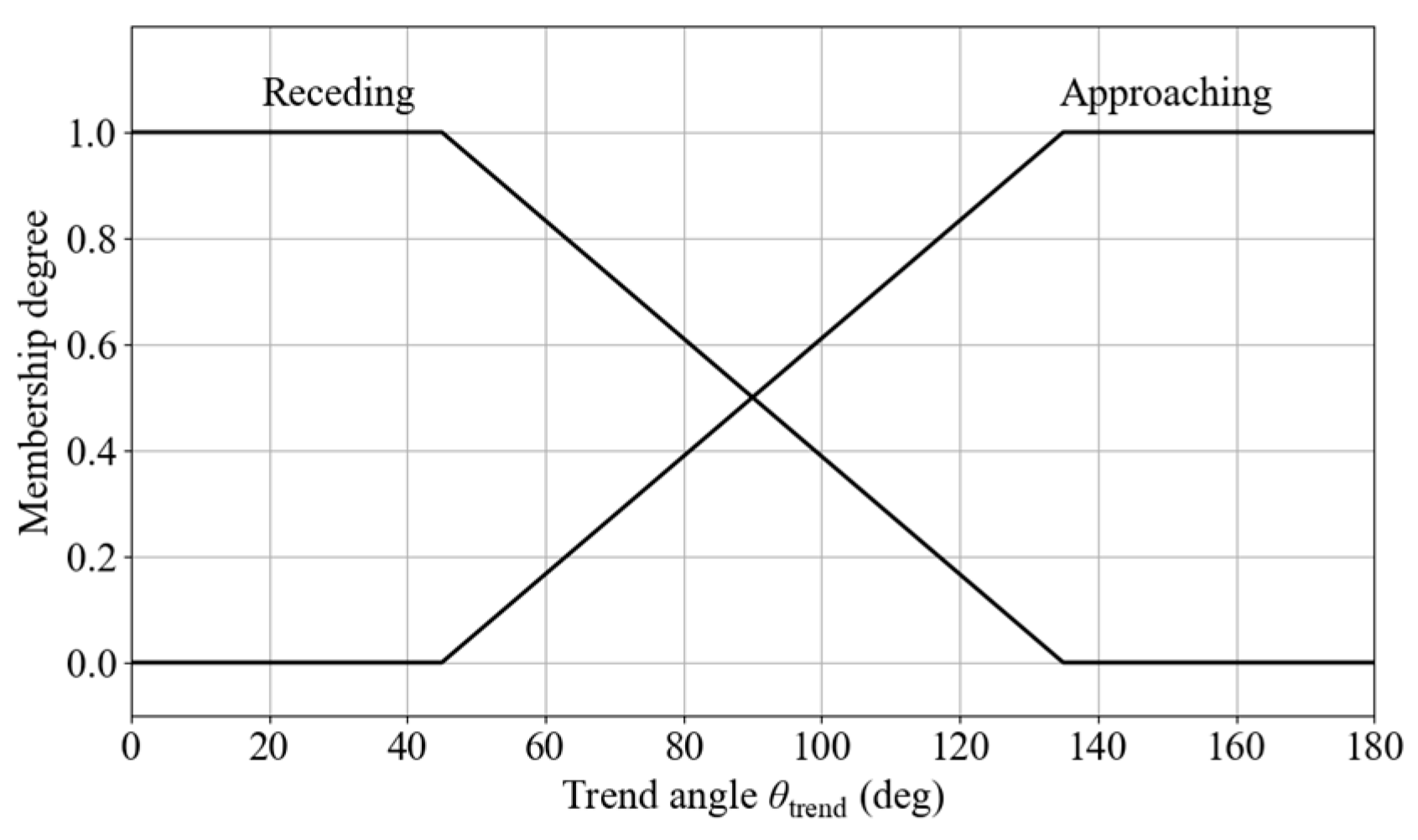
Figure 21.
Membership functions for trend angle.
Figure 21.
Membership functions for trend angle.
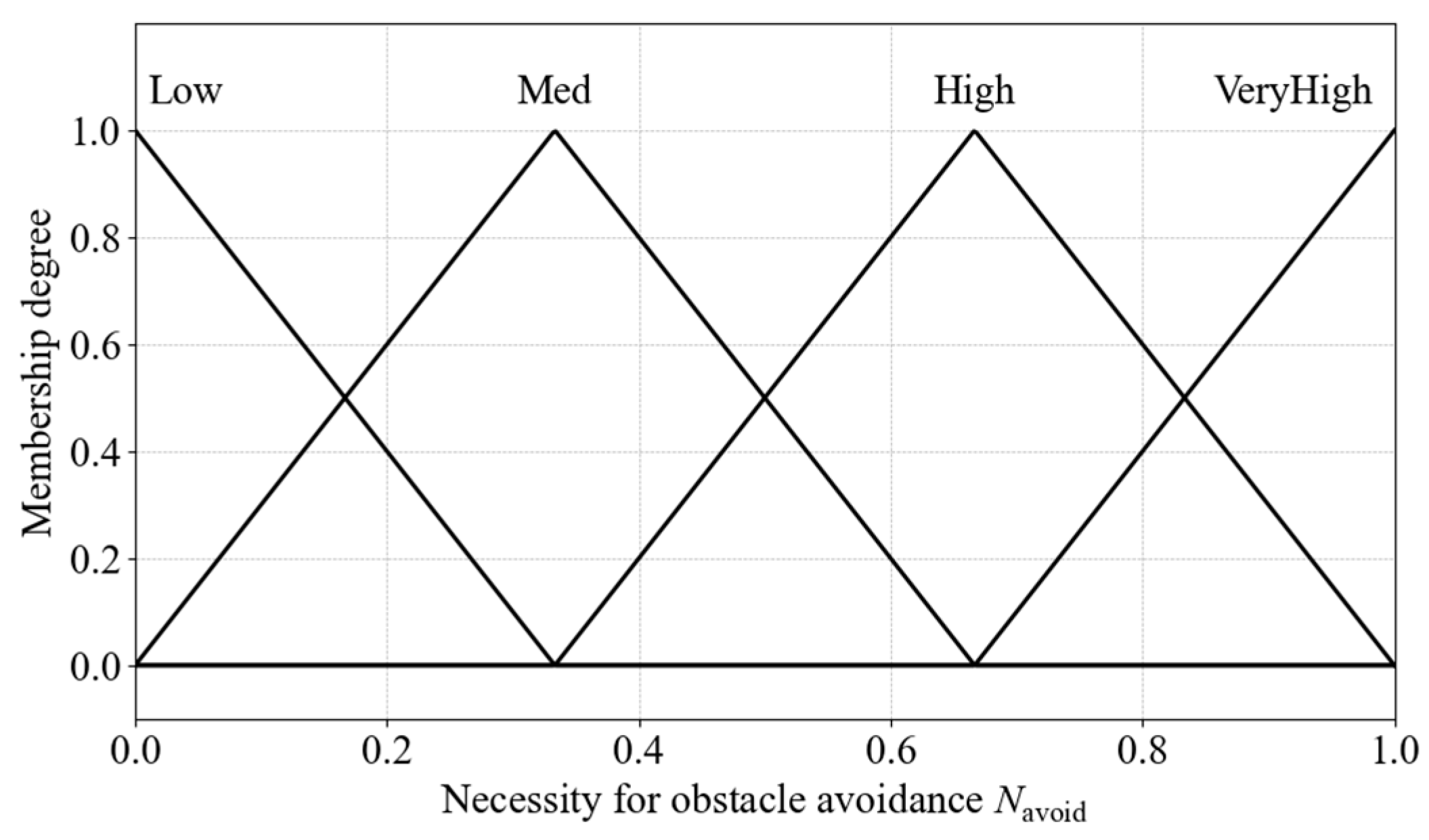
Figure 22.
Membership functions for obstacle avoidance necessity.
Figure 22.
Membership functions for obstacle avoidance necessity.
Figure 23.
FIS process for obstacle urgency.
Figure 23.
FIS process for obstacle urgency.
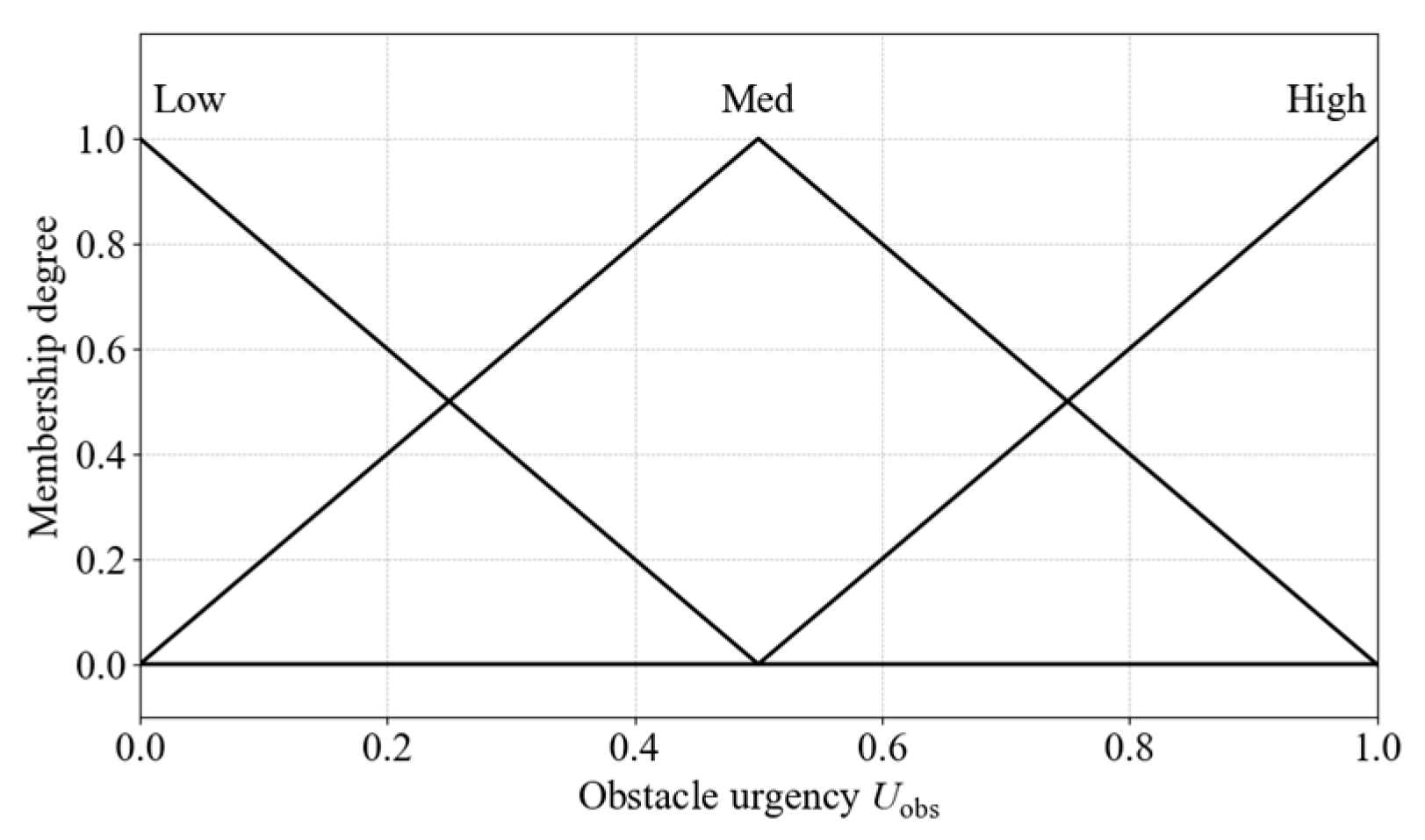
Figure 24.
Membership functions for obstacle urgency.
Figure 24.
Membership functions for obstacle urgency.
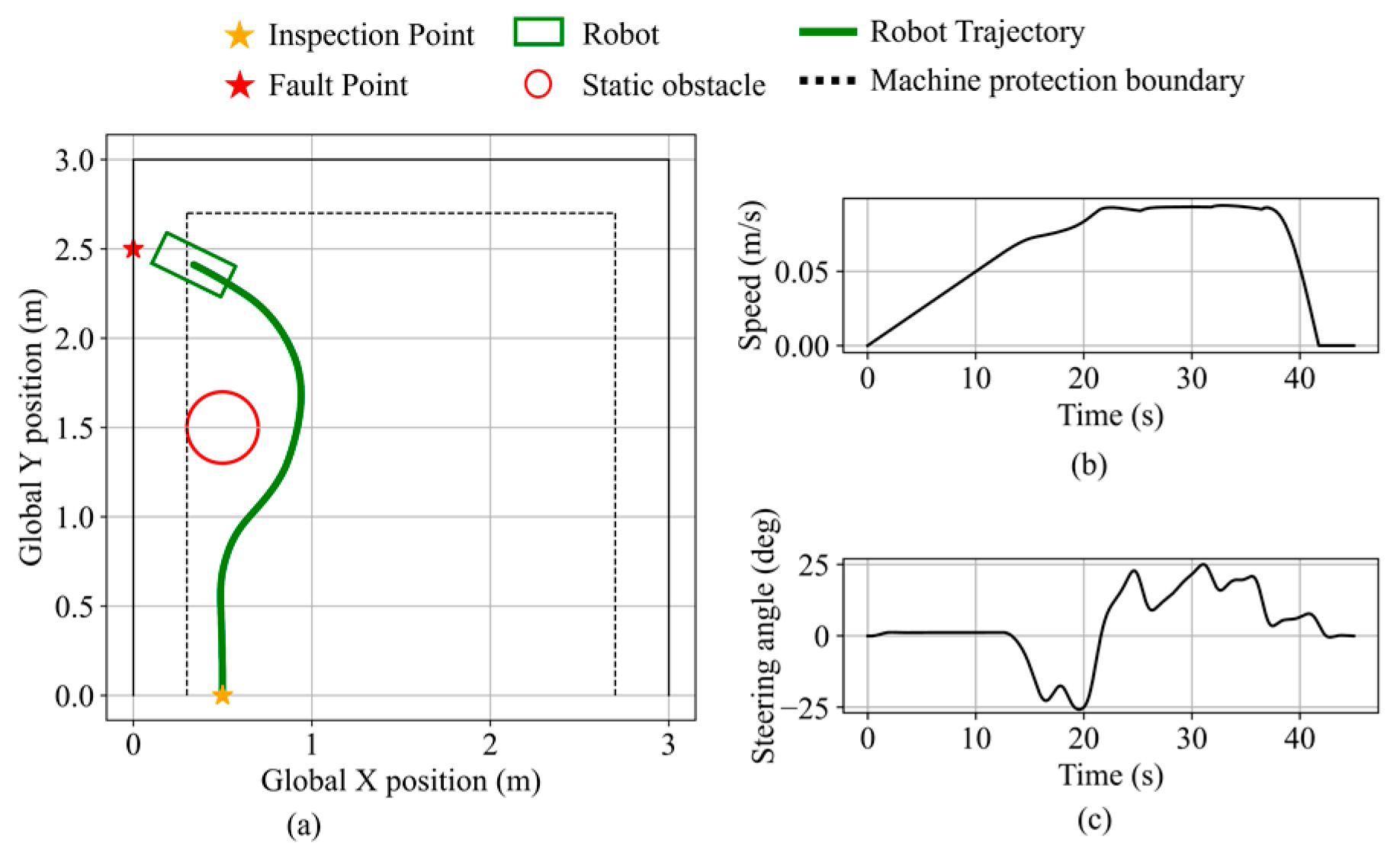
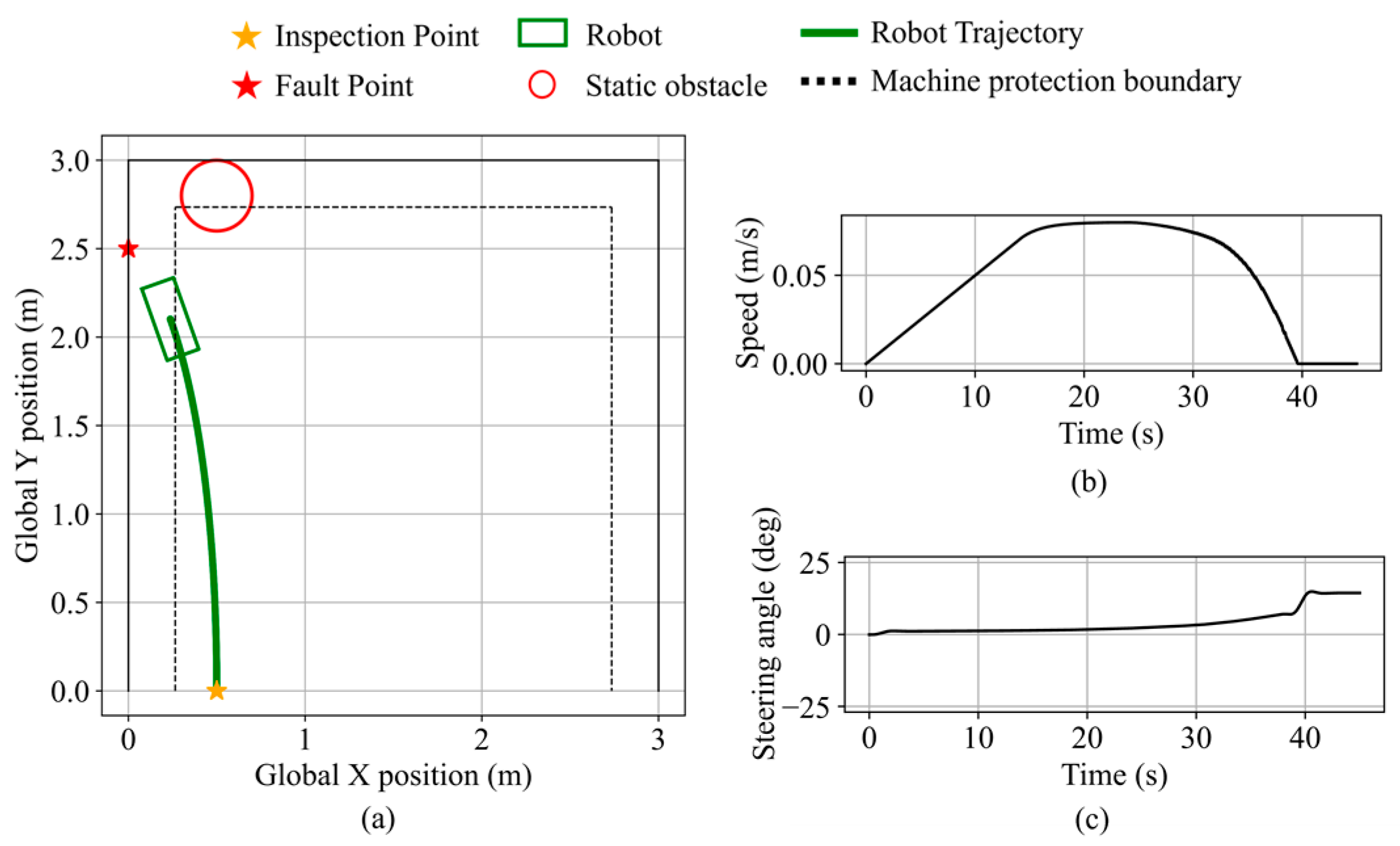
Figure 26.
Robot state during fault point search navigation validation. (a) Close-Range navigation validation. (b) Right-boundary navigation validation. (c) Boundary-following navigation validation. (d) Top-boundary navigation validation. (e,f) Left-boundary navigation validation.
Figure 26.
Robot state during fault point search navigation validation. (a) Close-Range navigation validation. (b) Right-boundary navigation validation. (c) Boundary-following navigation validation. (d) Top-boundary navigation validation. (e,f) Left-boundary navigation validation.
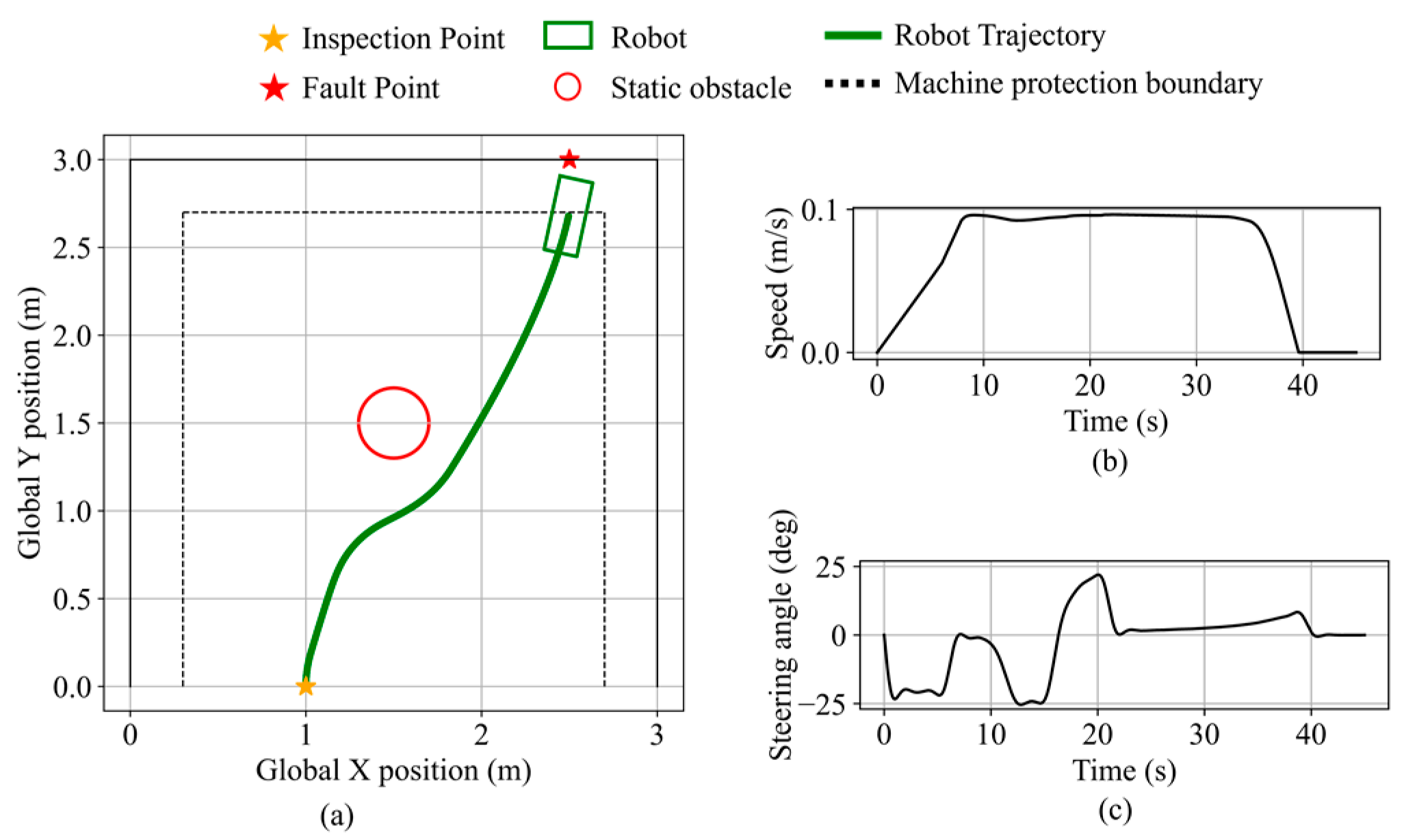
Figure 27.
Robot states during static obstacle avoidance in validation scenario 1. (a) Robot trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 27.
Robot states during static obstacle avoidance in validation scenario 1. (a) Robot trajectory. (b) Robot speed. (c) Robot steering angle.
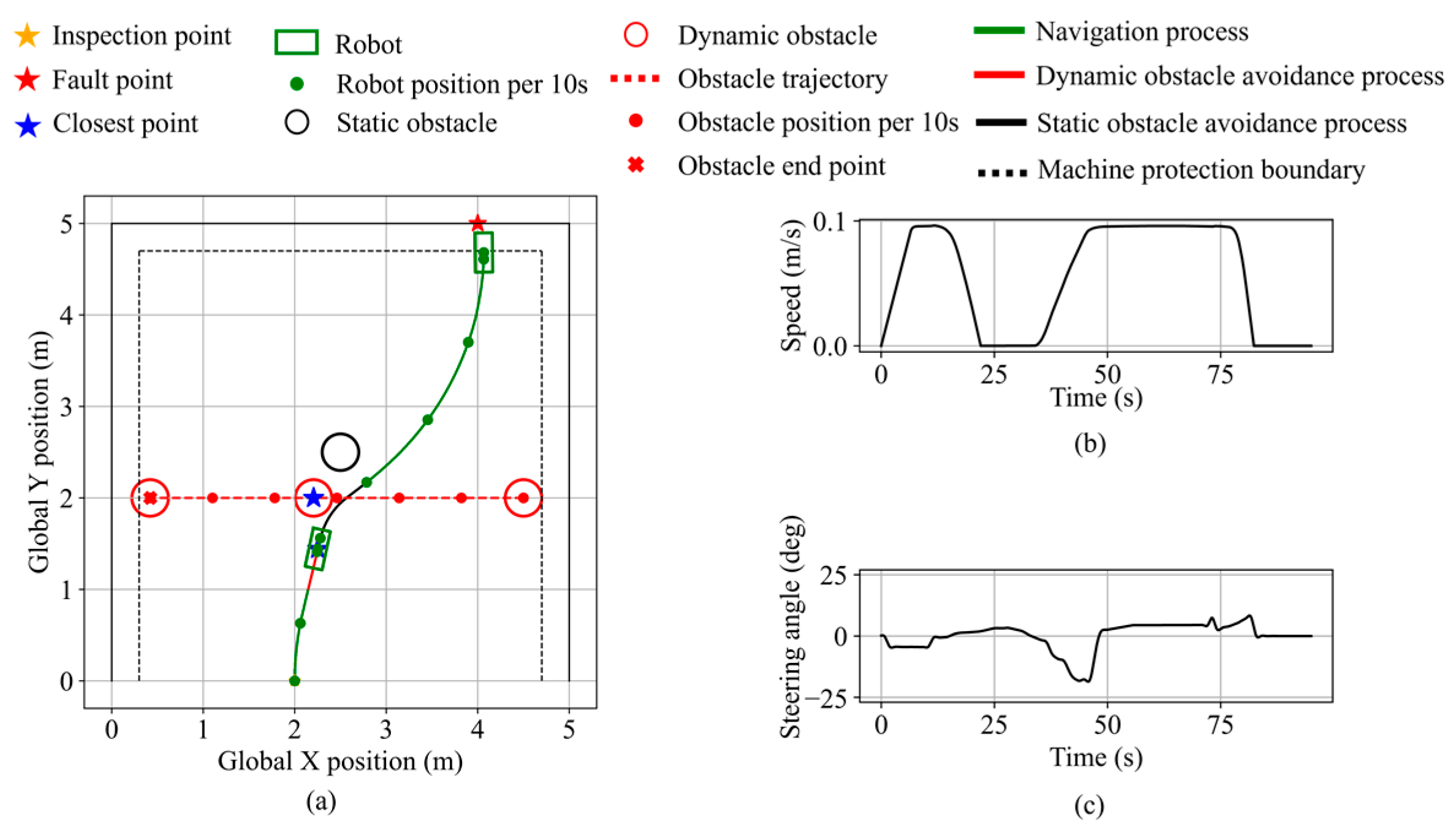
Figure 28.
Robot states during static obstacle avoidance in validation scenario 2. (a) Robot trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 28.
Robot states during static obstacle avoidance in validation scenario 2. (a) Robot trajectory. (b) Robot speed. (c) Robot steering angle.
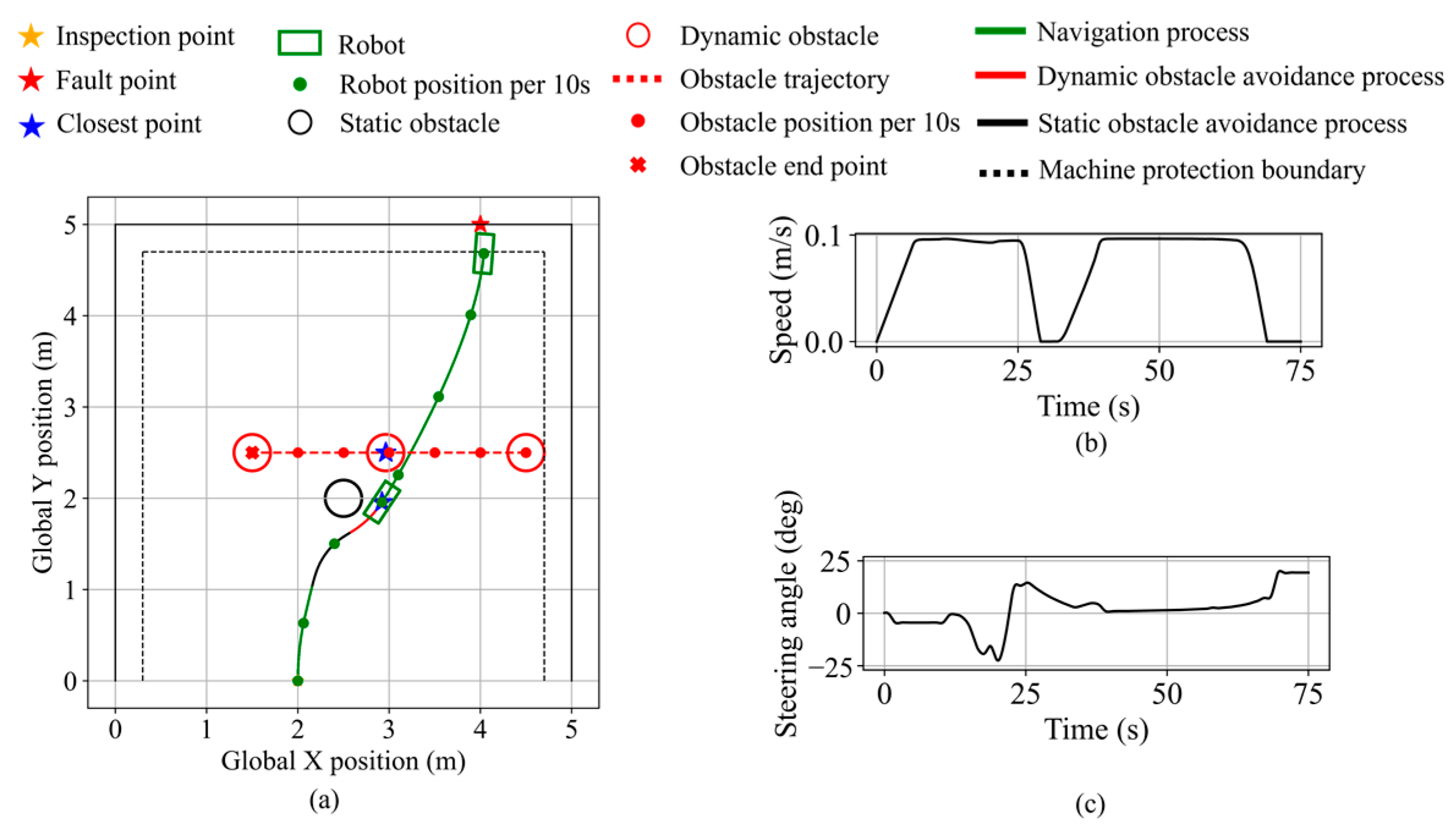
Figure 29.
Robot states during static obstacle avoidance in validation scenario 3. (a) Robot trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 29.
Robot states during static obstacle avoidance in validation scenario 3. (a) Robot trajectory. (b) Robot speed. (c) Robot steering angle.
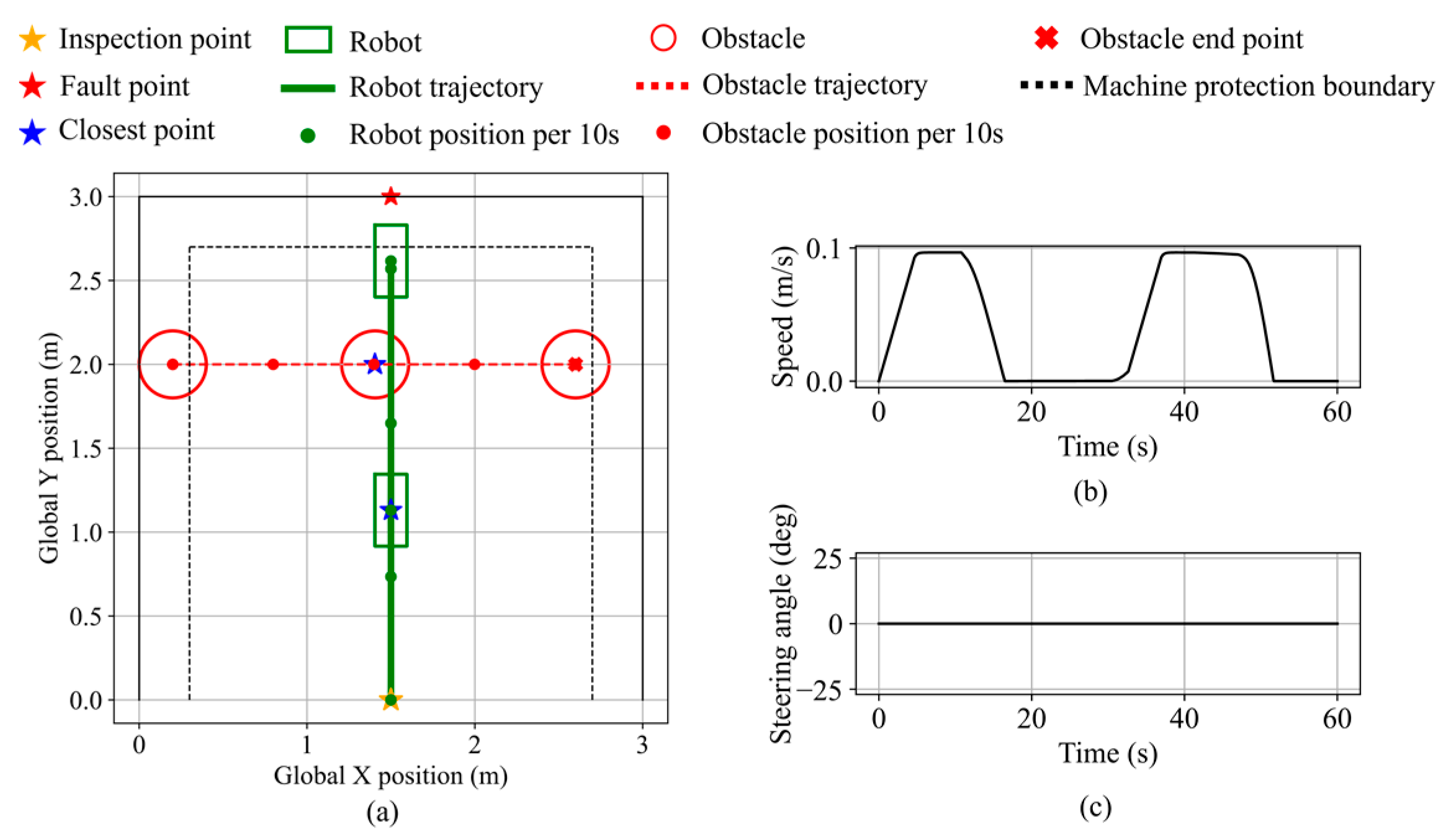
Figure 30.
Robot states during dynamic obstacle avoidance in validation scenario 1 and 2. (a) Dynamic obstacle approaching head-on. (b) Dynamic obstacle approaching from front-left. (c) MPC comparison test.
Figure 30.
Robot states during dynamic obstacle avoidance in validation scenario 1 and 2. (a) Dynamic obstacle approaching head-on. (b) Dynamic obstacle approaching from front-left. (c) MPC comparison test.
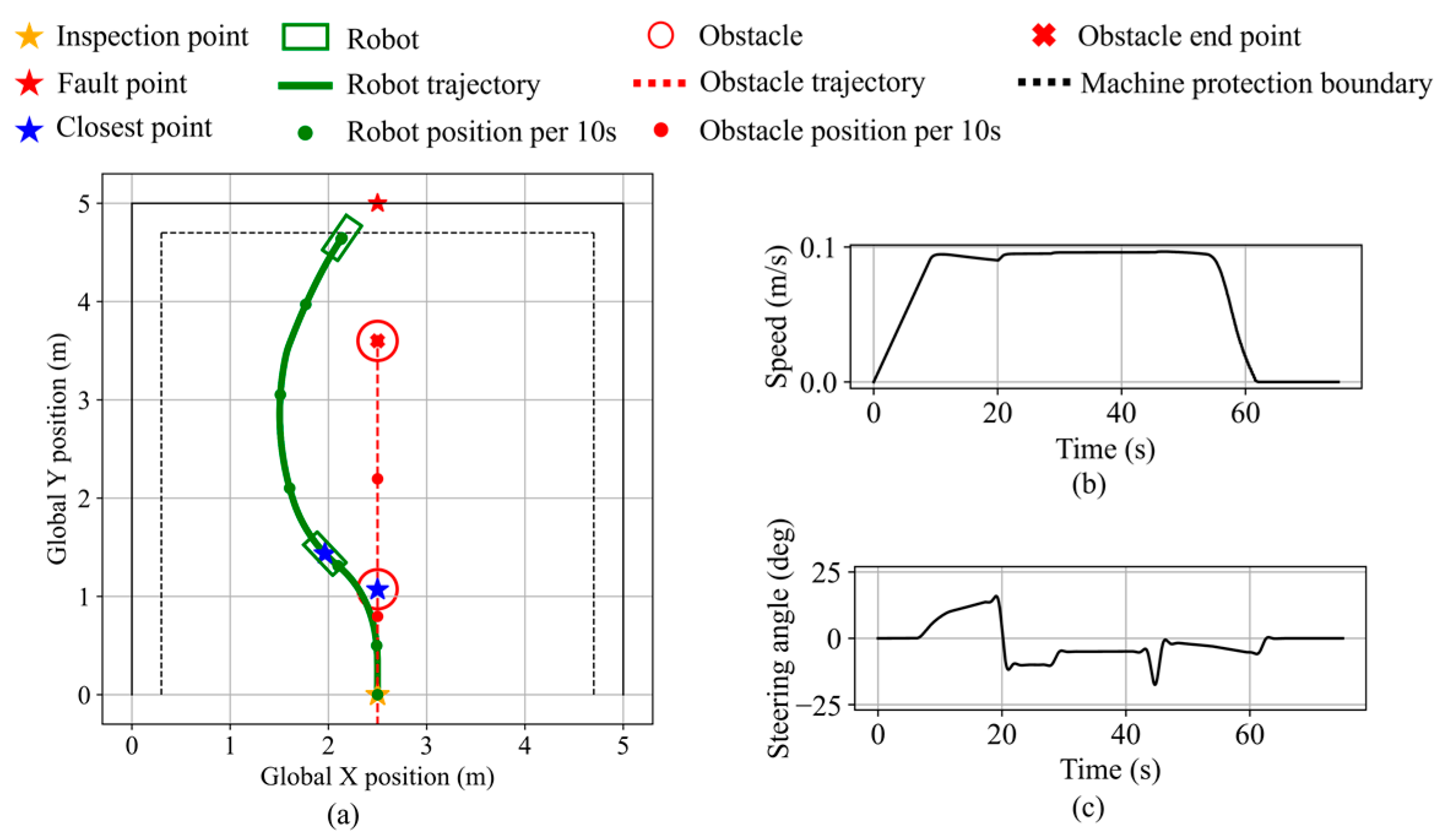
Figure 31.
Robot states during dynamic obstacle avoidance in validation scenario 3. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 31.
Robot states during dynamic obstacle avoidance in validation scenario 3. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 32.
Robot states during dynamic obstacle avoidance in validation scenario 4. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 32.
Robot states during dynamic obstacle avoidance in validation scenario 4. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 33.
Robot states during dynamic obstacle avoidance in validation scenario 5. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 33.
Robot states during dynamic obstacle avoidance in validation scenario 5. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 34.
Robot states during dynamic obstacle avoidance in validation scenario 6. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 34.
Robot states during dynamic obstacle avoidance in validation scenario 6. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 35.
Robot states during multi-objective planning in validation scenario 1. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 35.
Robot states during multi-objective planning in validation scenario 1. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 36.
Robot states during multi-objective planning in validation scenario 2. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Figure 36.
Robot states during multi-objective planning in validation scenario 2. (a) Robot and dynamic obstacle trajectory. (b) Robot speed. (c) Robot steering angle.
Table 1.
Navigation steering angle output rule base.
Table 1.
Navigation steering angle output rule base.
| Δθfault-boundary | θfault |
|---|
| Z | SP | SN | MP | MN | HP | HN |
|---|
| L | 0 | +L1 | −L1 | +L2 | −L2 | +L3 | −L3 |
| M | 0 | +L3 | −L3 | +L4 | −L4 | +L5 | −L5 |
| S | 0 | +L4 | −L4 | +L5 | −L5 | +L6 | −L6 |
Table 2.
Navigation-traction-acceleration-output rule base.
Table 2.
Navigation-traction-acceleration-output rule base.
| dboundary | Δθfault-boundary | θfault |
|---|
| Z | SP | SN | MP | MN | HP | HN |
|---|
| F | L/M/S | P6 | P5 | P5 | P4 | P4 | P3 | P3 |
| M | L/M/S | P5 | P4 | P4 | P3 | P3 | P2 | P2 |
| N | L | P2 | P2 | P2 | P2 | P2 | P2 | P2 |
| N | M/S | P4 | P3 | P3 | P2 | P2 | P1 | P1 |
| VN | L | P1 | P1 | P1 | P1 | P1 | P1 | P1 |
| VN | M/S | N4 | N3 | N3 | N2 | N2 | N1 | N1 |
Table 3.
Static obstacle-avoidance steering-angle-output rule base.
Table 3.
Static obstacle-avoidance steering-angle-output rule base.
| dboundary | θobs |
|---|
| Z | SP | SN | MP | MN | HP | HN |
|---|
| F, M | sgn(θfault) × L3 | −L2 | L2 | −L1 | L1 | 0 | 0 |
| N, VN | −sgn(θboundary) × L3 | −L2 | L2 | −L1 | L1 | 0 | 0 |
Table 4.
Static obstacle-avoidance traction-acceleration-output rule base.
Table 4.
Static obstacle-avoidance traction-acceleration-output rule base.
| dboundary | Δθfault-boundary | θsta_obs |
|---|
| Z | SP | SN | MP | MN | HP | HN |
|---|
| F, M | / | P2 | P3 | P3 | P4 | P4 | P5 | P5 |
| N | / | P1 | P2 | P2 | P3 | P3 | P4 | P4 |
| VN | S, M | N1 |
| VN | L | P1 | P2 | P2 | P3 | P3 | P4 | P4 |
Table 5.
Dynamic obstacle-avoidance steering-angle-output rule base.
Table 5.
Dynamic obstacle-avoidance steering-angle-output rule base.
| dboundary | θdyn_obs | θobs_v | |
|---|
| F | B | FL | L | BL | FR | R | BR |
|---|
| F, M | F, B | sgn(θfault) × L3 | sgn(θfault) × L3 | −L3 | 0 | L3 | L3 | 0 | −L3 |
| FL | 0 | 0 | 0 | 0 | 0 | L2 | 0 | −L2 |
| BL | 0 | 0 | 0 | 0 | 0 | L2 | 0 | 0 |
| L | 0 | 0 | 0 | 0 | 0 | L1 | 0 | 0 |
| FR | 0 | 0 | −L2 | 0 | L2 | 0 | 0 | 0 |
| BR | 0 | 0 | −L2 | 0 | 0 | 0 | 0 | 0 |
| R | 0 | 0 | −L1 | 0 | 0 | 0 | 0 | 0 |
Table 6.
Dynamic obstacle-avoidance steering-angle-output rule base during equipment protection.
Table 6.
Dynamic obstacle-avoidance steering-angle-output rule base during equipment protection.
| dboundary | θobs_v | | |
|---|
| F | B | FL | BL | FR | BR | L | R |
|---|
| N, VN | −sgn(θboundary) × L1 | −sgn(θboundary) × L2 | −sgn(θboundary) × L3 |
Table 7.
Dynamic obstacle-avoidance traction-acceleration-output rule base.
Table 7.
Dynamic obstacle-avoidance traction-acceleration-output rule base.
| dboundary | θdyn_obs | θobs_v | |
|---|
| F | B | FL | L | BL | FR | R | BR |
|---|
| F, M | F, B | sgn(θfault) × L3 | sgn(θfault) × L3 | −L3 | 0 | L3 | L3 | 0 | −L3 |
| FL | 0 | 0 | 0 | 0 | 0 | L2 | 0 | −L2 |
| BL | 0 | 0 | 0 | 0 | 0 | L2 | 0 | 0 |
| L | 0 | 0 | 0 | 0 | 0 | L1 | 0 | 0 |
| FR | 0 | 0 | −L2 | 0 | L2 | 0 | 0 | 0 |
| BR | 0 | 0 | −L2 | 0 | 0 | 0 | 0 | 0 |
| R | 0 | 0 | −L1 | 0 | 0 | 0 | 0 | 0 |
Table 8.
Obstacle-avoidance necessity-output rule base.
Table 8.
Obstacle-avoidance necessity-output rule base.
| Breached Level | Trend Angle | Block Angle | Necessity for Obstacle Avoidance |
|---|
| S | / | / | Low |
| PC | Approach | Block | High |
| Approach | NoBlock | Med |
| Recede | Block | Med |
| Recede | NoBlock | Low |
| E | Approach | Block | VeryHigh |
| Approach | NoBlock | High |
| Recede | Block | Med |
| Recede | NoBlock | Low |
Table 9.
Obstacle-urgency-output rule base.
Table 9.
Obstacle-urgency-output rule base.
| Breached Level | Trend Angle | Obstacle Urgency |
|---|
| S | / | Low |
| PC | Approach | Med |
| Recede | Low |
| E | Approach | High |
| Recede | Med |
Table 10.
Parameters of RoboCar 1/10.
Table 10.
Parameters of RoboCar 1/10.
| Parameter | Value | Unit |
|---|
| Mass | 2200 | g |
| Length | 429 | mm |
| Width | 190 | mm |
| Wheelbase | 250 | mm |
| Minimum radius of rotation | 500 | mm |
| Maximum speed | 2.78 | m/s |
Table 11.
Simulation parameters of RoboCar 1/10.
Table 11.
Simulation parameters of RoboCar 1/10.
| Scenarios | The Minimum Distance to the
Equipment (cm) | Distance From Front Center to
Fault Point (cm) |
|---|
| a | 7.7 | 12.5 |
| b | 10.9 | 23.2 |
| c | 7.6 | 25.6 |
| d | 7.4 | 27.5 |
| e | 6.8 | 11.1 |
| f | 6.4 | 9.2 |