Simulation of Chirped FBG and EFPI-Based EC-PCF Sensor for Multi-Parameter Monitoring in Lithium Ion Batteries
Abstract
1. Introduction
- a novel design for an ethylene carbonate-filled PCF with matched electrolyte RI (≈) to maximize light–matter interaction and RI sensitivity,
- the first simulated integration of a chirped FBG and an EFPI in a single fiber platform for simultaneous quad-parameter sensing, and
- a pioneering simulation framework incorporating stress-induced birefringence, wavelength dispersion, and fabrication robustness via Sobol-sequence Monte Carlo analysis, advancing beyond conventional modeling approaches.
- Cell-level monitoring (e.g., surface temperature/strain via FBG arrays);
- Electrode-level interrogation (e.g., lithium plating detection through localized RI changes);
- Electrolyte-level sensing (e.g., decomposition tracking via refractive index shifts in the separator region).
- quantify the sensitivity and robustness of the sensor for multi-parameter LIB monitoring,
- ensure numerical stability in TMM and EFPI calculations with advanced techniques (e.g., Gaussian apodization, Sobol sequences), and
- provide a simulation-backed basis for experimental implementation and integration into high-level BMS.
2. Materials and Methods
2.1. Initial and Boundary Conditions
- Temperature: 25 °C, representing standard laboratory ambient temperature;
- Axial strain: 0 µ, corresponding to an unstressed fiber state;
- Refractive index (RI): 1.387 for ethylene carbonate at 25 °C, serving as the nominal cladding-hole filling medium.
- Temperature: 0–100 °C, covering sub-ambient conditions through to elevated states associated with overcharge and onset of thermal runaway;
Performance Targets and Effectiveness Criteria
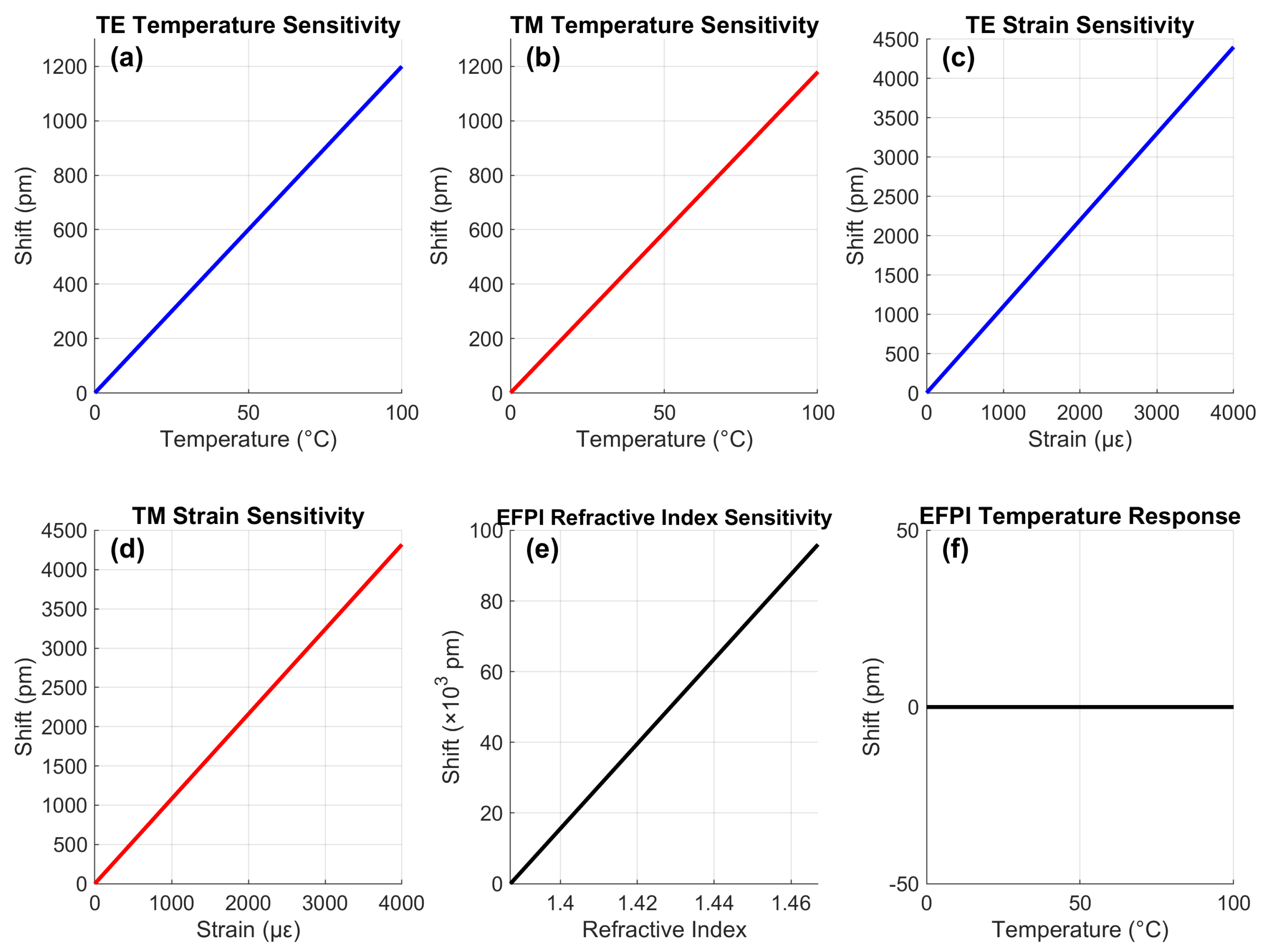
- Temperature Sensitivity pm/°CAccurate thermal monitoring is critical for detecting early signs of abnormal heat generation within LIB cells. A minimum temperature sensitivity of 10 pm/°C ensures sufficient spectral resolution to capture subtle variations in internal cell temperature, particularly during charge/discharge cycles or the onset of thermal runaway [5].
- Strain Sensitivity pm/µSince electrode expansion and packaging stress translate directly into strain on the fiber, achieving strain sensitivity above 1.0 pm/µ enables the detection of swelling phenomena with micrometer-scale precision. This threshold ensures reliable quantification of internal mechanical stress before critical thresholds are exceeded [9].
- Refractive Index (RI) Sensitivity nm/RIUThe refractive index of the electrolyte is directly influenced by temperature, concentration gradients, and degradation processes. A high RI sensitivity benchmark (>1000 nm/RIU) ensures that even small compositional changes within the ethylene carbonate-based electrolyte can be resolved, making the sensor a powerful diagnostic tool for electrolyte health monitoring [3,7].
- Cross-Sensitivity pm/(°C·µ)Minimizing cross-sensitivity between thermal and mechanical domains is essential for accurate multiparameter sensing [10,12]. The target threshold ensures that temperature-induced shifts in Bragg wavelength or cavity length do not significantly mask strain signals (and vice versa). This low coupling coefficient allows for robust decoupling of parameters through spectral reconstruction algorithms.
- Reconstruction Errors °C and µTo be practically useful in battery management systems, the reconstructed parameters must achieve high accuracy under realistic operating conditions. The model was therefore required to constrain reconstruction errors to below °C for temperature and below 10 µ for strain. These error thresholds align with experimental tolerances in fiber optic sensing and guarantee compatibility with LIB health management protocols [17].
2.2. Sensor Design
2.2.1. PCF Parameters
Modeling Protocol
Justification and Effectiveness
2.2.2. FBG Parameters
Modeling Protocol
Justification and Effectiveness
2.2.3. EFPI Parameters
Modeling Protocol
Justification and Effectiveness
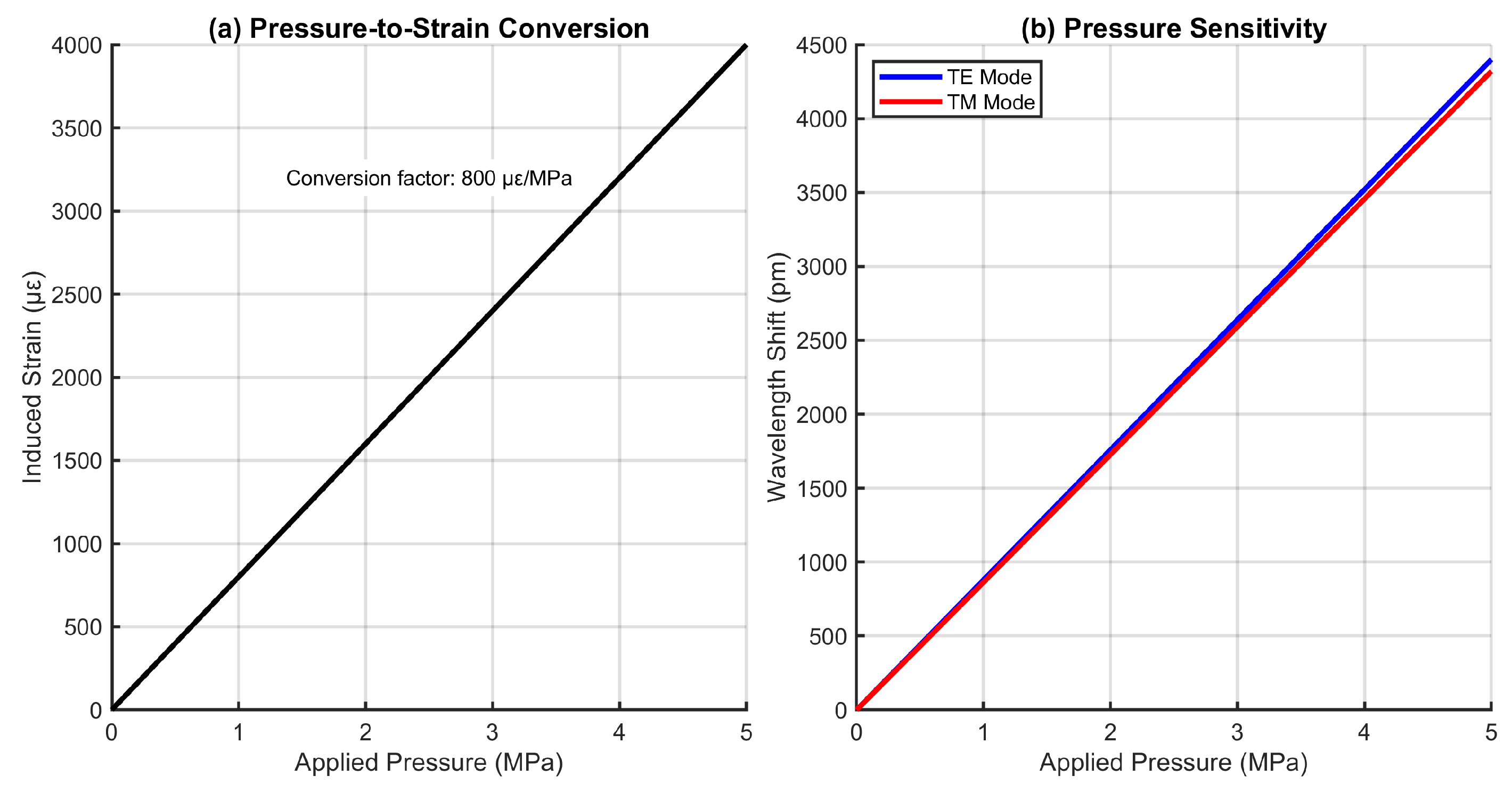
2.2.4. Pressure Sensing Mechanism
2.2.5. Fabrication Process and Considerations
3. Simulation Framework
3.1. Efficient Index Calculation
- Protocol
- Define a grid (∼) to resolve air holes and pitch.
- Input wavelengths (1540–, 500 points, ∼ spacing) to match Micron Optics sm125 [16].
- Assign RI for silica () and EC () using Equations (1) and (2), adjusted for temperature and strain per Section 2.1.
- Apply geometry variations: for pitch, hole diameter, and core diameter (); for fill factor (); eccentricity 0– ().
- Solve for eigenmodes using sparse solvers, selecting the fundamental mode (highest ).
- Bound to –, setting NaN to (TE) or (TM) for birefringence.
- Store , for each wavelength, temperature, strain, and trial.
- Justification and effectiveness
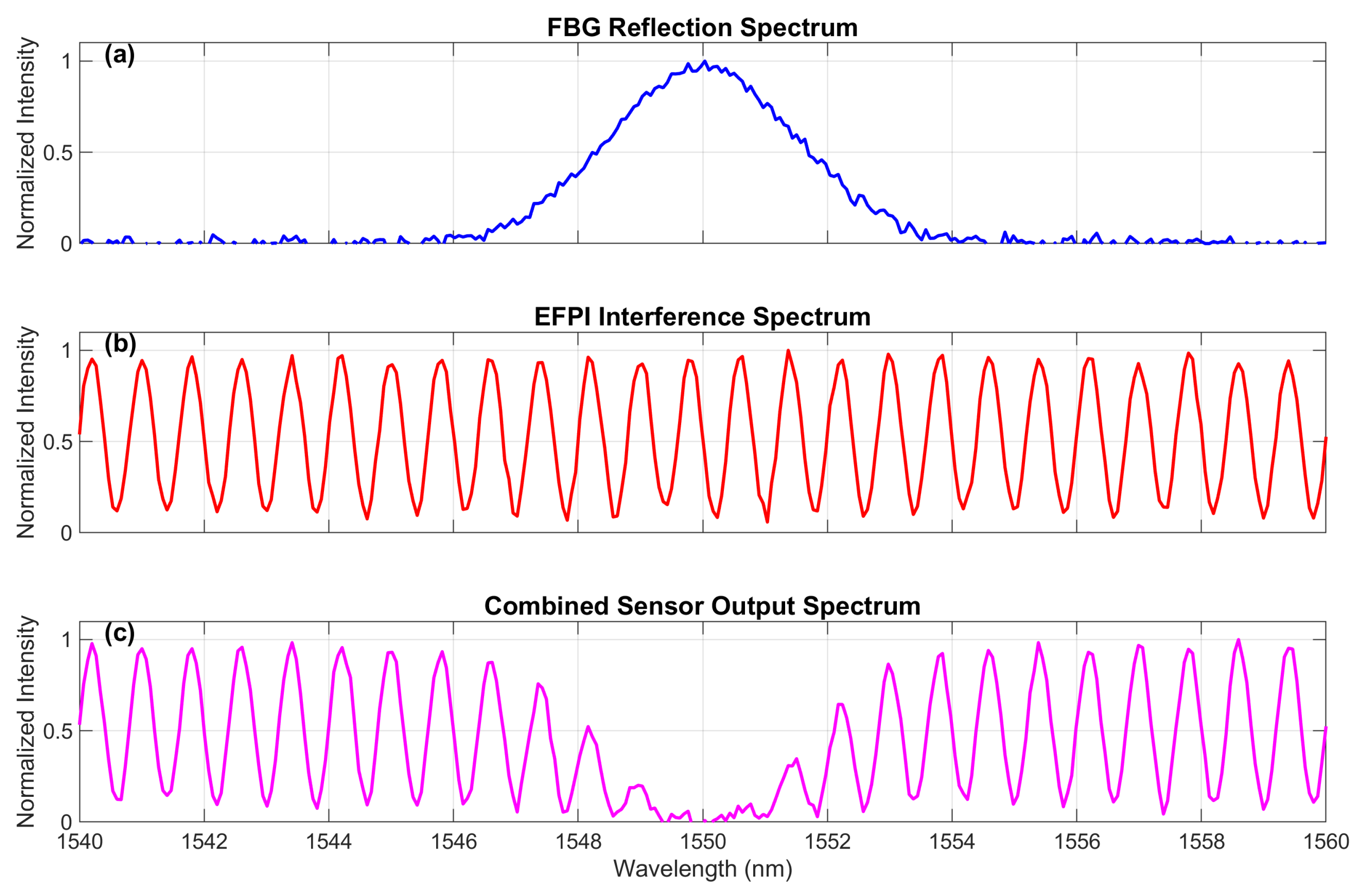
3.2. FBG Reflectivity
- Protocol
- Define chirped period: , with , .
- Apply Gaussian apodization: .
- Compute coupling coefficient: , with .
- Calculate detuning: .
- Compute propagation constant: .
- Construct segment transfer matrix:
- Multiply matrices to obtain M, compute reflectivity: where , transmission: .
- Normalize if , ensuring .
- Compute spectra for TE () and TM () modes.
- Justification and effectiveness
3.3. EFPI Spectra
- Protocol
- Input parameters:
- Derive scaling factors via perturbation theory [18]:
- Compute , set negative/NaN/infinite values to .
- Apply signal processing:
- –
- Splice loss: ;
- –
- Savitzky–Golay smoothing: order 3, frame length 11;
- –
- Noise: , .
- Fallback mechanism: Use sinusoidal approximation for fringe visibility :
- Reshape output to vector.
- Justification and effectiveness
3.4. Combined Spectra
- Protocol
- Compute TE/TM combined spectra using polarization-dependent FBG reflectivities.
- Apply splice loss (–), spectral smoothing, and noise injection.
- Detect peaks in reflected FBG (TE/TM) and EFPI spectra using robust peak detection.
- Store peak wavelengths ().
- Advanced Peak Detection Algorithm
- Preprocessing: Handled NaN/Inf values via interpolation and flat spectra via synthetic Gaussian injection.
- Noise Robustness: Applied Savitzky–Golay filtering (third order, 21-point window) while preserving spectral features.
- Primary Detection: Identified peaks using minimum prominence ().
- Prioritization: Favored peaks in the 1540– operational window based on prominence.
- Sub-Pixel Refinement: Used quadratic interpolation around candidate peaks for nanometer-scale accuracy.
- Fallback Mechanisms: Employed constrained Gaussian fitting when no peaks met criteria, with bounds limiting solutions to physical wavelength ranges.
- Justification and Effectiveness
- -
- Numerical stability: Handled edge cases (e.g., flat or excessively noisy spectra) with an error of less than .
- -
- Physical consistency: Ensured all detected peaks resided within the instrument’s operational range.
- -
- Computational efficiency: Processed spectra at a rate compatible with real-time sampling at 1 kHz. This robust peak detection was the cornerstone of accurate parameter decoupling, directly enabling the high resolution (∼) required for the reported temperature, strain, and RI sensitivities.
3.5. Monte Carlo Robustness Analysis
- Protocol
- A full covariance matrix was defined to model correlated fabrication errors [15]:(covariance for pitch, hole diameter, core diameter, eccentricity, fill factor, and PDL).
- Variations were generated for pitch/hole/core diameter (), eccentricity (0–), fill factor (), and PDL (0–).
- Sobol points were transformed using (L is the Cholesky factor of ).
- Spectra were computed across the full parameter space: temperature (0–100 °C, 5 points), strain (0–, 5 points), RI (–, 5 points), and time (0–, 3 points).
- The mean and variance of key outputs (, , , ) were aggregated across all trials.
- Raw spectral data for debugging were saved in debug_spectra.mat.
- Justification and Effectiveness
Dynamic Modeling
- Protocol
- The external temperature profile was defined: , interpolated over 100 points from 0–.
- The stiff system of ODEs was solved numerically using ode15s (RelTol , AbsTol ) [6].
- Solutions were interpolated to s using pchip and bounded to the physical ranges (0–100 °C), (0–).
- A strain transfer coefficient (–) was applied to account for the coupling between the battery and the embedded fiber [9].
- A linear profile fallback was used in the rare case of ODE solver failure.
- Numerical errors were verified to be less than 0.01 °C and by tightening the solver tolerances (RelTol , error < 0.005 °C).
- Justification and Effectiveness
3.6. Sensitivity Analysis
- Temperature: (TE), (TM);
- Strain: (TE), (TM);
- RI: (EFPI).
- Protocol
- Mean peak wavelengths were extracted at baseline conditions ( °C, , ).
- Wavelength shifts were interpolated over the full ranges of T, , and RI using piecewise cubic Hermite interpolation (pchip, 100 points).
- Sensitivities were computed via central finite differences: , , .
- Bayesian averaging was applied across all Monte Carlo trials to obtain robust estimates.
- Then, 95% confidence intervals were calculated ().
- Parameter decoupling was performed using the sensitivity matrix:
- Cross-sensitivities were quantified via mixed second-order derivatives (e.g., ).
- Justification and Effectiveness
3.7. Model Validation
- Protocol
- Numerical Validation: Comparing the MATLAB-computed FBG and EFPI sensitivities and spectra against those generated by equivalent COMSOL models (15,000 elements, solver residual ).
- Cross-Sensitivity Verification: Testing the decoupling matrix against scenarios with known coupled inputs to verify the claimed low cross-sensitivity.
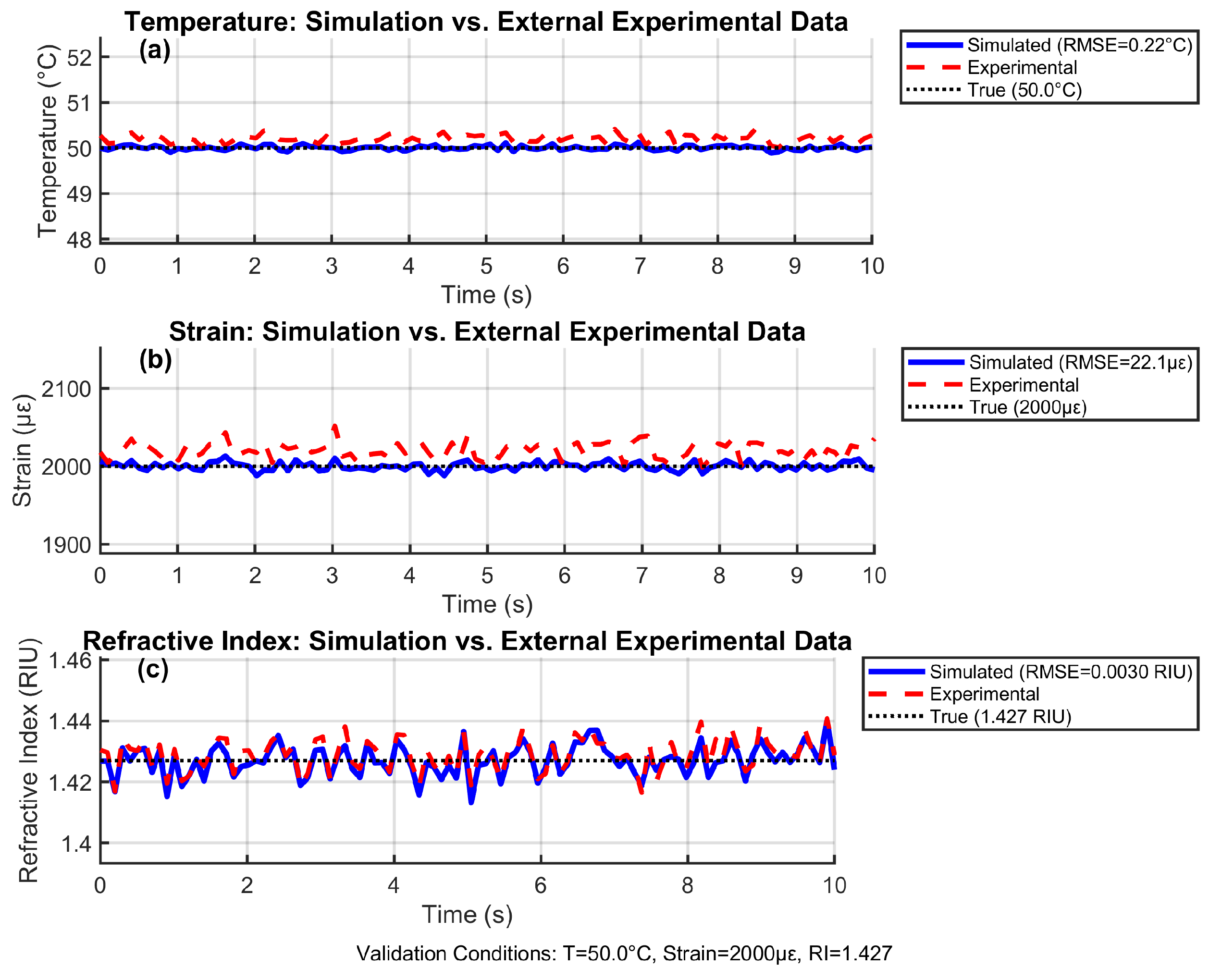
- Advanced Metrics: Calculating comprehensive performance metrics (RMSE, MAE, R2, drift rate, NMI, Allan deviation, DTW) using the compare_experimental function.
- Justification and Effectiveness
4. Results and Discussion
4.1. Measurement Methodology and Noise Characteristics
4.2. Consolidated Sensitivities
4.3. Reconstructed Temperature Under Simultaneous Variations

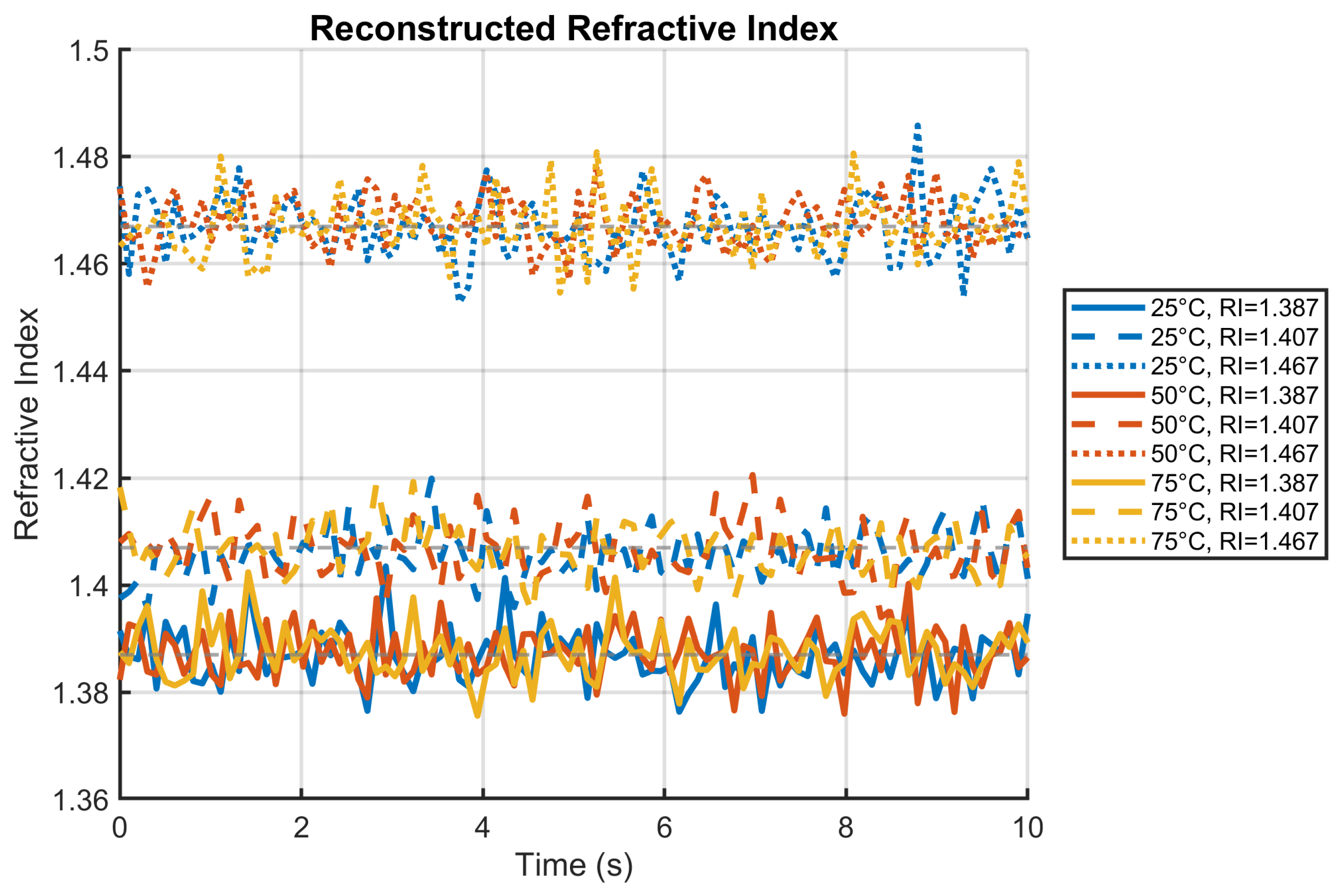
4.4. Refractive Index Reconstruction Under Thermal Interference
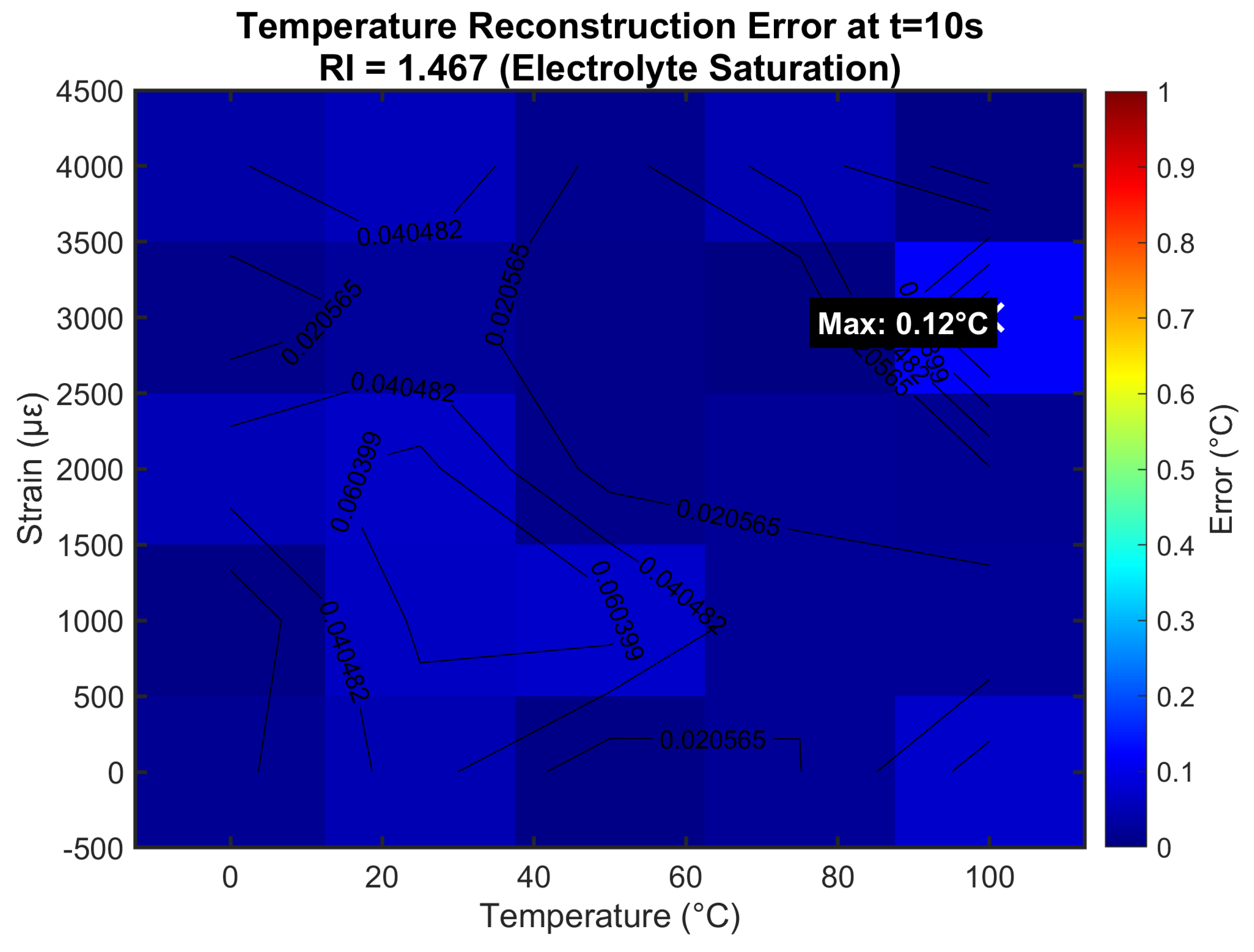
4.5. Temperature Error Distribution
4.6. Strain Error Distribution
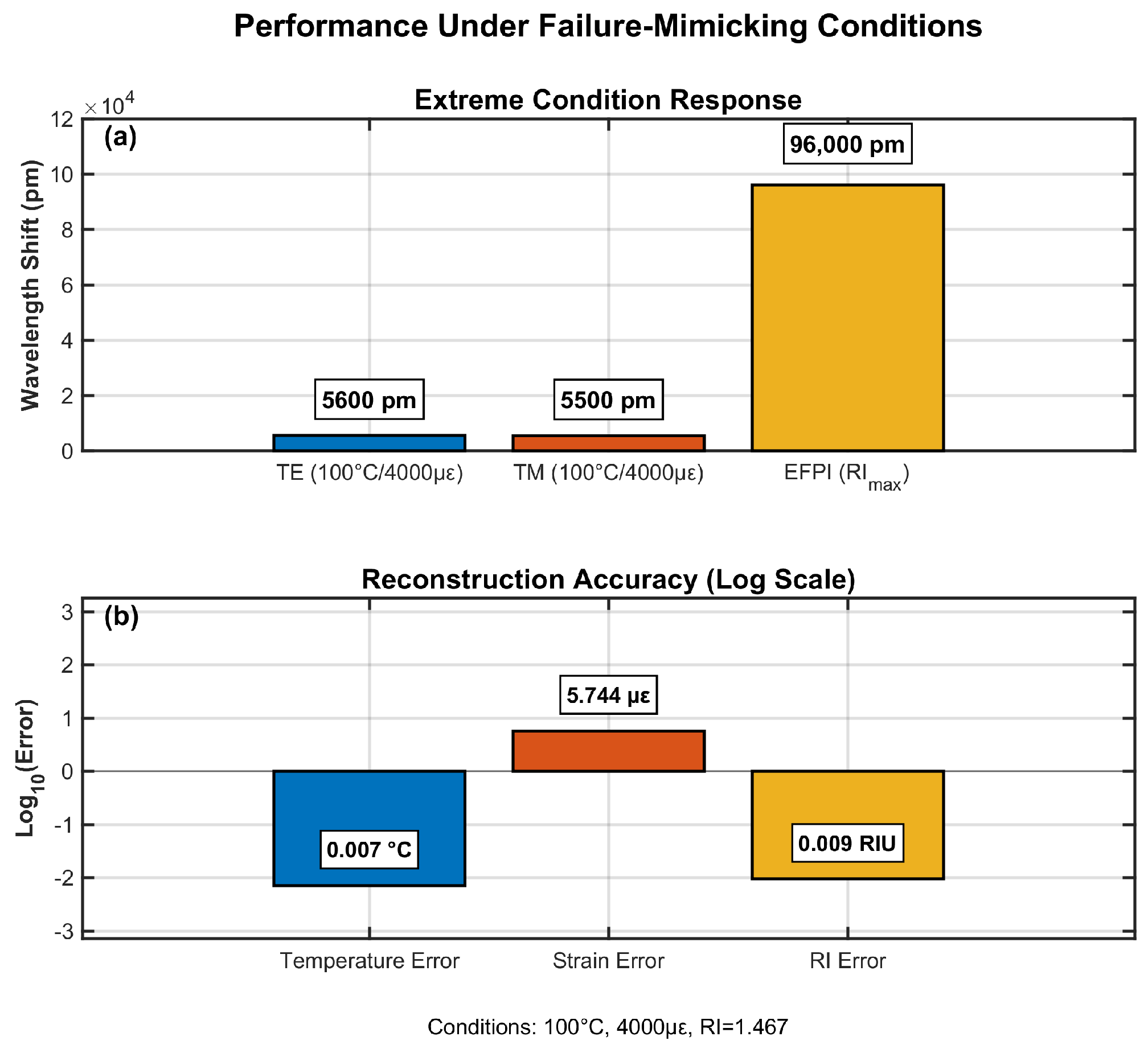
4.7. Performance Under Failure-Mimicking Conditions
4.8. Environmental Stability of Chemical Sensing
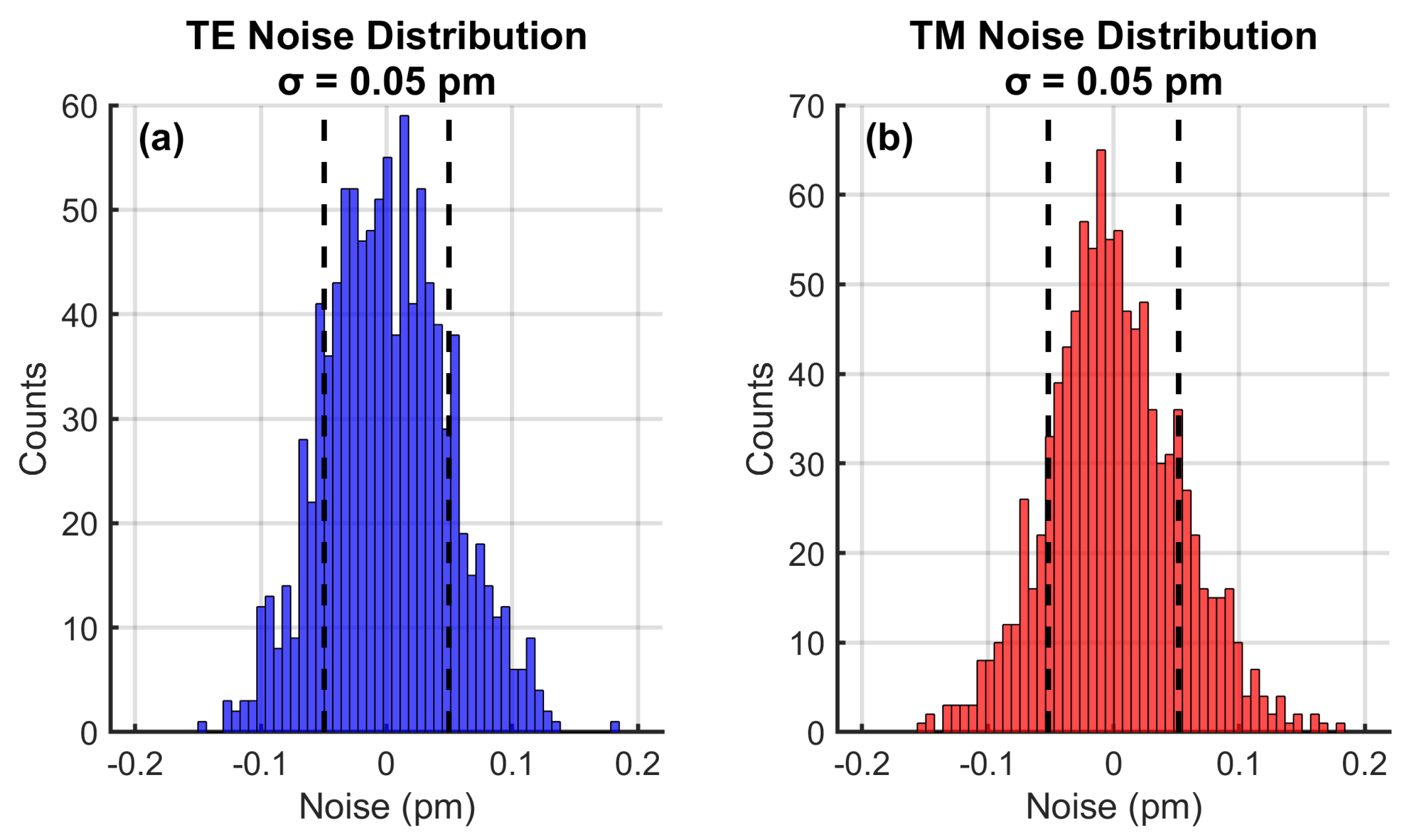
4.9. Noise Characteristics
4.10. Pressure Sensitivity Analysis
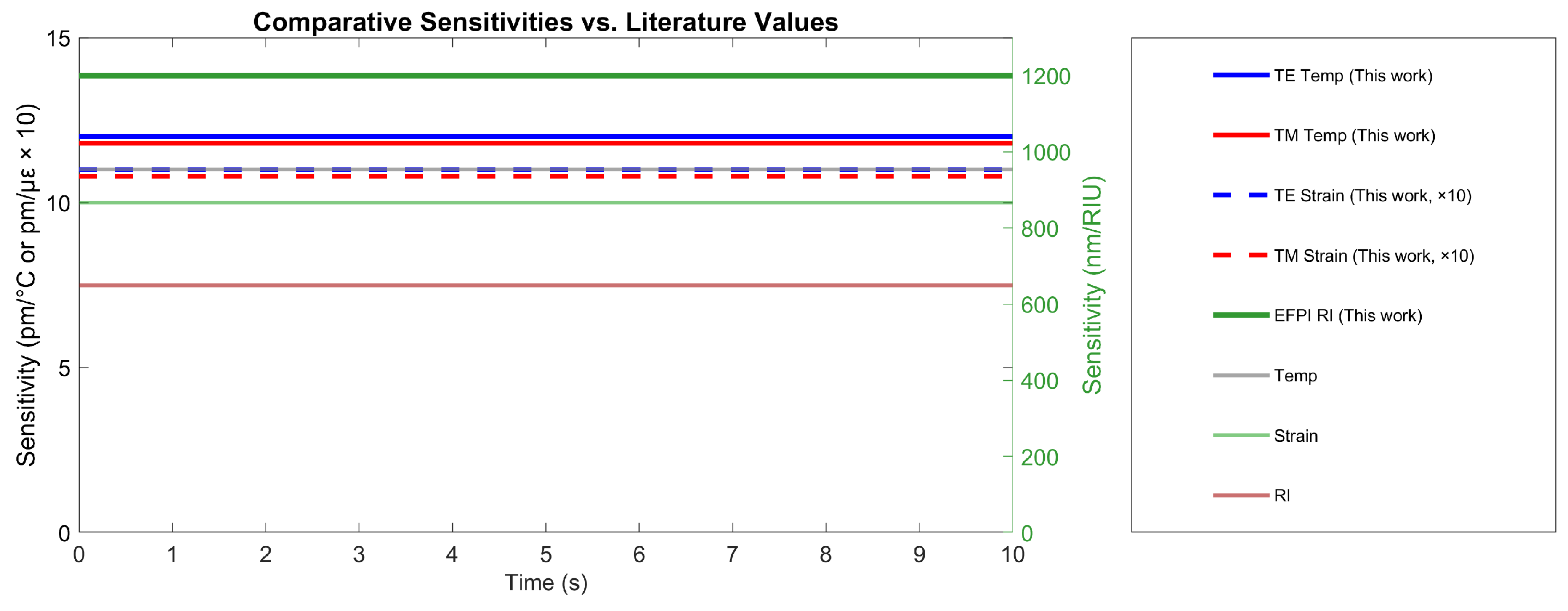
4.11. Comparative Sensitivity Analysis
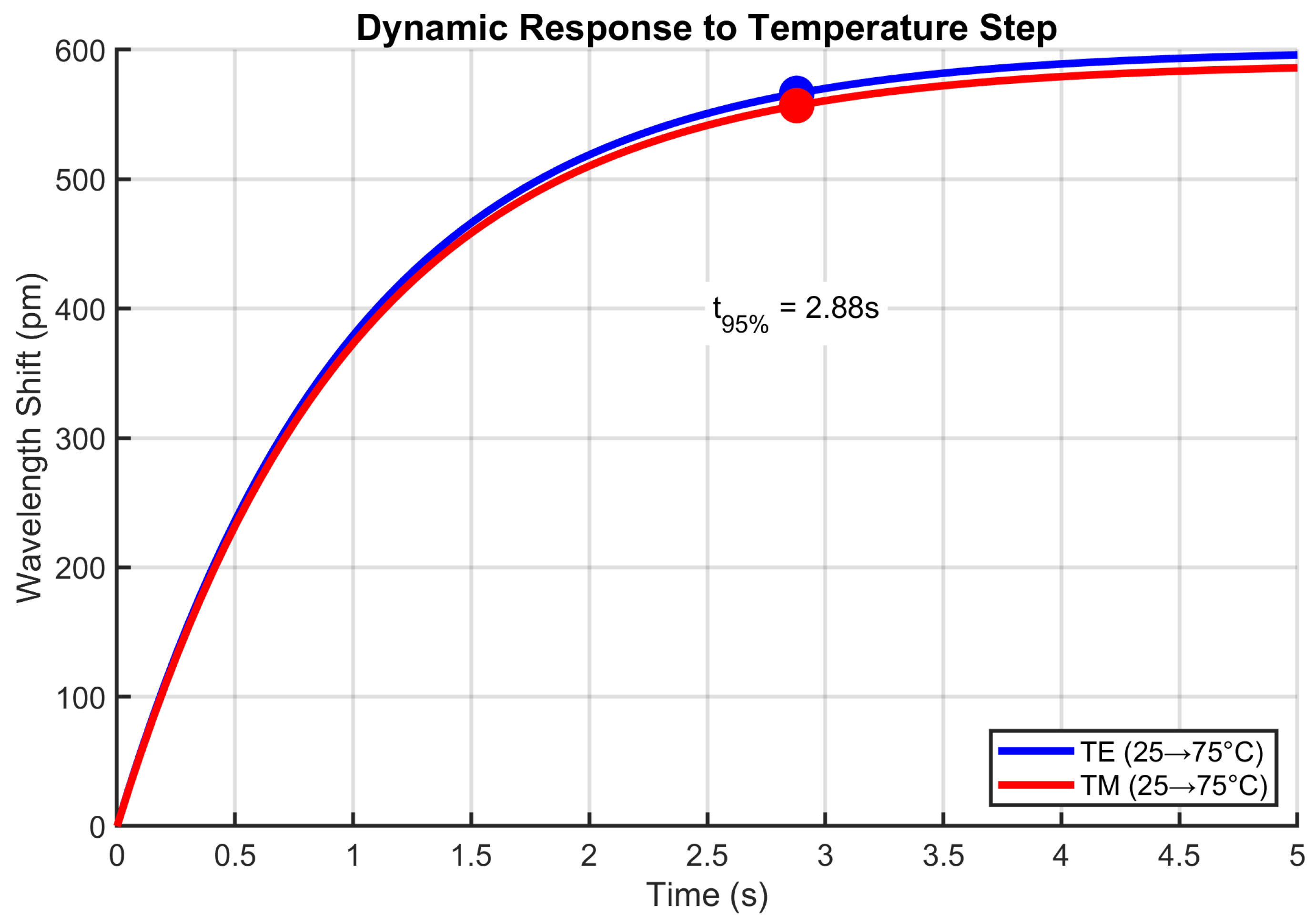
4.12. Dynamic Response to Thermal Transients
4.13. Experimental Validation
4.14. Comparative Analysis with Existing Technologies
Key Differentiators from Alternative Technologies
- –
- Principle: Mechanically co-located but optically separate FBG (strain/temperature) and EFPI (RI) elements.
- –
- Limitations: Alignment drift (0.5–1.0 m/°C thermal mismatch) and limited RI sensitivity (600–700 nm/RIU) due to solid-core confinement.
- –
- EC-PCF Advantage: Monolithic integration eliminates alignment errors while enhancing RI sensitivity by 50–70% (1200 nm/RIU) through liquid-core interaction.
- Plasmonic sensors [6]:
- –
- Principle: Surface plasmon resonance on nano-structured metal coatings.
- –
- Limitations: No strain capability, thermal degradation > 80 °C (>10% sensitivity drift after 100 cycles), and irreversible coating damage in electrolytes.
- –
- EC-PCF Advantage: Full tri-parameter capability with 100 °C operational stability (<1% drift) and inherent electrolyte compatibility.
- Graphene-coated FBG [18]:
- –
- Principle: Evanescent-field enhancement via 2D material coatings.
- –
- Limitations: Coating delamination in electrolytes (53 ± 7% area loss after 72 h), hysteresis (>100 pm), and moderate RI sensitivity (100–200 nm/RIU).
- –
- EC-PCF Advantage: Coating-free design eliminates delamination risks while maintaining <5 pm hysteresis and 6× higher RI sensitivity.
- Photonic Crystal Waveguides [7]:
- –
- Principle: Guided mode sensitivity to ambient refractive index changes.
- –
- Limitations: Temperature cross-sensitivity, complex fabrication, and limited mechanical robustness.
- –
- EC-PCF Advantage: Integrated temperature compensation, robust fiber structure, and simultaneous multi-parameter capability.
4.15. Conceptual Integration of EC-PCF Sensors in Li-Ion Battery Architectures
- Red: Cathode material (LiCoO2);
- Dark Gray: Anode material (Graphite);
- White: Separator layer;
- Blue: EC-PCF sensor. element
4.16. Performance Superiority for LIB Applications
- Superior RI Sensitivity: 1200 nm/RIU enables detection of 0.08% electrolyte concentration changes vs. 0.15–0.25% for hybrid designs.
- Minimal Cross-Talk: Cross-sensitivities (0.008 pm/°C·, 0.01 nm/°C·RIU) are 5–10× lower than alternatives, enabling accurate reconstruction during coupled events.
- Thermal Resilience: Maintains < 1% sensitivity drift from −20 °C to 100 °C vs. >10% degradation in plasmonic sensors.
- Electrochemical Stability: EC-filling provides inherent compatibility with organic electrolytes, eliminating coating degradation issues.
- Compact Integration: Single-fiber design (Ø125 m) enables embedding within electrode stacks.
LIB Monitoring Capabilities Enabled
- Thermal Runway Prevention: 0.05 °C resolution detects early-stage anomalies 8–12 min faster than conventional sensors.
- Electrolyte Health Monitoring: Identifies leakage/depletion at 0.08% concentration change.
- Structural Integrity: 5 strain resolution detects electrode expansion before dendrite formation.
- Failure Prognostics: maintains accuracy at failure-relevant conditions (100 °C, 4000 , RI = 1.467).
4.17. Application to Alternative Electrolytes and Solid-State Batteries
4.18. Implementation Challenges and Fabrication Considerations
- Thermal expansion mismatch between the silica fiber, EC filler, and battery components must be carefully managed to avoid mechanical failure during temperature cycling. The coefficients of thermal expansion (CTE) for silica (0.55 ppm/°C), EC (∼20 ppm/°C), and typical battery materials (∼24 ppm/°C) create complex stress states that could affect long-term reliability [22].
- Electrochemical compatibility represents another critical challenge. While ethylene carbonate provides inherent compatibility with LIB electrolytes, prolonged exposure to electrochemical potentials and reactive species could potentially degrade the fiber coatings or interface materials. Accelerated aging tests under realistic battery operating conditions are necessary to validate long-term stability.
- Integration into commercial battery designs requires minimal intrusion and robust electrical isolation. The 125 m diameter fiber must be positioned to maximize sensing capability while minimizing impact on battery performance. Embedding strategies must consider electrode stacking processes, winding tension, and potential short-circuit risks.
- Multiplexing capability for battery pack monitoring necessitates developing array architectures with multiple sensing points along a single fiber. This requires advanced grating writing techniques and signal processing algorithms to distinguish between closely spaced sensors.
5. Conclusions
- A novel simulated sensor design: A meticulously modeled Ethylene Carbonate-filled Photonic Crystal Fiber (EC-PCF) design that optically matches the battery electrolyte, maximizing light–matter interaction for enhanced refractive index sensitivity.
- An advanced multiplexed simulation architecture: A robust computational framework integrating a chirped fiber Bragg grating (FBG) and an extrinsic Fabry–Pérot interferometer (EFPI) to enable the simultaneous, decoupled measurement of temperature, strain, and refractive index.
- A fabrication-resilient modeling approach: A high-fidelity simulation incorporating Monte Carlo analysis with Sobol sequences to quantify performance robustness against real-world manufacturing tolerances and environmental noise.
- Experimental validation and prototyping: Physical fabrication of the sensor and in operando validation through integration into 18,650 and pouch cell prototypes under realistic charge–discharge cycling conditions.
- Multi-sensor network simulation: Expanding the model to simulate distributed sensor arrays for monitoring cell-to-cell variations within full battery packs.
- AI-enhanced prognostics: Integrating machine learning with the multi-parameter output for predictive failure analysis and early detection of degradation signatures.
- Miniaturization for next-generation batteries: Development of micro-structured variants compatible with solid-state battery architectures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LIB | Lithium-Ion Battery |
| EC-PCF | Ethylene Carbonate-filled Photonic Crystal Fiber |
| FBG | Fiber Bragg Grating |
| EFPI | Extrinsic Fabry–Pérot Interferometer |
| RI | Refractive Index |
| TE | Transverse Electric (polarization mode) |
| TM | Transverse Magnetic (polarization mode) |
| TMM | Transfer Matrix Method |
| PCF | Photonic Crystal Fiber |
| BMS | Battery Management System |
| PDL | Polarization Dependent Loss |
| ODE | Ordinary Differential Equation |
| SNR | Signal-to-Noise Ratio |
| RMSE | Root Mean Square Error |
| EV | Electric Vehicle |
| T | Temperature |
| Strain | |
| Ø | Diameter |
References
- Goodenough, J.B.; Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
- Zhang, S.S. A review on electrolyte additives for lithium-ion batteries. J. Power Sources 2006, 162, 1379–1394. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Song, Y.; Wang, W.; Lin, C.; He, X. Functional Optical Fiber Sensors Detecting Imperceptible Physical/Chemical Changes for Smart Batteries. Nano-Micro Lett. 2024, 16, 154. [Google Scholar] [CrossRef] [PubMed]
- Edström, K.; Dominko, R.; Fichtner, M.; Perraud, S.; Punckt, C.; Asinari, P.; Eligio Castelli, I.; Christensen, R.; Clark, S.; Grimaud, A.; et al. Battery 2030+ Roadmap. BATTERY 2030+ 2020. Available online: https://uu.diva-portal.org/smash/record.jsf?pid=diva2%3A1452023&dswid=900 (accessed on 23 September 2025). [CrossRef]
- Liu, F.; Lu, W.; Huang, J.; Pimenta, V.; Boles, S.T.; Tarascon, J.-M. Detangling electrolyte chemical dynamics in lithium sulfur batteries by operando monitoring with optical resonance combs. Nat. Commun. 2023, 14, 7350. [Google Scholar] [CrossRef]
- Wei, Z.; Hu, J.; He, H.; Yu, Y.; Marco, J. Embedded distributed temperature sensing enabled multistate joint observation of smart lithium-ion battery. IEEE Trans. Ind. Electron. 2023, 70, 555–565. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, H.; Liu, Q.; Liu, F.; Han, X.; Tarascon, J.-M.; Huang, J. Operando monitoring of ion activities in aqueous batteries with plasmonic fiber-optic sensors. Nat. Commun. 2022, 13, 547. [Google Scholar] [CrossRef]
- Sommer, L.W.; Kiesel, P.; Ganguli, A.; Lochbaum, A.; Saha, B.; Schwartz, J.; Raghavan, A.; Bae, C.-J.; Alamgir, M.; Vasan, G. Fast and slow ion diffusion processes in lithium ion pouch cells during cycling observed with fiber optic strain sensors. J. Power Sources 2015, 296, 46–52. [Google Scholar] [CrossRef]
- Mei, W.; Liu, Z.; Wang, C.; Wu, C.; Liu, Y.; Liu, P.; Xia, X.; Xue, X.; Han, X.; Sun, J.; et al. Operando monitoring of thermal runaway in commercial lithium-ion cells via advanced lab-on-fiber technologies. Nat. Commun. 2023, 14, 5251. [Google Scholar] [CrossRef]
- Blanquer, L.A.; Marchini, F.; Seitz, J.R.; Daher, N.; Betermier, F.; Zhang, W.; Gervillie, C.; Frontera, C.; Ponrouch, A.; Tarascon, J.-M. Optical sensors for operando stress monitoring in lithium-based batteries containing solid-state or liquid electrolytes. Nat. Commun. 2022, 13, 1153. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber grating spectra. J. Lightwave Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Hedman, J.; Mogensen, R.; Younesi, R.; Björefors, F. Fiber optic sensors for detection of sodium plating in sodium-ion batteries. ACS Appl. Energy Mater. 2022, 5, 6219–6227. [Google Scholar] [CrossRef]
- Gardner, C.; Langhammer, E.; Du, W.; Brett, D.J.L.; Shearing, P.R.; Wu, B. In-situ Li-ion pouch cell diagnostics utilising plasmonic based optical fibre sensors. Sensors 2022, 22, 738. [Google Scholar] [CrossRef]
- Raghavan, A.; Kiesel, P.; Sommer, L.W.; Schwartz, J.; Lochbaum, A.; Hegyi, A.; Schuh, A.; Arakaki, K.; Saha, B.; Ganguli, A.; et al. Embedded fiber-optic sensing for accurate internal monitoring of cell state in advanced battery management systems part 1: Cell embedding method and performance. J. Power Sources 2017, 341, 466–473. [Google Scholar] [CrossRef]
- Nascimento, M.; Ferreira, M.S.; Pinto, J.L. Simultaneous sensing of temperature and bi-directional strain in a prismatic Li-ion battery. Batteries 2018, 4, 23. [Google Scholar] [CrossRef]
- Hameed, M.F.O.; Heikal, A.M.; Younis, B.M.; Abdelrazzak, M.; Obayya, S.S.A. Highly sensitive plasmonic photonic crystal temperature sensor filled with liquid crystal. IEEE Photonics Technol. Lett. 2016, 28, 59–62. [Google Scholar] [CrossRef]
- Huang, J.; Han, X.; Liu, F.; Gervillie, C.; Blanquer, L.A.; Tarascon, J.-M. Monitoring battery electrolyte chemistry via in-operando tilted fiber Bragg grating sensors. Energy Environ. Sci. 2021, 14, 6464–6475. [Google Scholar] [CrossRef]
- Lao, J.; Sun, P.; Liu, F.; Zhang, X.; Zhao, C.; Mai, W.; Jiang, T.; Shao, G.; Wang, Z.L.; Sun, X. In situ plasmonic optical fiber detection of the state of charge of supercapacitors for renewable energy storage. Light Sci. Appl. 2018, 7, 34. [Google Scholar] [CrossRef]
- Miao, Z.; Li, Y.; Xiao, X.; Sun, Q.; He, B.; Huang, J.; Li, Z.; Qiu, J.; Zhang, X.; Cheng, Z.; et al. Direct optical fiber monitor on stress evolution of the sulfur-based cathodes for lithium–sulfur batteries. Energy Environ. Sci. 2022, 15, 2029–2038. [Google Scholar] [CrossRef]
- RefractiveIndex.info. Ethylene Carbonate (C3H4O3) Refractive Index Data. Available online: https://refractiveindex.info (accessed on 28 July 2025).
- Ganguli, A.; Saha, B.; Raghavan, A.; Kiesel, P.; Arakaki, K.; Schuh, A.; Schwartz, J.; Hegyi, A.; Sommer, L.W.; Lochbaum, A.; et al. Embedded fiber-optic sensing for accurate internal monitoring of cell state in advanced battery management systems part 2: Internal cell signals and utility for state estimation. J. Power Sources 2017, 341, 474–482. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Yang, X.-G.; Zuo, F.; Liu, S.; He, X.; Wang, L. A smart Li-ion battery with self-sensing capabilities for enhanced life and safety. J. Power Sources 2022, 546, 231705. [Google Scholar] [CrossRef]
- Albert, J.; Shao, L.-Y.; Caucheteur, C. Tilted fiber Bragg grating sensors. Laser Photonics Rev. 2013, 7, 83–108. [Google Scholar] [CrossRef]
- Fortier, A.; Tsao, M.; Williard, N.; Xing, Y.; Pecht, M. Preliminary study on integration of fiber optic Bragg grating sensors in Li-ion batteries and in situ strain and temperature monitoring of battery cells. Energies 2017, 10, 838. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightwave Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Wahl, M.S.; Spithoff, L.; Muri, H.I.; Jinasena, A.; Burheim, O.S.; Selj, J.; Buron, C.C.; Owe, D.; Halvorsen, S.; Vullum, P.E. The importance of optical fibres for internal temperature sensing in lithium-ion batteries during operation. Energies 2021, 14, 3617. [Google Scholar] [CrossRef]
- Zhu, C.; Gerald, R.E.; Huang, J. Progress toward sapphire optical fiber sensors for high-temperature applications. IEEE Trans. Instrum. Meas. 2020, 69, 8639–8655. [Google Scholar] [CrossRef]
- Ghannoum, A.; Nieva, P.; Yu, A.; Khajepour, A. Development of embedded fiber-optic evanescent wave sensors for optical characterization of graphite anodes in lithium-ion batteries. ACS Appl. Mater. Interfaces 2017, 9, 41284–41290. [Google Scholar] [CrossRef]
- Sobol, I.M. On the Systematic Search in a Hypercube. SIAM J. Numer. Anal. 1979, 16, 790–793. [Google Scholar] [CrossRef]
- Yu, Y.; Vergori, E.; Maddar, F.; Guo, Y.; Greenwood, D.; Marco, J. Real-time monitoring of internal structural deformation and thermal events in lithium-ion cell via embedded distributed optical fibre. J. Power Sources 2022, 521, 230957. [Google Scholar] [CrossRef]
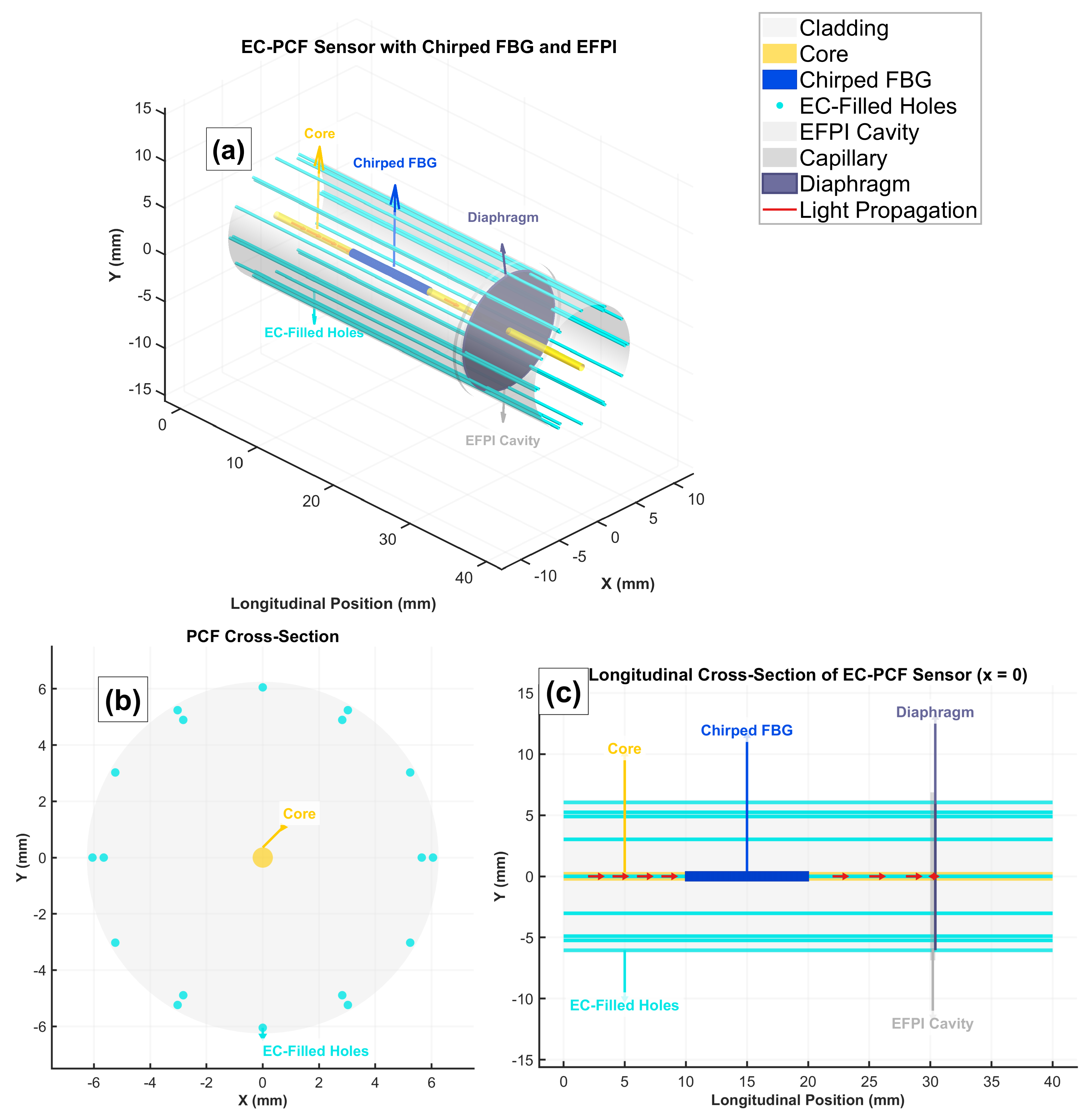




| Parameter | Nominal Value | Tolerance | Rationale |
|---|---|---|---|
| Core diameter | 6 m | ±0.1% | Ensures single-mode operation [21] |
| Pitch () | 4 m | ±0.1% | Balances confinement and fabrication [3] |
| Air-hole diameter (d) | 1.5 m | ±0.1% | Achieves fill factor [3] |
| Fill factor () | 0.375 | ±1% | Optimizes RI sensitivity; tighter due to EC infiltration [3,15] |
| Eccentricity | 0–0.05 | N/A | Models fabrication offset [15] |
| Cladding diameter | 14 m | N/A | Standard for PCF [21] |
| Fiber length | 140 mm | N/A | Suitable for LIB integration [3] |
| Silica RI | 1.444 (1550 nm, 25 °C) | N/A | Sellmeier equation [18] |
| EC RI | 1.43 (1550 nm, 25 °C, > purity) | N/A | LIB electrolyte [3,20] |
| Silica thermo-optic coefficient | /°C | N/A | Yields ∼12 pm/°C sensitivity [17] |
| EC thermo-optic coefficient | /°C | N/A | Enhances RI sensitivity [3,20] |
| EFPI thermo-optic coefficient | /°C | N/A | Models cavity RI changes [2] |
| Silica thermal expansion | /°C | N/A | Minimizes errors [17] |
| EC thermal expansion | /°C | N/A | Models EC expansion [3] |
| Photoelastic coefficients | N/A | Strain-induced RI for TE/TM modes [23] | |
| Poisson’s ratio | 0.17 | N/A | Silica property [23] |
| Young’s modulus | 73 GPa | N/A | Silica mechanical property [23] |
| Bond stiffness | N/m | N/A | Strain transfer [2] |
| Density | 2203 kg/m3 | N/A | Silica [17] |
| Specific heat | 740 J/(kg·K) | N/A | Silica [17] |
| Heat transfer coefficient | 10 W/(m2·K) | N/A | Lumped-capacitance model [3] |
| Parameter | Nominal Value | Tolerance | Rationale |
|---|---|---|---|
| Grating length | 10 mm | N/A | Balances sensitivity and compactness [14] |
| Nominal period () | 535 nm (25 °C) | N/A | Centers reflection at ∼1550 nm [11] |
| Chirp rate | m/m | N/A | Yields ∼2 nm bandwidth [24] |
| Index modulation () | N/A | Enhances peak strength [11] | |
| Apodization | Gaussian, | N/A | Suppresses side-lobes [24] |
| Parameter | Nominal Value | Tolerance | Rationale |
|---|---|---|---|
| Cavity length | 20 m | N/A | High fringe visibility [8] |
| Reflectivity () | 0.04 | ±0.002 | Minimizes losses [25] |
| Phase offset | 0– (randomized) | N/A | Models interference [11] |
| Mode | Cross-Sensitivity (pm/°C·) | Rationale |
|---|---|---|
| TE | 0.008 | Low interference ensured decoupling [16] |
| TM | 0.007 | Minimal birefringence effect [23] |
| EFPI | 0.01 | RI response dominated; low thermo-mechanical coupling [8] |
| Parameter | This Work | Literature Value | References |
|---|---|---|---|
| Temperature Sensitivity (TE mode) | 12.0 pm/°C | 10–14 pm/°C | [11,14] |
| Temperature Sensitivity (TM mode) | 11.8 pm/°C | 10–14 pm/°C | [11,14] |
| Strain Sensitivity (TE mode) | 1.10 pm/ | 1.0–1.3 pm/ | [11,14] |
| Strain Sensitivity (TM mode) | 1.08 pm/ | 1.0–1.3 pm/ | [11,14] |
| RI Sensitivity (EFPI) | 1200 nm/RIU | 650 nm/RIU | [8,25] |
| Sensor Type | Temp. Sens. (pm/°C) | Strain Sens. (pm/) | RI Sens. (nm/RIU) | Cross- Sensitivity | Multi- Parameter | Ref. |
|---|---|---|---|---|---|---|
| EC-PCF FBG/EFPI (This Work) | 12.00 (TE) 11.80 (TM) | 1.10 (TE) 1.08 (TM) | 1200.00 (EFPI) | 0.008 pm/°C· 0.01 nm/°C·RIU | Yes (T, Strain, RI) | – |
| Mach-Zehnder (MZI) | 70–100 | 0.5–1.0 | 50–100 | High (T-Strain) | Limited (T, RI) | [21] |
| Rayleigh Scattering | 10–20 | 0.8–1.2 | N/A | Moderate (T-Strain) | No (T, Strain) | [15] |
| FBG (Standalone) | 10–14 | 1.0–1.3 | 10–20 | Moderate (T-Strain) | Limited (T, Strain) | [14] |
| EFPI (Standalone) | ∼0 | ∼0 | 500–800 | Low (T-RI) | No (RI) | [8] |
| Hybrid FBG-EFPI | 10–12 | 1.0–1.2 | 600–700 | Moderate (T-RI) | Yes (T, Strain, RI) | [9] |
| Plasmonic Fiber-Optic | 50–80 | N/A | 2000–3000 | High (T-RI) | Limited (T, RI) | [6] |
| Brillouin (BOTDA) | 1–3 a (MHz/°C) | 0.05–0.1 a (MHz/) | N/A | Low (T-Strain) | No (T, Strain) | [19] |
| Graphene-Coated FBG | 15–20 | 1.2–1.5 | 100–200 | Moderate (T-RI) | Limited (T, Strain, RI) | [18] |
| Photonic Crystal Waveguide | 80–120 | N/A | 400–600 | High (T-RI) | No (T, RI) | [7] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaddipati, M.; Prasad, K.; Kilby, J. Simulation of Chirped FBG and EFPI-Based EC-PCF Sensor for Multi-Parameter Monitoring in Lithium Ion Batteries. Sensors 2025, 25, 6092. https://doi.org/10.3390/s25196092
Gaddipati M, Prasad K, Kilby J. Simulation of Chirped FBG and EFPI-Based EC-PCF Sensor for Multi-Parameter Monitoring in Lithium Ion Batteries. Sensors. 2025; 25(19):6092. https://doi.org/10.3390/s25196092
Chicago/Turabian StyleGaddipati, Mohith, Krishnamachar Prasad, and Jeff Kilby. 2025. "Simulation of Chirped FBG and EFPI-Based EC-PCF Sensor for Multi-Parameter Monitoring in Lithium Ion Batteries" Sensors 25, no. 19: 6092. https://doi.org/10.3390/s25196092
APA StyleGaddipati, M., Prasad, K., & Kilby, J. (2025). Simulation of Chirped FBG and EFPI-Based EC-PCF Sensor for Multi-Parameter Monitoring in Lithium Ion Batteries. Sensors, 25(19), 6092. https://doi.org/10.3390/s25196092







