Visuomotor Control Accuracy of Circular Tracking Movement According to Visual Information in Virtual Space
Abstract
1. Introduction
2. Materials and Methods
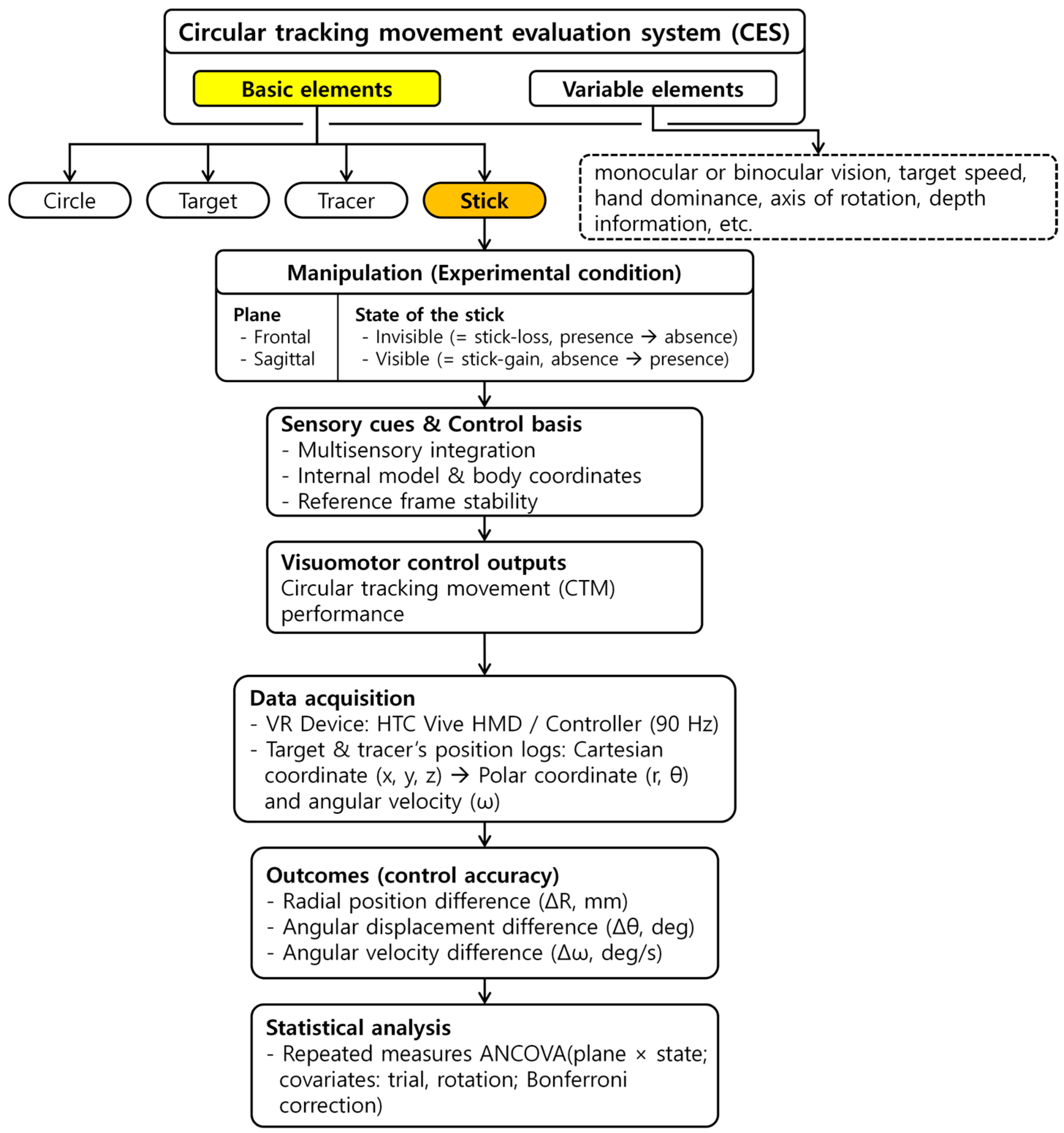
2.1. Research Framework
2.2. Participants
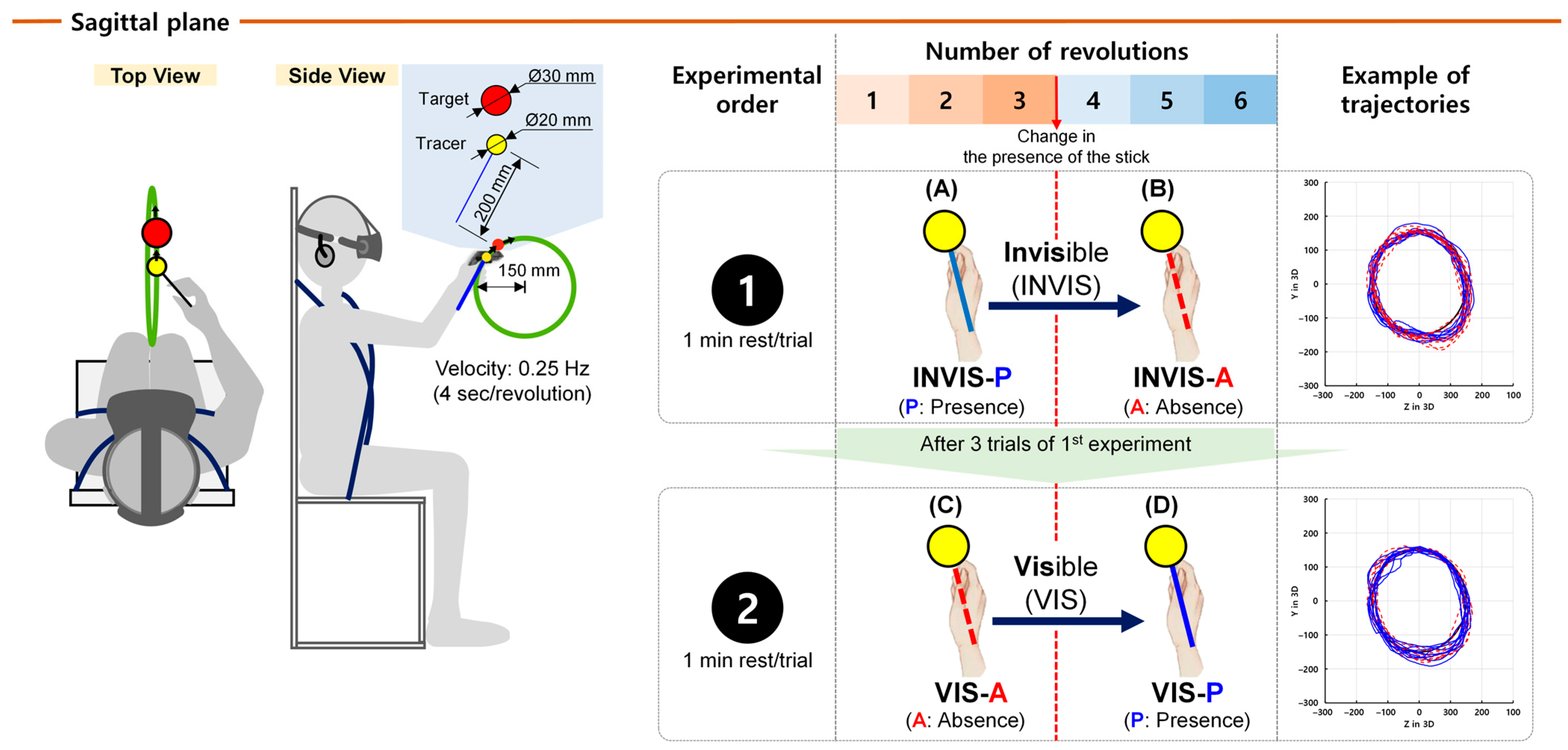
2.3. Experimental Task
2.4. Data Analysis
3. Results
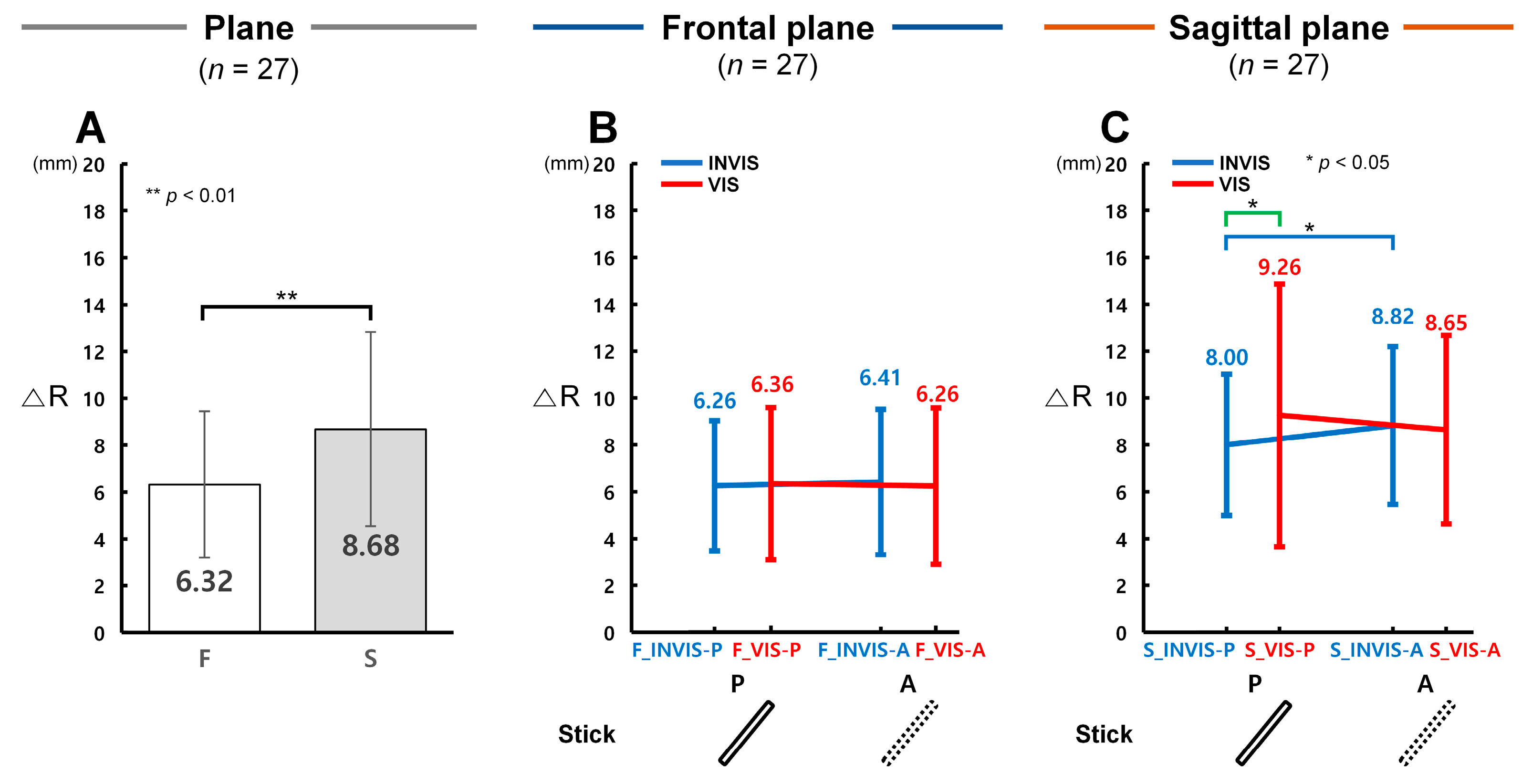
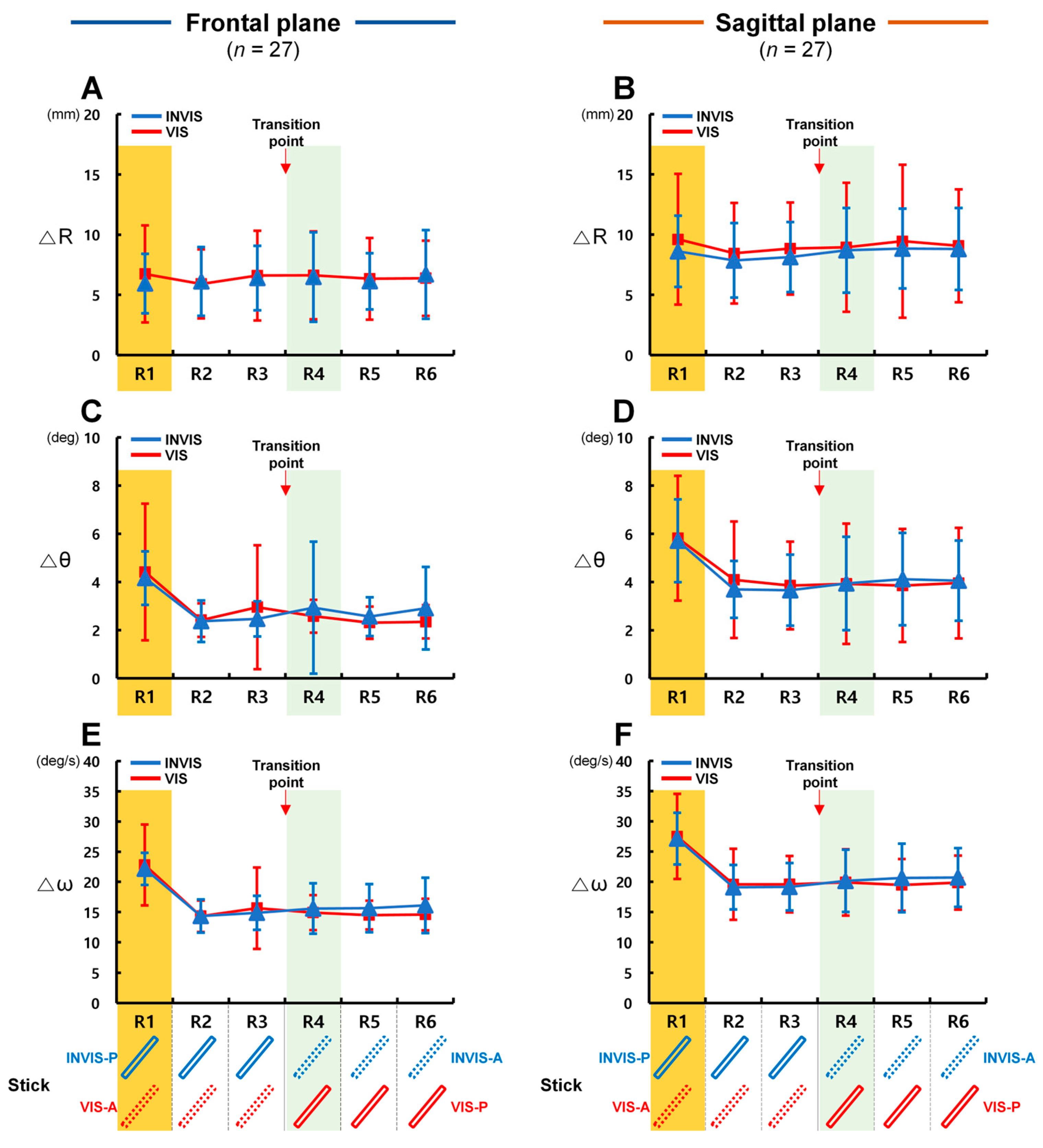
3.1. Control Accuracy in Terms of ΔR with the Presence of the Stick in CES
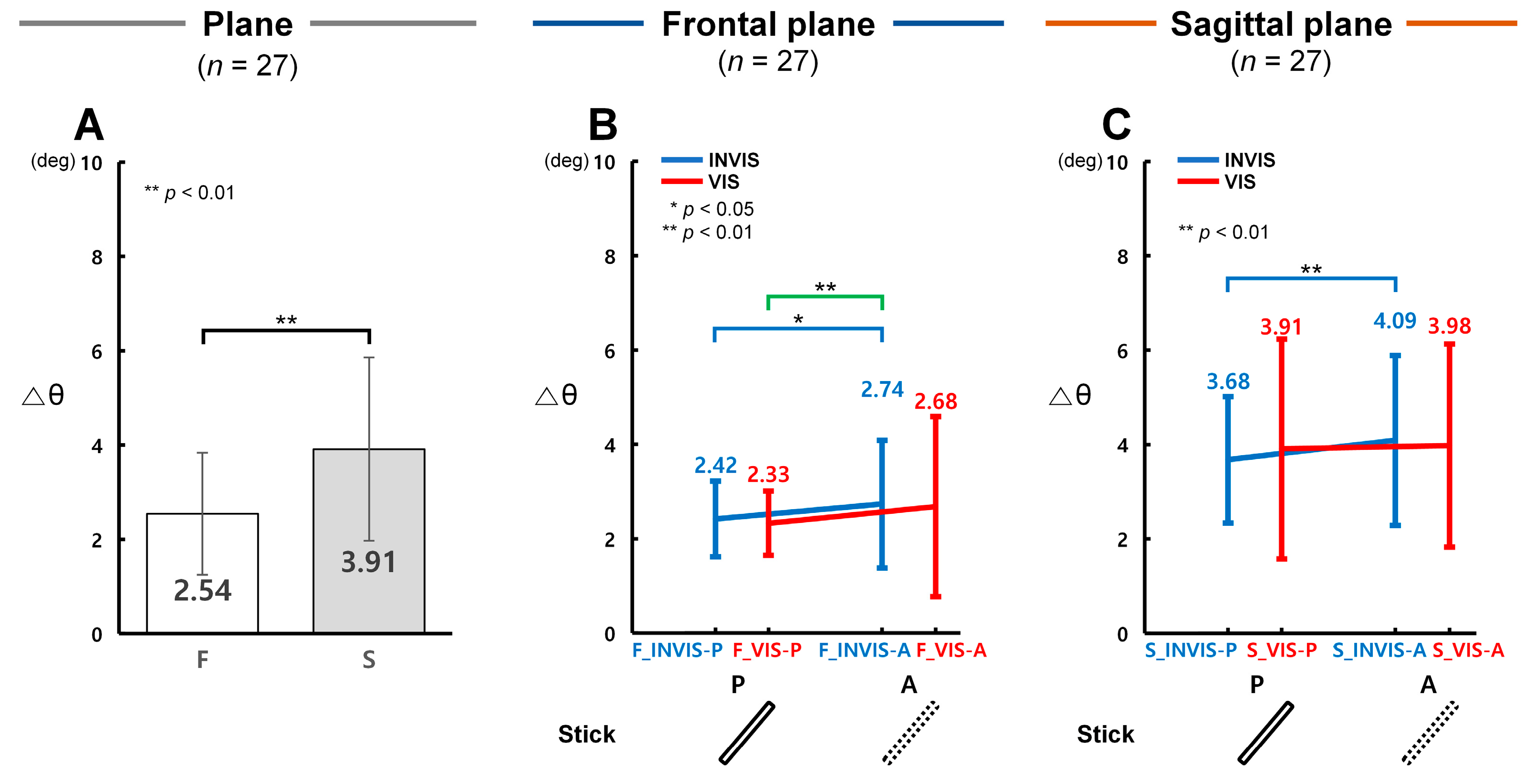
3.2. Control Accuracy in Terms of Δθ with the Presence of the Stick in CES
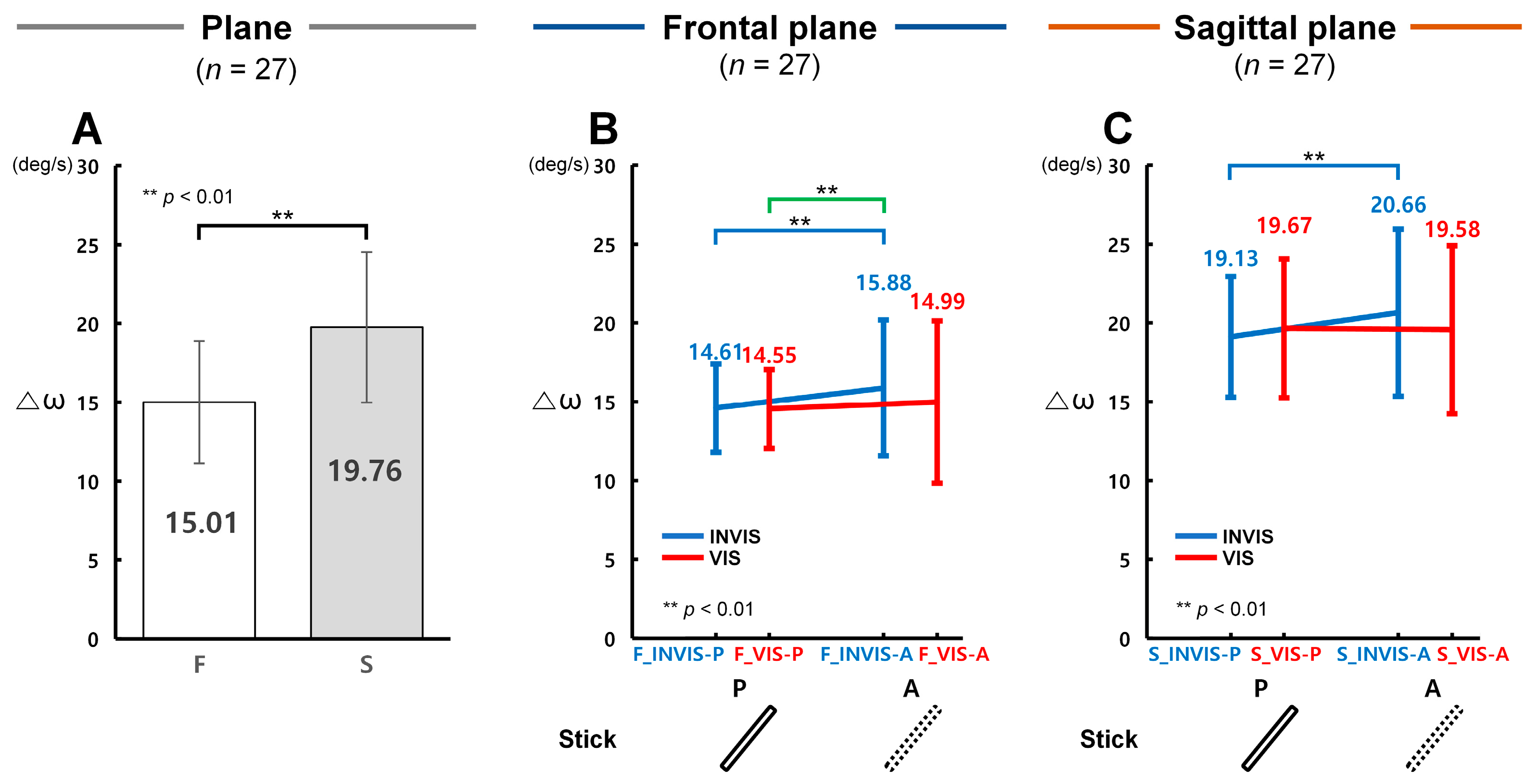
3.3. Control Accuracy in Terms of Δω with the Presence of the Stick in CES
4. Discussion
4.1. Differences in Control Accuracy with the Presence of the Stick in CES
4.2. Comparison of Control Accuracy Based on the Order of Stick Visibility in CTM
4.3. Further Research and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Georgopoulos, A.P.; Grillner, S. Visuomotor coordination in reaching and locomotion. Science 1989, 245, 1209–1210. [Google Scholar] [CrossRef]
- Steinberg, F.; Pixa, N.H.; Doppelmayr, M. Mirror visual feedback training improves intermanual transfer in a sport-specific task: A comparison between different skill levels. Neural Plast. 2016, 2016, 8628039. [Google Scholar] [CrossRef]
- Yokota, H.; Naito, M.; Mizuno, N.; Ohshima, S. Framework for visual feedback training based on a modified self organizing map to imitate complex motion. Proc. Inst. Mech. Eng. Technol. 2019, 234, 49–58. [Google Scholar] [CrossRef]
- Beggs, W.D.A.; Howarth, C.I. Movement control in a repetitive motor task. Nature 1970, 225, 752–753. [Google Scholar] [CrossRef]
- Van den Dobbelsteen, J.; Brenner, E.; Smeets, J. Endpoints of arm movements to visual targets. Exp. Brain Res. 2001, 138, 279–287. [Google Scholar] [CrossRef]
- Wolpert, D.M.; Ghahramani, Z. Computational principles of movement neuroscience. Nat. Neurosci. 2000, 3, 1212–1217. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Q.; Yin, X. Adaptive finite-time prescribed performance control of switched nonlinear systems with unknown actuator dead-zone. Int. J. Syst. Sci. 2019, 51, 133–145. [Google Scholar] [CrossRef]
- De Santis, A.; Siciliano, B.; De Luca, A.; Bicchi, A. An atlas of physical human–robot interaction. Mech. Mach. Theory 2008, 43, 253–270. [Google Scholar] [CrossRef]
- Haddadin, S.; Albu-Schaeffer, A.; Hirzinger, G. Safety Evaluation of Physical Human-Robot Interaction via Crash-Testing. In Proceedings of the Robotics: Science and Systems III, Wessling, Germany, 27–30 June 2007. [Google Scholar]
- Jo, H.; Choi, W.; Lee, G.; Park, W.; Kim, J. Analysis of visuo motor control between dominant hand and non-dominant hand for effective human-robot collaboration. Sensors 2020, 20, 6368. [Google Scholar] [CrossRef]
- Andersen, R.A.; Snyder, L.H.; Li, C.S.; Stricanne, B. Coordinate transformations in the representation of spatial information. Curr. Opin. Neurobiol. 1993, 3, 171–176. [Google Scholar] [CrossRef]
- Wolpert, D.M.; Ghahramani, Z.; Jordan, M.I. An internal model for sensorimotor integration. Science 1995, 269, 1880–1882. [Google Scholar] [CrossRef]
- O’Keefe, J.; Dostrovsky, J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971, 34, 171–175. [Google Scholar] [CrossRef]
- O’Keefe, J. Place units in the hippocampus of the freely moving rat. Exp. Neurol. 1976, 51, 78–109. [Google Scholar] [CrossRef]
- Hafting, T.; Fyhn, M.; Molden, S.; Moser, M.B.; Moser, E.I. Microstructure of a spatial map in the entorhinal cortex. Nature 2005, 436, 801–806. [Google Scholar] [CrossRef]
- Moser, E.I.; Kropff, E.; Moser, M.B. Place cells, grid cells, and the brain’s spatial representation system. Annu. Rev. Neurosci. 2008, 31, 69–89. [Google Scholar] [CrossRef]
- Moser, E.I.; Roudi, Y.; Witter, M.P.; Kentros, C.; Bonhoeffer, T.; Moser, M.B. Grid cells and cortical representation. Nat. Rev. Neurosci. 2014, 15, 466–481. [Google Scholar] [CrossRef]
- Hawkins, J.; Ahmad, S.; Cui, Y. A theory of how columns in the neocortex enable learning the structure of the world. Front. Neural Circuits 2017, 11, 81. [Google Scholar] [CrossRef]
- Hawkins, J.; Lewis, M.; Klukas, M.; Purdy, S.; Ahmad, S. A framework for intelligence and cortical function based on grid cells in the neocortex. Front. Neural Circuits 2019, 12, 121. [Google Scholar] [CrossRef]
- Lewis, M.; Purdy, S.; Ahmad, S.; Hawkins, J. Locations in the neocortex: A theory of sensorimotor object recognition using cortical grid cells. Front. Neural Circuits 2019, 13, 22. [Google Scholar] [CrossRef]
- Iwata, Y.; Yutaka, S. Periodic change in phase relationship between target and hand motion during visuo-manual tracking task: Behavioral evidence for intermittent control. Hum. Mov. Sci. 2014, 33, 211–226. [Google Scholar] [CrossRef]
- Miall, R.C.; Weir, D.J.; Stein, J.F. Intermittency in human manual tracking tasks. J. Mot. Behav. 1993, 25, 53–63. [Google Scholar] [CrossRef]
- Miall, R.C.; Weir, D.J.; Stein, J.F. Manual tracking of visual targets by trained monkeys. Behav. Brain Res. 1986, 20, 185–201. [Google Scholar] [CrossRef]
- Miall, R.C.; Weir, D.J.; Stein, J.F. Planning of movement parameters in a visuo-motor tracking task. Behav. Brain Res. 1988, 27, 1–8. [Google Scholar] [CrossRef]
- Engel, K.C.; Soechting, J.F. Manual tracking in two dimensions. J. Neurophysiol. 2000, 83, 3483–3496. [Google Scholar] [CrossRef]
- Roitman, A.V.; Pasalar, S.; Johnson, M.T.; Ebner, T.J. Position, direction of movement, and speed tuning of cerebellar Purkinje cells during circular manual tracking in monkey. J. Neurosci. 2005, 25, 9244–9257. [Google Scholar] [CrossRef]
- Roitman, A.V.; Pasalar, S.; Ebner, T.J. Single trial coupling of Purkinje cell activity to speed and error signals during circular manual tracking. Exp. Brain Res. 2008, 192, 241–251. [Google Scholar] [CrossRef]
- Hayashi, Y.; Sawada, Y. Transition from an antiphase error-correction mode to a synchronization mode in mutual hand tracking. Phys. Rev. E 2013, 88, 022704. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Kakei, S.; Kim, J. Motor control characteristics for circular tracking movements of human wrist. Adv. Robot. 2017, 31, 29–39. [Google Scholar] [CrossRef]
- Van Beers, R.J.; Wolpert, D.M.; Patrick, H. When feeling is more important than seeing in sensorimotor adaptation. Curr. Biol. 2002, 12, 834–837. [Google Scholar] [CrossRef]
- Choi, W.; Lee, J.; Yanagihara, N.; Li, L.; Kim, J. Development of a quantitative evaluation system for visuo-motor control in three-dimensional virtual reality space. Sci. Rep. 2018, 8, 13439. [Google Scholar] [CrossRef]
- Choi, W.; Yanagihara, N.; Li, L.; Kim, J.; Lee, J. Visuomotor control of intermittent circular tracking movements with visually guided orbits in 3D VR environment. PLoS ONE 2021, 16, e0251371. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.; Lee, J.; Li, L. Analysis of three-dimensional circular tracking movements based on temporo-spatial parameters in polar coordinates. Appl. Sci. 2020, 10, 621. [Google Scholar] [CrossRef]
- Lee, G.; Choi, W.; Jo, H.; Park, W.; Kim, J. Analysis of motor control strategy for frontal and sagittal planes of circular tracking movements using visual feedback noise from velocity change and depth information. PLoS ONE 2020, 15, e0241138. [Google Scholar] [CrossRef]
- Park, W.; Choi, W.; Jo, H.; Lee, G.; Kim, J. Analysis of control characteristics between dominant and non-dominant hands by transient responses of circular tracking movements in 3D virtual reality space. Sensors 2020, 20, 3477. [Google Scholar] [CrossRef]
- Kim, H.; Koike, Y.; Choi, W.; Lee, J. The effect of different depth planes during a manual tracking task in three-dimensional virtual reality space. Sci. Rep. 2023, 13, 21499. [Google Scholar] [CrossRef]
- Schmidt, R.A.; Lee, T.D.; Winstein, C.J.; Wulf, G.; Zelaznik, H.N. Motor Control and Learning: A Behavioral Emphasis, 6th ed.; Human Kinetics: Champaign, IL, USA, 2019; Available online: https://books.google.co.kr/books?id=RpBFDwAAQBAJ (accessed on 12 January 2025).
- Faul, F.; Erdfelder, E.; Lang, A.-G.; Buchner, A. G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 2007, 39, 175–191. [Google Scholar] [CrossRef]
- Hawkins, J.; Dawkins, R. A Thousand Brains: A New Theory of Intelligence; Basic Books: New York, NY, USA, 2022; Available online: https://books.google.co.kr/books?id=U46vzgEACAAJ (accessed on 12 January 2025).
- Slater, M.; Perez-Marcos, D.; Ehrsson, H.H.; Sanchez-Vives, M.V. Towards a digital body: The virtual arm illusion. Front. Hum. Neurosci. 2008, 2, 6. [Google Scholar] [CrossRef] [PubMed]
- Short, F.; Ward, R. Virtual limbs and body space: Critical features for the distinction between body space and near-body space. J. Exp. Psychol. Hum. Percept. Perform. 2009, 35, 1092–1103. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.; Li, L.; Satoh, S.; Hachimura, K. Multisensory integration in the virtual hand illusion with active movement. Biomed. Res. Int. 2016, 2016, 8163098. [Google Scholar] [CrossRef]
- Zhou, Y.; Popescu, V. Dynamic Redirection for VR Haptics with a Handheld Stick. IEEE Trans. Vis. Comput. Graph. 2023, 29, 2165–2175. [Google Scholar] [CrossRef]
- Kalaska, J. Reaching movements to visual targets: Neuronal representations of sensori-motor transformations. Semin. Neurosci. 1991, 3, 67–80. [Google Scholar] [CrossRef]
- Cardinali, L.; Frassinetti, F.; Brozzoli, C.; Urquizar, C.; Roy, A.C.; Farnè, A. Tool-use induces morphological updating of the body schema. Curr. Biol. 2009, 19, R478–R479. [Google Scholar] [CrossRef]
- Peeters, R.; Simone, L.; Nelissen, K.; Fabbri-Destro, M.; Vanduffel, W.; Rizzolatti, G.; Orban, G.A. The representation of tool use in humans and monkeys: Common and uniquely human features. J. Neurosci. 2009, 29, 11523–11539. [Google Scholar] [CrossRef]
- Hudson, T.E.; Wolfe, U.; Maloney, L.T. Speeded reaching movements around invisible obstacles. PLoS Comput. Biol. 2012, 8, e1002676. [Google Scholar] [CrossRef]
- Iriki, A.; Taoka, M. Triadic (ecological, neural, cognitive) niche construction: A scenario of human brain evolution extrapolating tool use and language from the control of reaching actions. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 10–23. [Google Scholar] [CrossRef]
- Van de Kamp, C.; Gawthrop, P.J.; Gollee, H.; Loram, I.D. Refractoriness in sustained visuo-manual control: Is the refractory duration intrinsic or does it depend on external system properties? PLoS Comput. Biol. 2013, 9, e1002843. [Google Scholar] [CrossRef] [PubMed]
- Brown, B. Dynamic visual acuity, eye movements and peripheral acuity for moving targets. Vision Res. 1972, 12, 305–321. [Google Scholar] [CrossRef]
- Keele, S.W.; Posner, M.I. Processing of visual feedback in rapid movements. J. Exp. Psychol. 1968, 77, 155–158. [Google Scholar] [CrossRef]
- Frey Law, L.A.; Avin, K.G. Endurance time is joint-specific: A modelling and meta-analysis investigation. Ergonomics 2010, 53, 109–129. [Google Scholar] [CrossRef] [PubMed]
- Dupuis, F.; Sole, G.; Wassinger, C.A.; Bielmann, M.; Bouyer, L.J.; Roy, J.-S. Fatigue, induced via repetitive upper-limb motor tasks, influences trunk and shoulder kinematics during an upper limb reaching task in a virtual reality environment. PLoS ONE 2021, 16, e0249403. [Google Scholar] [CrossRef] [PubMed]
- Beltran Martinez, K.; Nazarahari, M.; Rouhani, H. Breaking the Fatigue Cycle: Investigating the Effect of Work-Rest Schedules on Muscle Fatigue in Material Handling Jobs. Sensors 2023, 23, 9670. [Google Scholar] [CrossRef]
- Iqbal, U.; Latif, S.; Yan, Y.; Yu, L.; Shi, Y.; Cao, Y.; Liao, J. Reducing Arm Fatigue in Virtual Reality by Introducing 3D-Spatial Offset. IEEE Access 2021, 9, 62165–62178. [Google Scholar] [CrossRef]
- Niehorster, D.C.; Li, L.; Lappe, M. The Accuracy and Precision of Position and Orientation Tracking in the HTC Vive Virtual Reality System for Scientific Research. i-Perception 2017, 8, 2041669517708205. [Google Scholar] [CrossRef] [PubMed]
- Sansone, A.; Pace, G.; Carbone, G.; Crea, S. Robustness and Static-Positional Accuracy of the SteamVR (1.0) Virtual Reality Tracking System. Virtual Real. 2022, 26, 703–716. [Google Scholar] [CrossRef]
- Warburton, M.; Mon-Williams, M.; Mushtaq, F.; Morehead, J.R. Measuring Motion-to-Photon Latency for Sensorimotor Experiments with Virtual Reality Systems. Behav. Res. Methods 2023, 55, 3658–3678. [Google Scholar] [CrossRef]
- Stauffert, J.-P.; Niebling, F.; Latoschik, M.E. Latency and Cybersickness: Impact, Causes, and Measures. Front. Virtual Real. 2020, 1, 582204. [Google Scholar] [CrossRef]
- Zhao, C.; Beams, R.; Dahal, E.; Badano, A. Spatially Dependent Veiling Glare Degrades Image Quality in Medical Extended Reality. Virtual Reality 2024, 28, 11. [Google Scholar] [CrossRef]
- Nuanmeesri, S. The Affordable Virtual Learning Technology of Sea Salt Farming across Multigenerational Users through Improving Fitts’ Law. Sustainability 2024, 16, 7864. [Google Scholar] [CrossRef]
| Study | Summary | Components | Parameters |
|---|---|---|---|
| Choi et al. (2018) [31] | Comparison of visuomotor control in monocular and binocular vision | Visual field (monocular vs. binocular) | ΔR |
| Choi et al. (2020) [33] | Analysis of spatial–temporal parameter differences according to the body plane and target speed | Plane of body, velocity of target | ΔR, Δθ, Δω |
| Jo et al. (2020) [10] | Comparison of visuomotor control between dominant and non-dominant hands in terms of polar kinematic parameters and dimensionless squared jerk (DSJ) | Hand usage (dominant vs. nondominant) | ΔR, Δθ, Δa, dimensionless squared jerk (DSJ) |
| Lee at al. (2020) [34] | Visuomotor control assessment and strategy investigation based on depth information in the quadrant sections of the sagittal plane | Sagittal plane | ΔR, Δω |
| Park et al. (2020) [35] | Comparison of circular tracking movement characteristics between the dominant and non-dominant hands through transient response analysis | Transient response analysis and hand usage | Normalized initial peak velocity (IPV2), initial peak time (IPT2), time delay (TD2) |
| Choi et al. (2021) [32] | Visuomotor control analysis based on visible and invisible circular trajectories at different target speeds | Orbit | Δθ, Δω |
| Kim et al. (2023) [36] | Comparison of 3D tracking performance based on the rotation axis of the circular trajectory | Sagittal plane (0, 45, 90 deg) | ΔR |
| Ours | Comparison of control accuracy based on the presence of a stick and its presentation order | Stick | ΔR, Δθ, Δω |
| No. | Parameter | Image | Formula |
|---|---|---|---|
| 1 | Radial position difference |  | |
| 2 | Angular displacement difference | 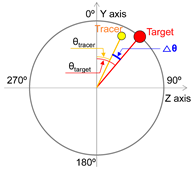 | |
| 3 | Angular velocity difference | 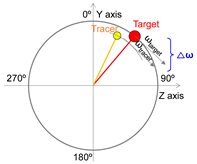 |
| State | Plane | Variable | State of the Stick | ΔSD (A-P) | Levene’s p-Value | |
|---|---|---|---|---|---|---|
| P | A | |||||
| INVIS | Frontal | ΔR | 2.78 | 3.10 | +0.32 | 0.875 |
| Δθ | 0.80 | 1.35 | +0.55 | 0.031 * | ||
| Δω | 2.80 | 4.31 | +1.51 | 0.063 | ||
| Sagittal | ΔR | 3.01 | 3.36 | +0.35 | 0.304 | |
| Δθ | 1.34 | 1.80 | +0.46 | 0.017 * | ||
| Δω | 3.82 | 5.30 | +1.48 | 0.021 * | ||
| VIS | Frontal | ΔR | 3.27 | 3.35 | +0.08 | 0.807 |
| Δθ | 0.68 | 1.91 | +1.23 | 0.059 | ||
| Δω | 2.51 | 5.15 | +2.64 | 0.139 | ||
| Sagittal | ΔR | 5.60 | 4.02 | −1.58 | 0.158 | |
| Δθ | 2.33 | 2.15 | −0.18 | 0.841 | ||
| Δω | 4.40 | 5.33 | +0.93 | 0.106 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Han, K.; Choi, W.; Kim, J. Visuomotor Control Accuracy of Circular Tracking Movement According to Visual Information in Virtual Space. Sensors 2025, 25, 5998. https://doi.org/10.3390/s25195998
Lee J, Han K, Choi W, Kim J. Visuomotor Control Accuracy of Circular Tracking Movement According to Visual Information in Virtual Space. Sensors. 2025; 25(19):5998. https://doi.org/10.3390/s25195998
Chicago/Turabian StyleLee, Jihyoung, Kwangyong Han, Woong Choi, and Jaehyo Kim. 2025. "Visuomotor Control Accuracy of Circular Tracking Movement According to Visual Information in Virtual Space" Sensors 25, no. 19: 5998. https://doi.org/10.3390/s25195998
APA StyleLee, J., Han, K., Choi, W., & Kim, J. (2025). Visuomotor Control Accuracy of Circular Tracking Movement According to Visual Information in Virtual Space. Sensors, 25(19), 5998. https://doi.org/10.3390/s25195998







