Numerical Study of Incidence Angle-Tuned, Guided-Mode Resonant, Metasurfaces-Based Sensors for Glucose and Blood-Related Analytes Detection
Abstract
1. Introduction
2. Materials and Methods
2.1. Analyzed Sensors’ Structures and Their Characteristics
2.2. The 1D- and 2D-Grating-Based Sensor Structures Simulated, Set A and B, Respectively
- A1
- The grating lamella and waveguide are both CsPbBr3;
- A2
- The grating lamella and waveguide are both Si3N4;
- A3
- The grating lamella is CsPbBr3 and the waveguide is Si3N4;
- A4
- The grating lamella is PVC, and the waveguide is CsPbBr3;
- A5
- The grating lamella is PVC, and the waveguide is Si3N4.
- B1
- The grating mesa and waveguide are both Si3N4;
- B2
- The grating mesa is CsPbBr3 and the waveguide is Si3N4;
- B3
- The grating mesa is PVC and the waveguide is Si3N4.
3. Results and Analysis
3.1. Reflectance Spectra and Characteristics of the Set A Sensors
3.2. 2D Grating Sensor at Normal Incidence
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GMR | Guided-mode resonance |
| DPN | Dip-pen nanolithography |
| RCWA | Rigorous coupled-wave analysis |
| FOM | Figure of merit |
| NIL | Nanoimprint lithography |
| PECVD | Plasma-enhanced chemical vapor deposition |
| SOI | Silicon on insulator |
References
- Zhou, Y.; Guo, Z.; Zhou, W.; Li, S.; Liu, Z.; Zhao, X.; Wu, X. High-Q guided mode resonance sensors based on shallow sub-wavelength grating structures. Nanotechnology 2020, 31, 325501. [Google Scholar] [CrossRef]
- Quaranta, G.; Basset, G.; Martin, O.J.F.; Gallinet, B. Recent Advances in Resonant Waveguide Gratings. Laser Photonics Rev. 2018, 12, 1800017. [Google Scholar] [CrossRef]
- Khaleque, T.; Magnusson, R. Light management through guided-mode resonances in thin-film silicon solar cells. J. Nanophotonics 2014, 8, 083995. [Google Scholar] [CrossRef]
- Magnusson, R.; Ko, Y.H. Guided-mode resonance nanophotonics: Fundamentals and applications. In Nanoengineering: Fabrication, Properties, Optics, and Devices XIII; Campo, E.M., Dobisz, E.A., Eldada, L.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2016; Volume 9927, p. 992702. [Google Scholar] [CrossRef]
- Qian, L.; Zhang, D.; Huang, Y.; Tao, C.; Hong, R.; Zhuang, S. Performance of a double-layer guided mode resonance filter with non-subwavelength grating period at oblique incidence. Opt. Laser Technol. 2015, 72, 42–47. [Google Scholar] [CrossRef]
- Menon, S.; Prosad, A.; Krishna, A.S.L.; Biswas, R.; Raghunathan, V. Resonant mode engineering in silicon compatible multilayer guided-mode resonance structures under Gaussian beam excitation condition. J. Opt. 2021, 23, 105001. [Google Scholar] [CrossRef]
- Zhang, W.; Kim, S.M.; Ganesh, N.; Block, I.D.; Mathias, P.C.; Wu, H.Y.; Cunningham, B.T. Deposited nanorod films for photonic crystal biosensor applications. J. Vac. Sci. Technol. A 2010, 28, 996–1001. [Google Scholar] [CrossRef]
- Canalejas-Tejero, V.; López, A.; Casquel, R.; Holgado, M.; Barrios, C.A. Sensitive metal layer-assisted guided-mode resonance SU8 nanopillar array for label-free optical biosensing. Sens. Actuators B Chem. 2016, 226, 204–210. [Google Scholar] [CrossRef]
- Kang, H.; Lee, D.; Yang, Y.; Oh, D.K.; Seong, J.; Kim, J.; Jeon, N.; Kang, D.; Rho, J. Emerging low-cost, large-scale photonic platforms with soft lithography and self-assembly. Photonics Insights 2023, 2, R04. [Google Scholar] [CrossRef]
- Xia, Y.; Whitesides, G.M. Soft Lithography. Angew. Chem. Int. Ed. 1998, 37, 550–575. [Google Scholar] [CrossRef]
- Guo, L.; Xu, L.; Liu, L. Sensitivity enhancement of guided mode resonance sensors under oblique incidence. Photonics Res. 2024, 12, 2667–2675. [Google Scholar] [CrossRef]
- Lan, H.; Ding, Y.; Liu, H. Nanoimprint Lithography: Principles, Processes and Materials; Nanotechnology Science and Technology Series; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2011. [Google Scholar]
- Kessel, A.; Frydendahl, C.; Indukuri, S.R.K.C.; Mazurski, N.; Arora, P.; Levy, U. Soft Lithography for Manufacturing Scalable Perovskite Metasurfaces with Enhanced Emission and Absorption. Adv. Opt. Mater. 2020, 8, 2001627. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, L.; Johnson, M.; Hillier, A.C.; Lu, M. One-step sol-gel imprint lithography for guided-mode resonance structures. Nanotechnology 2016, 27, 095302. [Google Scholar] [CrossRef]
- Gazzo, S.; Manfredi, G.; Pötzsch, R.; Wei, Q.; Alloisio, M.; Voit, B.; Comoretto, D. High refractive index hyperbranched polyvinylsulfides for planar one-dimensional all-polymer photonic crystals. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 73–80. [Google Scholar] [CrossRef]
- Zhan, Y.; Li, C.; Che, Z.; Shum, H.C.; Hu, X.; Li, H. Light management using photonic structures towards high-index perovskite optoelectronics: Fundamentals, designing, and applications. Energy Environ. Sci. 2023, 16, 4135–4163. [Google Scholar] [CrossRef]
- Das, S.; Gholipour, S.; Saliba, M. Perovskites for Laser and Detector Applications. Energy Environ. Mater. 2019, 2, 146–153. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Hong, B.; Wang, G. Optical waveguide in curved and welded perovskite nanowires. Sci. China Technol. Sci. 2023, 66, 1471–1479. [Google Scholar] [CrossRef]
- Sun, X.; Shao, Y.; Wang, C.; Yue, J.; Cui, A.; Tao, S.; Wang, S.; Zhang, D.; Zhou, D.; Chen, C. Organic-Inorganic Hybrid Integrated Optical Waveguide Gain Compensator Based on CsPbBr3 Perovskite Nanocrystals. IEEE Electron Device Lett. 2024, 45, 754–757. [Google Scholar] [CrossRef]
- Gebremichael, Z.T.; Alam, S.; Cefarin, N.; Pozzato, A.; Yohannes, T.; Schubert, U.S.; Hoppe, H.; Tormen, M. Controlling Metal Halide Perovskite Crystal Growth via Microcontact Printed Hydrophobic-Hydrophilic Templates. Cryst. Res. Technol. 2022, 57, 2100121. [Google Scholar] [CrossRef]
- Paquet, C.; Kumacheva, E. Nanostructured polymers for photonics. Mater. Today 2008, 11, 48–56. [Google Scholar] [CrossRef]
- Rumpf, R.C.; Johnson, E.G. Modeling fabrication to accurately place GMR resonances. Opt. Express 2007, 15, 3452–3464. [Google Scholar] [CrossRef]
- Cegielski, P.J.; Neutzner, S.; Porschatis, C.; Lerch, H.; Bolten, J.; Suckow, S.; Kandada, A.R.S.; Chmielak, B.; Petrozza, A.; Wahlbrink, T.; et al. Integrated perovskite lasers on a silicon nitride waveguide platform by cost-effective high throughput fabrication. Opt. Express 2017, 25, 13199–13206. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Y.; Sun, J.; Tan, S.; Li, Y.; Wang, X.; Cai, J.; Bai, J.; Lv, X.; Guo, W.; et al. Design Strategies and Emerging Applications of Perovskite-Based Sensors. SmartMat 2025, 6, e70022. [Google Scholar] [CrossRef]
- Knop, K. Rigorous diffraction theory for transmission phase gratings with deep rectangular grooves. J. Opt. Soc. Am. 1978, 68, 1206–1210. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Diffraction analysis of dielectric surface-relief gratings. J. Opt. Soc. Am. 1982, 72, 1385–1392. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of metallic surface-relief gratings. J. Opt. Soc. Am. A 1986, 3, 1780–1787. [Google Scholar] [CrossRef]
- Gallagher, N.C.; Whang, A.J. Solving slab lamellar grating problems by the singular-value-decomposition method. J. Opt. Soc. Am. A 1990, 7, 1701–1711. [Google Scholar] [CrossRef]
- Pai, D.M.; Awada, K.A. Analysis of dielectric gratings of arbitrary profiles and thicknesses. J. Opt. Soc. Am. A 1991, 8, 755–762. [Google Scholar] [CrossRef]
- Hava, S.; Auslender, M.; Rabinovich, D. Operator approach to electromagnetic coupled-wave calculations of lamellar gratings: Infrared optical properties of intrinsic silicon gratings. Appl. Opt. 1994, 33, 4807–4813. [Google Scholar] [CrossRef]
- Chateau, N.; Hugonin, J.P. Algorithm for the rigorous coupled-wave analysis of grating diffraction. J. Opt. Soc. Am. A 1994, 11, 1321–1331. [Google Scholar] [CrossRef]
- Li, L.; Haggans, C.W. Convergence of the coupled-wave method for metallic lamellar diffraction gratings. J. Opt. Soc. Am. A 1993, 10, 1184–1189. [Google Scholar] [CrossRef]
- Lalanne, P.; Morris, G.M. Highly improved convergence of the coupled-wave method for TM polarization. J. Opt. Soc. Am. A 1996, 13, 779–784. [Google Scholar] [CrossRef]
- Granet, G.; Guizal, B. Efficient implementation of the coupled-wave method for metallic lamellar gratings in TM polarization. J. Opt. Soc. Am. A 1996, 13, 1019–1023. [Google Scholar] [CrossRef]
- Auslender, M.; Hava, S. Scattering-matrix propagation algorithm in full-vectorial optics of multilayer grating structures. Opt. Lett. 1996, 21, 1765–1767. [Google Scholar] [CrossRef]
- Moharam, M.G.; Pommet, D.A.; Grann, E.B.; Gaylord, T.K. Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: Enhanced transmittance matrix approach. J. Opt. Soc. Am. A 1995, 12, 1077–1086. [Google Scholar] [CrossRef]
- Li, L. Use of Fourier series in the analysis of discontinuous periodic structures. J. Opt. Soc. Am. A 1996, 13, 1870–1876. [Google Scholar] [CrossRef]
- Li, L. New formulation of the Fourier modal method for crossed surface-relief gratings. J. Opt. Soc. Am. A 1997, 14, 2758–2767. [Google Scholar] [CrossRef]
- Brennan, M.C.; Krein, D.M.; Rowe, E.; McCleese, C.L.; Sun, L.; Berry, K.G.; Stevenson, P.R.; Susner, M.A.; Grusenmeyer, T.A. Fundamental optical constants and anti-reflection coating of melt-grown, polished CsPbBr3 crystals. MRS Commun. 2024, 14, 900–908. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, J.; Li, X.; Zhao, J.; Liu, L. Complex refractive indices measurements of polymers in visible and near-infrared bands. Appl. Opt. 2020, 59, 2337–2344. [Google Scholar] [CrossRef] [PubMed]
- Beliaev, L.Y.; Shkondin, E.; Lavrinenko, A.V.; Takayama, O. Optical, structural and composition properties of silicon nitride films deposited by reactive radio-frequency sputtering, low pressure and plasma-enhanced chemical vapor deposition. Thin Solid Films 2022, 763, 139568. [Google Scholar] [CrossRef]
- Friebel, M.; Meinke, M. Model function to calculate the refractive index of native hemoglobin in the wavelength range of 250–1100 nm dependent on concentration. Appl. Opt. 2006, 45, 2838–2842. [Google Scholar] [CrossRef] [PubMed]
- Misto; Purwandari, E.; Supriyadi; Arkundato, A.; Rohman, L.; Eko Cahyono, B. Analyses of Concentration and Wavelength Dependent Refractive Index of Sugar Solution Using Sellmeier Equation. J. Phys. Conf. Ser. 2021, 1825, 012030. [Google Scholar] [CrossRef]
- Ge, C.; Lu, M.; George, S.; Flood, T.A.; Wagner, C.; Zheng, J.; Pokhriyal, A.; Eden, J.G.; Hergenrother, P.J.; Cunningham, B.T. External cavity laser biosensor. Lab Chip 2013, 13, 1247–1256. [Google Scholar] [CrossRef]
- Drayton, A.; Barth, I.; Krauss, T.F. Chapter Five—Guided mode resonances and photonic crystals for biosensing and imaging. In Photonic Crystal Metasurface Optoelectronics; Semiconductors and Semimetals; Zhou, W., Fan, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 100, pp. 115–148. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R.; Bagby, J.S.; Moharam, M.G. Guided-mode resonances in planar dielectric-layer diffraction gratings. J. Opt. Soc. Am. A 1990, 8, 1470–1475. [Google Scholar] [CrossRef]
- Magnusson, R.; Wang, S.S. New principle for optical filters. Appl. Phys. Lett. 1992, 61, 1022–1024. [Google Scholar] [CrossRef]
- Magnusson, R.; Wang, S.S. Theory and applications of guided-mode resonance filters. Appl. Opt. 1993, 32, 2606–2613. [Google Scholar] [CrossRef]
- Wang, S.S.; Magnusson, R. Multilayer waveguide-grating filters. Appl. Opt. 1995, 34, 2414–2420. [Google Scholar] [CrossRef] [PubMed]
- Rosenblatt, D.; Sharon, A.; Friesem, A.A. Resonant Grating Waveguide Structures. IEEE J. Quantum Electron. 1997, 33, 2038–2059. [Google Scholar] [CrossRef]
- Norton, S.M.; Erdogan, T.; Morris, G.M. Coupled-mode theory of resonant-grating filters. J. Opt. Soc. Am. A 1997, 14, 629–639. [Google Scholar] [CrossRef]
- Sharon, A.; Rosenblatt, D.; Friesem, A.A. Narrow spectral bandwidths with grating waveguide structures. Appl. Phys. Lett. 1996, 69, 4154–4156. [Google Scholar] [CrossRef]
- Norton, S.M.; Morris, G.M.; Erdogan, T. Experimental investigation of resonant-grating filter lineshapes in comparison with theoretical models. J. Opt. Soc. Am. A 1998, 15, 464–472. [Google Scholar] [CrossRef]
- Priambodo, P.S.; Maldonado, T.A.; Magnusson, R. Fabrication and characterization of high-quality waveguide-mode resonant optical filters. Appl. Phys. Lett. 2003, 83, 3248–3250. [Google Scholar] [CrossRef]
- Sharon, A.; Rosenblatt, D.; Friesem, A.A. Light modulation with resonant grating–waveguide structures. Opt. Lett. 1996, 21, 1564–1566. [Google Scholar] [CrossRef] [PubMed]
- Lukosz, W. Principles and sensitivities of integrated optical and surface plasmon sensors for direct affinity sensing and immunosensing. Biosens. Bioelectron. 1991, 6, 215–225. [Google Scholar] [CrossRef]
- Nellen, P.; Lukosz, W. Integrated optical input grating couplers as direct affinity sensors. Biosens. Bioelectron. 1993, 8, 129–147. [Google Scholar] [CrossRef]
- Lukosz, W. Integrated optical chemical and direct biochemical sensors. Sens. Actuators B Chem. 1995, 29, 37–50. [Google Scholar] [CrossRef]
- Lukosz, W.; Clerc, D.; Nellen, P. Input and output grating couplers as integrated optical biosensors. Sens. Actuators A Phys. 1990, 25, 181–184. [Google Scholar] [CrossRef]
- Nellen, P.M.; Lukosz, W. Integrated optical input grating couplers as chemo- and immunosensors. Sens. Actuators B Chem. 1990, 1, 592–596. [Google Scholar] [CrossRef]
- Nellen, P.; Lukosz, W. Model experiments with integrated optical input grating couplers as direct immunosensors. Biosens. Bioelectron. 1991, 6, 517–525. [Google Scholar] [CrossRef]
- Clerc, D.; Lukosz, W. Integrated optical output grating coupler as refractometer and (bio-)chemical sensor. Sens. Actuators B Chem. 1993, 11, 461–465. [Google Scholar] [CrossRef]
- Lukosz, W.; Clerc, D.; Nellen, P.; Stamm, C.; Weiss, P. Output grating couplers on planar optical waveguides as direct immunosensors. Biosens. Bioelectron. 1991, 6, 227–232. [Google Scholar] [CrossRef]
- Huber, W.; Barner, R.; Fattinger, C.; Hübscher, J.; Koller, H.; Müller, F.; Schalatter, D.; Lukosz, W. Direct optical immunosensing (sensitivity and selectivity). Sens. Actuators B Chem. 1992, 6, 122–126. [Google Scholar] [CrossRef]
- Clerc, D.; Lukosz, W. Integrated optical output grating coupler as biochemical sensor. Sens. Actuators B Chem. 1994, 19, 581–586. [Google Scholar] [CrossRef]
- Abdulhalim, I. Biosensing configurations using guided wave resonant structures. In Proceedings of the Optical Waveguide Sensing and Imaging; Bock, W.J., Gannot, I., Tanev, S., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 211–228. [Google Scholar]
- Wawro, D.D.; Tibuleac, S.; Magnusson, R.; Liu, H. Optical fiber endface biosensor based on resonances in dielectric waveguide gratings. Proc. SPIE 2000, 3911, 86–94. [Google Scholar] [CrossRef]
- Cunningham, B.; Lin, B.; Qiu, J.; Li, P.; Pepper, J.; Hugh, B. A plastic colorimetric resonant optical biosensor for multiparallel detection of label-free biochemical interactions. Sens. Actuators B Chem. 2002, 85, 219–226. [Google Scholar] [CrossRef]
- Block, I.D.; Chan, L.L.; Cunningham, B.T. Photonic crystal optical biosensor incorporating structured low-index porous dielectric. Sens. Actuators B Chem. 2006, 120, 187–193. [Google Scholar] [CrossRef]
- Cunningham, B.; Li, P.; Lin, B.; Pepper, J. Colorimetric resonant reflection as a direct biochemical assay technique. Sens. Actuators B Chem. 2002, 81, 316–328. [Google Scholar] [CrossRef]
- Wang, J.J.; Chen, L.; Kwan, S.; Liu, F.; Deng, X. Resonant grating filters as refractive index sensors for chemical and biological detections. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2005, 23, 3006–3010. [Google Scholar] [CrossRef]
- Schmid, J.H.; Sinclair, W.; García, J.; Janz, S.; Lapointe, J.; Poitras, D.; Li, Y.; Mischki, T.; Lopinski, G.; Cheben, P.; et al. Silicon-on-insulator guided mode resonant grating for evanescent field molecular sensing. Opt. Express 2009, 17, 18371–18380. [Google Scholar] [CrossRef] [PubMed]
- Tiefenthaler, K.; Lukosz, W. Sensitivity of grating couplers as integrated-optical chemical sensors. J. Opt. Soc. Am. B 1989, 6, 209–220. [Google Scholar] [CrossRef]
- Krasnykov, O.; Auslender, M.; Abdulhalim, I. Optimizing the guided mode resonant structure for optical sensing in water. Phys. Express 2011, 1, 183–190. [Google Scholar]
- Bi, L.; Fan, X.; Zhao, H.; Liu, L.; Wei, X.; Niu, H.; Li, C.; Bai, C.; Fang, W. Enhanced sensing ability in multiple Fano resonance optical biosensor with high-contrast metastructures. Results Opt. 2022, 9, 100276. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, B.; Guo, Z.; Wu, X. Guided Mode Resonance Sensors with Optimized Figure of Merit. Nanomaterials 2019, 9, 837. [Google Scholar] [CrossRef]
- Liang, F.; Clarke, N.; Patel, P.; Loncar, M.; Quan, Q. Scalable photonic crystal chips for high sensitivity protein detection. Opt. Express 2013, 21, 32306–32312. [Google Scholar] [CrossRef]
- Huang, L.; Jin, R.; Zhou, C.; Li, G.; Xu, L.; Overvig, A.; Deng, F.; Chen, X.; Lu, W.; Alù, A.; et al. Ultrahigh-Q guided mode resonances in an All-dielectric metasurface. Nat. Commun. 2023, 14, 3433. [Google Scholar] [CrossRef]
- Qian, L.; Wang, K.; Bykov, D.A.; Xu, Y.; Zhu, L.; Yan, C. Improving the sensitivity of guided-mode resonance sensors under oblique incidence condition. Opt. Express 2019, 27, 30563–30575. [Google Scholar] [CrossRef] [PubMed]
- Cu, D.T.; Wu, H.W.; Chen, H.P.; Su, L.C.; Kuo, C.C. Exploiting Thin-Film Properties and Guided-Mode Resonance for Designing Ultrahigh-Figure-of-Merit Refractive Index Sensors. Sensors 2024, 24, 960. [Google Scholar] [CrossRef]
- Amedalor, R.; Karvinen, P.; Pesonen, H.; Turunen, J.; Niemi, T.; Bej, S. High-Q guided-mode resonance of a crossed grating with near-flat dispersion. Appl. Phys. Lett. 2023, 122, 161102. [Google Scholar] [CrossRef]
- Liu, B.; Chen, F. Adjustable slow light and optical switch in a black phosphorus metamaterial based on double plasmon-induced transparency. Phys. B Condens. Matter 2025, 714, 417423. [Google Scholar] [CrossRef]
- Liu, H.; Li, J.; Yang, H.; Wang, J.; Li, B.; Zhang, H.; Yi, Y. TiN-Only Metasurface Absorber for Solar Energy Harvesting. Photonics 2025, 12, 443. [Google Scholar] [CrossRef]
- Zhang, B.; Luo, Y. Dynamic optical tuning and sensing in L-shaped Dirac semimetal-based terahertz metasurfaces. Phys. Lett. A 2025, 541, 130419. [Google Scholar] [CrossRef]
- Li, L.; Chen, F. Tunable four-band metamaterial absorber and sensor based on a stacking double-ring Dirac semimetal structure design. Phys. Lett. A 2025, 544, 130489. [Google Scholar] [CrossRef]


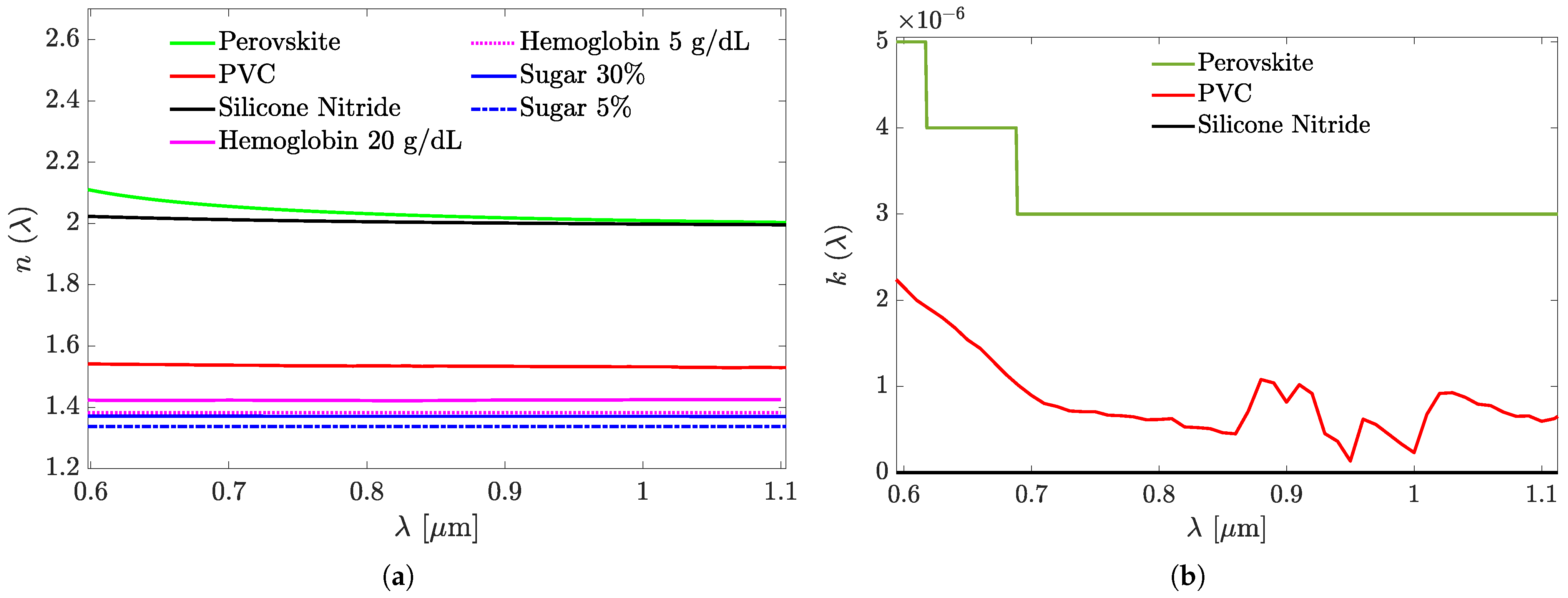
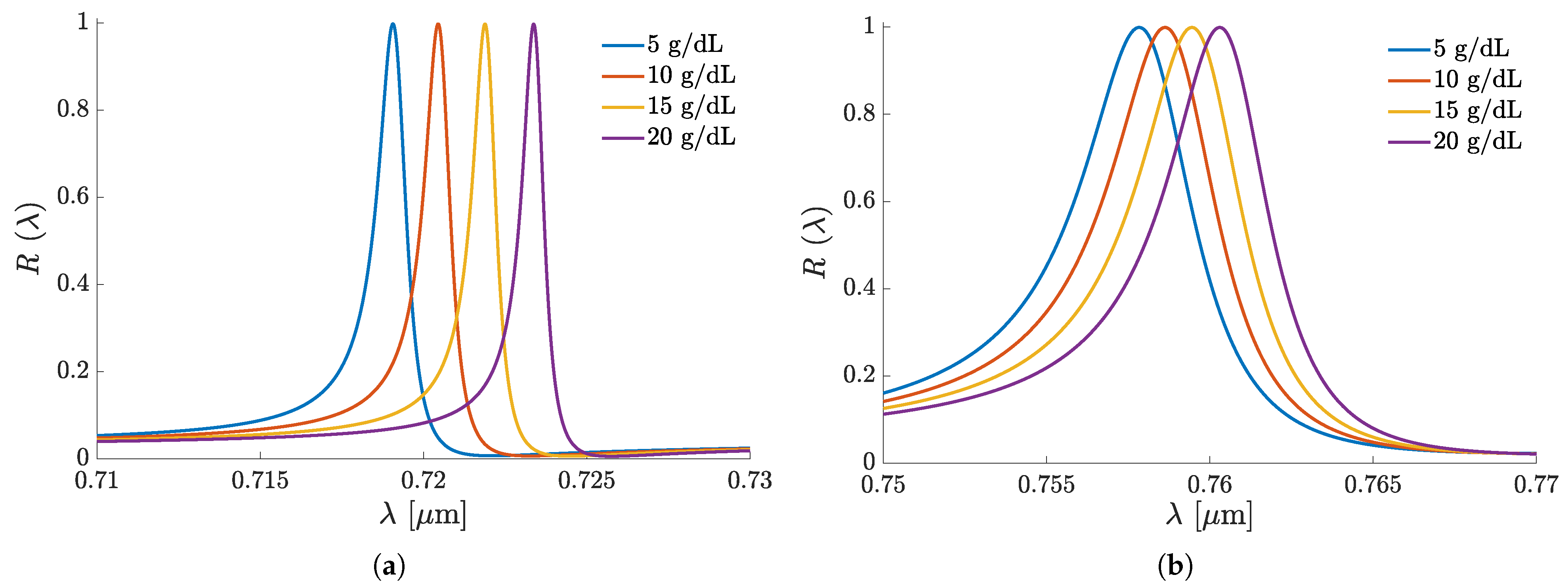
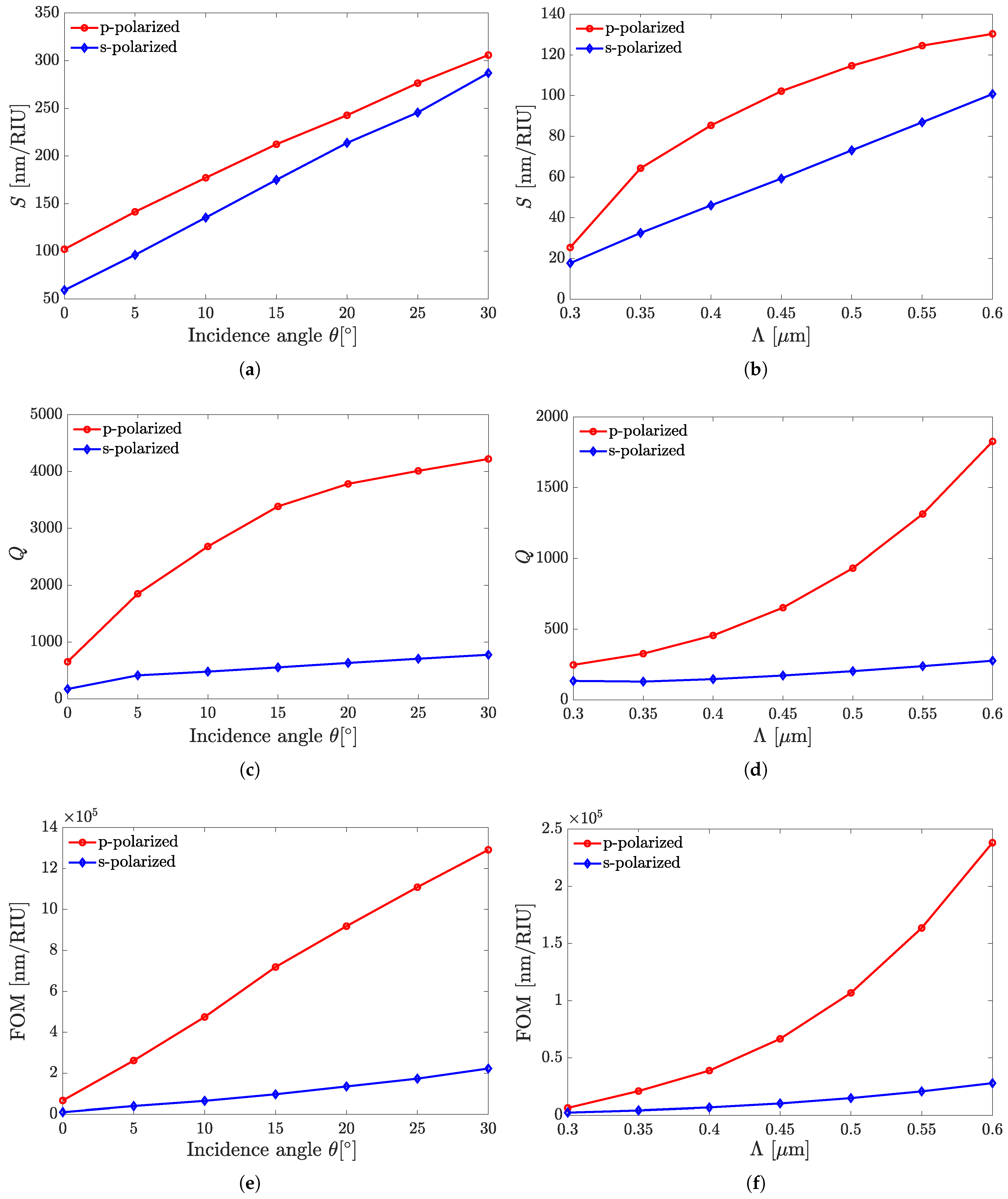
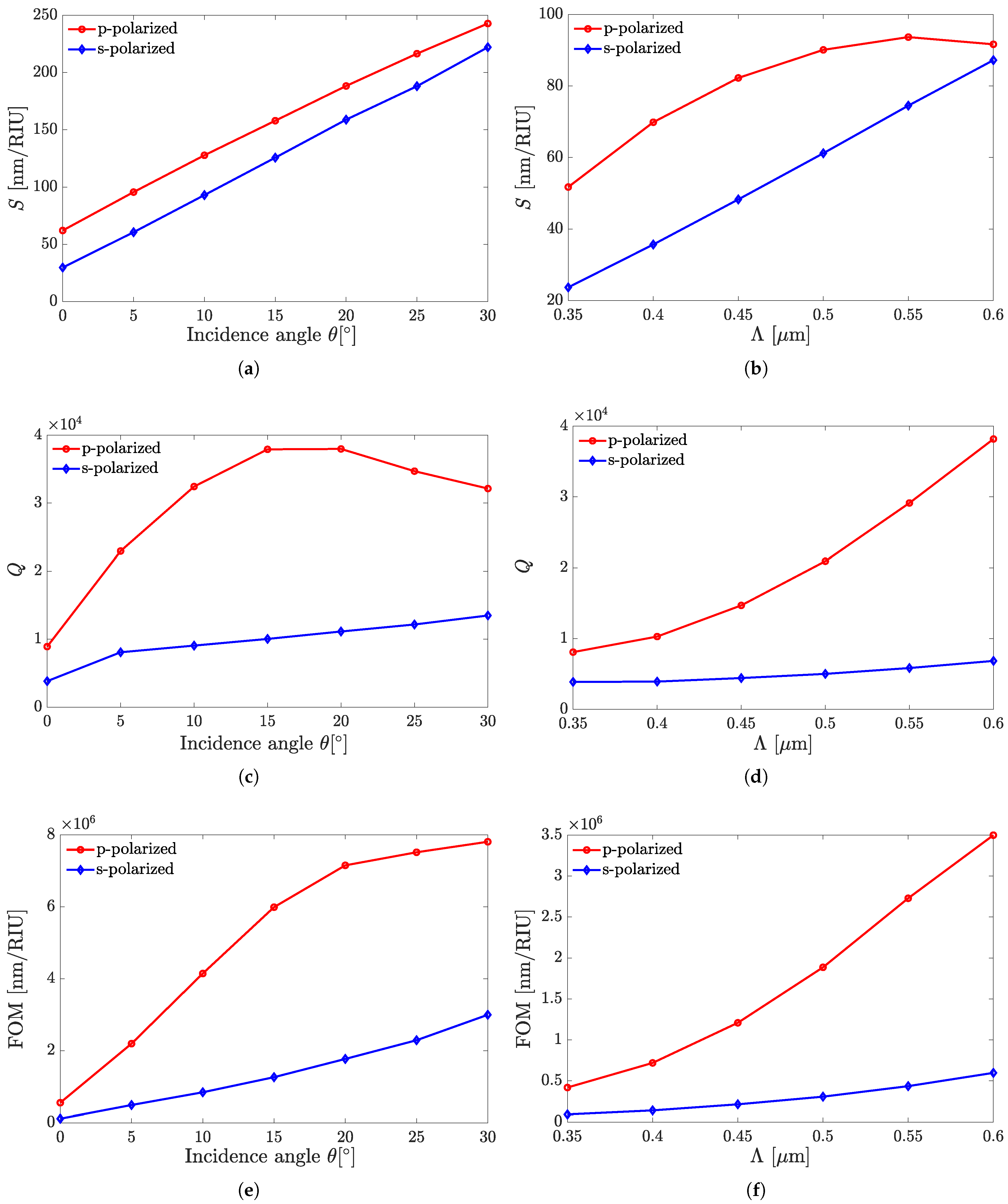
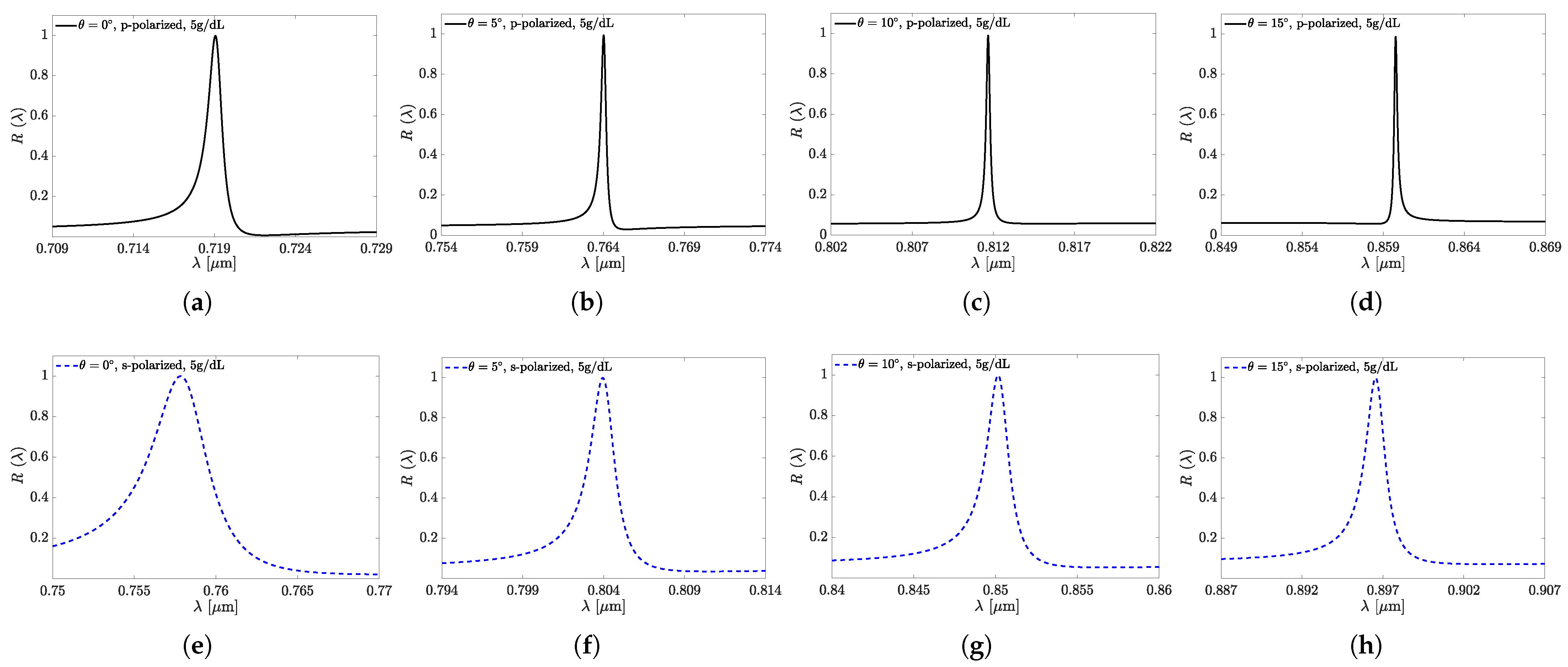

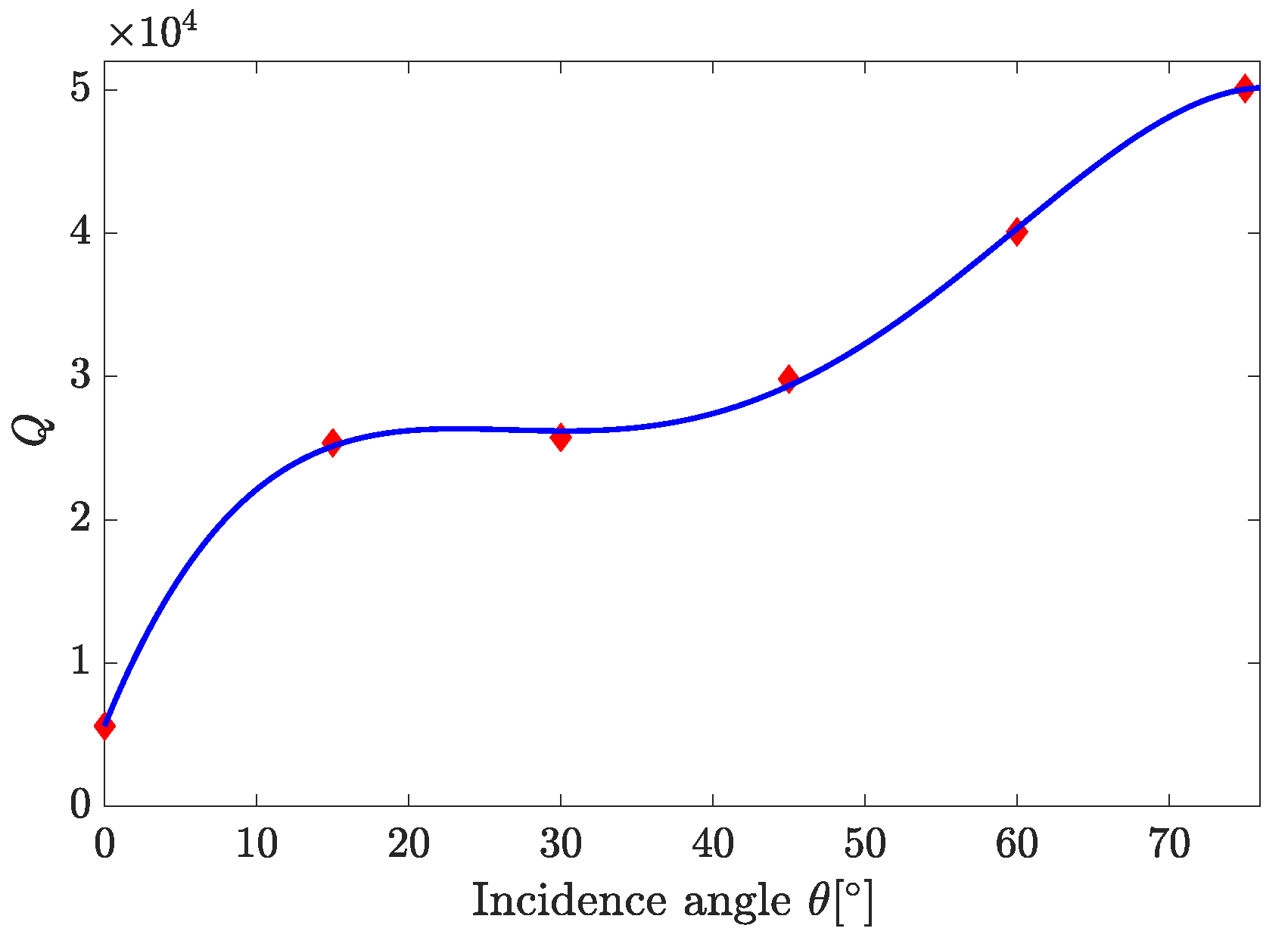

| Set A structures, s-polarized sensing modality | |||||||||
| Structure | S, nm/RIU | Q | FOM, nm/RIU | ||||||
| 0° | 30° | 60° | 0° | 30° | 60° | 0° | 30° | 60° | |
| A1 ∗ | 59 | 287 | – † | – † | – † | ||||
| A2 ⋄ | 55 | 277 | 441 | ||||||
| A3 ⋄ | 56 | 276 | 441 | ||||||
| A4 ∗ | 30 | 222 | – † | – † | – † | ||||
| A5 ⋄ | 30 | 216 | 355 | ||||||
| Set A structures, p-polarized sensing modality | |||||||||
| A1 ∗ | 102 | 306 | – † | – † | – † | ||||
| A2 ⋄ | 86 | 275 | 401 | ||||||
| A3 ⋄ | 88 | 276 | 402 | ||||||
| A4 ∗ | 62 | 243 | – † | – † | – † | ||||
| A5 ⋄ | 55 | 225 | 338 | ||||||
| Sensor Structure | Q | ||
|---|---|---|---|
| B1 | 82 | ||
| B2 | 83 | ||
| B3 | 67 |
| Sensor Type | Q | ||
|---|---|---|---|
| A5: s-polarized | 30 | ||
| A5: p-polarized | 54 | ||
| B3 | 67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fradkin, Z.; Piscklich, M.; Zohar, M.; Auslender, M. Numerical Study of Incidence Angle-Tuned, Guided-Mode Resonant, Metasurfaces-Based Sensors for Glucose and Blood-Related Analytes Detection. Sensors 2025, 25, 5852. https://doi.org/10.3390/s25185852
Fradkin Z, Piscklich M, Zohar M, Auslender M. Numerical Study of Incidence Angle-Tuned, Guided-Mode Resonant, Metasurfaces-Based Sensors for Glucose and Blood-Related Analytes Detection. Sensors. 2025; 25(18):5852. https://doi.org/10.3390/s25185852
Chicago/Turabian StyleFradkin, Zeev, Maxim Piscklich, Moshe Zohar, and Mark Auslender. 2025. "Numerical Study of Incidence Angle-Tuned, Guided-Mode Resonant, Metasurfaces-Based Sensors for Glucose and Blood-Related Analytes Detection" Sensors 25, no. 18: 5852. https://doi.org/10.3390/s25185852
APA StyleFradkin, Z., Piscklich, M., Zohar, M., & Auslender, M. (2025). Numerical Study of Incidence Angle-Tuned, Guided-Mode Resonant, Metasurfaces-Based Sensors for Glucose and Blood-Related Analytes Detection. Sensors, 25(18), 5852. https://doi.org/10.3390/s25185852







