InAsSb Photodiode-Based Infrared Radiation Thermometer for the Investigation of Droplet Surface Temperature Dynamics Within an Enclosed Combustion Chamber
Abstract
1. Introduction
2. Materials and Methods
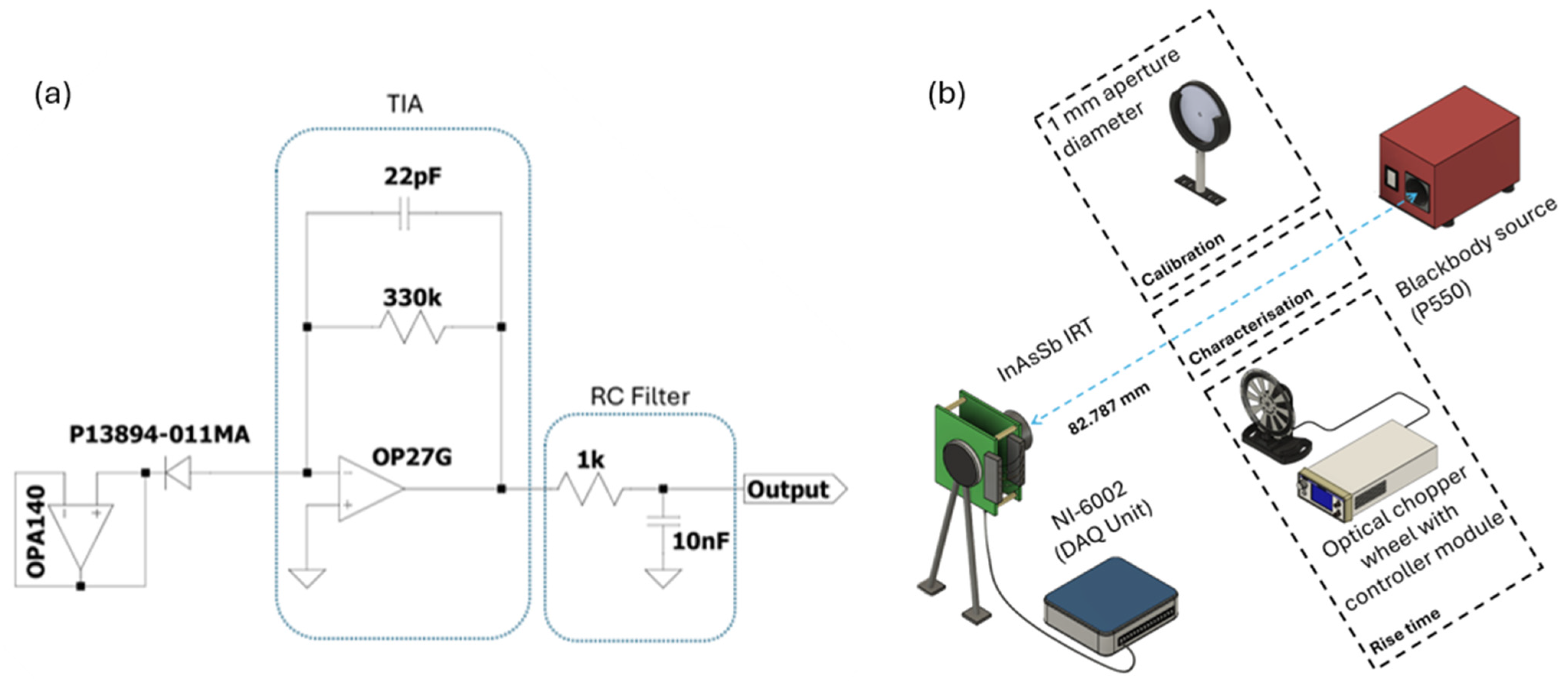
2.1. Instrument Design and Characterisation
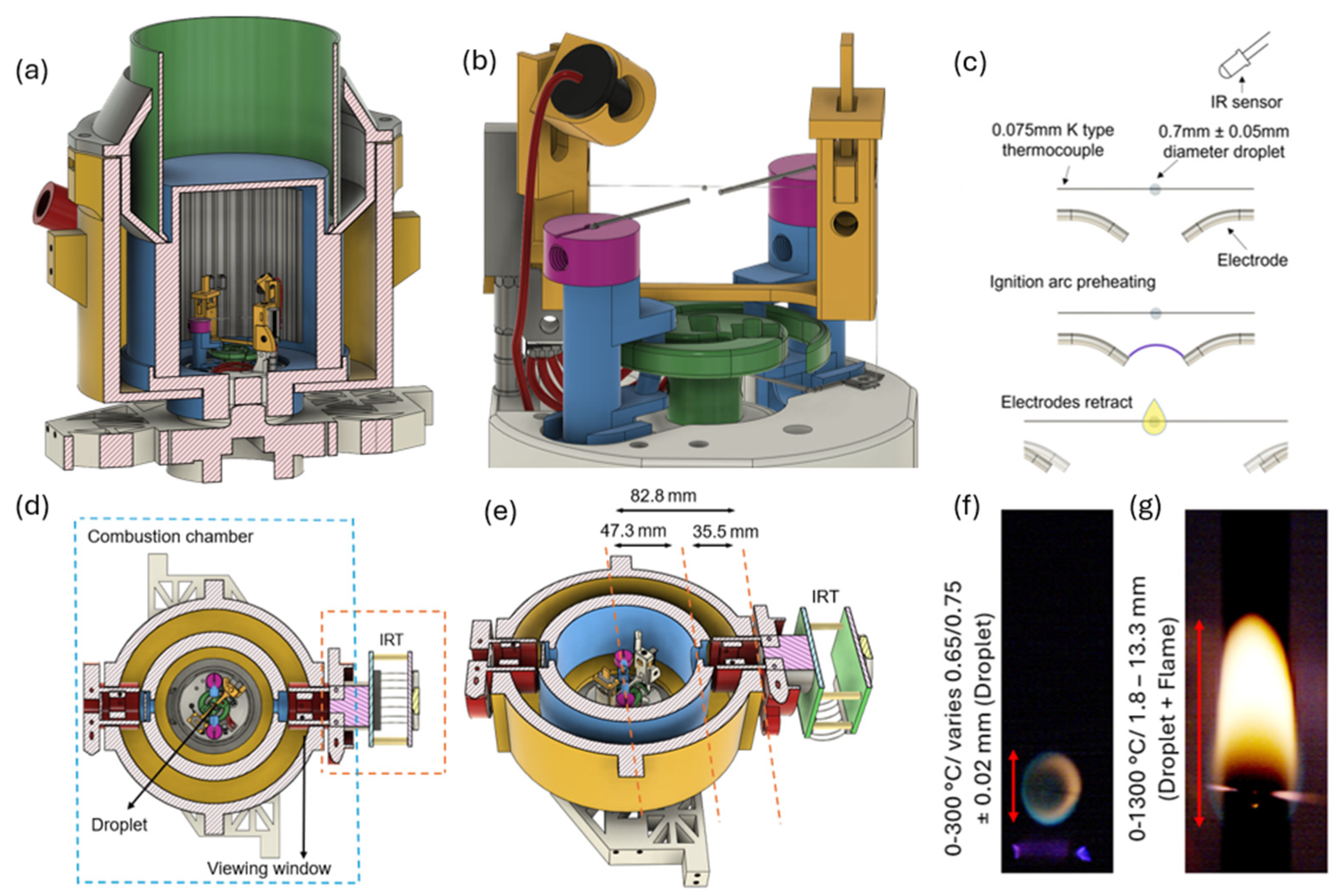
2.2. Droplet Closed Environment Combustion Chamber
3. Results and Discussion
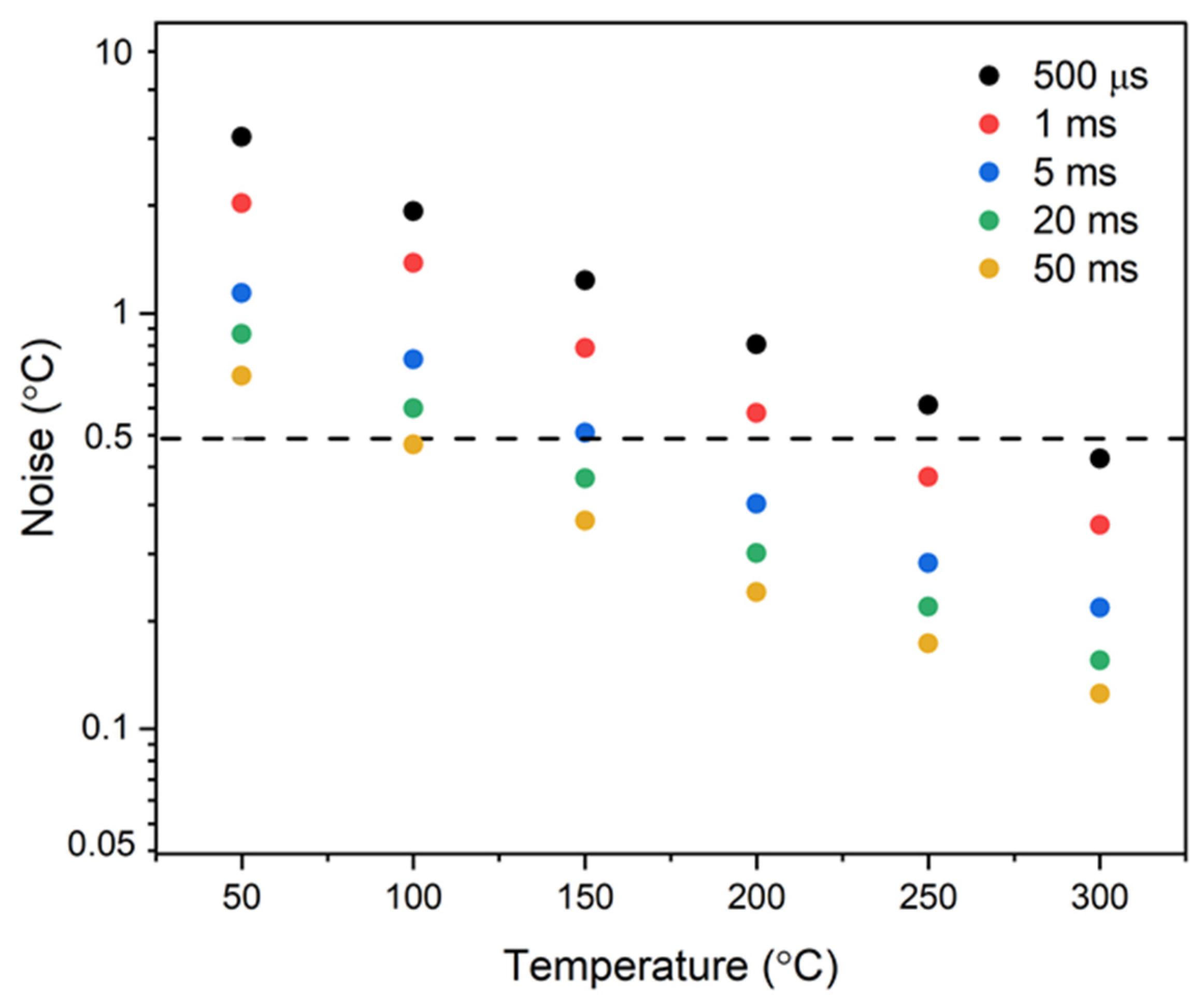
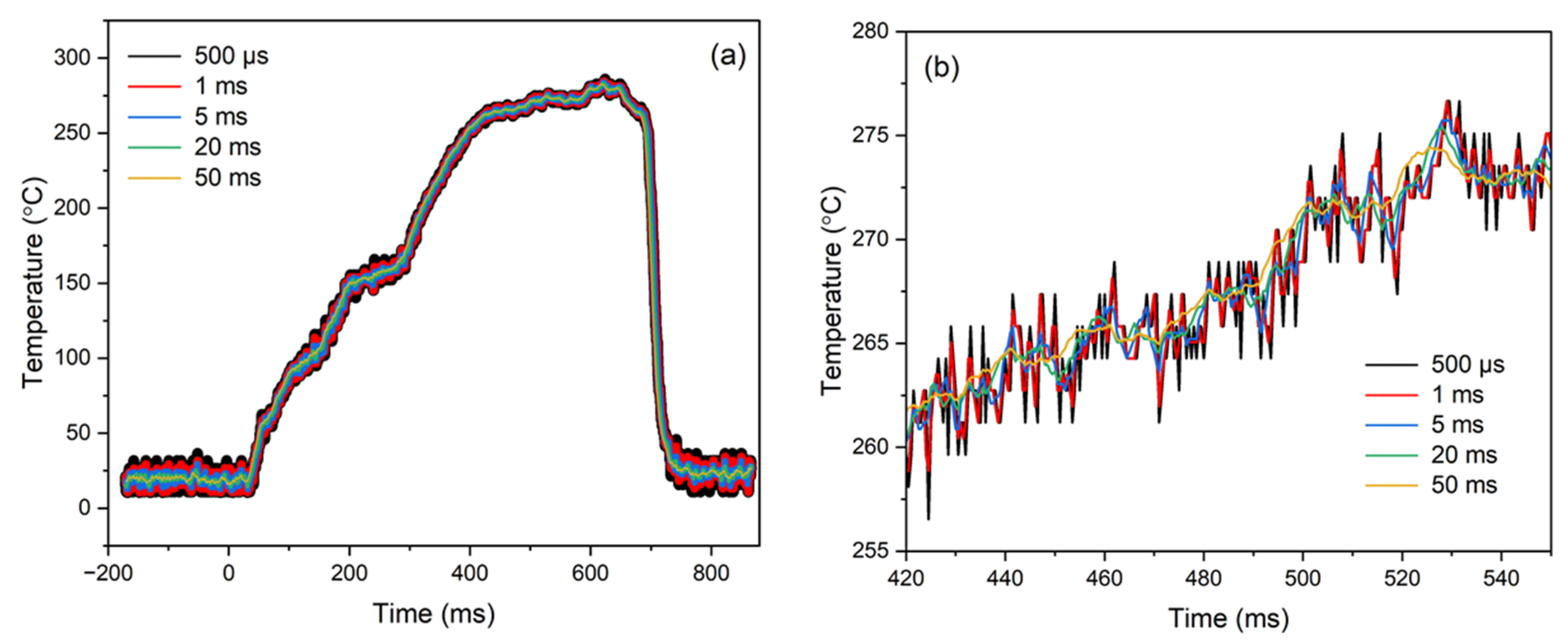
3.1. IRT Characterisation
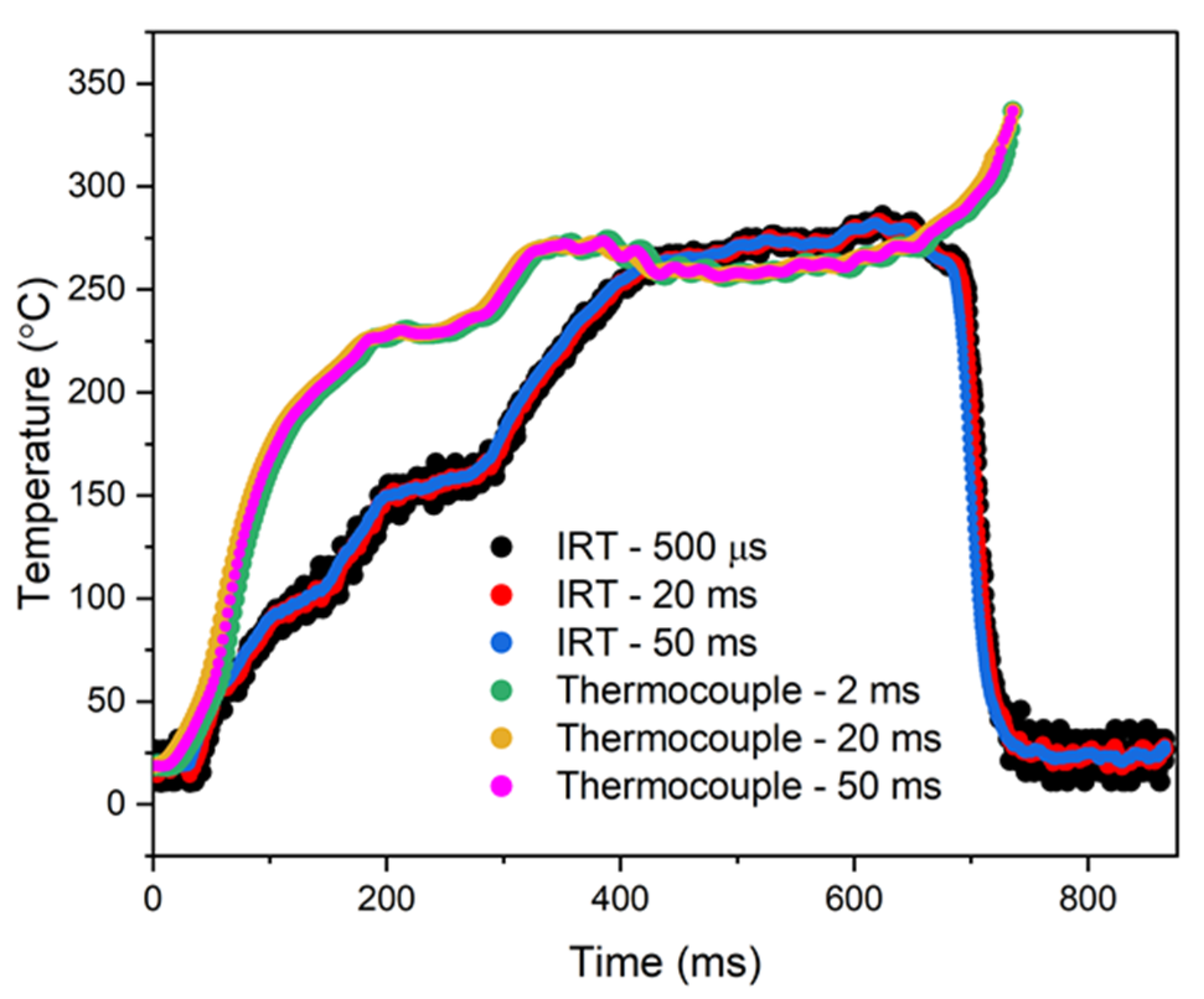
3.2. Surface Temperature Measurements of the Droplet
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jagadale, V.S.; Rao, D.C.K.; Deshmukh, D.; Hanstorp, D.; Mishra, Y.N. Modes of Atomization in Biofuel Droplets Induced by a Focused Laser Pulse. Fuel 2022, 315, 123190. [Google Scholar] [CrossRef]
- Karapateas, L.; Lai, Y.; Meng, X.; Zhang, Y.; Willmott, J.R.; Hobbs, M.J. Si APD-Based High Speed Infrared Radiation Thermometry for Analysing the Temperature Instability of a Combustion Chamber. Sensors 2024, 24, 7780. [Google Scholar] [CrossRef]
- Meng, X.; Lai, Y.; Zhang, Z.; Willmott, J.; Zhang, Y. Experimental Investigation of Kerosene Single Droplet Ignition and Combustion under Simulated High-Altitude Pressure and Temperature Conditions. Fuel 2025, 401, 135825. [Google Scholar] [CrossRef]
- Foust, H.C. Thermodynamics, Gas Dynamics, and Combustion; Springer: Cham, Switzerland, 2021; Available online: https://link.springer.com/book/10.1007/978-3-030-87387-5 (accessed on 11 December 2024).
- Tu, Y.; Liu, H.; Xu, S. Heat transfer and its influence on MILD combustion. In Fundamentals of Low Emission Flameless Combustion and Its Applications; Hosseini, S.E., Ed.; Academic Press: Cambridge, MA, USA, 2022; pp. 181–219. [Google Scholar]
- Liu, S.; Huang, Y.; He, Y.; Zhu, Y.; Wang, Z. Review of Development and Comparison of Surface Thermometry Methods in Combustion Environments: Principles, Current State of the Art, and Applications. Processes 2022, 10, 2528. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J.; Jin, Z.; Ren, G.; Ma, H. Multi-Component Model of Diesel Sprays Under High Injection Pressure. J. Shanghai Jiaotong Univ. 2018, 23, 264–268. [Google Scholar] [CrossRef]
- Luo, H. Experimental Investigations on Fuel Spray and Impingement for Gasoline Direct Injection Engines. In Internal Combustion Engine Technology and Applications of Biodiesel Fuel; Wang, E., Ed.; IntechOpen: London, UK, 2021; p. 95848. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Strizhak, P.A.; Volkov, R.S.; Vysokomornaya, O.V. Integral characteristics of water droplet evaporation in high temperature combustion products of typical flammable liquids using SP and IPI methods. Int. J. Therm. Sci. 2016, 108, 218–234. [Google Scholar] [CrossRef]
- Volkov, R.S.; Voytkov, I.S.; Strizhak, P.A. Temperature Fields of the Droplets and Gases Mixture. Appl. Sci. 2020, 10, 2212. [Google Scholar] [CrossRef]
- Omega Engineering. IRCO-BW. 2023. Available online: https://www.omega.co.uk/pptst/IRCO-BW.html (accessed on 11 December 2024).
- Gutiérrez, G.R.; van Keulen, F.; Goosen, J.F.L.; Aragón, A.M.; Bornheim, A. Enhancing the cooling performance of thermocouples: A power-constrained topology optimization procedure. Struct. Multidisc. Optim. 2024, 67, 189. [Google Scholar] [CrossRef]
- Voulgaropoulos, V.; Aguiar, G.M.; Markides, C.N.; Bucci, M. Simultaneous laser-induced fluorescence, particle image velocimetry and infrared thermography for the investigation of the flow and heat transfer characteristics of nucleating vapour bubbles. Int. J. Heat Mass Transf. 2022, 187, 122525. [Google Scholar] [CrossRef]
- Bai, B.; Yang, W.; Qi, X.; Che, Q.; Zhou, Q.; Sun, W.; Chen, S. Experimental study of thermocouple temperature measurement based on coherent anti-Stokes Raman spectroscopy. AIP Adv. 2013, 11, 115216. [Google Scholar] [CrossRef]
- Manullang, M.C.T.; Lin, Y.-H.; Lai, S.-J.; Chou, N.-K. Implementation of Thermal Camera for Non-Contact Physiological Measurement: A Systematic Review. Sensors 2021, 21, 7777. [Google Scholar] [CrossRef] [PubMed]
- Ito, Y.; Kita, Y.; Fukuhara, Y.; Nomura, M.; Sasahara, H. Development of In-Process Temperature Measurement of Grinding Surface with an Infrared Thermometer. J. Manuf. Mater. Process. 2022, 6, 44. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared Thermography for Temperature Measurement and Non-Destructive Testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef]
- Myakalwar, A.K.; Sandoval, C.; Velásquez, M.; Sbarbaro, D.; Sepúlveda, B.; Yáñez, J. LIBS as a Spectral Sensor for Monitoring Metallic Molten Phase in Metallurgical Applications—A Review. Minerals 2021, 11, 1073. [Google Scholar] [CrossRef]
- Hwang, J.-K. Methodology for the Emissivity Estimation of Radiation-Type Thermometers Using the Latent Heat Generated During the Phase Transformation of Steels. Infrared Phys. Technol. 2019, 105, 103166. [Google Scholar] [CrossRef]
- National Instruments. NI 9213 Specifications. Available online: https://www.ni.com/docs/en-US/bundle/ni-9213-specs/page/specs.html (accessed on 26 February 2025).
- National Instruments. USB-6002 Specifications. Available online: https://www.ni.com/docs/en-US/bundle/usb-6002-specs/resource/374371a.pdf (accessed on 11 December 2024).
- Rogalski, A. Infrared and Terahertz Detectors, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Rogalski, A. Comparison of photon and thermal detector performance. In Handbook of Infra-Red Detection Technologies; Elsevier: Amsterdam, The Netherlands, 2002; pp. 5–81. [Google Scholar]
- Subramanian, A.; Rodriguez-Saona, L. Fourier Transform Infrared (FTIR) Spectroscopy. In Infrared Spectroscopy for Food Quality Analysis and Control; Academic Press: Cambridge, MA, USA, 2009; pp. 145–178. [Google Scholar]
- Leonardo DRS. MCT’S Advantages as an Infrared Imaging Material; Leonardo, DRS: Dallas, TX, USA, 2010; Available online: www.drsinfrared.com (accessed on 11 December 2024).
- Xiang, Z.; Shi, M.; Zhou, N.; Zhang, C.; Ding, X.; Ni, Y.; Chen, D.; Mao, H. A Highly Accurate Method for Measuring Response Time of MEMS Thermopiles. Micromachines 2022, 13, 1717. [Google Scholar] [CrossRef]
- Rogalski, A.; Martyniuk, P.; Kopytko, M.; Madejczyk, P.; Krishna, S. InAsSb-Based Infrared Photodetectors: Thirty Years Later On. Sensors 2020, 20, 7047. [Google Scholar] [CrossRef]
- Hamamatsu Photonics. InAsSb Photovoltaic Detectors P13894 Series Datasheet; Hamamatsu Photonics: Iwata City, Japan, 2022; Available online: www.hamamatsu.com (accessed on 11 December 2024).
- Leonidas, E.; Ayvar-Soberanis, S.; Laalej, H.; Fitzpatrick, S.; Willmott, J.R. A Comparative Review of Thermocouple and Infrared Radiation Temperature Measurement Methods during the Machining of Metals. Sensors 2022, 22, 4693. [Google Scholar] [CrossRef]
- Yuan, H.; Yamamoto, H.; Nishino, J.; Shibata, G.; Ogawa, H. Optical Analysis on Diesel Combustion Processes of OME Blended FT Fuels by Rapid Compression-Expansion Machine. SSRN Prepr. 2024, 4748371. Available online: https://ssrn.com/abstract=4748371 (accessed on 10 September 2025).
- Song, Z.; Li, Z.; Liu, Z. Comparison of Emission Properties of Sustainable Aviation Fuels and Conventional Aviation Fuels: A Review. Appl. Sci. 2024, 14, 5484. [Google Scholar] [CrossRef]
- Lemoine, F.; Castanet, G. Temperature and chemical composition of droplets by optical measurement techniques: A state-of-the-art review. Exp. Fluids 2013, 54, 1572. [Google Scholar] [CrossRef]
- Leonidas, E.; Hobbs, M.J.; Ayvar-Soberanis, S.; Laalej, H.; Fisk, C.; Fitzpatrick, S.; Willmott, J.R. InAsSb Photodiode Fibre Optic Thermometry for High-Speed, near-Ambient Temperature Measurements. Sensors 2023, 23, 9514. [Google Scholar] [CrossRef]
- Lai, Y.; Liu, X.; Pan, M.; Davies, M.; Fisk, C.; King, D.; Zhang, Y.; Willmott, J. Advanced visualisation of biomass charcoal combustion dynamics using MWIR hyperspectral and LWIR thermal imaging under varied airflow conditions. Fuel 2024, 378, 132901. [Google Scholar] [CrossRef]
- Hobbs, M.J.; Barr, A.; Woolford, S.; Farrimond, D.; Clarke, S.D.; Tyas, A.; Willmott, J.R. High-Speed Infrared Radiation Thermometer for the Investigation of Early Stage Explosive Development and Fireball Expansion. Sensors 2022, 22, 6143. [Google Scholar] [CrossRef]
- Land Instruments International. SPOT—High Precision Pyrometers; LAND Instruments International: Dronfield, UK, 2016; Available online: https://www.ametek-land.com/-/media/ameteklandinstruments/documentation/products/fixedspotnoncontactthermometers/spot/ametek_land_spot_brochure_marcom0355_rev_15.pdf (accessed on 25 September 2024).
- Setyawana, H.Y.; Zhu, M. Cenosphere Formation and Combustion Characteristics of Single Droplets of Vacuum Residual Oils. Combust. Sci. Technol. 2025, 197, 59–76. [Google Scholar] [CrossRef]
- Südholt, B.A.; Witte, A.; Smallwood, G.J.; Mädler, L. Phase Changes in Burning Precursor-Laden Single Droplets Leading to Puffing and Micro-Explosion. Exp. Fluids 2024, 65, 170. [Google Scholar] [CrossRef]
- Li, W.; Riemer, N.; Xu, L.; Wang, Y.; Adachi, K.; Shi, Z.; Zhang, D.; Zheng, Z.; Laskin, A. Microphysical properties of atmospheric soot and organic particles: Measurements, modeling, and impacts. npj Clim. Atmos. Sci. 2024, 7, 65. [Google Scholar] [CrossRef]
- Waluyo, B.; Wardana, I.; Yuliati, L.; Sasongko, M.N.; Setiyo, M. The role of polar ethanol induction in various iso-octane ethanol fuel blends during single droplet combustion. Fuel Process. Technol. 2020, 199, 106275. [Google Scholar] [CrossRef]
- Raghuram, S.; Vasudevan, R. Thermodynamic Analysis of Evaporation of Levitated Binary and Ternary Liquid Fuel Droplets under Normal Gravity. ISRN Thermodyn. 2012, 2012, 167281. [Google Scholar] [CrossRef][Green Version]
- Edwards, T. Reference Jet Fuels for Combusting Testing. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Cung, K.; Kalaskar, V.; Mitchell, R.; Wallace, J.; Briggs, T.; Smith, E.; Michlberger, A.; Williams, D.R.; Bitsis, C. Improved Combustion Efficiency in Methanol/Renewable Diesel Dual Fuel Combustion by Advanced Injection Timing and Increased Intake Temperature: Single-Cylinder Experiment. SAE Tech. Pap. 2023, 2023-01-1641. [Google Scholar] [CrossRef]
- Qi, J.; Eri, Q.; Kong, B.; Zhang, Y. The normal spectral emittance of the real surface from worked aero-engine nozzle. Appl. Therm. Eng. 2019, 150, 641–650. [Google Scholar] [CrossRef]
- Główka, M.; Wójcik, J.K.; Boberski, P.; Woszczyński, P.J.; Sabura, E. Highly Efficient Process for Producing a Jet-A1 Biofuel Component Through Hydroprocessing Soybean Oil over Ni and Pt Catalysts. Energies 2024, 17, 6195. [Google Scholar] [CrossRef]
- Fujinawa, A.; Jean-Philyppe, J.; Panahi, A.; Chang, D.; Schiemann, M.; Levendis, Y.A.; Bergthorson, J.M.; Mi, X.C. Combustion Behavior of Single Iron Particles—Part II: A Theoretical Analysis Based on a Zero-Dimensional Model. Appl. Energy Combust. Sci. 2023, 14, 100145. [Google Scholar] [CrossRef]
- Girin, O.G. Self-Sustained Regimes of Liquid Aerosol Detonation. Proc. R. Soc. A 2019, 475, 20190325. [Google Scholar] [CrossRef]
- Xu, Q.; Yan, F.; Fan, Y.; Gong, M. Inhibition of Polycyclic Aromatic Hydrocarbons Formation During Supercritical Water Gasification of Sewage Sludge by H2O2 Combined with Catalyst. Water 2024, 16, 3235. [Google Scholar] [CrossRef]
- Slabaugh, S.P.; Clavette, P.A.; Blouch, R.J. Fuel Temperature Effects on Combustion Stability of a High-Pressure Liquid-Fueled Swirl Flame. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2025. [Google Scholar]
- Coates, P.; Lowe, S. The Fundamentals of Radiation Thermometers; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Planas-Cuchi, E.; Chatris, J.M.; López, C.; Arnaldos, J.; Casal, J. Determination of Flame Emissivity in Hydrocarbon Pool Fires Using Infrared Thermography. Fire Technol. 2003, 39, 261–273. [Google Scholar] [CrossRef]
- Pastor, E.; Rigueiro, A.; Zárate, L.; Giménez, A.; Arnaldos, J.; Planas, E. Experimental Methodology for Characterizing Flame Emissivity of Small Scale Forest Fires Using Infrared Thermography Techniques. In Proceedings of the IV International Conference on Forest Fire Research 2002 Wildland Fire Safety Summit, Coimbra, Portugal, 19 November 2002; pp. 1–11. Available online: http://hdl.handle.net/2117/7201 (accessed on 31 March 2025).
- Langsdale, M.F.; Wooster, M.; Harrison, J.J.; Koehl, M.; Hecker, C.; Hook, S.J.; Abbott, E.; Johnson, W.R.; Maturilli, A.; Poutier, L.; et al. Spectral Emissivity (SE) Measurement Uncertainties across 2.5–14 μm Derived from a Round-Robin Study Made across In-ternational Laboratories. Remote Sens. 2021, 13, 102. [Google Scholar] [CrossRef]
- Parent, G.; Acem, Z.; Lechêne, S.; Boulet, P. Measurement of Infrared Radiation Emitted by the Flame of a Vegetation Fire. Int. J. Therm. Sci. 2010, 49, 555–562. [Google Scholar] [CrossRef]
- Zalosh, R. Appendix A: Flame Radiation Review. In Handbook of Combustion; Wiley-VCH: Weinheim, Germany, 2014. [Google Scholar] [CrossRef]
- Pavlasek, P.; Elliott, C.J.; Pearce, J.V.; Duris, S.; Palencar, R.; Koval, M.; Machin, G. Machin Hysteresis Effects and Strain-Induced Homogeneity Effects in Base Metal Ther-mo-couples. Int. J. Thermophys. 2015, 36, 467–481. [Google Scholar] [CrossRef]
- Ageyeva, T.; Horváth, S.; Kovács, J.G. In-Mold Sensors for Injection Molding: On the Way to Industry 4.0. Sensors 2019, 19, 3551. [Google Scholar] [CrossRef] [PubMed]
- Galfetti, L. Experimental Measurements and Numerical Modelling of Conductive and Radiative Heat Transfer in Polytetrafluoroethylene. In Proceedings of the RTO Applied Vehicle Technology Panel (AVT) Symposium on Advanced Flow Management: Part B-Heat Transfer and Cooling in Propulsion and Power Systems, Loen, Norway, 7–11 May 2001; Available online: https://apps.dtic.mil/sti/pdfs/ADA419259.pdf (accessed on 31 March 2025).

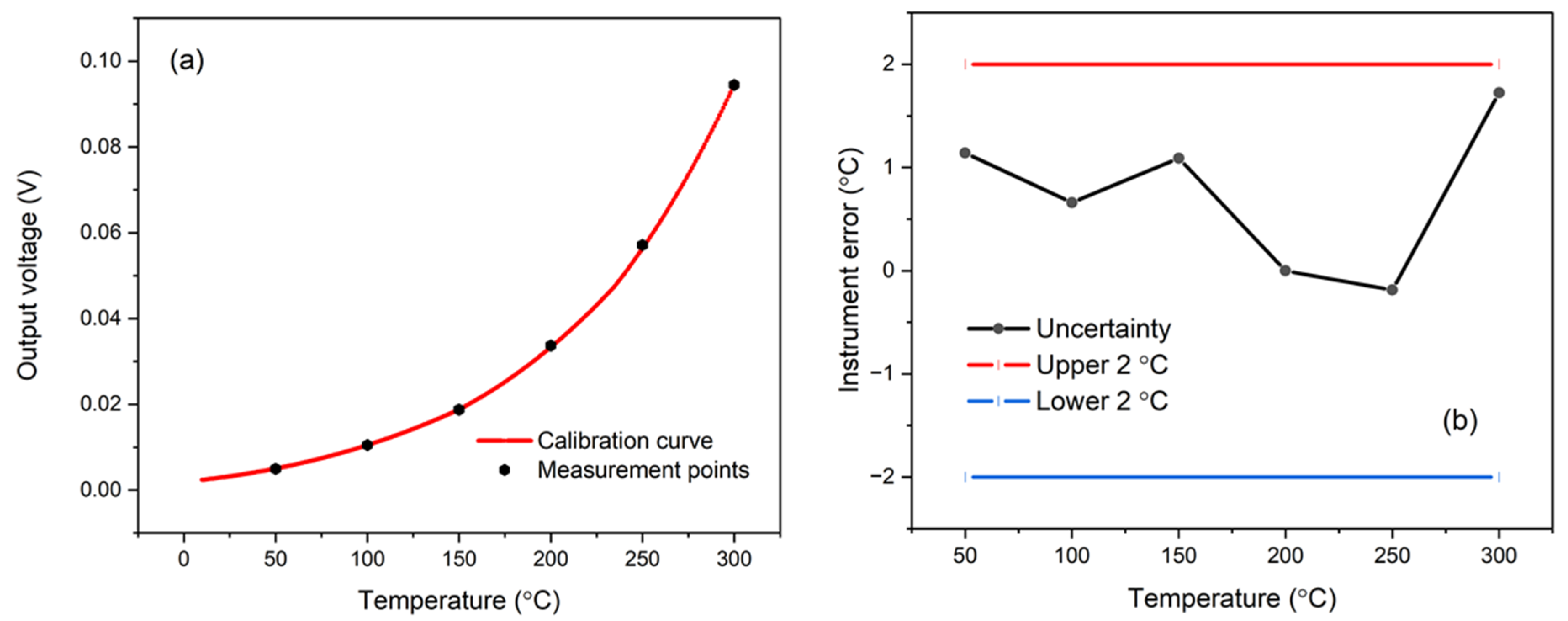
| Target/Reference Temperature (°C) | Blackbody and Thermocouple Contribution to Uncertainty (%) | NI 6002-DAQ-Induced Calibration Uncertainty (%) | |
| Calibration Uncertainties | 100 | 0.3/0.4 | 0.003 |
| Target/Reference Temperature (°C) | IRT Measurement Variability (%) | Mean-IRT Interpolation Deviation (%) | |
| Measurement Uncertainties | 100 | 1.73 | 1.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karapateas, L.; Leonidas, E.; Meng, X.; Lai, Y.; Zhang, Y.; Willmott, J.R.; Hobbs, M.J. InAsSb Photodiode-Based Infrared Radiation Thermometer for the Investigation of Droplet Surface Temperature Dynamics Within an Enclosed Combustion Chamber. Sensors 2025, 25, 5780. https://doi.org/10.3390/s25185780
Karapateas L, Leonidas E, Meng X, Lai Y, Zhang Y, Willmott JR, Hobbs MJ. InAsSb Photodiode-Based Infrared Radiation Thermometer for the Investigation of Droplet Surface Temperature Dynamics Within an Enclosed Combustion Chamber. Sensors. 2025; 25(18):5780. https://doi.org/10.3390/s25185780
Chicago/Turabian StyleKarapateas, Louis, Emilios Leonidas, Xiangfei Meng, Yufeng Lai, Yang Zhang, Jon R. Willmott, and Matthew J. Hobbs. 2025. "InAsSb Photodiode-Based Infrared Radiation Thermometer for the Investigation of Droplet Surface Temperature Dynamics Within an Enclosed Combustion Chamber" Sensors 25, no. 18: 5780. https://doi.org/10.3390/s25185780
APA StyleKarapateas, L., Leonidas, E., Meng, X., Lai, Y., Zhang, Y., Willmott, J. R., & Hobbs, M. J. (2025). InAsSb Photodiode-Based Infrared Radiation Thermometer for the Investigation of Droplet Surface Temperature Dynamics Within an Enclosed Combustion Chamber. Sensors, 25(18), 5780. https://doi.org/10.3390/s25185780








