An Analytical Model of Motion Artifacts in a Measured Arterial Pulse Signal—Part I: Accelerometers and PPG Sensors
Abstract
1. Introduction
2. Materials and Methods
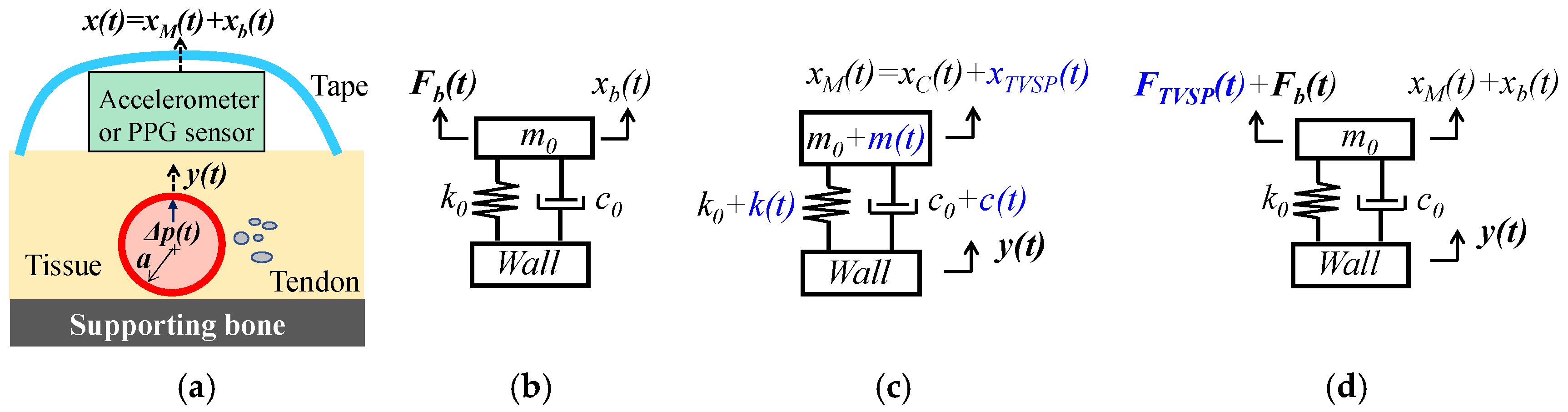
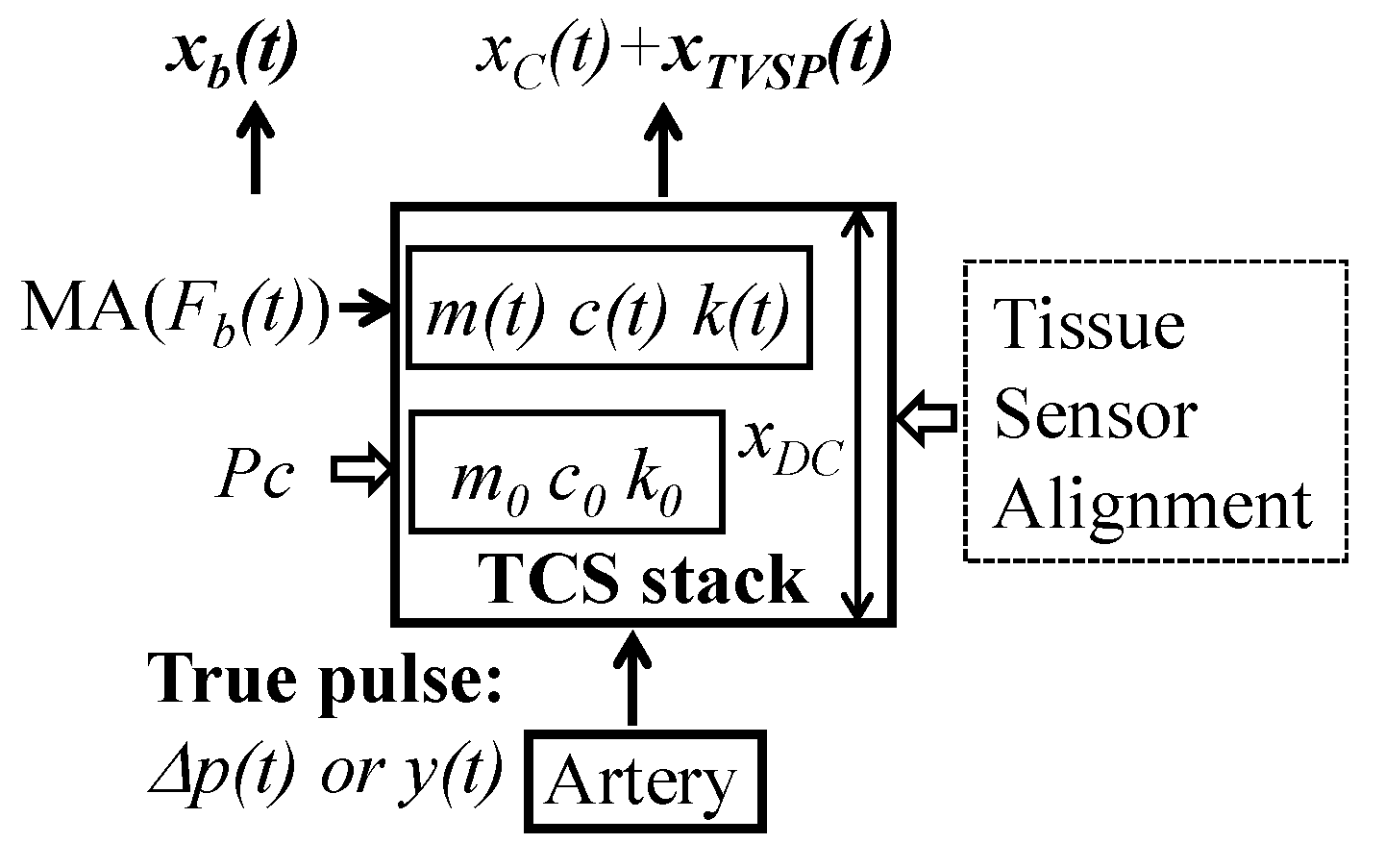
2.1. Arterial Wall Displacement as the True Pulse Signal
2.1.1. MA as Baseline Drift and TVSP
2.1.2. MA as Equivalent Forces
2.2. Pulsatile Pressure as the True Pulse Signal
2.2.1. MA as Baseline Drift and TVSP
2.2.2. MA as Equivalent Forces
2.3. Numerical Calculation
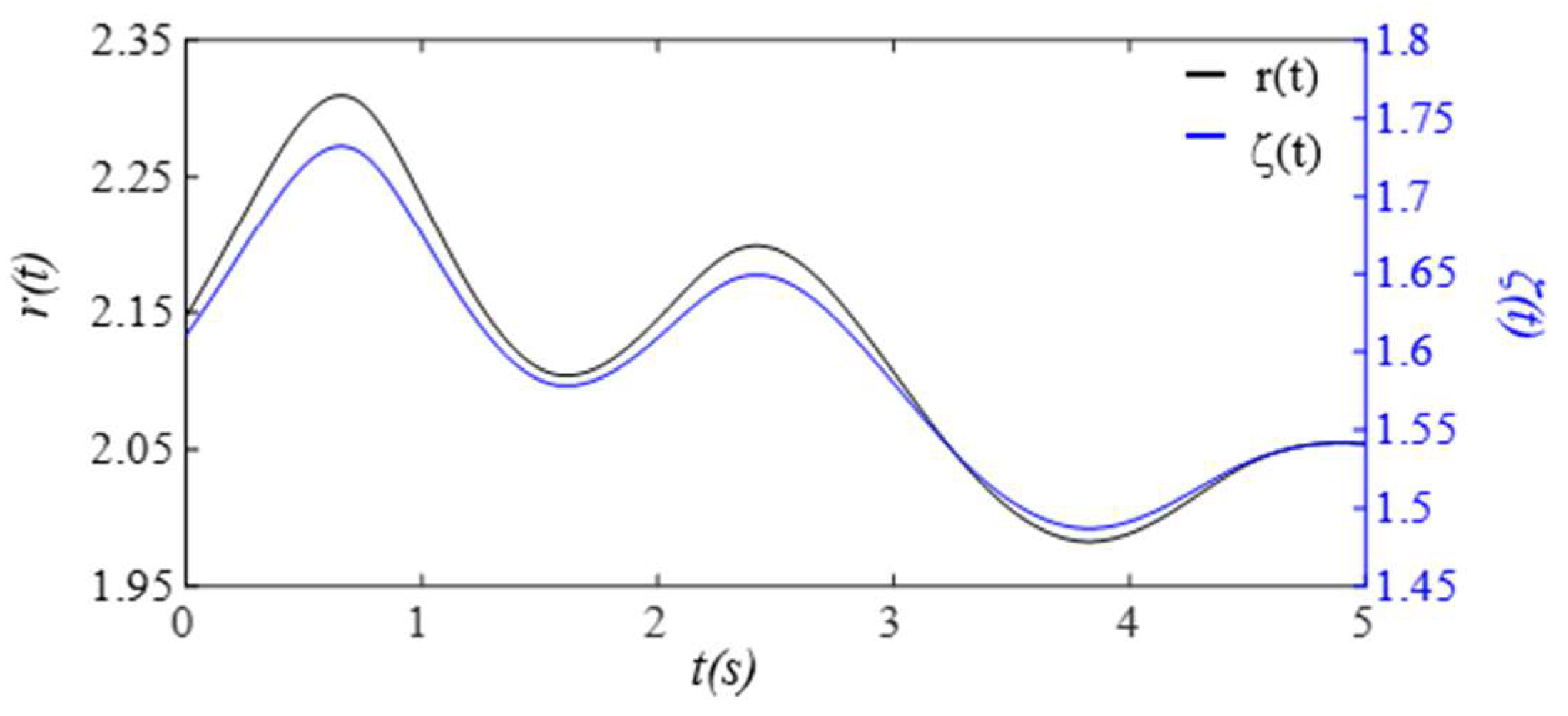
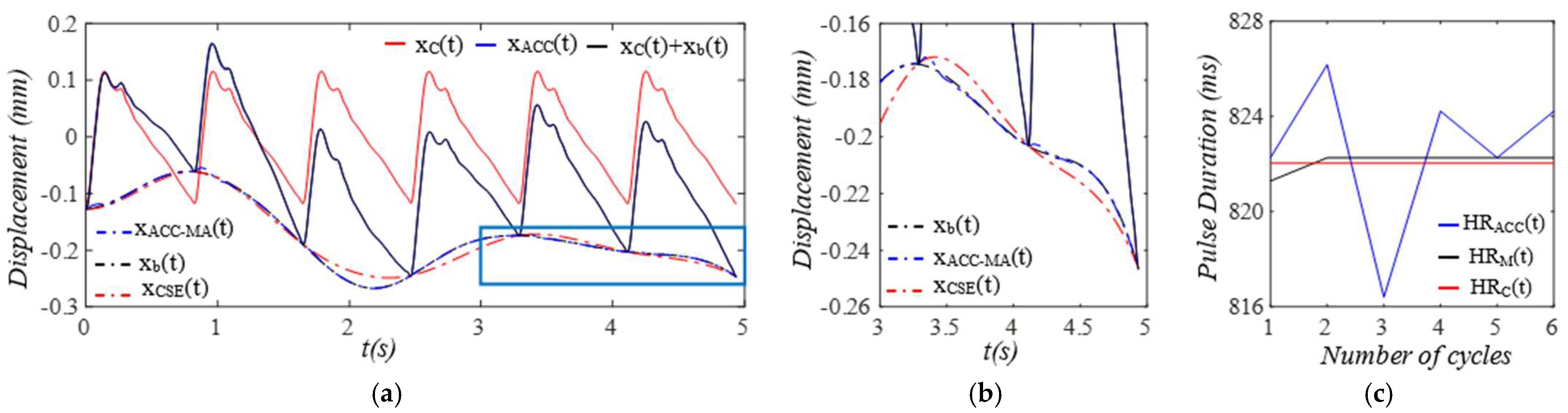
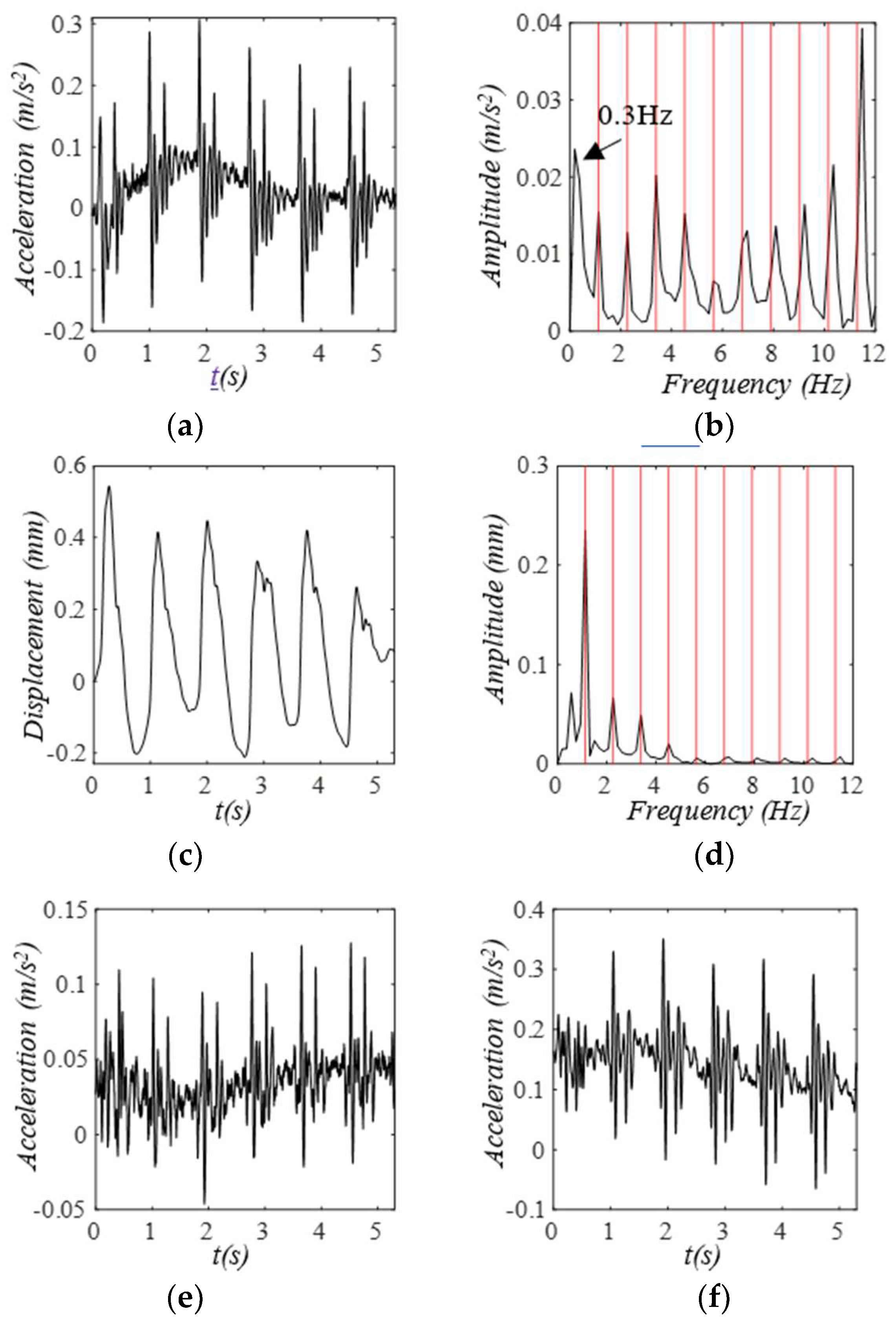
3. Results
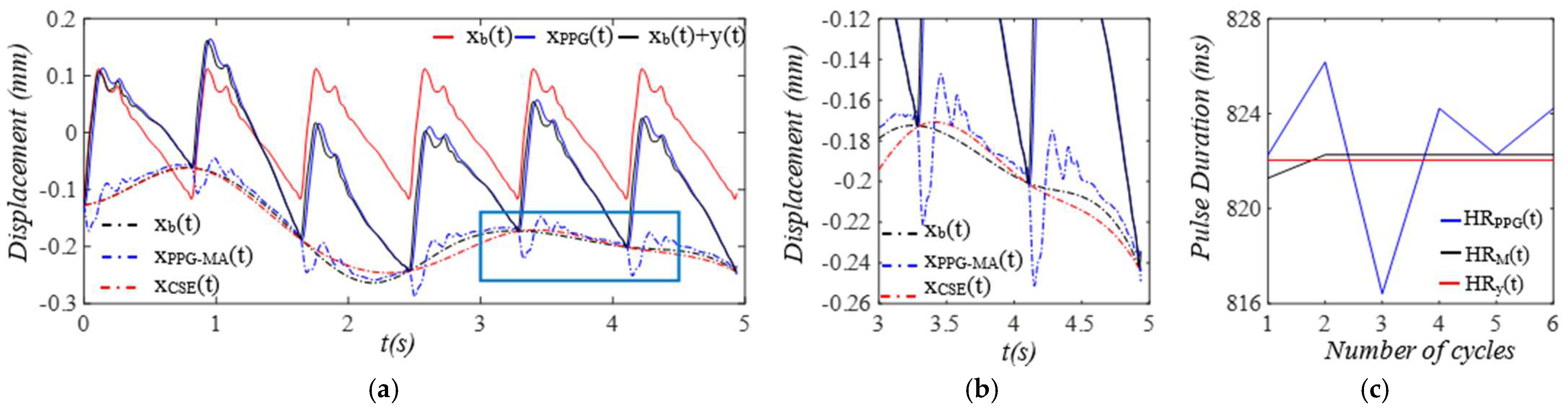
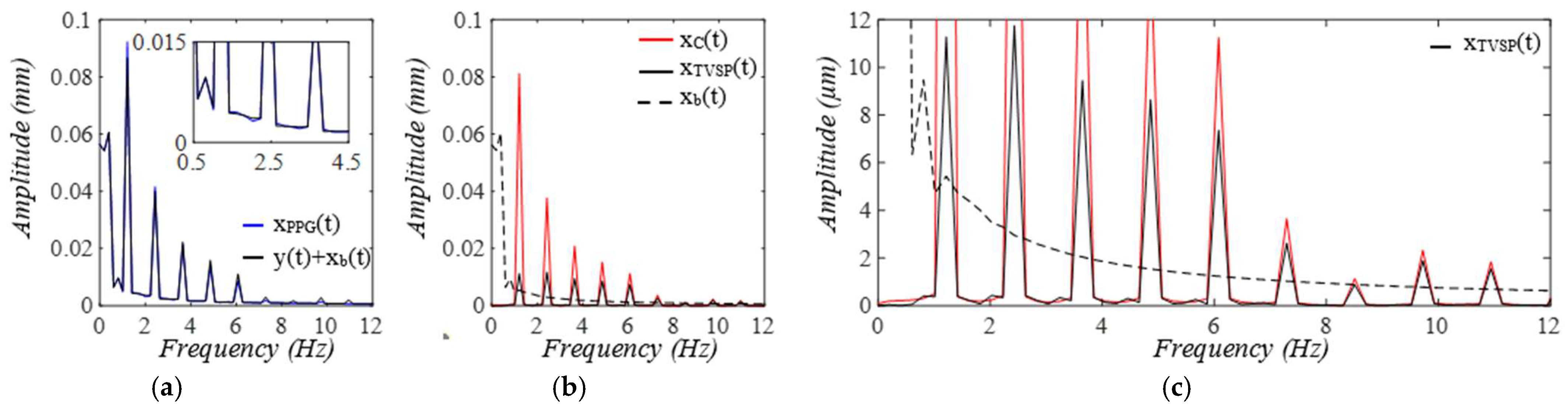
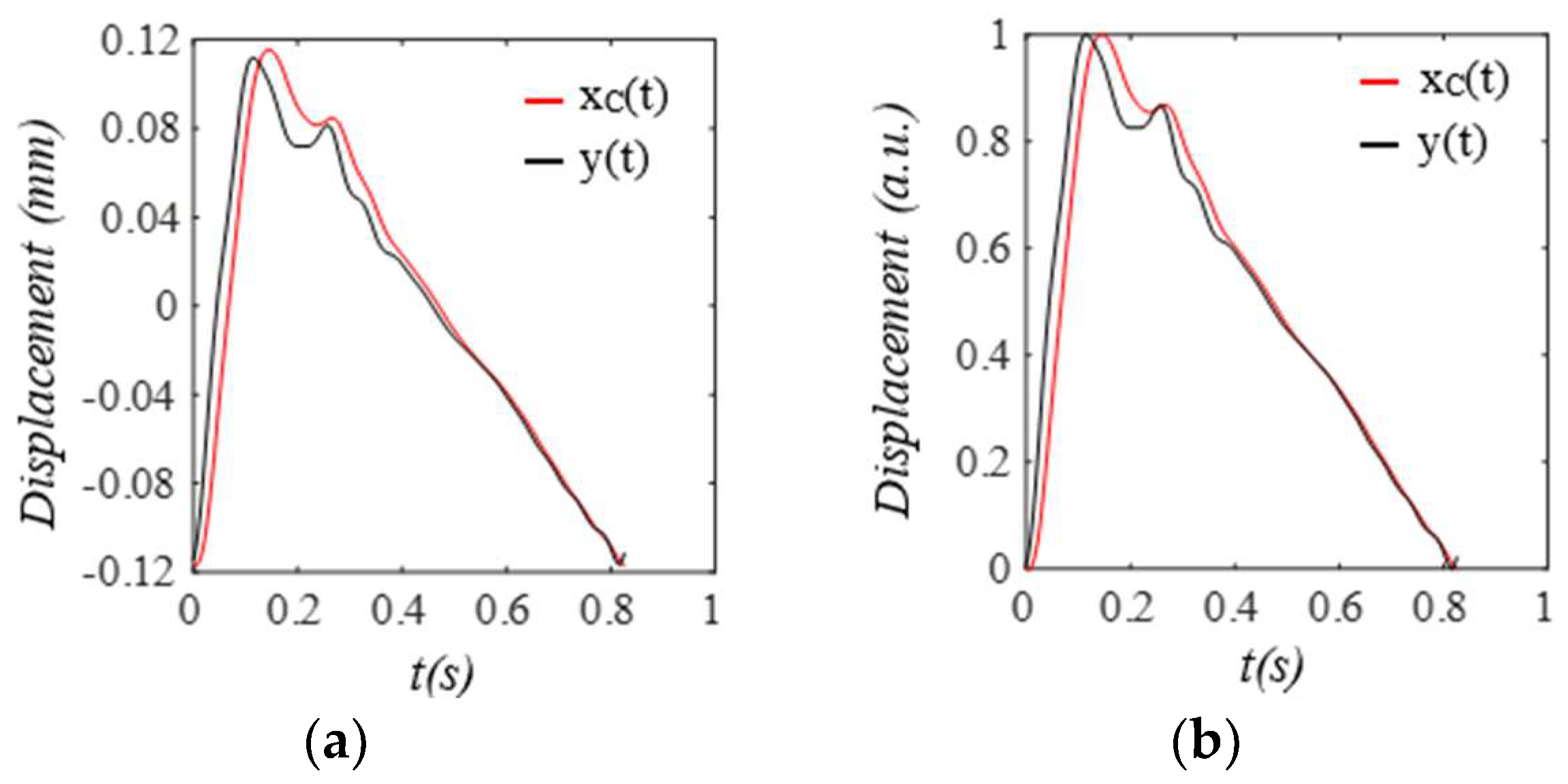
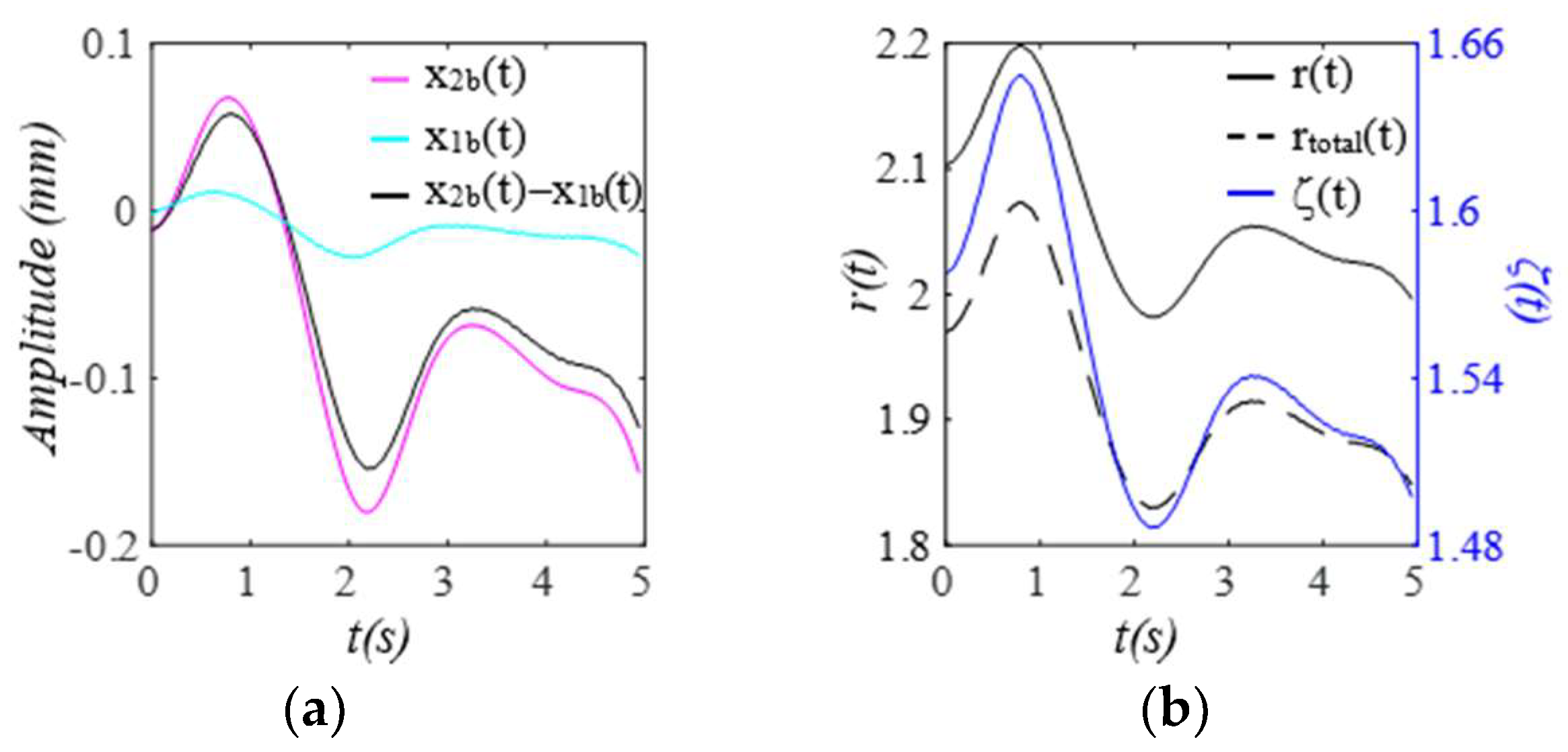
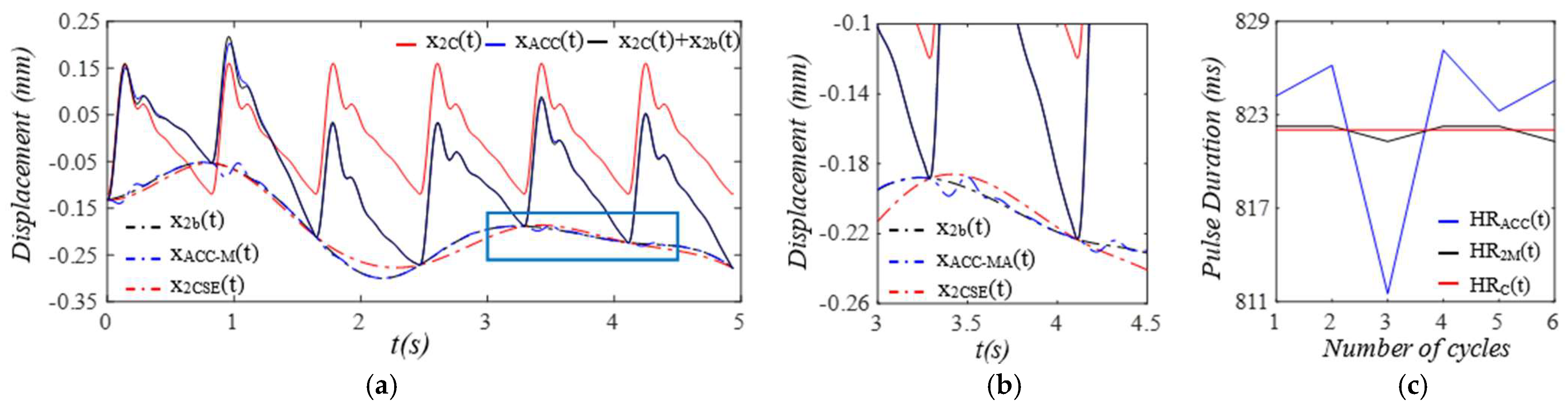
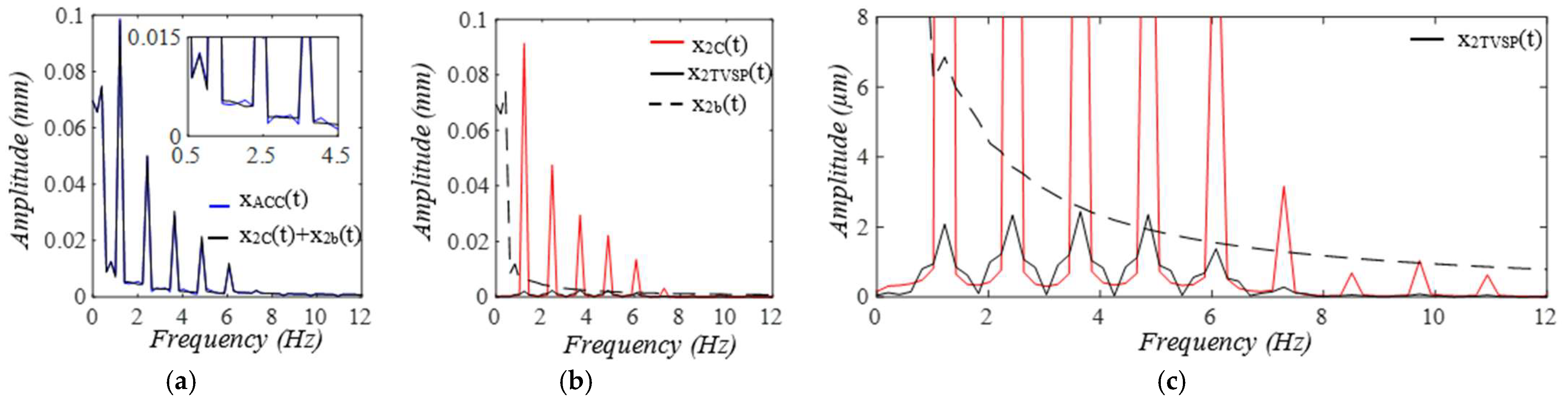
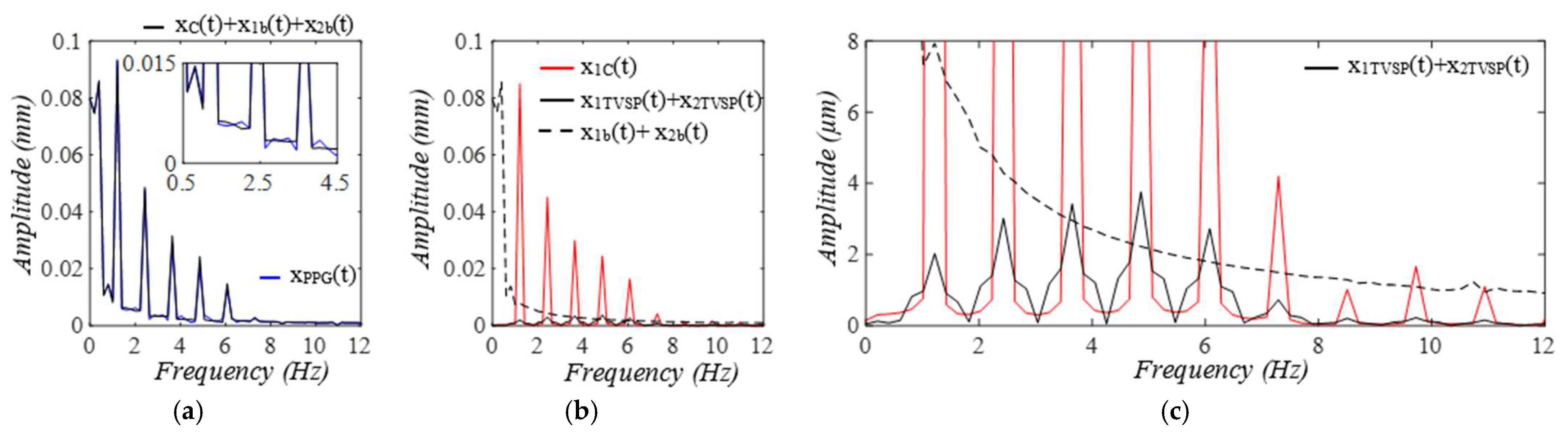
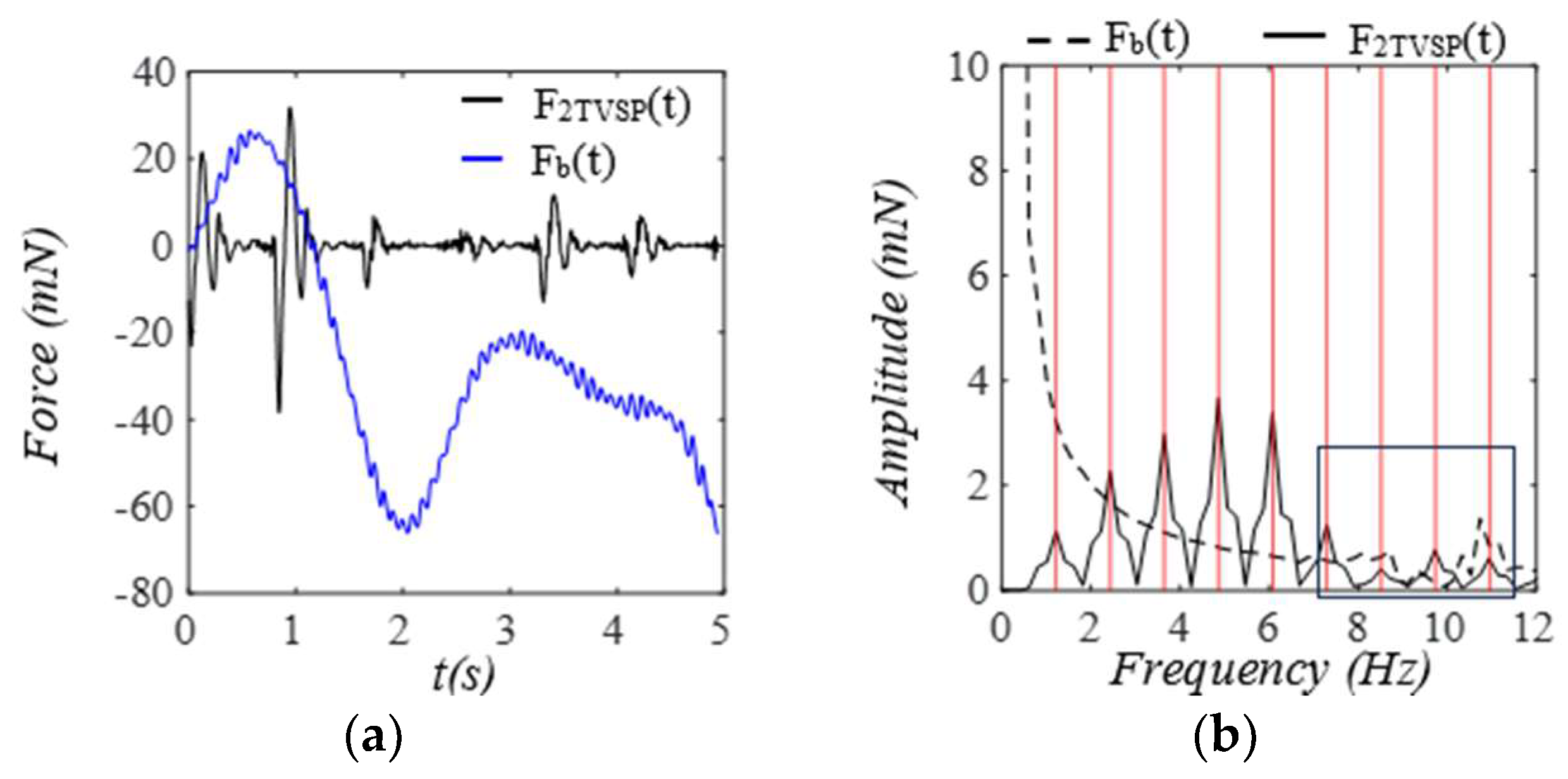
3.1. Arterial Wall Displacement as the True Pulse Signal
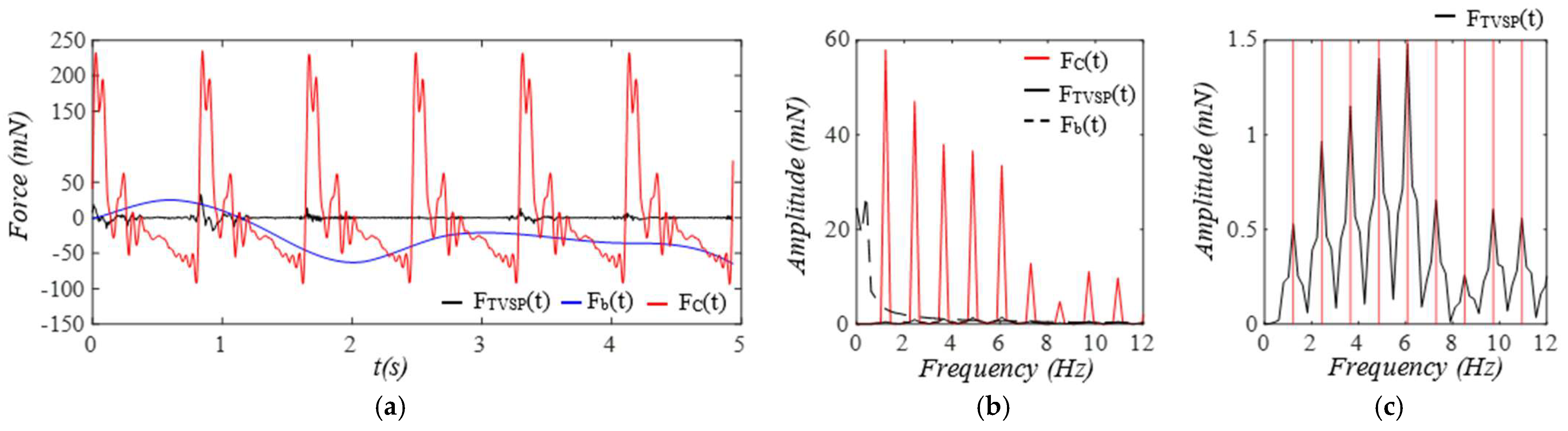
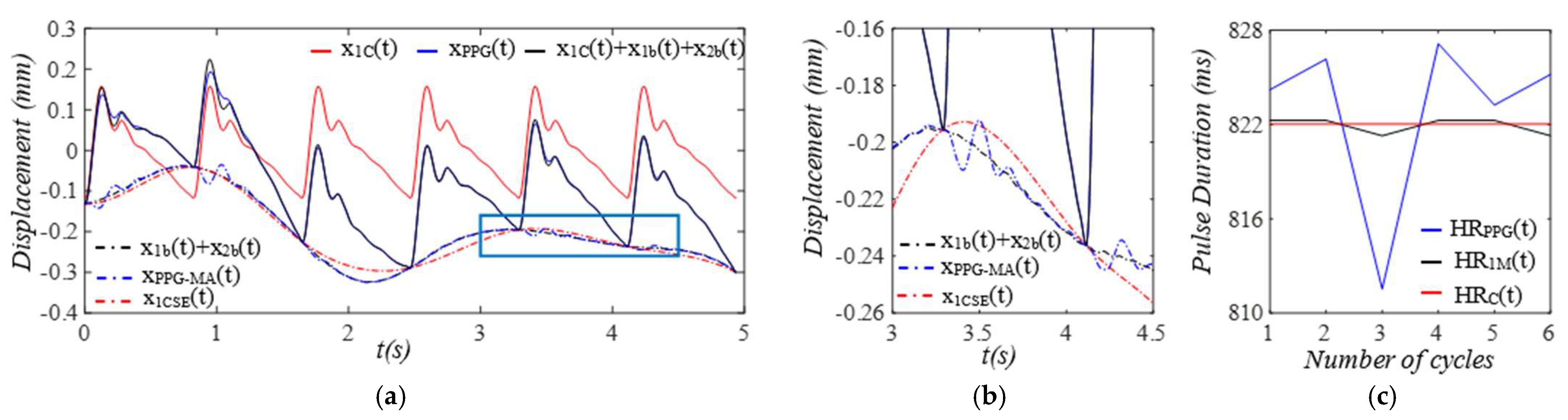
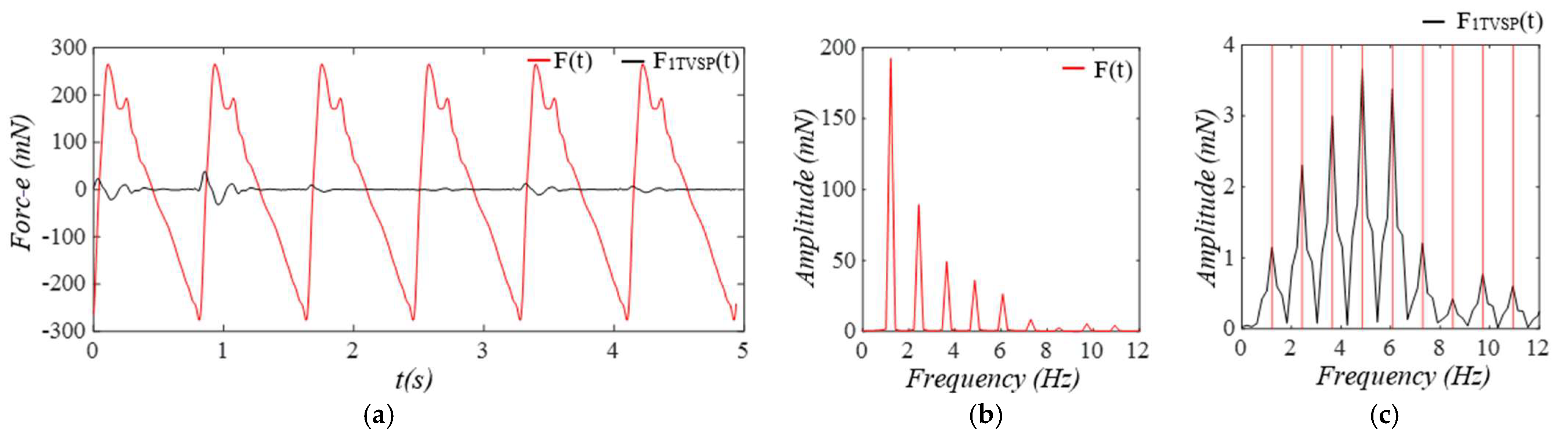
3.2. Pulsatile Pressure as the True Pulse Signal
4. Discussion
4.1. A Full Consideration of the Transmission Path in a Measured Pulse Signal
4.1.1. Comparison with the Current Studies on Pulse Measurement and MA
4.1.2. Existence of TVSPs
4.2. Baseline Drift Versus TVSP-Generated Distortion
4.3. Comparisons with the Related Studies on PPG Signals
4.4. Future Work for Quantification of MA and the TCS Stack
4.5. The Fixing of an Accelerometer and a PPG Sensor
4.6. y(t) Versus as the True Pulse Signal
4.7. Study Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BD | Baseline drift |
| DOF | Degree-of-freedom |
| TVSP | Time-varying system parameter |
| MA | Motion artifact |
| TCS | Tissue–Contact–Sensor |
| HR | Heart Rate |
References
- Elgendi, M. On the Analysis of Fingertip Photoplethysmogram Signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Sun, N.; Yao, Y.; Hao, L.; Xu, L.; Greenwald, S.E. Quantitative Comparison of the Performance of Piezoresistive, Piezoelectric, Acceleration, and Optical Pulse Wave Sensors. Front. Physiol. 2020, 10, 1563. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Reynolds, L.; Alberts, T.; Vahala, L.; Hao, Z. Model-based analysis of arterial pulse signals for tracking changes in arterial wall parameters: A pilot study. Biomech. Model. Mechanobiol. 2019, 18, 1629–1638. [Google Scholar] [CrossRef]
- Hao, Z. Harmonics of Pulsatile Pressure at Different Ages and Its Effect on Other Pulsatile Parameters and Waveform-Based Clinical Indices. J. Eng. Sci. Med. Diagn. Ther. 2024, 7, 011001. [Google Scholar] [CrossRef]
- Ding, X.; Yan, B.P.; Zhang, Y.-T.; Liu, J.; Zhao, N.; Tsang, H.K. Pulse Transit Time Based Continuous Cuffless Blood Pressure Estimation: A New Extension and A Comprehensive Evaluation. Sci. Rep. 2017, 7, 11554. [Google Scholar] [CrossRef]
- Xu, L.; Zhou, S.; Wang, L.; Yao, Y.; Hao, L.; Qi, L.; Yao, Y.; Han, H.; Mukkamala, R.; Greenwald, S.E. Improving the accuracy and robustness of carotid-femoral pulse wave velocity measurement using a simplified tube-load model. Sci. Rep. 2022, 12, 5147. [Google Scholar] [CrossRef]
- Hao, Z. Relations of Radial Vibration of the Arterial Wall to Pulsatile Parameters in Blood Flow for Extraction of Arterial Indices. J. Eng. Sci. Med. Diagn. Ther. 2023, 6, 011002. [Google Scholar] [CrossRef]
- Hoog Antink, C.; Mai, Y.; Peltokangas, M.; Leonhardt, S.; Oksala, N.; Vehkaoja, A. Accuracy of heart rate variability estimated with reflective wrist-PPG in elderly vascular patients. Sci. Rep. 2021, 11, 8123. [Google Scholar] [CrossRef] [PubMed]
- Hao, Z. A 2-DOF Model of the Artery-Sensor System for Interpreting Variability in Measured Arterial Pulse Waveform. IEEE Sens. J. 2023, 23, 22668–22678. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, D.; Wang, K.; Li, N.; Wang, X. Baseline wander correction in pulse waveforms using wavelet-based cascaded adaptive filter. Comput. Biol. Med. 2007, 37, 716–731. [Google Scholar] [CrossRef] [PubMed]
- Kan, L.; Jianqing, L.; Jianfeng, W.; Gaozhi, X. A cascade filter for pulse wave baseline drift elimination. In Proceedings of the 2012 5th International Congress on Image and Signal Processing, Nanjing, China, 16–18 October 2012; pp. 1495–1499. [Google Scholar] [CrossRef]
- Liu, H.; Chen, F.; Hartmann, V.; Khalid, S.G.; Hughes, S.; Zheng, D. Comparison of different modulations of photoplethysmography in extracting respiratory rate: From a physiological perspective. Physiol. Meas. 2020, 41, 094001. [Google Scholar] [CrossRef]
- Chon, K.H.; Dash, S.; Ju, K. Estimation of respiratory rate from photoplethysmogram data using time-frequency spectral estimation. IEEE Trans. Biomed. Eng. 2009, 56, 2054–2063. [Google Scholar] [CrossRef] [PubMed]
- Pollreisz, D.; Taherinejad, N. Detection and Removal of Motion Artifacts in PPG Signals. Mob. Netw. Appl. 2022, 27, 728–738. [Google Scholar] [CrossRef]
- Noorlandt, R.; Drijkoningen, G. On the mechanical vibrator-earth contact geometry and its dynamics. Geophysics 2016, 81, P37–P45. [Google Scholar] [CrossRef]
- Pandey, R.K.; Chao, P.C.P. A Dual-Channel PPG Readout System with Motion-Tolerant Adaptability for OLED-OPD Sensors. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 36–51. [Google Scholar] [CrossRef]
- Hao, Z. A Vibrating-String Model for Closed-Loop Wave Transmission and Reflection Between the Aorta and Periphery. J. Eng. Sci. Med. Diagn. Ther. 2023, 6, 041001. [Google Scholar] [CrossRef]
- Wang, Z.-C.; Ren, W.-X.; Chen, G. Time–frequency analysis and applications in time-varying/nonlinear structural systems: A state-of-the-art review. Adv. Struct. Eng. 2018, 21, 1562–1584. [Google Scholar] [CrossRef]
- Charlton, P.; Mariscal-Harana, J.; Vennin, S.; Li, Y.; Chowienczyk, P.; Alastruey, J. Modeling arterial pulse waves in healthy ageing: A database for in silico evaluation of haemodynamics and pulse wave indices. Am. J. Physiol.-Heart Circ. Physiol. 2019, 317, H1062–H1085. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Andreozzi, E.; Centracchio, J.; Esposito, D.; Bifulco, P. A Comparison of Heart Pulsations Provided by Forcecardiography and Double Integration of Seismocardiogram. Bioengineering 2022, 9, 167. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, N.; Xu, J.; Liu, Z.; Zhou, Y.; Yang, Y.; Li, S.; Huang, Y.; Jiang, S. Flexible electronics for cardiovascular healthcare monitoring. Innovation 2023, 4, 100485. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Zhu, T.; Kang, Z.; Zeng, X.; Zhou, B.; Zhou, Y.; Mu, J.; Yin, Z. Strategies for Achieving High-Performance Photomultiplication-Type Organic Photodetectors and Their Promising Applications. Nano Energy 2024, 132, 110399. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, H.; Jang, J.; Lee, J.; Kim, M.; Lee, J.; Kim, H.; Yoo, S.; Yoo, H.J. Sticker-Type Hybrid Photoplethysmogram Monitoring System Integrating CMOS IC with Organic Optical Sensors. IEEE J. Emerg. Sel. Top. Circuits Syst. 2017, 7, 50–59. [Google Scholar] [CrossRef]
- Di Lascio, N.; Gemignani, V.; Bruno, R.M.; Bianchini, E.; Stea, F.; Ghiadoni, L.; Faita, F. Noninvasive Assessment of Carotid Pulse Pressure Values: An Accelerometric-Based Approach. IEEE Trans. Biomed. Eng. 2016, 63, 869–875. [Google Scholar] [CrossRef] [PubMed]
- Arathy, R.; Nabeel, P.M.; Abhidev, V.V.; Sivaprakasam, M.; Joseph, J. An Accelerometric Sensor System With Integrated Hydrostatic Pressure Correction to Assess Carotid Arterial Stiffness. IEEE Sens. J. 2021, 21, 11163–11175. [Google Scholar] [CrossRef]
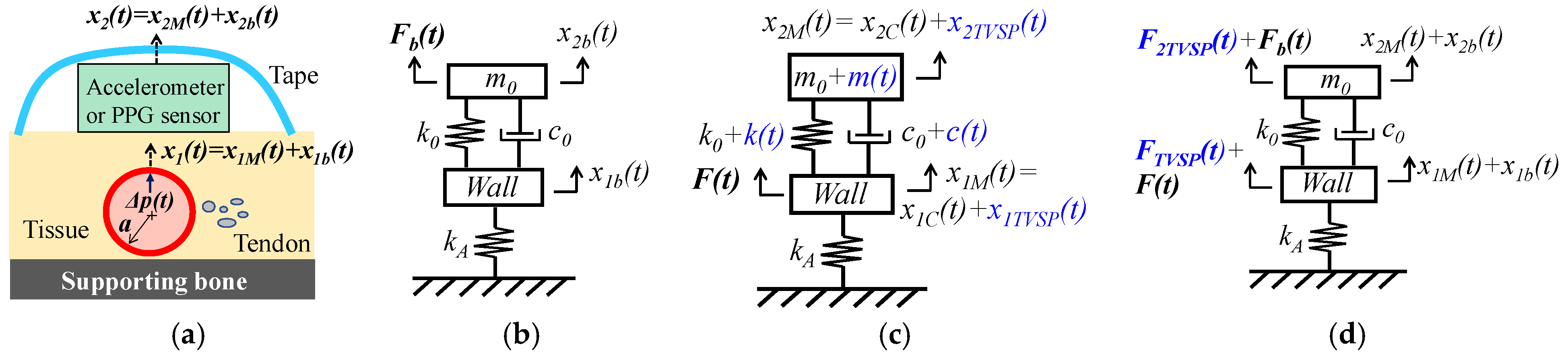


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.M.; Toraskar, S.; Hasan, M.; Hao, Z. An Analytical Model of Motion Artifacts in a Measured Arterial Pulse Signal—Part I: Accelerometers and PPG Sensors. Sensors 2025, 25, 5710. https://doi.org/10.3390/s25185710
Rahman MM, Toraskar S, Hasan M, Hao Z. An Analytical Model of Motion Artifacts in a Measured Arterial Pulse Signal—Part I: Accelerometers and PPG Sensors. Sensors. 2025; 25(18):5710. https://doi.org/10.3390/s25185710
Chicago/Turabian StyleRahman, Md Mahfuzur, Subodh Toraskar, Mamun Hasan, and Zhili Hao. 2025. "An Analytical Model of Motion Artifacts in a Measured Arterial Pulse Signal—Part I: Accelerometers and PPG Sensors" Sensors 25, no. 18: 5710. https://doi.org/10.3390/s25185710
APA StyleRahman, M. M., Toraskar, S., Hasan, M., & Hao, Z. (2025). An Analytical Model of Motion Artifacts in a Measured Arterial Pulse Signal—Part I: Accelerometers and PPG Sensors. Sensors, 25(18), 5710. https://doi.org/10.3390/s25185710





