Characterization of Sub-Resonant Dielectric Spheres by Millimeter-Wave Scattering Measurements
Abstract
Highlights
- Sub-wavelength-sized alumina ceramic spheres are characterized with good accuracy with respect to their size and relative permittivity from scattering measurements at millimeter-wave frequencies.
- The characterization procedure is explained in detail and systematic error sources are analyzed.
- Sub-resonant scattering measurements allow the characterization of relatively smaller particles with respect to traditional resonance-based methods.
- Alternatively, for a given particle size, sub-resonant characterization allows use of a lower operating frequency and, thus, simpler equipment.
Abstract
1. Introduction
2. Materials and Methods
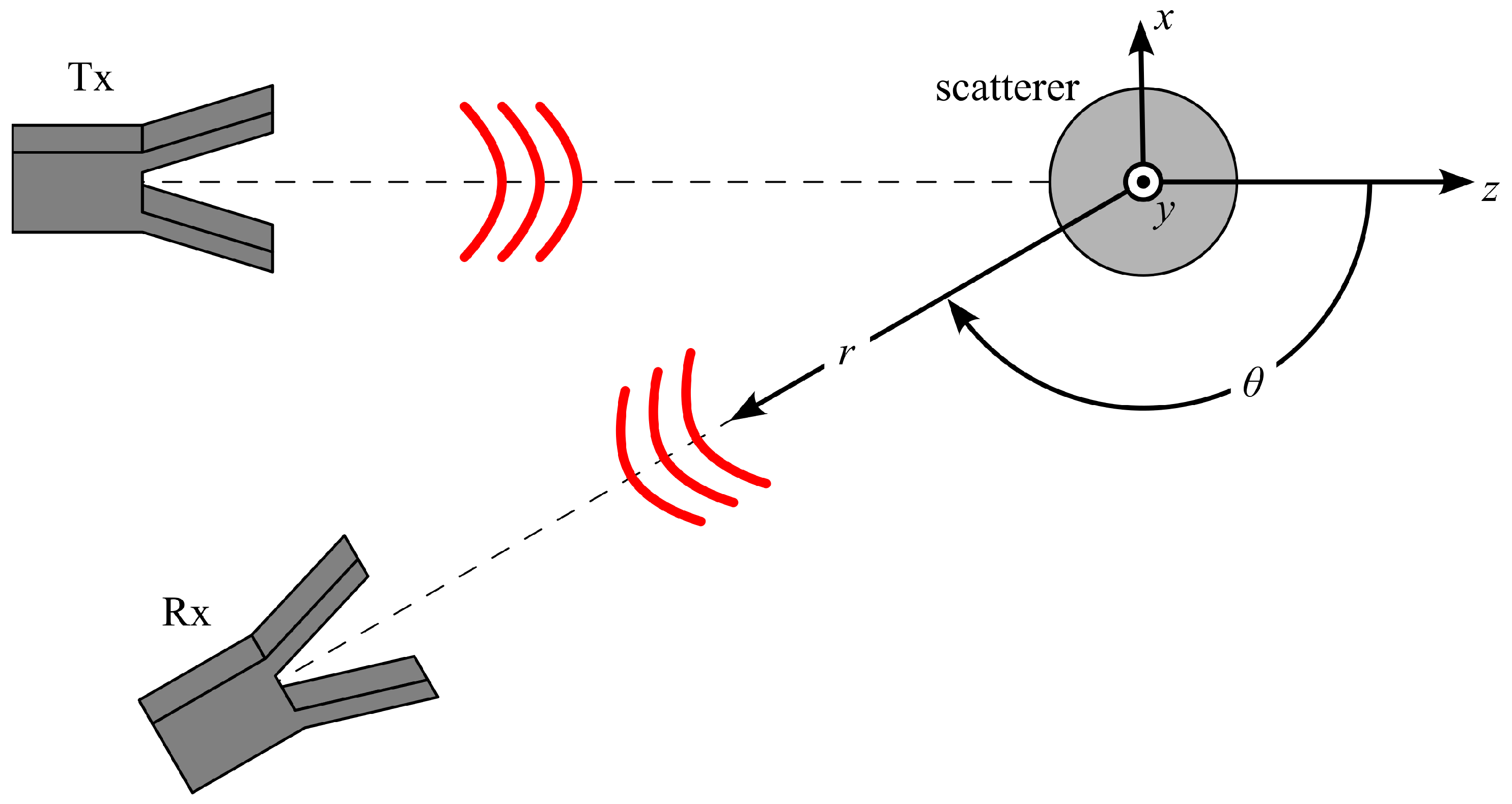
2.1. Scattering of a Dielectric Sphere
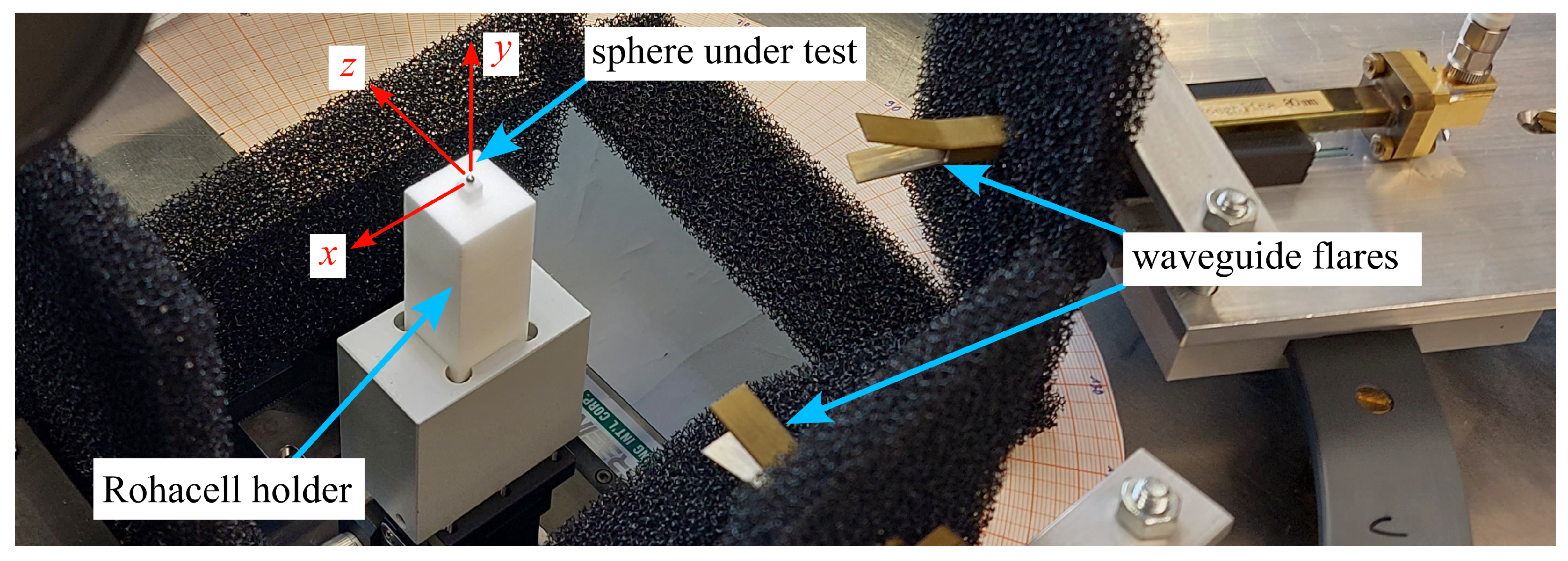
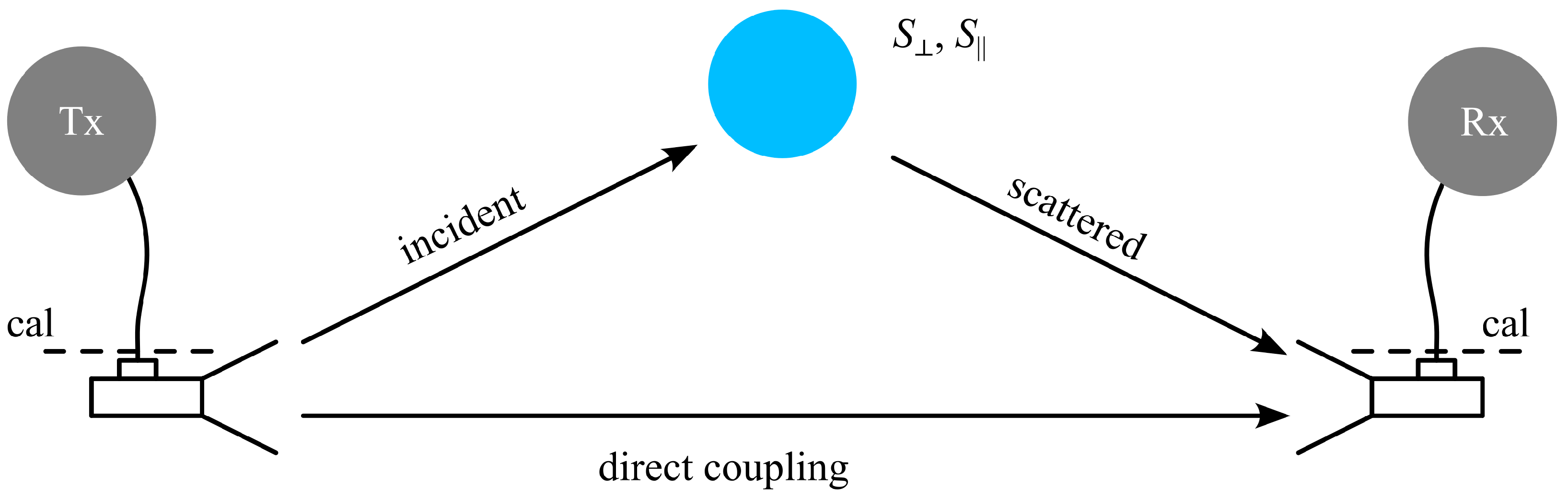
2.2. Measurement of Bi-Static Sphere Scattering
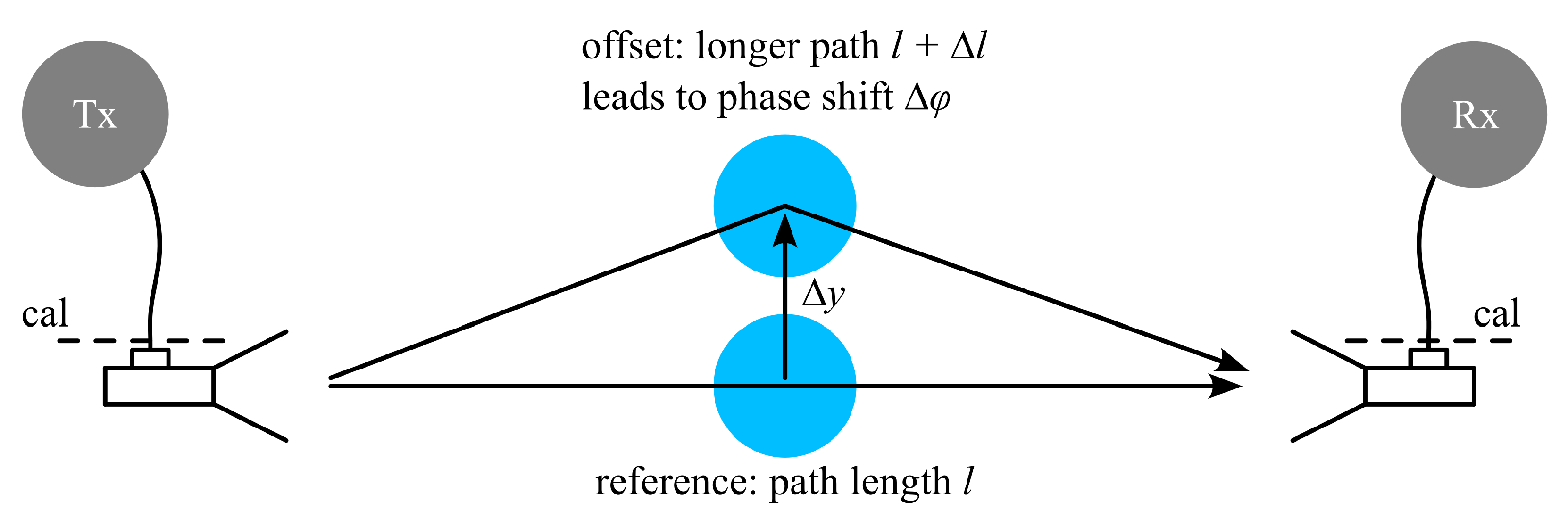
2.3. Post-Processing and Parameter Extraction
3. Results and Discussion
3.1. Results
3.2. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lorenz, L. Lysbevægelsen i og uden for en af Plane Lysbølger Belyst Kugle; Det Kongelige Danske Videnskabernes Selskabs Skrifter: Copenhagen, Denmark, 1890. [Google Scholar]
- Logan, N. Survey of some early studies of the scattering of plane waves by a sphere. Proc. IEEE 1965, 53, 773–785. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Baltes, H.P. Inverse Scattering Problems in Optics; Springer: Berlin, Germany, 1980. [Google Scholar]
- Conwell, P.R.; Rushforth, C.K.; Benner, R.E.; Hill, S.C. Efficient automated algorithm for the sizing of dielectric microspheres using the resonance spectrum. J. Opt. Soc. Am. A 1984, 1, 1181–1187. [Google Scholar] [CrossRef]
- Hill, S.C.; Rushforth, C.K.; Benner, R.E.; Conwell, P.R. Sizing dielectric spheres and cylinders by aligning measured and computed resonance locations: Algorithm for multiple orders. Appl. Opt. 1985, 24, 2380–2390. [Google Scholar] [CrossRef]
- Salzman, G.; Hiebert, R.; Jett, J.; Bartholdi, M. High-speed single particle sizing by light scattering in a flow system. In Proceedings of the Optics in Metrology and Quality Assurance, Los Angeles, CA, USA, 4–7 February 1980; Volume 220, pp. 23–27. [Google Scholar]
- Sierra, A.Q.; Delgado Mora, A.V. Size–shape determination of nonspherical particles in suspension by means of full and depolarized static light scattering. Appl. Opt. 1995, 34, 6256–6262. [Google Scholar] [CrossRef] [PubMed]
- Litvinenko, A.L.; Nekrasov, V.M.; Strokotov, D.I.; Moskalensky, A.E.; Chernyshev, A.V.; Shilova, A.N.; Karpenko, A.A.; Maltsev, V.P. Blood platelet quantification by light scattering: From morphology to activation. Anal. Methods 2021, 13, 3233–3241. [Google Scholar] [CrossRef]
- Saleh, H.; Tortel, H.; Leroux, C.; Coudreuse, A.; Litman, A.; Geffrin, J.M. Approach to control permittivity and shape of centimeter-sized additive manufactured objects: Application to microwave scattering experiments. IEEE Trans. Antennas Propag. 2020, 69, 983–991. [Google Scholar] [CrossRef]
- Young, J.D. Constitutive Parameter Measurements Using the Scattering Technique; Technical Report; NASA: Greenbelt, MD, USA, 1967.
- Yu, J.; Peters, L. Measurement of constitutive parameters using the Mie solution of a scattering sphere. Proc. IEEE 1970, 58, 876–885. [Google Scholar] [CrossRef][Green Version]
- Yu, J.; Peters, L.; Castello, D. A refractive index chart for a scattering sphere. IEEE Trans. Antennas Propag. 1970, 18, 75–83. [Google Scholar][Green Version]
- Greenberg, J.M.; Pedersen, N.E.; Pedersen, J.C. Microwave analog to the scattering of light by nonspherical particles. J. Appl. Phys. 1961, 32, 233–242. [Google Scholar] [CrossRef]
- Eyraud, C.; Geffrin, J.M.; Sabouroux, P.; Chaumet, P.C.; Tortel, H.; Giovannini, H.; Litman, A. Validation of a 3D bistatic microwave scattering measurement setup. Radio Sci. 2008, 43, 1–12. [Google Scholar] [CrossRef]
- Gustafson, B.Å. Microwave analog to light scattering measurements: A modern implementation of a proven method to achieve precise control. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 663–672. [Google Scholar] [CrossRef]
- Gustafson, B.Å. Scaled analogue experiments in electromagnetic scattering. In Light Scattering Reviews 4: Single Light Scattering and Radiative Transfer; Springer: Berlin/Heidelberg, Germany, 2009; pp. 3–30. [Google Scholar]
- Hage, J.I.; Greenberg, J.M.; Wang, R.T. Scattering from arbitrarily shaped particles: Theory and experiment. Appl. Opt. 1991, 30, 1141–1152. [Google Scholar] [CrossRef]
- Aden, A. Electromagnetic scattering from spheres with sizes comparable to the wavelength. J. Appl. Phys. 1951, 22, 601–605. [Google Scholar] [CrossRef]
- Geffrin, J.M.; García-Cámara, B.; Gómez-Medina, R.; Albella, P.; Froufe-Pérez, L.; Eyraud, C.; Litman, A.; Vaillon, R.; González, F.; Nieto-Vesperinas, M.; et al. Magnetic and electric coherence in forward-and back-scattered electromagnetic waves by a single dielectric subwavelength sphere. Nat. Commun. 2012, 3, 1171. [Google Scholar] [CrossRef] [PubMed]
- Merchiers, O.; Eyraud, C.; Geffrin, J.M.; Vaillon, R.; Stout, B.; Sabouroux, P.; Lacroix, B. Microwave measurements of the full amplitude scattering matrix of a complex aggregate: A database for the assessment of light scattering codes. Opt. Express 2010, 18, 2056–2075. [Google Scholar] [CrossRef]
- Renard, J.B.; Geffrin, J.M.; Valencia, V.T.; Tortel, H.; Ménard, F.; Rannou, P.; Milli, J.; Berthet, G. Number of independent measurements required to obtain reliable mean scattering properties of irregular particles having a small size parameter, using microwave analogy measurements. J. Quant. Spectrosc. Radiat. Transf. 2021, 272, 107718. [Google Scholar] [CrossRef]
- Schuerman, D.; Wang, R.; Gustafson, B.; Schaefer, R. Systematic studies of light scattering. 1: Particle shape. Appl. Opt. 1981, 20, 4039–4050. [Google Scholar] [CrossRef]
- Zerull, R.H.; Giese, R.H.; Weiss, K. Scattering functions of nonspherical dielectric and absorbing particles vs Mie theory. Appl. Opt. 1977, 16, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Dey, U.; Li, Y.; Hesselbarth, J. Millimeter-Wave Resonant Spectroscopy of Sub-Wavelength Dielectric Particle. In Proceedings of the 2021 IEEE MTT-S International Microwave Symposium (IMS), Atlanta, GA, USA, 7–25 June 2021; pp. 485–488. [Google Scholar]
- Phillips, D.T.; Wyatt, P.J.; Berkman, R.M. Measurement of the Lorenz-Mie scattering of a single particle: Polystyrene latex. J. Colloid Interf. Sci. 1970, 34, 159–162. [Google Scholar] [CrossRef]
- Marshall, T.R.; Parmenter, C.S.; Seaver, M. Characterization of polymer latex aerosols by rapid measurement of 360 light scattering patterns from individual particles. J. Colloid Interface Sci. 1976, 55, 624–636. [Google Scholar] [CrossRef]
- Gastine, M.; Courtois, L.; Dormann, J. Electromagnetic Resonances of Free Dielectric Spheres. IEEE Trans. Microw. Theory Tech. 1967, 15, 694–700. [Google Scholar] [CrossRef]
- Jansen, C.; Krumbholz, N.; Geise, R.; Enders, A.; Koch, M. Scaled radar cross section measurements with terahertz-spectroscopy up to 800 GHz. In Proceedings of the 2009 3rd European Conference on Antennas and Propagation, Berlin, Germany, 23–27 March 2009; pp. 3645–3648. [Google Scholar]
- Iwaszczuk, K.; Heiselberg, H.; Jepsen, P.U. Terahertz radar cross section measurements. Opt. Express 2010, 18, 26399–26408. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Rycaj, K.; Chen, X.; Tang, D.G. Cancer stem cells and cell size: A causal link? Semin. Cancer Biol. 2015, 35, 191–199. [Google Scholar] [CrossRef] [PubMed]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004. [Google Scholar]
- Tzarouchis, D.; Sihvola, A. Light scattering by a dielectric sphere: Perspectives on the Mie resonances. Appl. Sci. 2018, 8, 184. [Google Scholar] [CrossRef]
- Dey, U.; Hesselbarth, J. Subwavelength Particle Spectroscopy by Measurements of Electromagnetic Scattering at Millimeter-Wave Frequency. IEEE Trans. Microw. Theory Tech. 2022, 70, 699–710. [Google Scholar] [CrossRef]
- Larsson, C.; Gustafsson, M. Wideband measurements of the forward RCS and the extinction cross section. Appl. Comput. Electromagn. Soc. J. (ACES) 2013, 28, 1145–1152. [Google Scholar]
- Molla, J.; Heidinger, R.; Ibarra, A.; Link, G. Dielectric properties of alumina/zirconia composites at millimeter wavelengths. J. Appl. Phys. 1993, 73, 7667–7671. [Google Scholar] [CrossRef]
- Wiscombe, W.J. Improved Mie scattering algorithms. Appl. Opt. 1980, 19, 1505–1509. [Google Scholar] [CrossRef]
- Penn, S.J.; Alford, N.M.; Templeton, A.; Wang, X.; Xu, M.; Reece, M.; Schrapel, K. Effect of porosity and grain size on the microwave dielectric properties of sintered alumina. J. Am. Ceram. Soc. 1997, 80, 1885–1888. [Google Scholar] [CrossRef]

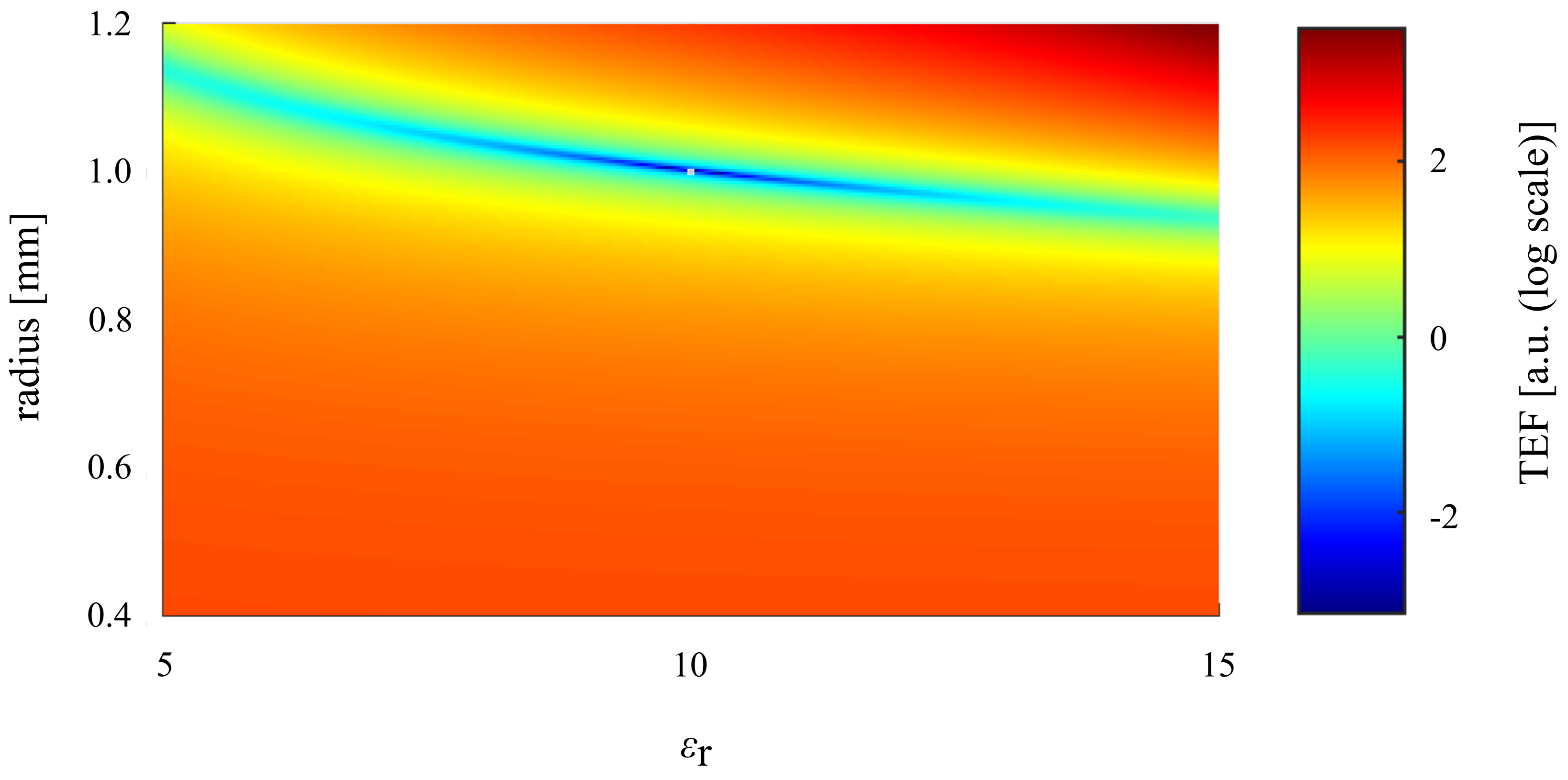

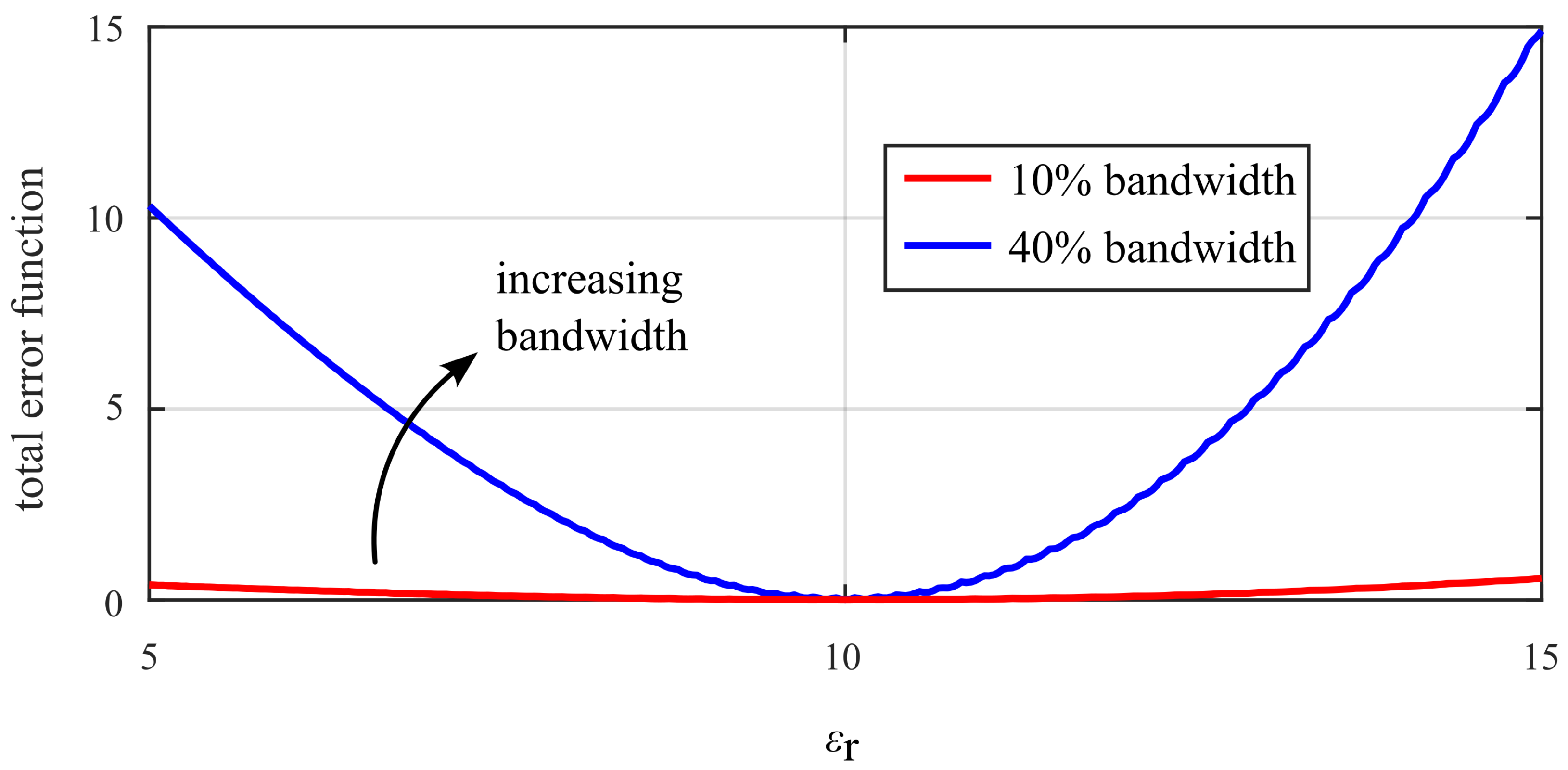
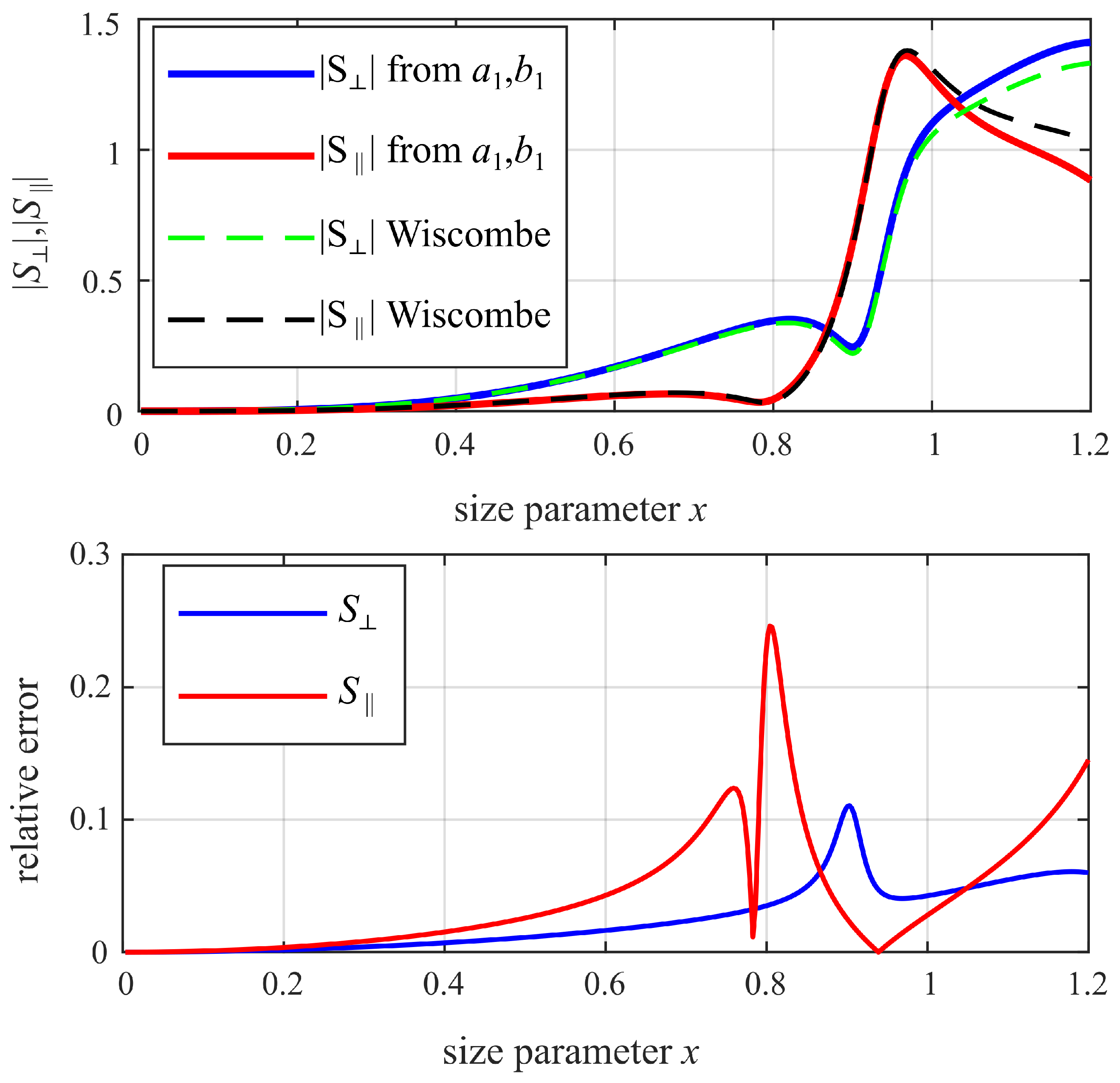
| Sphere | Mechanically Measured Radius [mm] | Extracted Radius [mm] | Extracted |
|---|---|---|---|
| #1 | 0.998 | 1.006 | 9.967 |
| #2 | 0.793 | 0.794 | 10.900 |
| #3 | 0.599 | 0.596 | 10.633 |
| #4 | 0.498 | 0.497 | 12.033 |
| #5 | 0.396 | 0.394 | 12.867 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lippoldt, M.; Hesselbarth, J. Characterization of Sub-Resonant Dielectric Spheres by Millimeter-Wave Scattering Measurements. Sensors 2025, 25, 5687. https://doi.org/10.3390/s25185687
Lippoldt M, Hesselbarth J. Characterization of Sub-Resonant Dielectric Spheres by Millimeter-Wave Scattering Measurements. Sensors. 2025; 25(18):5687. https://doi.org/10.3390/s25185687
Chicago/Turabian StyleLippoldt, Max, and Jan Hesselbarth. 2025. "Characterization of Sub-Resonant Dielectric Spheres by Millimeter-Wave Scattering Measurements" Sensors 25, no. 18: 5687. https://doi.org/10.3390/s25185687
APA StyleLippoldt, M., & Hesselbarth, J. (2025). Characterization of Sub-Resonant Dielectric Spheres by Millimeter-Wave Scattering Measurements. Sensors, 25(18), 5687. https://doi.org/10.3390/s25185687






