A GRU-KAN Surrogate Model with Genetic Algorithm Uniform Sampling for Active Magnetic Bearings–Rotor Critical Speed Prediction
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.2.1. Dynamic Modeling Methods for AMB–Rotors
1.2.2. Surrogate Model Methods
1.3. Contributions
- An evolutionary uniform design guided by a composite discrepancy metric is proposed. The scheme balances space filling with factor coupling and yields representative training sets suited to control–dynamics analysis.
- A surrogate that combines gated recurrent units with a Kolmogorov–Arnold network is formulated to capture nonlinear interactions between controller parameters and rotor dynamics. In conjunction with the GAUD, this approach improves the data efficiency and predication capacity relative to conventional surrogates and clarifies controller–plant interactions.
- The integrated GRU-KAN-UD workflow replaces repeated finite element simulations with rapid surrogate evaluation, enabling fast parametric exploration and early-stage design studies, thereby lowering the computational burden without compromising modeling fidelity.
2. AMB System Model
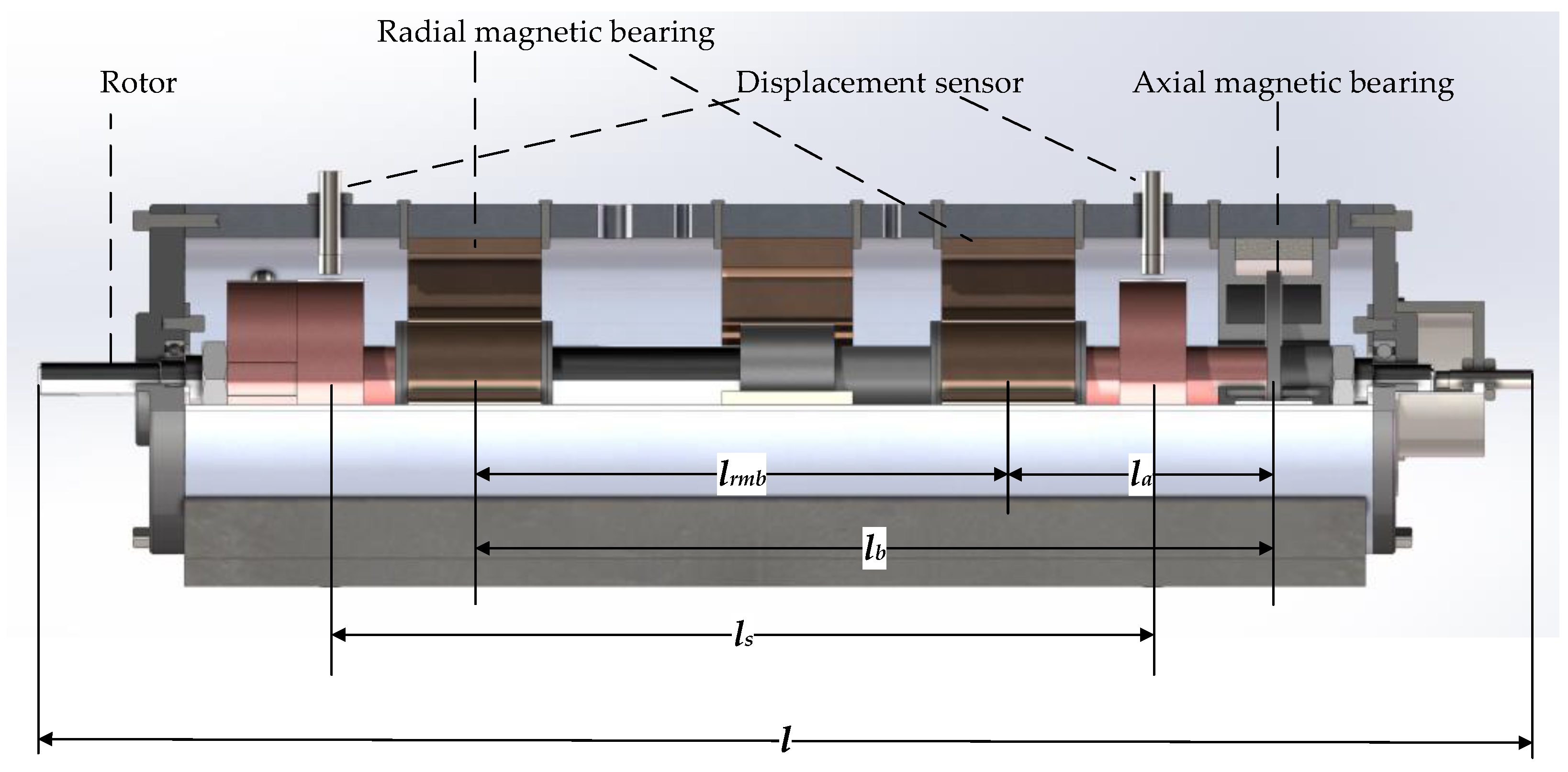
2.1. Construction of the AMB–Rotor Dynamic Model
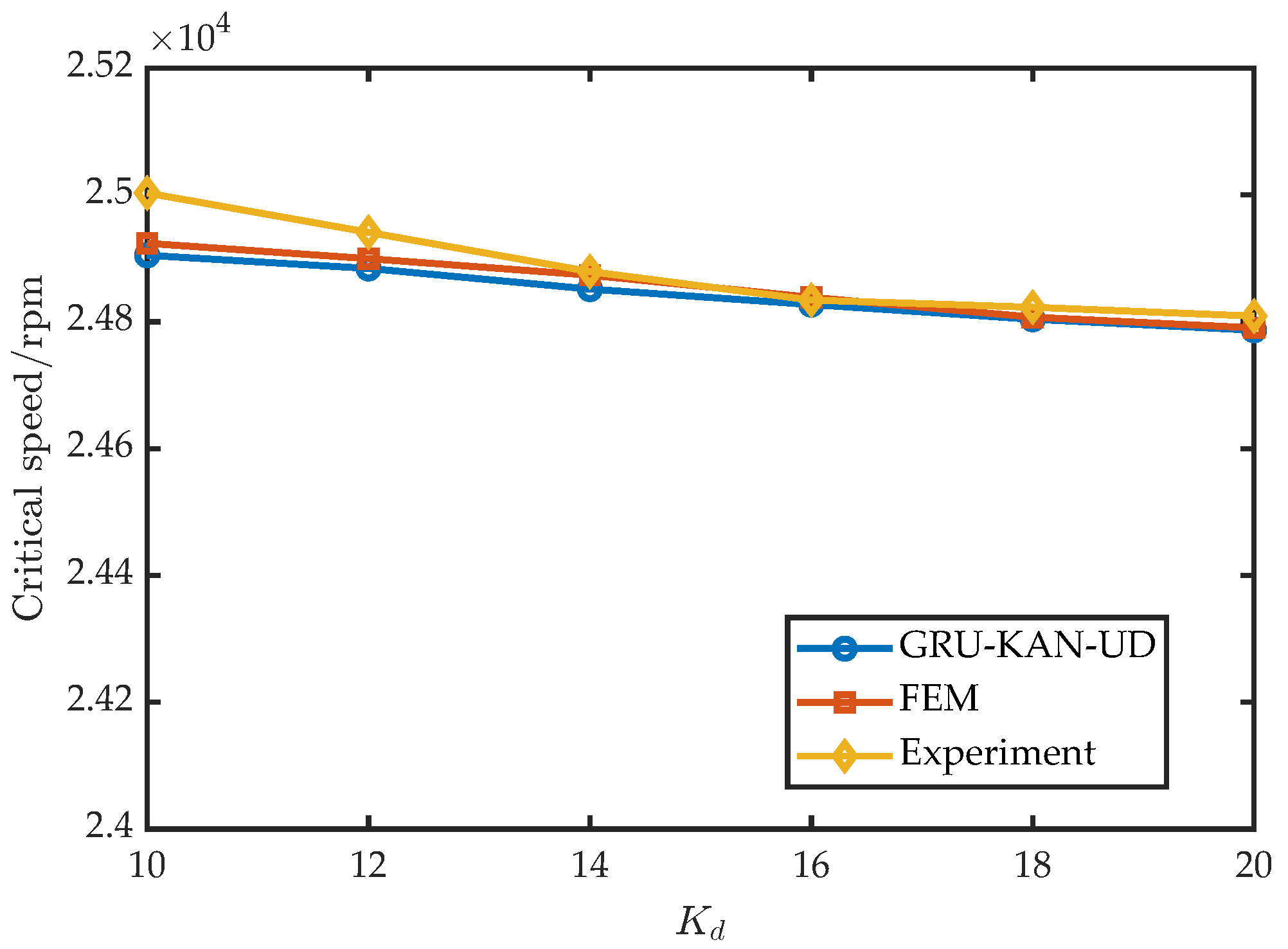
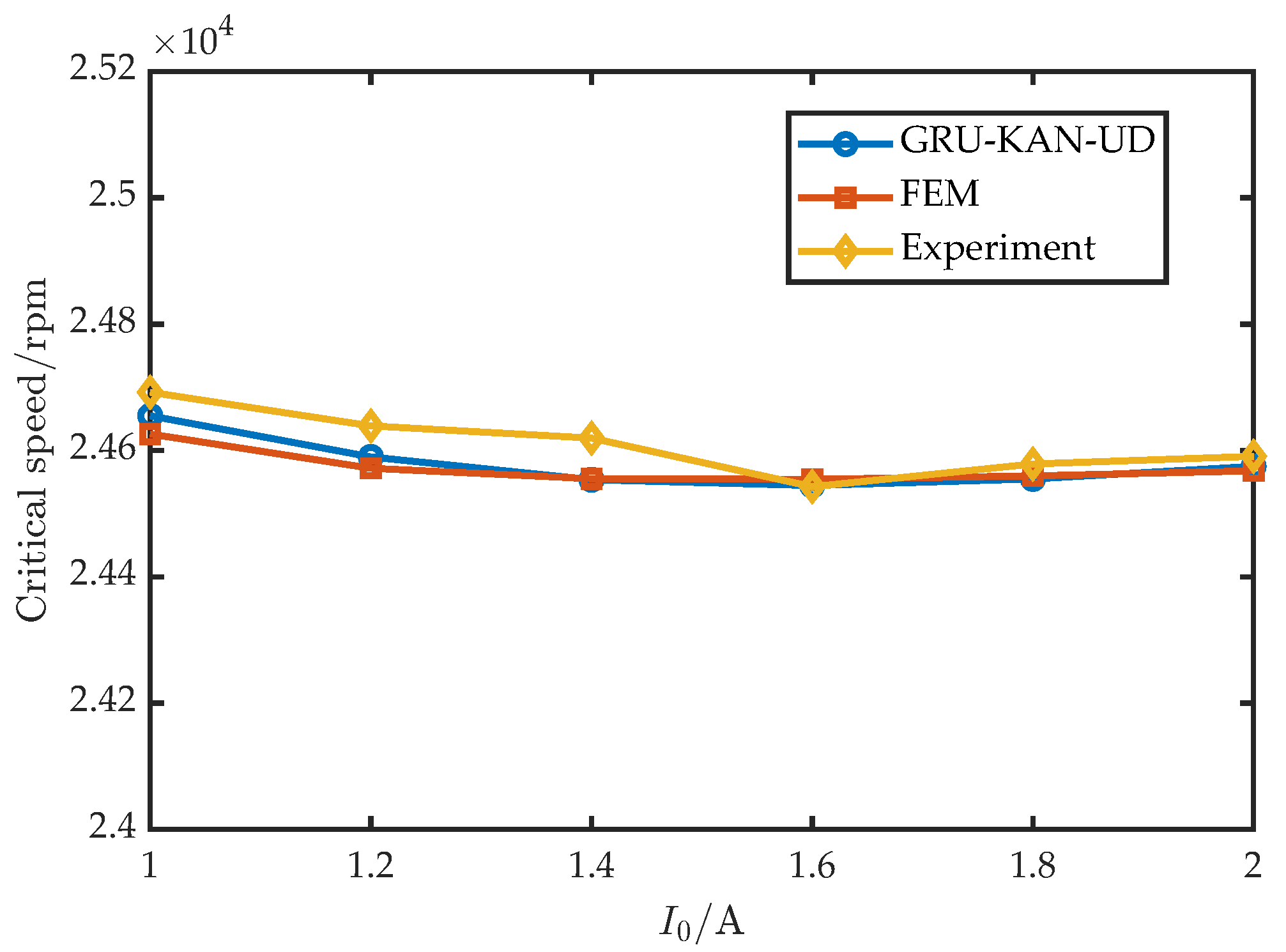
2.2. Effects of Individual Control Parameters on Critical Speed
3. Surrogate Modeling of Control Parameters Versus Critical Speed
3.1. Surrogate Model Framework
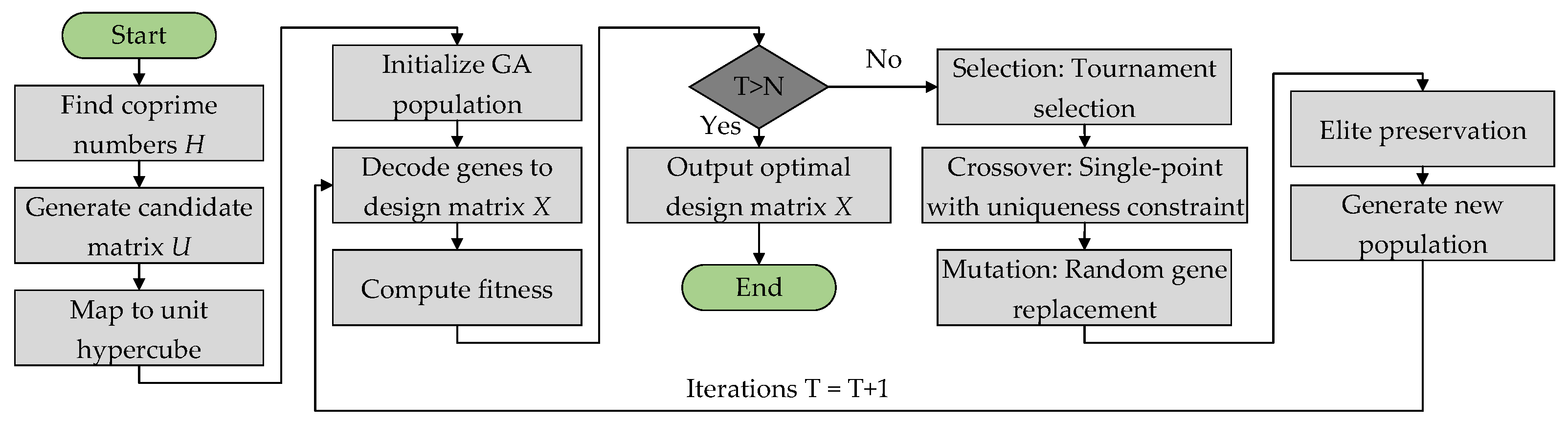
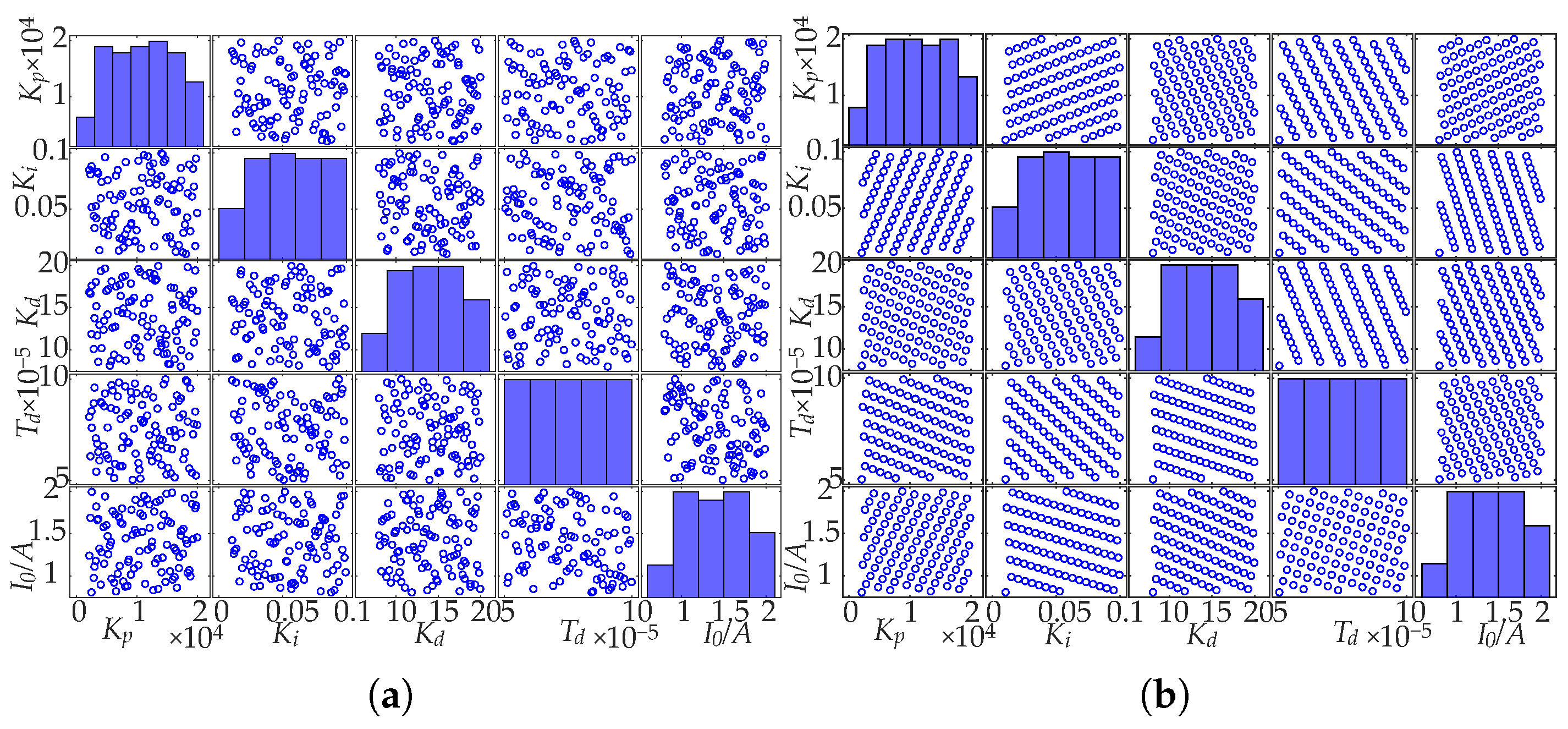
3.1.1. Uniform Design Sampling
3.1.2. Support Vector Regression
3.1.3. Kriging
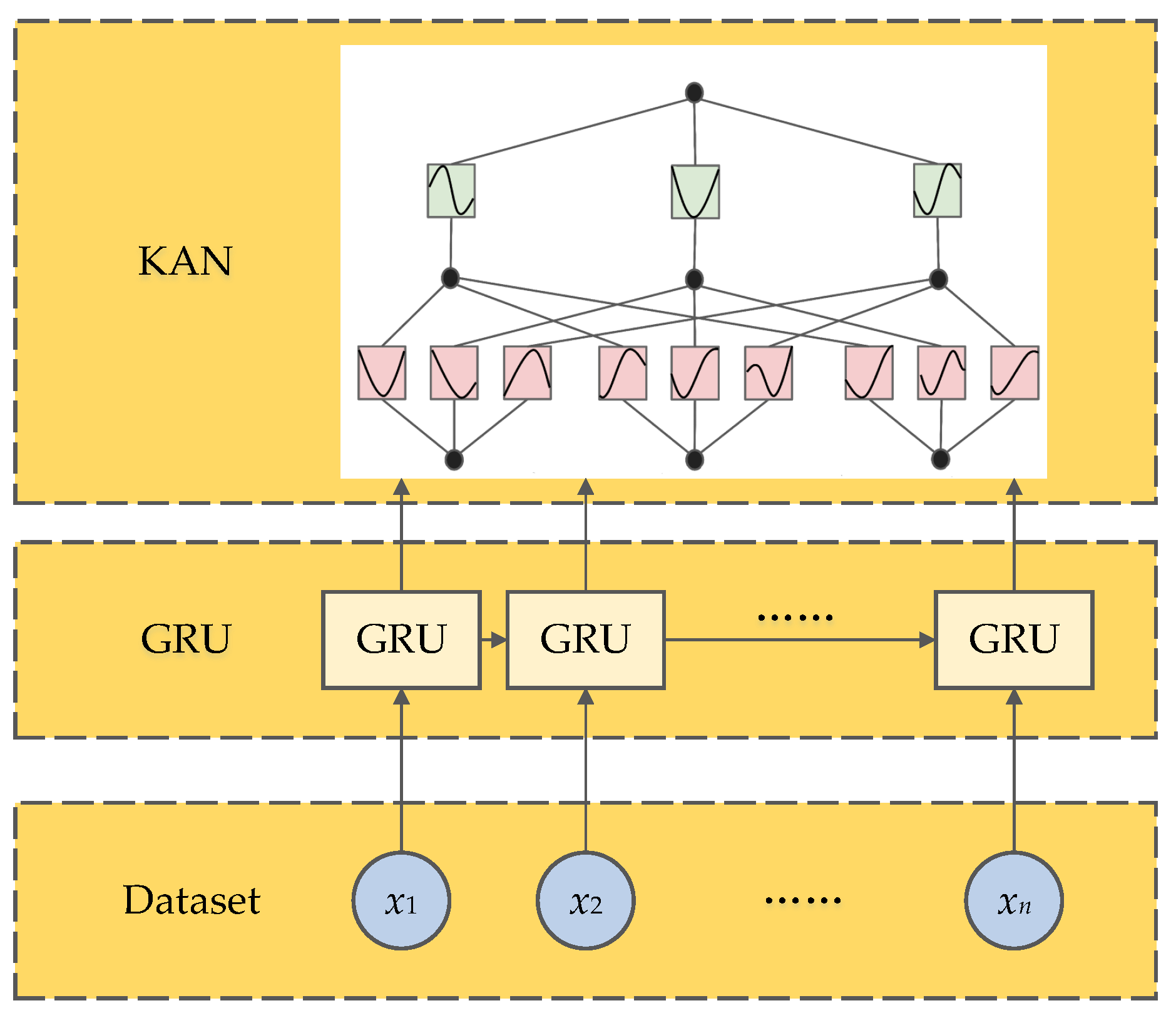
3.1.4. Gated Recurrent Unit–Kolmogorov–Arnold Network
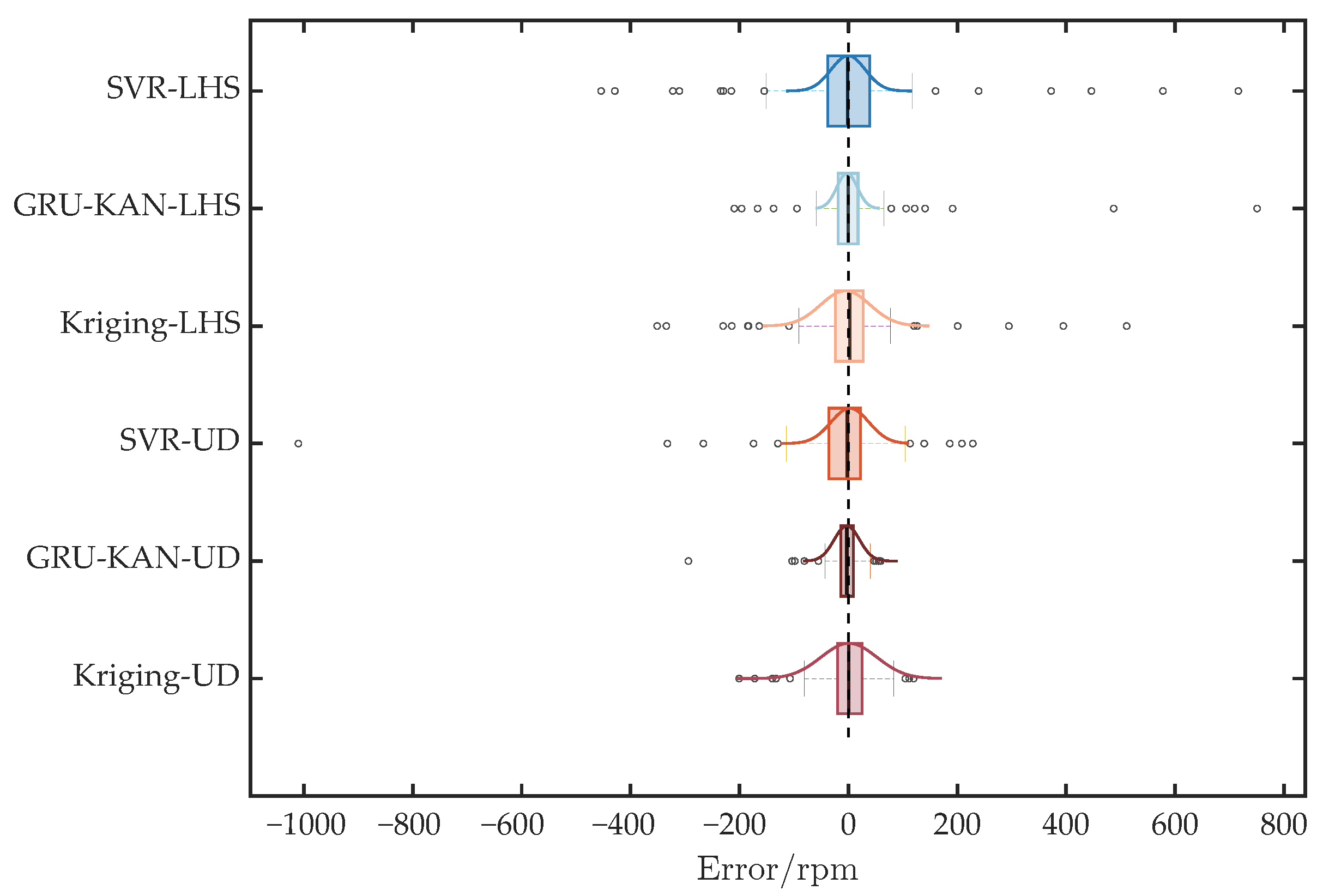
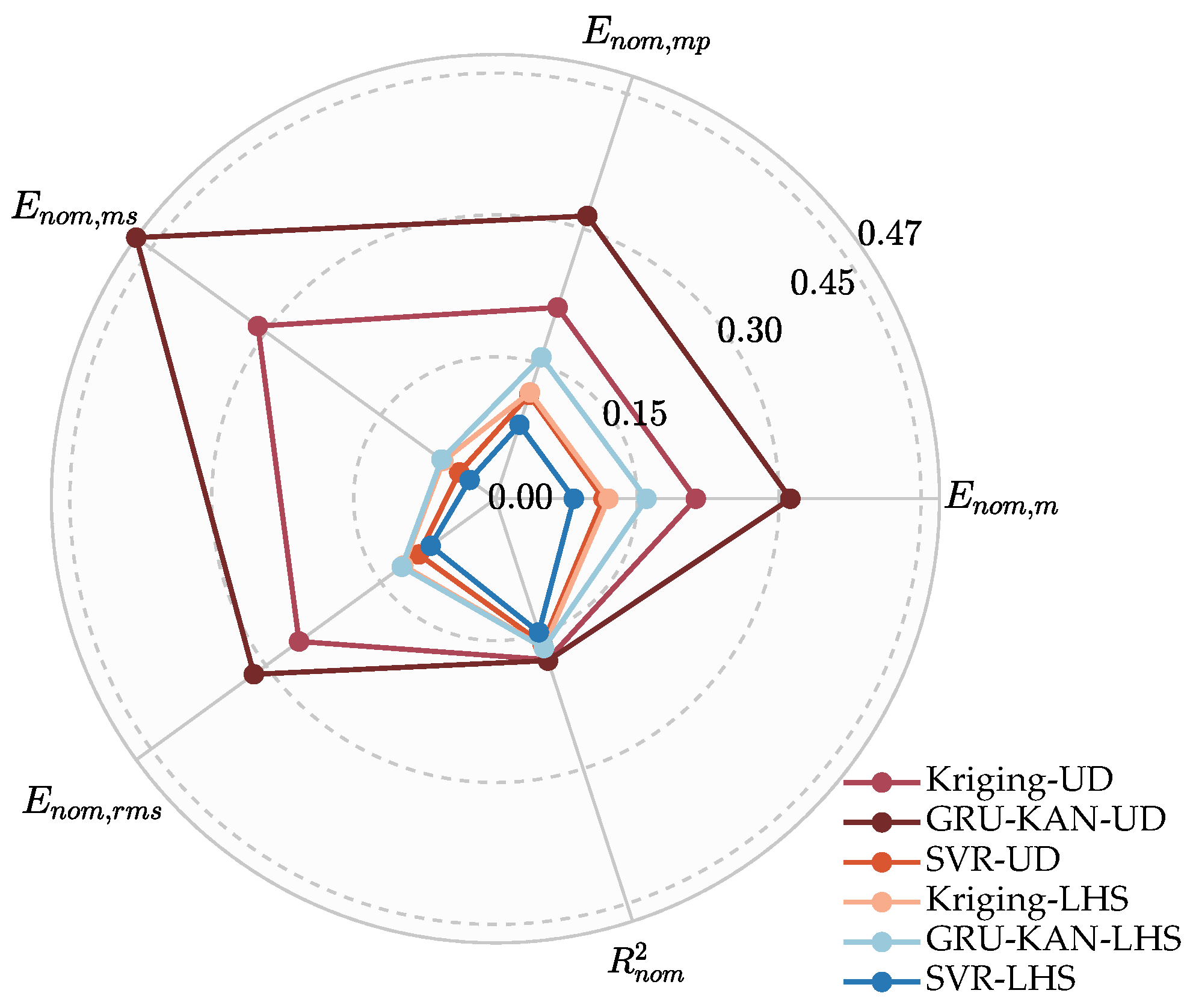
3.2. Model Result Analysis
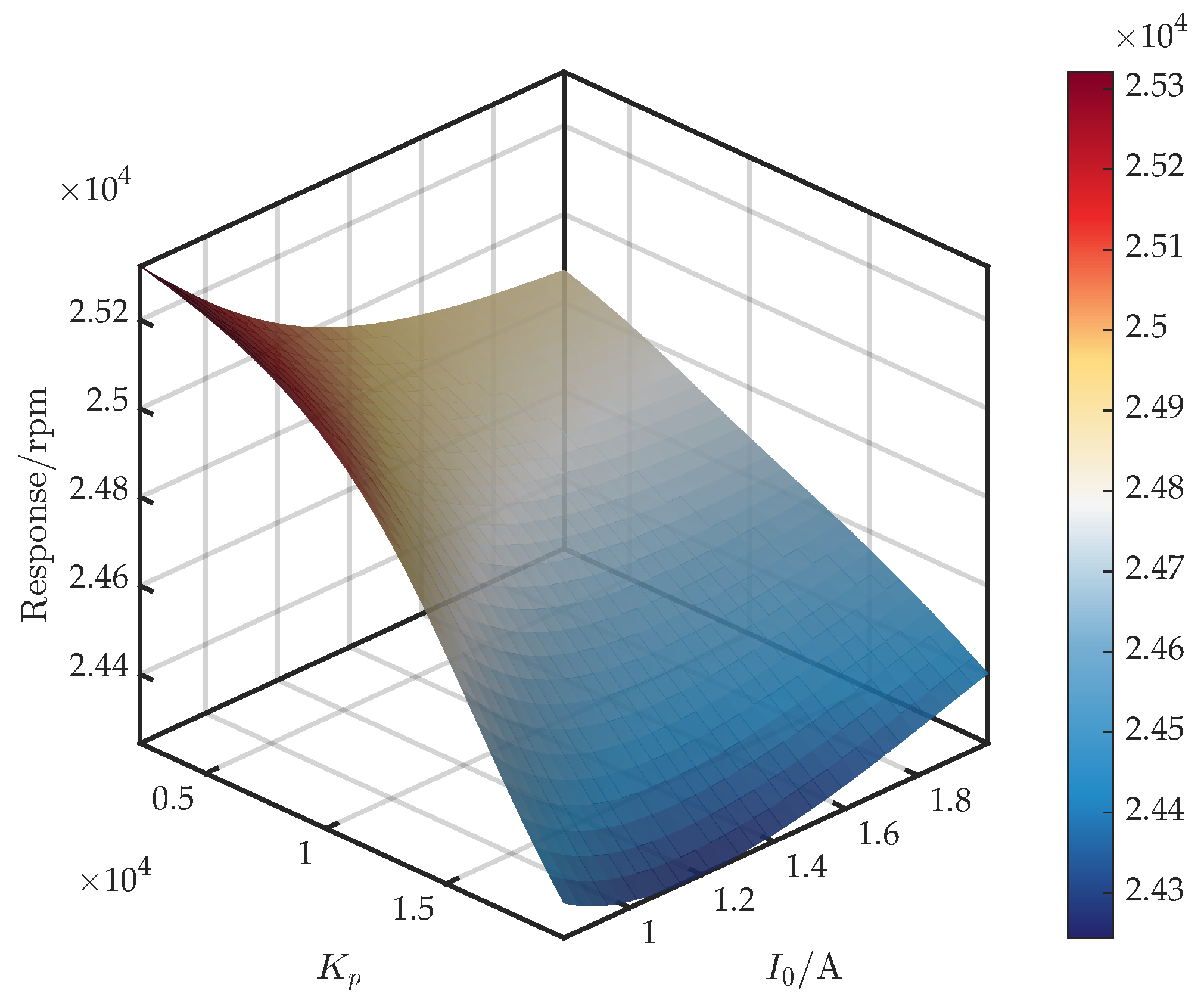
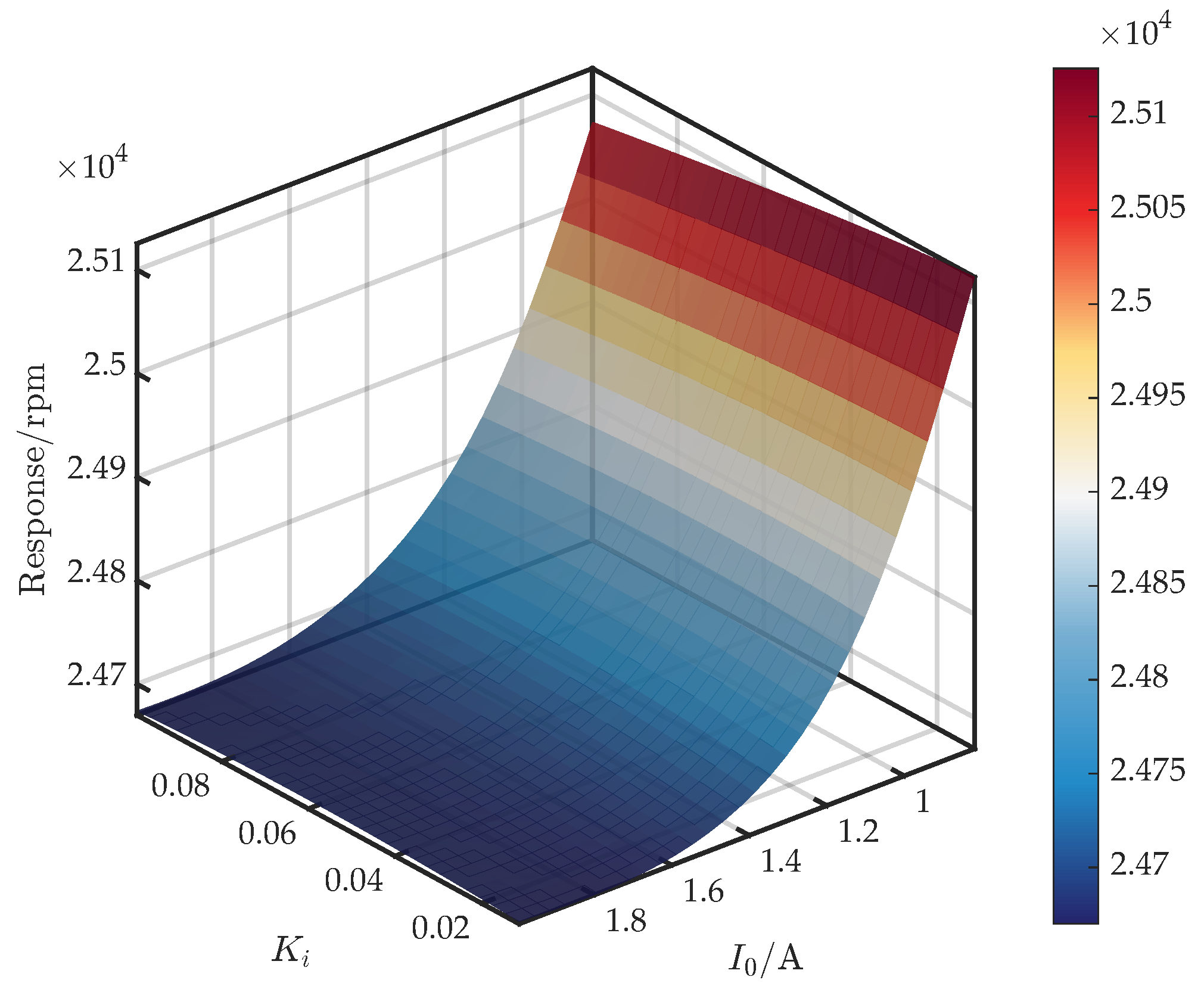
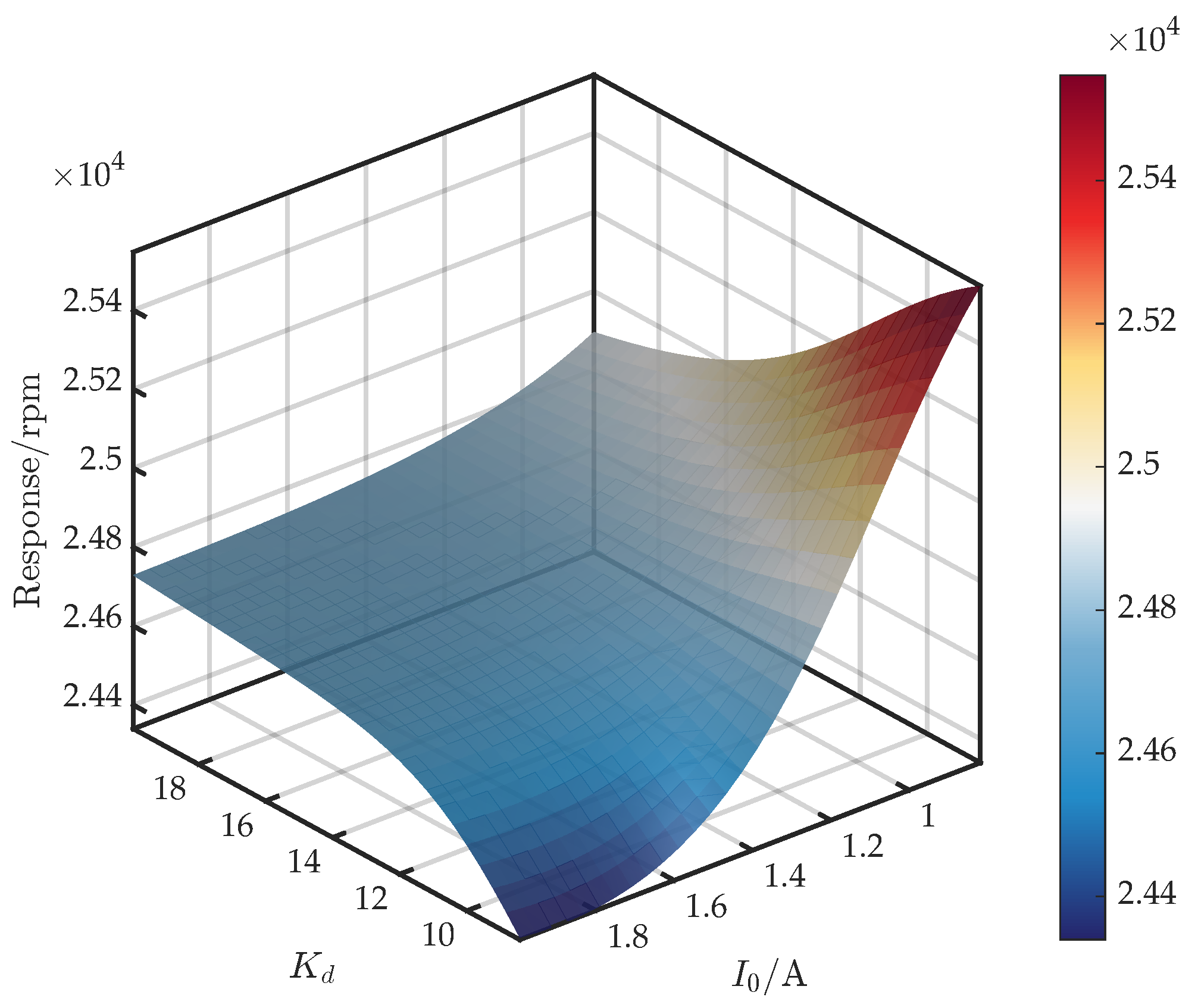
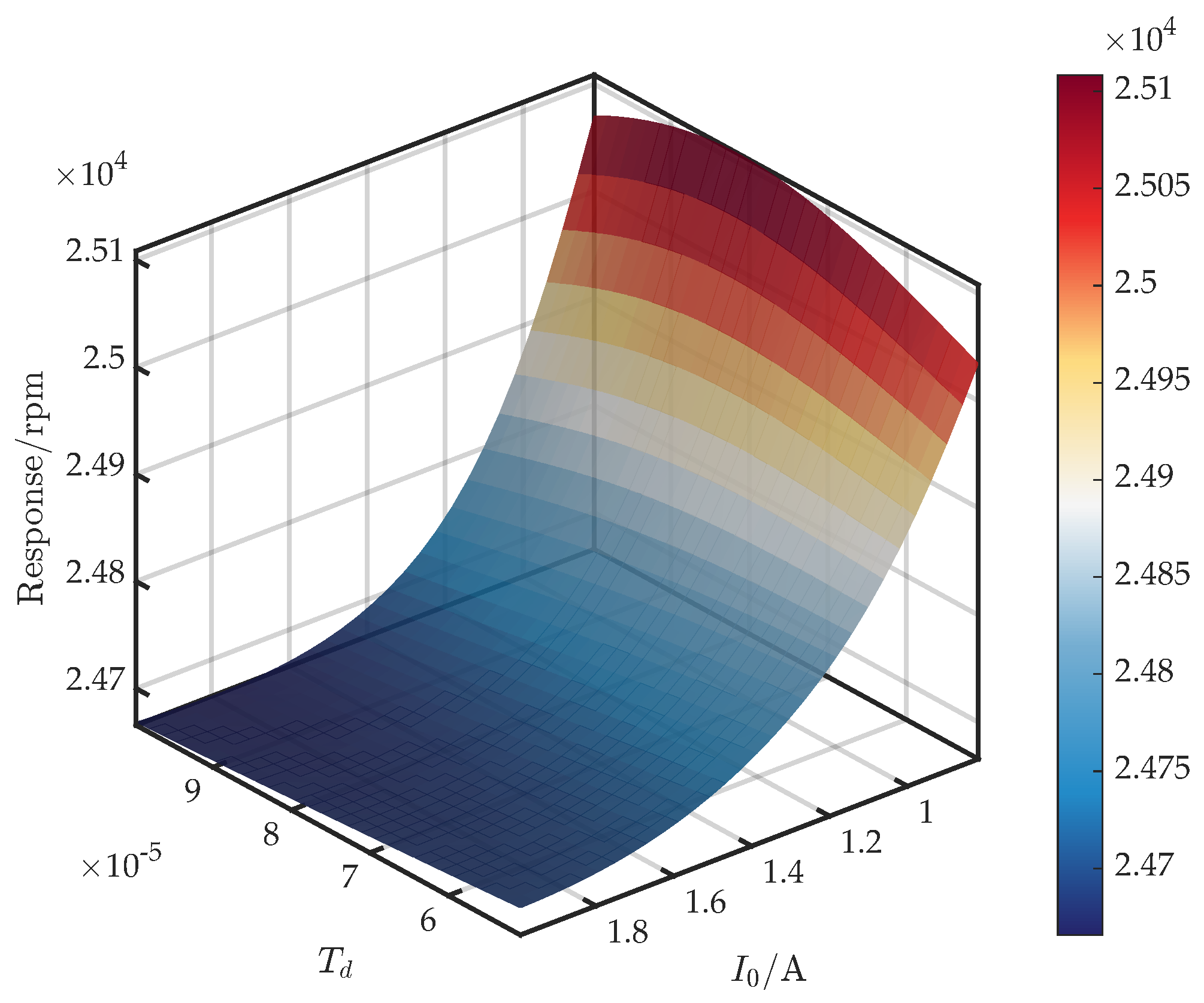
3.3. Analysis of Control Parameter Coupling and Critical Speed
4. Experimental Validation
5. Conclusions
- We introduce a surrogate-based method for the analysis of the coupling between the control parameters and the AMB–rotor’s first critical speed. The GRU-KAN-UD surrogate achieves a mean absolute error of rpm and a mean absolute percentage error of %. The experimental results confirm the surrogate’s feasibility and precision, providing a solid theoretical and practical foundation for AMB–rotor dynamic modeling.
- Compared with FEM, the trained surrogate model reduces the computation time from s to s while maintaining high fidelity, demonstrating a significant speed advantage.
- Unlike single-parameter studies, the surrogate approach captures the interaction effects among controller gains, offering a more comprehensive dynamic analysis.
- We propose a genetic algorithm-enhanced uniform design for sample selection, improving the robustness of surrogate training. The resulting GRU-KAN-UD attains the highest goodness of fit among all candidates () and the lowest mean absolute error in cross-validation ( rpm), with error reductions of over 60% relative to Kriging-LHS and over 70% relative to SVR-LHS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Falkowski, K.; Kurnyta-Mazurek, P.; Szolc, T.; Henzel, M. Radial magnetic bearings for rotor–shaft support in electric jet engine. Energies 2022, 15, 3339. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, W. Review on Key Development of Magnetic Bearings. Machines 2025, 13, 113. [Google Scholar] [CrossRef]
- Zhu, Z.; Qi, G.; Xu, J.; Li, X. Dynamic Modeling of the Support System for Vehicle-Mounted Spherical Magnetic Suspension Flywheel Battery. IEEE Trans. Energy Convers. 2023, 39, 322–333. [Google Scholar] [CrossRef]
- Uzhegov, N.; Smirnov, A.; Park, C.H.; Ahn, J.H.; Heikkinen, J.; Pyrhönen, J. Design aspects of high-speed electrical machines with active magnetic bearings for compressor applications. IEEE Trans. Ind. Electron. 2017, 64, 8427–8436. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, H.; Ma, X.; Ju, Z. Study on PID tuning strategy based on dynamic stiffness for radial active magnetic bearing. ISA Trans. 2018, 80, 458–474. [Google Scholar] [CrossRef]
- Wei, Z.; Song, C.; Li, J.; Li, M. Research on vibration characteristics of magnetic suspension bearing-rotor system under variable supporting stiffness. Bearing 2022, 3, 15–22. [Google Scholar]
- Kumar, P.; Tiwari, R. Finite element modelling, analysis and identification using novel trial misalignment approach in an unbalanced and misaligned flexible rotor system levitated by active magnetic bearings. Mech. Syst. Signal Process. 2021, 152, 107454. [Google Scholar] [CrossRef]
- Kumar, P.; Tiwari, R. Dynamic analysis and identification of unbalance and misalignment in a rigid rotor with two offset discs levitated by active magnetic bearings: A novel trial misalignment approach. Propuls. Power Res. 2021, 10, 58–82. [Google Scholar] [CrossRef]
- Mushi, S.E.; Lin, Z.; Allaire, P.E. Design, construction, and modeling of a flexible rotor active magnetic bearing test rig. IEEE/ASME Trans. Mechatronics 2011, 17, 1170–1182. [Google Scholar] [CrossRef]
- van Rensburg, J.J.; Van Schoor, G.; Van Vuuren, P.; van Rensburg, A.J. Non-linear model of rotor delevitation in an active magnetic bearing system including parameter estimation. Measurement 2017, 109, 256–267. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, H.; Ju, Z. Dynamic stiffness analysis and measurement of radial active magnetic bearing in magnetically suspended molecular pump. Sci. Rep. 2020, 10, 1401. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Du, L.; Sun, Q.; Bai, J. A Disturbance Compensation Control Strategy for Rotational Speed Standard Device Based on AMB System. Sensors 2024, 24, 3093. [Google Scholar] [CrossRef]
- Hutterer, M.; Schrödl, M. Modeling and mu-synthesis control of a flexible rotor stabilized by active magnetic bearings including current free control. J. Sound Vib. 2023, 546, 117439. [Google Scholar] [CrossRef]
- Sugimoto, H.; Chiba, A. Dynamic modeling and experimental validations of passing through critical speeds by high acceleration in one-axis actively positioned bearingless motors. IEEE Trans. Ind. Appl. 2021, 57, 6956–6964. [Google Scholar] [CrossRef]
- Shata, A.M.A.H.; Hamdy, R.A.; Abdelkhalik, A.S.; El-Arabawy, I. A fractional order PID control strategy in active magnetic bearing systems. Alex. Eng. J. 2018, 57, 3985–3993. [Google Scholar] [CrossRef]
- Song, X.; Lv, L.; Sun, W.; Zhang, J. A radial basis function-based multi-fidelity surrogate model: Exploring correlation between high-fidelity and low-fidelity models. Struct. Multidiscip. Optim. 2019, 60, 965–981. [Google Scholar] [CrossRef]
- Chelladurai, S.J.S.; Murugan, K.; Ray, A.P.; Upadhyaya, M.; Narasimharaj, V.; Gnanasekaran, S. Optimization of process parameters using response surface methodology: A review. Mater. Today Proc. 2021, 37, 1301–1304. [Google Scholar] [CrossRef]
- Cai, F.; Huang, X. Study on Trajectory Optimization of Hypersonic Vehicle Based on Neural Network. Front. Energy Res. 2022, 10, 884624. [Google Scholar] [CrossRef]
- Sinou, J.J.; Denimal, E. Reliable crack detection in a rotor system with uncertainties via advanced simulation models based on kriging and Polynomial Chaos Expansion. Eur. J. Mech.-A/Solids 2022, 92, 104451. [Google Scholar] [CrossRef]
- Zhou, Z.; Dai, Y.; Wang, G.; Li, S.; Pang, J.; Zhan, S. Thermal displacement prediction model of SVR high-speed motorized spindle based on SA-PSO optimization. Case Stud. Therm. Eng. 2022, 40, 102551. [Google Scholar] [CrossRef]
- Shuai, H.; Li, F. Physics-informed kolmogorov-arnold networks for power system dynamics. IEEE Open Access J. Power Energy 2025, 12, 46–58. [Google Scholar] [CrossRef]
- Tian, J.; Hou, M.; Bian, H.; Li, J. Variable surrogate model-based particle swarm optimization for high-dimensional expensive problems. Complex Intell. Syst. 2023, 9, 3887–3935. [Google Scholar] [CrossRef]
- Bogoclu, C.; Roos, D.; Nestorović, T. Local Latin hypercube refinement for multi-objective design uncertainty optimization. Appl. Soft Comput. 2021, 112, 107807. [Google Scholar] [CrossRef]
- Sheikholeslami, R.; Razavi, S. Progressive Latin Hypercube Sampling: An efficient approach for robust sampling-based analysis of environmental models. Environ. Model. Softw. 2017, 93, 109–126. [Google Scholar] [CrossRef]
- Xiang, B.; Shi, Z.; Wen, T.; Liu, H. Attitude stabilization control of three-axis inertial stabilized platform using magnetically suspension system. Measurement 2025, 253, 117858. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. Recent advances and applications of surrogate models for finite element method computations: A review. Soft Comput. 2022, 26, 13709–13733. [Google Scholar] [CrossRef]
- Han, Z.; Xu, C.; Qiao, J.; Liu, F.; Chi, J.; Meng, G.; Zhang, K.; Song, W. Recent progress of efficient global aerodynamic shape optimization using surrogate-based approach. Acta Aeronaut. Astronaut. Sin. 2020, 41, 30–70. [Google Scholar]
- Lü, Q.; Chan, C.L.; Low, B.K. Probabilistic evaluation of ground-support interaction for deep rock excavation using artificial neural network and uniform design. Tunn. Undergr. Space Technol. 2012, 32, 1–18. [Google Scholar] [CrossRef]
- Cui, J.; Li, J.; Zhao, W.; Zhai, X.; Liu, W.; Chen, C. Research on High Altitude Simulation Test of Aero-engine Based on Genetic Algorithm Optimization Uniform Design. J. Ordnance Equip. Eng. 2023, 44, 285–289. [Google Scholar]
- Gu, J.; Hua, W.; Yu, W.; Zhang, Z.; Zhang, H. Surrogate model-based multiobjective optimization of high-speed PM synchronous machine: Construction and comparison. IEEE Trans. Transp. Electrif. 2022, 9, 678–688. [Google Scholar] [CrossRef]
- Qian, J.; Yi, J.; Cheng, Y.; Liu, J.; Zhou, Q. A sequential constraints updating approach for Kriging surrogate model-assisted engineering optimization design problem. Eng. Comput. 2020, 36, 993–1009. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Li, B.; Zou, X.; Cai, F. The multi-stage adding strategy on Kriging and applied to cavitation optimization of centrifugal impeller. J. Northwestern Polytech. Univ. 2024, 42, 467–476. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, Z.; Chen, W.A.; Liu, M.; Ruan, Y. A revolutionary neural network architecture with interpretability and flexibility based on Kolmogorov—Arnold for solar radiation and temperature forecasting. Appl. Energy 2025, 378, 124844. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Bias current (A) | 1.4 |
| Number of coil turns | 171 |
| Pole area (mm2) | 742 |
| One side air gap (mm) | 0.8 |
| Parameter | Variable | Value |
|---|---|---|
| Rotor mass (kg) | m | 4.3 |
| Total rotor length (mm) | l | 502 |
| Distance between radial AMB centers (mm) | 192 | |
| Distance between end sensor centers (mm) | 296 | |
| Right AMB to thrust disk distance (mm) | 287.5 | |
| Left AMB to thrust disk distance (mm) | 95.5 |
| Control Parameter | Range |
|---|---|
| [2000, 20,000] | |
| [0.01, 0.1] | |
| [8, 20] | |
| [, ] | |
| (A) | [0.8, 2] |
| Model | Hyperparameter | Range/Options |
|---|---|---|
| GRU-KAN | Batch size | {16, 32, 64, 128} |
| Learning rate | ||
| Hidden dimension | integers | |
| GRU layers | integers | |
| SVR | Kernel type | {linear, poly, rbf, sigmoid} |
| Regularization strength | ||
| Epsilon tube width | ||
| Kriging | Kernel type | {rbf, matern} |
| Length scale | ||
| Constant value | ||
| Noise level |
| Method | (rpm) | (%) | (rpm) | SD (rpm) | ||
|---|---|---|---|---|---|---|
| SVR-LHS | 83.03 | 150.31 | 0.8157 | |||
| SVR-UD | 60.21 | 126.97 | 0.8877 | |||
| Kriging-LHS | 57.60 | 105.77 | 0.9087 | |||
| Kriging-UD | 32.47 | 49.58 | 0.9829 | |||
| GRU-KAN-LHS | 43.06 | 103.97 | 0.9118 | |||
| GRU-KAN-UD | 22.06 | 40.32 | 0.9887 |
| Model/Test Type | Critical Speed (rpm) | (rpm) | (%) |
|---|---|---|---|
| GRU-KAN-UD | 24,866.08 | 51.92 | |
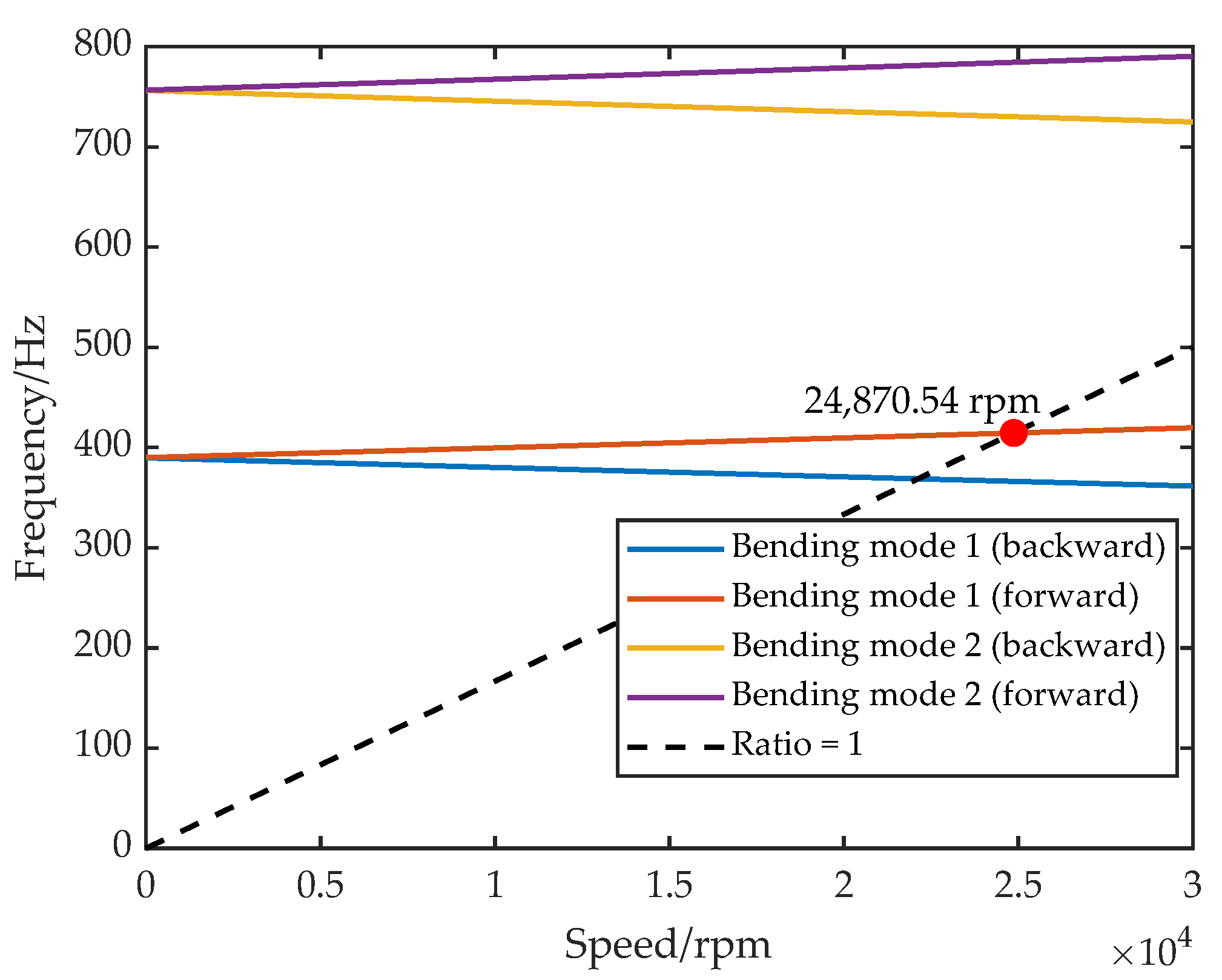
| FEA | 24,870.54 | 47.46 | |
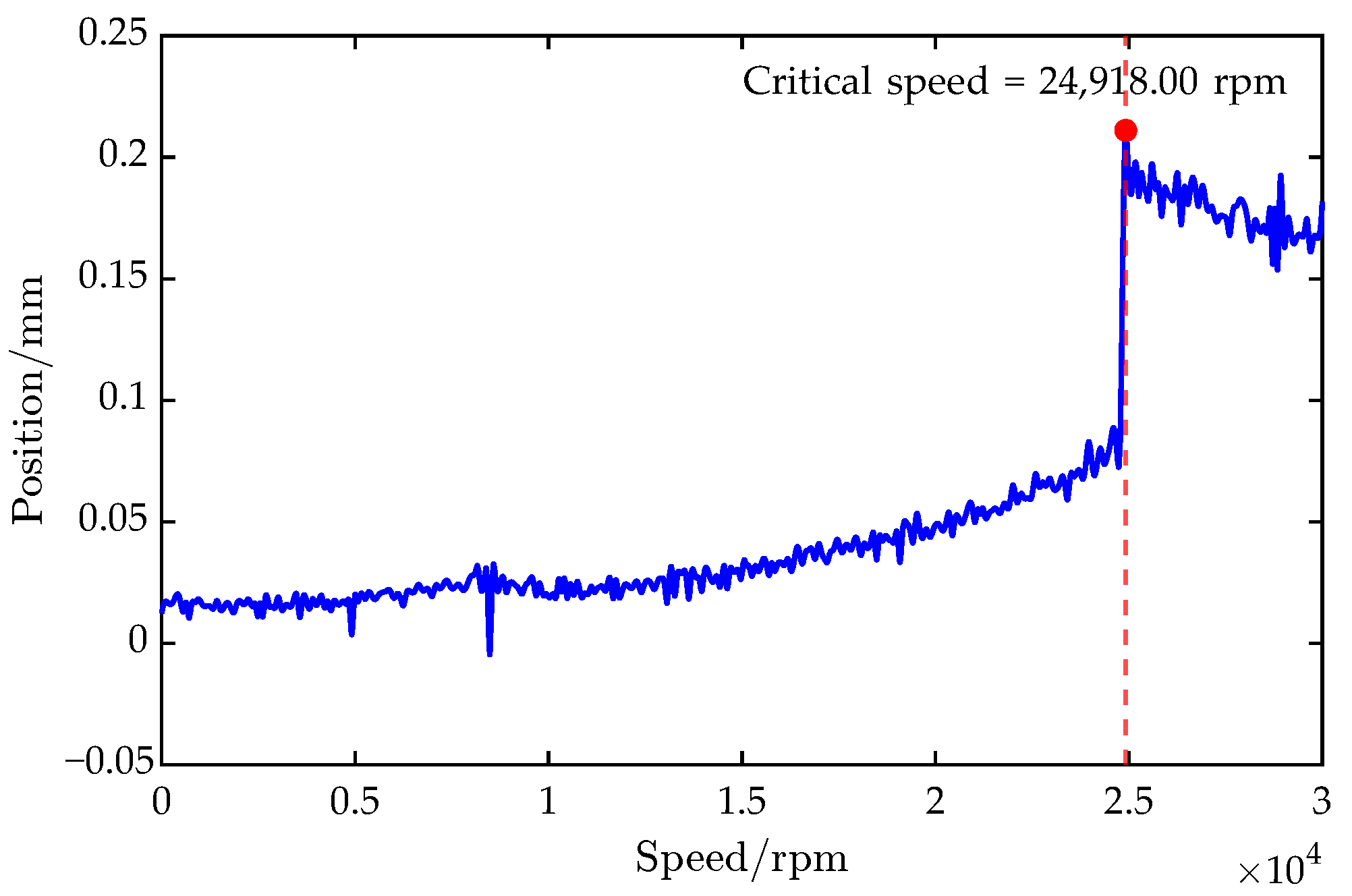
| Acceleration test | 24,918.00 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, J.; Li, J.; Cai, F.; Zhao, Z.; Liu, Y. A GRU-KAN Surrogate Model with Genetic Algorithm Uniform Sampling for Active Magnetic Bearings–Rotor Critical Speed Prediction. Sensors 2025, 25, 5680. https://doi.org/10.3390/s25185680
Cui J, Li J, Cai F, Zhao Z, Liu Y. A GRU-KAN Surrogate Model with Genetic Algorithm Uniform Sampling for Active Magnetic Bearings–Rotor Critical Speed Prediction. Sensors. 2025; 25(18):5680. https://doi.org/10.3390/s25185680
Chicago/Turabian StyleCui, Jiahang, Jianghong Li, Feichao Cai, Zhenmin Zhao, and Yuxi Liu. 2025. "A GRU-KAN Surrogate Model with Genetic Algorithm Uniform Sampling for Active Magnetic Bearings–Rotor Critical Speed Prediction" Sensors 25, no. 18: 5680. https://doi.org/10.3390/s25185680
APA StyleCui, J., Li, J., Cai, F., Zhao, Z., & Liu, Y. (2025). A GRU-KAN Surrogate Model with Genetic Algorithm Uniform Sampling for Active Magnetic Bearings–Rotor Critical Speed Prediction. Sensors, 25(18), 5680. https://doi.org/10.3390/s25185680






