Development of an Equivalent Circuit to Analyze the Receiving Characteristics of a Class IV Flextensional Transducer
Abstract
1. Introduction
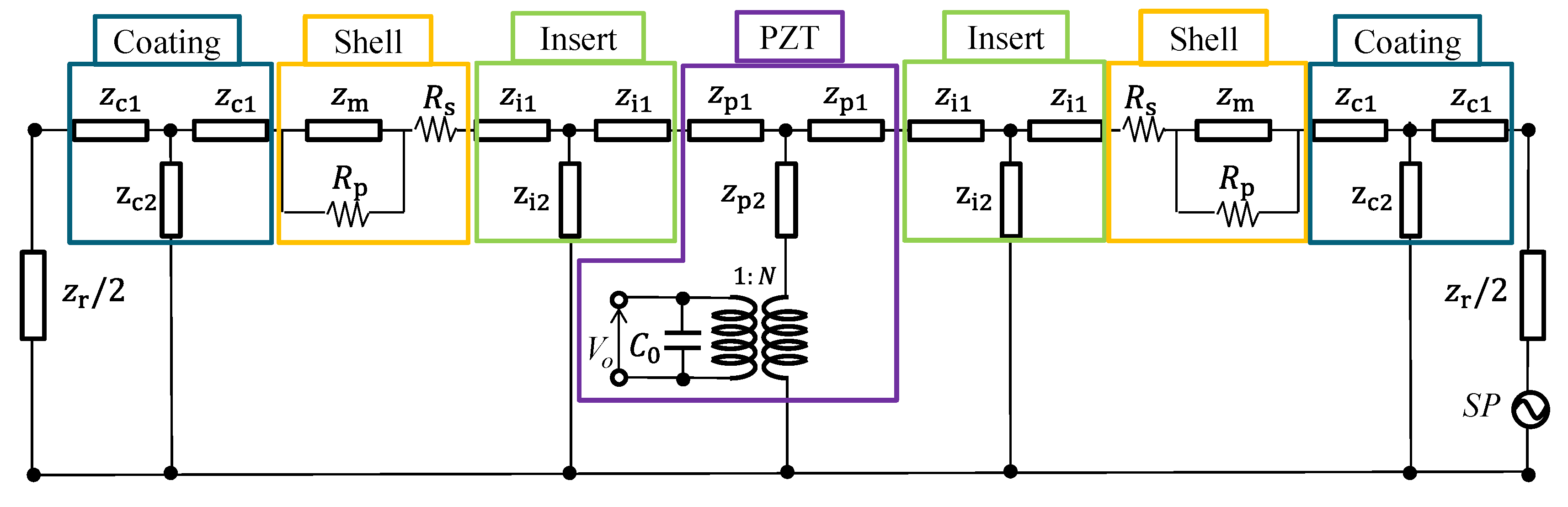
2. Equivalent Circuit of the Class IV FH
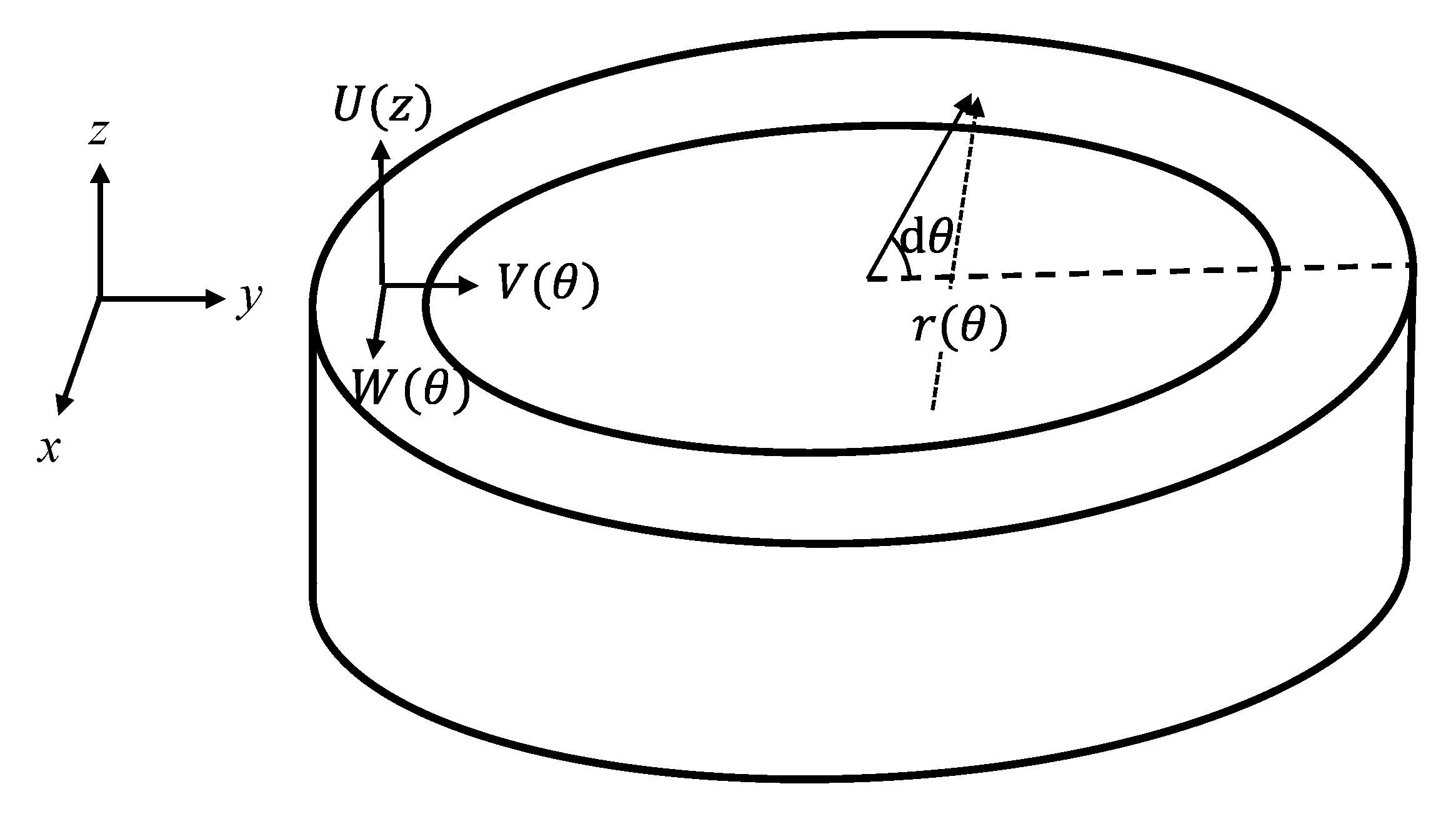
2.1. Shell and End-Plate
2.2. Piezoceramic Stack, Insert, and Coating
2.3. Radiation Impedance
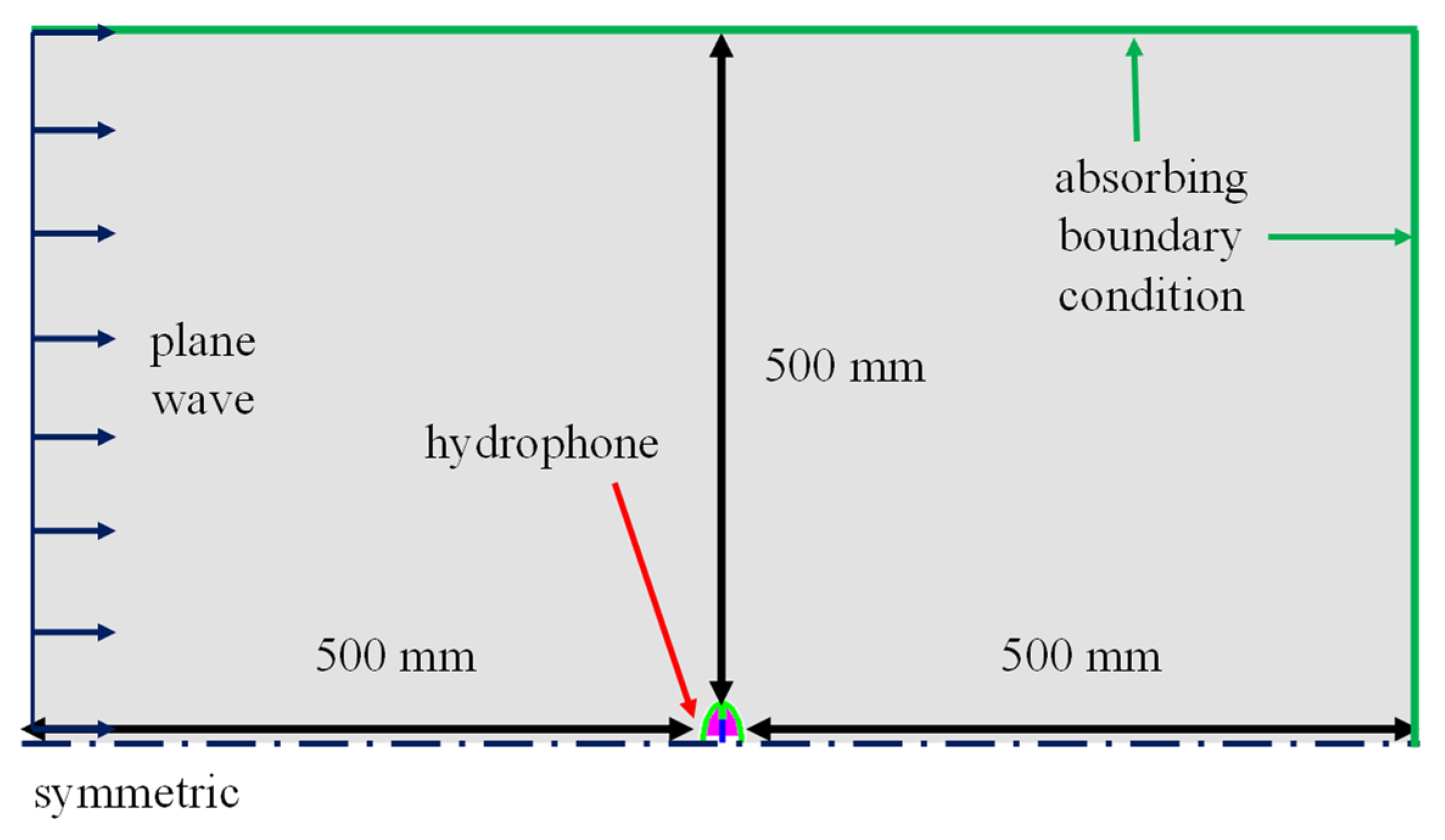
3. Finite Element Analysis
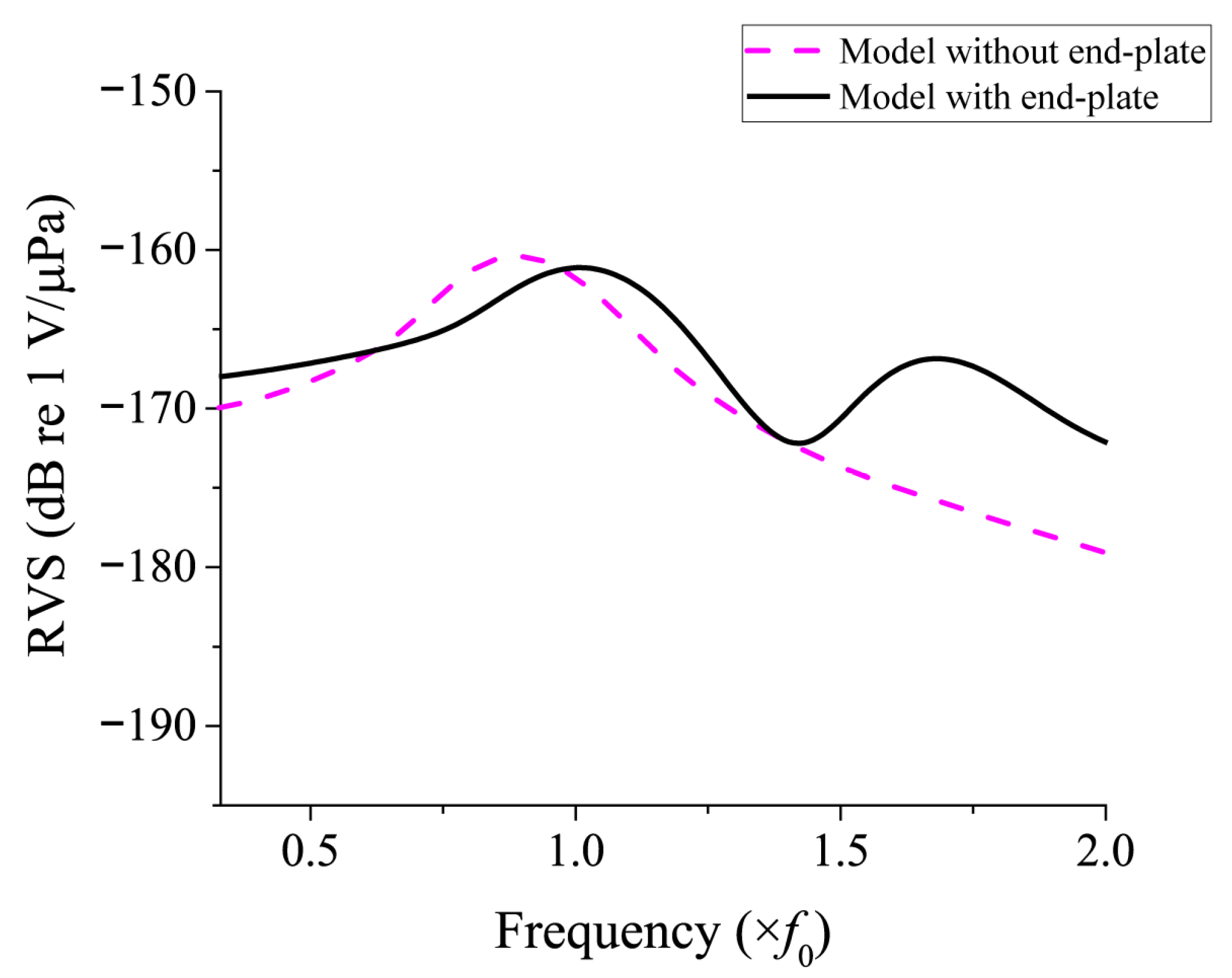
4. Model Validation and Parameter Sweep Analysis
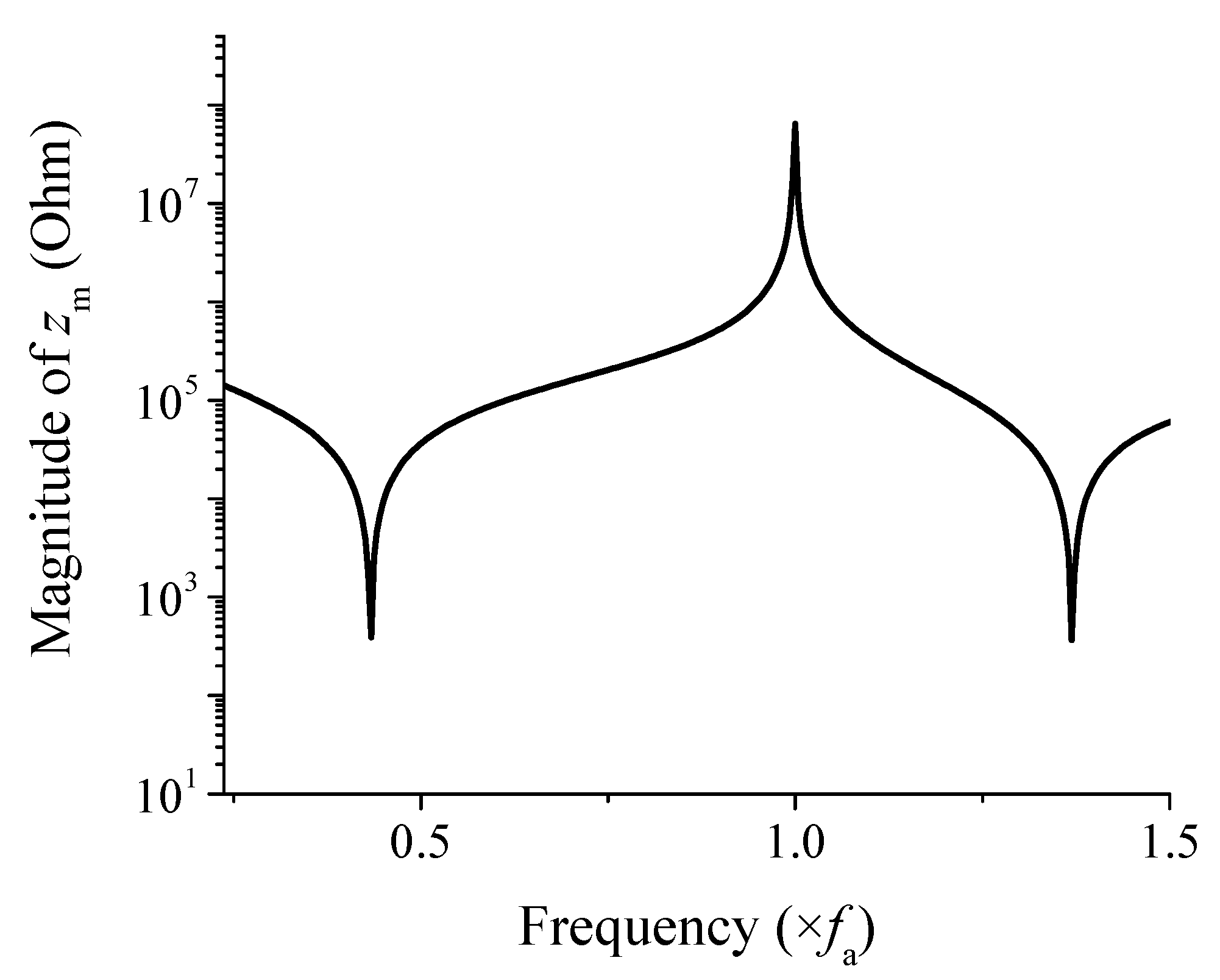
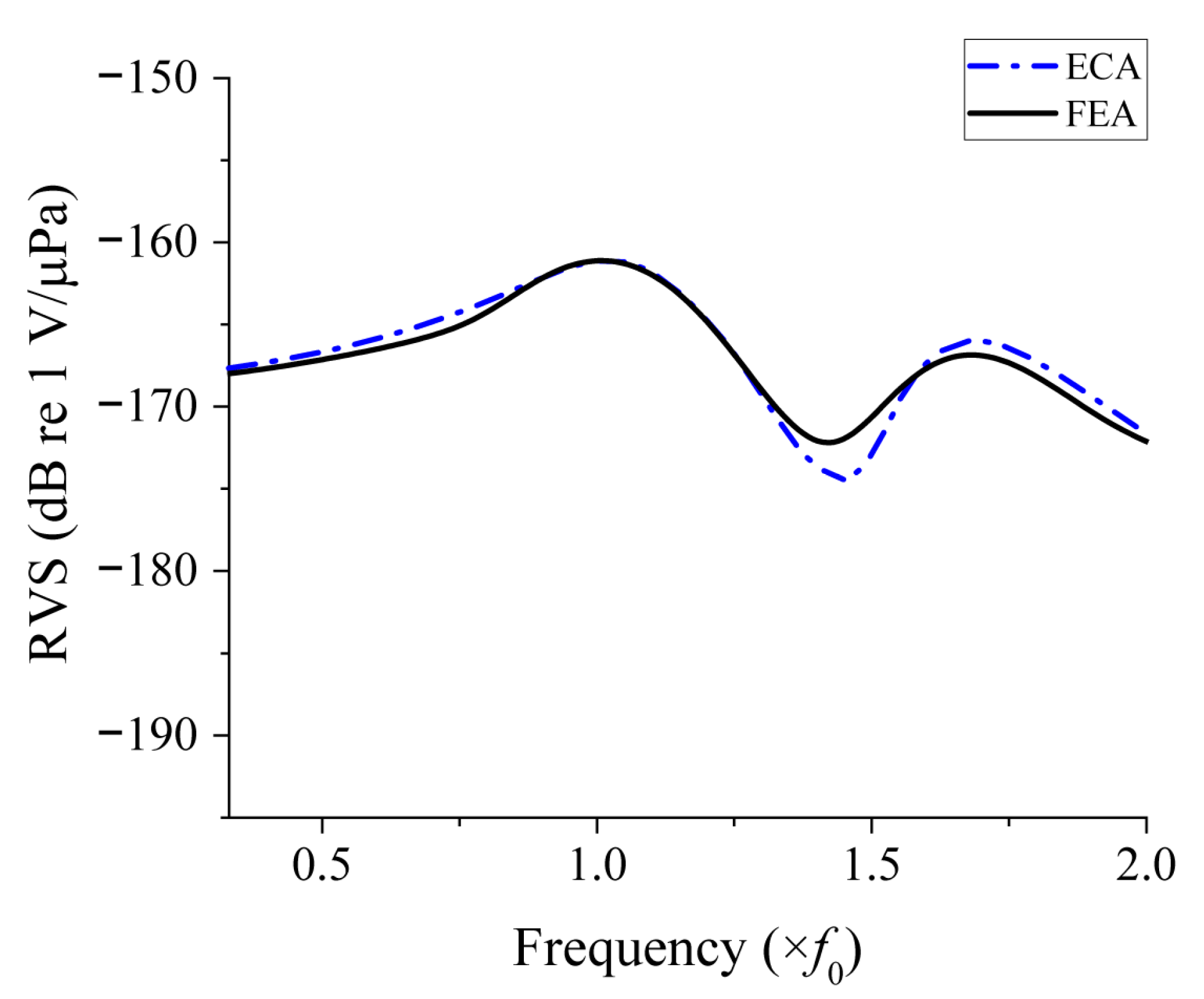
4.1. Comparison of Results from ECA and FEA
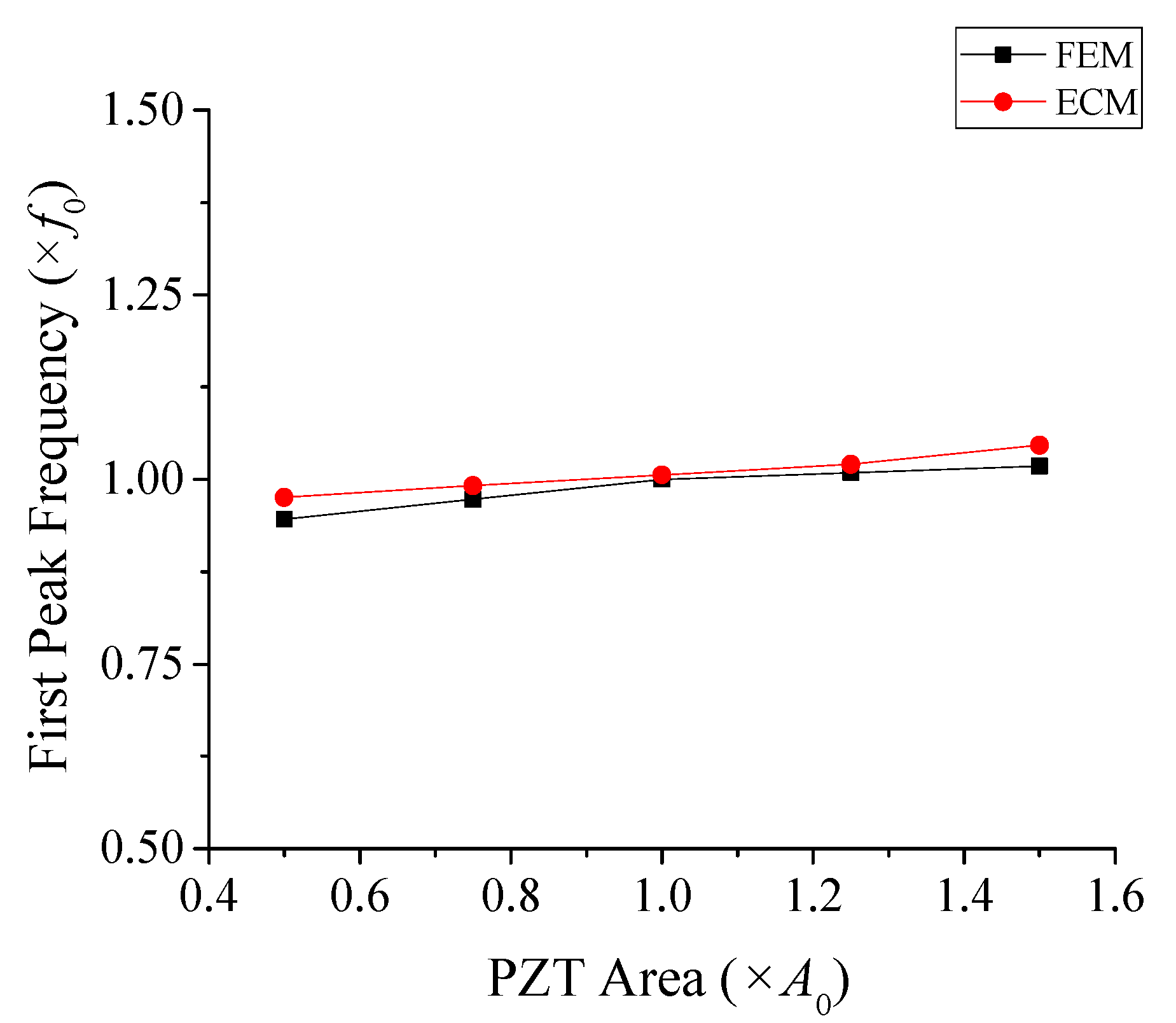
4.2. Parameter Sweep Analysis via the Equivalent Circuit Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rolt, K.D. History of the flextensional electroacoustic transducer. J. Acoust. Soc. Am. 1990, 87, 1340–1349. [Google Scholar] [CrossRef]
- Brigham, G.; Glass, B. Present status in flextensional transducer technology. J. Acoust. Soc. Am. 1980, 68, 1046–1052. [Google Scholar] [CrossRef]
- Decarpigny, J.-N.; Hamonic, B.; Wilson, O.B. The design of low frequency underwater acoustic projectors: Present status and future trends. IEEE J. Ocean. Eng. 1991, 16, 107–122. [Google Scholar] [CrossRef]
- Guo, R.; Li, S.; Li, T.; Sun, X.; Lin, L.; Sun, S. Analysis and design of low frequency and high power flextensional transducer with double-grooves. Appl. Acoust. 2019, 149, 25–31. [Google Scholar] [CrossRef]
- Fang, H.; Liu, Y.; Zhao, T.; Liu, Y.; Li, K.; Sun, D.; Zhang, D. Design of a flextensional transducer with adjustable prestress. J. Phys. Conf. Ser. 2021, 2012, 012017. [Google Scholar] [CrossRef]
- Zhou, T.; Lan, Y.; Zhang, Q.; Yuan, J.; Li, S.; Lu, W. A conformal driving class IV flextensional transducer. Sensors 2018, 18, 2102. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Lan, Y.; Zhou, T.; Lu, W. Numerical and experimental investigation of a negative-curvature variable-shell flextensional transducer. J. Acoust. Soc. Am. 2023, 153, 505–516. [Google Scholar] [CrossRef]
- Feeney, A.; Tweedie, A.; Mathieson, A.; Lucas, M. A miniaturized class IV flextensional ultrasonic transducer. Phys. Procedia 2016, 87, 10–15. [Google Scholar] [CrossRef]
- Varadan, V.V.; Chin, L.C.; Varadan, V.K. Finite-element modeling of flextensional electroacoustic transducers. Smart Mater. Struct. 1993, 2, 201. [Google Scholar] [CrossRef]
- Zhang, Y.-M.; Chen, H.; Dai, L.-X.; Hu, H.-P.; Fan, G.-F.; Lv, W.-Z. Analysis on performance of flextensional piezoelectric hydrophone. In Proceedings of the Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Chengdu, China, 27–30 October 2017. [Google Scholar]
- Garrett, S.L.; Danielson, D.A. Flextensional Hydrophone. U.S. Patent 4,951,271, 21 August 1990. [Google Scholar]
- Kim, G.; Kim, D.; Roh, Y. Design of Wideband Flextensional Hydrophone. Sensors 2024, 24, 4941. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Gao, S.; Wu, D.; Zhang, Q. Simulation Design of Class IV Flextensional Transducer. In Proceedings of the 2024 3rd International Symposium on Sensor Technology and Control (ISSTC), Zhuhai, China, 25–27 October 2024; pp. 19–22. [Google Scholar]
- Zheng, J.; Li, S.; Wang, B. Design of low-frequency broadband flextensional transducers based on combined particle swarm optimization and finite element method. Smart Mater. Struct. 2021, 30, 105002. [Google Scholar] [CrossRef]
- Kim, Y.; Yoo, J.; Lim, Y.; Min, S.; Lee, S.; Kim, H. High-frequency, multiband projector using 1–3 connectivity lithium niobate composites with an inversion layer. IEEE Sens. J. 2023, 23, 13000–13009. [Google Scholar] [CrossRef]
- Debus, J.-C.; Hamonic, B.; Damiri, B. Analysis of a flextensional transducer using piece-part equivalent circuit models: Determination of the shell contribution. In Proceedings of the OCEANS, Brest, France, 13–16 September 1994; Volume 282, pp. II/289–II/294. [Google Scholar]
- Oswin, J.R. Electro-Acoustic Energy Conversion in Class IV Flextensional Transducers. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 1995. [Google Scholar]
- Brigham, G.A. In-plane free vibrations of tapered oval rings. J. Acoust. Soc. Am. 1973, 54, 451–460. [Google Scholar] [CrossRef]
- Brigham, G.A. Analysis of the class-IV flextensional transducer by use of wave mechanics. J. Acoust. Soc. Am. 1974, 56, 31–39. [Google Scholar] [CrossRef]
- Lam, Y. Mathematical model of a class IV flextensional transducer and its numerical solution. Appl. Acoust. 1992, 36, 123–144. [Google Scholar] [CrossRef]
- Butler, J.L.; Sherman, C.H. Transducer Models. In Transducers and Arrays for Underwater Sound, 2nd ed.; Springer: New York, NY, USA, 2016; pp. 320–375. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Radiation and reception of acoustic waves. In Fundamentals of Acoustics, 4th ed.; John Wiley & Sons: New York, NY, USA, 2000; pp. 184–188. [Google Scholar]
- Henry, W.A. Regression analysis: Statistical modeling of a response variable. Technometrics 1999, 41, 367–368. [Google Scholar] [PubMed]
- Kim, H.; Roh, Y. Design and fabrication of a wideband Tonpilz transducer with a void head mass. Sens. Actuators A Phys. 2016, 239, 137–143. [Google Scholar] [CrossRef]
- Wilson, O.B.C., II. Equivalent circuits for transducers. In Introduction to Theory and Design of Sonar Transducers; Peninsula Publishing: Los Altos, CA, USA, 1988; pp. 11–43. [Google Scholar]




| Structural Parameter | Symbol | Value [mm] |
|---|---|---|
| Semi-major axis length | a | 29.4 |
| Semi-minor axis length | b | 14.5 |
| Shell thickness | h | 4.6 |
| Shell height | L0 | 54.0 |
| Normalization Factor | −1 | 0 | 1 | |
|---|---|---|---|---|
| Parameter | ||||
| kb (N/m) | 1.1 × 106 | 1.2 × 106 | 1.3 × 106 | |
| Rs (Ohm) | 5.0 × 104 | 1.0 × 105 | 1.5 × 105 | |
| Rp (Ohm) | 1.0 × 105 | 2.0 × 105 | 3.0 × 105 | |
| Acoustic Property | ECA | FEA |
|---|---|---|
| 1st peak frequency (×f0) | 1.00 | 1.01 |
| 2nd peak frequency (×f0) | 1.69 | 1.68 |
| 1st peak level (dB) | −161.3 | −161.1 |
| 2nd peak level (dB) | −166.0 | −166.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, E.; Roh, Y. Development of an Equivalent Circuit to Analyze the Receiving Characteristics of a Class IV Flextensional Transducer. Sensors 2025, 25, 5661. https://doi.org/10.3390/s25185661
Kang E, Roh Y. Development of an Equivalent Circuit to Analyze the Receiving Characteristics of a Class IV Flextensional Transducer. Sensors. 2025; 25(18):5661. https://doi.org/10.3390/s25185661
Chicago/Turabian StyleKang, Eunseo, and Yongrae Roh. 2025. "Development of an Equivalent Circuit to Analyze the Receiving Characteristics of a Class IV Flextensional Transducer" Sensors 25, no. 18: 5661. https://doi.org/10.3390/s25185661
APA StyleKang, E., & Roh, Y. (2025). Development of an Equivalent Circuit to Analyze the Receiving Characteristics of a Class IV Flextensional Transducer. Sensors, 25(18), 5661. https://doi.org/10.3390/s25185661







