Unsupervised Hyperspectral Band Selection Using Spectral–Spatial Iterative Greedy Algorithm
Abstract
1. Introduction
- (1)
- A novel unsupervised Spectral–Spatial Iterative Greedy Algorithm-based band selection method is proposed. To the best of our knowledge, this is the first time that the IG algorithm is used to solve the band selection problem.
- (2)
- By conducting clustering on all bands and constructing a K-NNG for each cluster, our proposed SSIGA enables efficient neighborhood solution construction, which helps to facilitate efficient local search using spectral information.
- (3)
- We designed an effective objective function that can evaluate the quality of the solution by calculating the average information entropy of all the bands in the solution and the average mutual information between the bands, as well as the Fisher score of each band. Experimental results show that SSIGA outperforms several state-of-the-art methods.
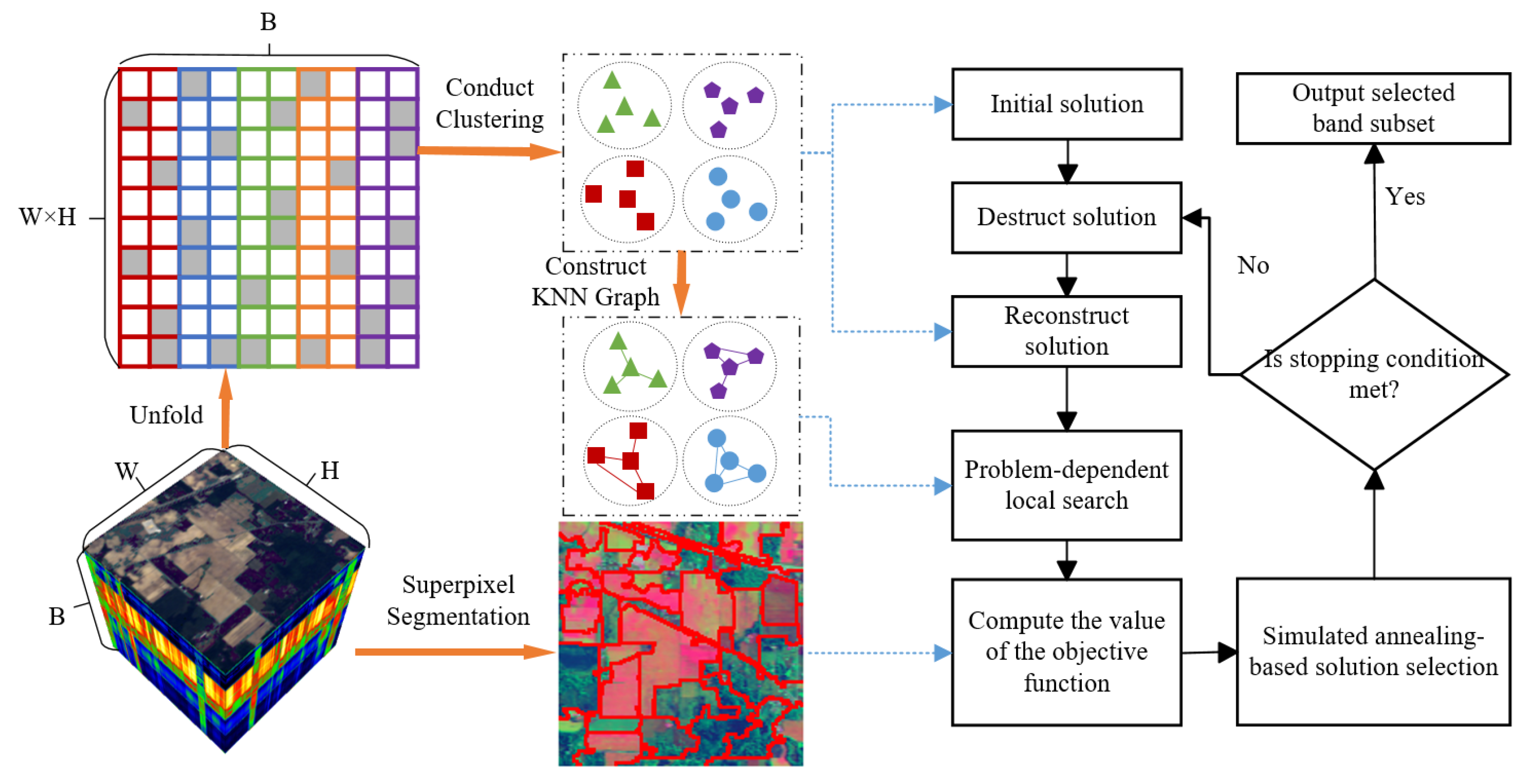
2. Method
2.1. Iterative Greedy Algorithm
2.2. Iterative Greedy Algorithm Based on Simulated Annealing
| Algorithm 1 Framework of IGA. |
|
| Algorithm 2 The algorithm of the SSIGA method. |
|
2.3. Initialization of the Solution
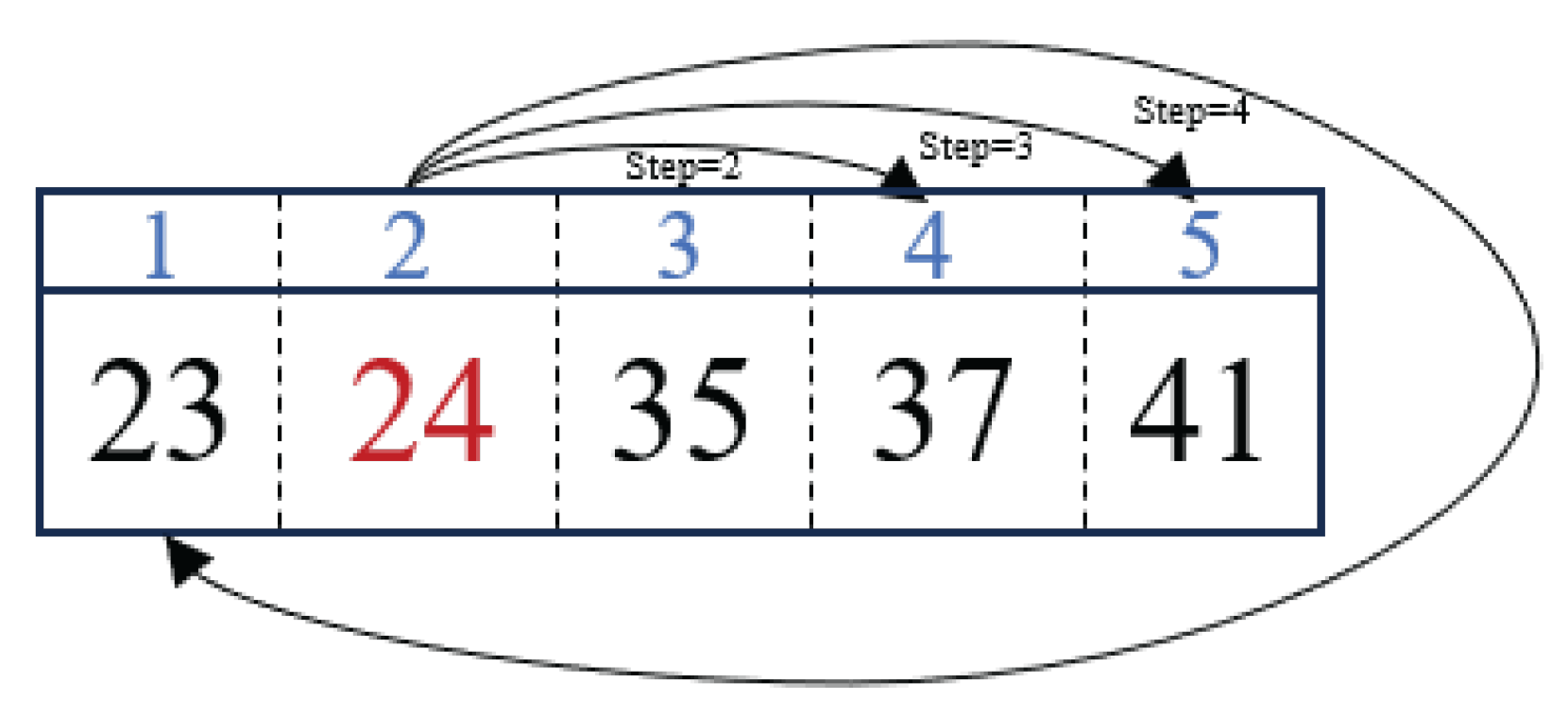
2.4. Destruction and Reconstruction Operator
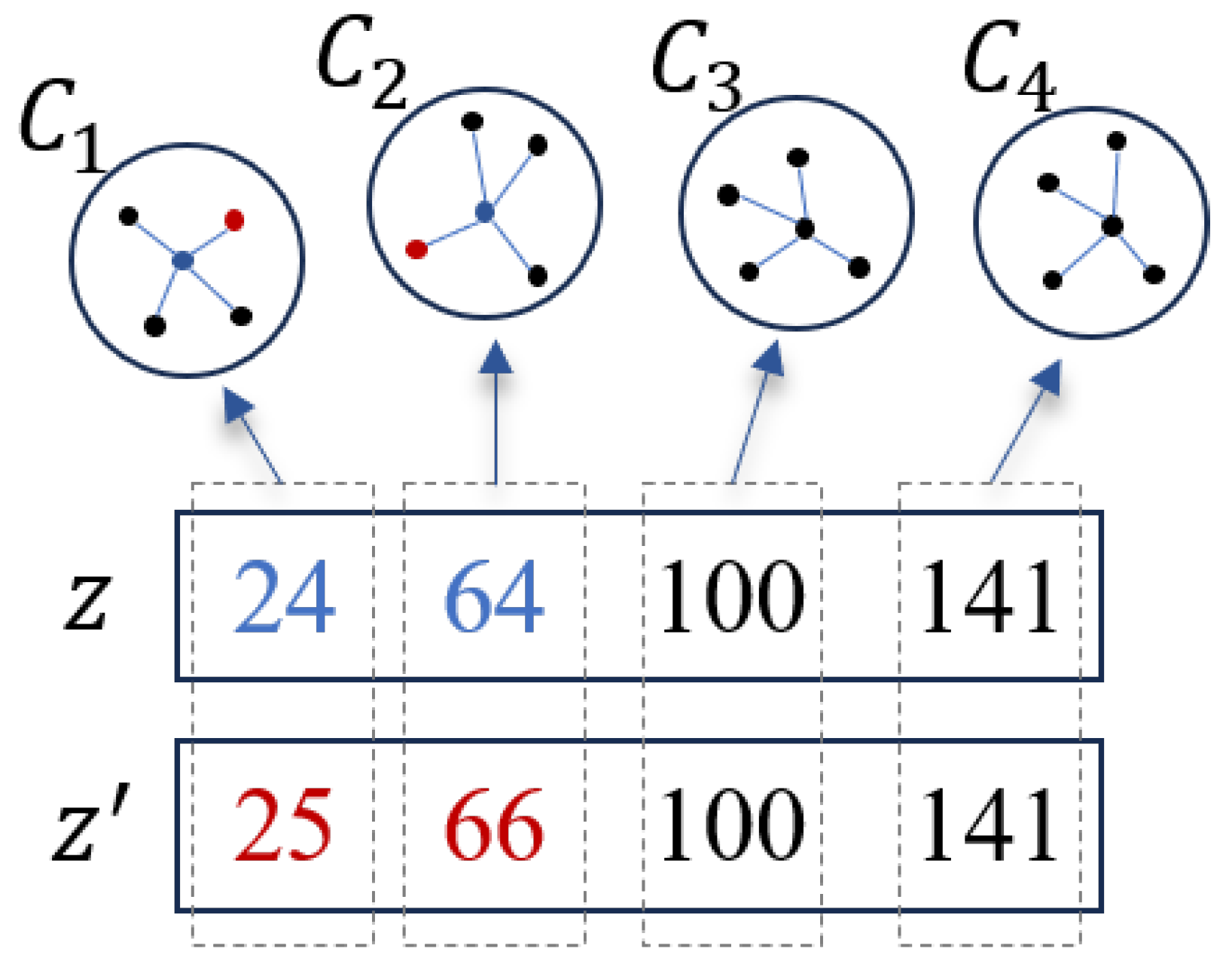
2.5. Spectral Information-Based Local Search
2.6. Objective Function Based on Spatial–Spectral Prior
3. Experiments and Discussion
3.1. Datasets
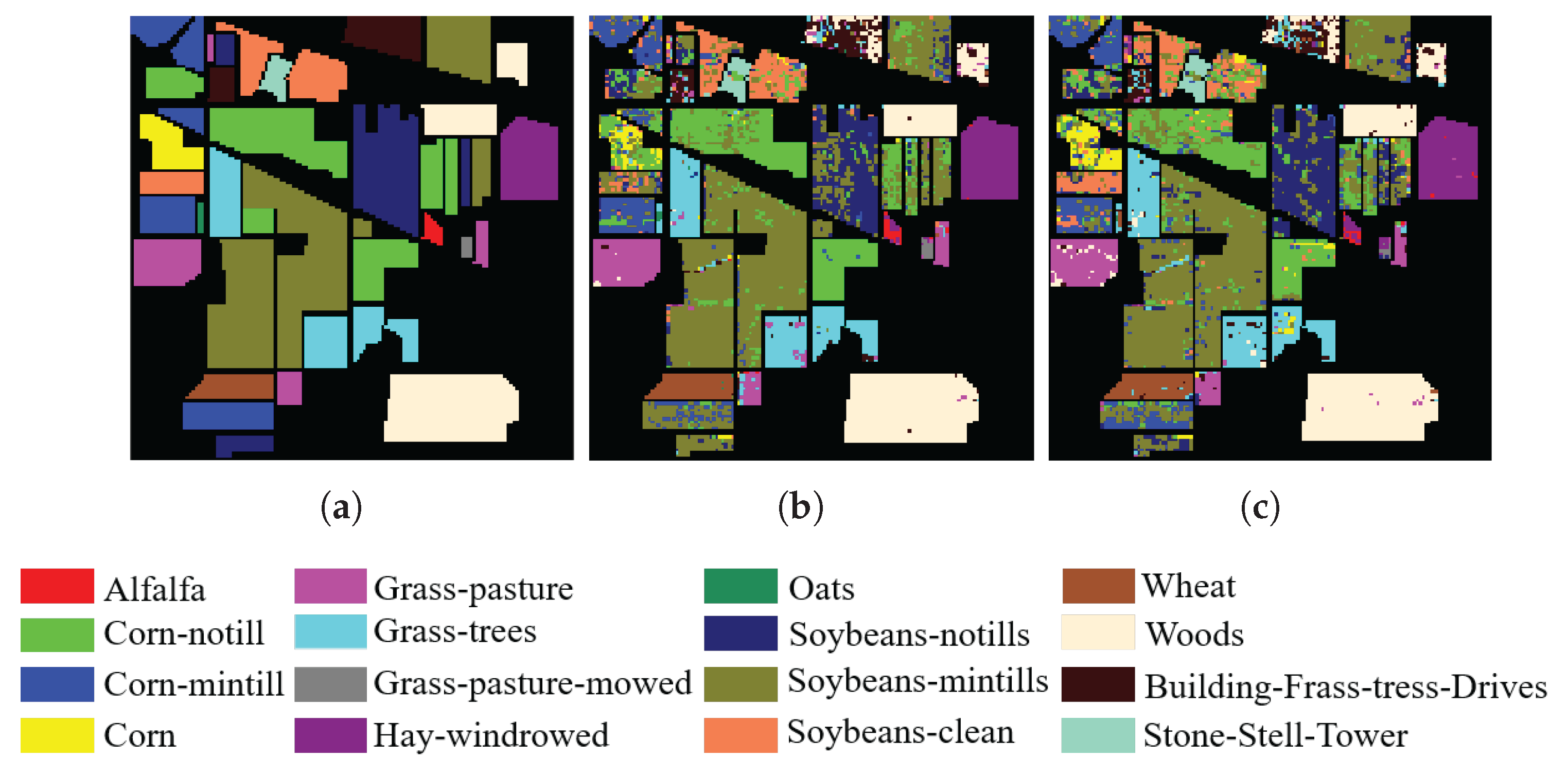
3.1.1. Indian Pines
3.1.2. Kennedy Space Center
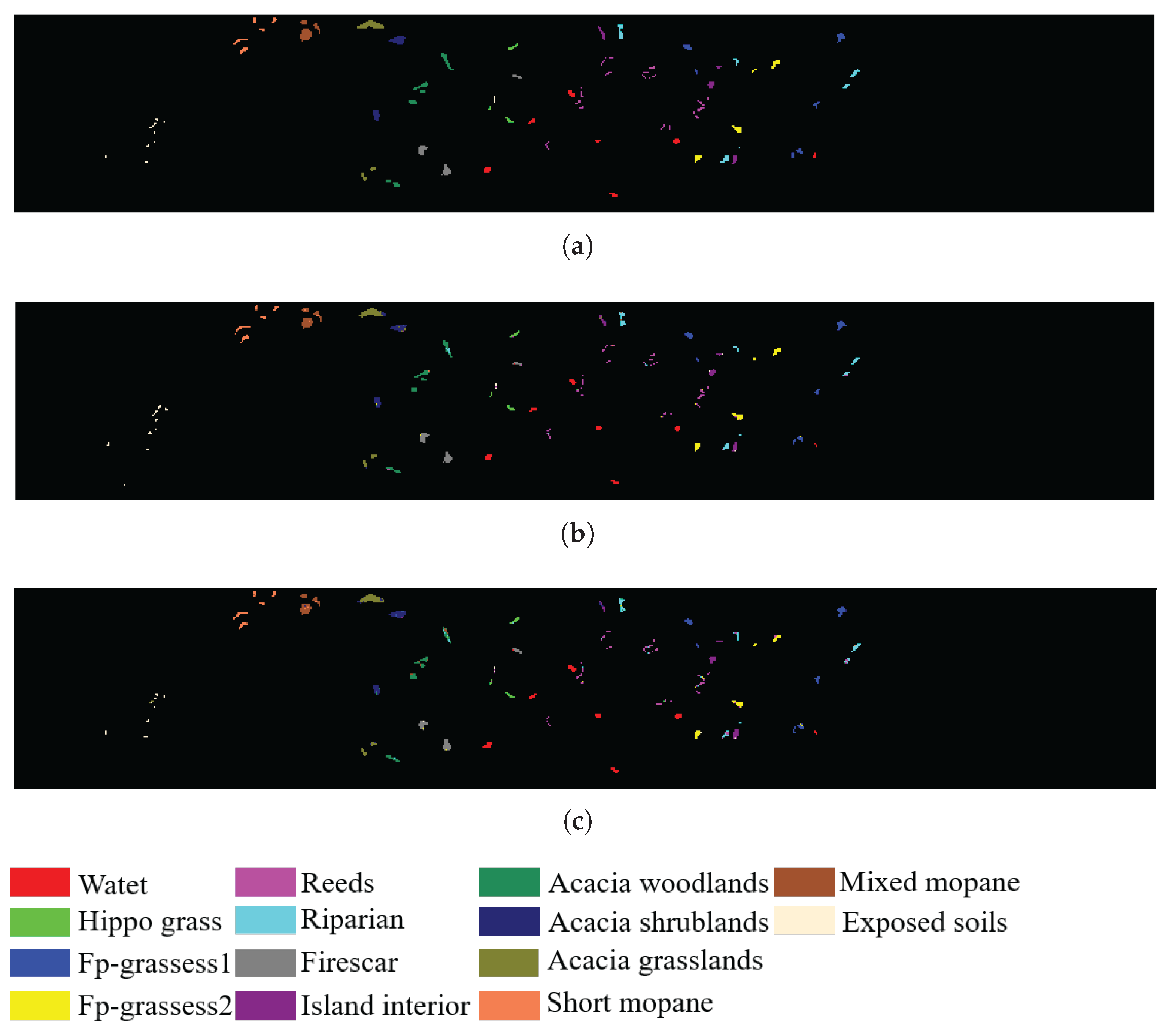
3.1.3. Botswana
3.2. Experiment Setup
3.2.1. ASPS
3.2.2. DSC
3.2.3. E-FDPC
3.2.4. FNGBS
3.2.5. HLFC
3.2.6. MBBS-VC
3.2.7. SNEA
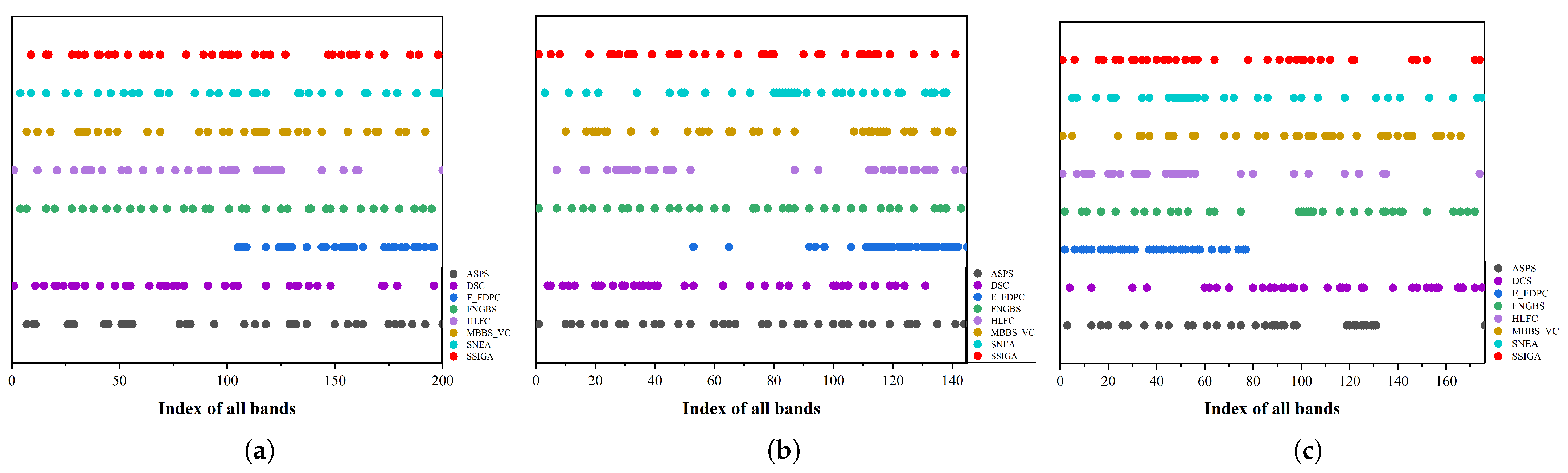
3.3. Experimental Results and Discussion
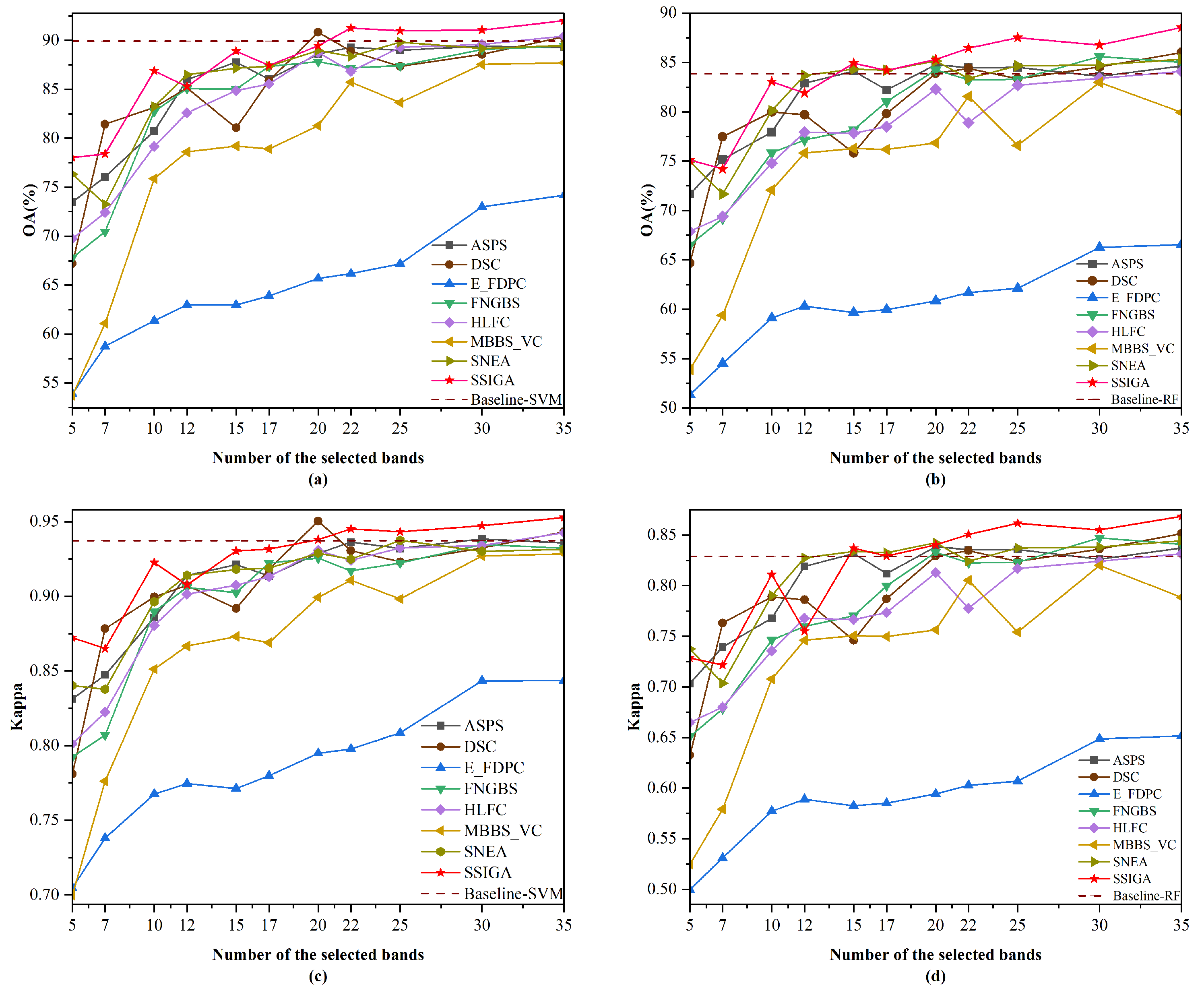
3.3.1. Comparison with State-of-the-Art Methods
3.3.2. Ablation Study
3.3.3. Execution Time
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BS | Band Selection |
| HSIs | Hyperspectral remote sensing images |
| SSIGA | Spectral–Spatial Iterative Greedy Algorithm |
| K-NNGs | K-Nearest Neighbor Graphs |
| IGA | Iterative Greedy Algorithm |
| ERS | Entropy Rate Superpixel |
| KSC | Kennedy Space Center |
| ASPS | Adaptive Subspace Partition Strategy |
| DSC | Deep Subspace Clustering |
| E-FDPC | Enhanced Fast Density-Peak-based Clustering |
| FNGBS | Fast Neighborhood Grouping for Band Selection |
| HLFC | Hierarchical Latent Feature Clustering |
| MBBS-VC | Multi-task Bee Band Selection With Variable-Size Clustering |
| SNEA | Structure-Conserved Neighborhood-Grouped Evolutionary Algorithm |
| SVM | Support Vector Machine |
| RF | Random Forest |
| RBF | Radial Basis Function |
| OA | Overall Accuracy |
| AOA | Average Overall Accuracy |
References
- Shang, X.; Song, M.; Wang, Y.; Yu, C.; Yu, H.; Li, F.; Chang, C.-I. Target-Constrained Interference-Minimized Band Selection for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6044–6064. [Google Scholar] [CrossRef]
- Chang, C.-I.; Kuo, Y.-M.; Hu, P.F. Unsupervised Rate Distortion Function-Based Band Subset Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Launeau, P.; Kassouk, Z.; Debaine, F.; Roy, R.; Mestayer, P.G.; Boulet, C.; Rouaud, J.-M.; Giraud, M. Airborne Hyperspectral Mapping of Trees in an Urban Area. Int. J. Remote Sens. 2017, 38, 1277–1311. [Google Scholar] [CrossRef]
- An, D.; Zhao, G.; Chang, C.; Wang, Z.; Li, P.; Zhang, T.; Jia, J. Hyperspectral Field Estimation and Remote-Sensing Inversion of Salt Content in Coastal Saline Soils of the Yellow River Delta. Int. J. Remote Sens. 2016, 37, 455–470. [Google Scholar] [CrossRef]
- Tan, K.; Zhu, L.; Wang, X. A Hyperspectral Feature Selection Method for Soil Organic Matter Estimation Based on an Improved Weighted Marine Predators Algorithm. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–11. [Google Scholar] [CrossRef]
- Saputro, A.H.; Handayani, W. Wavelength Selection in Hyperspectral Imaging for Prediction Banana Fruit Quality. In Proceedings of the 2017 International Conference on Electrical Engineering and Informatics (ICELTICs), Banda Aceh, Indonesia, 18–20 October 2017; IEEE: Piscataway, NJ, USA, 2018; pp. 226–230. [Google Scholar]
- Cheng, E.; Wang, F.; Peng, D.; Zhang, B.; Zhao, B.; Zhang, W.; Hu, J.; Lou, Z.; Yang, S.; Zhang, H.; et al. A GT-LSTM Spatio-Temporal Approach for Winter Wheat Yield Prediction: From the Field Scale to County Scale. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–18. [Google Scholar] [CrossRef]
- Dong, Y.; Du, B.; Zhang, L.; Zhang, L. Dimensionality Reduction and Classification of Hyperspectral Images Using Ensemble Discriminative Local Metric Learning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2509–2524. [Google Scholar] [CrossRef]
- Sun, W.; Tian, L.; Xu, Y.; Zhang, D.; Du, Q. Fast and Robust Self-Representation Method for Hyperspectral Band Selection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5087–5098. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, J.; Chen, C.L.P. Dimension Reduction Using Spatial and Spectral Regularized Local Discriminant Embedding for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1082–1095. [Google Scholar] [CrossRef]
- Li, B.; Zhang, P.; Zhang, J.; Jing, L. Unsupervised Double Weight Graphs Based Discriminant Analysis for Dimensionality Reduction. Int. J. Remote Sens. 2020, 41, 2209–2238. [Google Scholar] [CrossRef]
- Paul, A.; Chaki, N. Dimensionality Reduction of Hyperspectral Images Using Pooling. Pattern Recognit. Image Anal. 2019, 29, 72–78. [Google Scholar] [CrossRef]
- Li, D.; Shen, Y.; Kong, F.; Liu, J.; Wang, Q. Spectral–Spatial Prototype Learning-Based Nearest Neighbor Classifier for Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Zhao, E.; Qu, N.; Wang, Y.; Gao, C.; Duan, S.-B.; Zeng, J.; Zhang, Q. Thermal Infrared Hyperspectral Band Selection via Graph Neural Network for Land Surface Temperature Retrieval. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–14. [Google Scholar] [CrossRef]
- Qiao, X.; Roy, S.K.; Huang, W. Multiscale Neighborhood Attention Transformer With Optimized Spatial Pattern for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- He, Y.; Tu, B.; Liu, B.; Li, J.; Plaza, A. 3DSS-Mamba: 3D-Spectral-Spatial Mamba for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Zhou, W.; Kamata, S.; Wang, H.; Wong, M.S.; Hou, H. Mamba-in-Mamba: Centralized Mamba-Cross-Scan in Tokenized Mamba Model for Hyperspectral Image Classification. Neurocomputing 2025, 613, 128751. [Google Scholar] [CrossRef]
- Sellami, A.; Farah, M.; Farah, I.R.; Solaiman, B. Hyperspectral Imagery Semantic Interpretation Based on Adaptive Constrained Band Selection and Knowledge Extraction Techniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1337–1347. [Google Scholar] [CrossRef]
- Sun, W.; Peng, J.; Yang, G.; Du, Q. Correntropy-Based Sparse Spectral Clustering for Hyperspectral Band Selection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 484–488. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, L.; Zhang, L.; Lai, Y.M. A Dissimilarity-Weighted Sparse Self-Representation Method for Band Selection in Hyperspectral Imagery Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4374–4388. [Google Scholar] [CrossRef]
- Serpico, S.B.; Bruzzone, L. A New Search Algorithm for Feature Selection in Hyperspectral Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1360–1367. [Google Scholar] [CrossRef]
- Taşkın, G.; Kaya, H.; Bruzzone, L. Feature Selection Based on High Dimensional Model Representation for Hyperspectral Images. IEEE Trans. Image Process. 2017, 26, 2918–2928. [Google Scholar] [CrossRef]
- Cao, X.; Wei, C.; Ge, Y.; Feng, J.; Zhao, J.; Jiao, L. Semi-Supervised Hyperspectral Band Selection Based on Dynamic Classifier Selection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1289–1298. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, X.; Lu, X. Discovering Diverse Subset for Unsupervised Hyperspectral Band Selection. IEEE Trans. Image Process. 2017, 26, 51–64. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Li, Q.; Li, X. Hyperspectral Band Selection via Adaptive Subspace Partition Strategy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4940–4950. [Google Scholar] [CrossRef]
- Chang, C.-I.; Du, Q.; Sun, T.-L.; Althouse, M.L.G. A Joint Band Prioritization and Band-Decorrelation Approach to Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Chang, C.-I.; Wang, S. Constrained Band Selection for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1575–1585. [Google Scholar] [CrossRef]
- Jia, S.; Tang, G.; Zhu, J.; Li, Q. A Novel Ranking-Based Clustering Approach for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 88–102. [Google Scholar] [CrossRef]
- Shahwani, H.; Bui, T.D.; Jeong, J.P.; Shin, J. A Stable Clustering Algorithm Based on Affinity Propagation for VANETs. In Proceedings of the 2017 19th International Conference on Advanced Communication Technology (ICACT), Pyeongchang, Republic of Korea, 19–22 February 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 501–504. [Google Scholar]
- Martinez-Uso, A.; Pla, F.; Sotoca, J.M.; GarcÍa-Sevilla, P. Clustering-Based Hyperspectral Band Selection Using Information Measures. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4158–4171. [Google Scholar] [CrossRef]
- Su, H.; Du, Q.; Chen, G.; Du, P. Optimized Hyperspectral Band Selection Using Particle Swarm Optimization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2659–2670. [Google Scholar] [CrossRef]
- Yang, H.; Du, Q.; Chen, G. Particle Swarm Optimization-Based Hyperspectral Dimensionality Reduction for Urban Land Cover Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 544–554. [Google Scholar] [CrossRef]
- Wang, Q.; Song, C.; Dong, Y.; Cheng, F.; Tong, L.; Du, B.; Zhang, X. Unsupervised Hyperspectral Band Selection via Structure-Conserved and Neighborhood-Grouped Evolutionary Algorithm. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–19. [Google Scholar] [CrossRef]
- Li, S.; Peng, B.; Fang, L.; Zhang, Q.; Cheng, L.; Li, Q. Hyperspectral Band Selection via Difference Between Intergroups. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–10. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, X. Optimal Clustering Framework for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2018, 16, 5522319. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-Clustering-Based Hyperspectral Band Selection by Contextual Analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Jia, S.; Yuan, Y.; Li, N.; Liao, J.; Huang, Q.; Jia, X.; Xu, M. A Multiscale Superpixel-Level Group Clustering Framework for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Zhao, H.; Bruzzone, L.; Guan, R.; Zhou, F.; Yang, C. Spectral-Spatial Genetic Algorithm-Based Unsupervised Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9616–9632. [Google Scholar] [CrossRef]
- Wan, Y.; Chen, C.; Zhang, L.; Gong, X.; Zhong, Y. Adaptive Multistrategy Particle Swarm Optimization for Hyperspectral Remote Sensing Image Band Selection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5520115. [Google Scholar] [CrossRef]
- Su, H.; Yong, B.; Du, Q. Hyperspectral Band Selection Using Improved Firefly Algorithm. IEEE Geosci. Remote Sens. Lett. 2016, 13, 68–72. [Google Scholar] [CrossRef]
- Su, H.; Cai, Y.; Du, Q. Firefly-Algorithm-Inspired Framework With Band Selection and Extreme Learning Machine for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 309–320. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Q.; Ma, H.; Yu, H. A Hybrid Gray Wolf Optimizer for Hyperspectral Image Band Selection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- He, C.; Zhang, Y.; Gong, D.; Song, X.; Sun, X. A Multitask Bee Colony Band Selection Algorithm With Variable-Size Clustering for Hyperspectral Images. IEEE Trans. Evol. Computat. 2022, 26, 1566–1580. [Google Scholar] [CrossRef]
- Wu, M.; Ou, X.; Lu, Y.; Li, W.; Yu, D.; Liu, Z.; Ji, C. Heterogeneous Cuckoo Search-Based Unsupervised Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Jacobs, L.W.; Brusco, M.J. Note: A Local-Search Heuristic for Large Set-Covering Problems. Nav. Res. Logist. 1995, 42, 1129–1140. [Google Scholar] [CrossRef]
- Zhao, F.; Zhuang, C.; Wang, L.; Dong, C. An Iterative Greedy Algorithm With Q -Learning Mechanism for the Multiobjective Distributed No-Idle Permutation Flowshop Scheduling. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3207–3219. [Google Scholar] [CrossRef]
- Karimi-Mamaghan, M.; Mohammadi, M.; Pasdeloup, B.; Meyer, P. Learning to Select Operators in Meta-Heuristics: An Integration of Q-Learning into the Iterated Greedy Algorithm for the Permutation Flowshop Scheduling Problem. Eur. J. Oper. Res. 2023, 304, 1296–1330. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J. Simulated Annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Lee, S.; Kim, S.B. Parallel Simulated Annealing with a Greedy Algorithm for Bayesian Network Structure Learning. IEEE Trans. Knowl. Data Eng. 2020, 32, 1157–1166. [Google Scholar] [CrossRef]
- Ribas, I.; Companys, R.; Tort-Martorell, X. An Iterated Greedy Algorithm for the Flowshop Scheduling Problem with Blocking. Omega 2011, 39, 293–301. [Google Scholar] [CrossRef]
- Wang, J.; Ye, M.; Xiong, F.; Qian, Y. Cross-Scene Hyperspectral Feature Selection via Hybrid Whale Optimization Algorithm With Simulated Annealing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2473–2483. [Google Scholar] [CrossRef]
- Ruiz, R.; Stützle, T. A Simple and Effective Iterated Greedy Algorithm for the Permutation Flowshop Scheduling Problem. Eur. J. Oper. Res. 2007, 177, 2033–2049. [Google Scholar] [CrossRef]
- Huang, Y.-Y.; Pan, Q.-K.; Huang, J.-P.; Suganthan, P.; Gao, L. An Improved Iterated Greedy Algorithm for the Distributed Assembly Permutation Flowshop Scheduling Problem. Comput. Ind. Eng. 2021, 152, 107021. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, J.; Gong, M. Unsupervised Hyperspectral Band Selection by Fuzzy Clustering With Particle Swarm Optimization. IEEE Geosci. Remote Sens. Lett. 2017, 14, 773–777. [Google Scholar] [CrossRef]
- Luo, X.; Xue, R.; Yin, J. Information-Assisted Density Peak Index for Hyperspectral Band Selection. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1870–1874. [Google Scholar] [CrossRef]
- Zeng, M.; Cai, Y.; Cai, Z.; Liu, X.; Hu, P.; Ku, J. Unsupervised Hyperspectral Image Band Selection Based on Deep Subspace Clustering. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1889–1893. [Google Scholar] [CrossRef]
- Zhou, P.; Chen, J.; Fan, M.; Du, L.; Shen, Y.-D.; Li, X. Unsupervised Feature Selection for Balanced Clustering. Knowl.-Based Syst. 2020, 193, 105417. [Google Scholar] [CrossRef]
- Haklı, H.; Uğuz, H. A Novel Particle Swarm Optimization Algorithm with Levy Flight. Appl. Soft Comput. 2014, 23, 333–345. [Google Scholar] [CrossRef]
- Gong, M.; Zhang, M.; Yuan, Y. Unsupervised Band Selection Based on Evolutionary Multiobjective Optimization for Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 544–557. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, L.C.; Zhang, X.; Sun, T. Hyperspectral Band Selection Based on Trivariate Mutual Information and Clonal Selection. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4092–4105. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Li, X. A Fast Neighborhood Grouping Method for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5028–5039. [Google Scholar] [CrossRef]
- Wang, J.; Tang, C.; Liu, X.; Zhang, W.; Li, W.; Zhu, X.; Wang, L.; Zomaya, A.Y. Region-Aware Hierarchical Latent Feature Representation Learning-Guided Clustering for Hyperspectral Band Selection. IEEE Trans. Cybern. 2023, 53, 5250–5263. [Google Scholar] [CrossRef]




| Class | Name | Training Samples | Testing Samples |
|---|---|---|---|
| 1 | Alfalfa | 5 | 41 |
| 2 | Corn-notill | 143 | 1285 |
| 3 | Corn-mintill | 83 | 747 |
| 4 | Grass-pasture | 24 | 213 |
| 5 | Corn | 49 | 434 |
| 6 | Grass-trees | 73 | 657 |
| 7 | Grass-pasture-mowed | 3 | 25 |
| 8 | Hay-windrowed | 48 | 430 |
| 9 | Oats | 2 | 18 |
| 10 | Soybeans-notills | 98 | 874 |
| 11 | Soybeans-mintills | 246 | 2209 |
| 12 | Soybeans-clean | 60 | 533 |
| 13 | Wheat | 21 | 184 |
| 14 | Woods | 127 | 1138 |
| 15 | Building-Grass-Tress-Drives | 39 | 347 |
| 16 | Stone-Steel-Tower | 10 | 83 |
| Class | Name | Training Samples | Testing Samples |
|---|---|---|---|
| 1 | Water | 27 | 243 |
| 2 | Hippo grass | 11 | 90 |
| 3 | Fp-grassess1 | 26 | 225 |
| 4 | Fp-grassess2 | 22 | 193 |
| 5 | Reeds | 27 | 242 |
| 6 | Riparian | 27 | 242 |
| 7 | Firescar | 26 | 233 |
| 8 | Island interior | 21 | 182 |
| 9 | Acacia woodlands | 32 | 282 |
| 10 | Acacia shrublands | 25 | 223 |
| 11 | Acacia grasslands | 31 | 274 |
| 12 | Short mopane | 19 | 162 |
| 13 | Mixed mopane | 27 | 241 |
| 14 | Exposed soils | 10 | 85 |
| Class | Name | Training Samples | Testing Samples |
|---|---|---|---|
| 1 | Scrub | 77 | 684 |
| 2 | Willow swamp | 25 | 218 |
| 3 | CP hammock | 26 | 230 |
| 4 | CP/Oak | 26 | 226 |
| 5 | Slash pine | 17 | 144 |
| 6 | Oak/Broadleaf | 23 | 206 |
| 7 | Hardwood swamp | 11 | 94 |
| 8 | Graminoid marsh | 44 | 387 |
| 9 | Spartina marsh | 52 | 468 |
| 10 | Catiail marsh | 41 | 363 |
| 11 | Salt marsh | 42 | 377 |
| 12 | Mud flats | 51 | 452 |
| 13 | Water | 93 | 834 |
| Parameters | Values |
|---|---|
| Simulate annealing initial temperature, T | 1000 |
| Maximum numuber of iterations, | 2000 |
| Number of superpixels, N | 300 |
| Dataset | Classifier | SSIGA | ASPS [25] | DSC [54] | E-FDPC [28] | FNGBS [61] | HLFC [62] | MBBS-VC [41] | SNEA [33] |
|---|---|---|---|---|---|---|---|---|---|
| Indian Pines | AOA(RF) | 72.80 | 69.91 | 70.47 | 62.13 | 71.68 | 70.44 | 70.61 | 69.91 |
| Kappa(RF) | 70.46 | 67.63 | 68.19 | 59.59 | 69.45 | 68.18 | 68.36 | 67.64 | |
| AOA(SVM) | 70.88 | 66.69 | 67.07 | 56.54 | 69.85 | 66.68 | 66.82 | 67.70 | |
| Kappa(SVM) | 82.19 | 80.93 | 80.50 | 74.64 | 81.59 | 79.78 | 80.80 | 79.94 | |
| Botswana | AOA(RF) | 83.45 | 81.45 | 79.97 | 60.21 | 79.02 | 77.98 | 73.78 | 82.02 |
| Kappa(RF) | 81.44 | 80.43 | 78.91 | 58.81 | 77.93 | 76.83 | 72.57 | 81.02 | |
| AOA(SVM) | 87.25 | 85.05 | 84.53 | 64.55 | 83.57 | 83.57 | 77.57 | 85.42 | |
| Kappa(SVM) | 92.32 | 90.76 | 90.50 | 78.40 | 89.56 | 89.91 | 86.36 | 90.71 | |
| KSC | AOA(RF) | 86.68 | 82.85 | 84.39 | 85.71 | 84.18 | 86.56 | 80.56 | 85.11 |
| Kappa(RF) | 85.42 | 81.34 | 82.95 | 84.37 | 82.75 | 85.29 | 78.79 | 83.73 | |
| AOA(SVM) | 90.11 | 86.25 | 87.55 | 88.09 | 87.27 | 89.66 | 83.26 | 88.24 | |
| Kappa(SVM) | 93.03 | 89.79 | 91.16 | 90.81 | 90.70 | 92.64 | 87.33 | 91.56 |
| Dataset | Local Search | Fisher score | AOA | Kappa |
|---|---|---|---|---|
| Indian Pines | ✓ | 64.93 | 76.98 | |
| ✓ | 68.33 | 79.27 | ||
| ✓ | ✓ | 70.88 | 82.19 | |
| Botswana | ✓ | 83.06 | 89.97 | |
| ✓ | 85.41 | 90.15 | ||
| ✓ | ✓ | 87.25 | 92.32 | |
| KSC | ✓ | 86.39 | 90.01 | |
| ✓ | 89.08 | 92.29 | ||
| ✓ | ✓ | 90.11 | 93.03 |
| Dataset | ASPS | DSC | E-FDPC | FNGBS | HLFC | MBBS-VC | SNEA | SSIGA |
|---|---|---|---|---|---|---|---|---|
| Indian Pines | 0.11 | 14.27 | 0.29 | 0.05 | 55.44 | 62.90 | 4.80 | 30.58 |
| Botswana | 1.22 | 206.07 | 0.58 | 0.45 | 41.51 | 1224.76 | 5.72 | 138.93 |
| KSC | 1.24 | 208.97 | 0.62 | 0.47 | 52.56 | 1257.03 | 5.88 | 155.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Wang, W. Unsupervised Hyperspectral Band Selection Using Spectral–Spatial Iterative Greedy Algorithm. Sensors 2025, 25, 5638. https://doi.org/10.3390/s25185638
Yang X, Wang W. Unsupervised Hyperspectral Band Selection Using Spectral–Spatial Iterative Greedy Algorithm. Sensors. 2025; 25(18):5638. https://doi.org/10.3390/s25185638
Chicago/Turabian StyleYang, Xin, and Wenhong Wang. 2025. "Unsupervised Hyperspectral Band Selection Using Spectral–Spatial Iterative Greedy Algorithm" Sensors 25, no. 18: 5638. https://doi.org/10.3390/s25185638
APA StyleYang, X., & Wang, W. (2025). Unsupervised Hyperspectral Band Selection Using Spectral–Spatial Iterative Greedy Algorithm. Sensors, 25(18), 5638. https://doi.org/10.3390/s25185638





