Designand Implementation of a Novel Wideband HF Communication System Based on NC-OFDM and Probabilistic Shaping
Abstract
1. Introduction
2. System Model
2.1. Transmitter
2.2. Receiver
3. Principle of the Proposed Scheme
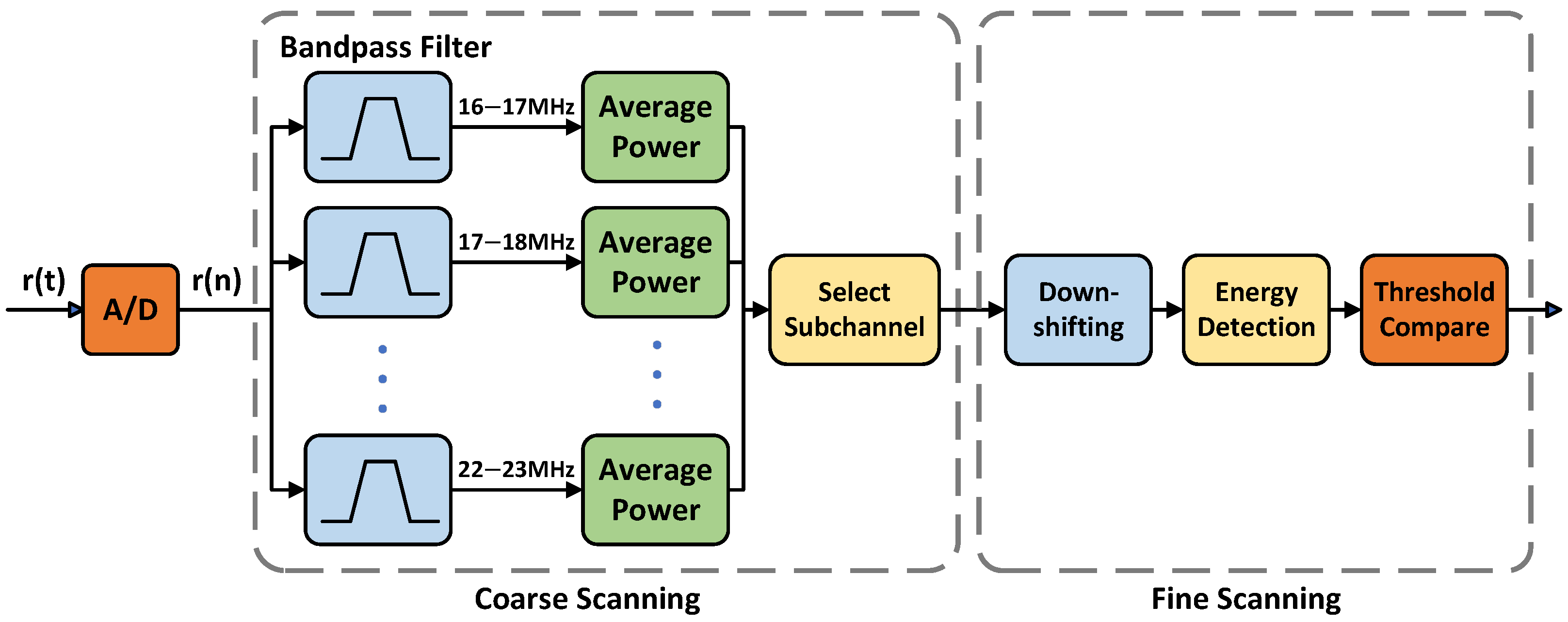
3.1. Dynamic Spectrum Sensing
3.2. NC-OFDM
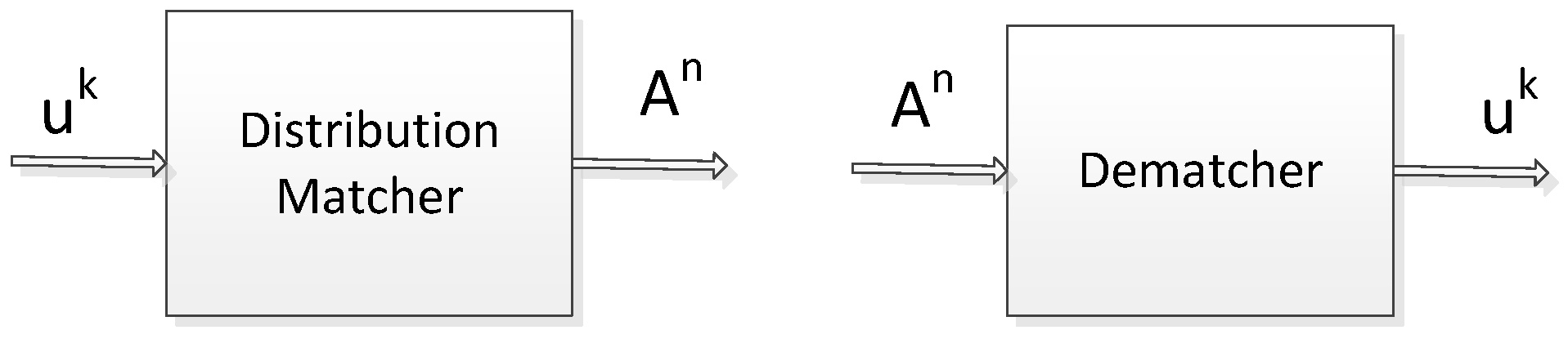
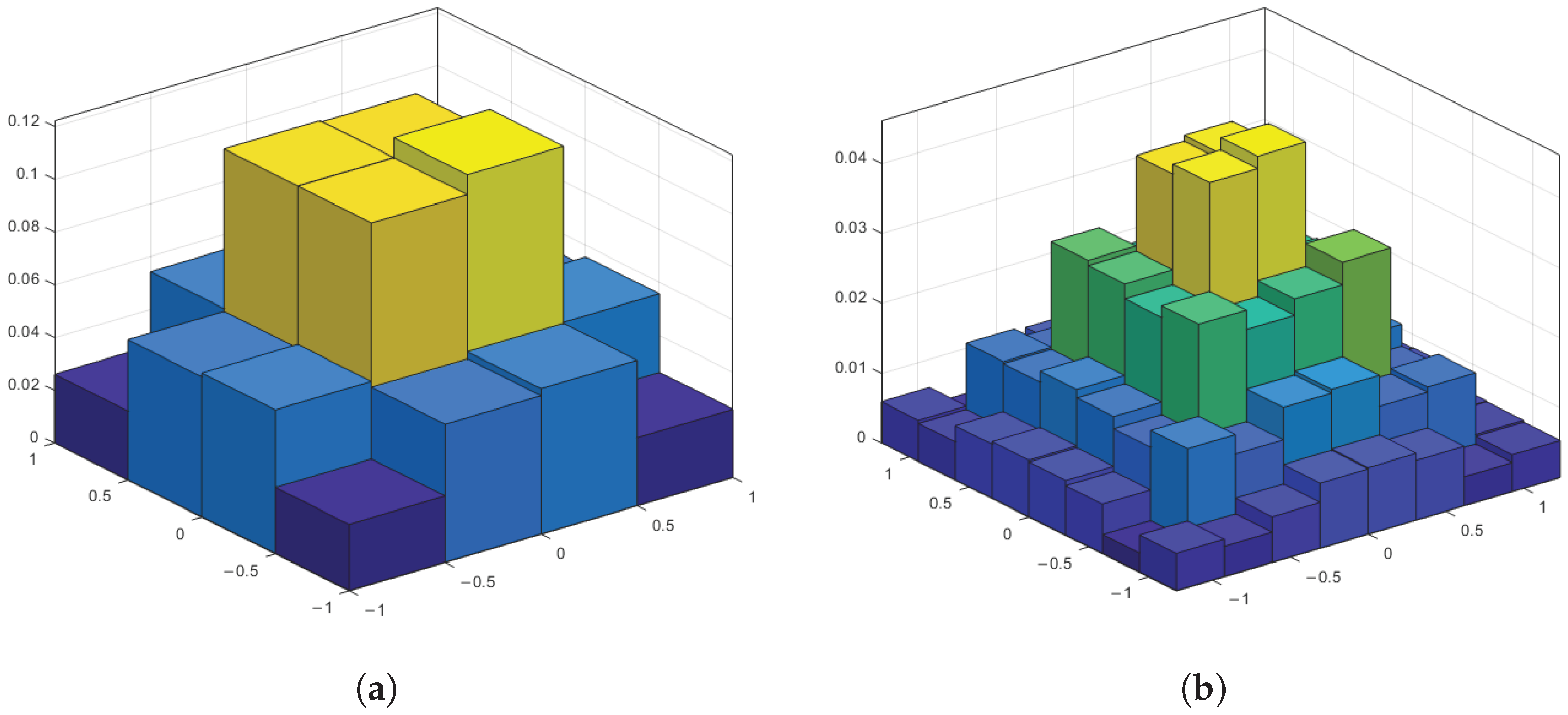
3.3. Probabilistic Shaping Coded Modulation
3.4. Soft Demodulation Algorithm
4. Simulation Results and Discussions
4.1. Dynamic Spectrum Sensing and NC-OFDM Signal Spectrum
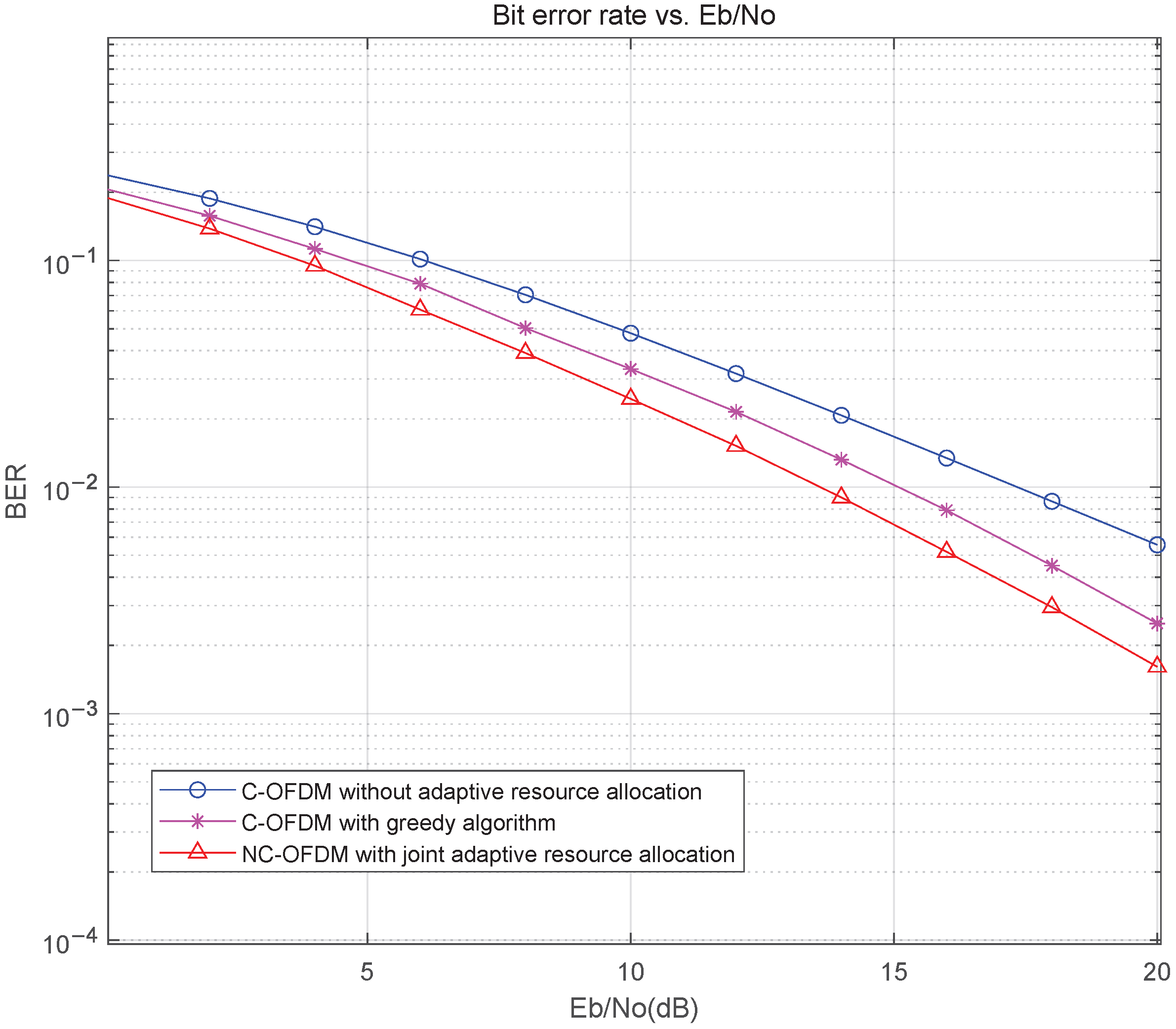
4.2. BER Performance Comparison of NC-OFDM and C-OFDM
4.3. PAPR Performance Comparison of NC-OFDM and C-OFDM
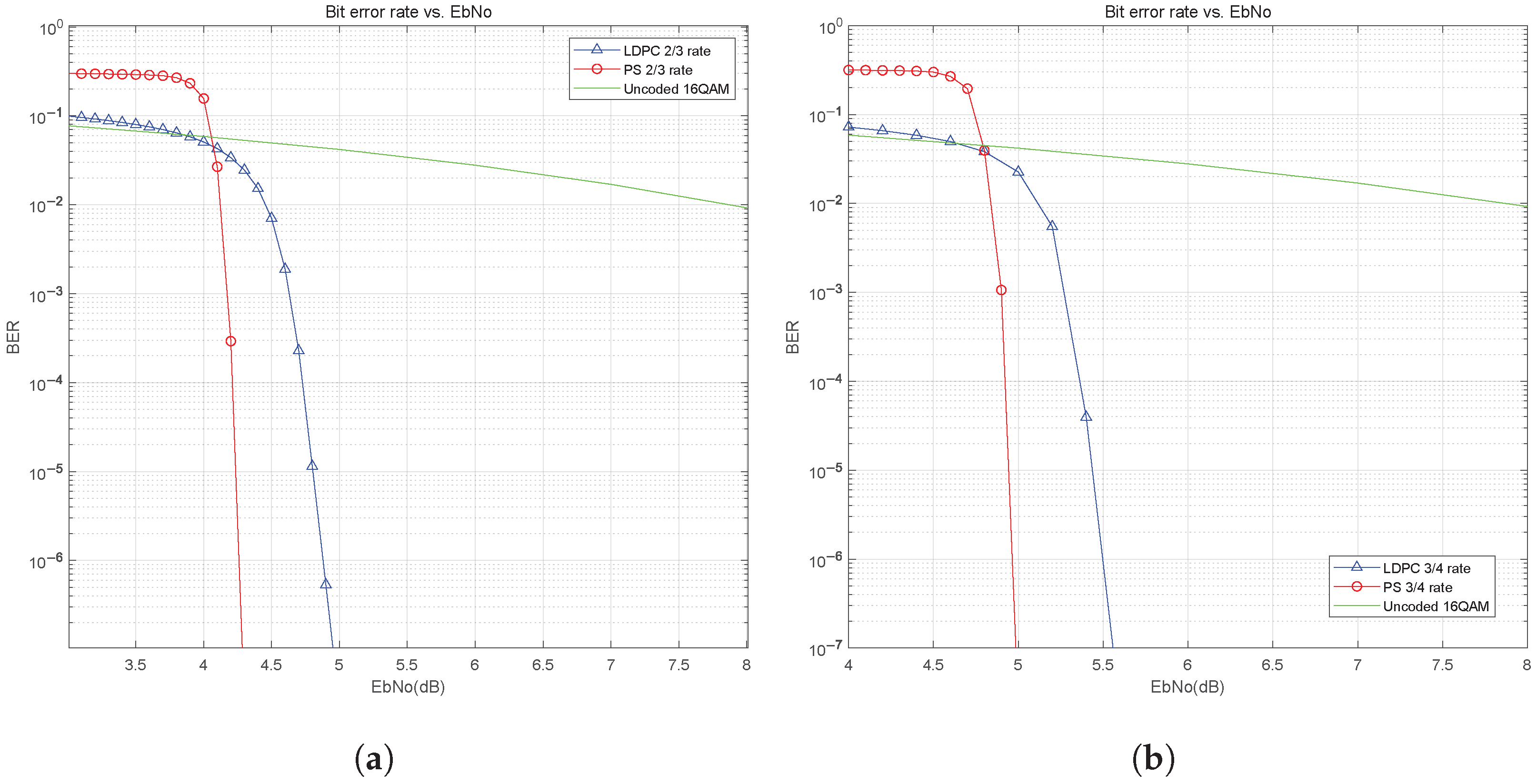
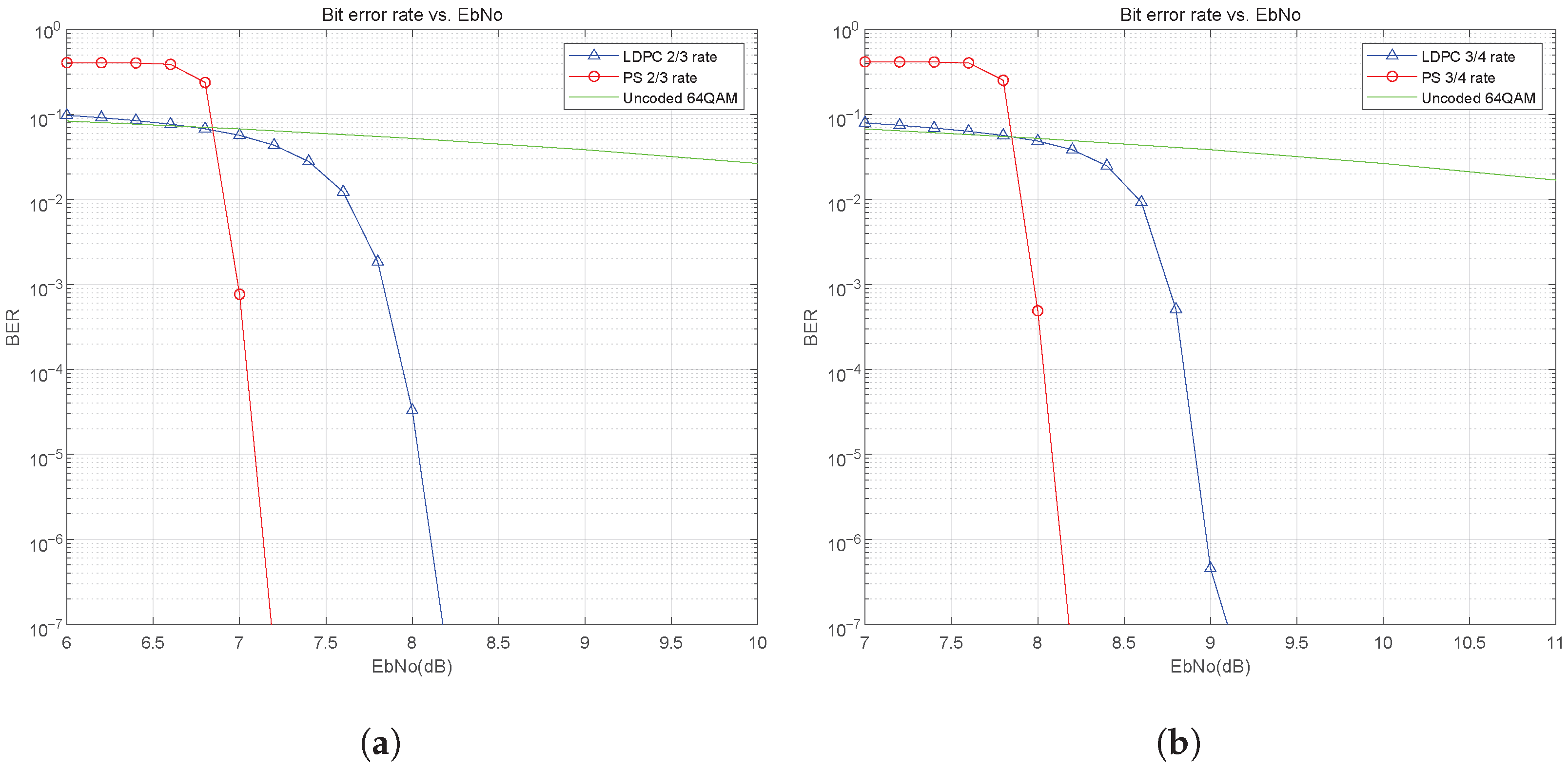
4.4. Performance Analysis of NC-OFDM with LDPC Coding in the HF ITS Channel
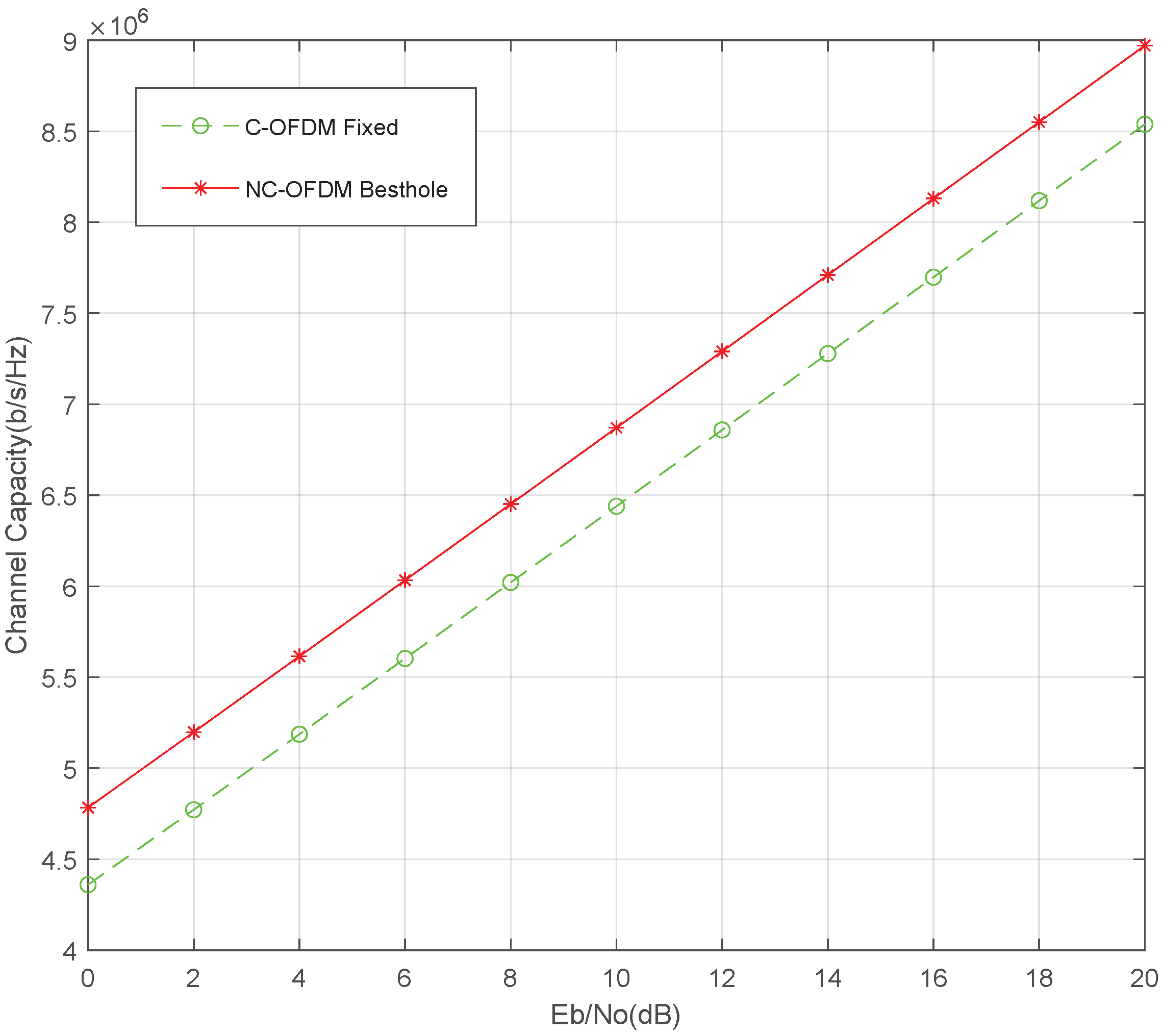
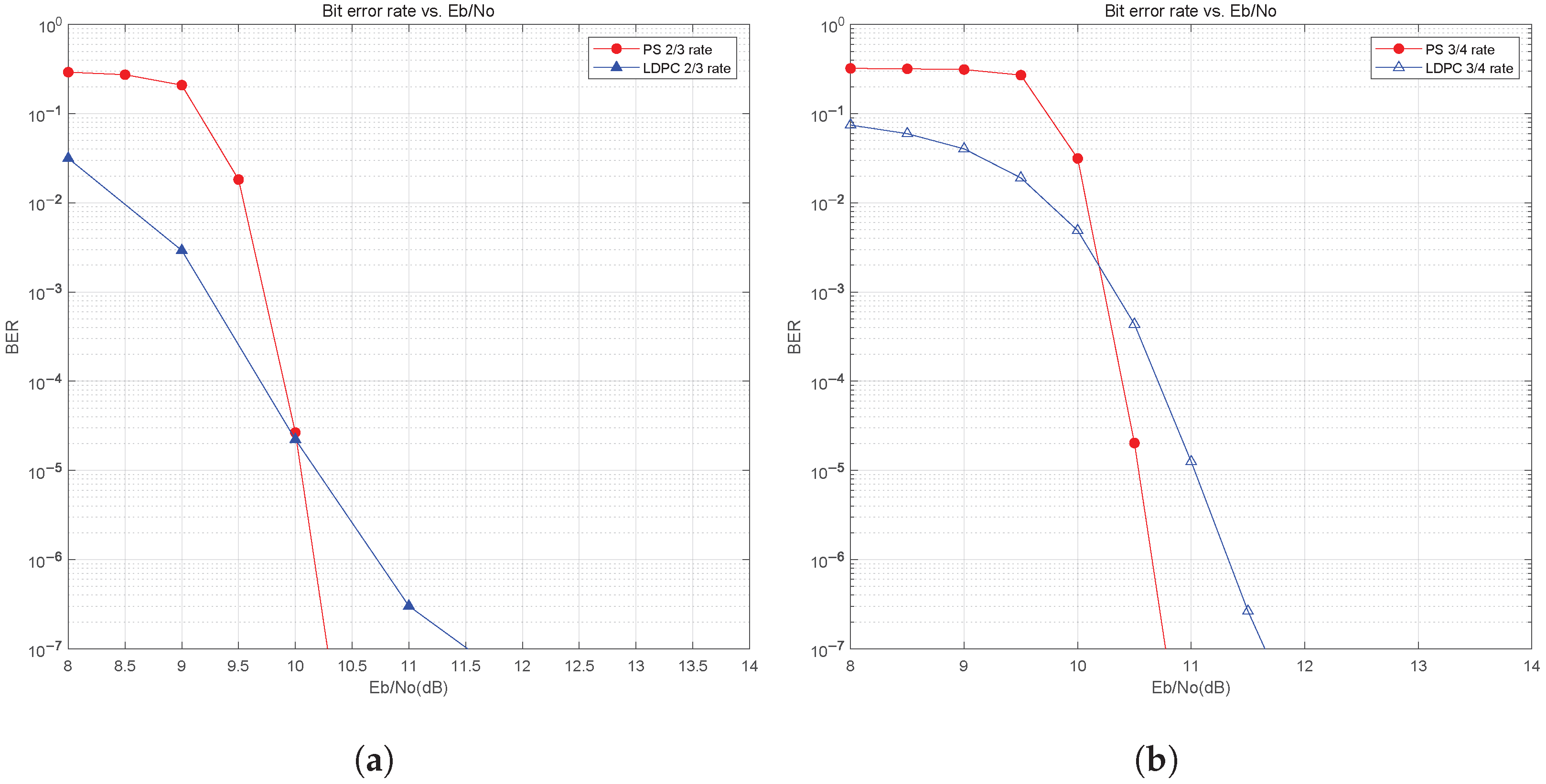
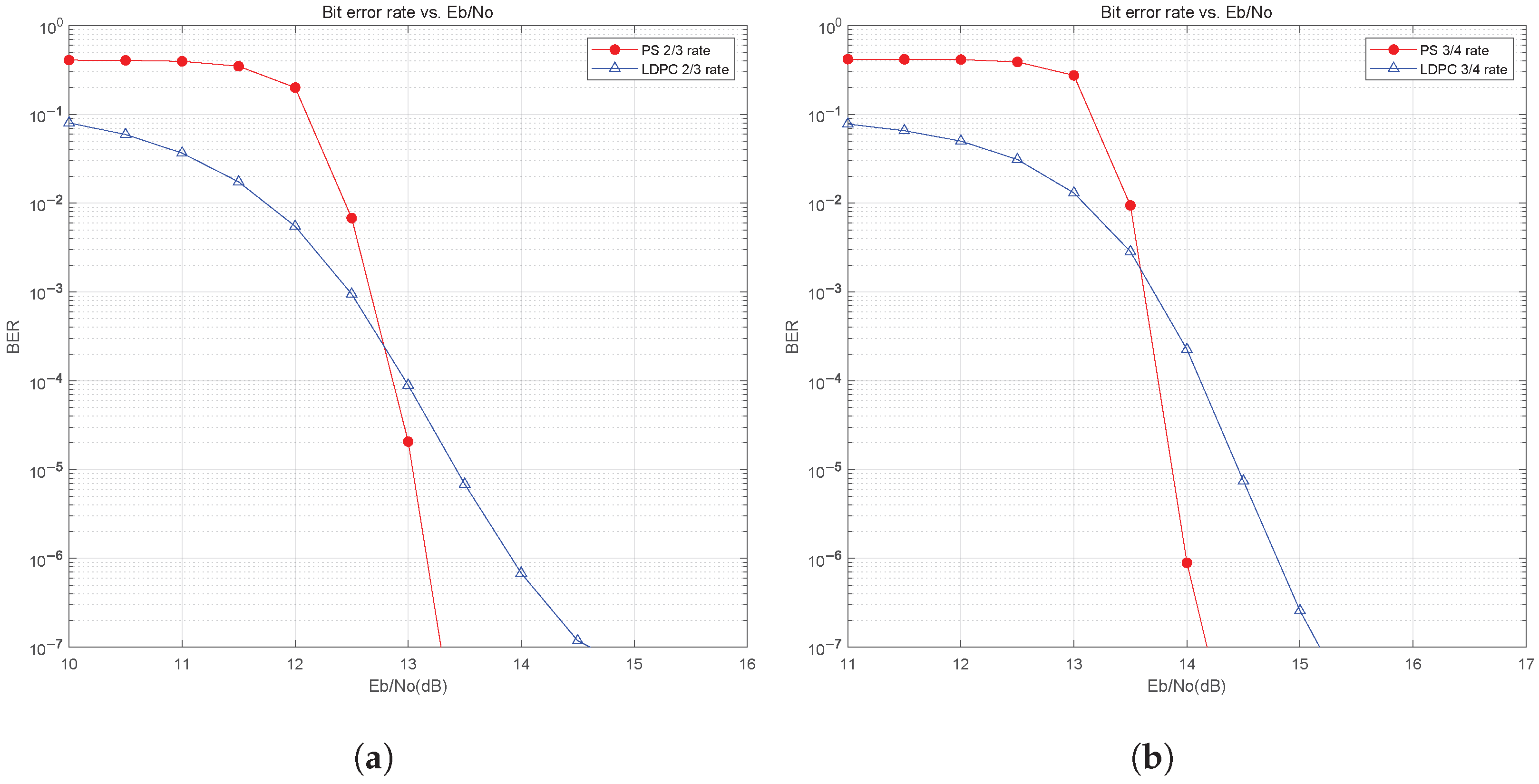
4.5. Performance Simulation of NC-OFDM+LDPC+PS in HF Channel
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Johnson, E.E.; Koski, E.; Furman, W.N. Third-Generation and Wideband HF Radio Communications; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Wang, J.; Ding, G.; Wang, H. HF communications: Past, present, and future. China Commun. 2018, 15, 1–9. [Google Scholar] [CrossRef]
- Hervás, M.; Bergadà, P.; Alsina-Pagès, R.M. Ionospheric narrowband and wideband HF soundings for communications purposes: A review. Sensors 2020, 20, 2486. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zeng, F.; Ge, L.; Chen, S.; Yang, B.; Xuan, G. Design and implementation of novel HF OFDM communication systems. In Proceedings of the 2012 IEEE 14th International Conference on Communication Technology, Chengdu, China, 9–11 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1088–1092. [Google Scholar]
- Vogler, L.E.; Hoffmeyer, J.A. A model for wideband HF propagation channels. Radio Sci. 1993, 28, 1131–1142. [Google Scholar] [CrossRef]
- Mastrangelo, J.F.; Lemmon, J.J.; Vogler, L.E.; Hoffmeyer, J.A.; Pratt, L.E.; Behm, C.J. A new wideband high frequency channel simulation system. IEEE Trans. Commun. 2002, 45, 26–34. [Google Scholar] [CrossRef]
- Nilsson, J.E.; Giles, T.C. Wideband Multi-Carrier Transmission for Military HF Communication; IEEE: Piscataway, NJ, USA, 1997; Volume 2. [Google Scholar]
- Chun-rong, K.; Ying, L. A multi-band OFDM system in HF communications. In Proceedings of the 2006 8th international Conference on Signal Processing, Guilin, China, 16–20 November 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 4. [Google Scholar]
- Ibrahim, A.A.; Abdelaziz, A.M.; Salah, M.M. OFDM over wideband ionospheric HF channel: Channel modelling & optimal subcarrier power allocation. In Proceedings of the 2018 35th National Radio Science Conference (NRSC), Cairo, Egypt, 20–22 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 300–308. [Google Scholar]
- Ibrahim, A.A.; Abdelaziz, A.M.; Salah, M.M. Performance of single carrier cyclic prefix versus ofdm over wideband hf ionospheric channel. In Proceedings of the 2019 36th National Radio Science Conference (NRSC), Port Said, Egypt, 16–18 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 92–99. [Google Scholar]
- Koski, E.; Furman, W. Applying cognitive radio concepts to HF communications. In Proceedings of the The Institution of Engineering and Technology 11th International Conference on Ionospheric radio Systems and Techniques (IRST 2009), Edinburgh, UK, 28–30 April 2009; IET: Stevenage, UK, 2009; pp. 1–6. [Google Scholar]
- Melián-Gutiérrez, L.; Zazo, S.; Blanco-Murillo, J.L.; Pérez-Álvarez, I.; García-Rodríguez, A.; Pérez-Díaz, B. Efficiency improvement of HF communications using cognitive radio principles. In Proceedings of the 12th IET International Conference on Ionospheric Radio Systems and Techniques (IRST 2012), York, UK, 15–17 May 2012; IET: Stevenage, UK, 2012; p. 22. [Google Scholar]
- Ivanov, V.; Ivanov, D.; Ryabova, N.; Belgibaev, R. Development of Methods for Spectral Monitoring of HF Interference to Determine the Availability of Ionospheric Radio Channels. In Proceedings of the 2024 Wave Electronics and its Application in Information and Telecommunication Systems (WECONF), St. Petersburg, Russia, 3–7 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–5. [Google Scholar]
- Rajbanshi, R.; Wyglinski, A.M.; Minden, G.J. An Efficient Implementation of NC-OFDM Transceivers for Cognitive Radios. In Proceedings of the 2006 1st International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Mykonos, Greece, 8–10 June 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–5. [Google Scholar]
- Wang, W.; Gao, J.; Bai, Y. Non-contiguous channel bonding via NC-OFDM for using TV white spaces. In Proceedings of the 2013 3rd International Conference on Consumer Electronics, Communications and Networks, Xianning, China, 20–22 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 427–430. [Google Scholar]
- Wang, Y.; Niu, H.; Zhao, Q.; Wang, L.; Gao, Y.; Lin, Z. NC-OFDM Satellite Communication Based on Compressed Spectrum Sensing. Sensors 2022, 22, 3800. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Zhang, S.; Gu, P.; Wu, L. On the design of MLC-LDPC-OFDM in DRM MF and HF channels. In Proceedings of the 2014 Sixth International Conference on Wireless Communications and Signal Processing (WCSP), Hefei, China, 23–25 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Li, X.B.; Zhang, S.; Zhao, F.H.; Zhang, H.W. A multi-base station cooperative algorithm for LDPC-OFDM system in the HF channel. In Proceedings of the 2014 International Conference on Wireless Communication and Sensor Network, Wuhan, China, 13–14 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 21–27. [Google Scholar]
- Smith, B.P.; Kschischang, F.R. A pragmatic coded modulation scheme for high-spectral-efficiency fiber-optic communications. J. Light. Technol. 2012, 30, 2047–2053. [Google Scholar] [CrossRef]
- Fehenberger, T.; Alvarado, A.; Böcherer, G.; Hanik, N. On probabilistic shaping of quadrature amplitude modulation for the nonlinear fiber channel. J. Light. Technol. 2016, 34, 5063–5073. [Google Scholar] [CrossRef]
- Weimin, K.; Hongwen, Y. High spectral efficient coded modulation scheme based on constellation shaping. Syst. Eng. Electron. 2021, 43, 1686. [Google Scholar]
- Zhi, Z.; Binghua, Q.; Ping, Z. Low-density parity-check codes and high spectral efficiency modulation. In Proceedings of the 14th IEEE Proceedings on Personal, Indoor and Mobile Radio Communications, 2003, PIMRC 2003, Beijing, China, 7–10 September 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 1, pp. 444–448. [Google Scholar]
- Muchandi, N.; Khanai, R. Cognitive radio spectrum sensing: A survey. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3233–3237. [Google Scholar]
- Nasrallah, A.; Hamza, A.; Boukaba, T.; Baudoin, G.; Messani, A. Energy detection with adaptive threshold for cognitive radio. In Proceedings of the 2018 International Conference on Communications and Electrical Engineering (ICCEE), El Oued, Algeria, 17–18 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Grunheid, R.; Bolinth, E.; Rohling, H. A blockwise loading algorithm for the adaptive modulation technique in OFDM systems. In Proceedings of the IEEE 54th Vehicular Technology Conference, VTC Fall 2001, Proceedings (Cat. No. 01CH37211), Atlantic City, NJ, USA, 7–11 October 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 2, pp. 948–951. [Google Scholar]
- Schulte, P.; Böcherer, G. Constant composition distribution matching. IEEE Trans. Inf. Theory 2015, 62, 430–434. [Google Scholar] [CrossRef]
- Ramabadran, T.V. A coding scheme for m-out-of-n codes. IEEE Trans. Commun. 1990, 38, 1156–1163. [Google Scholar] [CrossRef]
- Jones, C. An efficient coding system for long source sequences. IEEE Trans. Inf. Theory 1981, 27, 280–291. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Pasupathy, S. Optimal nonuniform signaling for Gaussian channels. IEEE Trans. Inf. Theory 2002, 39, 913–929. [Google Scholar] [CrossRef]






| Solutions | Waveforms | Dynamic Spectrum Sensing | Spectral Efficiency |
|---|---|---|---|
| SC HF [10] | Single Carrier | No | Low |
| SC-CR HF [12] | Single Carrier | Yes | Medium |
| OFDM HF [7] | C-OFDM | No | Medium |
| Our proposed | NC-OFDM | Yes | High |
| Parameter | Value |
|---|---|
| Frequency band | 16 MHz∼23 MHz |
| Maximum bandwidth | 1 MHz |
| Signal bandwidth | 500 KHz |
| Channel maximum delay | 70 us |
| Channel maximum doppler | 0.1 Hz |
| Subcarrier spacing | 39.0625 Hz |
| CP length | 6.4 ms |
| FFT/IFFT size | 25,600 |
| QAM modulation | 16QAM, 64QAM |
| System code rate | 2/3, 3/4 |
| LDPC code length | 64,800 |
| LDPC code rate | 4/5 |
| CCDM code rate | 11/15, 9/10 1 or 8/5, 37/20 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Bai, Y.; Hu, Z. Designand Implementation of a Novel Wideband HF Communication System Based on NC-OFDM and Probabilistic Shaping. Sensors 2025, 25, 5596. https://doi.org/10.3390/s25175596
Yang R, Bai Y, Hu Z. Designand Implementation of a Novel Wideband HF Communication System Based on NC-OFDM and Probabilistic Shaping. Sensors. 2025; 25(17):5596. https://doi.org/10.3390/s25175596
Chicago/Turabian StyleYang, Rifei, Yong Bai, and Zhuhua Hu. 2025. "Designand Implementation of a Novel Wideband HF Communication System Based on NC-OFDM and Probabilistic Shaping" Sensors 25, no. 17: 5596. https://doi.org/10.3390/s25175596
APA StyleYang, R., Bai, Y., & Hu, Z. (2025). Designand Implementation of a Novel Wideband HF Communication System Based on NC-OFDM and Probabilistic Shaping. Sensors, 25(17), 5596. https://doi.org/10.3390/s25175596






