PM2.5 Concentration Prediction: Ultrahigh Spatiotemporal Resolution Achieved by Combining Machine Learning and Low-Cost Sensors
Abstract
1. Introduction
2. Literature Review
2.1. Target Variable
2.2. Prediction Variables
2.3. Model Development and Construction
3. Materials and Methods
3.1. Study Area
3.2. LCS Monitoring Campaign
3.2.1. Monitoring Time Period
3.2.2. Monitoring Tools
3.3. Correction of Low-Cost Sensor Data
3.3.1. Data Used for Correction
3.3.2. Correction Method for Low-Cost Sensor Data
3.4. Prediction Variables
3.4.1. Land Cover Data
3.4.2. Road Network Data
3.4.3. Meteorological Data
3.5. Modeling Data Preprocessing Method
3.5.1. Preprocessing of Sampling Point LCS Data
3.5.2. Meteorological Data Preprocessing
3.5.3. Grid Center Coordinate Transformation
3.5.4. Calculating Land Use Raster Statistics Within the Buffer Zone and Matching Target Variables and Prediction Variables
3.6. Stacking Model and Explainable Methods
3.6.1. Modeling Approach
3.6.2. Evaluation of Model Performance
3.6.3. Explainability Method Based on SHAP
4. Results
4.1. Correction Results of Low-Cost Sensors
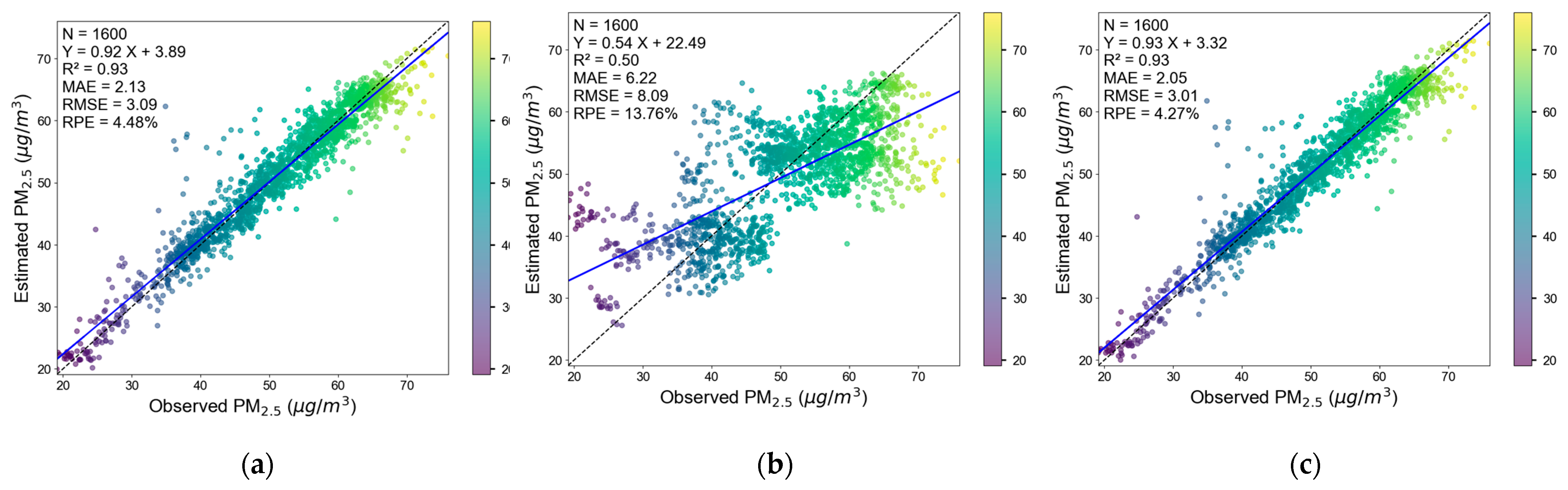
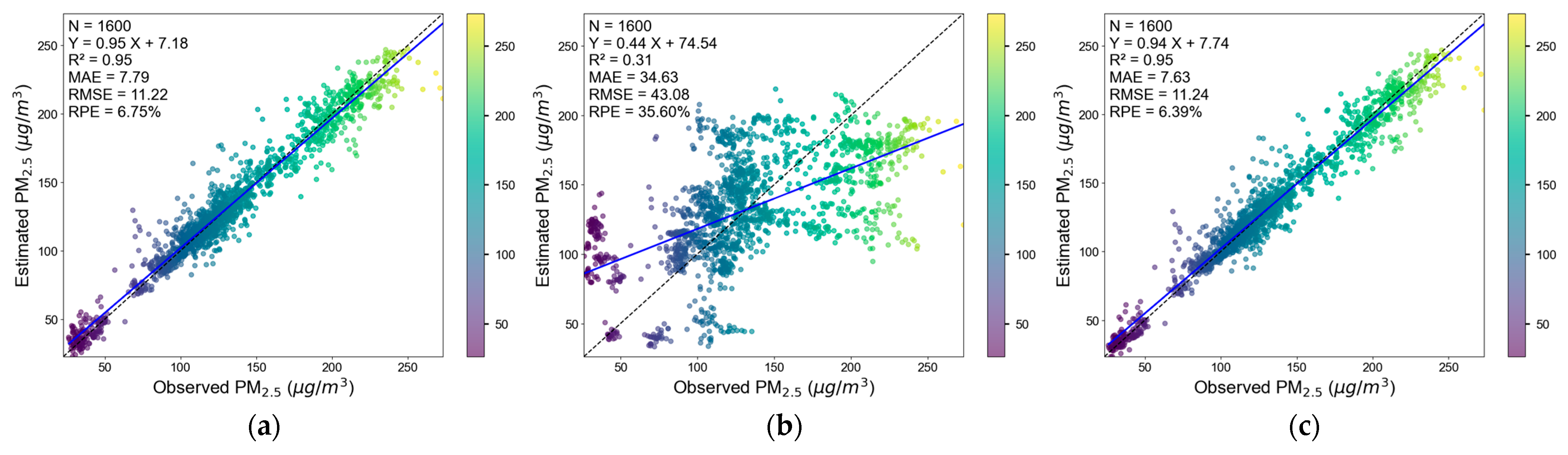
4.2. Stacking Model Evaluation Results
4.2.1. Evaluation Results of the Model Based on Corrected Low-Cost Sensor Data
4.2.2. Evaluation Results of the Model Based on Uncorrected Low-Cost Sensor Data
4.2.3. Independent Verification of Prediction Results and National Environmental Monitoring Station Data
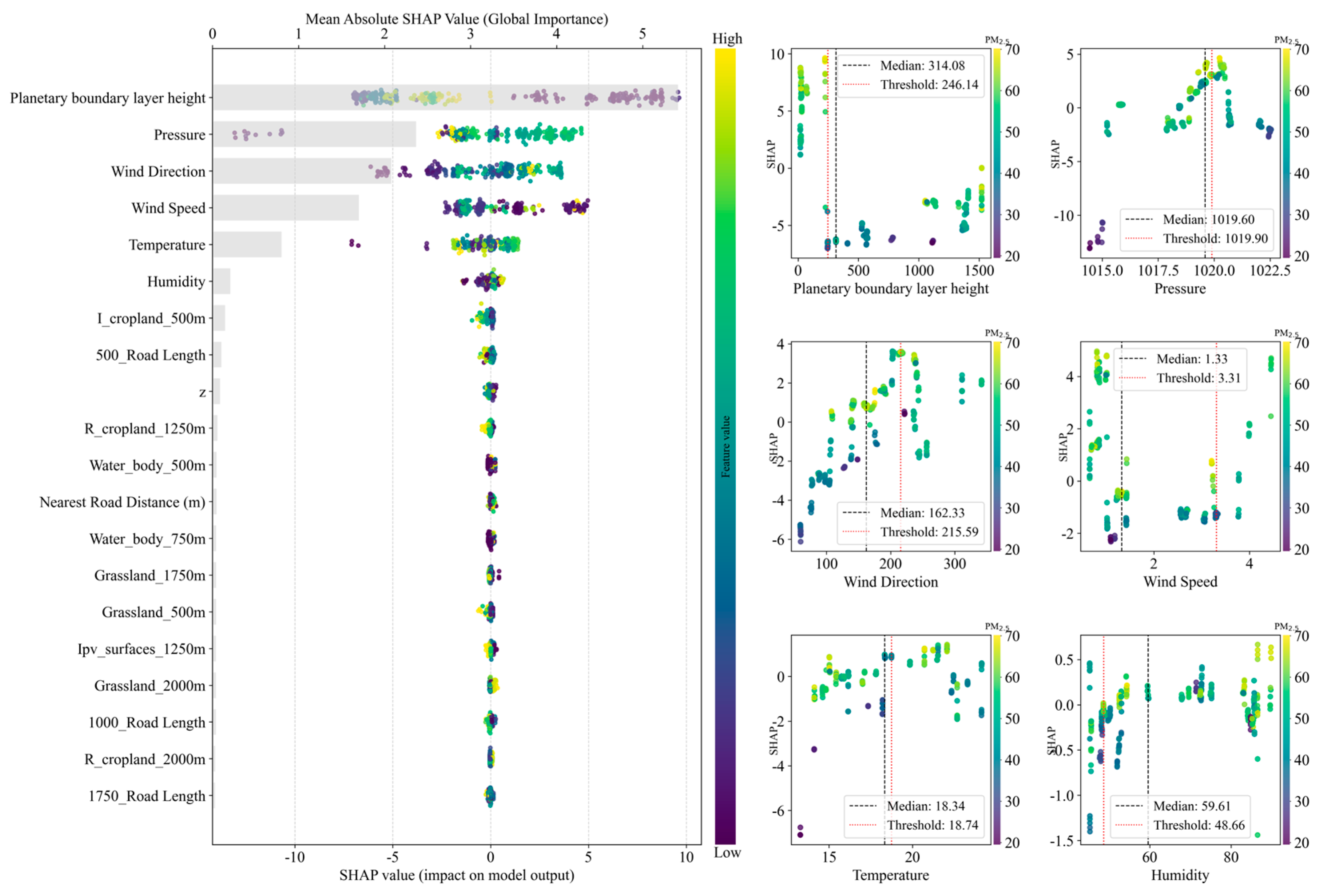
4.2.4. Feature Importance
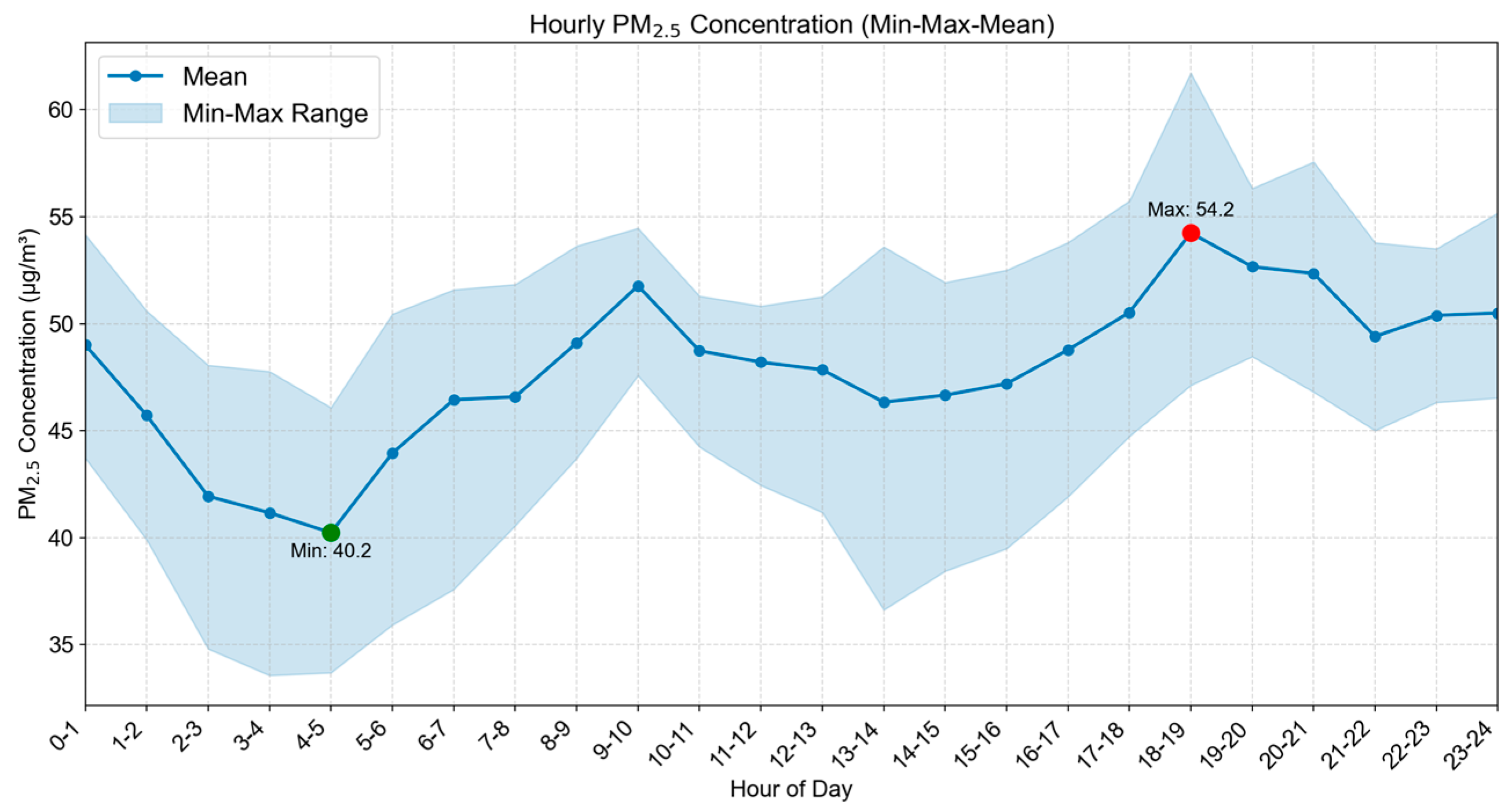
4.3. Spatiotemporal Analysis
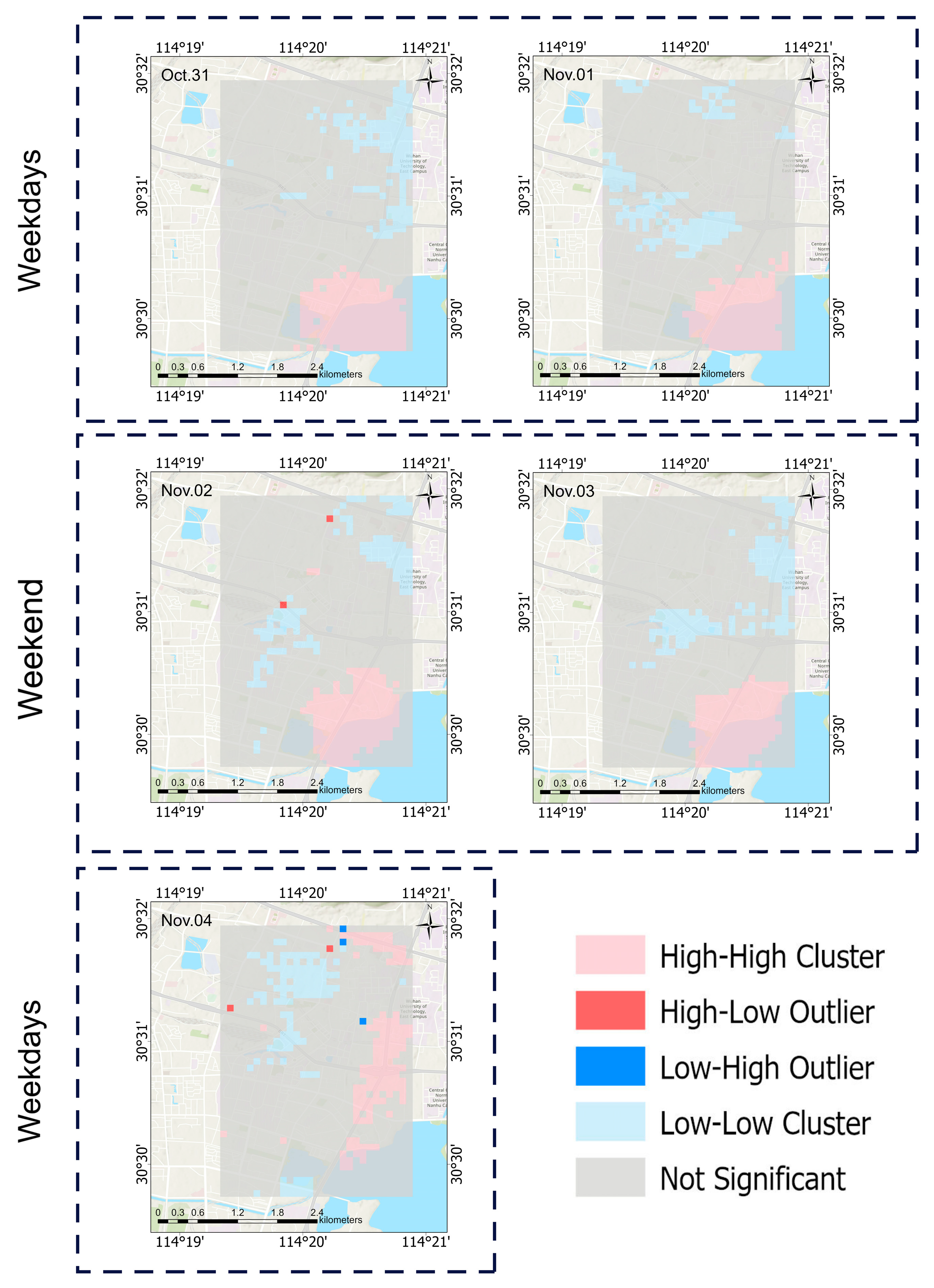
4.4. Spatial Autocorrelation Analysis
5. Discussion
5.1. Limitations
5.2. Future Works
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Enkhjargal, O.; Lamchin, M.; Chambers, J.; You, X.Y. Linear and Nonlinear Land Use Regression Approach for Modelling PM2.5 Concentration in Ulaanbaatar, Mongolia during Peak Hours. Remote Sens. 2023, 15, 1174. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating Ground-Level PM2.5 in China Using Satellite Remote Sensing. Environ. Sci. Technol. 2014, 48, 7197–7206. [Google Scholar] [CrossRef]
- Brokamp, C.; Jandarov, R.; Hossain, M.; Ryan, P. Predicting Daily Urban Fine Particulate Matter Concentrations Using a Random Forest Model. Environ. Sci. Technol. 2018, 52, 4173–4179. [Google Scholar] [CrossRef]
- Zou, B.; Chen, J.; Zhai, L.; Fang, X.; Zheng, Z. Satellite Based Mapping of Ground PM2.5 Concentration Using Generalized Additive Modeling. Remote Sens. 2017, 9, 1. [Google Scholar] [CrossRef]
- Feng, S.; Gao, D.; Liao, F.; Zhou, F.; Wang, X. The Health Effects of Ambient PM2.5 and Potential Mechanisms. Ecotoxicol. Environ. Saf. 2016, 128, 67–74. [Google Scholar] [CrossRef]
- Wu, J.; Xie, W.; Li, J. Application of Land Use Regression Model in the Study of Spatiotemporal Variation of Atmospheric Pollution. Environ. Sci. 2016, 37, 413–419. [Google Scholar]
- Cheng, L.X.; Tao, J.H.; Yu, C.; Zhang, Y.; Fan, M.; Wang, Y.P.; Chen, Y.L.; Zhu, L.L.; Gu, J.B.; Chen, L.F. Research on Remote Sensing Retrieval of Tropospheric NO2 Column Concentration Using GF-5 Satellite Atmospheric Trace Gas Differential Absorption Spectrometer. J. Remote Sens. 2021, 25, 2313–2325. [Google Scholar]
- Chao, C.-Y.; Zhang, H.; Hammer, M.; Zhan, Y.; Kenney, D.; Martin, R.V.; Biswas, P. Integrating Fixed Monitoring Systems with Low-Cost Sensors to Create High-Resolution Air Quality Maps for the Northern China Plain Region. ACS Earth Space Chem. 2021, 5, 2986–2997. [Google Scholar] [CrossRef]
- Lee, H.J. Benefits of High Resolution PM2.5 Prediction using Satellite MAIAC AOD and Land Use Regression for Exposure Assessment: California Examples. Environ. Sci. Technol. 2019, 53, 12151–12161. [Google Scholar] [CrossRef] [PubMed]
- Messier, K.P.; Chambliss, S.E.; Gani, S.; Alvarez, R.; Brauer, M.; Choi, J.J.; Hamburg, S.P.; Kerckhoffs, J.; LaFranchi, B.; Lunden, M.M.; et al. Mapping Air Pollution with Google Street View Cars: Efficient Approaches with Mobile Monitoring and Land Use Regression. Environ. Sci. Technol. 2018, 52, 11971–11979. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Song, Y. Land Use Quantile Regression Modeling of Fine Particulate Matter in Australia. Remote Sens. 2022, 14, 1370. [Google Scholar] [CrossRef]
- Minet, L.; Liu, R.; Valois, M.-F.; Xu, J.; Weichenthal, S.; Hatzopoulou, M. Development and Comparison of Air Pollution Exposure Surfaces Derived from On-Road Mobile Monitoring and Short-Term Stationary Sidewalk Measurements. Environ. Sci. Technol. 2018, 52, 3327–3334. [Google Scholar] [CrossRef] [PubMed]
- Geng, G.; Murray, N.L.; Chang, H.H.; Liu, Y. The Sensitivity of Satellite-Based PM2.5 Estimates to Its Inputs: Implications to Model Development in Data-Poor Regions. Environ. Int. 2018, 121, 550–560. [Google Scholar] [CrossRef]
- Zeng, X.; Ruan, F.; Peng, Y. Spatial Distribution of Health Effects of PM2.5 Pollution in China Based on Spatial Grid Scale. China Environ. Sci. 2019, 39, 2624–2632. [Google Scholar]
- Jain, S.; Presto, A.A.; Zimmerman, N. Spatial Modeling of Daily PM2.5, NO2, and CO Concentrations Measured by a Low-Cost Sensor Network: Comparison of Linear, Machine Learning, and Hybrid Land Use Models. Environ. Sci. Technol. 2021, 55, 8459–8468. [Google Scholar] [CrossRef] [PubMed]
- Bi, J.; Burnham, D.; Zuidema, C.; Schumacher, C.; Gassett, A.J.; Szpiro, A.A.; Kaufman, J.D.; Sheppard, L. Evaluating Low-Cost Monitoring Designs for PM2.5 Exposure Assessment with a Spatiotemporal Modeling Approach. Environ. Pollut. 2024, 343, 123227. [Google Scholar] [CrossRef]
- Huang, Y. Research on Spatiotemporal Characteristics and Functional Data Analysis of PM2.5: Based on Data from 9 Monitoring Stations in Nanchang City. Master’s Thesis, Jiangxi University of Finance and Economics, Nanchang, China, 2022. [Google Scholar]
- Zhang, S.; Chen, P.; Zhang, Y.; Zhu, C.; Zhang, C.; Lu, J.; Wu, M.; Yang, X. Estimating Hourly Surface PM2.5 Concentrations with Full Spatiotemporal Coverage in China Using Himawari-8/9 AOD and a Two-Stage Model. Atmos. Pollut. Res. 2025, 16, 102519. [Google Scholar] [CrossRef]
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS Aerosol Products over Land and Ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ‘16), New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Shikhovtsev, A.Y.; Kovadlo, P.G.; Kiselev, A.V.; Eselevich, M.V.; Lukin, V.P. Application of Neural Networks to Estimation and Prediction of Seeing at the Large Solar Telescope Site. Publ. Astron. Soc. Pac. 2023, 135, 014503. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, X.; Qing, C.; Su, C.; Yang, Q.; Wang, Z. Blind Restoration of Images Distorted by Atmospheric Turbulence Based on Deep Transfer Learning. Photonics 2022, 9, 582. [Google Scholar] [CrossRef]
- Yang, Q.; Kim, J.; Cho, Y.; Lee, W.-J.; Lee, D.-W.; Yuan, Q.; Wang, F.; Zhou, C.; Zhang, X.; Xiao, X.; et al. A Synchronized Estimation of Hourly Surface Concentrations of Six Criteria Air Pollutants with GEMS Data. npj Clim. Atmos. Sci. 2023, 6, 94. [Google Scholar] [CrossRef]
- Xu, S.; Zou, B.; Xiong, Y.; Wan, N.; Feng, H.; Hu, C.; Lin, Y. High spatiotemporal resolution mapping of PM2.5 concentrations under a pollution scene assumption. J. Clean. Prod. 2021, 326, 129409. [Google Scholar] [CrossRef]
- Yang, N.; Shi, H.; Tang, H.; Yang, X. Geographical and Temporal Encoding for Improving the Estimation of PM2.5 Concentrations in China Using End-to-End Gradient Boosting. Remote Sens. Environ. 2022, 269, 112828. [Google Scholar] [CrossRef]
- Benaida, M.; Abnane, I.; Idri, A. Stacked ensembles for one-step and multi-step ahead BGL forecasting. Biomed. Signal Process. Control 2026, 112, 108536. [Google Scholar] [CrossRef]
- Chen, M.; Xin, J.; Tang, Q.; Hu, T.; Zhou, Y.; Zhou, J. Explainable machine learning model for load-deformation correlation in long-span suspension bridges using XGBoost-SHAP. Dev. Built Environ. 2024, 20, 100569. [Google Scholar] [CrossRef]
- Qi, M.; Hankey, S. Using Street View Imagery to Predict Street-Level Particulate Air Pollution. Environ. Sci. Technol. 2021, 55, 2173–2181. [Google Scholar] [CrossRef]
- Qi, M.; Dixit, K.; Marshall, J.D.; Zhang, W.; Hankey, S. National Land Use Regression Model for NO2 Using Street View Imagery and Satellite Observations. Environ. Sci. Technol. 2022, 56, 12785–12795. [Google Scholar] [CrossRef] [PubMed]








| Monitoring Time | Date | ||||
|---|---|---|---|---|---|
| 10/31/2024 | 11/1/2024 | 11/2/2024 | 11/3/2024 | 11/4/2024 | |
| 6am–7am | √ | √ | √ | √ | |
| 7am–8am | √ | √ | √ | √ | |
| 8am–9am | √ | √ | √ | √ | |
| 9am–10am | √ | ||||
| 11am–12am | √ | √ | |||
| 12am–1pm | √ | √ | |||
| 1pm–2pm | √ | √ | |||
| 2pm–3pm | √ | ||||
| 4pm–5pm | √ | √ | |||
| 5pm–6pm | √ | √ | |||
| 6pm–7pm | √ | √ | |||
| 7pm–8pm | √ | ||||
| 9pm–10pm | √ | √ | |||
| 10pm–11pm | √ | √ | |||
| Equipment Number | Effective Monitoring Hours (h) | Co-Location Start Time | Co-Location End Time |
|---|---|---|---|
| 1 | 141 | 9/10/2024 | 10/30/2024 |
| 2 | 134 | 9/10/2024 | 10/30/2024 |
| 3 | 144 | 9/10/2024 | 10/30/2024 |
| 4 | 167 | 9/10/2024 | 10/30/2024 |
| Type Number | Variable Name |
|---|---|
| 0 | Filled value |
| 10 | Rainfed cropland |
| 11 | Herbaceous cover cropland |
| 20 | Irrigated cropland |
| 51 | Open evergreen broadleaved forest |
| 52 | Closed evergreen broadleaved forest |
| 61 | Open deciduous broadleaved forest (0.15 < fc < 0.4) |
| 62 | Closed deciduous broadleaved forest (fc > 0.4) |
| 71 | Open evergreen needle-leaved forest (0.15 < fc < 0.4) |
| 72 | Closed evergreen needle-leaved forest (fc > 0.4) |
| 121 | Evergreen shrubland |
| 130 | Grassland |
| 181 | Swamp |
| 182 | Marsh |
| 183 | Flooded flat |
| 190 | Impervious surfaces |
| 200 | Bare areas |
| 210 | Water body |
| Variable Name | Type of Data and Source | Predictor Variable Description | Unit | Buffer Zone Radius (m) |
|---|---|---|---|---|
| Filled value_radius m | Land use data (GLC_FCS30 fine land cover data, 2022) | Filled value | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 |
| R_cropland_radius m | Rainfed cropland | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Hc_cropland_radius m | Herbaceous cover cropland | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| I_cropland_radius m | Irrigated cropland | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Oeb_forest_radius m | Open evergreen broadleaved forest | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Ceb_forest_radius m | Closed evergreen broadleaved forest | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Odb_forest_radius m | Open deciduous broadleaved forest | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Cdb_forest_radius m | Closed deciduous broadleaved forest | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Oen_forest_radius m | Open evergreen needle-leaved forest | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Cen_forest_radius m | Closed evergreen needle-leaved forest | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| E_shrubland_radius m | Evergreen shrubland | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Grassland_radius m | Grassland | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Swamp_radius m | Swamp | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Marsh_radius m | Marsh | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Fld_flat_radius m | Flooded flat | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Ipv_surfaces_radius m | Impervious surfaces | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Bare areas_radius m | Bare areas | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Water body_radius m | Water body | 1 | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| x | Geospatial variables (Cartesian coordinates converted from latitude and longitude) | gx | 1 | NA |
| y | gy | 1 | NA | |
| z | gz | 1 | NA | |
| Radius_Road Length | Road network data (Open Street Map, 2024) | The length of all major roads within the buffer zone of the specified radius | m | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 |
| Nearest Road Distance (m) | The minimum distance from the center of the raster corresponding to the buffer zone to the nearest major road | m | 50, 250, 500, 750, 1000, 1250, 1500, 1750, 2000 | |
| Temperature | Meteorological station data (Environmental meteorological data service platform, China ground meteorological station hourly data standard version) | The temperature monitored by meteorological stations | ℃ | NA |
| Pressure | The air pressure monitored by meteorological stations | Pa | NA | |
| Wind Speed | 2-min average wind speed | m·s−1 | NA | |
| Wind Direction | 2-min average wind direction | degree | NA | |
| Humidity | The relative humidity monitored by meteorological stations | % | NA | |
| Planetary boundary layer height | Reanalyzing meteorological data (ERA5 reanalysis dataset, ERA: European Centre for Medium-Range Weather Forecast Reanalysis) | Planetary boundary layer height | kilometer | NA |
| Low-Cost Sensors | Equipment Number | Correction Equation | Adjusted R2 | RMSE | MRE |
|---|---|---|---|---|---|
| SDL307 | 1 | Corrected PM2.5 = PM2.5 × 0.265 + temperature × 0.268 − relative humidity × 0.1 + 6.378 | 0.927 | 4.129 | 10.98% |
| 2 | Corrected PM2.5 = PM2.5 × 0.315 + temperature × 0.173 − relative humidity × 0.06 + 5.487 | 0.922 | 4.377 | 12.31% | |
| 3 | Corrected PM2.5 = PM2.5 × 0.229 − relative humidity × 0.159 + 17.48 | 0.926 | 4.728 | 10.69% | |
| 4 | Corrected PM2.5 = PM2.5 × 0.458 − temperature × 0.156 − relative humidity × 0.12 + 15.366 | 0.908 | 4.904 | 6.85% |
| Low-Cost Sensors | Equipment Number | PM2.5 | Temperature | Relative Humidity | Constant | ||||
|---|---|---|---|---|---|---|---|---|---|
| Significance | VIF | Significance | VIF | Significance | VIF | Significance | VIF | ||
| SDL307 | 1 | <0.001 | 1.153 | <0.001 | 1.429 | <0.001 | 1.267 | 0.043 | <0.001 |
| 2 | <0.001 | 1.104 | 0.018 | 1.367 | 0.046 | 1.254 | 0.101 | <0.001 | |
| 3 | <0.001 | 1.057 | - | - | <0.001 | 1.057 | <0.001 | <0.001 | |
| 4 | <0.001 | 1.065 | 0.04 | 1.338 | <0.001 | 1.345 | <0.001 | <0.001 | |
| Low-Cost Sensors | Equipment Number | Min (μg/m3) | Max (μg/m3) | Mean (μg/m3) |
|---|---|---|---|---|
| SDL307 after correction | 1 | 5.94 | 272.72 | 58.06 |
| 2 | 4.86 | 220.08 | 51.46 | |
| 3 | 5.26 | 282.35 | 81.20 | |
| 4 | 2.84 | 139.32 | 46.39 | |
| SDL307 before correction | 1 | 5.72 | 73.08 | 21.41 |
| 2 | 5.93 | 71.61 | 21.66 | |
| 3 | 6.04 | 66.99 | 25.03 | |
| 4 | 4.42 | 65.02 | 24.40 | |
| National Environmental Station Instruments | - | 1.00 | 77.00 | 23.21 |
| Min | Max | Mean | |
|---|---|---|---|
| PM2.5 Concentration (μg/m3) | 43.1004 | 52.7418 | 47.9068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Chen, J.; You, R.; He, Q. PM2.5 Concentration Prediction: Ultrahigh Spatiotemporal Resolution Achieved by Combining Machine Learning and Low-Cost Sensors. Sensors 2025, 25, 5527. https://doi.org/10.3390/s25175527
Li J, Chen J, You R, He Q. PM2.5 Concentration Prediction: Ultrahigh Spatiotemporal Resolution Achieved by Combining Machine Learning and Low-Cost Sensors. Sensors. 2025; 25(17):5527. https://doi.org/10.3390/s25175527
Chicago/Turabian StyleLi, Junfeng, Jiaqi Chen, Ran You, and Qingqing He. 2025. "PM2.5 Concentration Prediction: Ultrahigh Spatiotemporal Resolution Achieved by Combining Machine Learning and Low-Cost Sensors" Sensors 25, no. 17: 5527. https://doi.org/10.3390/s25175527
APA StyleLi, J., Chen, J., You, R., & He, Q. (2025). PM2.5 Concentration Prediction: Ultrahigh Spatiotemporal Resolution Achieved by Combining Machine Learning and Low-Cost Sensors. Sensors, 25(17), 5527. https://doi.org/10.3390/s25175527








