Utilization of BiLSTM- and GAN-Based Deep Neural Networks for Automated Power Amplifier Optimization over X-Parameters
Abstract
1. Introduction
2. Proposed Optimization Method Based on DNNs
| Algorithm 1 Proposed automated methodology based on BiLSTM-based DNNs and GAN for modeling and sizing PA |
| 1: Combination of EDA tool (here, Keysight ADS) with numerical analyzer (here, Matlab) for co-design simulations; |
| 2: Extraction of incident port waves through independent TCAD physical simulator leading to provide the X-parameter data of employed HEMT device; |
| 3: Training the regression BiLSTM-based DNN through X-parameters; |
| 4: Implementation of multi-objective optimizations leading to predict the optimal hyperparameters of network; |
| 5: GAN network training for predicting the optimal gate and drain impedances of employed HEMT device that these impedances will be inserted to the SRFT method for generating MNs of PA; |
| 6: Construction of classification BiLSTM-based DNN for predicting the optimal PA configuration that is modeled through the achieved optimal impedances in the previous step; |
| 7: Training the regression BiLSTM-based DNN for estimating the optimal design parameters leading to obtain the targeted specifications. |
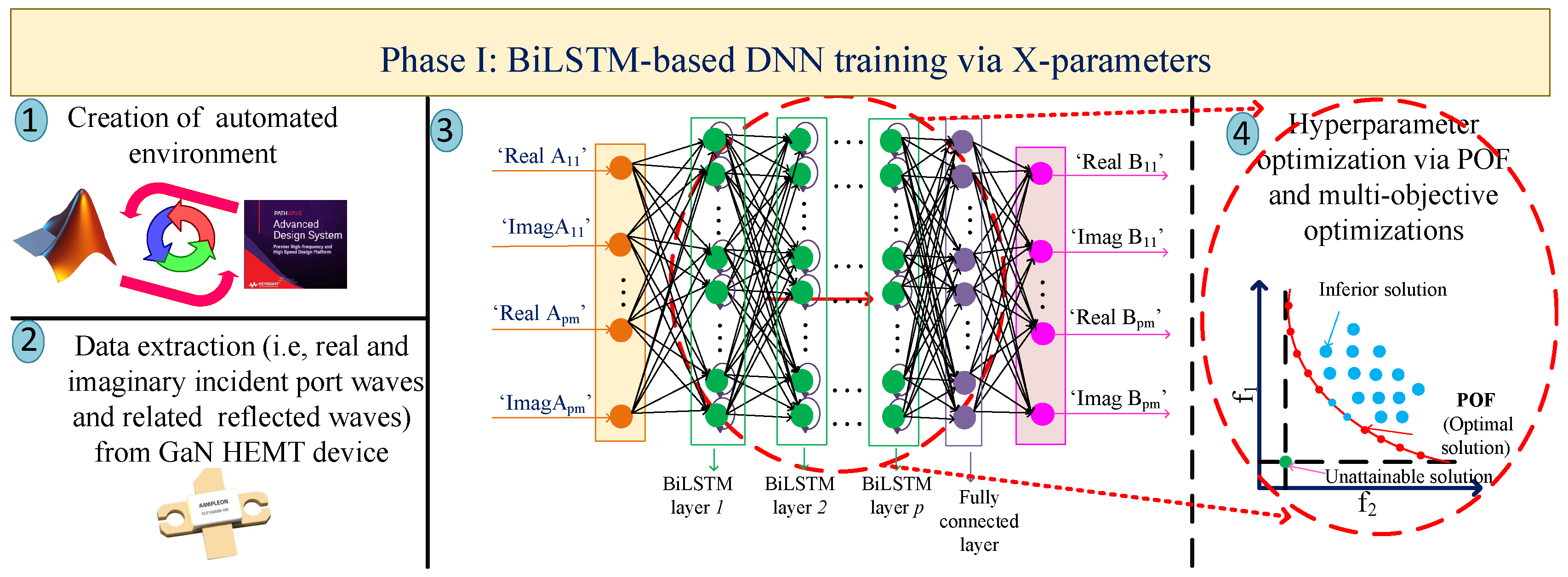
2.1. Phase I: BiLSTM-Based DNN Construction with the Help of X-Parameters
2.2. Phase II: GAN Training for Obtaining the Optimal Impedances of the HEMT Device
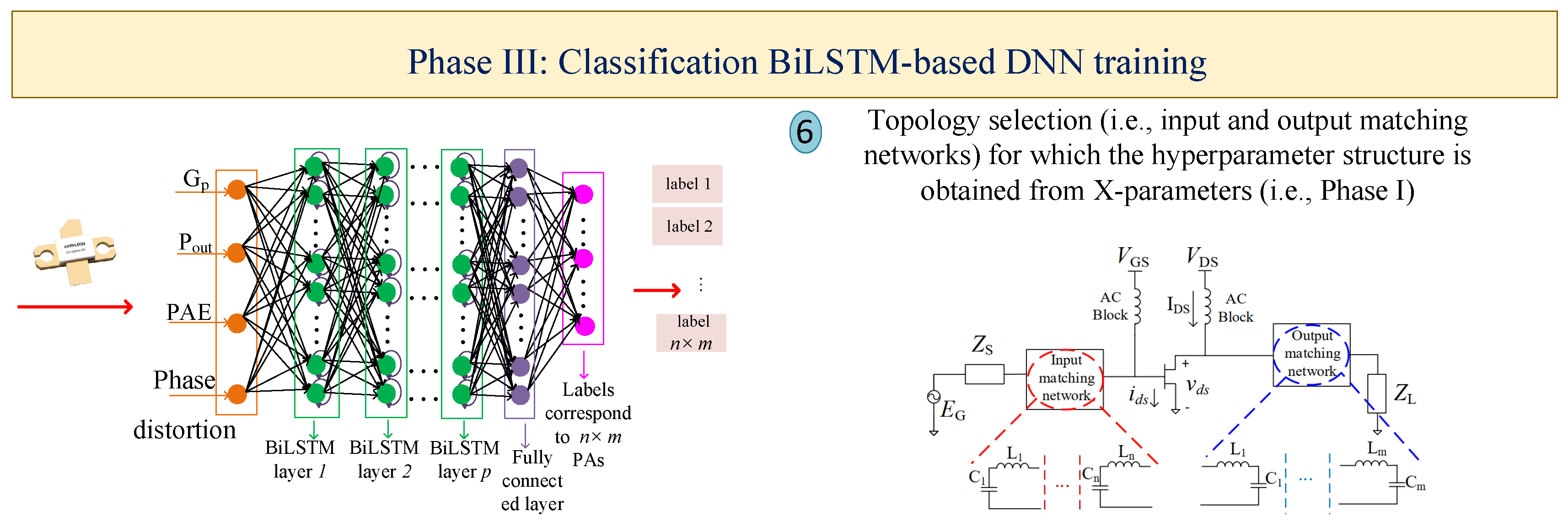
2.3. Phase III: Classification BiLSTM-Based DNN for Obtaining the Optimal Configuration
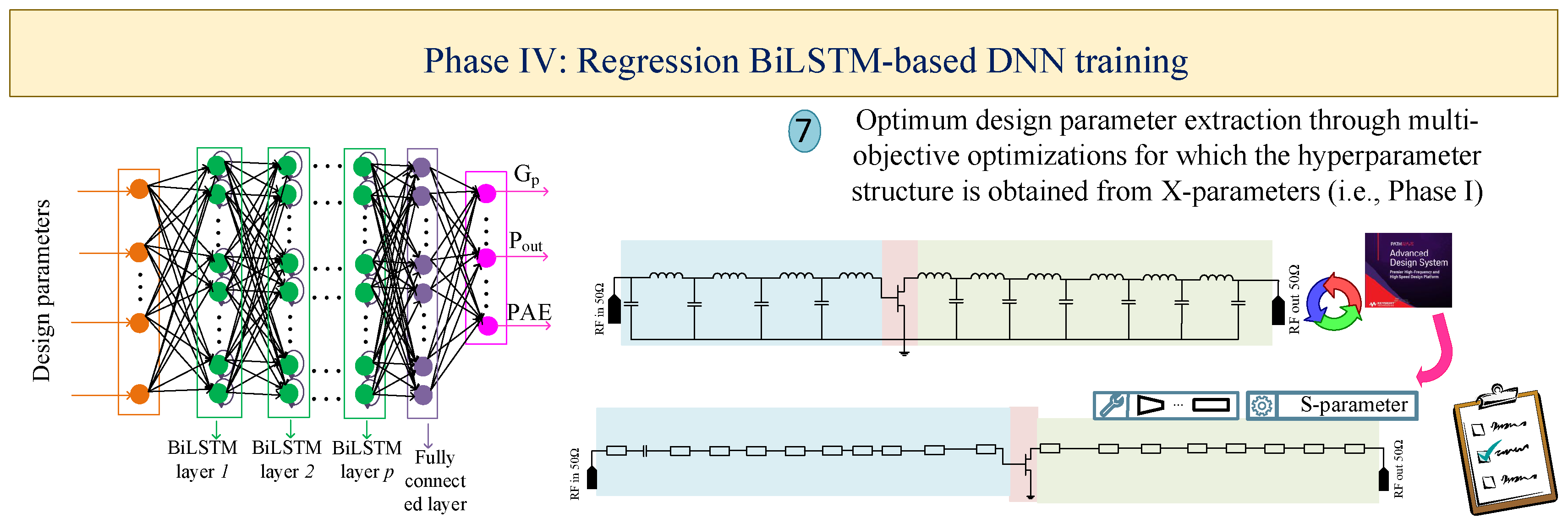
2.4. Phase IV: Regression BiLSTM-Based DNN for Obtaining the Optimal Geometric Parameters
3. Practical Execution of Various DNNs
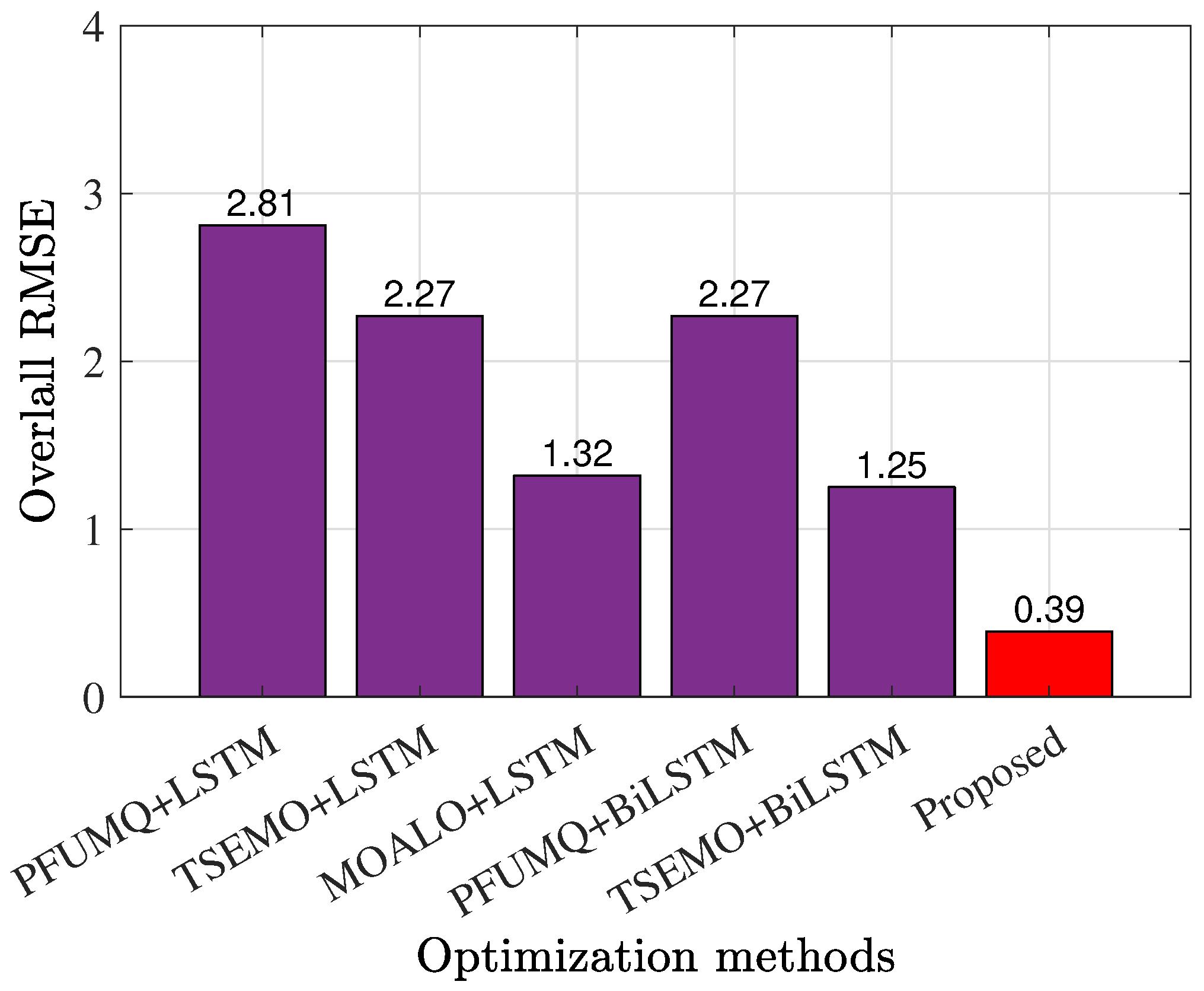
4. Simulation Results of Optimized PA Through Automated Proposed Methodology
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Samira Delwar, T.; Siddique, A.; Aras, U.; Lee, Y.; Ryu, J.Y. A μ-GA Oriented ANN-Driven: Parameter Extraction of 5G CMOS Power Amplifier. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2024, 32, 1569–1577. [Google Scholar] [CrossRef]
- Xu, Z.; Zhai, J.; Yu, Z.; Zhou, J.; Zhang, N.; Yu, C.; Hao, Z.C. A Grid-Based Competitive Mixture of Experts Approach for Partition Optimization of the Multidimensional Magnitude-Selective Affine-Function Behavioral Model. IEEE Trans. Microwave Theory Tech. 2025, 73, 4442–4454. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Q.; Gao, K.; Liu, X.; Chen, W.; Feng, H.; Feng, Z.; Ghannouchi, F.M. A Novel Digital Predistortion Coefficients Prediction Technique for Dynamic PA Nonlinearities Using Artificial Neural Networks. IEEE Microwave Wireless Tech. Lett. 2024, 34, 1115–1118. [Google Scholar] [CrossRef]
- Chang, Z.; Hu, X.; Li, B.; Yao, Q.; Yao, Y.; Wang, W.; Ghannouchi, F.M. A Residual Selectable Modeling Method Based on Deep Neural Network for Power Amplifiers With Multiple States. IEEE Microwave Wireless Tech. Lett. 2024, 34, 1043–1046. [Google Scholar] [CrossRef]
- Amini, A.R.; Boumaiza, S. A Time-Domain Multi-Tone Distortion Model for Effective Design of High Power Amplifiers. IEEE Access 2022, 10, 23152–23166. [Google Scholar] [CrossRef]
- Javid-Hosseini, S.H.; Ghazanfarianpoor, P.; Nayyeri, V.; Colantonio, P. A Unified Neural Network-Based Approach to Nonlinear Modeling and Digital Predistortion of RF Power Amplifier. IEEE Trans. Microwave Theory Tech. 2024, 72, 5031–5038. [Google Scholar] [CrossRef]
- Wu, H.; Chen, W.; Liu, X.; Feng, Z.; Ghannouchi, F.M. A Uniform Neural Network Digital Predistortion Model of RF Power Amplifiers for Scalable Applications. IEEE Trans. Microwave Theory Tech. 2022, 70, 4885–4899. [Google Scholar] [CrossRef]
- Fischer-Bühner, A.; Anttila, L.; Turunen, M.; Dev Gomony, M.; Valkama, M. Augmented Phase-Normalized Recurrent Neural Network for RF Power Amplifier Linearization. IEEE Trans. Microwave Theory Tech. 2025, 73, 412–422. [Google Scholar] [CrossRef]
- Tang, Y.; Peng, J.; He, S.; You, F.; Wang, X.; Zhong, T.; Bian, Y.; Pang, B. Bandwidth-Scalable Digital Predistortion Using Multigroup Aggregation Neural Network for PAs. IEEE Microwave Wireless Tech. Lett. 2024, 34, 1387–1390. [Google Scholar] [CrossRef]
- Zhou, H.; Chang, H.; Widén, D.; Fornstedt, L.; Melin, G.; Fager, C. AI-Assisted Deep-Learning-Based Design of High-Efficiency Class F Power Amplifiers. IEEE Microwave Wireless Tech. Lett. 2025, 35, 690–693. [Google Scholar] [CrossRef]
- Jaraut, P.; Abdelhafiz, A.; Chenini, H.; Hu, X.; Helaoui, M.; Rawat, M.; Chen, W.; Boulejfen, N.; Ghannouchi, F.M. Augmented Convolutional Neural Network for Behavioral Modeling and Digital Predistortion of Concurrent Multiband Power Amplifiers. IEEE Trans. Microwave Theory Tech. 2021, 69, 4142–4156. [Google Scholar] [CrossRef]
- Ren, J.; Song, A.; Xu, Z.; Hu, H. An Integrated Scheme of FIR and Augmented Real-Valued Time-Delay Neural Network of Harmonic Cancellation Digital Predistortion Model for High-Frequency Power Amplifier. IEEE Microwave Wireless Tech. Lett. 2024, 34, 951–954. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, X.; Liu, T.; Li, X.; Wang, W.; Ghannouchi, F.M. Attention-Based Deep Neural Network Behavioral Model for Wideband Wireless Power Amplifiers. IEEE Microwave Wireless Compon. Lett. 2020, 30, 82–85. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, H.; Xin, J.; Li, L.; Ye, Z.; Wang, Y. Deep Neural Networks-Based Direct-Current Operation Prediction and Circuit Migration Design. Electronics 2023, 12, 2780. [Google Scholar] [CrossRef]
- Shobayo, O.; Saatchi, R. Developments in Deep Learning Artificial Neural Network Techniques for Medical Image Analysis and Interpretation. Diagnostics 2025, 15, 1072. [Google Scholar] [CrossRef]
- Li, R.; Yao, Z.; Wang, Y.; Lin, Y.; Ohtsuki, T.; Gui, G.; Sari, H. Behavioral Modeling of Power Amplifiers Leveraging Multi-Channel Convolutional Long Short-Term Deep Neural Network. IEEE Trans. Veh. Technol. 2025, 1–5. [Google Scholar] [CrossRef]
- Watanabe, T.; Ohseki, T.; Kanno, I. Hardware-efficient Neural Network Digital Predistortion for Terahertz Power Amplifiers Using DeepShift and Pruning. IEEE Access 2025, 119772–119788. [Google Scholar] [CrossRef]
- Wang, J.; Han, R.; Zhang, Q.; Jiang, C.; Chang, H.; Zhou, K.; Liu, F. Learnable Edge-Located Activation Neural Network for Digital Predistortion of RF Power Amplifiers. IEEE Trans. Microwave Theory Tech. 2025, 1–14. [Google Scholar] [CrossRef]
- Zhou, M.; Li, S.; Yuan, P.; Zhang, J.; Zhang, J.; Yang, L.; Zhu, H. GNN-Assisted Deep Reinforcement Learning for Cell-Free Massive MIMO Systems with Nonlinear Power Amplifiers and Low-Resolution ADCs. IEEE Internet Things J. 2025, 12, 33041–33055. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, J.; Chen, X.; Guo, Y. An ANN-Based GaN HEMT Large-Signal Model With High Near-Threshold Accuracy and Its Application in Class-AB MMIC PA Design. IEEE Trans. Microwave Theory Tech. 2025, 1–13. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Wei, Y.; Meng, S.; Yang, T.; Wang, C. Inverse Design of Broadband Optimal Power Amplifiers Enabled by Deep Learning. IEEE Trans. Microwave Theory Tech. 2025, 1–15. [Google Scholar] [CrossRef]
- Kouhalvandi, L.; Matekovits, L. Hyperparameter Optimization of Long Short-Term Memory-Based Forecasting DNN for Antenna Modeling Through Stochastic Methods. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 725–729. [Google Scholar] [CrossRef]
- Wu, M.; Qu, Y.; Guo, J.; Yu, C.; Cai, J. Design of Doherty Power Amplifier Using Load-pull X-Parameters. In Proceedings of the 2021 IEEE MTT-S International Wireless Symposium (IWS), Nanjing, China, 23–26 May 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Kouhalvandi, L.; Catoggio, E.; Guerrieri, S.D. Synergic Exploitation of TCAD and Deep Neural Networks for Nonlinear FinFET Modeling. In Proceedings of the IEEE EUROCON 2023—20th International Conference on Smart Technologies, Turin, Italy, 6–8 July 2023; pp. 542–546. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, J.; Liu, J.; Yan, F.; Chen, C.; Yang, J. Multi-Objective Coverage Optimization for 3D Heterogeneous Wireless Sensor Networks. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2025, 1–1. [Google Scholar] [CrossRef]
- Li, Y.; Wu, X.; Gong, W.; Xu, M.; Wang, Y.; Gu, Q. Evolutionary Competitive Multiobjective Multitasking: One-Pass Optimization of Heterogeneous Pareto Solutions. IEEE Trans. Evol. Comput. 2024, 1–1. [Google Scholar] [CrossRef]
- Wang, H.; Rodriguez-Fernandez, A.E.; Uribe, L.; Deutz, A.; Cortés-Piña, O.; Schütze, O. A Newton Method for Hausdorff Approximations of the Pareto Front Within Multi-objective Evolutionary Algorithms. IEEE Trans. Evol. Comput. 2024, 1–1. [Google Scholar] [CrossRef]
- Yarman, S. Design of Ultra Wideband Power Transfer Networks; Wiley: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Song, H.; Wang, Z.; Zhang, X. Defending Against Adversarial Attack Through Generative Adversarial Networks. IEEE Signal Process Lett. 2025, 32, 1730–1734. [Google Scholar] [CrossRef]
- Kouhalvandi, L.; Ceylan, O.; Ozoguz, S. Multi-objective Efficiency and Phase Distortion Optimizations for Automated Design of Power Amplifiers Through Deep Neural Networks. In Proceedings of the 2021 IEEE MTT-S International Microwave Symposium (IMS), Atlanta, GA, USA, 7–25 June 2021; pp. 233–236. [Google Scholar] [CrossRef]
- Ohiri, U.; Guo, X.T. Atomistic Materials and TCAD Device Modeling and Simulation of Ultrawide Bandgap (UWBG) Materials and UWBG Heterointerfaces. In Proceedings of the 2024 IEEE Nanotechnology Materials and Devices Conference (NMDC), Salt Lake City, UT, USA, 21–24 October 2024; pp. 5–8. [Google Scholar] [CrossRef]
- Dolatnezhadsomarin, A.; Khorram, E.; Yousefikhoshbakht, M. Numerical algorithms for generating an almost even approximation of the Pareto front in nonlinear multi-objective optimization problems. Appl. Soft Comput. 2024, 165, 112001. [Google Scholar] [CrossRef]
- Karahan, E.A.; Liu, Z.; Sengupta, K. Deep-Learning-Based Inverse-Designed Millimeter-Wave Passives and Power Amplifiers. IEEE J. Solid-State Circuits 2023, 58, 3074–3088. [Google Scholar] [CrossRef]
- Mendes, L.; Silva, J.; Lourenço, N.; Vaz, J.C.; Martins, R.; Passos, F. Fully Automatically Synthesized mm-Wave Low-Noise Amplifiers for 5G/6G Applications. IEEE Trans. Microwave Theory Tech. 2025, 73, 4828–4841. [Google Scholar] [CrossRef]
- Liu, B.; Xue, L.; Fan, H.; Ding, Y.; Imran, M.; Wu, T. An Efficient and General Automated Power Amplifier Design Method Based on Surrogate Model Assisted Hybrid Optimization Technique. IEEE Trans. Microwave Theory Tech. 2025, 73, 926–937. [Google Scholar] [CrossRef]
- Hang Chai, S.; Chae, H.; Yu, H.; Pan, D.Z.; Li, S. A D-Band InP Power Amplifier Featuring Fully AI-Generated Passive Networks. IEEE Microwave Wireless Tech. Lett. 2025, 35, 824–827. [Google Scholar] [CrossRef]
- Wei, Y.C.; Li, J.H.; Cai, D.Y.; Meng, F.Y.; Kim, N.Y.; Wu, Y.L.; Wang, C. A Flexible Automated Design Method for Broadband Matching Networks in Power Amplifiers. IEEE Trans. Microwave Theory Tech. 2025, 73, 4779–4790. [Google Scholar] [CrossRef]
- Ling, R.; Zhang, Z.; Xuan, X. Dual-Frequency Power Amplifiers’ Design Based on Improved Multiobjective Particle Swarm Optimization Algorithm. IEEE Microw. Wirel. Technol. Lett. 2025, 1–4. [Google Scholar] [CrossRef]

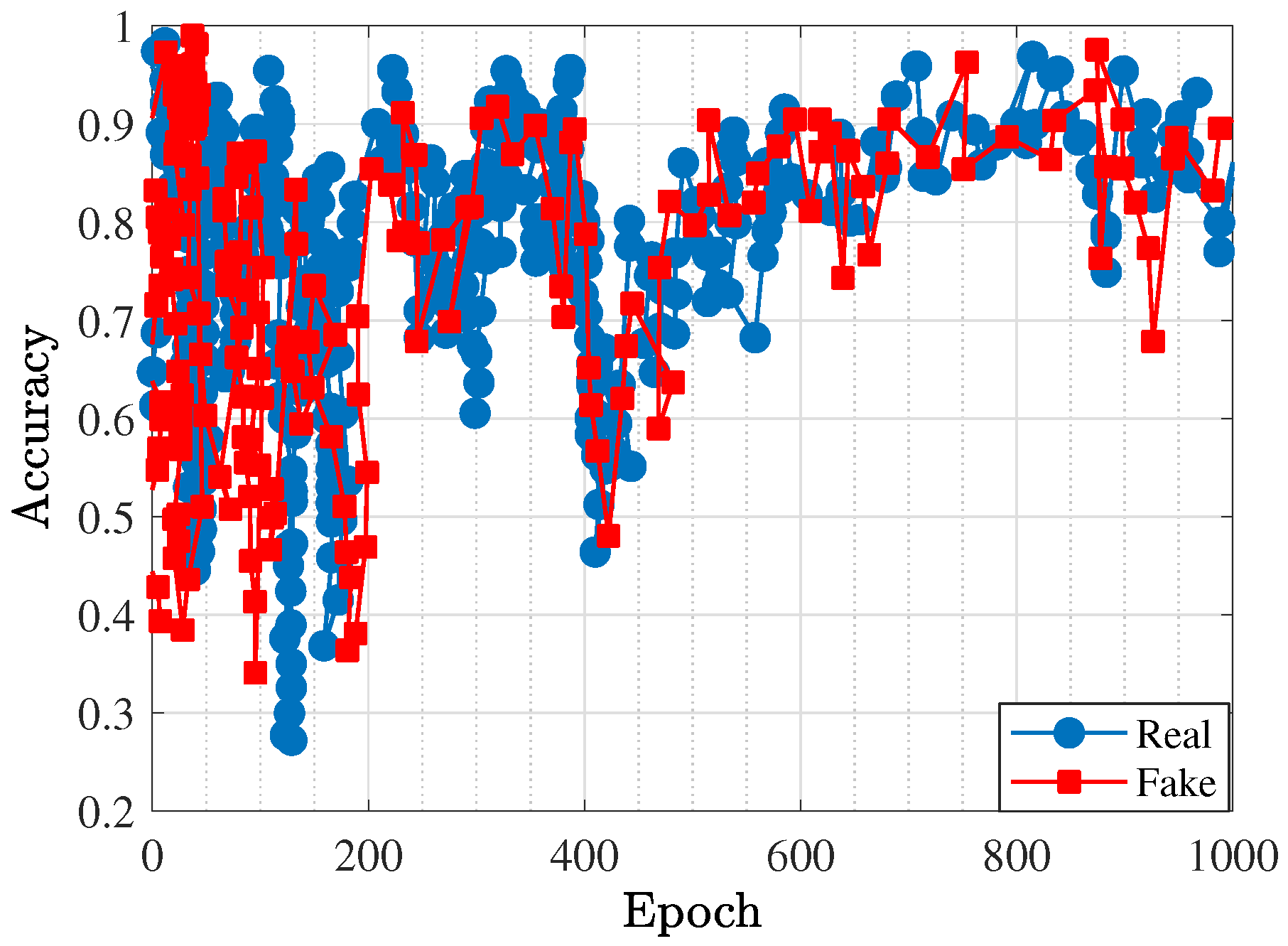

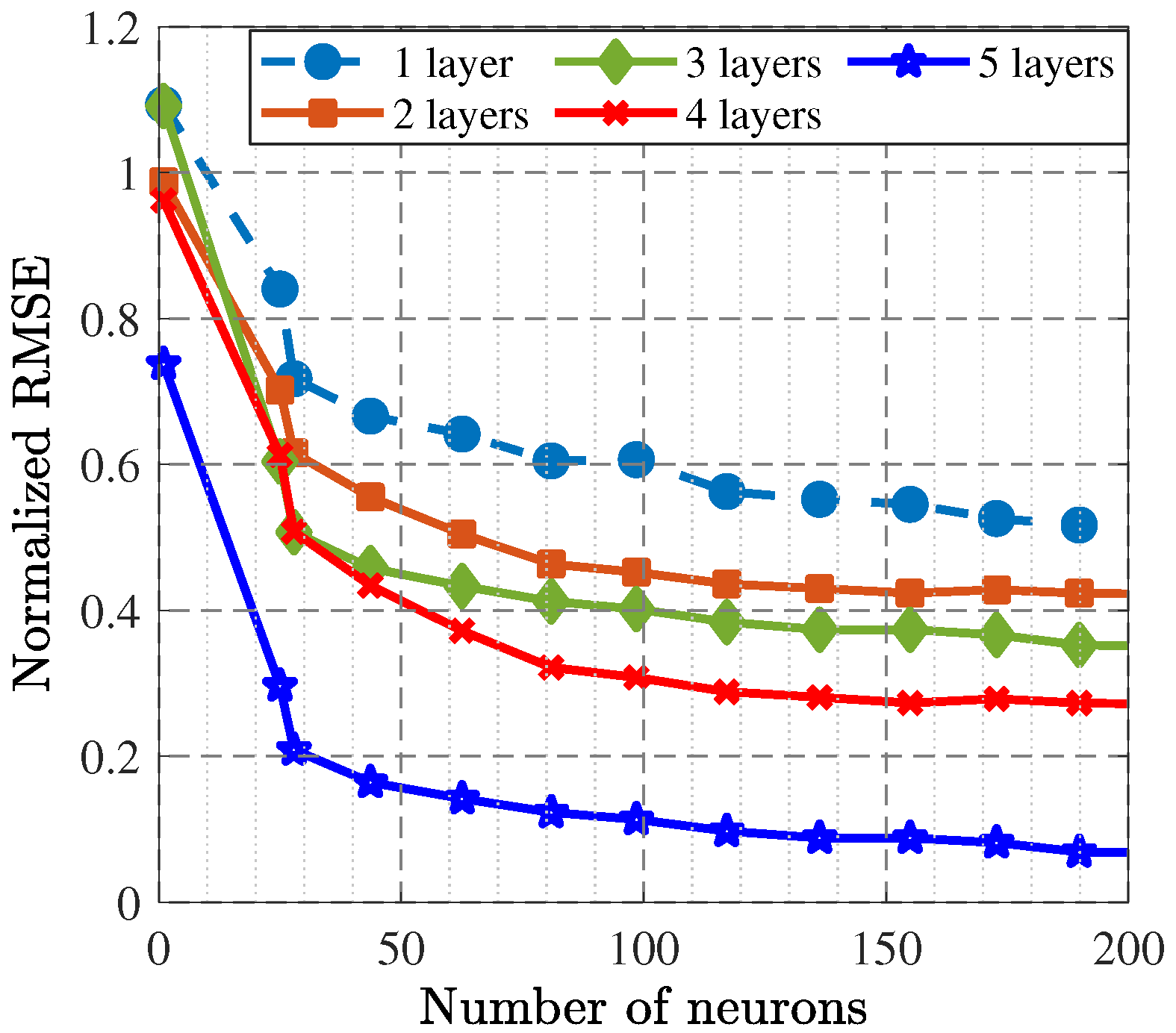
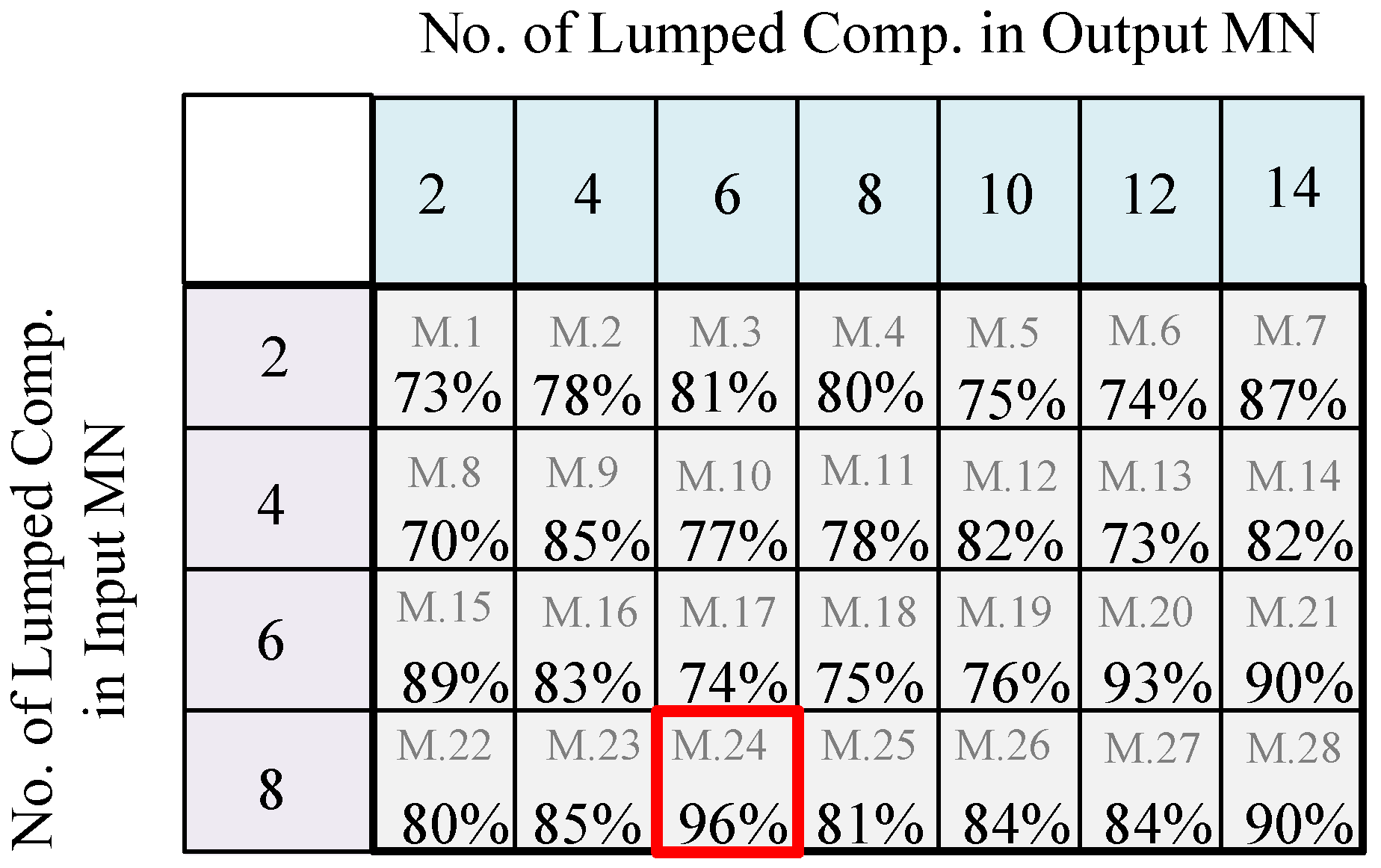
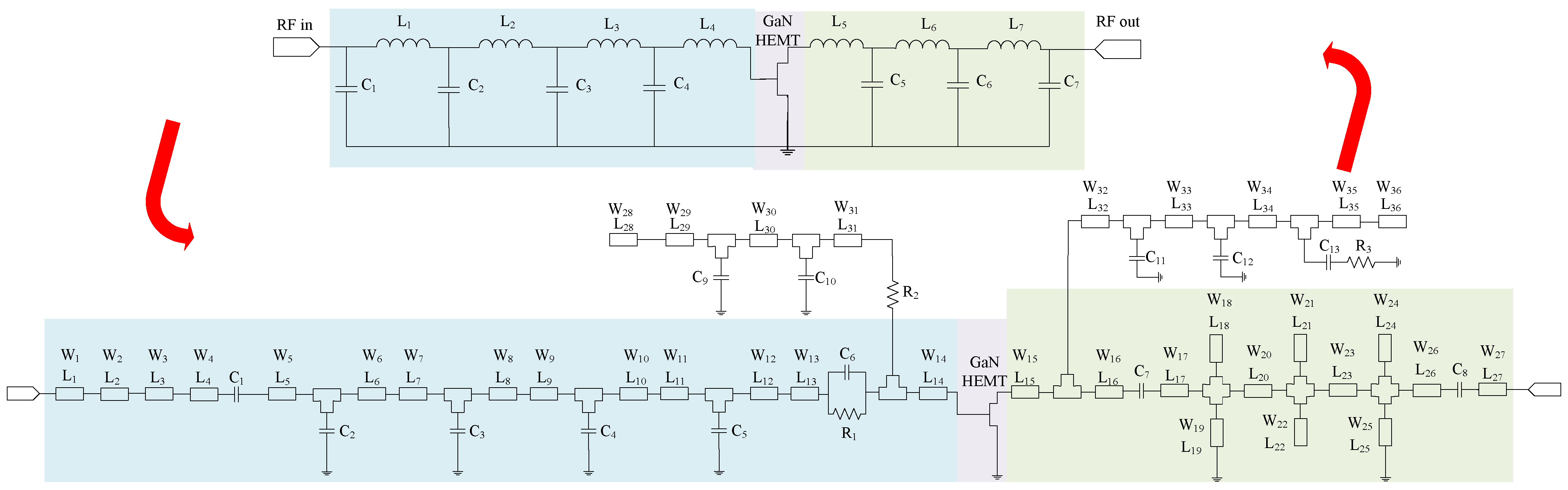
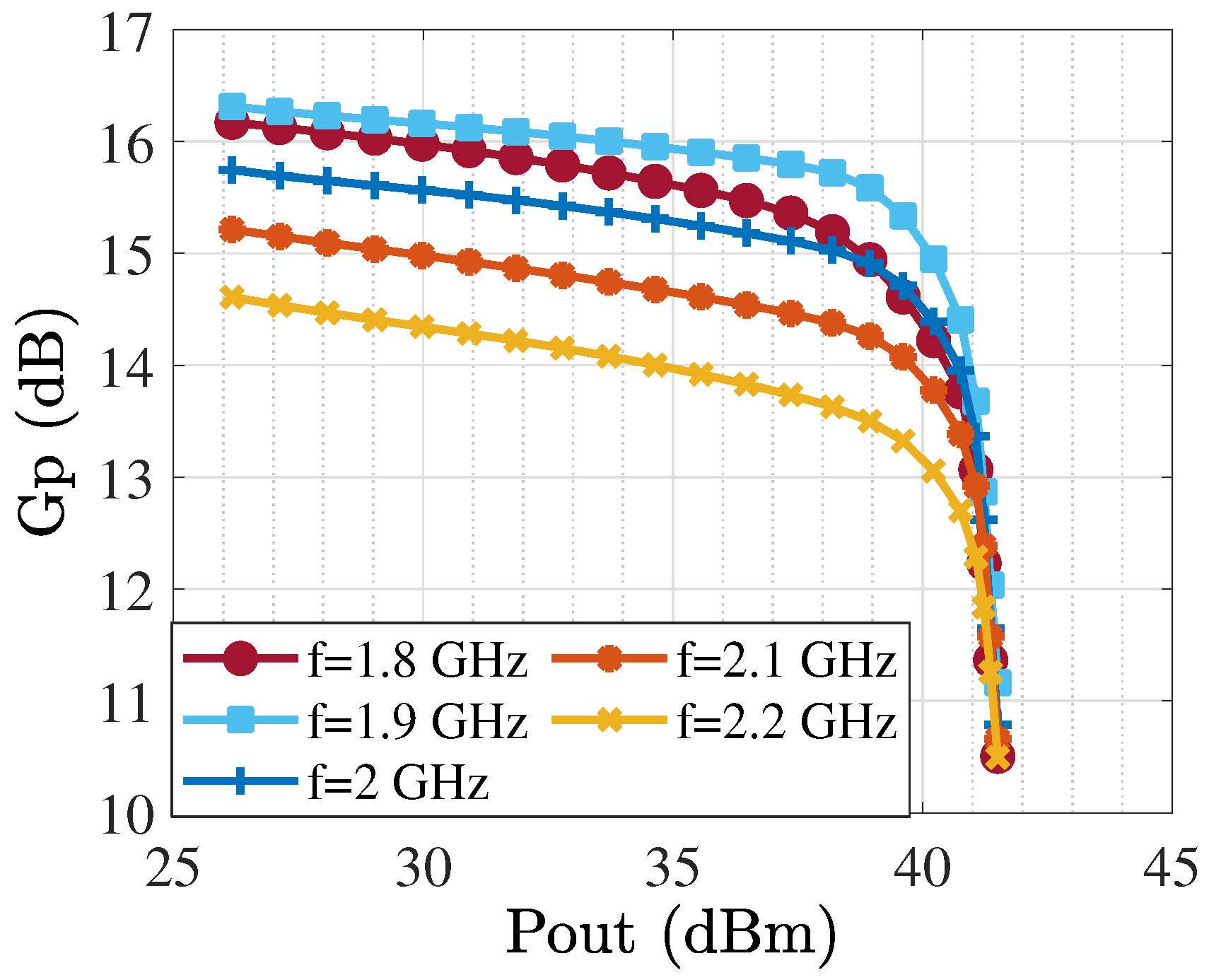

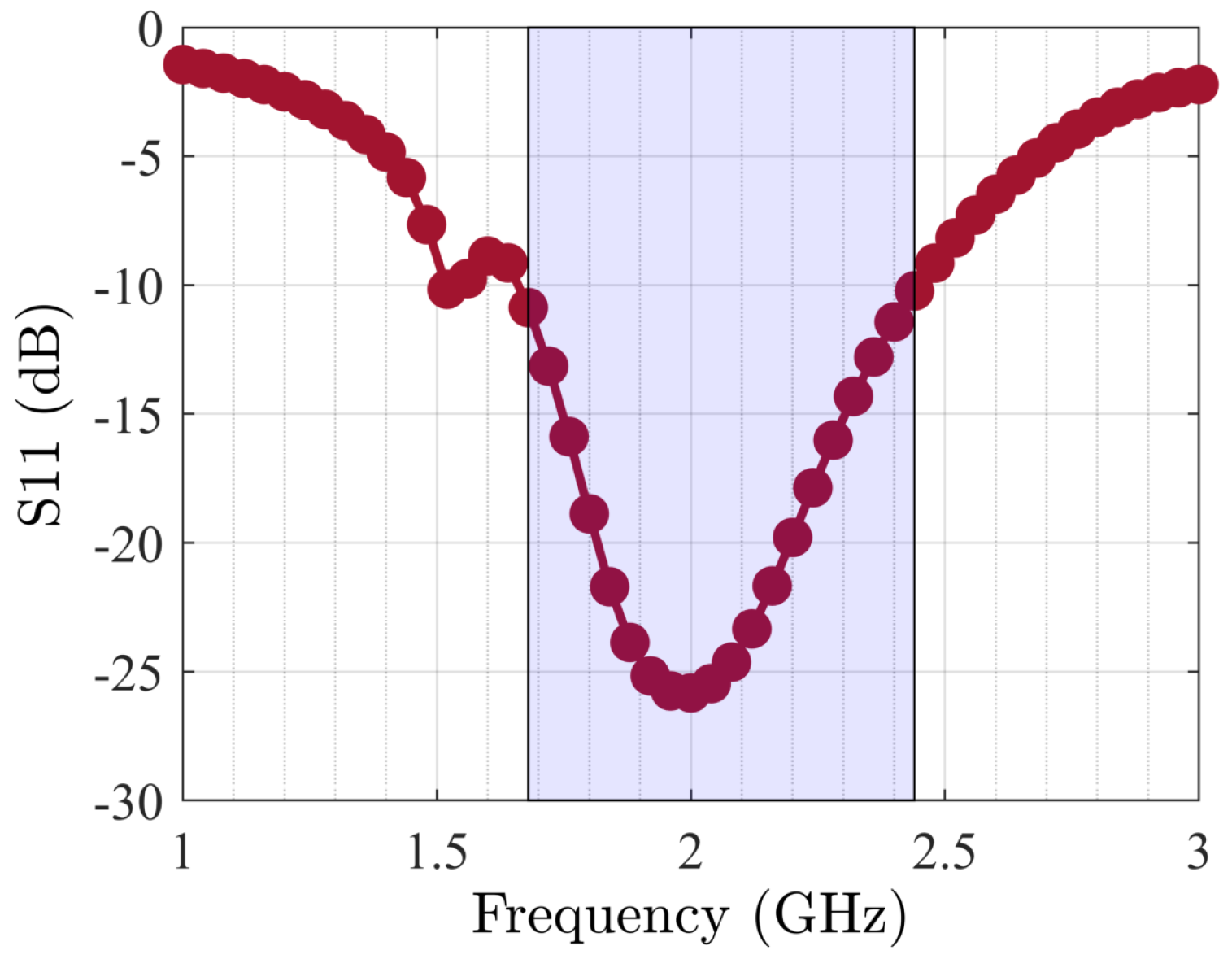
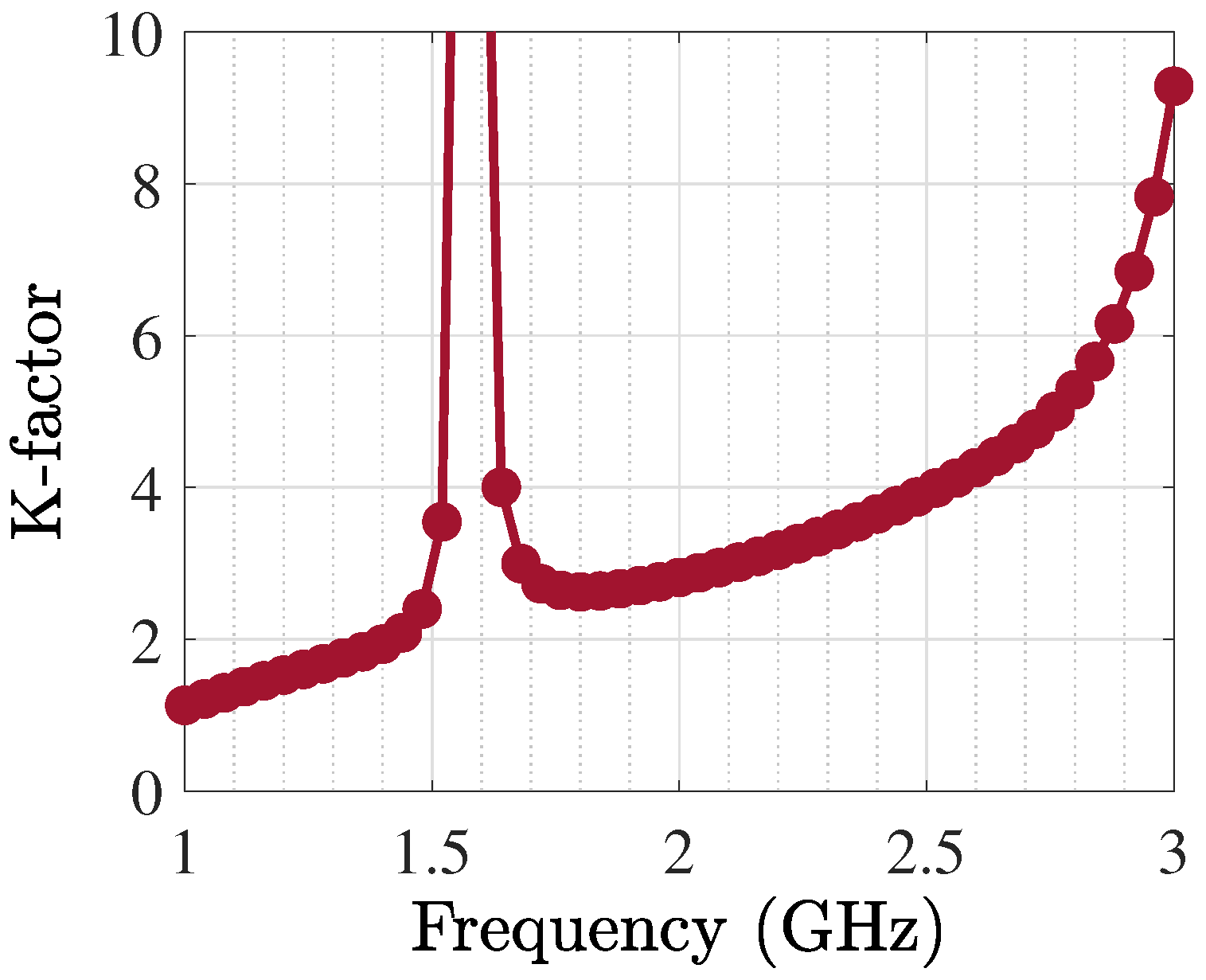
| Freq. (GHz) | Gate Impedance | Drain Impedance | PAE (%) | (dBm) | (dB) |
|---|---|---|---|---|---|
| 1.8 | 4.8-j5.8 | 20-j36 | 63 | 40 | 17.5 |
| 1.9 | 4.6-j3.9 | 21-j29.02 | 60.71 | 40.04 | 16.8 |
| 2 | 4.5-j3.4 | 21.02-j32.93 | 60.09 | 39.74 | 16.9 |
| 2.1 | 5.02-j2.5 | 19.81-j32.29 | 62.07 | 41 | 16.59 |
| 2.2 | 5.25-j1.8 | 18.23-j29.59 | 61.62 | 41.29 | 16.99 |
| 3.5 | 1.7 | ||
| 25.3 | 0.3 | ||
| 143 | 0.15 | ||
| 27.7 | 0.3 | ||
| 9.3 | 4.3 | ||
| 12.7 | 1.3 | ||
| 3.15 | 2.2 |
| 4.8 | 1.5 | 4.1 | 1 | ||||
| 4.0 | 1.5 | 3.7 | 1 | ||||
| 3.0 | 1.5 | 5.3 | 1 | ||||
| 1.07 | 3 | 5.3 | 1 | ||||
| 1.5 | 1 | 3.7 | 1 | ||||
| 1.5 | 4 | 3.7 | 1 | ||||
| 1.5 | 3.7 | 8 | 1 | ||||
| 1.5 | 3.7 | 1 | 1 | ||||
| 1.5 | 4.1 | 1 | 8 | ||||
| 1.6 | 1 | 3.6 | 8 | ||||
| 1.7 | 1 | 1.6 | 1 | ||||
| 1.8 | 1 | 5.5 | 1 | ||||
| 3 | 2 | 6.8 | 26.4 | ||||
| 1 | 0.2 | 1.6 | 26.4 | ||||
| 1 | 0.2 | 3.4 | 1 | ||||
| 1 | 8.16 | 1.7 | 1 | ||||
| 1 | 1.6 | 1.6 | 1 | ||||
| 1 | 5.4 | 1.6 | 8 | ||||
| 40.9 | 0.28 | 0.04 | 1.08 | ||||
| 3.6 | 1.6 | 27.50 | 24.5 | ||||
| 10e3 | 2.2 | 2.2 | 10e3 | ||||
| 10e6 | 10 | 10 | 10 |
| Ref. | Method | Goal(s) of paper |
|---|---|---|
| [10] | Deep learning-based CNN | - Estimating the scattering parameters of pixelated electromagnetic layouts |
| [33] | Deep CNN-based surrogate model | - Estimating scattering parameters |
| [34] | Pareto optimization | - Automatic design of low-noise amplifier with CMOS-based technology |
| [35] | Bayesian neural network | - Reducing the simulation consumption time for automatically designing a Doherty PA |
| [36] | Machine learning | - Designing a PA with 250 nm indium phosphide technology |
| [37] | Simulated annealing algorithm | - Presenting a design method for matching networks of PAs |
| [38] | Differential evolution multi-objective particle swarm optimization algorithm | - Improving the global search capability in the optimization process |
| This work | Co-implementation of a GAN with BiLSTM-based DNNs with multi-objective optimizations | - Obtaining the optimal hyperparameters of DNNs; |
| - Predicting the optimal gate and drain impedances of the transistor; - Estimating the optimal PA structure; - Optimizing the PA’s design parameters for improving the overall specifications. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kouhalvandi, L. Utilization of BiLSTM- and GAN-Based Deep Neural Networks for Automated Power Amplifier Optimization over X-Parameters. Sensors 2025, 25, 5524. https://doi.org/10.3390/s25175524
Kouhalvandi L. Utilization of BiLSTM- and GAN-Based Deep Neural Networks for Automated Power Amplifier Optimization over X-Parameters. Sensors. 2025; 25(17):5524. https://doi.org/10.3390/s25175524
Chicago/Turabian StyleKouhalvandi, Lida. 2025. "Utilization of BiLSTM- and GAN-Based Deep Neural Networks for Automated Power Amplifier Optimization over X-Parameters" Sensors 25, no. 17: 5524. https://doi.org/10.3390/s25175524
APA StyleKouhalvandi, L. (2025). Utilization of BiLSTM- and GAN-Based Deep Neural Networks for Automated Power Amplifier Optimization over X-Parameters. Sensors, 25(17), 5524. https://doi.org/10.3390/s25175524






