ECACS: An Enhanced Certificateless Authentication Scheme for Smart Car Sharing
Abstract
1. Introduction
- (1)
- We propose an efficient CLS authentication scheme for smart car-sharing scenarios, built upon the fuzzy extractor and the CRT. Compared with existing authentication schemes, our scheme provides decoupled, fine-grained authentication, supports dynamic user revocation, and eliminates computation on the user side.
- (2)
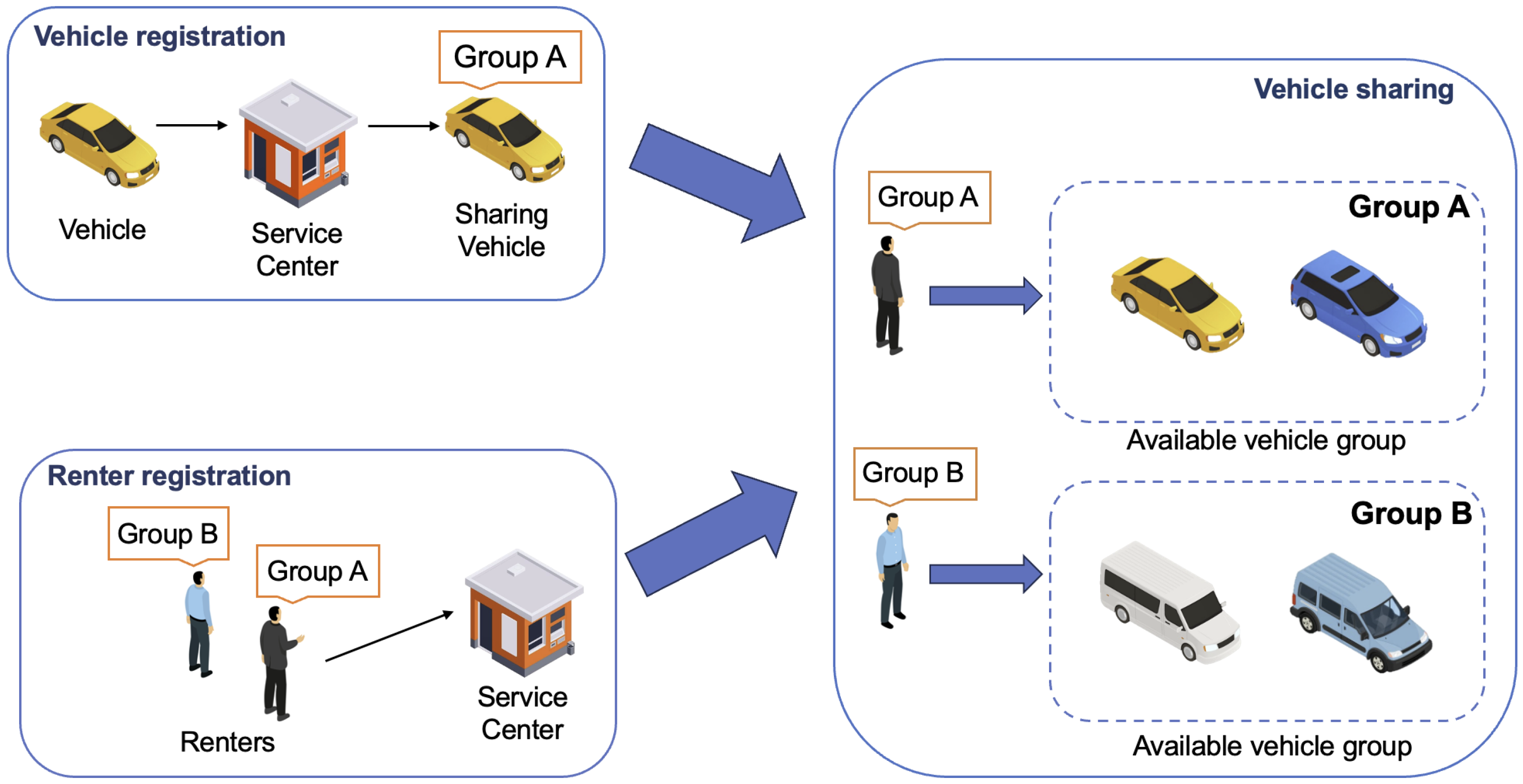
- We introduce a novel category-range authentication framework where vehicles are organized into distinct categories with unique identifiers. This enables users to access any vehicle within an authorized category, instead of a single specific one in most IoV frameworks, thereby enhancing the flexibility and efficiency of the rental process.
- (3)
- We conduct a comprehensive security analysis of our scheme and benchmark its performance against related works. The results demonstrate that our proposal achieves provable security and exhibits competitive overhead in terms of computation, communication, and dynamic membership management.
2. Related Works
3. Preliminaries
3.1. Elliptic Curve Cryptography
3.2. Chinese Remainder Theorem
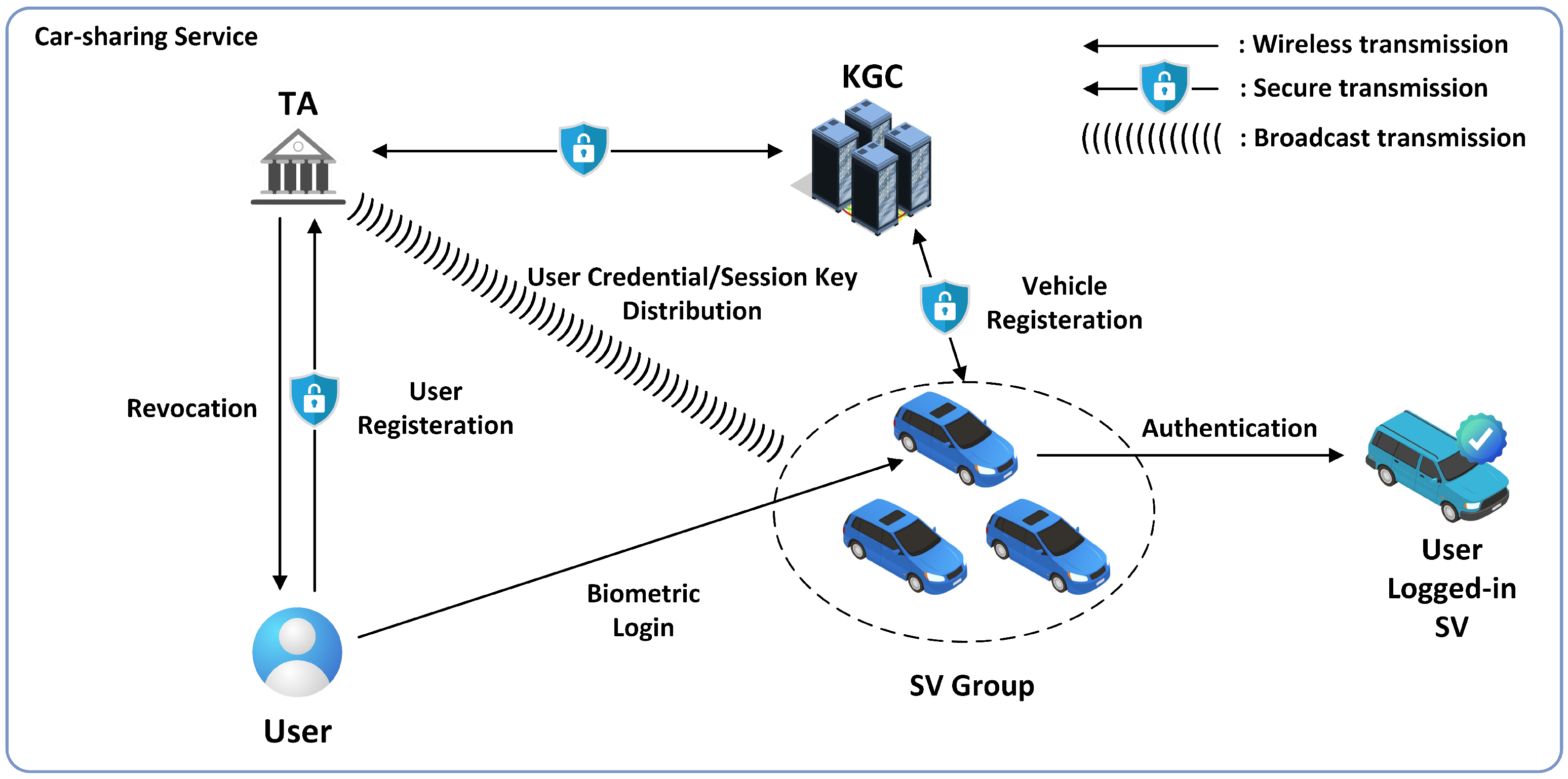
3.3. System Model
- TA: It represents the service center in smart car-sharing, which is a fully trusted authority that generates the system parameters and manages the service membership of users within the system by distributing and updating the group identifier. Moreover, it is also responsible for generating pseudonyms for users and can track and reveal their real identities when malicious behaviors occur.
- KGC: It represents a key generation center that generates the partial private keys for vehicles and the private keys for users and is considered to be a semi-trusted third party.
- SV: It represents a vehicle in the car-sharing service. In our scheme, SVs are classified into individual categories based on their characteristics (e.g., model and capacity). After an SV is logged in by a legitimate renter via biometric information, it can authenticate with other verified SVs by generating signatures utilizing the derived group identifier.
- User: It represents the actual user of the car-sharing service. Additionally, it is important to emphasize that no local computational abilities are required for users in our proposed scheme.
3.4. Security Model
- (1)
- Vehicle Registration Query: When receiving this query from with as input, generates the related information for the corresponding vehicle.
- (2)
- User Registration Query: When receiving this query from with as input, generates the related information for the corresponding user.
- (3)
- Reveal Vehicle Partial Key Query: When receiving this query from with as input, returns the corresponding .
- (4)
- Reveal User Private Key Query: When receiving this query from with as input, returns the corresponding .
- (5)
- Reveal Vehicle Secret Query: When receiving this query from with as input, returns the corresponding .
- (6)
- Reveal Vehicle Public Key Query: When receiving this query from with as input, returns the corresponding .
- (7)
- Reveal User Public Key Query: When receiving this query from with as input, returns the corresponding .
- (8)
- Replace Vehicle Public Key Query: When receiving this query from with as input, replaces the public key of the corresponding vehicle with .
- (9)
- Replace User Public Key Query: When receiving this query from with as input, replaces the public key of the corresponding user with .
- (10)
- Sign Query: When receiving this query from with as input, outputs a legitimate signature .
- Sign Query has never been queried with the submitted tuple.
- Reveal User Private Key Query and Replace User Public Key Query have never been queried with the pseudonym by .
- is a valid signature for the submitted tuple.
- (1)
- Vehicle Registration Query: When receiving this query from with as input, generates the related information for the corresponding vehicle.
- (2)
- User Registration Query: When receiving this query from with as input, generates the related information for the corresponding user.
- (3)
- Reveal User Private Key Query: When receiving this query from with as input, returns the corresponding .
- (4)
- Reveal Vehicle Secret Query: When receiving this query from with as input, returns the corresponding .
- (5)
- Reveal Vehicle Public Key Query: When receiving this query from with as input, returns the corresponding .
- (6)
- Reveal User Public Key Query: When receiving this query from with as input, returns the corresponding .
- (7)
- Sign Query: When receiving this query from with as input, outputs a legitimate signature .
- Sign Query has never been queried with the submitted tuple.
- Reveal Vehicle Secret Query has never been queried with the pseudonym by .
- is a valid signature for the submitted tuple.
4. Proposed Scheme
4.1. Setup
- (1)
- Given as the security parameter, TA chooses a cyclic group of order q with P as its generator. Then, TA randomly selects and calculates .
- (2)
- Then, TA selects five secure hash functions: , , , , .
- (3)
- KGC randomly selects and calculates .
- (4)
- TA selects n unique prime numbers and calculates . Then, for each , TA calculates , , individually.
- (5)
- Finally, TA calculates and publishes the system parameters, which are denoted as .
4.2. Registration
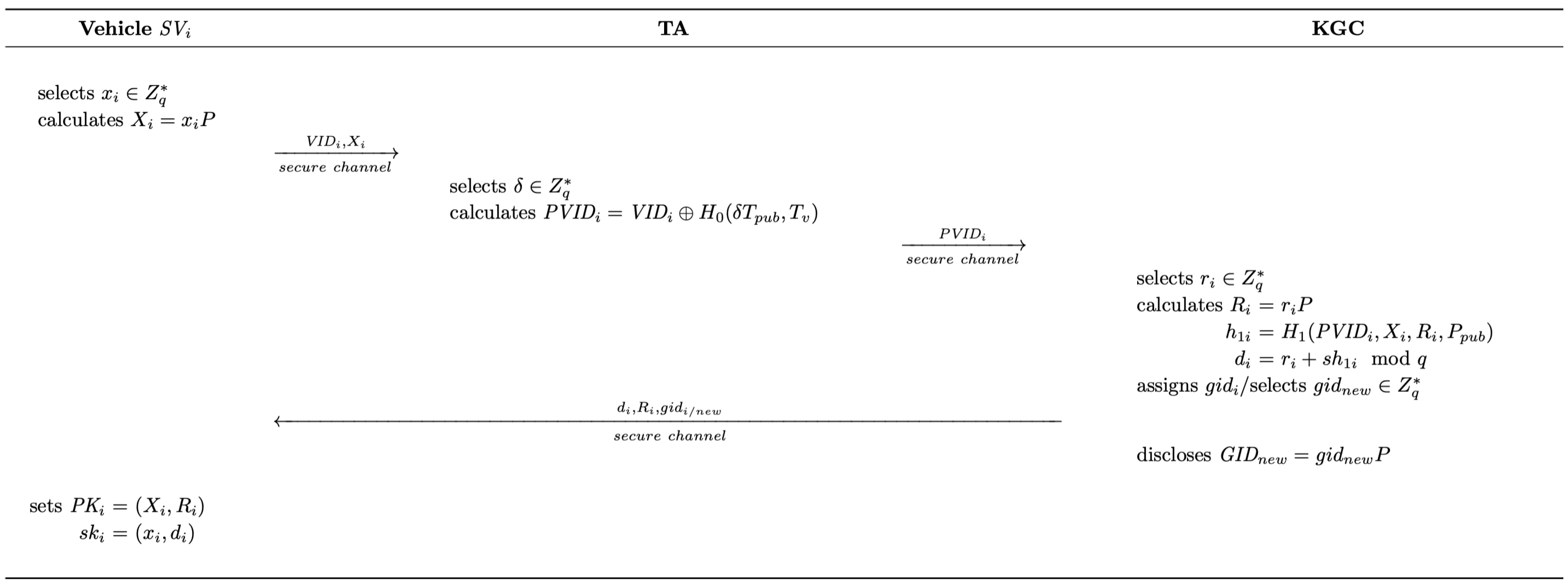
4.2.1. Vehicle Registration
- (1)
- A vehicle first randomly selects and calculates . Then, it sends to TA through a secure channel, where denotes the unique identifier of .
- (2)
- Upon receiving the request from , TA randomly selects and calculates , where is the current timestamp. Consequently, TA transmits to KGC through a secure channel.
- (3)
- After receiving information from TA, KGC randomly selects and calculates , , . Then, based on the characteristics of the vehicle (e.g., model, capacity), KGC assigns an existing or creates a new class identifier to and transmits to through a secure channel. Note that every time after a new class identifier is created and assigned, KGC calculates and discloses it to all the entities within the system.
- (4)
- After obtaining the message from KGC, sets its public key as and its private key as .
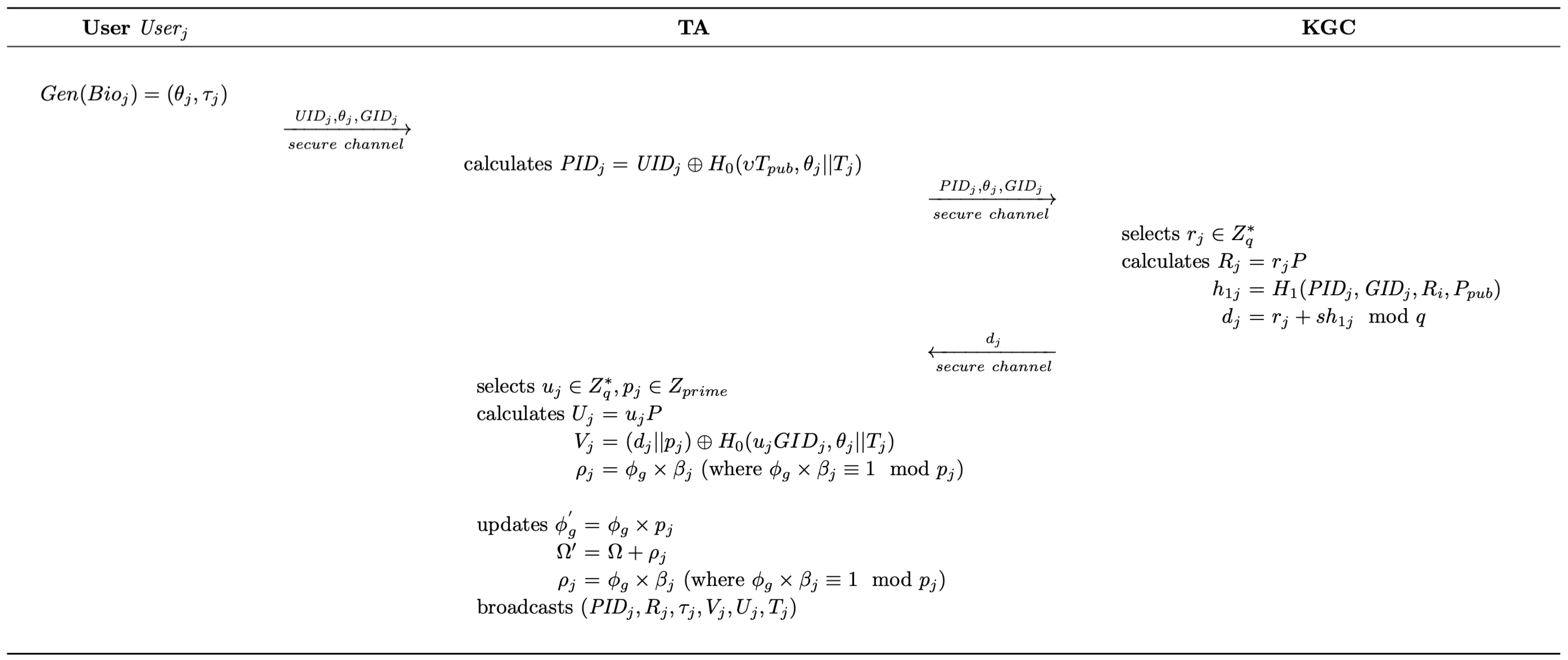
4.2.2. User Registration
- (1)
- With the real user identity , the target category identifier , and the biometric information acquired from , TA first utilizes the fuzzy extractor to calculate . Then, TA randomly selects and calculates , where is the current timestamp. Consequently, TA transmits to KGC through a secure channel.
- (2)
- Upon receiving the data of TA, KGC randomly selects and calculates . Then, KGC calculates the credential for and transmits it to TA via a secure channel, where .
- (3)
- Next, TA randomly selects and an identifier update secret . Then, TA calculates and .
- (4)
- TA calculates , and records the parameters in a list L.
- (5)
- Finally, TA updates with , with and broadcasts through a public channel.
4.2.3. Group Identifier Distribution
4.3. Authentication
4.3.1. User Login
- (1)
- Upon receiving the biometric data from , utilizes the fuzzy extractor to obtain .
- (2)
- Next, calculates , and checks whether the equation holds. If not, rejects the request. Otherwise, succeeds in the login process.
4.3.2. Signing
- (1)
- randomly selects and calculates .
- (2)
- then acquires the hash values by calculating and , where denotes the current timestamp and .
- (3)
- calculates , where denotes the multiplicative inverse of z on .
- (4)
- Finally, constructs the signature and sends the tuple to the receiver.
4.3.3. Verification
- (1)
- Upon receiving the message, vehicle will first check its freshness and will abort it if the timestamp is considered invalid. Then, as mentioned in the signing process, will extract z from stored locally by calculating , where denotes the identifier update secret obtained during the user login phase.
- (2)
- With the received parameters, calculates and .
- (3)
- Finally, checks whether the equation holds. If not, the authentication process fails. Otherwise, accepts as a valid signature from .
4.4. User Logout
- Upon service termination of , randomly selects and calculates and , where denotes the current timestamp. Then, transmits to TA and KGC. When receiving the message, TA and KGC can verify its authenticity by checking whether the equation holds.
- After successful verification, based on the received , KGC randomly selects and generates the corresponding credential for with operations described in the User registration section, which are then transmitted to TA.
- According to the received information, TA retrieves the relevant parameters from the list L, selects a new identifier update secret , and calculates , where is the current timestamp.
- TA then updates the recorded parameters in list L with , which is calculated based on the newly generated .
- Finally, TA updates and with , , and broadcasts via a public channel. Additionally, TA performs the operations described in the Group identifier distribution section to prevent potential illegal access with the outdated group identifier.
4.5. Revocation
- TA first acquires the corresponding by searching the maintained list L and updates by calculating .
- Next, TA randomly selects and calculates , , and , where denotes the current timestamp.
- TA then broadcasts to all SVs within the system.
- Upon receiving the update message from TA, each SV first checks the timestamp of the message. If the message is fresh, then vehicles will continue to check whether the equation holds. If not, then the update process is aborted. Otherwise, a new group identifier can be calculated with , where denotes the individual identifier update secret held by each SV within the system.
5. Security Analysis
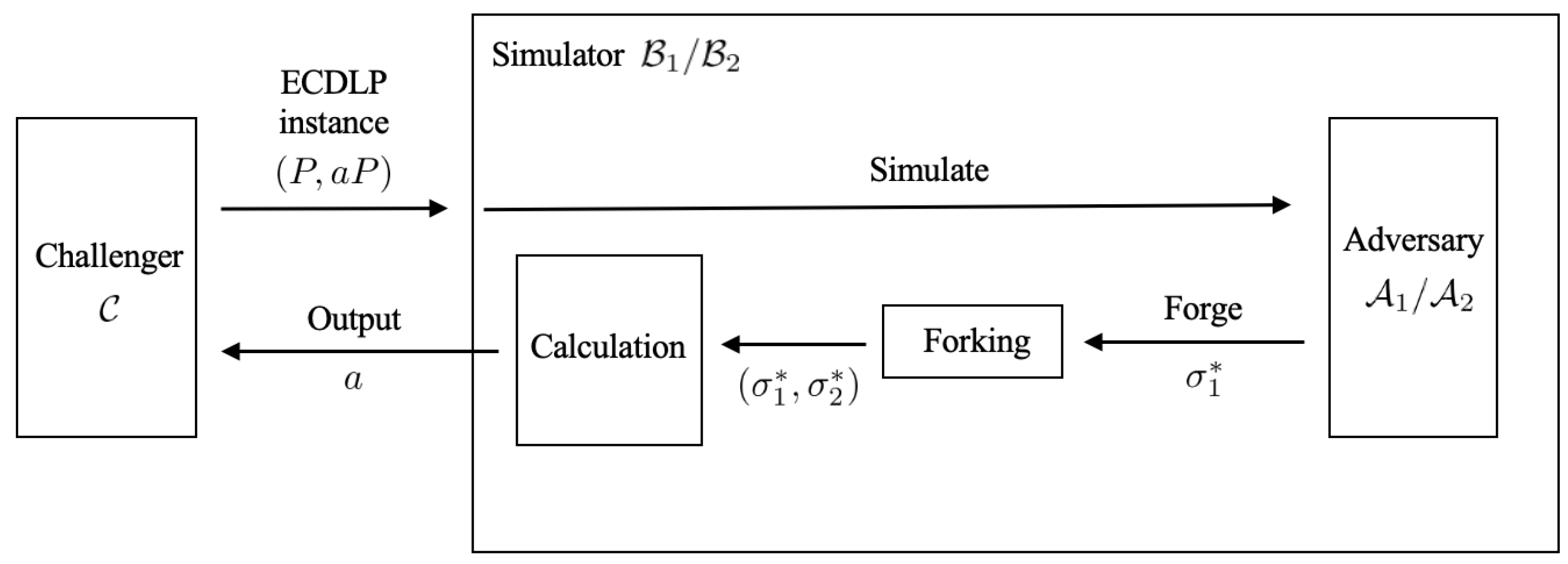
5.1. Security Proof
- (1)
- Hash Query: will respond to the hash queries from as follows:
- (a)
- Query: When receiving an hash query with , if , returns . Otherwise, selects , adds the tuple to , and then returns . Note that the and here generally represent a random string and a point on the defined elliptic curve.
- (b)
- Query: When receiving an hash query with , if , returns . Otherwise, selects , adds the tuple to , and then returns .
- (c)
- Query: When receiving an hash query with , if the corresponding tuple , then returns . Otherwise, selects , adds to , and then returns .
- (d)
- Query: When receiving an hash query with , if the corresponding tuple , then returns . Otherwise, selects , adds to , and then returns .
- (2)
- Vehicle Registration Query: When receives a Vehicle Registration Query from with as input, if exists in , returns ⊥. Otherwise, selects and calculates , and . Then, adds to and to .
- (3)
- User Registration Query: When receives a User Registration Query from with as input, if exists in , returns ⊥. Otherwise, continues the game as follows:
- If , selects and calculates . Then, adds the tuple to and the tuple to , where is selected from the existing records in .
- If , selects and calculates . Then, adds to and to , where is selected from the existing records in .
- (4)
- Reveal Vehicle Partial Key Query: When receives a Reveal Vehicle Partial Key Query from with as input, if the tuple , returns the corresponding . Otherwise, first executes the Vehicle Registration Query with as input and then returns the corresponding .
- (5)
- Reveal User Private Key Query: When receives a Reveal User Private Key Query from with as input, if , aborts the game. Otherwise, continues the game as follows:
- If , returns the corresponding .
- If , first executes the User Registration Query and then returns the corresponding .
- (6)
- Reveal Vehicle Secret Query: When receives a Reveal Vehicle Secret Query from with as input, returns if . Otherwise, first executes the Vehicle Registration Query with as input and then returns the corresponding .
- (7)
- Reveal Vehicle Public Key Query: When receives a Reveal Public Key Query from with as input, if , returns the corresponding . Otherwise, first executes the Vehicle Registration Query with as input and then returns the corresponding .
- (8)
- Reveal User Public Key Query: When receives a Reveal User Public Key Query from with as input, if , returns the corresponding . Otherwise, first executes the User Registration Query with as input and then returns the corresponding .
- (9)
- Replace Vehicle Public Key Query: When receives a Replace Vehicle Public Key Query from with as input, sets as s new public key and updates the record in .
- (10)
- Replace User Public Key Query: When receives a Replace User Public Key Query from with as input, sets as ’s new public key and updates the record in .
- (11)
- Sign Query: When receives a Sign Query from with as input, first checks whether and exist in and . If not, first executes the Vehicle Registration Query and User Registration Query with the input identities. Then, after acquiring the corresponding records, continues the game as follows:
- If , selects and obtains , from . Then, calculates , . Then, adds to and to , where . Finally, returns to .
- If , selects and obtains , from . Then, sets , , where . Then, adds to and to , where . Finally, returns to .
- (1)
- Hash Query: answers the Hash Query the same as in Game I.
- (2)
- Vehicle Registration Query: When receives a Vehicle Registration Query from with as input, if exists in , returns ⊥. Otherwise, continue the game as follows.
- If , selects and calculates , and . Then, sets and adds the tuple to and to .
- If , selects and calculates , , and . Then, adds the tuple to and to .
- (3)
- User Registration Query: When receives a User Registration Query from with as input, if exists in , returns ⊥. Otherwise, selects and calculates . Then, adds the tuple to and the tuple to , where is selected from the existing records in .
- (4)
- Reveal User Private Key Query: When receives a Reveal User Private Key Query from with as input, if the tuple , returns the corresponding . Otherwise, first executes the User Registration Query with as input and then returns the corresponding .
- (5)
- Reveal Vehicle Secret Query: When receives a Reveal Vehicle Secret Query from with as input, if , aborts the game. Otherwise, continues the game as follows:
- If , returns the corresponding .
- If , first executes the Vehicle Registration Query and then returns the corresponding .
- (6)
- Reveal Vehicle Public Key Query: When receives a Reveal Public Key Query from with as input, if , returns the corresponding . Otherwise, first executes the Vehicle Registration Query with as input and then returns the corresponding .
- (7)
- Reveal User Public Key Query: When receives a Reveal User Public Key Query from with as input, if , returns the corresponding . Otherwise, first executes the User Registration Query with as input and then returns the corresponding .
- (8)
- Sign Query: When receives a Sign Query from with as input, first checks whether and exist in and . If not, first executes the Vehicle Registration Query and User Registration Query with the input identities. Then, after acquiring the corresponding records, continues the game as follows:
- If , selects and obtains , from . Then, calculates , . Then, adds to and to . Finally, returns to .
- If , selects and obtains , from . Then, sets and calculates , where . then adds to and to , where . Finally, returns to .
5.2. Security Features
5.2.1. Message Authenticity and Integrity
5.2.2. Anonymity
5.2.3. Traceability
5.2.4. Revocability
5.2.5. Resistance Against Replay Attacks
5.2.6. Resistance Against MITM Attacks
6. Performance Evaluation
6.1. Experiment Environment
6.2. Functional Properties
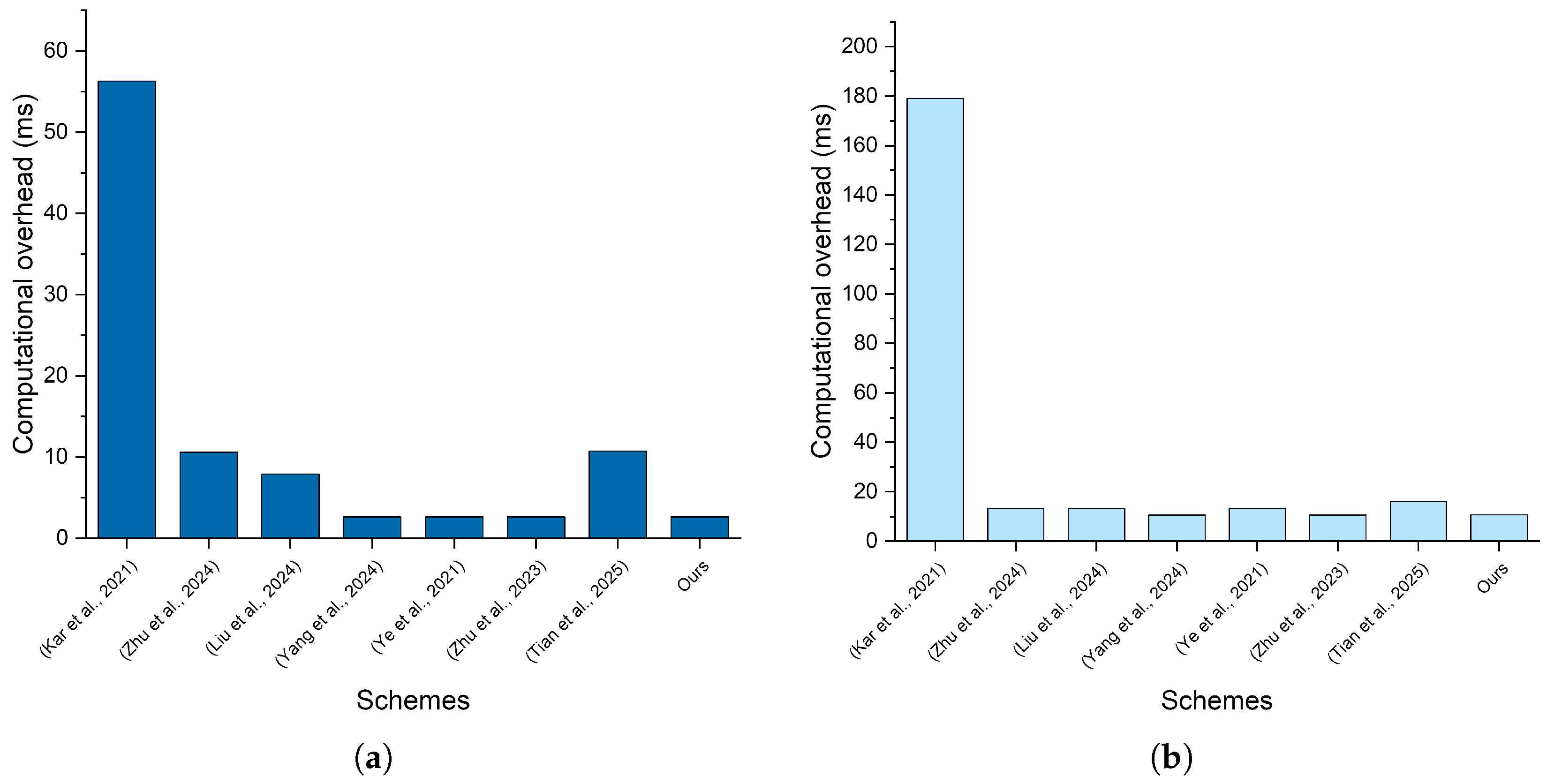
6.3. Computational Overhead
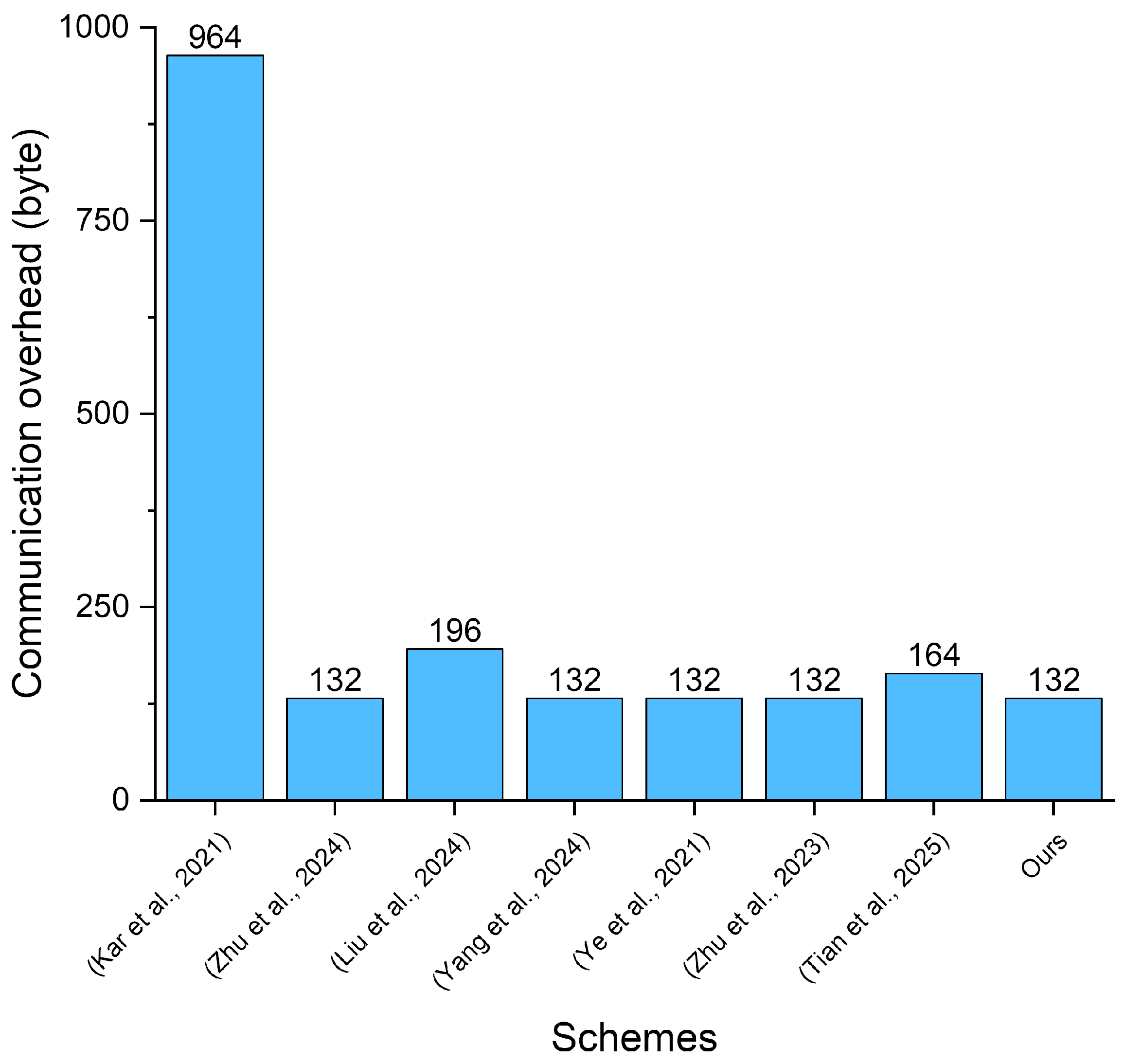
6.4. Communication Overhead
6.5. Revocation Feature
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rajkumar, Y.; Santhosh Kumar, S. A comprehensive survey on communication techniques for the realization of intelligent transportation systems in IoT based smart cities. Peer-Peer Netw. Appl. 2024, 17, 1263–1308. [Google Scholar] [CrossRef]
- Ji, B.; Zhang, X.; Mumtaz, S.; Han, C.; Li, C.; Wen, H.; Wang, D. Survey on the internet of vehicles: Network architectures and applications. IEEE Commun. Stand. Mag. 2020, 4, 34–41. [Google Scholar] [CrossRef]
- Karabulut, M.A.; Shah, A.S.; Ilhan, H.; Pathan, A.S.K.; Atiquzzaman, M. Inspecting VANET with various critical aspects—A systematic review. Ad Hoc Netw. 2023, 150, 103281. [Google Scholar] [CrossRef]
- Vélez, A.M.A. Economic impacts, carbon footprint and rebound effects of car sharing: Scenario analysis assessing business-to-consumer and peer-to-peer car sharing. Sustain. Prod. Consum. 2023, 35, 238–249. [Google Scholar] [CrossRef]
- Statista Market Insights. Car-Sharing–Worldwide. Available online: https://www.statista.com/outlook/mmo/shared-mobility/car-sharing/worldwide (accessed on 26 May 2025).
- Huang, C.; Lu, R.; Ni, J.; Shen, X. DAPA: A decentralized, accountable, and privacy-preserving architecture for car sharing services. IEEE Trans. Veh. Technol. 2020, 69, 4869–4882. [Google Scholar] [CrossRef]
- Liu, Y.; He, D.; Bao, Z.; Luo, M.; Peng, C. PEACS: A Privacy-Enhancing and Accountable Car Sharing System. IEEE Internet Things J. 2024, 11, 16422–16435. [Google Scholar] [CrossRef]
- Zhu, D.; Guan, Y. Secure and Lightweight Conditional Privacy-Preserving Identity Authentication Scheme for VANET. IEEE Sens. J. 2024, 24, 35743–35756. [Google Scholar] [CrossRef]
- Yue, Q.; Jiang, W.; Lei, H. A lightweight certificateless aggregate signature scheme without pairing for VANETs. Sci. Rep. 2025, 15, 23663. [Google Scholar] [CrossRef]
- Rajkumar, Y.; Kumar, S.S. An elliptic curve cryptography based certificate-less signature aggregation scheme for efficient authentication in vehicular ad hoc networks. Wirel. Netw. 2024, 30, 335–362. [Google Scholar] [CrossRef]
- Mundhe, P.; Verma, S.; Venkatesan, S. A comprehensive survey on authentication and privacy-preserving schemes in VANETs. Comput. Sci. Rev. 2021, 41, 100411. [Google Scholar] [CrossRef]
- AlMarshoud, M.; Sabir Kiraz, M.; Al-Bayatti, A.H. Security, privacy, and decentralized trust management in VANETs: A review of current research and future directions. ACM Comput. Surv. 2024, 56, 1–39. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Tian, Y. ISC-CPPA: Improverd-security certificateless conditional privacy-preserving authentication scheme with revocation. IEEE Trans. Veh. Technol. 2022, 71, 12304–12314. [Google Scholar] [CrossRef]
- Al-Mekhlafi, Z.G.; Al-Janabi, H.D.K.; Al-Shareeda, M.A.; Mohammed, B.A.; Alshudukhi, J.S.; Al-Dhlan, K.A. Fog computing and blockchain technology based certificateless authentication scheme in 5G-assisted vehicular communication. Peer-Peer Netw. Appl. 2024, 17, 3703–3721. [Google Scholar] [CrossRef]
- Hou, Y.; Cao, Y.; Xiong, H.; Sun, Z.; Mumtaz, S.; Tian, D. CASKA-CRT: Chinese remainder theorem empowered certificateless aggregate signcryption scheme with key agreement in IoVs. IEEE Trans. Intell. Veh. 2024, 9, 6814–6829. [Google Scholar] [CrossRef]
- Raya, M.; Hubaux, J.P. Securing vehicular ad hoc networks. J. Comput. Secur. 2007, 15, 39–68. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, R.; Lin, X.; Shen, X.; Su, J. An efficient pseudonymous authentication scheme with strong privacy preservation for vehicular communications. IEEE Trans. Veh. Technol. 2010, 59, 3589–3603. [Google Scholar] [CrossRef]
- Di, C.; Wu, W. A Novel Identity-Based Mutual Authentication Scheme for Vehicle Ad Hoc Networks. Wirel. Commun. Mob. Comput. 2022, 2022, 7881079. [Google Scholar] [CrossRef]
- Umar, M.; Islam, S.H.; Mahmood, K.; Ahmed, S.; Ghaffar, Z.; Saleem, M.A. Provable secure identity-based anonymous and privacy-preserving inter-vehicular authentication protocol for VANETS using PUF. IEEE Trans. Veh. Technol. 2021, 70, 12158–12167. [Google Scholar] [CrossRef]
- Li, Q.; Hsu, C.F.; Raymond Choo, K.K.; He, D. A Provably Secure and Lightweight Identity-Based Two-Party Authenticated Key Agreement Protocol for Vehicular Ad Hoc Networks. Secur. Commun. Netw. 2019, 2019, 7871067. [Google Scholar] [CrossRef]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless public key cryptography. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, 30 November–4 December 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 452–473. [Google Scholar]
- Ma, K.; Zhou, Y.; Wang, Y.; Dong, C.; Xia, Z.; Yang, B.; Zhang, M. An efficient certificateless signature scheme with provably security and its applications. IEEE Syst. J. 2023, 17, 5636–5647. [Google Scholar] [CrossRef]
- Malip, A.; Ng, S.L.; Li, Q. A certificateless anonymous authenticated announcement scheme in vehicular ad hoc networks. Secur. Commun. Netw. 2014, 7, 588–601. [Google Scholar] [CrossRef]
- Zhong, H.; Han, S.; Cui, J.; Zhang, J.; Xu, Y. Privacy-preserving authentication scheme with full aggregation in VANET. Inf. Sci. 2019, 476, 211–221. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Zhang, K.; Li, J.; Luo, Y. A conditional privacy-preserving certificateless aggregate signature scheme in the standard model for VANETs. IEEE Access 2022, 10, 15605–15618. [Google Scholar] [CrossRef]
- Shim, K.A. Security analysis of conditional privacy-preserving authentication schemes for VANETs. IEEE Access 2023, 11, 33956–33963. [Google Scholar] [CrossRef]
- Zheng, H.; Luo, M.; Zhang, Y.; Peng, C.; Feng, Q. A security-enhanced pairing-free certificateless aggregate signature for vehicular Ad-Hoc networks. IEEE Syst. J. 2022, 17, 3822–3833. [Google Scholar] [CrossRef]
- Cheng, G.; Huang, J.; Wang, Y.; Zhao, J.; Kong, L.; Deng, S.; Yan, X. Conditional privacy-preserving multi-domain authentication and pseudonym management for 6G-enabled IoV. IEEE Trans. Inf. Forensics Secur. 2023, 19, 10206–10220. [Google Scholar] [CrossRef]
- Yin, D.; Gong, B. A Lightweight Certificateless Mutual Authentication Scheme Based on Signatures for IIoT. IEEE Internet Things J. 2024, 11, 26852–26865. [Google Scholar] [CrossRef]
- Lin, H.T.; Jhuang, W.L. Blockchain-Based Lightweight Certificateless Authenticated Key Agreement Protocol for V2V Communications in IoV. IEEE Internet Things J. 2024, 11, 27744–27759. [Google Scholar] [CrossRef]
- Gu, Y.; Shen, L.; Gao, C.; Zhu, T. Efficient and Secure Certificateless Aggregate Signature Scheme in Vehicle Networks. Netinfo Secur. 2024, 24, 188–202. [Google Scholar]
- Genc, Y.; Aytas, N.; Akkoc, A.; Afacan, E.; Yazgan, E. ELCPAS: A new efficient lightweight certificateless conditional privacy preserving authentication scheme for IoV. Veh. Commun. 2023, 39, 100549. [Google Scholar] [CrossRef]
- Ali, I.; Chen, Y.; Ullah, N.; Kumar, R.; He, W. An efficient and provably secure ECC-based conditional privacy-preserving authentication for vehicle-to-vehicle communication in VANETs. IEEE Trans. Veh. Technol. 2021, 70, 1278–1291. [Google Scholar] [CrossRef]
- Li, X.; Yin, X.; Ning, J. RelCLAS: A Reliable Malicious KGC-Resistant Certificateless Aggregate Signature Protocol for Vehicular Ad Hoc Networks. IEEE Internet Things J. 2023, 10, 21100–21114. [Google Scholar] [CrossRef]
- Xiong, W.; Wang, R.; Wang, Y.; Zhou, F.; Luo, X. CPPA-D: Efficient conditional privacy-preserving authentication scheme with double-insurance in VANETs. IEEE Trans. Veh. Technol. 2021, 70, 3456–3468. [Google Scholar] [CrossRef]
- Gong, Z.; Gao, T.; Guo, N. PCAS: Cryptanalysis and improvement of pairing-free certificateless aggregate signature scheme with conditional privacy-preserving for VANETs. Ad Hoc Netw. 2023, 144, 103134. [Google Scholar] [CrossRef]
- Ali, I.; Hassan, A.; Li, F. Authentication and privacy schemes for vehicular ad hoc networks (VANETs): A survey. Veh. Commun. 2019, 16, 45–61. [Google Scholar] [CrossRef]
- Wu, W.; Ye, F. IPCAS: An improved conditional privacy-preserving certificateless aggregate signature scheme without bilinear pairing for VANETs. J. Syst. Archit. 2024, 152, 103175. [Google Scholar] [CrossRef]
- Paliwal, S.; Cherukuri, A.K.; Gao, X.Z. Dynamic private Modulus based password conditional privacy preserving authentication and key-agreement protocol for VANET. Wirel. Pers. Commun. 2022, 123, 2061–2088. [Google Scholar] [CrossRef]
- Roeschlin, M.; Vaas, C.; Rasmussen, K.B.; Martinovic, I. Bionyms: Driver-centric message authentication using biometric measurements. In Proceedings of the 2018 IEEE Vehicular Networking Conference (VNC), Taipei, Taiwan, 5–7 December 2018; pp. 1–8. [Google Scholar]
- Islam, S.H.; Obaidat, M.S.; Vijayakumar, P.; Abdulhay, E.; Li, F.; Reddy, M.K.C. A robust and efficient password-based conditional privacy preserving authentication and group-key agreement protocol for VANETs. Future Gener. Comput. Syst. 2018, 84, 216–227. [Google Scholar] [CrossRef]
- Cui, J.; Liu, X.; Zhong, H.; Zhang, J.; Wei, L.; Bolodurina, I.; He, D. A Practical and Provably Secure Authentication and Key Agreement Scheme for UAV-Assisted VANETs for Emergency Rescue. IEEE Trans. Netw. Sci. Eng. 2024, 11, 1454–1468. [Google Scholar] [CrossRef]
- Azees, M.; Rajasekaran, A.S.; Vijayakumar, P.; Karuppiah, M. Hybrid CMOS Memristor Based Biometric OBU Authentication and Anonymous Mutual Authentication for Secure Communication in Fog-Based VANETs. IEEE Trans. Intell. Transp. Syst. 2024, 25, 11117–11129. [Google Scholar] [CrossRef]
- Wang, L.; Xu, J.; Qin, B.; Wen, M.; Chen, K. An Efficient Fuzzy Certificateless Signature-Based Authentication Scheme Using Anonymous Biometric Identities for VANETs. IEEE Trans. Dependable Secur. Comput. 2025, 22, 292–307. [Google Scholar] [CrossRef]
- Huang, X.; Mu, Y.; Susilo, W.; Wong, D.S.; Wu, W. Certificateless signatures: New schemes and security models. Comput. J. 2012, 55, 457–474. [Google Scholar] [CrossRef]
- Pointcheval, D.; Stern, J. Security arguments for digital signatures and blind signatures. J. Cryptol. 2000, 13, 361–396. [Google Scholar] [CrossRef]
- Bellare, M.; Neven, G. Multi-signatures in the plain public-key model and a general forking lemma. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 390–399. [Google Scholar]
- Kar, J.; Liu, X.; Li, F. CL-ASS: An efficient and low-cost certificateless aggregate signature scheme for wireless sensor networks. J. Inf. Secur. Appl. 2021, 61, 102905. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, Y.; Wang, J.; Yang, B.; Zhang, M. A Lightweight Cross-Domain Direct Identity Authentication Protocol for VANETs. IEEE Internet Things J. 2024, 11, 37741–37757. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Li, L.; Zhang, X.; Niu, S. A Certificateless Anonymous Cross-Domain Authentication Scheme Assisted by Blockchain for Internet of Vehicles. Wirel. Commun. Mob. Comput. 2022, 2022, 3488977. [Google Scholar] [CrossRef]
- Yang, X.; Li, S.; Yang, L.; Du, X.; Wang, C. Efficient and Security-Enhanced Certificateless Aggregate Signature-Based Authentication Scheme With Conditional Privacy Preservation for VANETs. IEEE Trans. Intell. Transp. Syst. 2024, 25, 12256–12268. [Google Scholar] [CrossRef]
- Ye, X.; Xu, G.; Cheng, X.; Li, Y.; Qin, Z. Certificateless-Based Anonymous Authentication and Aggregate Signature Scheme for Vehicular Ad Hoc Networks. Wirel. Commun. Mob. Comput. 2021, 2021, 6677137. [Google Scholar] [CrossRef]
- Zhu, F.; Yi, X.; Abuadbba, A.; Khalil, I.; Huang, X.; Xu, F. A security-enhanced certificateless conditional privacy-preserving authentication scheme for vehicular ad hoc networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10456–10466. [Google Scholar] [CrossRef]
- Tian, J.; Wang, Y.; Shen, Y. A Security-Enhanced Certificateless Anonymous Authentication Scheme with High Computational Efficiency for Mobile Edge Computing. IEEE Trans. Netw. Serv. Manag. 2025, 22, 3555–3572. [Google Scholar] [CrossRef]

| Scheme | Technologies | Unforgeability | GA a | DB b |
|---|---|---|---|---|
| [33] | ECC, Short signature | Type II weak | ✕ | ✕ |
| [34] | ECC, Registration-based encryption | ✔ | ✕ | ✕ |
| [35] | ECC, Private key double insurance | Type I weak | ✕ | ✕ |
| [36] | ECC, Pseudonym mechanism, Low resource consumption | Type I weak | ✕ | ✕ |
| [41] | ECC, Password-based auth., Vehicle membership alteration | ✔ | ✔ | ✕ |
| [42] | Chebyshev chaotic map, Fuzzy verification, Honeywords | ✔ | ✔ | ✕ |
| [43] | Bilinear mapping, CMOS memristor-based auth. | ✔ | ✔ | ✕ |
| [44] | ECC, Fuzzy extractor, Biometric-based auth. | ✔ | ✔ | ✕ |
| Symbol | Definition |
|---|---|
| Security parameter | |
| TA | Trust Authority |
| KGC | Key generation center |
| Sharing vehicle | |
| User | |
| s | Secret key of KGC |
| t | Secret key of TA |
| System parameters | |
| Identity of the vehicle | |
| Pseudonym of the vehicle | |
| Identity of the user | |
| Pseudonym of the user | |
| Public key of the vehicle | |
| Private key of the vehicle | |
| Private key of the user | |
| Category identifier | |
| z | Group identifier |
| Signature | |
| Identifier update secret | |
| Timestamp |
| Symbol | Meaning | Time (ms) |
|---|---|---|
| Bilinear Pairing | 27.844 | |
| Pairing-based Scalar Multiplication | 9.027 | |
| Pairing-based Point Addition | 0.055 | |
| Scalar Multiplication | 2.632 | |
| Point Addition | 0.018 | |
| Hash to Point Operation | 5.433 | |
| General Secure Hash | 0.001 |
| Scheme | Pairing-Free | Unforgeability | Revocation | User Decoupling | Category Range Selection |
|---|---|---|---|---|---|
| [48] | ✕ | ✔ | ✕ | ✕ | ✕ |
| [49] | ✔ | ✔ | ✔ | ✕ | ✕ |
| [50] | ✔ | ✔ | ✔ | ✕ | ✕ |
| [51] | ✔ | ✔ | ✕ | ✕ | ✕ |
| [52] | ✔ | ✕ | ✕ | ✕ | ✕ |
| [53] | ✔ | ✕ | ✕ | ✕ | ✕ |
| [54] | ✔ | ✔ | ✕ | ✔ | ✕ |
| Our scheme | ✔ | ✔ | ✔ | ✔ | ✔ |
| Scheme | Computational Overhead | Communication Overhead (byte) | |
|---|---|---|---|
| Signature Generation (ms) | Signature Validation (ms) | ||
| [48] | |||
| [49] | |||
| [50] | |||
| [51] | |||
| [52] | |||
| [53] | |||
| [54] | |||
| Our scheme | |||
| Scheme | Support Revocation | Method | Overhead Complexity |
|---|---|---|---|
| [48] | ✕ | N/A | N/A |
| [49] | ✔ | Revocation list | Linear |
| [50] | ✔ | Blockchain database | Linear |
| [51] | ✕ | N/A | N/A |
| [52] | ✔ | Revocation list | Linear |
| [53] | ✕ | N/A | N/A |
| [54] | ✕ | N/A | N/A |
| Our scheme | ✔ | CRT | Constant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Kou, X.; Yang, T. ECACS: An Enhanced Certificateless Authentication Scheme for Smart Car Sharing. Sensors 2025, 25, 5441. https://doi.org/10.3390/s25175441
Shen Z, Kou X, Yang T. ECACS: An Enhanced Certificateless Authentication Scheme for Smart Car Sharing. Sensors. 2025; 25(17):5441. https://doi.org/10.3390/s25175441
Chicago/Turabian StyleShen, Zhuowei, Xiao Kou, and Taiyao Yang. 2025. "ECACS: An Enhanced Certificateless Authentication Scheme for Smart Car Sharing" Sensors 25, no. 17: 5441. https://doi.org/10.3390/s25175441
APA StyleShen, Z., Kou, X., & Yang, T. (2025). ECACS: An Enhanced Certificateless Authentication Scheme for Smart Car Sharing. Sensors, 25(17), 5441. https://doi.org/10.3390/s25175441







