Machine Learning Approaches for Geospatial Modeling of Urban Land Surface Temperature: Assessing Geographical Compactness, Interpretability, and Causal Inference
Abstract
1. Introduction
2. Research Method and Materials
2.1. Study Area and the Remote Sensing Data
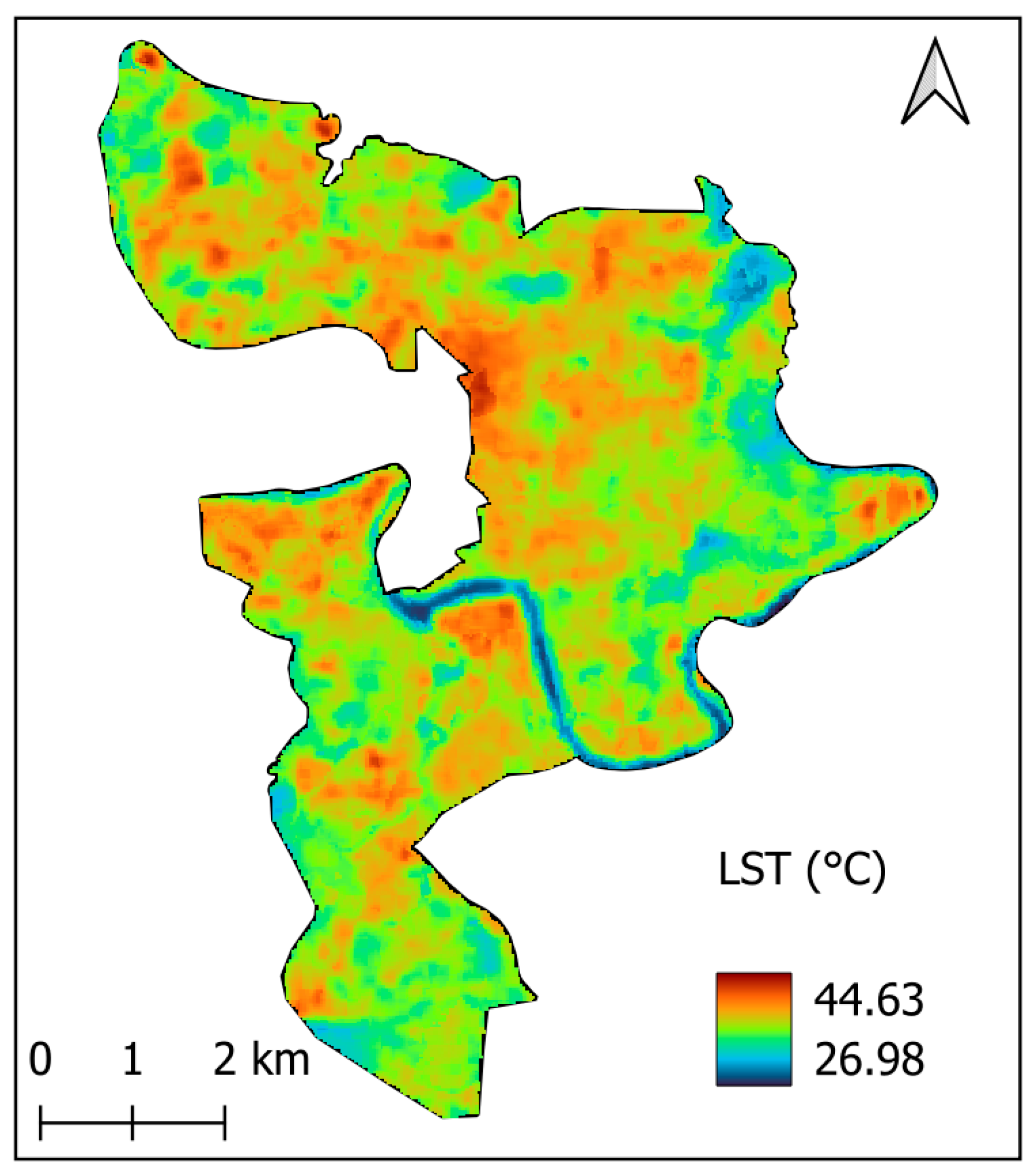
2.2. Land Surface Temperature Retrieval and Assessment of Heat Stress
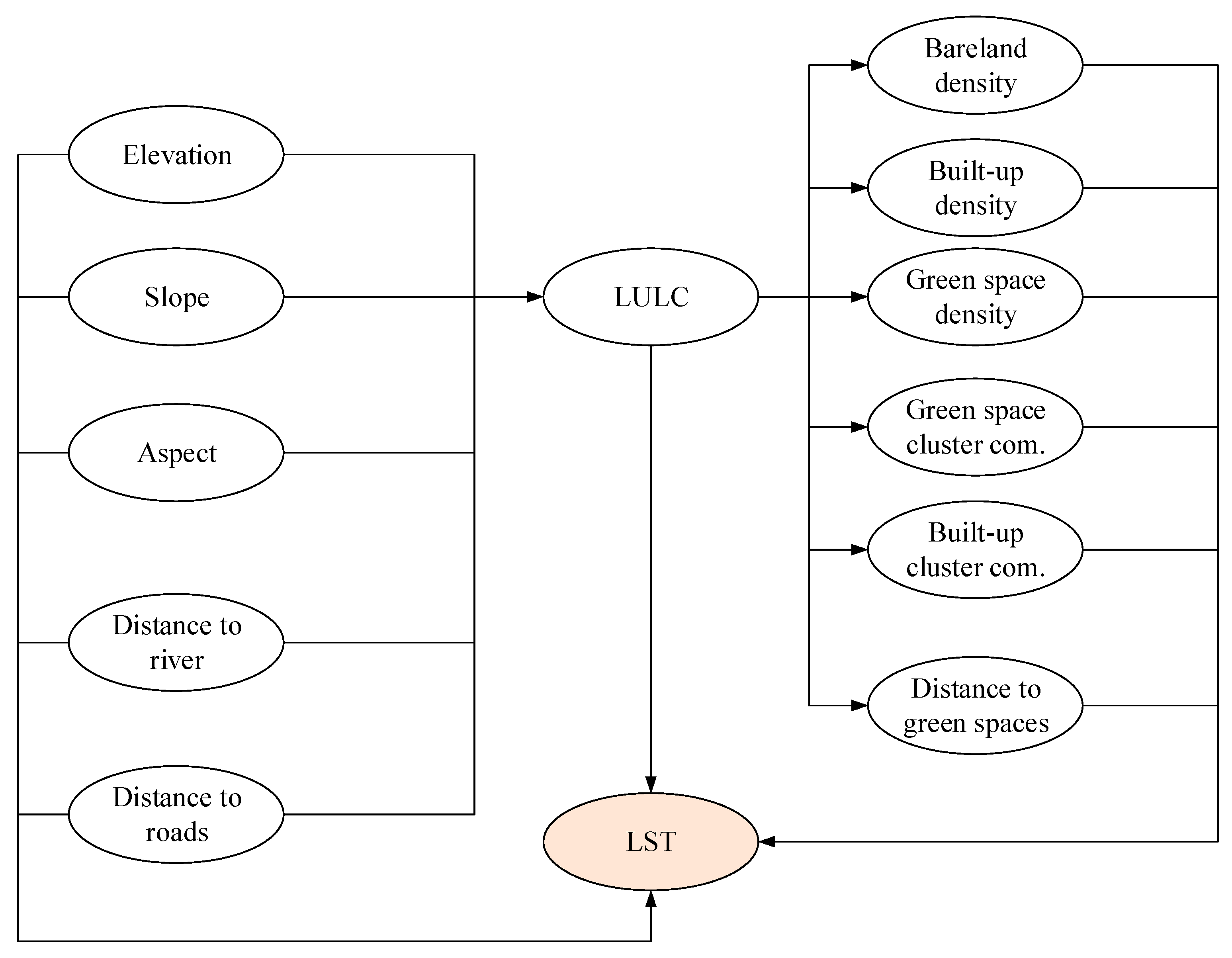
2.3. Remote Sensing-Based Feature Selection
2.3.1. Topographical Features
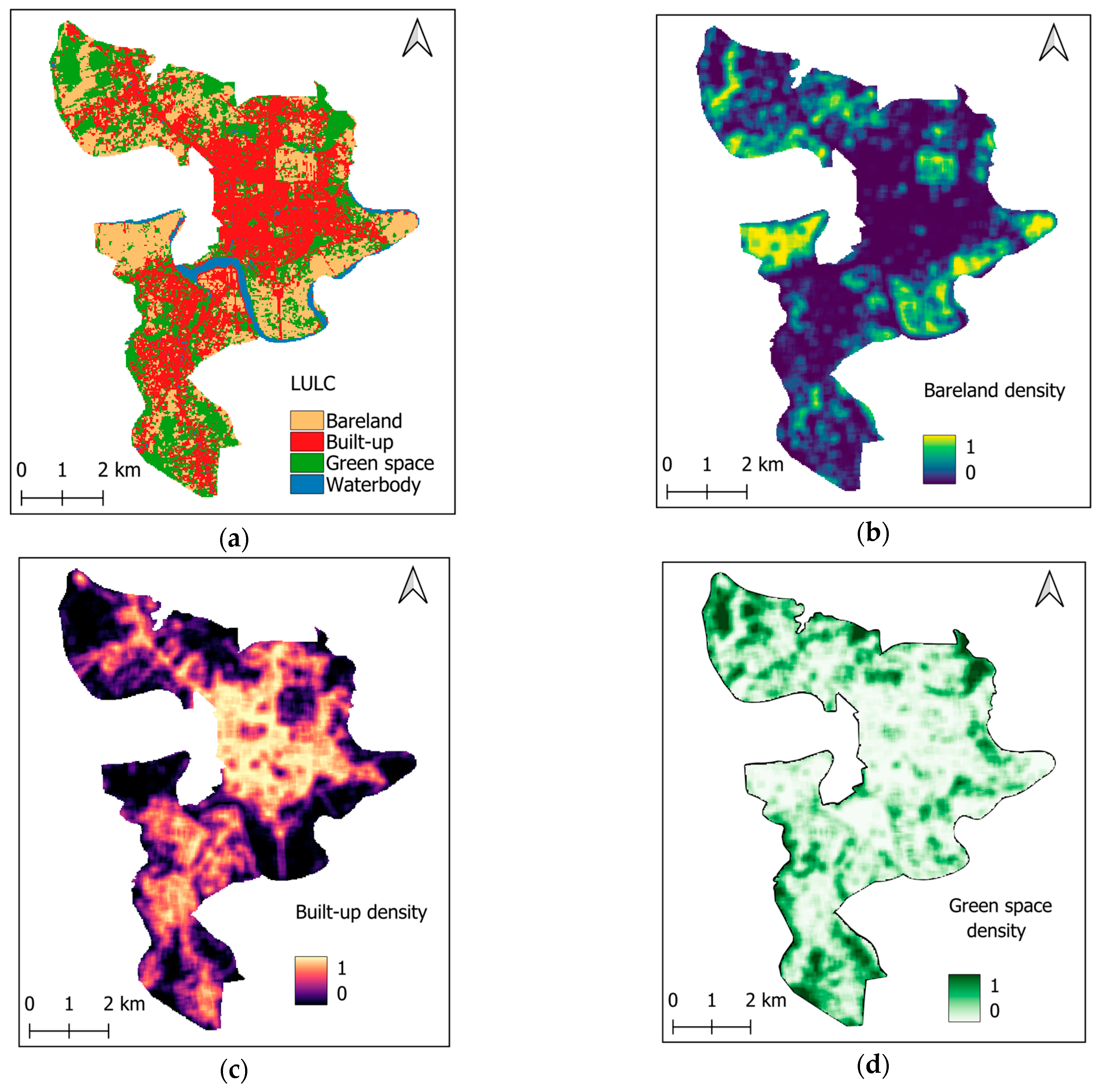
2.3.2. LULC and Density-Related Features
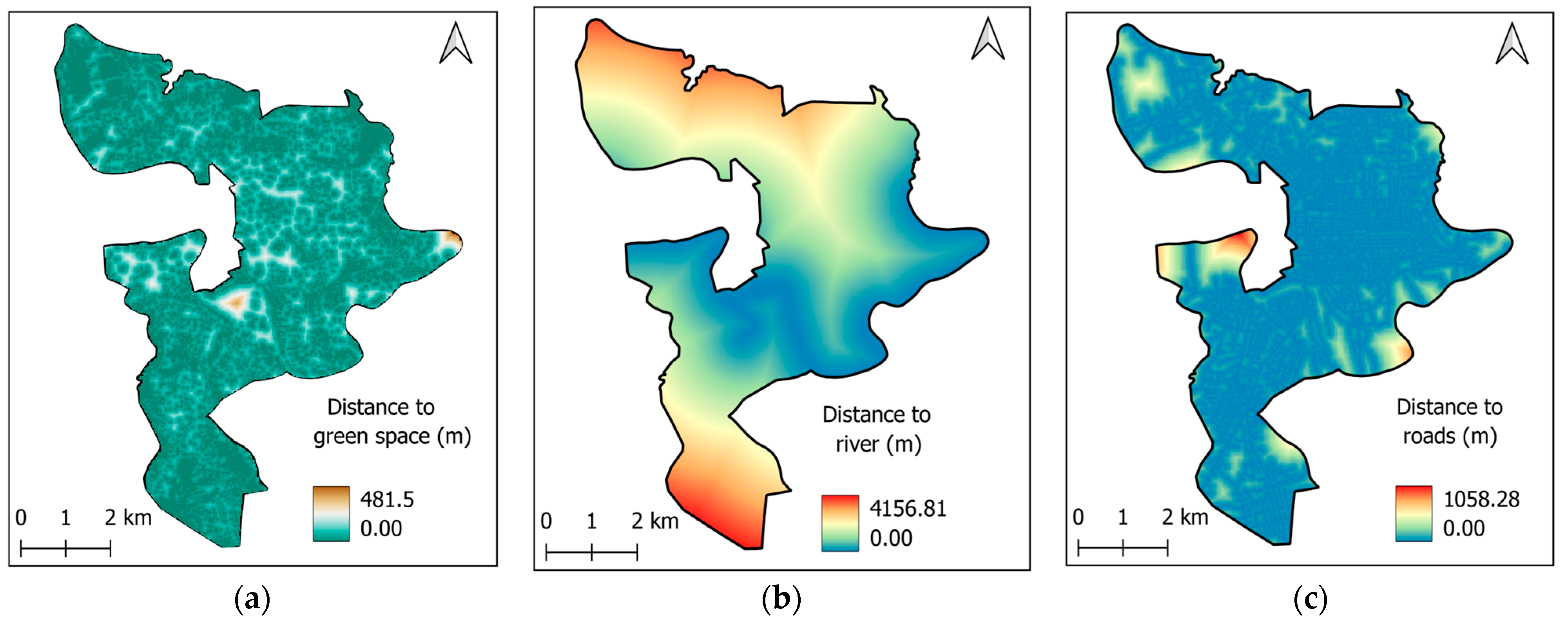
2.3.3. Proximity Features
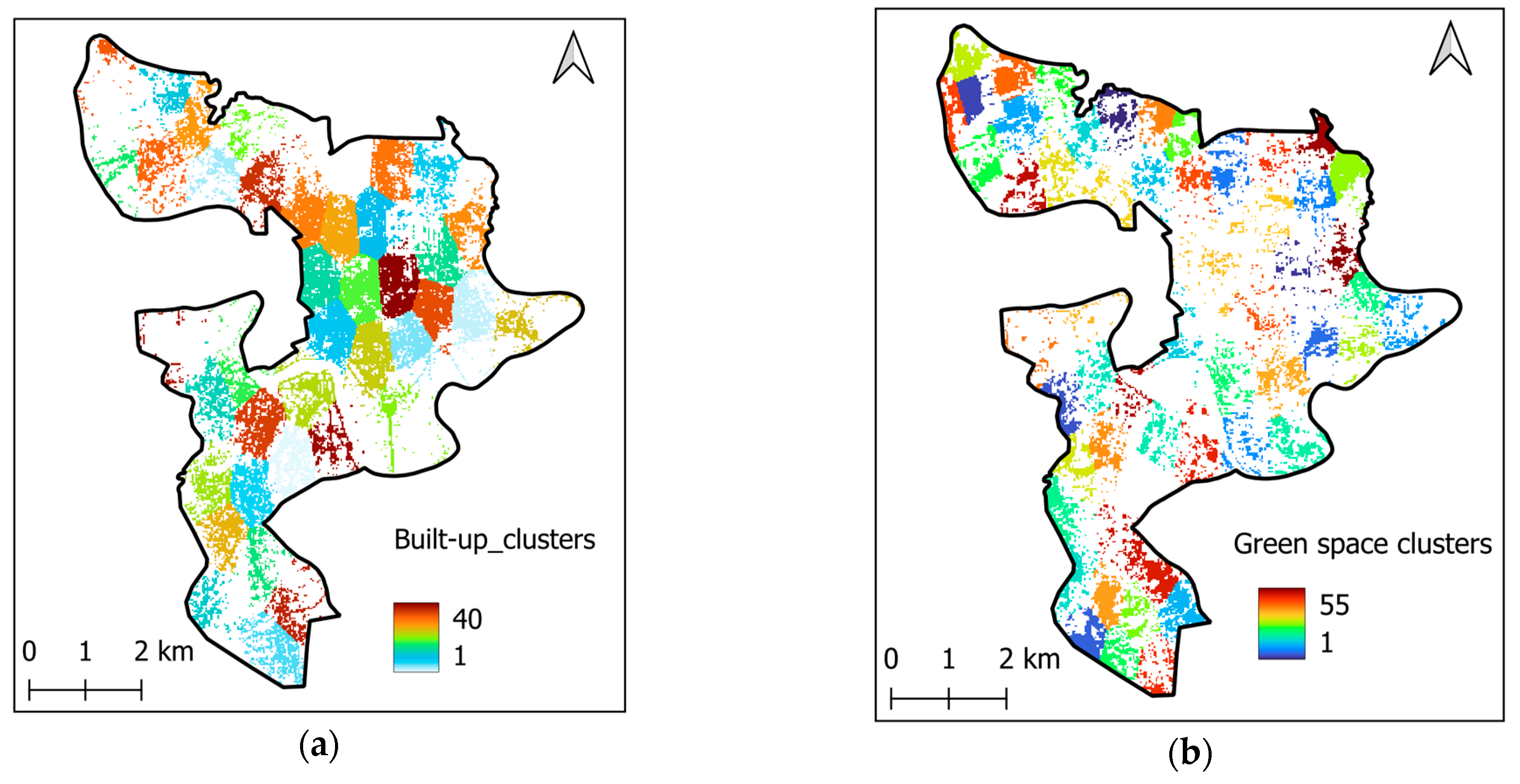
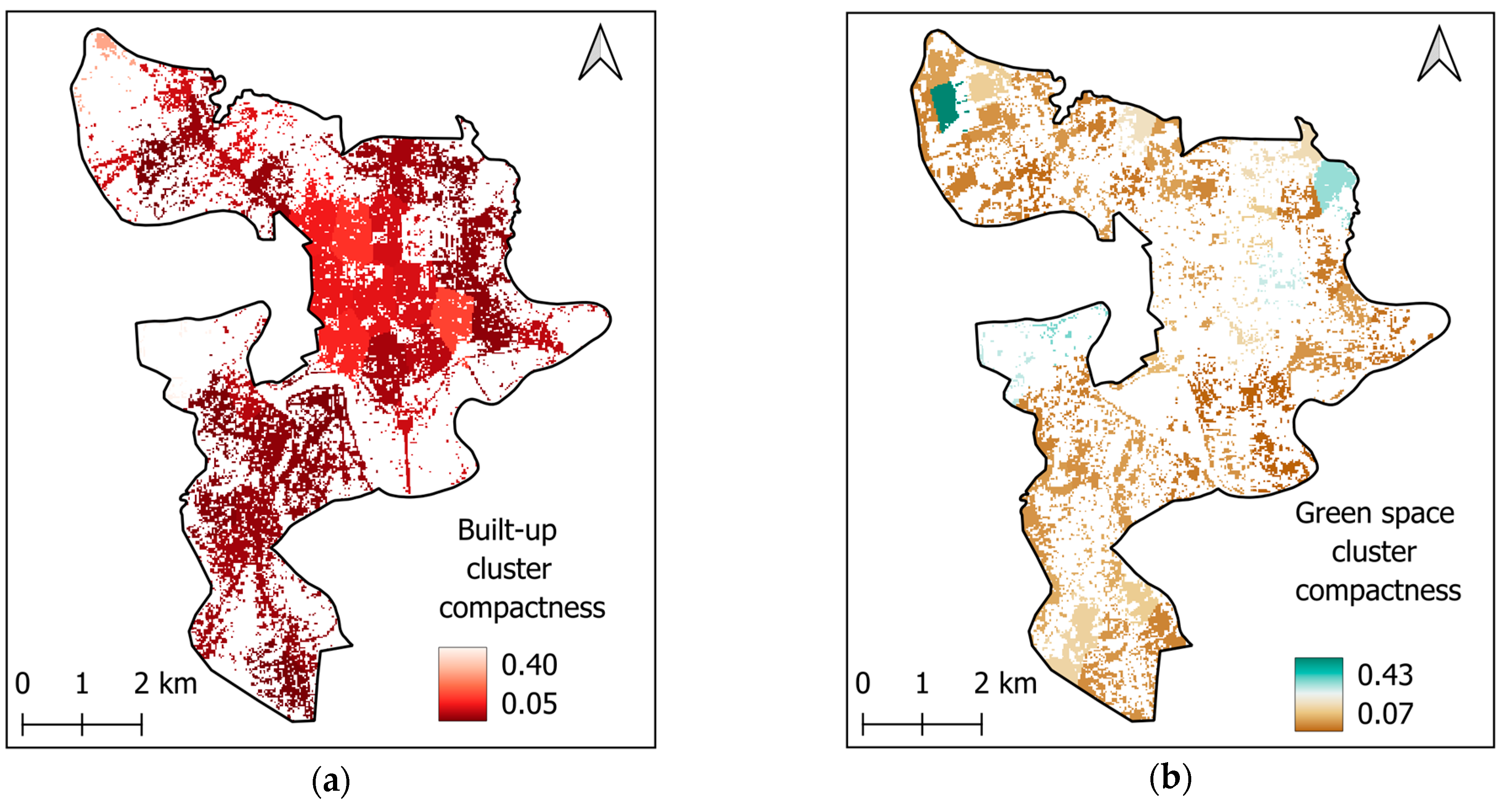
2.3.4. Geographical Compactness Assessment Based on k-Means Clustering and the Polsby–Popper Index
2.4. Modeling Approach
2.4.1. CatBoost Regressor
2.4.2. Convolutional Neural Network Regressor
2.5. Model Evaluation
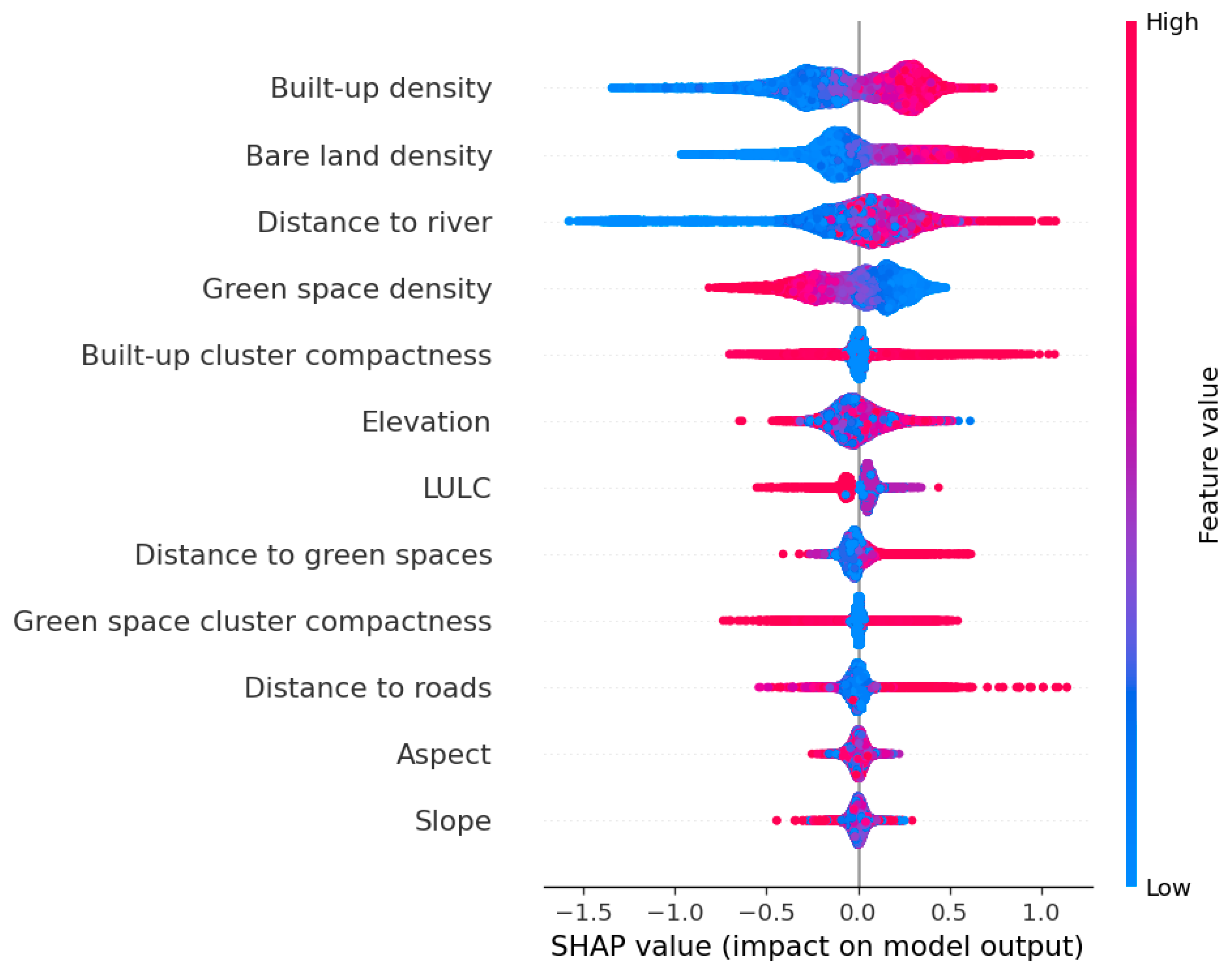
2.6. Shapley Additive Explanations (SHAP) for Feature Analysis
2.7. Machine Learning-Based Causal Inference
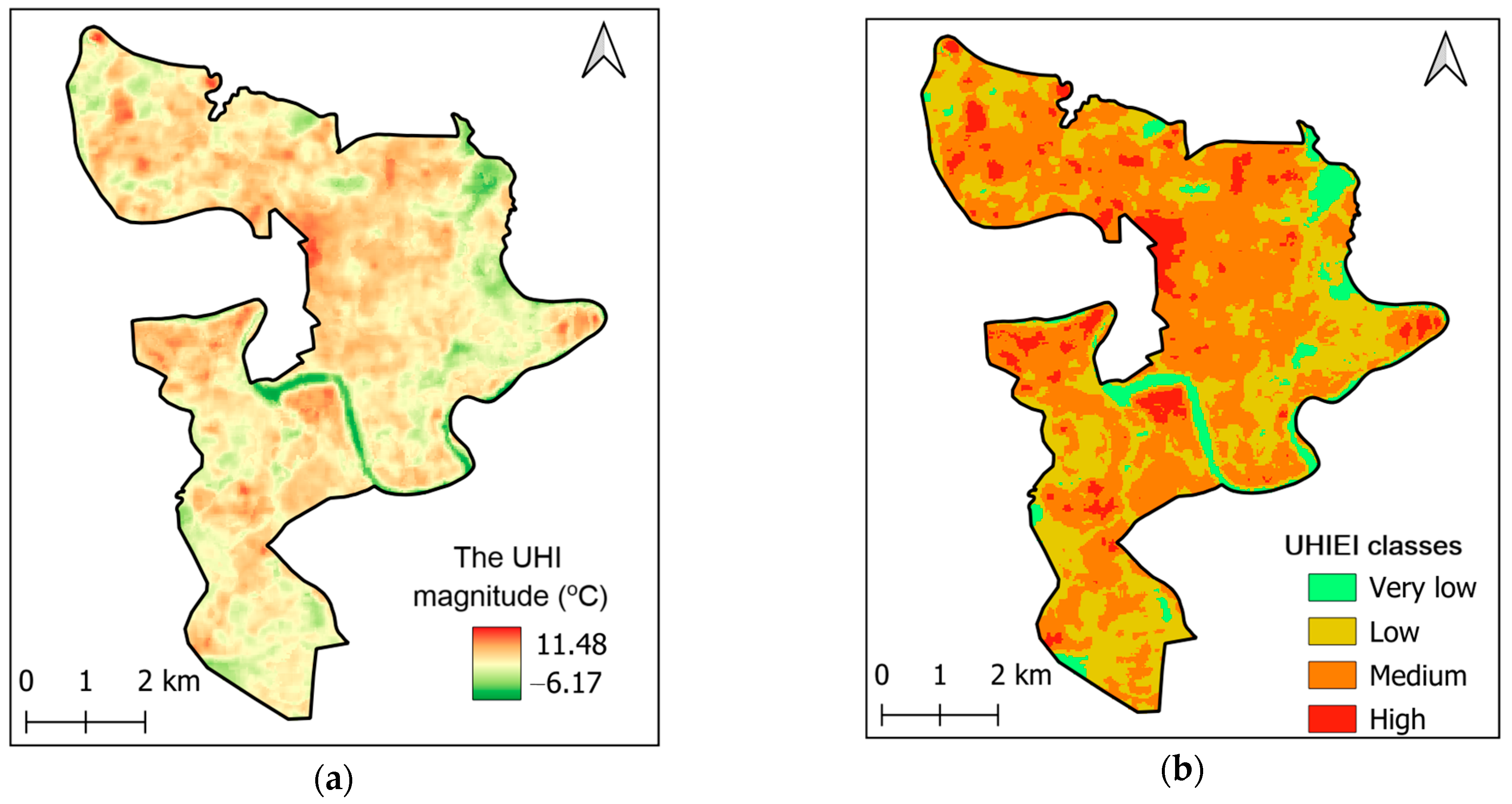
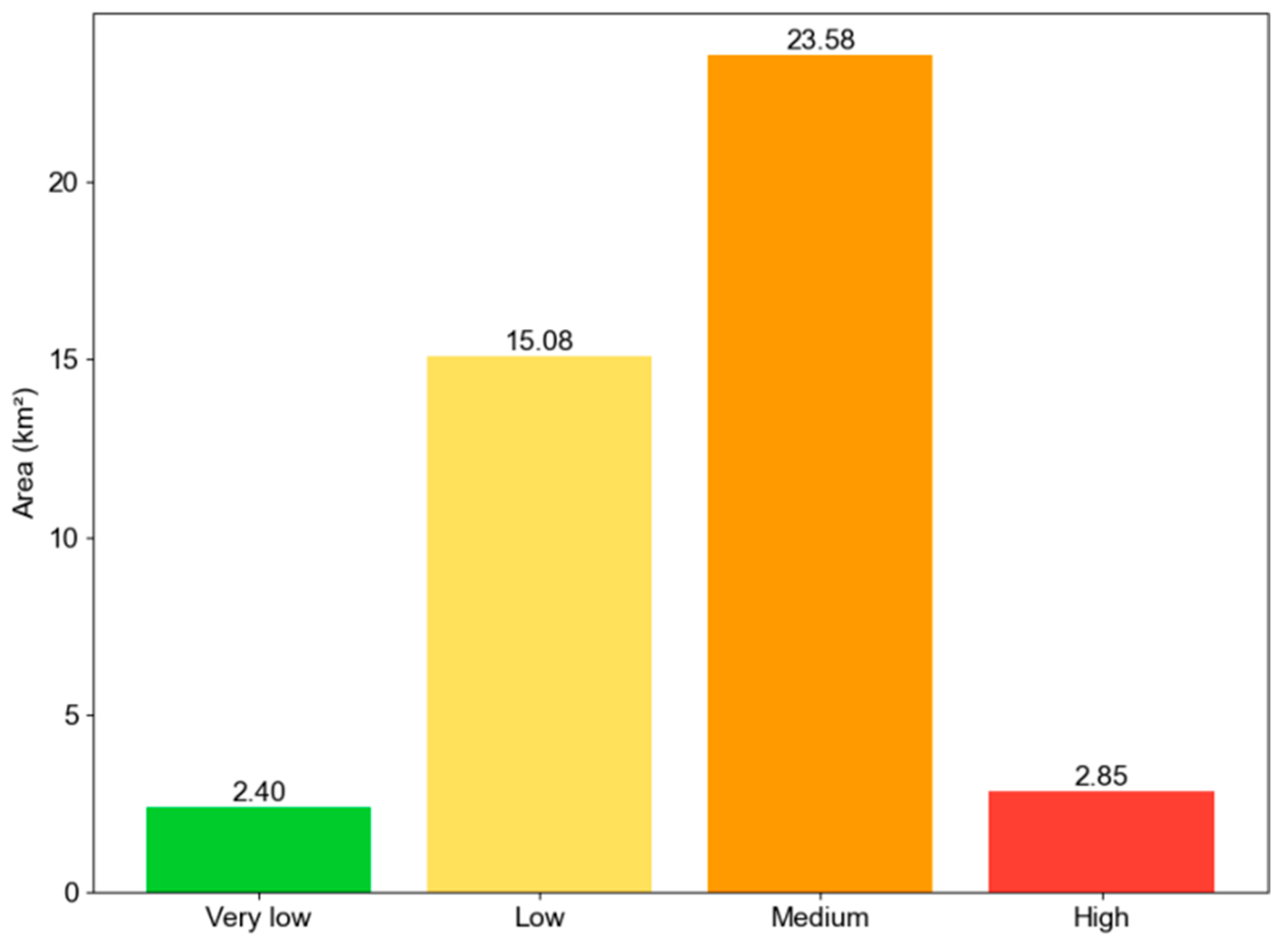
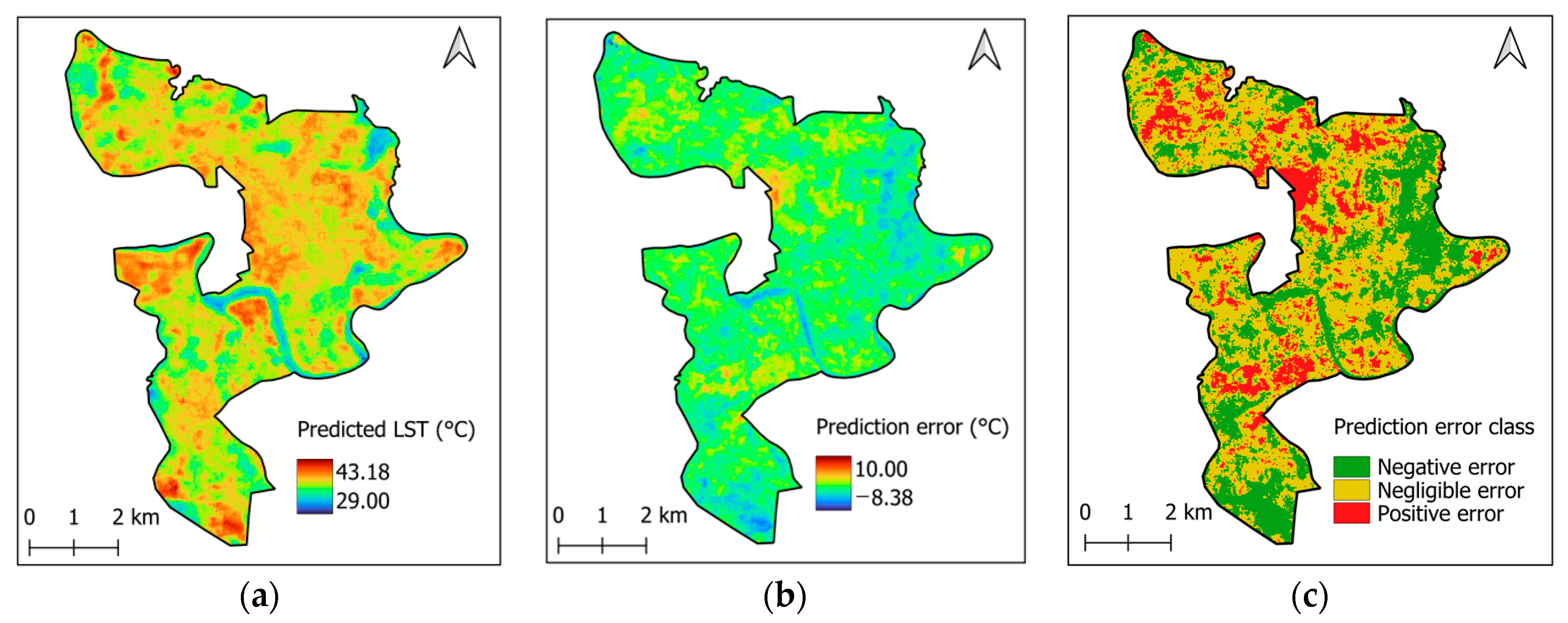
3. Prediction Results
4. Discussion
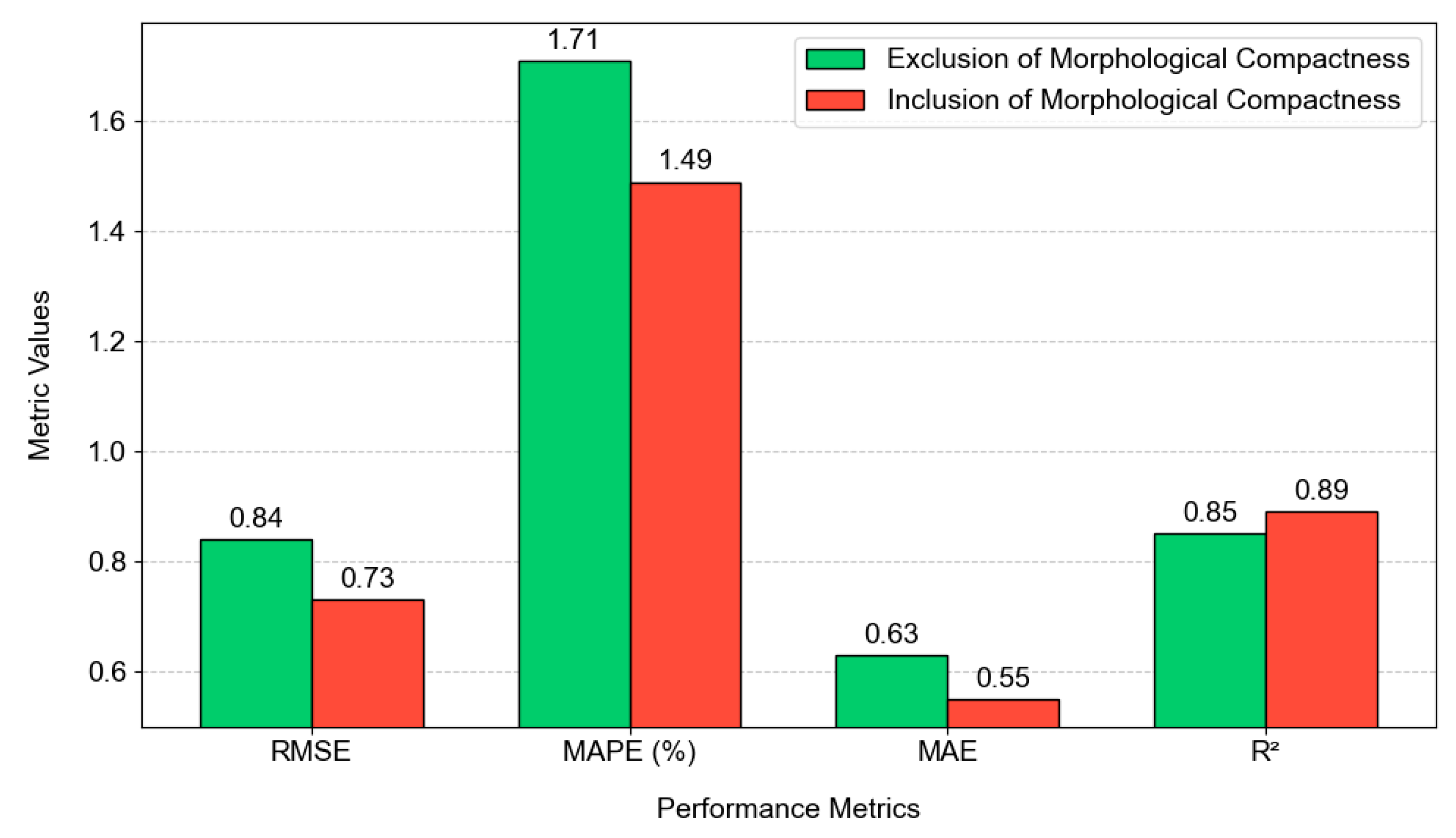
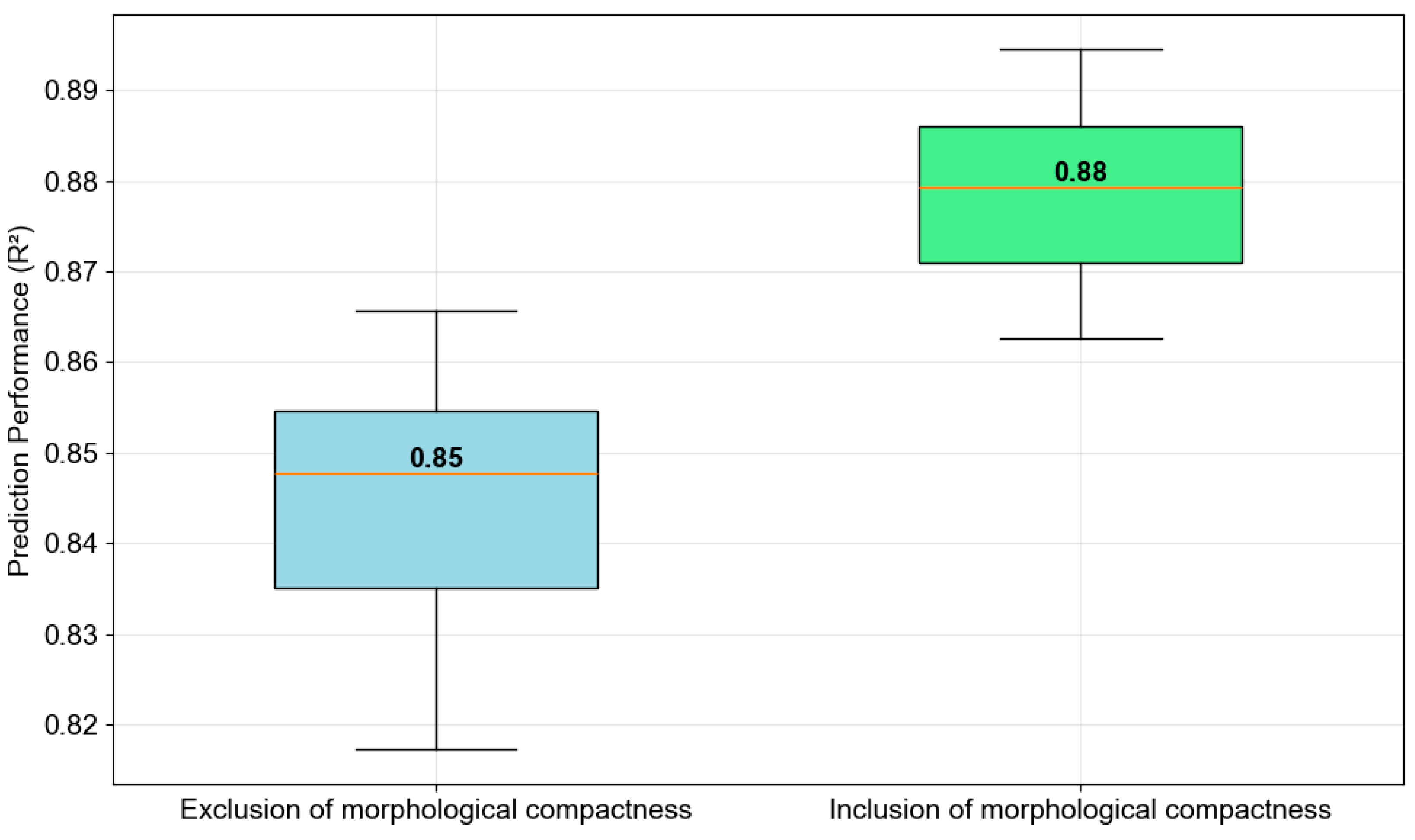
4.1. Machine Learning Performance
4.2. Implications for Urban Heat Stress Mitigation
4.3. Limitations and Future Works
5. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- UN. 68% of the World Population Projected to Live in Urban Areas by 2050, Says UN; Department of Economic and Social Affairs, United Nations: New York, NY, USA, 2018; Available online: https://www.un.org/uk/desa/68-world-population-projected-live-urban-areas-2050-says-un (accessed on 17 June 2025).
- Seto, K.C.; Güneralp, B.; Hutyra, L.R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef] [PubMed]
- Eshetie, S.M. Exploring urban land surface temperature using spatial modelling techniques: A case study of Addis Ababa city, Ethiopia. Sci. Rep. 2024, 14, 6323. [Google Scholar] [CrossRef] [PubMed]
- Hoang, T.L.T.; Dao, H.N.; Cu, P.T.; Tran, V.T.T.; Tong, T.P.; Hoang, S.T.; Vuong, V.V.; Nguyen, T.N. Assessing heat index changes in the context of climate change: A case study of Hanoi (Vietnam). Front. Earth Sci. 2022, 10, 897601. [Google Scholar] [CrossRef]
- Thanh, P.N.; Le Van, T.; Thi, X.A.T.; Hai, A.N.; Le Cong, C.; Gagnon, A.S.; Pham, N.T.; Anh, D.T.; Dinh, V.N. Predicting drought stress under climate change in the Southern Central Highlands of Vietnam. Environ. Monit. Assess. 2024, 196, 636. [Google Scholar] [CrossRef]
- Pham-Thanh, H.; Pham-Thi, L.; Phan, H.; Fink, A.H.; van der Linden, R.; Phan-Van, T. Heatwaves in Vietnam: Characteristics and relationship with large-scale climate drivers. Int. J. Climatol. 2024, 44, 4725–4740. [Google Scholar] [CrossRef]
- Pham Thi, L.; Pham Thanh, H.; Phan Van, T.; Vu Thuan, Y. Variability of heatwaves across Vietnam in recent decades. Vietnam J. Earth Sci. 2023, 45, 517–530. [Google Scholar] [CrossRef]
- Le Hung, T.; Zablotskii, V.R.; Zenkov, I.V.; Vu, D.T.; Dao, K.H. Relationship between the Land Surface Temperature and Land Cover Types, a Case Study in Hanoi City, Vietnam. Izv. Atmos. Ocean. Phys. 2022, 58, 1111–1120. [Google Scholar] [CrossRef]
- Chakrabortty, R.; Pramanik, M.; Hasan, M.M.; Halder, B.; Pande, C.B.; Moharir, K.N.; Zhran, M. Mitigating Urban Heat Islands in the Global South: Data-driven Approach for Effective Cooling Strategies. Earth Syst. Environ. 2025, 9, 447–474. [Google Scholar] [CrossRef]
- Khalil, M.; Kumar, J.S. Assessing Urban Heat Island Intensity in Damascus City Using Google Earth Engine and Landsat 8 and 9: A Comparative Analysis. Remote Sens. Earth Syst. Sci. 2025, 8, 576–592. [Google Scholar] [CrossRef]
- Waleed, M.; Sajjad, M. Leveraging cloud-based computing and spatial modeling approaches for land surface temperature disparities in response to land cover change: Evidence from Pakistan. Remote Sens. Appl. Soc. Environ. 2022, 25, 100665. [Google Scholar] [CrossRef]
- Kara, Y.; Yavuz, V.; Lupo, A.R. Multi-Index Assessment of Surface Urban Heat Island (SUHI) Dynamics in Samsun Using Google Earth Engine. Atmosphere 2025, 16, 712. [Google Scholar] [CrossRef]
- Duan, X.; Haseeb, M.; Tahir, Z.; Mahmood, S.A.; Tariq, A.; Jamil, A.; Ullah, S.; Abdullah-Al-Wadud, M. A geospatial and statistical analysis of land surface temperature in response to land use land cover changes and urban heat island dynamics. Sci. Rep. 2025, 15, 4943. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Pham, P.A.H.; Huynh, T.C.; Cao, M.-T.; Bui, D.-T. Geospatial urban heat mapping with interpretable machine learning and deep learning: A case study in Hue City, Vietnam. Earth Sci. Inform. 2024, 18, 64. [Google Scholar] [CrossRef]
- Al-Hameedi, W.M.M.; Chen, J.; Faichia, C.; Nath, B.; Al-Shaibah, B.; Al-Aizari, A. Geospatial Analysis of Land Use/Cover Change and Land Surface Temperature for Landscape Risk Pattern Change Evaluation of Baghdad City, Iraq, Using CA–Markov and ANN Models. Sustainability 2022, 14, 8568. [Google Scholar] [CrossRef]
- Sidiqui, P.; Roös, P.B.; Herron, M.; Jones, D.S.; Duncan, E.; Jalali, A.; Allam, Z.; Roberts, B.J.; Schmidt, A.; Tariq, M.A.U.R.; et al. Urban Heat Island vulnerability mapping using advanced GIS data and tools. J. Earth Syst. Sci. 2022, 131, 266. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Zhou, Y.; Liu, D.; Wang, H. The dominant factors and influence of urban characteristics on land surface temperature using random forest algorithm. Sustain. Cities Soc. 2022, 79, 103722. [Google Scholar] [CrossRef]
- Tanoori, G.; Soltani, A.; Modiri, A. Machine Learning for Urban Heat Island (UHI) Analysis: Predicting Land Surface Temperature (LST) in Urban Environments. Urban Clim. 2024, 55, 101962. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Tran, V.-D.; Huynh, T.-C. From Data to Insights: Modeling Urban Land Surface Temperature Using Geospatial Analysis and Interpretable Machine Learning. Sensors 2025, 25, 1169. [Google Scholar] [CrossRef]
- Bushenkova, A.; Soares, P.M.M.; Johannsen, F.; Lima, D.C.A. Towards an improved representation of the urban heat island effect: A multi-scale application of XGBoost for madrid. Urban Clim. 2024, 55, 101982. [Google Scholar] [CrossRef]
- Bansal, P.; Quan, S.J. Examining temporally varying nonlinear effects of urban form on urban heat island using explainable machine learning: A case of Seoul. Build. Environ. 2024, 247, 110957. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, R.; Rui, J.; Yu, Y. Revealing the impact of urban spatial morphology on land surface temperature in plain and plateau cities using explainable machine learning. Sustain. Cities Soc. 2025, 118, 106046. [Google Scholar] [CrossRef]
- Mansourmoghaddam, M.; Rousta, I.; Ghafarian Malamiri, H.; Sadeghnejad, M.; Krzyszczak, J.; Ferreira, C.S.S. Modeling and Estimating the Land Surface Temperature (LST) Using Remote Sensing and Machine Learning (Case Study: Yazd, Iran). Remote Sens. 2024, 16, 454. [Google Scholar] [CrossRef]
- Ghorbany, S.; Hu, M.; Yao, S.; Wang, C. Towards a Sustainable Urban Future: A Comprehensive Review of Urban Heat Island Research Technologies and Machine Learning Approaches. Sustainability 2024, 16, 4609. [Google Scholar] [CrossRef]
- Mohammad, P.; Goswami, A.; Chauhan, S.; Nayak, S. Machine learning algorithm based prediction of land use land cover and land surface temperature changes to characterize the surface urban heat island phenomena over Ahmedabad city, India. Urban Clim. 2022, 42, 101116. [Google Scholar] [CrossRef]
- Pande, C.B.; Egbueri, J.C.; Costache, R.; Sidek, L.M.; Wang, Q.; Alshehri, F.; Din, N.M.; Gautam, V.K.; Chandra Pal, S. Predictive modeling of land surface temperature (LST) based on Landsat-8 satellite data and machine learning models for sustainable development. J. Clean. Prod. 2024, 444, 141035. [Google Scholar] [CrossRef]
- Hou, H.; Longyang, Q.; Su, H.; Zeng, R.; Xu, T.; Wang, Z.-H. Prioritizing environmental determinants of urban heat islands: A machine learning study for major cities in China. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103411. [Google Scholar] [CrossRef]
- Suthar, G.; Kaul, N.; Khandelwal, S.; Singh, S. Predicting land surface temperature and examining its relationship with air pollution and urban parameters in Bengaluru: A machine learning approach. Urban Clim. 2024, 53, 101830. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.; Qiao, X. Evaluating the impact of urbanization patterns on LST and UHI effect in Afghanistan’s Cities: A machine learning approach for sustainable urban planning. Environ. Dev. Sustain. 2025. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Tan, P.Y.; Rinaldi, B.M. Landscapes for compact cities. J. Landsc. Archit. 2019, 14, 4–7. [Google Scholar] [CrossRef]
- Xing, X.; Shi, W.; Wu, X.; Liu, Y.; Wang, X.; Zhang, Y. Towards a more compact urban form: A spatial-temporal study on the multi-dimensional compactness index of urban form in China. Appl. Geogr. 2024, 171, 103368. [Google Scholar] [CrossRef]
- Yan, H.; Wang, K.; Lin, T.; Zhang, G.; Sun, C.; Hu, X.; Ye, H. The Challenge of the Urban Compact Form: Three-Dimensional Index Construction and Urban Land Surface Temperature Impacts. Remote Sens. 2021, 13, 1067. [Google Scholar] [CrossRef]
- Polsby, D.D.; Popper, R.D. The Third Criterion: Compactness as a Procedural Safeguard against Partisan Gerrymandering. Yale Law Policy Rev. 1991, 9, 301–353. [Google Scholar] [CrossRef]
- Shukla, A.; Jain, K. Critical analysis of spatial-temporal morphological characteristic of urban landscape. Arab. J. Geosci. 2019, 12, 112. [Google Scholar] [CrossRef]
- Calhoun, Z.D.; Willard, F.; Ge, C.; Rodriguez, C.; Bergin, M.; Carlson, D. Estimating the effects of vegetation and increased albedo on the urban heat island effect with spatial causal inference. Sci. Rep. 2024, 14, 540. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, S.; Liang, X.; Guan, Q. Causal inference of urban heat island effect and its spatial heterogeneity: A case study of Wuhan, China. Sustain. Cities Soc. 2024, 115, 105850. [Google Scholar] [CrossRef]
- Assaf, G.; Hu, X.; Assaad, R.H. Mining and modeling the direct and indirect causalities among factors affecting the Urban Heat Island severity using structural machine learned Bayesian networks. Urban Clim. 2023, 49, 101570. [Google Scholar] [CrossRef]
- Zhang, Y.; Weibo, M.; Nan, W.; Lijun, Z.; Qingwu, H.; Shaogang, L.; Li, H. Detection of driving factors and critical thresholds for carbon sequestration capacity in urban agglomerations using a combined causal inference and machine learning approach. GISci. Remote Sens. 2025, 62, 2483492. [Google Scholar] [CrossRef]
- Mallick, J.; Alqadhi, S. Explainable artificial intelligence models for proposing mitigation strategies to combat urbanization impact on land surface temperature dynamics in Saudi Arabia. Urban Clim. 2025, 59, 102259. [Google Scholar] [CrossRef]
- Ullah, S.; Qiao, X.; Abbas, M. Addressing the impact of land use land cover changes on land surface temperature using machine learning algorithms. Sci. Rep. 2024, 14, 18746. [Google Scholar] [CrossRef]
- Ta Huu, C.; Phan Van, T.; Mai Van, K.; Vu Van, T.; Hoang Phuc, L.; Lohpaisankrit, W.; Bao Pham, Q.; Trong Nguyen, T.; Nguyen Thanh, P. Spatiotemporal Variability of Hot Days in Association with the Large-Scale Atmospheric Drivers over Vietnam. Adv. Meteorol. 2023, 2023, 6612199. [Google Scholar] [CrossRef]
- Rhee, J.; Seonyoung, P.; Lu, Z. Relationship between land cover patterns and surface temperature in urban areas. GISci. Remote Sens. 2014, 51, 521–536. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- GEE. USGS Landsat 8 Level 2, Collection 2, Tier 1. 2024 Earth Engine Data Catalog. Available online: https://developers.google.com/earth-engine/datasets/catalog/LANDSAT_LC08_C02_T1_L2 (accessed on 19 May 2024).
- Hou, H.; Estoque, R.C. Detecting Cooling Effect of Landscape from Composition and Configuration: An Urban Heat Island Study on Hangzhou. Urban For. Urban Green. 2020, 53, 126719. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Petrou, I.; Kassomenos, P. Estimating the importance of environmental factors influencing the urban heat island for urban areas in Greece: A machine learning approach. J. Environ. Manag. 2024, 368, 122255. [Google Scholar] [CrossRef]
- Martin-Vide, J.; Sarricolea, P.; Moreno-García, M.C. On the definition of urban heat island intensity: The “rural” reference. Front. Earth Sci. 2015, 3, 24. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, J.; Yang, X.; Fang, C.; Liang, Y. Quantifying the seasonal contribution of coupling urban land use types on Urban Heat Island using Land Contribution Index: A case study in Wuhan, China. Sustain. Cities Soc. 2019, 44, 666–675. [Google Scholar] [CrossRef]
- Lu, L.; Weng, Q.; Xiao, D.; Guo, H.; Li, Q.; Hui, W. Spatiotemporal Variation of Surface Urban Heat Islands in Relation to Land Cover Composition and Configuration: A Multi-Scale Case Study of Xi’an, China. Remote Sens. 2020, 12, 2713. [Google Scholar] [CrossRef]
- Rengma, N.S.; Yadav, M. A generic machine learning-based framework for predictive modeling of land surface temperature. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-4/W2-2022, 95–102. [Google Scholar] [CrossRef]
- Zhao, W.; Duan, S.-B.; Li, A.; Yin, G. A practical method for reducing terrain effect on land surface temperature using random forest regression. Remote Sens. Environ. 2019, 221, 635–649. [Google Scholar] [CrossRef]
- Khandelwal, S.; Goyal, R.; Kaul, N.; Mathew, A. Assessment of land surface temperature variation due to change in elevation of area surrounding Jaipur, India. Egypt. J. Remote Sens. Space Sci. 2018, 21, 87–94. [Google Scholar] [CrossRef]
- Phan, T.N.; Kappas, M.; Tran, T.P. Land Surface Temperature Variation Due to Changes in Elevation in Northwest Vietnam. Climate 2018, 6, 28. [Google Scholar] [CrossRef]
- He, J.; Zhao, W.; Li, A.; Wen, F.; Yu, D. The impact of the terrain effect on land surface temperature variation based on Landsat-8 observations in mountainous areas. Int. J. Remote Sens. 2019, 40, 1808–1827. [Google Scholar] [CrossRef]
- Patel, S.; Indraganti, M.; Jawarneh, R.N. A comprehensive systematic review: Impact of Land Use/Land Cover (LULC) on Land Surface Temperatures (LST) and outdoor thermal comfort. Build. Environ. 2024, 249, 111130. [Google Scholar] [CrossRef]
- Kafy, A.A.; Rahman, M.S.; Faisal, A.-A.; Hasan, M.M.; Islam, M. Modelling future land use land cover changes and their impacts on land surface temperatures in Rajshahi, Bangladesh. Remote Sens. Appl. Soc. Environ. 2020, 18, 100314. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Nguyen, Q.-L. Geospatial Analysis and Machine Learning Framework for Urban Heat Island Intensity Prediction: Natural Gradient Boosting and Deep Neural Network Regressors with Multisource Remote Sensing Data. Sustainability 2025, 17, 4287. [Google Scholar] [CrossRef]
- Wai, C.Y.; Tariq, M.A.U.R.; Muttil, N.; Chau, H.-W. Assessing Socio-Economic Vulnerabilities to Urban Heat: Correlations with Land Use and Urban Morphology in Melbourne, Australia. Land 2025, 14, 958. [Google Scholar] [CrossRef]
- Liu, W.; Jia, B.; Li, T.; Zhang, Q.; Ma, J. Correlation Analysis between Urban Green Space and Land Surface Temperature from the Perspective of Spatial Heterogeneity: A Case Study within the Sixth Ring Road of Beijing. Sustainability 2022, 14, 13492. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, F.; Zhang, M.; Meng, Q.; Jim, C.Y.; Shi, J.; Tan, M.L.; Ma, X. Landscape and vegetation traits of urban green space can predict local surface temperature. Sci. Total Environ. 2022, 825, 154006. [Google Scholar] [CrossRef]
- Park, C.Y.; Lee, D.K.; Asawa, T.; Murakami, A.; Kim, H.G.; Lee, M.K.; Lee, H.S. Influence of urban form on the cooling effect of a small urban river. Landsc. Urban Plan. 2019, 183, 26–35. [Google Scholar] [CrossRef]
- Hathway, E.A.; Sharples, S. The interaction of rivers and urban form in mitigating the Urban Heat Island effect: A UK case study. Build. Environ. 2012, 58, 14–22. [Google Scholar] [CrossRef]
- Cao, A.; Li, Q.; Meng, Q. Effects of Orientation of Urban Roads on the Local Thermal Environment in Guangzhou City. Procedia Eng. 2015, 121, 2075–2082. [Google Scholar] [CrossRef]
- Ni, X.; Huang, H.; Zhou, S.; Su, B.; Meng, Y.; Huang, Z. Spatial data mining and O-D hotspots discovery in cities based on an O-D hotspots clustering model using vehicles’ GPS data: A case study in the morning rush hours in Beijing, China. In Proceedings of the 4th ACM SIGSPATIAL International Workshop on Safety and Resilience, Seattle, WA, USA, 6 November 2018. [Google Scholar]
- Zawadzka, J.E.; Harris, J.A.; Corstanje, R. A simple method for determination of fine resolution urban form patterns with distinct thermal properties using class-level landscape metrics. Landsc. Ecol. 2021, 36, 1863–1876. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Sarif, M.O.; Gupta, R.D. Comparative evaluation between Shannon’s entropy and spatial metrics in exploring the spatiotemporal dynamics of urban morphology: A case study of Prayagraj City, India (1988–2018). Spat. Inf. Res. 2021, 29, 961–979. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Tran, Q.T.; Ngo, C.T.; Nguyen, D.D.; Tran, V.Q. Solar energy prediction through machine learning models: A comparative analysis of regressor algorithms. PLoS ONE 2025, 20, e0315955. [Google Scholar] [CrossRef]
- Vishwakarma, D.K.; Kumar, P.; Yadav, K.K.; Ali, R.; Markuna, S.; Chauhan, S.; Heddam, S.; Kuriqi, A.; Srivastava, A.; Alam, M.; et al. Evaluation of CatBoost Method for Predicting Weekly Pan Evaporation in Subtropical and Sub-Humid Regions. Pure Appl. Geophys. 2024, 181, 719–747. [Google Scholar] [CrossRef]
- Ige, A.O.; Sibiya, M. State-of-the-Art in 1D Convolutional Neural Networks: A Survey. IEEE Access 2024, 12, 144082–144105. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, M.; Liu, K. Deep neural networks for global wildfire susceptibility modelling. Ecol. Indic. 2021, 127, 107735. [Google Scholar] [CrossRef]
- Ishida, K.; Ercan, A.; Nagasato, T.; Kiyama, M.; Amagasaki, M. Use of one-dimensional CNN for input data size reduction in LSTM for improved computational efficiency and accuracy in hourly rainfall-runoff modeling. J. Environ. Manag. 2024, 359, 120931. [Google Scholar] [CrossRef]
- Hoa, P.V.; Binh, N.A.; Hong, P.V.; An, N.N.; Thao, G.T.P.; Hanh, N.C.; Ngo, P.T.T.; Bui, D.T. One-dimensional deep learning driven geospatial analysis for flash flood susceptibility mapping: A case study in North Central Vietnam. Earth Sci. Inform. 2024, 17, 4419–4440. [Google Scholar] [CrossRef]
- Hu, L.; Yan, C. Evaluation of Landslide Susceptibility of Mangshan Mountain in Zhengzhou Based on GWO-1D CNN Model. Sustainability 2024, 16, 5086. [Google Scholar] [CrossRef]
- Chou, J.-S.; Chen, L.-Y.; Liu, C.-Y. Forensic-based investigation-optimized extreme gradient boosting system for predicting compressive strength of ready-mixed concrete. J. Comput. Des. Eng. 2023, 10, 425–445. [Google Scholar] [CrossRef]
- Lundberg, S. An Introduction to Explainable AI with Shapley Values. 2018. SHAP. Available online: https://shap.readthedocs.io/ (accessed on 27 February 2024).
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Islam, M.R.; Shahfahad; Talukdar, S.; Rihan, M.; Rahman, A. Evaluating cooling effect of blue-green infrastructure on urban thermal environment in a metropolitan city: Using geospatial and machine learning techniques. Sustain. Cities Soc. 2024, 113, 105666. [Google Scholar] [CrossRef]
- Zhu, S.; Yan, Y.; Zhao, B.; Wang, H. Assessing the impact of adjacent urban morphology on street temperature: A multisource analysis using random forest and SHAP. Build. Environ. 2025, 267, 112326. [Google Scholar] [CrossRef]
- Guo, R.; Yang, B.; Guo, Y.; Li, H.; Li, Z.; Zhou, B.; Hong, B.; Wang, F. Machine learning-based prediction of outdoor thermal comfort: Combining Bayesian optimization and the SHAP model. Build. Environ. 2024, 254, 111301. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, C.; Meadows, M.E.; Feng, M. Pixel level spatial variability modeling using SHAP reveals the relative importance of factors influencing LST. Environ. Monit. Assess. 2023, 195, 407. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Huang, G.; Zhang, M. Comparative Analysis of the Seasonal Driving Factors of the Urban Heat Environment Using Machine Learning: Evidence from the Wuhan Urban Agglomeration, China, 2020. Atmosphere 2024, 15, 671. [Google Scholar] [CrossRef]
- Pearl, J. Statistics and causal inference: A review. Test 2003, 12, 281–345. [Google Scholar] [CrossRef]
- Brewer, L.E.; Wright, J.M.; Rice, G.; Neas, L.; Teuschler, L. Causal inference in cumulative risk assessment: The roles of directed acyclic graphs. Environ. Int. 2017, 102, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Athey, S. Stable learning establishes some common ground between causal inference and machine learning. Nat. Mach. Intell. 2022, 4, 110–115. [Google Scholar] [CrossRef]
- Hair, J.F., Jr.; Sarstedt, M. Data, measurement, and causal inferences in machine learning: Opportunities and challenges for marketing. J. Mark. Theory Pract. 2021, 29, 65–77. [Google Scholar] [CrossRef]
- Brand, J.E.; Zhou, X.; Xie, Y. Recent Developments in Causal Inference and Machine Learning. Annu. Rev. Sociol. 2023, 49, 81–110. [Google Scholar] [CrossRef]
- Wong, T.; Yeh, P. Reliable Accuracy Estimates from k-Fold Cross Validation. IEEE Trans. Knowl. Data Eng. 2020, 32, 1586–1594. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Ajin, R.S.; Segoni, S.; Fanti, R. Optimization of SVR and CatBoost models using metaheuristic algorithms to assess landslide susceptibility. Sci. Rep. 2024, 14, 24851. [Google Scholar] [CrossRef]
- Yao, Z.; Chen, M.; Zhan, J.; Zhuang, J.; Sun, Y.; Yu, Q.; Yu, Z. Refined Landslide Susceptibility Mapping by Integrating the SHAP-CatBoost Model and InSAR Observations: A Case Study of Lishui, Southern China. Appl. Sci. 2023, 13, 12817. [Google Scholar] [CrossRef]
- USGS. Landsat 8-9 Collection 2 (C2) Level 2 Science Product (L2SP) Guide; US Geological Survey: Reston, VA, USA, 2020. Available online: https://www.usgs.gov/media/files/landsat-8-9-collection-2-level-2-science-product-guide (accessed on 12 August 2025).
- Cook, M.J. Atmospheric Compensation for a Landsat Land Surface Temperature Product. Ph.D. Thesis, Rochester Institute of Technology, Rochester, NY, USA, 2014. Available online: http://scholarworks.rit.edu/theses/8513 (accessed on 12 August 2025).
- Giridharan, R.; Emmanuel, R. The impact of urban compactness, comfort strategies and energy consumption on tropical urban heat island intensity: A review. Sustain. Cities Soc. 2018, 40, 677–687. [Google Scholar] [CrossRef]
- Aram, F.; Higueras García, E.; Solgi, E.; Mansournia, S. Urban green space cooling effect in cities. Heliyon 2019, 5, e01339. [Google Scholar] [CrossRef]
- Schwaab, J. Sprawl or compactness? How urban form influences urban surface temperatures in Europe. City Environ. Interact. 2022, 16, 100091. [Google Scholar] [CrossRef]
- Choi, Y.; Suh, J.; Kim, S.-M. GIS-Based Solar Radiation Mapping, Site Evaluation, and Potential Assessment: A Review. Appl. Sci. 2019, 9, 1960. [Google Scholar] [CrossRef]
- Kotharkar, R.; Vidyasagar, A. Cooling efficacy assessment of urban green spaces using machine learning-based multivariate landscape analysis. Sustain. Cities Soc. 2025, 130, 106541. [Google Scholar] [CrossRef]
- Zhou, W.; Cao, F.; Wang, G. Effects of Spatial Pattern of Forest Vegetation on Urban Cooling in a Compact Megacity. Forests 2019, 10, 282. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhan, Y.; Yu, T.; Ren, X. Urban green effects on land surface temperature caused by surface characteristics: A case study of summer Beijing metropolitan region. Infrared Phys. Technol. 2017, 86, 35–43. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, K.; Ren, Y.; Li, M.; Ji, R.; Wu, X.; Yan, H.; Lin, T.; Zhang, G.; Zhou, X.; et al. 3D compact form as the key role in the cooling effect of greenspace landscape pattern. Ecol. Indic. 2024, 160, 111776. [Google Scholar] [CrossRef]
- Masoudi, M.; Tan, P.Y. Multi-year comparison of the effects of spatial pattern of urban green spaces on urban land surface temperature. Landsc. Urban Plan. 2019, 184, 44–58. [Google Scholar] [CrossRef]

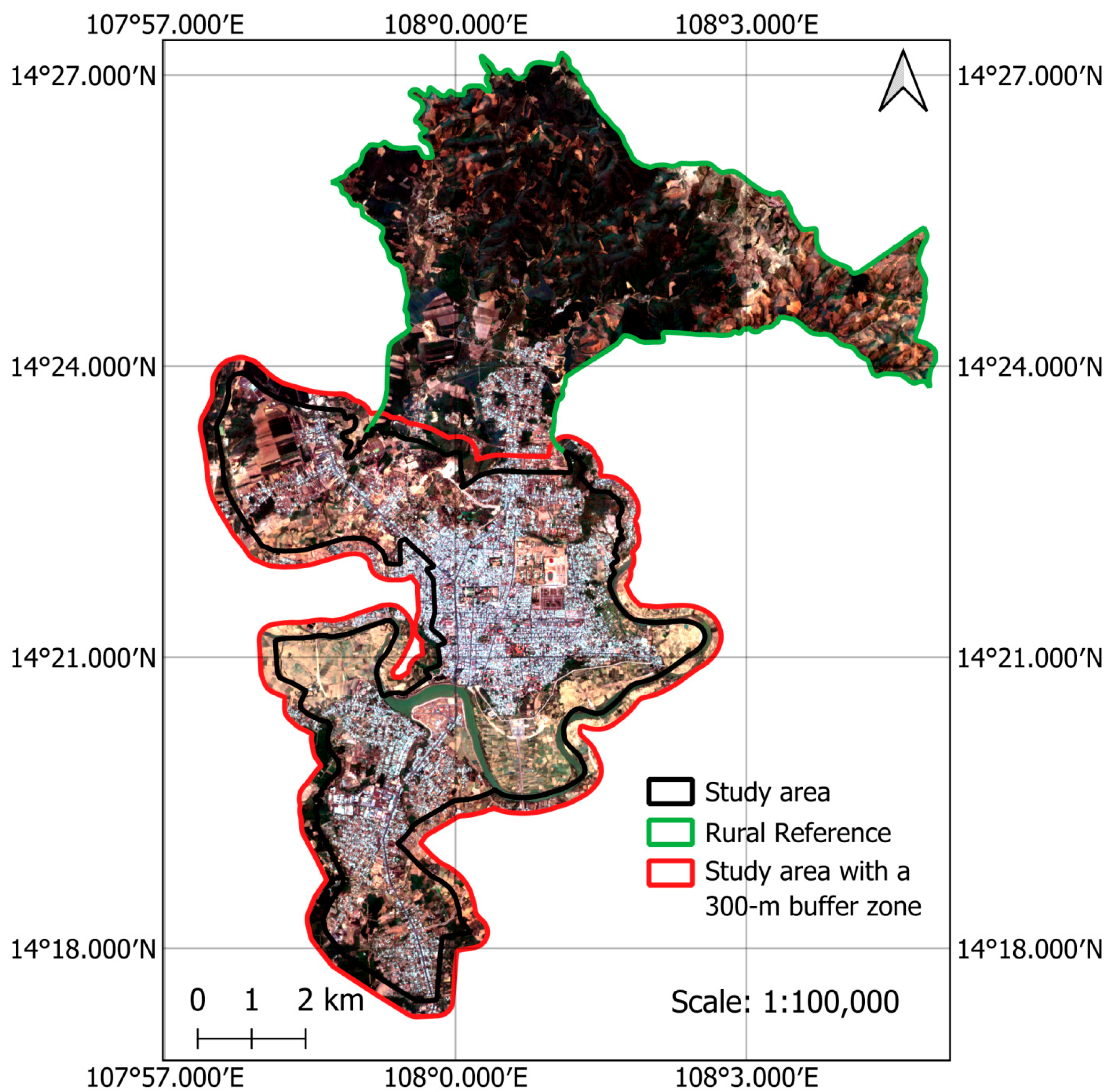
| Dataset | Filtered Date | Bands | Resolution | Number of Images in Collection |
|---|---|---|---|---|
| Landsat 8 | 1 January 2024–31 March 2024 1 December 2024–31 December 2024 | SR_4, SR_5, and ST_B10 | 30 m | 7 |
| Sentinel-2 | 1 January 2024–31 December 2024 | B2, B3, B4, B5, B6, B7, B8, B8A, B11, B12 | 10 m (B2, B3, B4, and B8) 20 m (B5, B6, B7, B8A, B11, and B12) | 29 |
| NASA SRTM Digital Elevation 30 m | Elevation | 30 m | 1 |
| Category | Variables | Data Source |
|---|---|---|
| Topographic features | Elevation | NASA SRTM Digital Elevation 30 m |
| Slope | ||
| Aspect | ||
| LULC | LULC | RF-based classification using Sentinel-2’s spectral bands |
| Urban morphology | Bare land density | Computed from LULC maps using morphological mean filters |
| Built-up density | ||
| Green space density | ||
| Proximity features | Distance to green spaces | Calculated using geometry objects and distance measurements |
| Distance to river | ||
| Distance to roads | ||
| Geographical Compactness | Built-up cluster compactness | Computed using k-means clustering and the Polsby–Popper index |
| Green space cluster compactness |
| Indices | Notation | Equations | Explanation |
|---|---|---|---|
| Root Mean Square Error | RMSE | This index computes the standard deviation of prediction errors and indicates the average differences between actual and predicted LST values. | |
| Mean Absolute Percentage Error | MAPE | MAPE expresses the prediction errors as a percentage of actual values; this index shows the relative magnitude of the error. | |
| Mean Absolute Error | MAE | This index computes the average absolute value of the errors. Compared to RMSE, MAE is more robust to outliers in the dataset. | |
| Coefficient of determination | R2 | This metric represents the proportion of variation in urban LST explained by the model. |
| Phase | Metrics | CatBoost | CNN |
|---|---|---|---|
| Training | RMSE | 0.50 | 0.68 |
| MAPE (%) | 1.03 | 1.40 | |
| MAE | 0.38 | 0.51 | |
| R2 | 0.95 | 0.90 | |
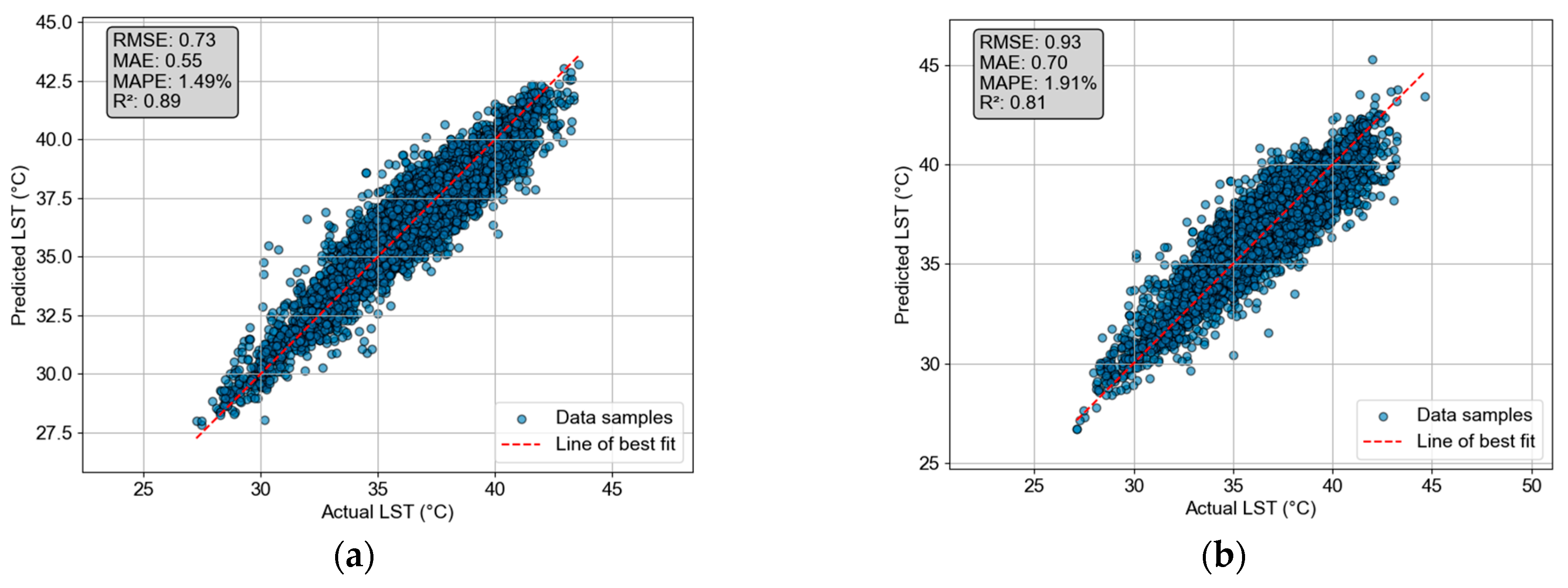
| Testing | RMSE | 0.73 | 0.93 |
| MAPE (%) | 1.49 | 1.91 | |
| MAE | 0.55 | 0.70 | |
| R2 | 0.89 | 0.81 |
| Variable | Unit | ATE | Placebo Test p-Value |
|---|---|---|---|
| Bare land density | % | 0.0404 °C | 0.1336 |
| Built-up density | % | 0.0623 °C | 0.4002 |
| Greenspace density | % | −0.0087 °C | 0.4534 |
| Distance to green spaces | m | 0.0043 °C | 0.3611 |
| Distance to river | m | 0.0001 °C | 0.4057 |
| Distance to roads | m | 0.0002 °C | 0.4389 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoang, N.-D. Machine Learning Approaches for Geospatial Modeling of Urban Land Surface Temperature: Assessing Geographical Compactness, Interpretability, and Causal Inference. Sensors 2025, 25, 5380. https://doi.org/10.3390/s25175380
Hoang N-D. Machine Learning Approaches for Geospatial Modeling of Urban Land Surface Temperature: Assessing Geographical Compactness, Interpretability, and Causal Inference. Sensors. 2025; 25(17):5380. https://doi.org/10.3390/s25175380
Chicago/Turabian StyleHoang, Nhat-Duc. 2025. "Machine Learning Approaches for Geospatial Modeling of Urban Land Surface Temperature: Assessing Geographical Compactness, Interpretability, and Causal Inference" Sensors 25, no. 17: 5380. https://doi.org/10.3390/s25175380
APA StyleHoang, N.-D. (2025). Machine Learning Approaches for Geospatial Modeling of Urban Land Surface Temperature: Assessing Geographical Compactness, Interpretability, and Causal Inference. Sensors, 25(17), 5380. https://doi.org/10.3390/s25175380






