ADBM: Adversarial Diffusion Bridge Model for Denoising of 3D Point Cloud Data
Abstract
1. Introduction
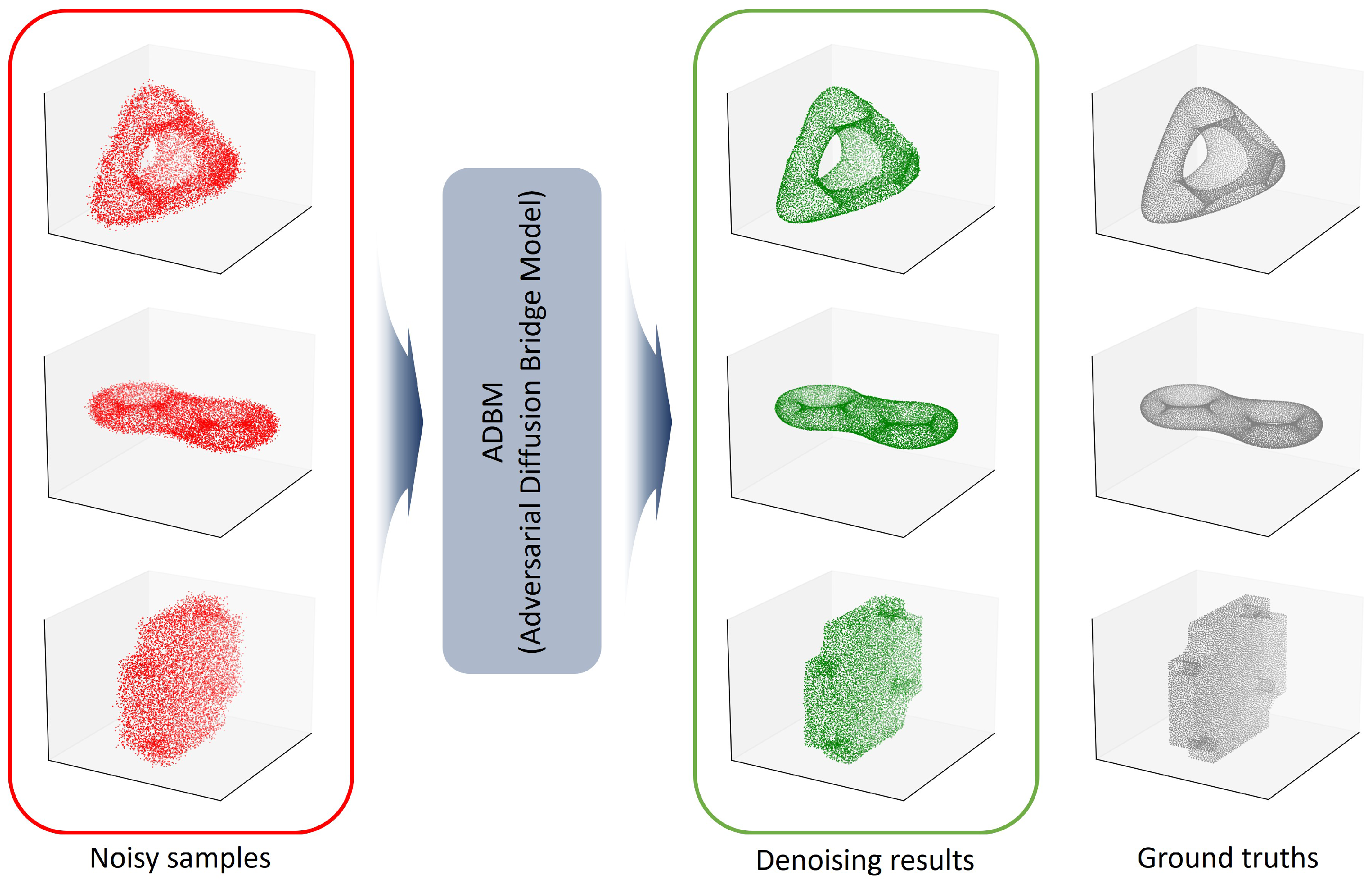
- We propose ADBM, a novel denoising framework that integrates adversarial learning into a diffusion bridge model, enhancing robustness and generation quality for 3D point cloud restoration.
- We design an adversarial training objective specifically formulated for diffusion-based point cloud denoising, which reconstructs fine-grained geometric details of the 3D point cloud.
- We perform comparative evaluations on the PU-Net and PC-Net datasets, using the latter solely for testing, and demonstrate that ADBM achieves state-of-the-art denoising performance with strong generalization across unseen objects categories and varying resolutions.
2. Related Work
2.1. Traditional Denoising Methods
2.2. Deep Learning-Based Methods
2.3. Adversarial Training Approaches
3. Methods
3.1. Diffusion Bridge Training
3.2. Adversarial Training Method
3.3. Implementation
| Algorithm 1: Training of Adversarial Diffusion Bridge Model |
 |
4. Experiments
4.1. Datasets
4.2. Evaluation Measure
4.3. Training Details
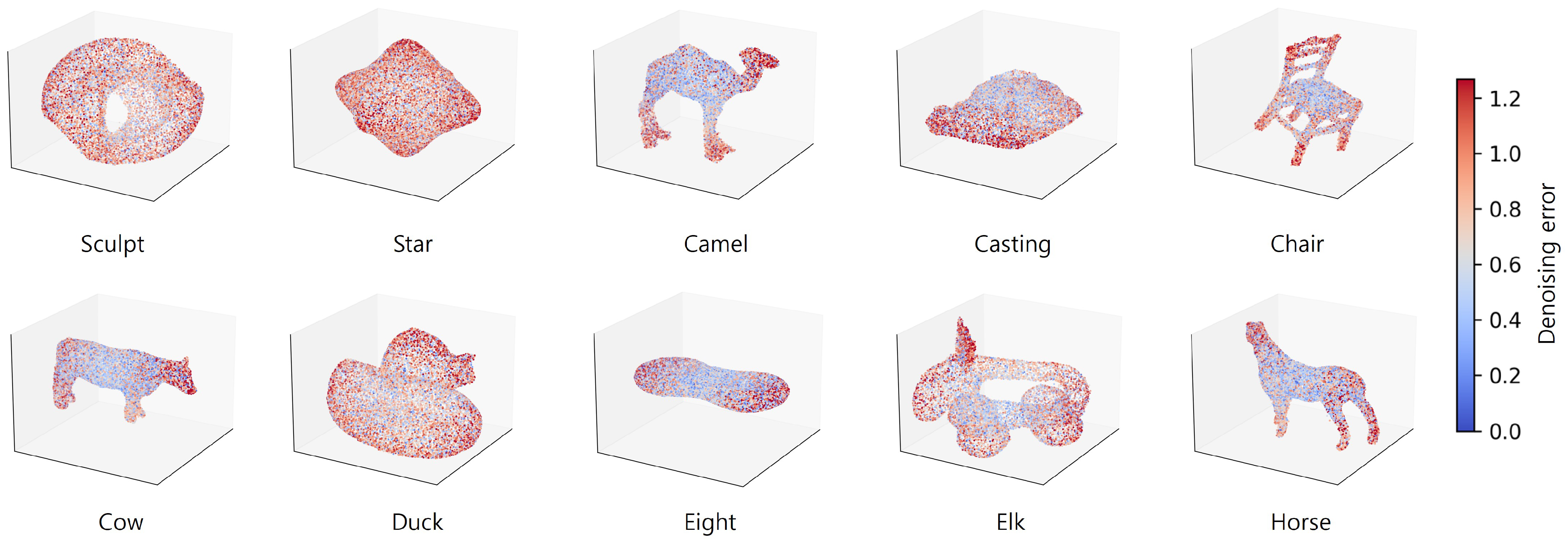
4.4. Experimental Results
4.5. Ablation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Behera, S.; Anand, B.; Rajalakshmi, P. YoloV8 Based Novel Approach for Object Detection on LiDAR Point Cloud. In Proceedings of the 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, 24–27 June 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, C.; Wei, X.; Xie, X.; Tomizuka, M.; Keutzer, K.; Zhang, S. Open-Vocabulary Point-Cloud Object Detection without 3D Annotation. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 1190–1199. [Google Scholar] [CrossRef]
- Qi, C.R.; Litany, O.; He, K.; Guibas, L. Deep Hough Voting for 3D Object Detection in Point Clouds. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9276–9285. [Google Scholar] [CrossRef]
- Nagavarapu, S.C.; Abraham, A.; Selvaraj, N.M.; Dauwels, J. A Dynamic Object Removal and Reconstruction Algorithm for Point Clouds. In Proceedings of the 2023 IEEE International Conference on Service Operations and Logistics, and Informatics (SOLI), Singapore, 11–13 December 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Luo, K.; Yu, H.; Chen, X.; Yang, Z.; Wang, J.; Cheng, P.; Mian, A. 3D point cloud-based place recognition: A survey. Artif. Intell. Rev. 2024, 57, 83. [Google Scholar] [CrossRef]
- Ding, Z.; Sun, Y.; Xu, S.; Pan, Y.; Peng, Y.; Mao, Z. Recent Advances and Perspectives in Deep Learning Techniques for 3D Point Cloud Data Processing. Robotics 2023, 12, 100. [Google Scholar] [CrossRef]
- Shamim, S.; un Nabi Jafri, S.R. Enhanced vehicle localization with low-cost sensor fusion for urban 3D mapping. PLoS ONE 2025, 20, e0318710. [Google Scholar] [CrossRef] [PubMed]
- Sang, H. Application of UAV-based 3D modeling and visualization technology in urban planning. Adv. Eng. Technol. Res. 2024, 12, 912. [Google Scholar] [CrossRef]
- Cheng, Q.; Sun, P.; Yang, C.; Yang, Y.; Liu, P.X. A morphing-Based 3D point cloud reconstruction framework for medical image processing. Comput. Methods Programs Biomed. 2020, 193, 105495. [Google Scholar] [CrossRef] [PubMed]
- Beetz, M.; Banerjee, A.; Grau, V. Point2Mesh-Net: Combining Point Cloud and Mesh-Based Deep Learning for Cardiac Shape Reconstruction; Springer: Cham, Switzerland, 2022; pp. 280–290. [Google Scholar] [CrossRef]
- Han, X.F.; Jin, J.S.; Wang, M.J.; Jiang, W. Guided 3D point cloud filtering. Multimed. Tools Appl. 2018, 77, 17397–17411. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, G.; Wu, S.; Liu, Y.; Gao, Y. Guided point cloud denoising via sharp feature skeletons. Vis. Comput. 2017, 33, 857–867. [Google Scholar] [CrossRef]
- Yadav, S.K.; Reitebuch, U.; Skrodzki, M.; Zimmermann, E.; Polthier, K. Constraint-based point set denoising using normal voting tensor and restricted quadratic error metrics. Comput. Graph. 2018, 74, 234–243. [Google Scholar] [CrossRef]
- Liu, Z.; Xiao, X.; Zhong, S.; Wang, W.; Li, Y.; Zhang, L.; Xie, Z. A feature-preserving framework for point cloud denoising. Comput.-Aided Des. 2020, 127, 102857. [Google Scholar] [CrossRef]
- Rakotosaona, M.; Barbera, V.L.; Guerrero, P.; Mitra, N.J.; Ovsjanikov, M. PointCleanNet: Learning to Denoise and Remove Outliers from Dense Point Clouds. Comput. Graph. Forum 2020, 39, 185–203. [Google Scholar] [CrossRef]
- Luo, S.; Hu, W. Score-Based Point Cloud Denoising. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 4563–4572. [Google Scholar] [CrossRef]
- Vogel, M.; Tateno, K.; Pollefeys, M.; Tombari, F.; Rakotosaona, M.J.; Engelmann, F. P2P-Bridge: Diffusion Bridges for 3D Point Cloud Denoising; Springer: Cham, Switzerland, 2025; pp. 184–201. [Google Scholar] [CrossRef]
- Wang, G.; Jiao, Y.; Xu, Q.; Wang, Y.; Yang, C. Deep Generative Learning via Schrödinger Bridge. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Volume 139, pp. 10794–10804. [Google Scholar]
- De Bortoli, V.; Thornton, J.; Heng, J.; Doucet, A. Diffusion Schrödinger Bridge with Applications to Score-Based Generative Modeling. Adv. Neural Inf. Process. Syst. 2021, 34, 17695–17709. [Google Scholar]
- Shi, Y.; De Bortoli, V.; Deligiannidis, G.; Doucet, A. Conditional simulation using diffusion Schrödinger bridges. In Proceedings of the Thirty-Eighth Conference on Uncertainty in Artificial Intelligence, Eindhoven, The Netherlands, 1–5 August 2022; Volume 180, pp. 1792–1802. [Google Scholar]
- Tong, A.; Malkin, N.; Fatras, K.; Atanackovic, L.; Zhang, Y.; Huguet, G.; Wolf, G.; Bengio, Y. Simulation-free Schrödinger bridges via score and flow matching. arXiv 2024, arXiv:2307.03672. [Google Scholar] [CrossRef]
- Ko, M.; Kim, E.; Choi, Y.H. Adversarial Training of Denoising Diffusion Model Using Dual Discriminators for High-Fidelity Multi-Speaker TTS. IEEE Open J. Signal Process. 2024, 5, 577–587. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhao, C.; Cai, W.; Dong, C. Semantic-guided Adversarial Diffusion Model for Self-supervised Shadow Removal. arXiv 2024, arXiv:2407.01104. [Google Scholar]
- Liu, Y.; Chen, L.; Liu, H. De novo protein backbone generation based on diffusion with structured priors and adversarial training. bioRxiv 2022. [Google Scholar] [CrossRef]
- Yang, L.; Qian, H.; Zhang, Z.; Liu, J.; Cui, B. Structure-Guided Adversarial Training of Diffusion Models. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–21 June 2024; pp. 7256–7266. [Google Scholar] [CrossRef]
- Yu, L.; Li, X.; Fu, C.W.; Cohen-Or, D.; Heng, P.A. PU-Net: Point Cloud Upsampling Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2790–2799. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Adv. Neural Inf. Process. Syst. 2017, 30, 5099–5108. [Google Scholar]

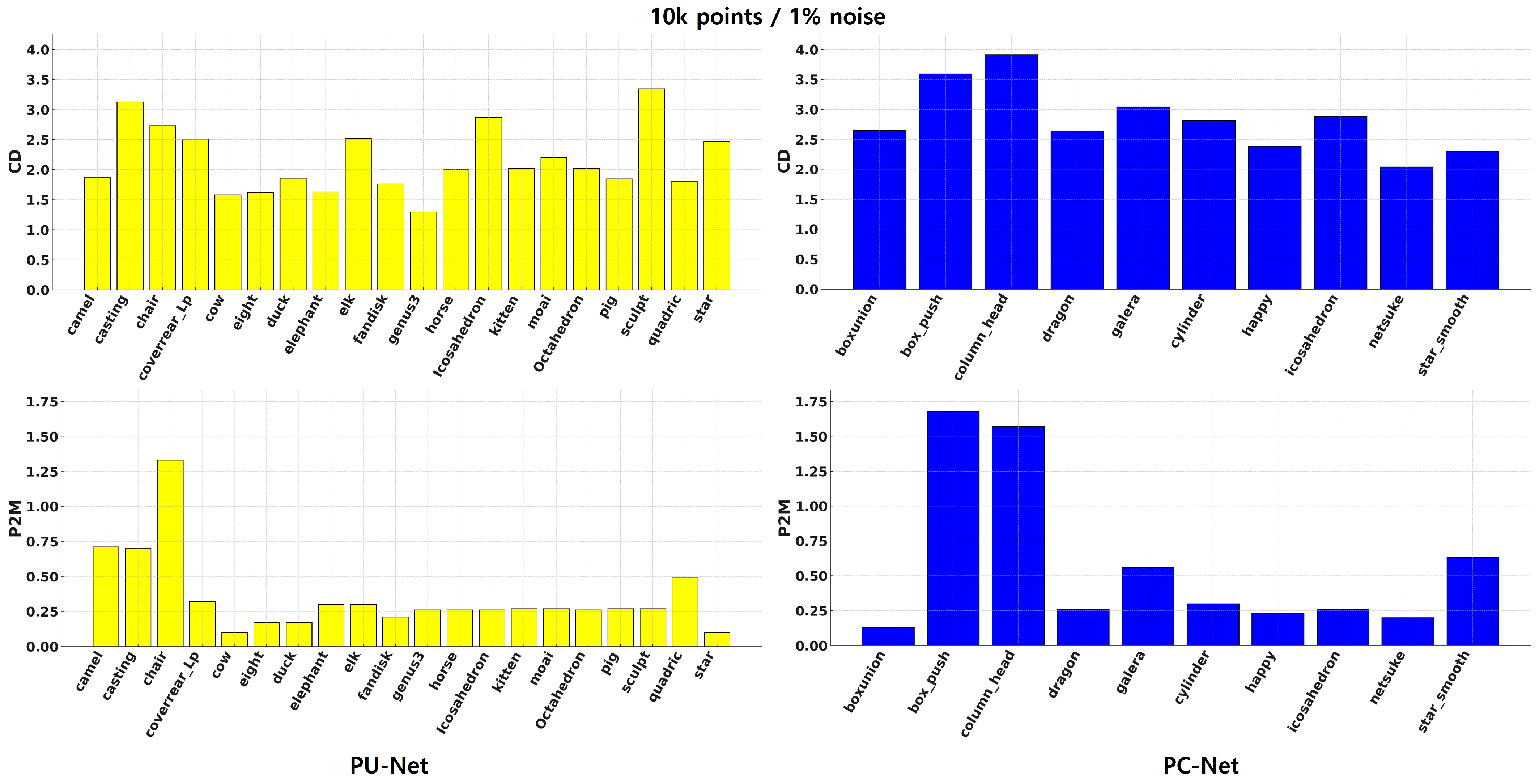

| Dataset | Number of Points Gaussian Noise Level Method/Metric | Points | Points | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1% | 2% | 3% | 1% | 2% | 3% | ||||||||
| CD | P2M | CD | P2M | CD | P2M | CD | P2M | CD | P2M | CD | P2M | ||
| PU-Net [26] | PC-Net [15] | 3.52 | 1.15 | 7.47 | 3.97 | 13.1 | 8.74 | 1.05 | 0.35 | 1.45 | 0.61 | 2.29 | 1.29 |
| ScoreDenoise [16] | 2.52 | 0.46 | 3.69 | 1.07 | 4.71 | 1.94 | 0.72 | 0.15 | 1.29 | 0.57 | 1.93 | 1.04 | |
| P2P-Bridge [17] | 2.45 | 0.39 | 3.27 | 0.86 | 4.07 | 1.47 | 0.60 | 0.09 | 0.95 | 0.35 | 1.63 | 0.90 | |
| ADBM (ours) | 2.18 | 0.34 | 3.15 | 0.77 | 3.98 | 1.40 | 0.57 | 0.08 | 0.90 | 0.32 | 1.61 | 0.88 | |
| PC-Net [15] | PC-Net [15] | 3.85 | 1.22 | 6.04 | 1.45 | 5.87 | 1.29 | 0.29 | 0.11 | 0.51 | 0.25 | 3.25 | 1.08 |
| ScoreDenoise [16] | 3.37 | 0.95 | 4.52 | 1.16 | 6.78 | 1.94 | 1.07 | 0.17 | 1.66 | 0.35 | 2.49 | 0.66 | |
| P2P-Bridge [17] | 2.87 | 0.63 | 4.52 | 0.92 | 5.65 | 1.34 | 0.92 | 0.12 | 1.39 | 0.26 | 2.17 | 0.51 | |
| ADBM (ours) | 2.82 | 0.59 | 4.43 | 0.86 | 5.57 | 1.27 | 0.90 | 0.11 | 1.37 | 0.25 | 2.14 | 0.49 | |
| Number of Points | Points | Points | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gaussian Noise Level | 1% | 2% | 3% | 1% | 2% | 3% | ||||||
| /Metric | CD | P2M | CD | P2M | CD | P2M | CD | P2M | CD | P2M | CD | P2M |
| Base (w/o ADBM) | 2.45 | 0.39 | 3.27 | 0.86 | 4.07 | 1.47 | 0.60 | 0.09 | 0.95 | 0.35 | 1.63 | 0.90 |
| 0.5 | 2.28 | 0.38 | 3.28 | 0.85 | 4.06 | 1.46 | 0.59 | 0.09 | 0.91 | 0.34 | 1.54 | 0.82 |
| 0.7 | 2.18 | 0.34 | 3.15 | 0.77 | 3.98 | 1.40 | 0.57 | 0.08 | 0.90 | 0.32 | 1.61 | 0.88 |
| 0.9 | 2.30 | 0.38 | 3.32 | 0.87 | 4.10 | 1.47 | 0.60 | 0.09 | 0.97 | 0.37 | 1.70 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nam, C.; Lee, S.J. ADBM: Adversarial Diffusion Bridge Model for Denoising of 3D Point Cloud Data. Sensors 2025, 25, 5261. https://doi.org/10.3390/s25175261
Nam C, Lee SJ. ADBM: Adversarial Diffusion Bridge Model for Denoising of 3D Point Cloud Data. Sensors. 2025; 25(17):5261. https://doi.org/10.3390/s25175261
Chicago/Turabian StyleNam, Changwoo, and Sang Jun Lee. 2025. "ADBM: Adversarial Diffusion Bridge Model for Denoising of 3D Point Cloud Data" Sensors 25, no. 17: 5261. https://doi.org/10.3390/s25175261
APA StyleNam, C., & Lee, S. J. (2025). ADBM: Adversarial Diffusion Bridge Model for Denoising of 3D Point Cloud Data. Sensors, 25(17), 5261. https://doi.org/10.3390/s25175261







