Acoustics-Augmented Diagnosis Method for Rolling Bearings Based on Acoustic–Vibration Fusion and Knowledge Transfer
Abstract
1. Introduction
- (1)
- SLKNet is proposed, employing a super-large-kernel size of 160. Serving as the core model for acoustic–vibration signal feature extraction, its super-large-kernel significantly enhances global fault feature capture capability, while the lightweight design ensures efficient deployment in industrial scenarios.
- (2)
- Given that research on the heterogeneous transfer between vibration and acoustic signals remains relatively insufficient, an acoustic–vibration feature fusion method based on symmetric feature transfer theory is introduced. Utilizing SLKNet as the backbone network to construct dual-path feature mapping, this method drives feature distribution alignment and enforces semantic consistency constraints within a shared subspace, effectively bridging the discrepancies arising from physical dimensions and feature distributions. This feature-level transfer strategy offers a novel solution perspective for vibration–acoustic cross-modal transfer, fundamentally distinct from existing paradigms of model tuning or data generation.
- (3)
- Building upon the proposed acoustic–vibration fusion method, a vibration–acoustic knowledge distillation transfer pathway is constructed by exploring the intrinsic consistency between the knowledge distillation framework and symmetric feature mapping theory, establishing it as the core pathway for cross-modal knowledge transfer. Through joint distillation, deep abstract features from the intermediate layers and discriminative knowledge from the output layer of the vibration-trained teacher model are transferred to the acoustically trained student model. This process achieves deep guidance of vibration information over acoustic fault knowledge—an innovative application of distillation technology in the field of vibration–acoustic knowledge enhancement.
- (4)
- Comprehensive validation experiments and evaluation methods for acoustic–vibration knowledge transfer are designed. This includes a transfer benchmark based on the maximum mean discrepancy (MMD) alignment, covering both acoustic-to-acoustic transfer and vibration-to-acoustic transfer scenarios to provide a rigorous reference for cross-modal gain evaluation. Furthermore, cross-condition deep feature space visualization is introduced to intuitively reveal the model transferability and robustness.
2. Related Works
2.1. Feasibility Study of Acoustic–Vibration Transfer
- (1)
- Homology of fault knowledge hypothesis:
- (2)
- Feature projection hypothesis:
2.2. Transfer Learning
2.3. Knowledge Distillation
- (1)
- Hard loss: the cross-entropy loss with the true labels at T = 1.
- (2)
- Soft loss: the Kullback–Leibler (KL) divergence loss between the softened output distributions of the teacher and student models, computed at temperature T.
3. Proposed Methodology
3.1. Transfer Diagnosis Scenario
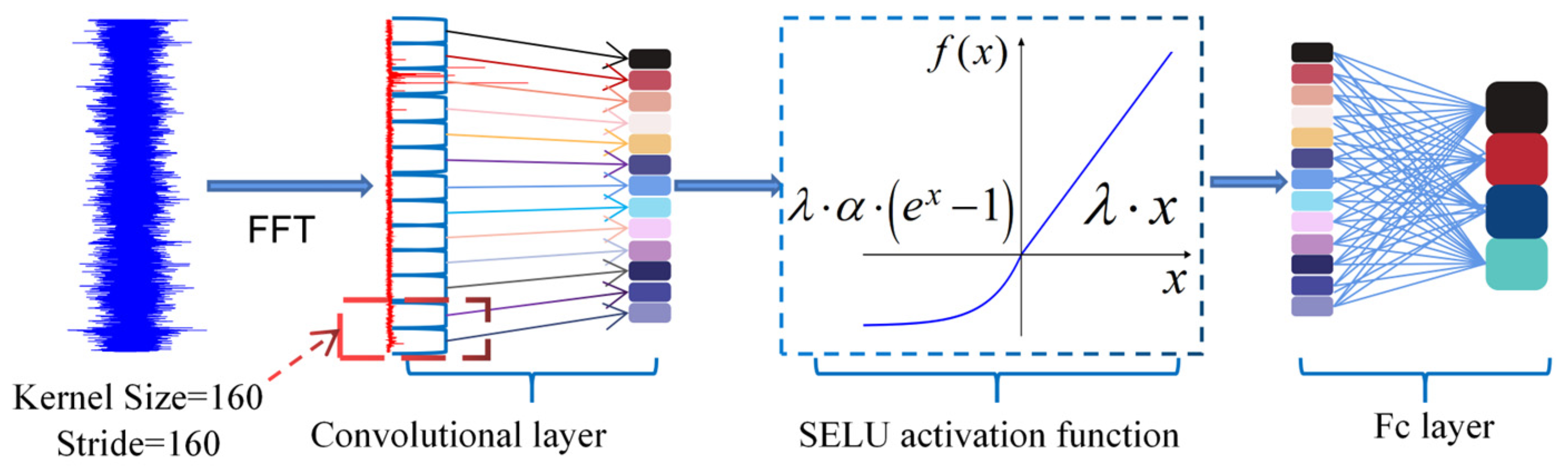
3.2. Super-Large-Kernel Lightweight Convolutional Neural Network
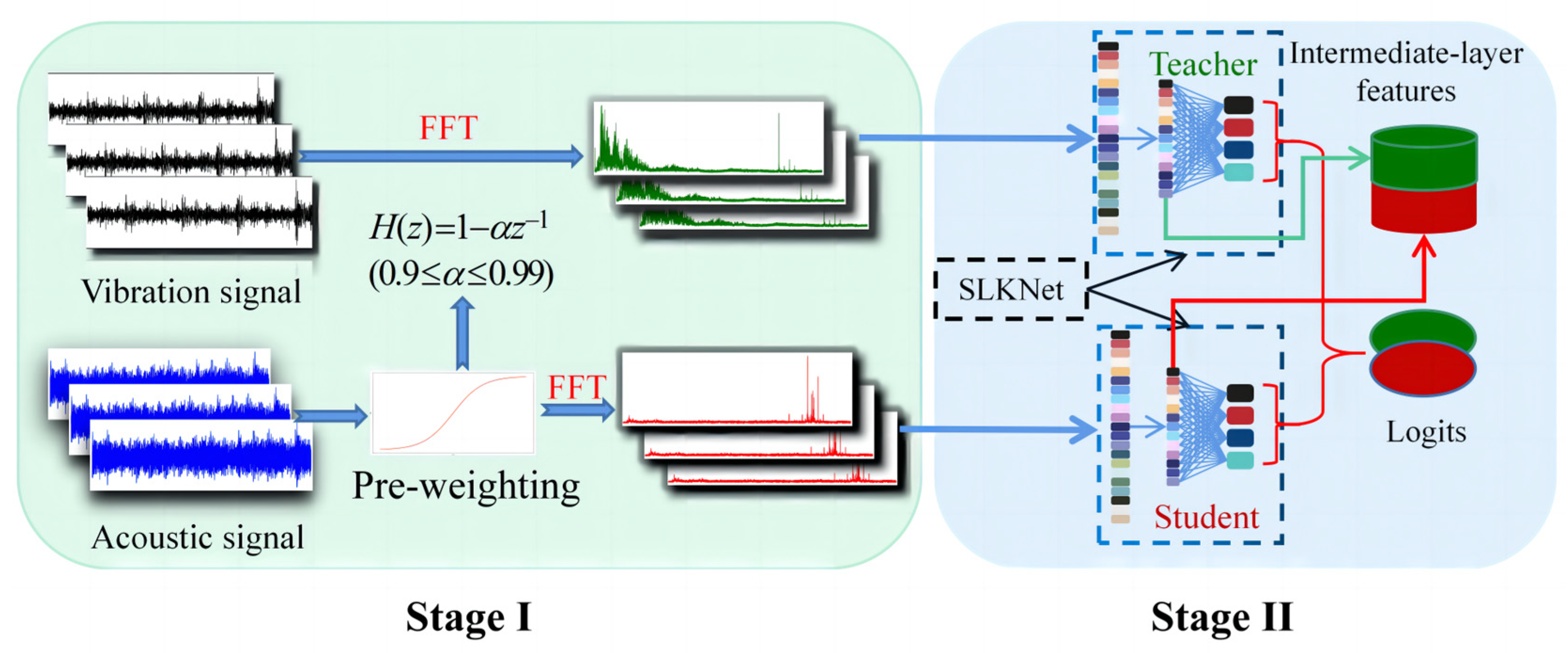
3.3. Acoustic–Vibration Feature Fusion Method
3.4. Constructing the Vibration–Acoustic Knowledge Distillation Transfer Pathway
3.4.1. Intermediate-Layer Feature Alignment
3.4.2. Output-Layer Knowledge Transfer
3.5. Acoustic–Vibration Knowledge Transfer Diagnosis Method Based on Joint Knowledge Distillation
- (1)
- Collecting vibration and acoustic signals from bearings under multiple loads and health states to establish cross-condition transfer tasks.
- (2)
- Implementing SLKNet as the unified backbone for feature extraction and knowledge fusion.
- (3)
- Applying pre-emphasis to acoustic signals for high-frequency compensation, converting all signals to amplitude spectra via FFT, and mapping them to a shared subspace Z through SLKNet’s dual branches to fuse cross-modal features.
- (4)
- Constructing vibration-based teacher models and acoustic-based student models using parameter-independent SLKNet instances and transferring vibration knowledge via joint optimization of feature-layer cosine alignment loss and output-layer KL divergence loss .
- (5)
- Evaluating the student model on cross-load acoustic test sets using accuracy, confusion matrices, and t-SNE visualizations, with benchmarking against MMD-based transfer learning. Subsequently, the enhanced acoustic model, based on vibration transfer, was deployed on a Raspberry Pi platform. This lightweight deployment aimed to validate the model and benchmark its real-time inference performance for edge computing.
4. Experimental Validation
4.1. Case Study I: Self-Collected Experimental Bearing Dataset
4.1.1. Dataset Description
4.1.2. Experimental Results
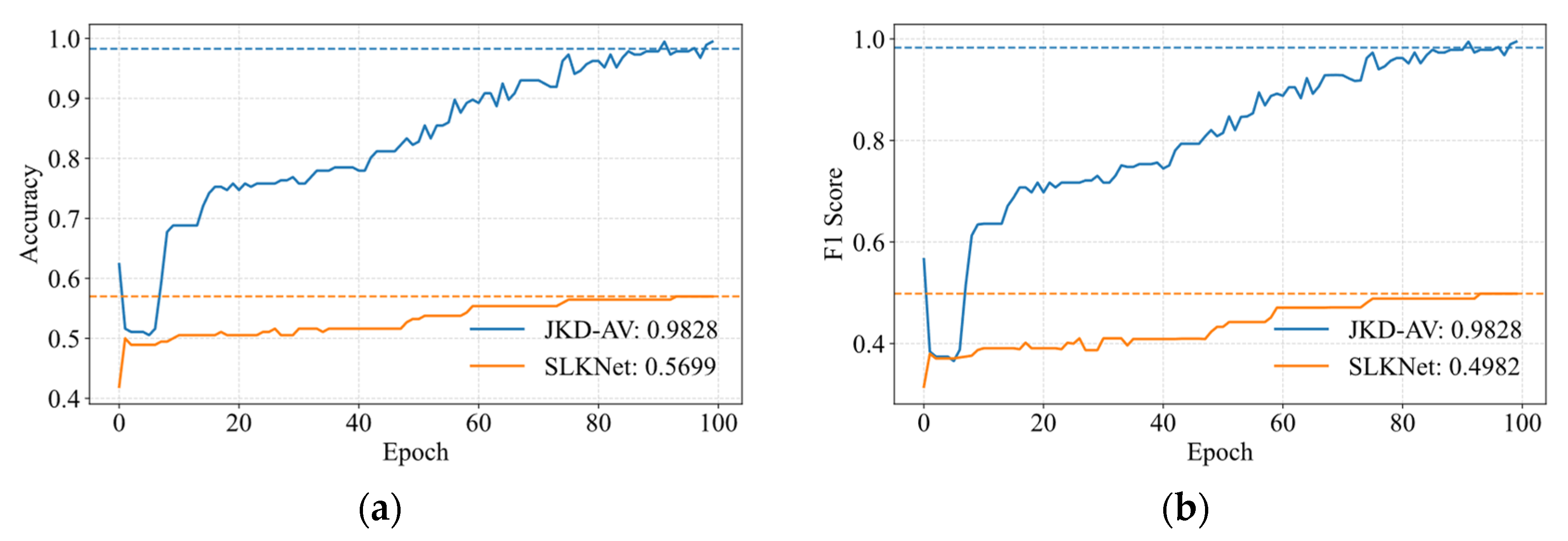
4.1.3. Ablation Study
- (1)
- The acoustic baseline SLKNet without knowledge distillation.
- (2)
- The vibration–acoustic knowledge transfer method KD-AV employing basic distillation.
- (3)
- The proposed joint knowledge distillation method JKD-AV.
4.1.4. Comparative Experiments
- (1)
- Support vector machines’ processing of acoustic signals established SLKNet’s advantage over classical machine learning.
- (2)
- The maximum mean discrepancy alignment for acoustic signals served as a feature transfer baseline to investigate noise interference.
- (3)
- The MMD-based vibration-to-acoustic transfer provided a benchmark for conventional distribution alignment.
4.2. Case Study II: BJTU-RAO Bogie Dataset
4.2.1. Dataset Description
4.2.2. Experimental Results
4.2.3. Comparative Experiments
4.3. Deployment of Models to Embedded Devices
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Angelopoulos, A.; Michailidis, E.T.; Nomikos, N.; Trakadas, P.; Hatziefremidis, A.; Voliotis, S.; Zahariadis, T. Tackling Faults in the Industry 4.0 Era—A Survey of Machine-Learning Solutions and Key Aspects. Sensors 2020, 20, 109. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Qu, W.; Wang, W.; Dong, L.; Wan, S. Multi-fault Diagnosis Model of Rolling Bearing Based on Improved CNN-GRU Model. Available online: https://link.cnki.net/urlid/33.1088.TH.20250521.1526.010 (accessed on 15 August 2025).
- Yong, Y. Methodologies for Acoustic-Based Diagnosis of Rotating Machinery Under Industrial Environmental Condition; Sichuan University: Chengdu, China, 2023. [Google Scholar] [CrossRef]
- Malla, C.; Panigrahi, I. Review of Condition Monitoring of Rolling Element Bearing Using Vibration Analysis and Other Techniques. J. Vib. Eng. Technol. 2019, 7, 407–414. [Google Scholar] [CrossRef]
- Izaz, R.; Hyewon, L.; Soo, K.H. Mechanical fault detection based on machine learning for robotic RV reducer using electrical current signature analysis: A data-driven approach. J. Comput. Des. Eng. 2022, 9, 417–433. [Google Scholar] [CrossRef]
- Raouf, I.; Kumar, P.; Kim, H.S. Deep learning-based fault diagnosis of servo motor bearing using the attention-guided feature aggregation network. Expert Syst. Appl. 2024, 258, 125137. [Google Scholar] [CrossRef]
- Raouf, I.; Kumar, P.; Lee, H.Y.W.; Kim, H.S. Transfer Learning-Based Intelligent Fault Detection Approach for the Industrial Robotic System. Mathematics 2023, 11, 945. [Google Scholar] [CrossRef]
- Sharma, K.; Goyal, D.; Kanda, R. Intelligent Fault Diagnosis of Bearings based on Convolutional Neural Network using Infrared Thermography. Proc. Inst. Mech. Eng. Part J—J. Eng. Tribol. 2022, 236, 2439–2446. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Guo, Y. Unknown fault feature extraction of rolling bearings under variable speed conditions based on statistical complexity measures. Mech. Syst. Signal Process. 2022, 172, 108964. [Google Scholar] [CrossRef]
- Cui, H.; Guan, Y.; Chen, H. Rolling element fault diagnosis based on VMD and sensitivity MCKD. IEEE Access 2021, 9, 120297–120308. [Google Scholar] [CrossRef]
- Li, X.Z.; Xing, Z.T.; Xiang, L.; Chen, Y.; Hu, A.J. Memory-augmented prototypical meta-learning method for bearing fault identification under few-sample conditions. Neurocomputing 2025, 635, 129996. [Google Scholar] [CrossRef]
- Li, X.; Chen, H.; Li, S.H.; Wei, D.; Zou, X.Y.; Si, L.; Shao, H.D. Multi-kernel weighted joint domain adaptation network for cross-condition fault diagnosis of rolling bearings. Reliab. Eng. Syst. Saf. 2025, 261, 111109. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, Y.H.; Wang, M.H.; Zhao, H.L.; Zhou, Q.H. Multisource-Multitarget Partial Domain Adaptation for Bearing Fault Diagnosis. IEEE Internet Things J. 2025, 12, 15897–15910. [Google Scholar] [CrossRef]
- Baydar, N.; Ball, A. Detection of gear failures via vibration and acoustic signals using wavelet transform. Mech. Syst. Signal Process. 2003, 17, 787–804. [Google Scholar] [CrossRef]
- Yadav, S.K.; Tyagi, K.; Shah, B.; Kalra, P.K. Audio Signature-Based Condition Monitoring of Internal Combustion Engine Using FFT and Correlation Approach. IEEE Trans. Instrum. Meas. 2011, 60, 1217–1226. [Google Scholar] [CrossRef]
- Lu, W.; Jiang, W.; Pan, S.; Xiang, S. Mechanical fault diagnosis based on texture features of acoustic images by near-field acoustic holography. J. Vib. Eng. 2013, 26, 617–623. [Google Scholar]
- Wang, R.; Liu, F.K.; Hou, F.T.; Jiang, W.K.; Hou, Q.L.; Yu, L.J. A Non-Contact Fault Diagnosis Method for Rolling Bearings Based on Acoustic Imaging and Convolutional Neural Networks. IEEE Access 2020, 8, 132761–132774. [Google Scholar] [CrossRef]
- Hou, J.J.; Ma, J.; Fang, Z.P.; Ming, W.Y.; He, W.B. Bearing Fault Diagnosis Based on Spatial Features of 2.5 Dimensional Sound Field. Shock. Vib. 2019, 2019, 4678491. [Google Scholar] [CrossRef]
- Li, C.; Chen, C.Z.; Gu, X.J. Acoustic-Based Rolling Bearing Fault Diagnosis Using a Co-Prime Circular Microphone Array. Sensors 2023, 23, 3050. [Google Scholar] [CrossRef]
- Wei, X.Y.; Ding, L.S.; Wang, D.Z.; Ma, L.Q.; Chen, C.Y. A lightweight complex-domain acoustic feature extraction method for rotating machinery fault detection. Meas. Sci. Technol. 2024, 35, 9. [Google Scholar] [CrossRef]
- Gu, Y.K.; Wang, P.Z.; Li, Y.; You, K.S.; Qiu, G.Q. An adaptive acoustic signal reconstruction and fault diagnosis method for rolling bearings based on SSDAE-MobileViT. Meas. Sci. Technol. 2025, 36, 016190. [Google Scholar] [CrossRef]
- Sun, X.M.; Yang, Y.H.; Chen, C.Z.; Tian, M.; Du, S.N.; Wang, Z.Q. A Multi-Branch Convolution and Dynamic Weighting Method for Bearing Fault Diagnosis Based on Acoustic-Vibration Information Fusion. Actuators 2025, 14, 17. [Google Scholar] [CrossRef]
- Yan, X.A.; Jiang, D.; Xiang, L.; Xu, Y.D.; Wang, Y.L. CDTFAFN: A novel coarse-to-fine dual-scale time-frequency attention fusion network for machinery vibro-acoustic fault diagnosis. Inf. Fusion 2024, 112, 102554. [Google Scholar] [CrossRef]
- Lian, Y.; Wang, J.R.; Li, Z.L.; Liu, W.; Huang, L.M.; Jiang, X.X. Residual attention guided vision transformer with acoustic-vibration signal feature fusion for cross-domain fault diagnosis. Adv. Eng. Inform. 2025, 64, 103003. [Google Scholar] [CrossRef]
- Chen, X.H.; Xue, Y.H.; Huang, M.J.; Yang, R. Multi-Modal Self-Supervised Learning for Cross-Domain One-Shot Bearing Fault Diagnosis. In Proceedings of the 12th IFAC Symposium on Fault Detection, Supervision and Safety for Technical Processes (SAFEPROCESS), Ferrara, Italy, 4–7 June 2024; pp. 746–751. [Google Scholar]
- Di Maggio, L.G. Intelligent Fault Diagnosis of Industrial Bearings Using Transfer Learning and CNNs Pre-Trained for Audio Classification. Sensors 2023, 23, 211. [Google Scholar] [CrossRef]
- Zhang, F.; Lai, P.; Wang, Q.; Li, T.; Zhang, W. TCRNN: A Cross-domain Knowledge Transfer Acoustic Bearing Fault Diagnosis Method for Data Unbalance Issue. In Proceedings of the International Conference on the Efficiency and Performance Engineering Network, Huddersfield, UK, 29 August–1 September 2023; pp. 921–933. [Google Scholar]
- Wu, P.; Yu, G.Y.; Han, Y.M.; Ma, B. Cross-Domain Acoustic Diagnosis Method of Rotating Machinery Based on Vibration and Acoustic Migration. IEEE Trans. Reliab. 2025, 1–15. [Google Scholar] [CrossRef]
- Li, Z. Acoustic-Based Methods for Fault Diagnosis; Metallurgical Industry Press: Beijing, China, 1989. [Google Scholar]
- Wu, C. Research on the Fault Diagnosis Method Andits Application to Rotating Machinery by Vibro-acoustic Data Fusion; Zhejiang University: Hangzhou, China, 2021. [Google Scholar]
- Liu, T.; Wang, Z.; Wu, X.; Li, M. Application of Transfer Learning in Mechanical Equipment Intelligent Diagnosis:Literature Review. J. Kunming Univ. Sci. Technol. (Nat. Sci.) 2024, 49, 154–169. [Google Scholar] [CrossRef]
- Lei, Y.G.; Yang, B.; Jiang, X.W.; Jia, F.; Li, N.P.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q.A. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Day, O.; Khoshgoftaar, T.M. A survey on heterogeneous transfer learning. J. Big Data 2017, 4, 29. [Google Scholar] [CrossRef]
- Yan, R.Q.; Shen, F.; Sun, C.; Chen, X.F. Knowledge Transfer for Rotary Machine Fault Diagnosis. IEEE Sens. J. 2020, 20, 8374–8393. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. Comput. Sci. 2015, 14, 38–39. [Google Scholar]
- Wang, T.; Liu, T.; Wang, Z.; Pu, H. Applied Research on Bearing Fault Diagnosis Based on Knowledge Distillation and Transfer Learning. J. Comput. Eng. Appl. 2023, 59, 289–297. [Google Scholar] [CrossRef]
- Xiao, J.; Liu, C.; Wang, X.; Wang, Z.; Wu, X. A Fault Diagnosis Method for Variable Condition Equipment Based on Knowledge Transfer and Improved Residual Neural Networks. IEEE Trans. Instrum. Meas. 2025, 74, 3508216. [Google Scholar] [CrossRef]
- Ding, A.; Qin, Y.; Wang, B.; Guo, L.; Jia, L.; Cheng, X. Evolvable graph neural network for system-level incremental fault diagnosis of train transmission systems. Mech. Syst. Signal Process. 2024, 210, 15. [Google Scholar] [CrossRef]
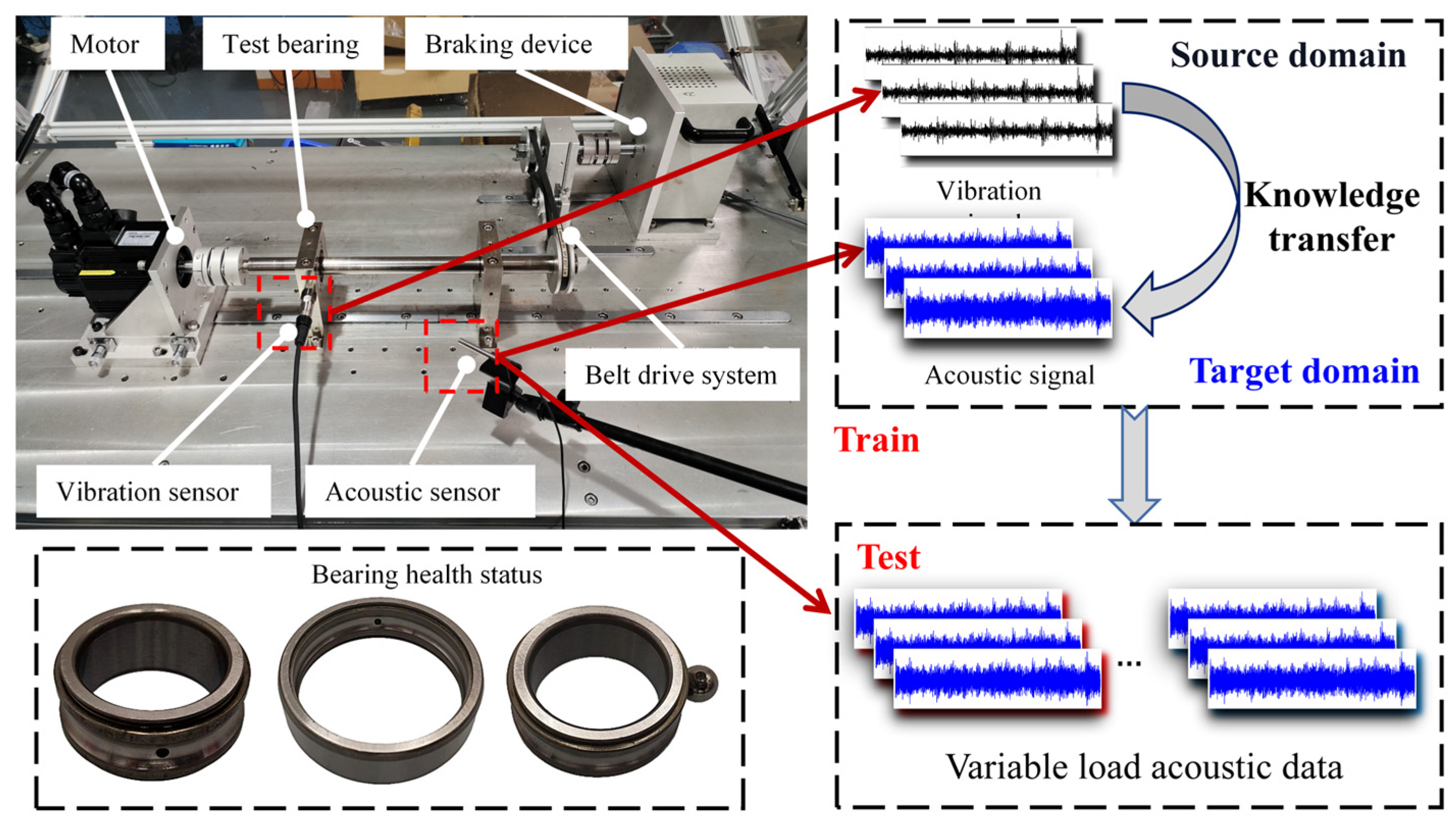
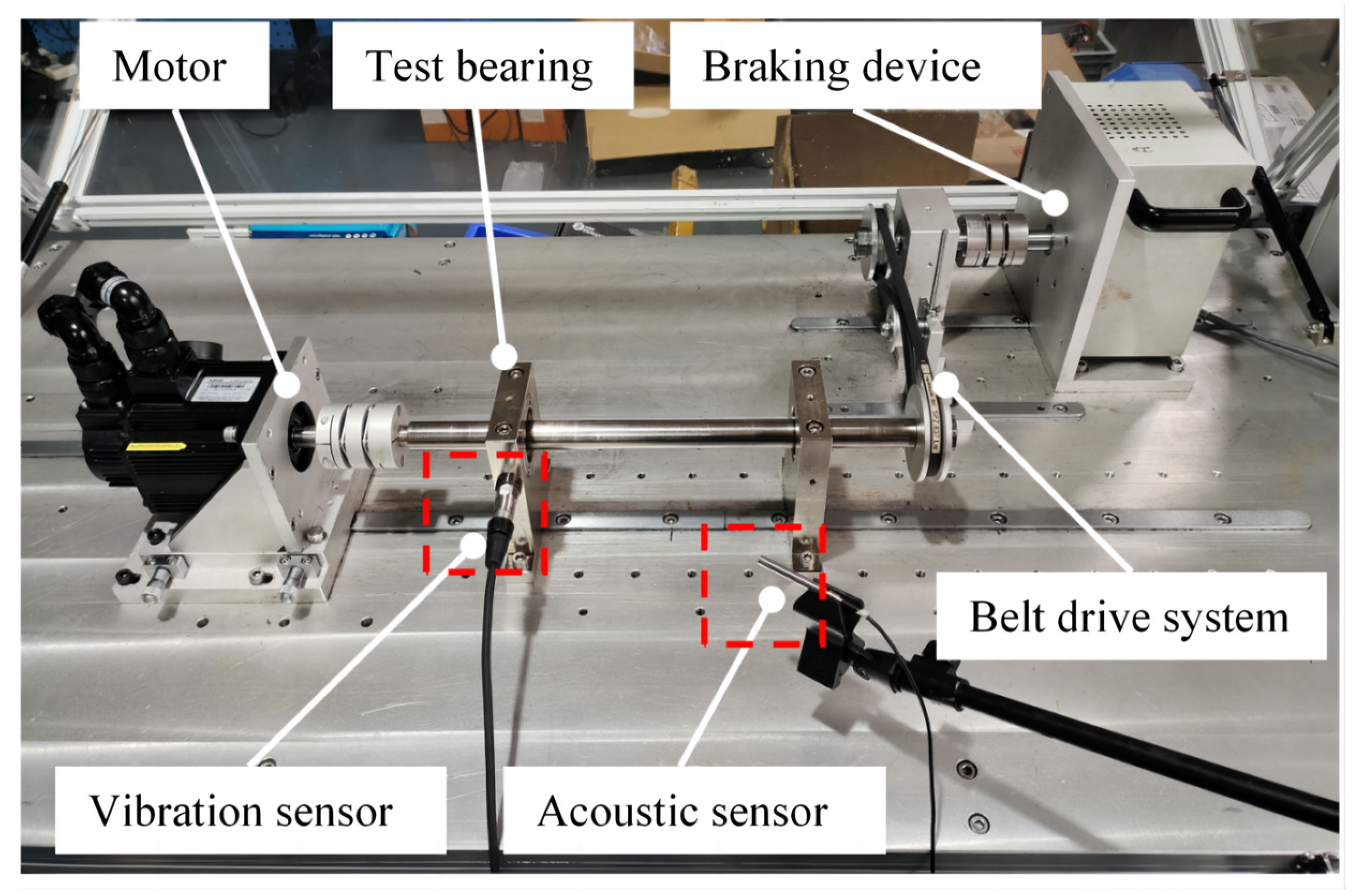

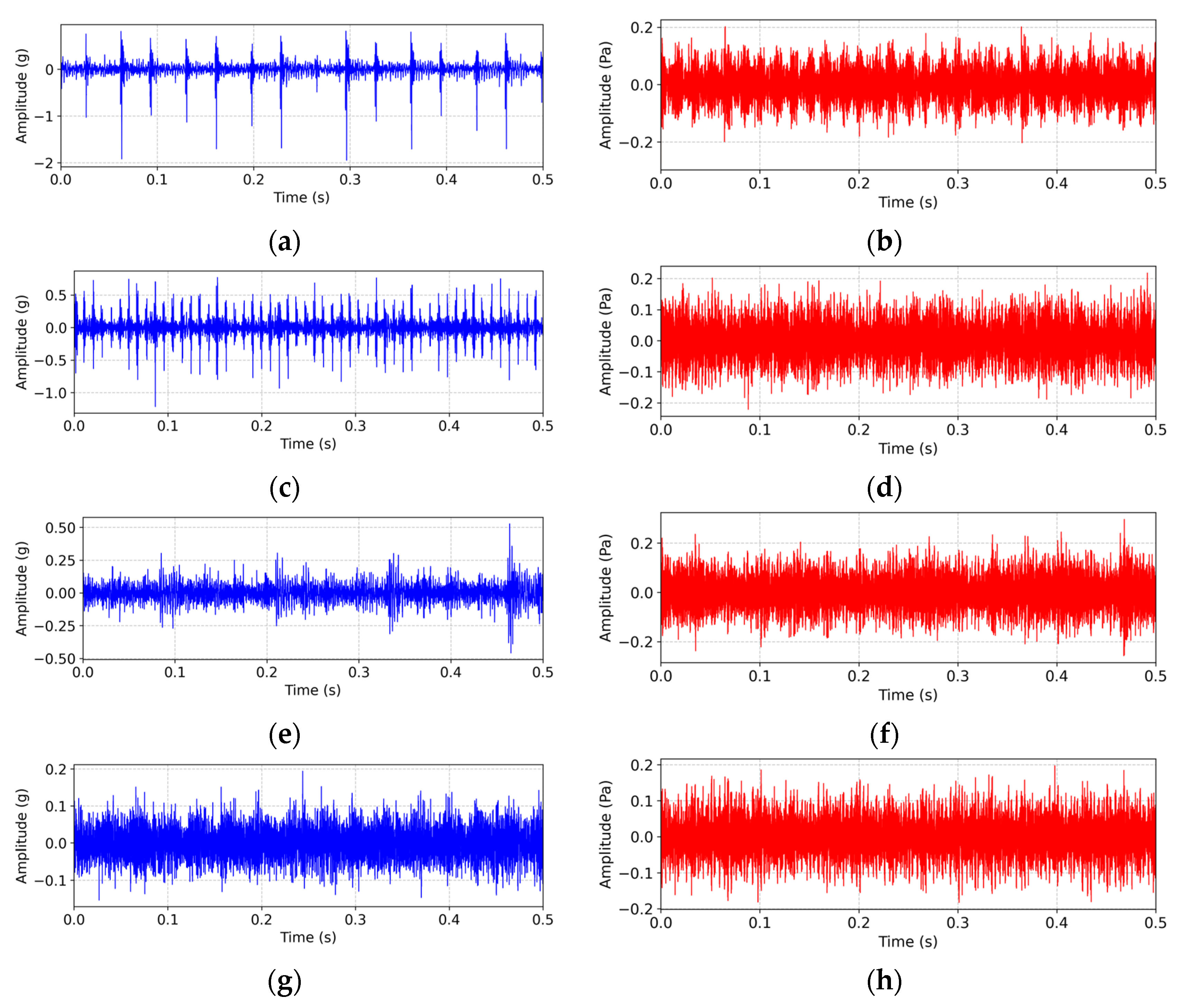
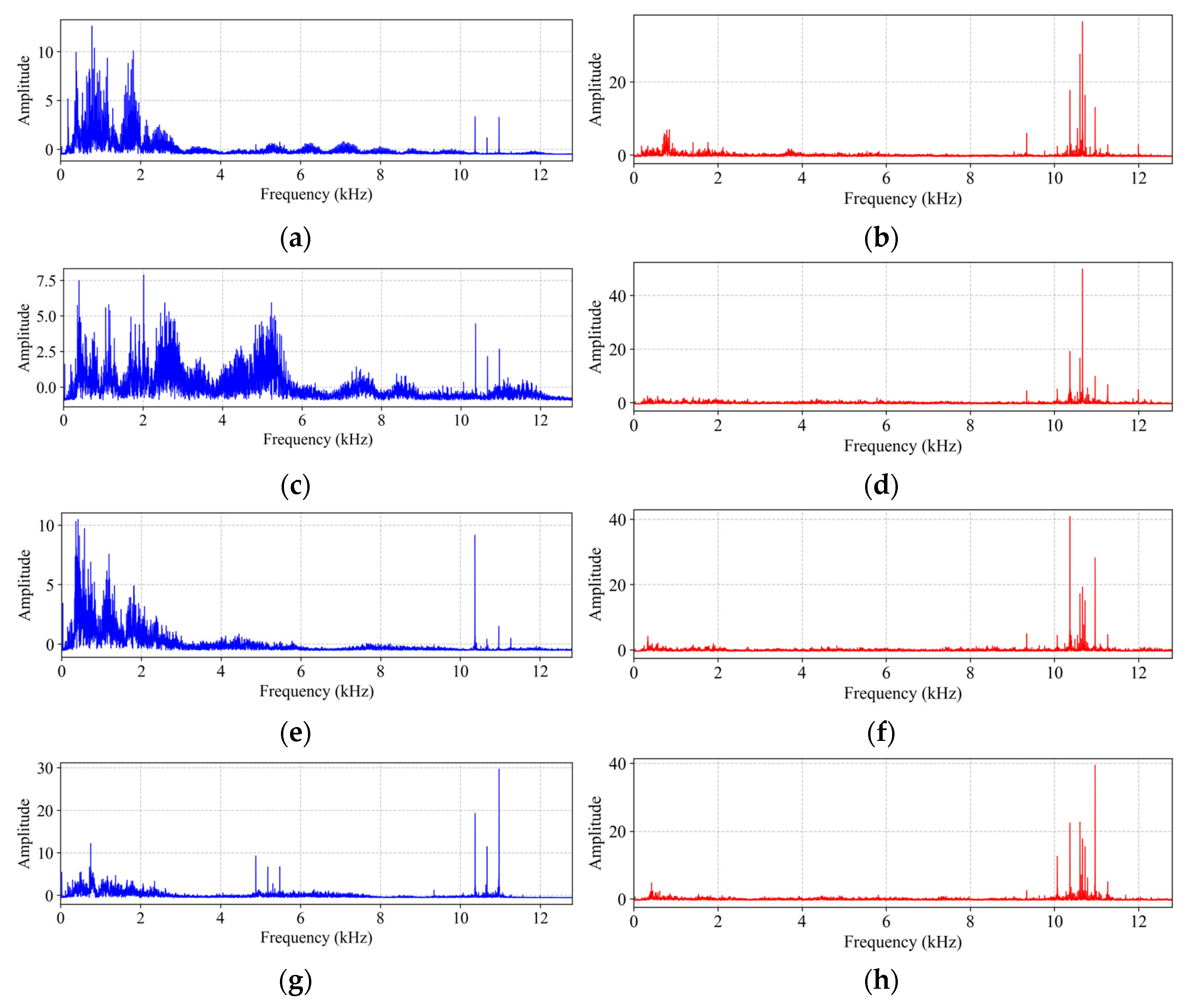
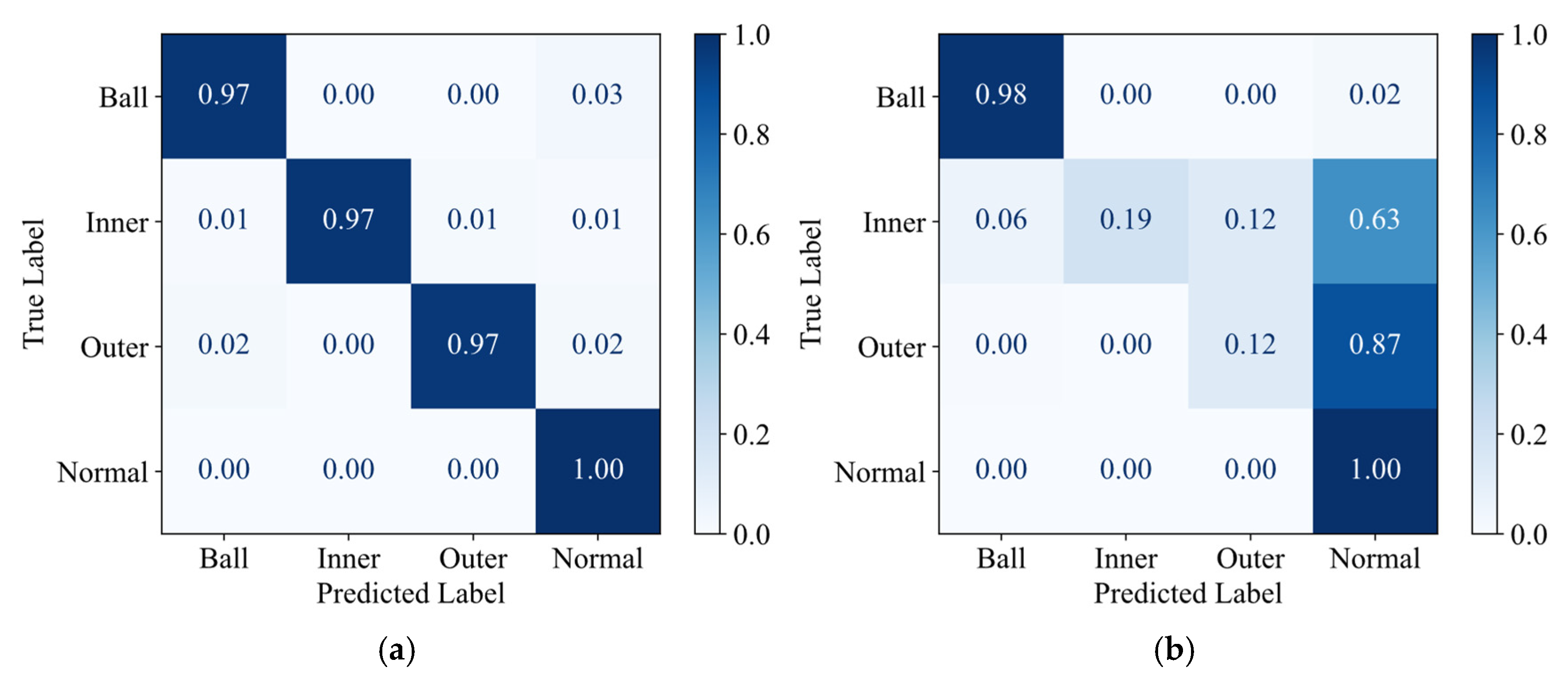




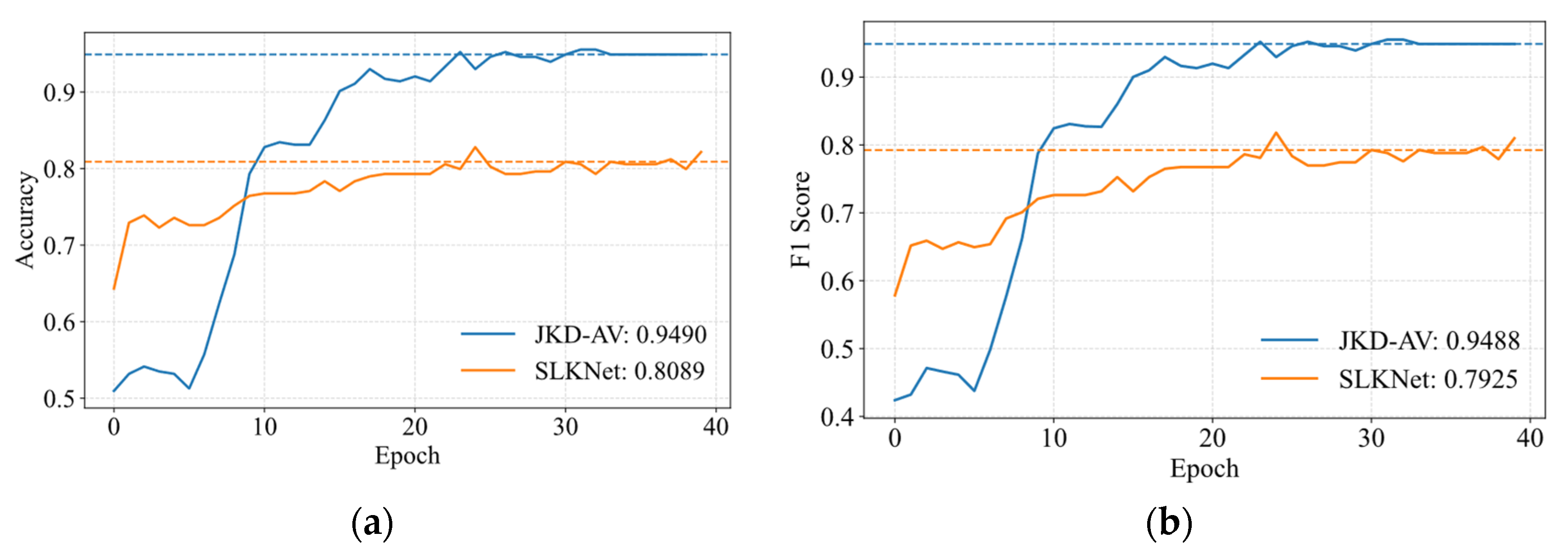

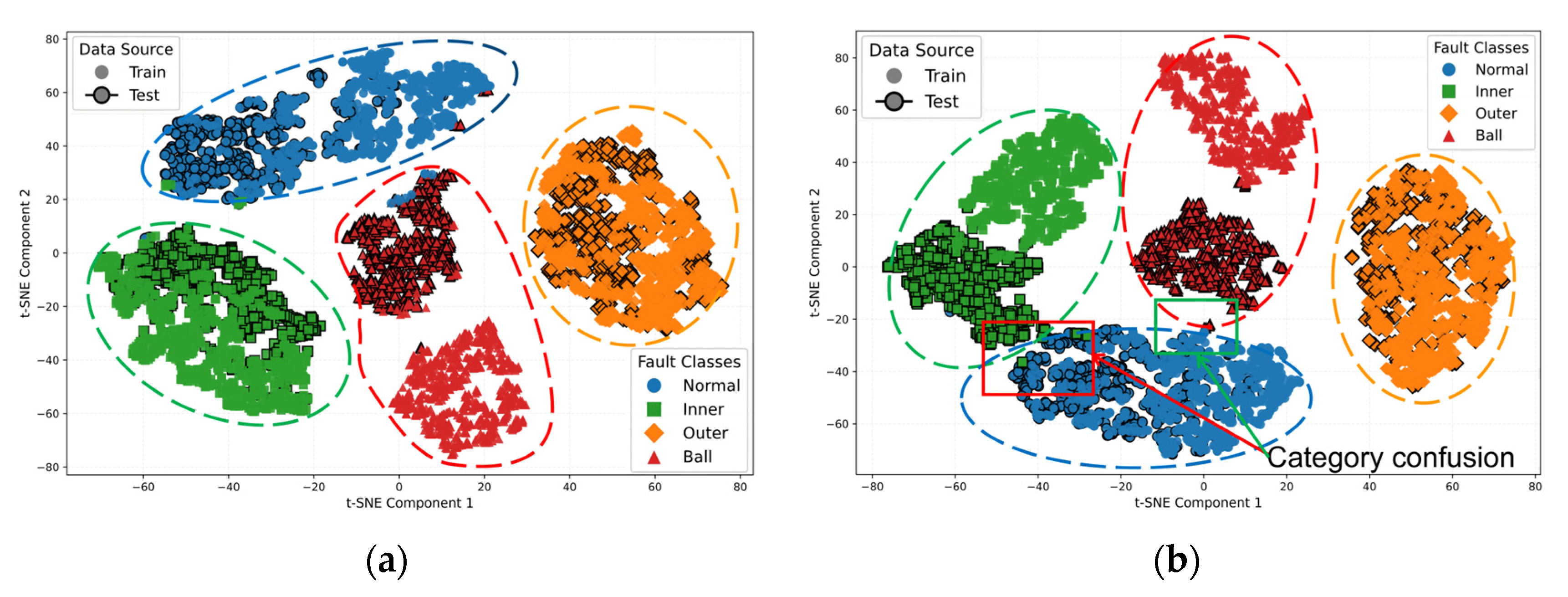
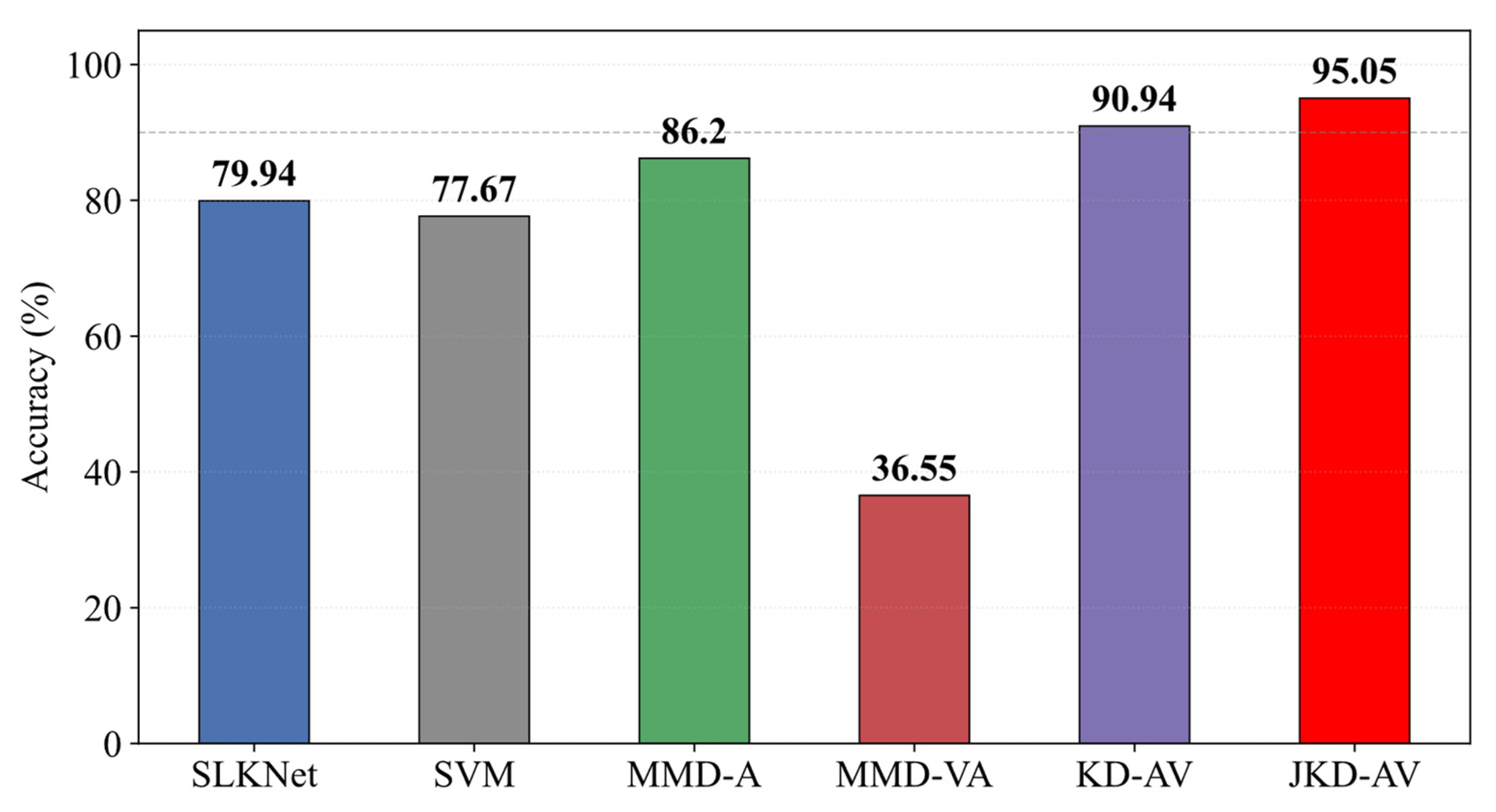

| Dataset | Health States | Label | Working Conditions | Number of Single-Mode Samples |
|---|---|---|---|---|
| A | Ball fault | 0 | 30 Hz_0 Nm | 1860 |
| Inner race fault | 1 | |||
| Outer race fault | 2 | |||
| Normal | 3 | |||
| B | Ball fault | 0 | 30 Hz_3 Nm | 1860 |
| Inner race fault | 1 | |||
| Outer race fault | 2 | |||
| Normal | 3 | |||
| C | Ball fault | 0 | 30 Hz_6 Nm | 1860 |
| Inner race fault | 1 | |||
| Outer race fault | 2 | |||
| Normal | 3 |
| Transfer Task | Training Set | Validation and Test Sets | |
|---|---|---|---|
| Source Domain (Vibration) | Target Domain (Acoustic) | ||
| A → B | Dataset A | Dataset A | Dataset B |
| A → C | Dataset A | Dataset A | Dataset C |
| B → C | Dataset B | Dataset B | Dataset C |
| Method | A → B | A → C | B → C | |||
|---|---|---|---|---|---|---|
| Accuracy | F1-Score | Accuracy | F1-Score | Accuracy | F1-Score | |
| SLKNet | 92.95% | 92.86% | 63.74% | 59.50% | 88.89% | 89.05% |
| KD-AV | 98.39% | 98.40% | 94.86% | 95.60% | 94.80% | 94.80% |
| JKD-AV | 99.58% | 99.58% | 97.85% | 97.85% | 97.49% | 97.48% |
| Method | A → B | A → C | B → C | |||
|---|---|---|---|---|---|---|
| Accuracy | F1-Score | Accuracy | F1-Score | Accuracy | F1-Score | |
| SLKNet | 92.95% | 92.86% | 63.74% | 59.50% | 88.89% | 89.05% |
| SVM | 40.68% | 37.23% | 74.13% | 64.49% | 75.03% | 66.46% |
| MMD-A | 95.22% | 95.15% | 90.38% | 90.41% | 96.06% | 96.05% |
| MMD-VA | 37.4% | 33.42% | 59.80% | 54.10% | 34.29% | 25.26% |
| KD-AV | 98.39% | 98.40% | 94.86% | 95.60% | 94.80% | 94.80% |
| JKD-AV | 99.58% | 99.58% | 97.85% | 97.85% | 97.49% | 97.48% |
| Model Size | Total Params | Test Time (Single Sample)/μs |
|---|---|---|
| 0.03 M | 325 | 134 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, F.; Liu, C.; He, F.; Bai, Z. Acoustics-Augmented Diagnosis Method for Rolling Bearings Based on Acoustic–Vibration Fusion and Knowledge Transfer. Sensors 2025, 25, 5190. https://doi.org/10.3390/s25165190
Xue F, Liu C, He F, Bai Z. Acoustics-Augmented Diagnosis Method for Rolling Bearings Based on Acoustic–Vibration Fusion and Knowledge Transfer. Sensors. 2025; 25(16):5190. https://doi.org/10.3390/s25165190
Chicago/Turabian StyleXue, Fangyong, Chang Liu, Feifei He, and Zeping Bai. 2025. "Acoustics-Augmented Diagnosis Method for Rolling Bearings Based on Acoustic–Vibration Fusion and Knowledge Transfer" Sensors 25, no. 16: 5190. https://doi.org/10.3390/s25165190
APA StyleXue, F., Liu, C., He, F., & Bai, Z. (2025). Acoustics-Augmented Diagnosis Method for Rolling Bearings Based on Acoustic–Vibration Fusion and Knowledge Transfer. Sensors, 25(16), 5190. https://doi.org/10.3390/s25165190






