Soft Shear Sensing of Robotic Twisting Tasks Using Reduced-Order Conductivity Modeling
Abstract
1. Introduction
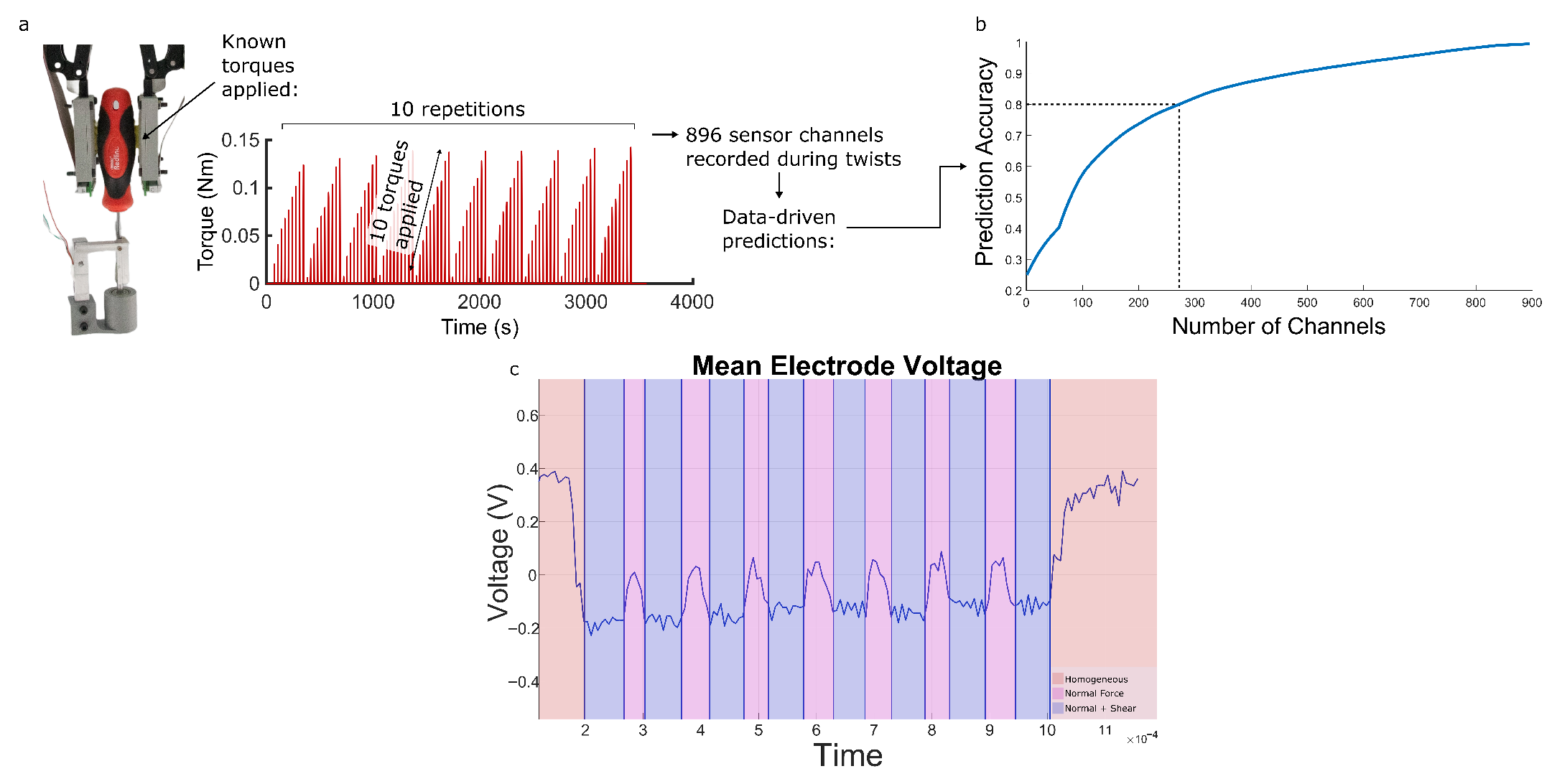
2. Experimental Section
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, Z.; Deng, Z.; Fang, B.; Yang, Y.; Sun, F. A review on sensory perception for dexterous robotic manipulation. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221095974. [Google Scholar] [CrossRef]
- Hegde, C. Sensing in Soft Robotics. ACS Nano 2023, 17, 15277–15307. [Google Scholar] [CrossRef] [PubMed]
- Zangrandi, A.; D’Alonzo, M.; Cipriani, C.; Di Pino, G. Neurophysiology of slip sensation and grip reaction: Insights for hand prosthesis control of slippage. J. Neurophysiol. 2021, 126, 477–492. [Google Scholar] [CrossRef]
- Nakazawa, N.; Ikeura, R.; Inooka, H. Characteristics of human fingertips in the shearing direction. Biol. Cybern. 2000, 82, 207–214. [Google Scholar] [CrossRef]
- Kyberd, P. Slip detection strategies for automatic grasping in prosthetic hands. Sensors 2023, 23, 4433. [Google Scholar] [CrossRef]
- Aksoy, B.; Hao, Y.; Grasso, G.; Digumarti, K.M.; Cacucciolo, V.; Shea, H. Shielded soft force sensors. Nat. Commun. 2022, 13, 4649. [Google Scholar] [CrossRef]
- Aksoy, B.; Digumarti, K.M.; Shea, H. Soft monolithic shielded sensors to measure shear and normal forces for local slip detection. Adv. Mater. Technol. 2024, 9, 2400486. [Google Scholar] [CrossRef]
- Platkiewicz, J.; Lipson, H.; Hayward, V. Haptic edge detection through shear. Sci. Rep. 2016, 6, 23551. [Google Scholar] [CrossRef]
- Lepora, N.F. Soft Biomimetic Optical Tactile Sensing with the TacTip: A Review. IEEE Sens. J. 2021, 21, 21131–21143. [Google Scholar] [CrossRef]
- Yuan, W.; Li, R.; Srinivasan, M.A.; Adelson, E.H. Measurement of shear and slip with a GelSight tactile sensor. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 304–311. [Google Scholar] [CrossRef]
- Tiwana, M.I.; Shashank, A.; Redmond, S.J.; Lovell, N.H. Characterization of a capacitive tactile shear sensor for application in robotic and upper limb prostheses. Sens. Actuators A Phys. 2011, 165, 164–172. [Google Scholar] [CrossRef]
- Roberts, P.; Damian, D.D.; Shan, W.; Lu, T.; Majidi, C. Soft-matter capacitive sensor for measuring shear and pressure deformation. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3529–3534. [Google Scholar] [CrossRef]
- Hwang, E.S.; Seo, J.h.; Kim, Y.J. A polymer-based flexible tactile sensor for both normal and shear load detections and its application for robotics. J. Microelectromech. Syst. 2007, 16, 556–563. [Google Scholar] [CrossRef]
- Lee, H.K.; Chung, J.; Chang, S.I.; Yoon, E. Normal and shear force measurement using a flexible polymer tactile sensor with embedded multiple capacitors. J. Microelectromech.Syst. 2008, 17, 934–942. [Google Scholar] [CrossRef]
- Xu, R.; Yurkewich, A.; Patel, R.V. Curvature, torsion, and force sensing in continuum robots using helically wrapped FBG sensors. IEEE Robot. Autom. Lett. 2016, 1, 1052–1059. [Google Scholar] [CrossRef]
- Baimukashev, D.; Kappassov, Z.; Varol, H.A. Shear, torsion and pressure tactile sensor via plastic optofiber guided imaging. IEEE Robot. Autom. Lett. 2020, 5, 2618–2625. [Google Scholar] [CrossRef]
- Domenici, C.; De Rossi, D.; Bacci, A.; Bennati, S. Shear stress detection in an elastic layer by a piezoelectric polymer tactile sensor. IEEE Trans. Electr. Insul. 1989, 24, 1077–1081. [Google Scholar] [CrossRef]
- Cheney, M.; Isaacson, D.; Newell, J.C. Electrical impedance tomography. SIAM Rev. 1999, 41, 85–101. [Google Scholar] [CrossRef]
- Park, K.; Yuk, H.; Yang, M.; Cho, J.; Lee, H.; Kim, J. A biomimetic elastomeric robot skin using electrical impedance and acoustic tomography for tactile sensing. Sci. Robot. 2022, 7, eabm7187. [Google Scholar] [CrossRef]
- Hardman, D.; Thuruthel, T.G.; Iida, F. Multimodal information structuring with single-layer soft skins and high-density electrical impedance tomography. Sci. Robot. 2025, 10, eadq2303. [Google Scholar] [CrossRef]
- Abdelwahed, M.; Pitti, A.; Romain, O.; Ouezdou, F.B. Use of multi-frequency electrical impedance tomography as tactile sensor for material discrimination. In Proceedings of the 2020 5th International Conference on Advanced Robotics and Mechatronics (ICARM), Shenzhen, China, 18–21 December 2020; pp. 588–594. [Google Scholar] [CrossRef]
- Chen, H.; Yang, X.; Wang, P.; Geng, J.; Ma, G.; Wang, X. A Large-Area Flexible Tactile Sensor for Multi-Touch and Force Detection Using Electrical Impedance Tomography. IEEE Sens. J. 2022, 22, 7119–7129. [Google Scholar] [CrossRef]
- Xin, W.; Zhu, F.; Wang, P.; Xie, Z.; Tang, Z.; Laschi, C. Electrical impedance tomographic shape sensing for soft robots. IEEE Robot. Autom. Lett. 2023, 8, 1555–1562. [Google Scholar] [CrossRef]
- Hardman, D.; Thuruthel, T.G.; Iida, F. Tactile perception in hydrogel-based robotic skins using data-driven electrical impedance tomography. Mater. Today Electron. 2023, 4, 100032. [Google Scholar] [CrossRef]
- Park, H.; Kim, W.; Jeon, S.; Na, Y.; Kim, J. Graph-structured super-resolution for geometry- generalized tomographic tactile sensing: Application to humanoid faces. IEEE Trans. Robot. 2025, 41, 558–572. [Google Scholar] [CrossRef]
- Park, H.; Kim, J. Data-Driven Investigation on Anisotropic Electrical Impedance Tomography for Robotic Shear Tactile Sensing. In Proceedings of the 2023 20th International Conference on Ubiquitous Robots (UR), Honolulu, HI, USA, 25–28 June 2023; pp. 59–63. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, D.; Cho, H.; Park, I.; Kim, J. Soft nanocomposite based multi-point, multi-directional strain mapping sensor using anisotropic electrical impedance tomography. Sci. Rep. 2017, 7, 39837. [Google Scholar] [CrossRef] [PubMed]
- Hughes, J.; Gilday, K.; Scimeca, L.; Garg, S.; Iida, F. Flexible, adaptive industrial assembly: Driving innovation through competition: Flexible manufacturing. Intell. Serv. Robot. 2020, 13, 169–178. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, J.; Wang, B.; Huang, J.; Bao, G. Continuous adaptive gaits manipulation for three-fingered robotic hands via bioinspired fingertip contact events. Biomim. Intell. Robot. 2024, 4, 100144. [Google Scholar] [CrossRef]
- Radwin, R.G. Biomechanical aspects of hand tools. In Musculoskeletal Disorders in the Workplace: Principles and Practice; Mosby: Maryland Heights, MO, USA, 2007; pp. 246–263. [Google Scholar]
- Kim, K.; Hong, J.H.; Bae, K.; Lee, K.; Lee, D.J.; Park, J.; Zhang, H.; Sang, M.; Ju, J.E.; Cho, Y.U.; et al. Extremely durable electrical impedance tomography–based soft and ultrathin wearable e-skin for three-dimensional tactile interfaces. Sci. Adv. 2024, 10, eadr1099. [Google Scholar] [CrossRef] [PubMed]
- Tegin, J.; Wikander, J. Tactile sensing in intelligent robotic manipulation—A review. Ind. Robot 2005, 32, 64–70. [Google Scholar] [CrossRef]
- Zhu, J.; Snowden, J.C.; Verdejo, J.; Chen, E.; Zhang, P.; Ghaednia, H.; Schwab, J.H.; Mueller, S. EIT-kit: An electrical impedance tomography toolkit for health and motion sensing. In Proceedings of the UIST 2021—34th Annual ACM Symposium on User Interface Software and Technology, Virtual, USA, 10–14 October 2021; Association for Computing Machinery, Inc.: New York, NY, USA, 2021; pp. 400–413. [Google Scholar] [CrossRef]
- Hardman, D.; George Thuruthel, T.; Iida, F. Self-healing ionic gelatin/glycerol hydrogels for strain sensing applications. NPG Asia Mater. 2022, 14, 11. [Google Scholar] [CrossRef]
- Glover, J.D.; Yang, X.; Long, R.; Pham, J.T. Creasing in microscale, soft static friction. Nat. Commun. 2023, 14, 2362. [Google Scholar] [CrossRef]
- Biasi, N.; Gargano, A.; Arcarisi, L.; Carbonaro, N.; Tognetti, A. Physics-based simulation and machine learning for the practical implementation of EIT-based tactile sensors. IEEE Sens. J. 2022, 22, 4186–4196. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trehan, D.; Hardman, D.; Iida, F. Soft Shear Sensing of Robotic Twisting Tasks Using Reduced-Order Conductivity Modeling. Sensors 2025, 25, 5159. https://doi.org/10.3390/s25165159
Trehan D, Hardman D, Iida F. Soft Shear Sensing of Robotic Twisting Tasks Using Reduced-Order Conductivity Modeling. Sensors. 2025; 25(16):5159. https://doi.org/10.3390/s25165159
Chicago/Turabian StyleTrehan, Dhruv, David Hardman, and Fumiya Iida. 2025. "Soft Shear Sensing of Robotic Twisting Tasks Using Reduced-Order Conductivity Modeling" Sensors 25, no. 16: 5159. https://doi.org/10.3390/s25165159
APA StyleTrehan, D., Hardman, D., & Iida, F. (2025). Soft Shear Sensing of Robotic Twisting Tasks Using Reduced-Order Conductivity Modeling. Sensors, 25(16), 5159. https://doi.org/10.3390/s25165159





