A Spline Curve Fitting Model for Towed Streamer Positioning in Marine Seismic Exploration
Abstract
1. Introduction
2. Spline Curve Fitting Method
2.1. Spline Curve Model
2.2. Observation Error Equations
2.3. Hydrophone Position Estimation
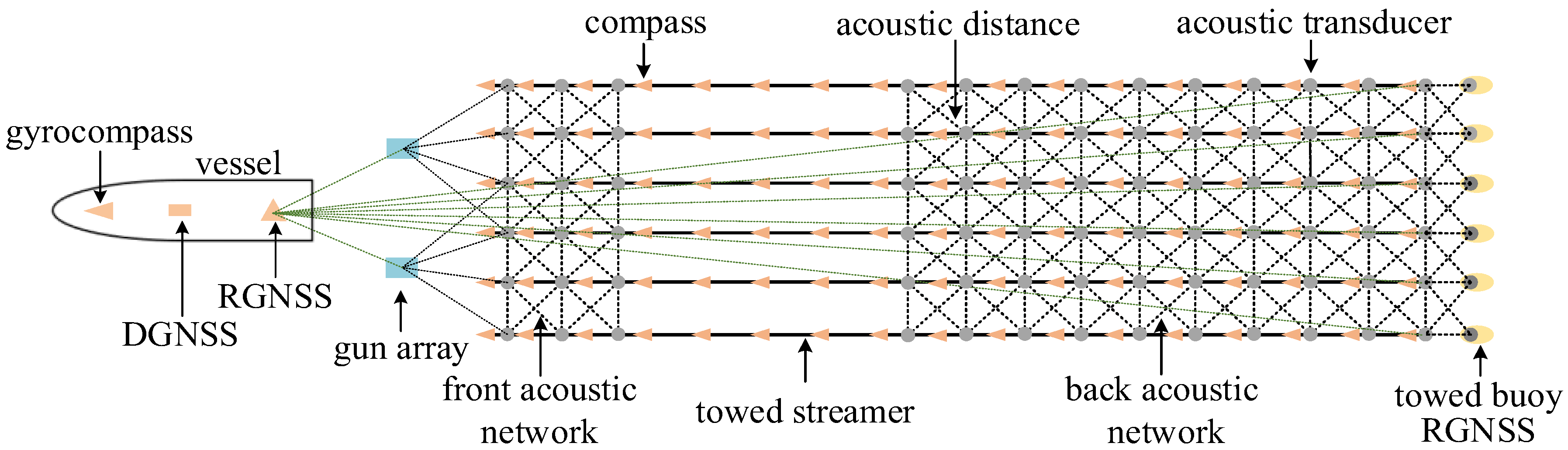
3. Experiments and Results Analysis
3.1. Simulation Experiment
3.2. Field Experiment
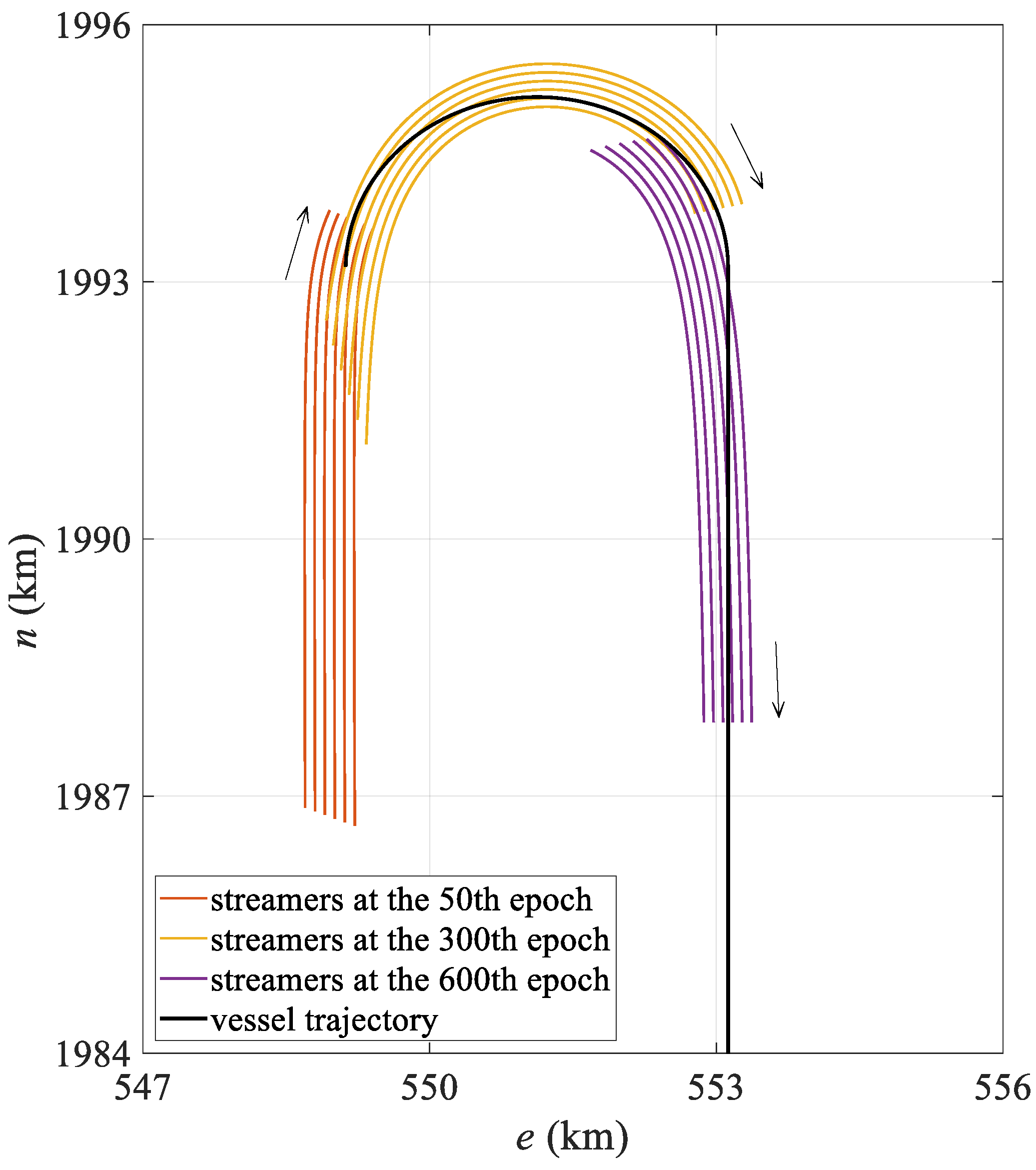
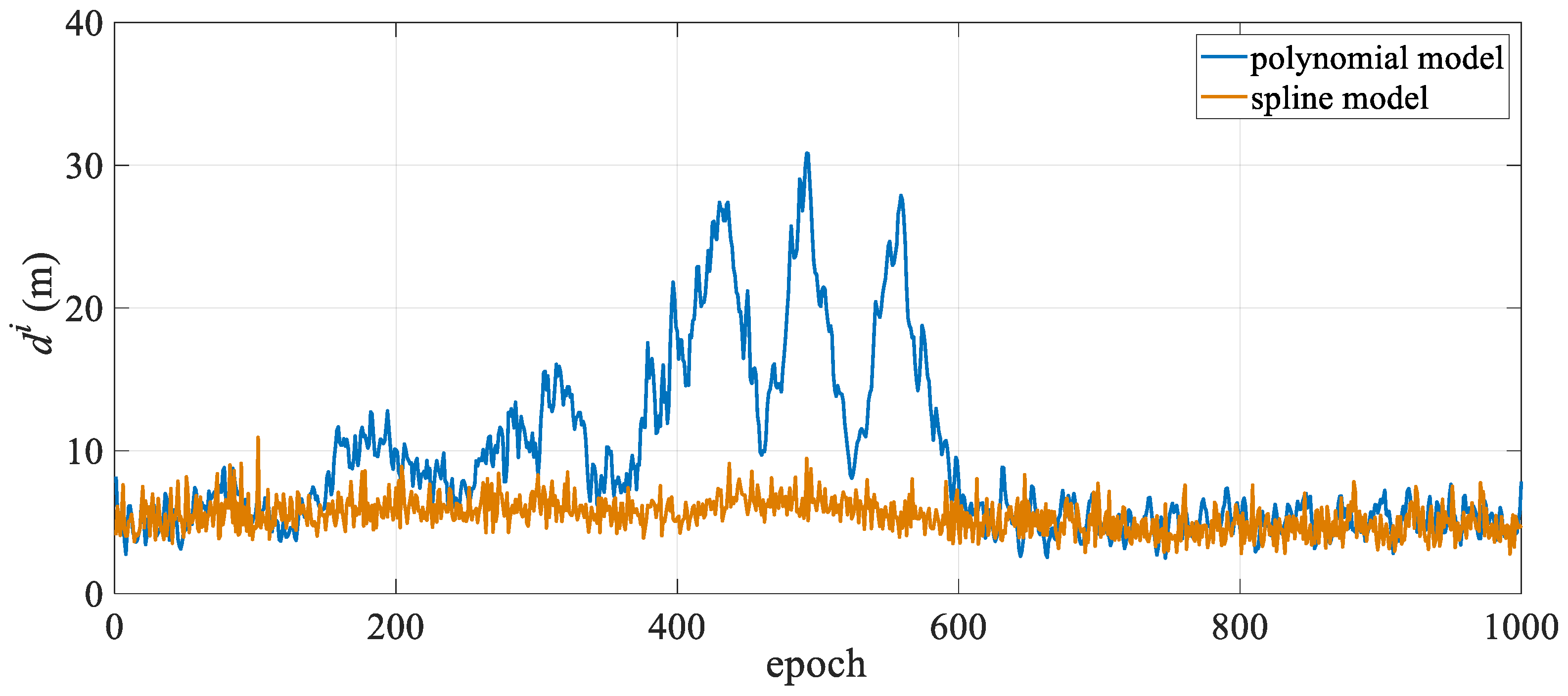
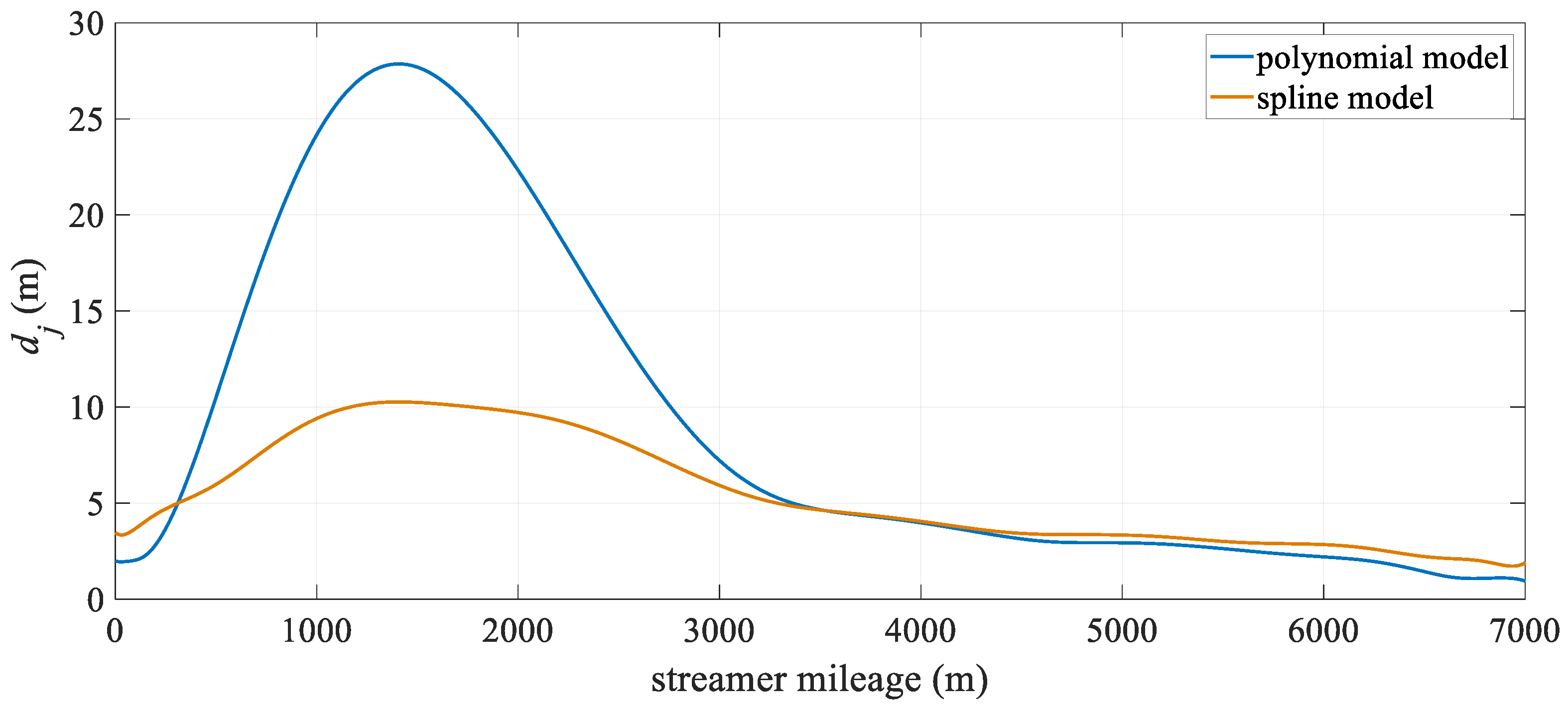
3.2.1. Case I: 6-Streamer Scenario
3.2.2. Case II: 10-Streamer Scenario
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gikas, V.; Cross, P.A.; Ridyard, D. Reliability analysis in dynamic systems: Implications for positioning marine seismic networks. Geophysics 1999, 64, 1014–1022. [Google Scholar] [CrossRef]
- Musser, J.A.; Ridyard, D.; Hupkens, D.E. Streamer positioning for advanced 3D and 4D applications. Mar. Imag. 2002, 28, 1–4. [Google Scholar]
- Gilbert, D. Seismic streamer position and shape estimation. In Proceedings of the OCEANS 81, Boston, MA, USA, 16–18 September 1981; pp. 1077–1081. [Google Scholar]
- Gilbert, D. Performance characteristics of a three-dimensional array shape estimator. In Proceedings of the OCEANS 82, Washington, DC, USA, 20–22 September 1982; pp. 140–145. [Google Scholar]
- Zinn, N.D.; Rapatz, P.J.V. Positioning networks in 3D marine seismic. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 1993; p. OTC-7078-MS. [Google Scholar]
- Goutorbe, B.; Combier, V. On the reconstruction of the shape of a seismic streamer. Geophysics 2010, 75, H1–H6. [Google Scholar] [CrossRef]
- Egeland, G. Array shape estimation. In Proceedings of the OCEANS 82, Washington, DC, USA, 20–22 September 1982; pp. 121–122. [Google Scholar]
- Combier, V. Single streamer positioning. Lithos 2006, 8, 113–118. [Google Scholar]
- Morgan, J.G. The challenge of precisely positioning a 3D seismic survey. Navigation 1983, 30, 261–272. [Google Scholar] [CrossRef]
- Jubinski, P. A test of the accuracy of a magnetic compass-based streamer location system. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 1985; p. OTC-4996-MS. [Google Scholar]
- Krail, P.M.; Brysk, H. The shape of a marine streamer in a cross current. Geophysics 1989, 54, 302–308. [Google Scholar] [CrossRef]
- Gikas, V.N. Least squares filtering and testing for positioning and quality control during 3d marine seismic surveys. Doctoral dissertation, Newcastle University, Newcastle, UK, 1996. [Google Scholar]
- Zinn, N.; Rapatz, P.J.V. Reliability analysis in marine seismic networks. Oceanogr. Lit. Rev. 1995, 10, 847. [Google Scholar] [CrossRef]
- Bole, J.R., Jr.; Dakin, D.T. Sound velocity measurements for seismic streamers. Sea Technol. 1998, 39, 73–78. [Google Scholar]
- Court, I.N. Streamer compass validation and verification. Geophysics 1993, 58, 589–592. [Google Scholar] [CrossRef]
- Yi, C.; Cao, G.; Fang, S.; Sun, S. Fitting of offshore towed streamer shapes. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 702–704. [Google Scholar]
- Zhang, Z.; Wang, Z.; Dong, S.; Ma, Z.; Qu, C. Integrated navigation and positioning data processing in offshore multi-sources and multi-streamers seismic survey. Geophys. Prosp. Petro. 2013, 52, 630–635. [Google Scholar]
- Zhang, H.; Ruan, F.; Hu, G. Key positioning algorithm of marine 3D towed streamer integrated navigation system. J. Geomatics Sci. Technol. 2019, 36, 441–446. [Google Scholar]
- Yao, Y.; Yi, W.; Song, W. Processing methods for navigation data of offshore towed streamer exploration. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 698–701. [Google Scholar]
- Yi, C. Study on Key Techniques of Navigation & Positioning Data Processing and System Development in Marine Seismic Streamer Operation. Ph.D. Dissertation, Wuhan University, Wuhan, China, 2013. [Google Scholar]
- Yu, W.; Wu, P.; Zhang, H.; Hu, G.; Ruan, F.; Dai, W.; Kuang, C. Offshore towed-streamer seismic positioning based on polynomial curve fitting. Acta Geod. Cartogr. Sin. 2022, 51, 772. [Google Scholar]
- Yu, W.; Duan, C.; Kuang, C.; Zhang, H.; Wu, P.; Dai, W. Offshore towed-streamer positioning based on variance component estimation. Ocean Eng. 2023, 278, 114355. [Google Scholar] [CrossRef]
- Duan, C.; Zhang, H.; Kuang, C.; Yu, W.; Ruan, F.; Dai, W. Multi-streamer positioning algorithm based on curvilinear integral for seismic exploration. Oil Geophys. Prospect. 2022, 57, 1317–1324. [Google Scholar]
- Duan, C.; Kuang, C.; Zhang, H.; Sang, K.; Yang, B.; Ruan, F. Multi-sensor fusion positioning for marine towed streamers: Modeling, evaluation and comparison. IEEE Trans. Instrum. Meas. 2024, 73, 9512014. [Google Scholar] [CrossRef]
- Duan, C. Research on key algorithms and software development for post-processing of offshore streamer positioning. Master’s Thesis, Central South University, Changsha, China, 2023. [Google Scholar]
- Sang, K.; Kuang, C.; Lv, L.; Liu, H.; Zhang, H.; Yang, Y.; Yang, B. A hybrid harmonic curve model for multi-streamer hydrophone positioning in seismic exploration. Sensors 2024, 24, 8025. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Liu, Y.; Chen, G.; Tang, Q.; Feng, Y.; Wen, Y. Sequential GNSS-Acoustic seafloor point positioning with modeling of sound speed variation. J. Geod. 2023, 97, 115. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, T.; Liu, Y.; Wang, S.; Chen, G.; Li, M.; Tang, Q.; Feng, Y. Precise GNSS-Acoustic seafloor positioning with sound speed from global ocean analysis. Satell. Navig. 2025, 6, 16. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, G.; Fan, Z.; Ma, H.; Wang, Z.; Sun, Q. Vessel and buoy positioning system based on RT-PPP. J. Geomatics Sci. Technol. 2019, 36, 233–237. [Google Scholar]
- Court, I.N. Applications of acoustics to source-array and streamer tow-point positioning. Geophysics 1991, 56, 558–564. [Google Scholar] [CrossRef]
- Shen, Y.; Tao, B. Practical Methods for Surveying Data Processing; Surveying and Mapping Publishing: Beijing, China, 2012; pp. 35–41. [Google Scholar]
- Duan, C.; Zhang, H.; Kuang, C.; Yu, W.; Yang, B. Design and realization of a marine 3D towed-streamer navigation and positioning data processing system. Geophys. Prosp. Petro. 2023, 62, 80–86. [Google Scholar]
- Duan, C.; Zhang, H.; Kuang, C.; Yu, W.; Yang, B. SimStr: A C++ program for offshore seismic towed-streamer positioning data simulation. Geophysics 2024, 89, F11–F21. [Google Scholar] [CrossRef]
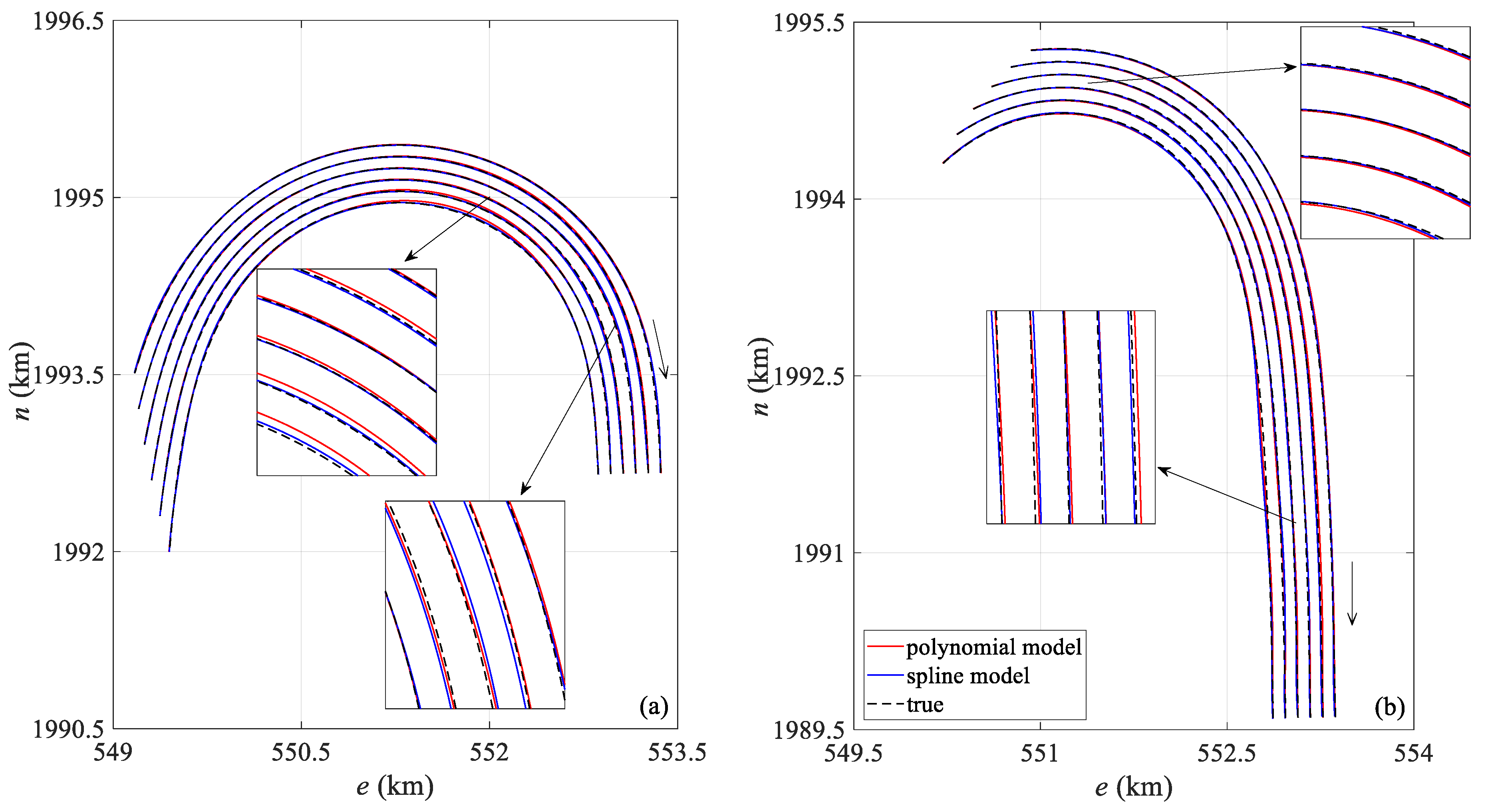

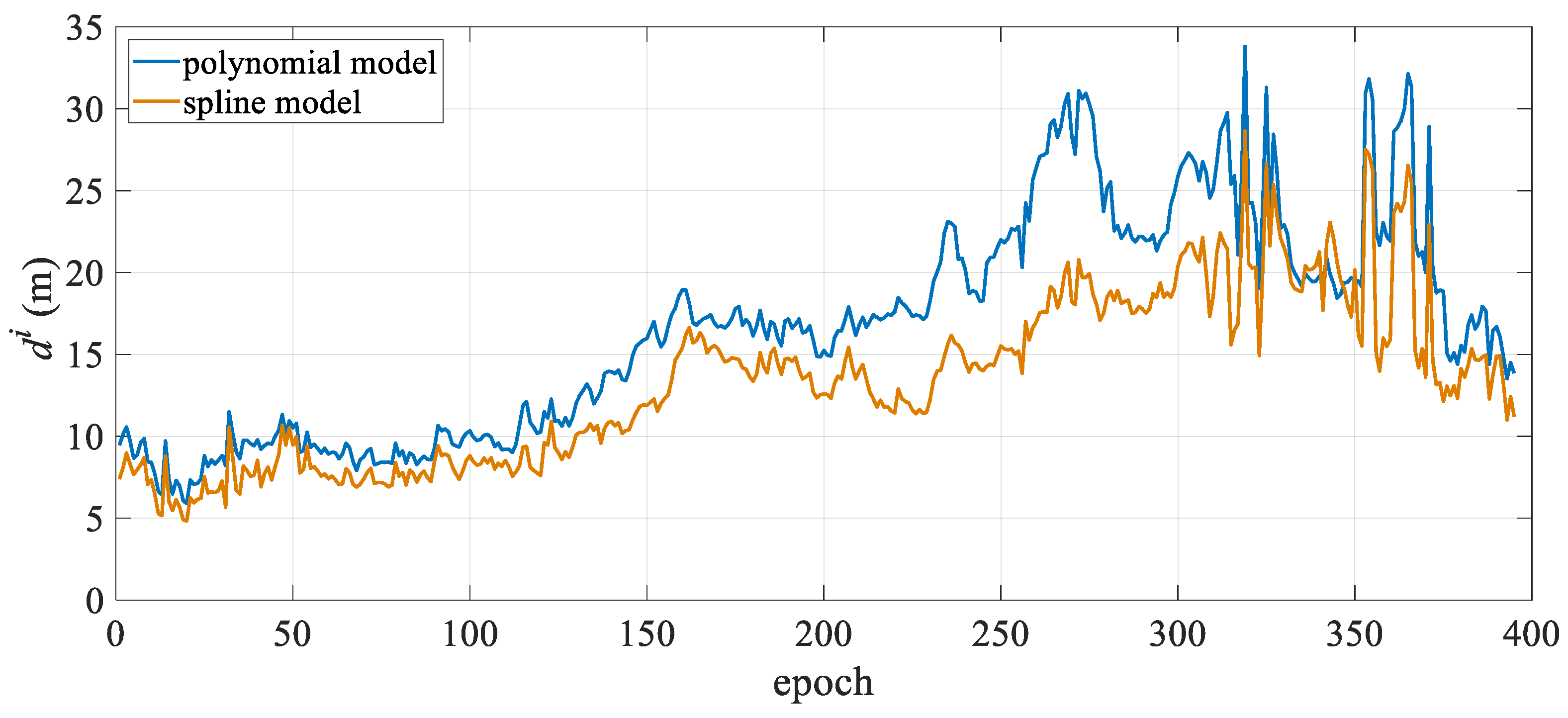
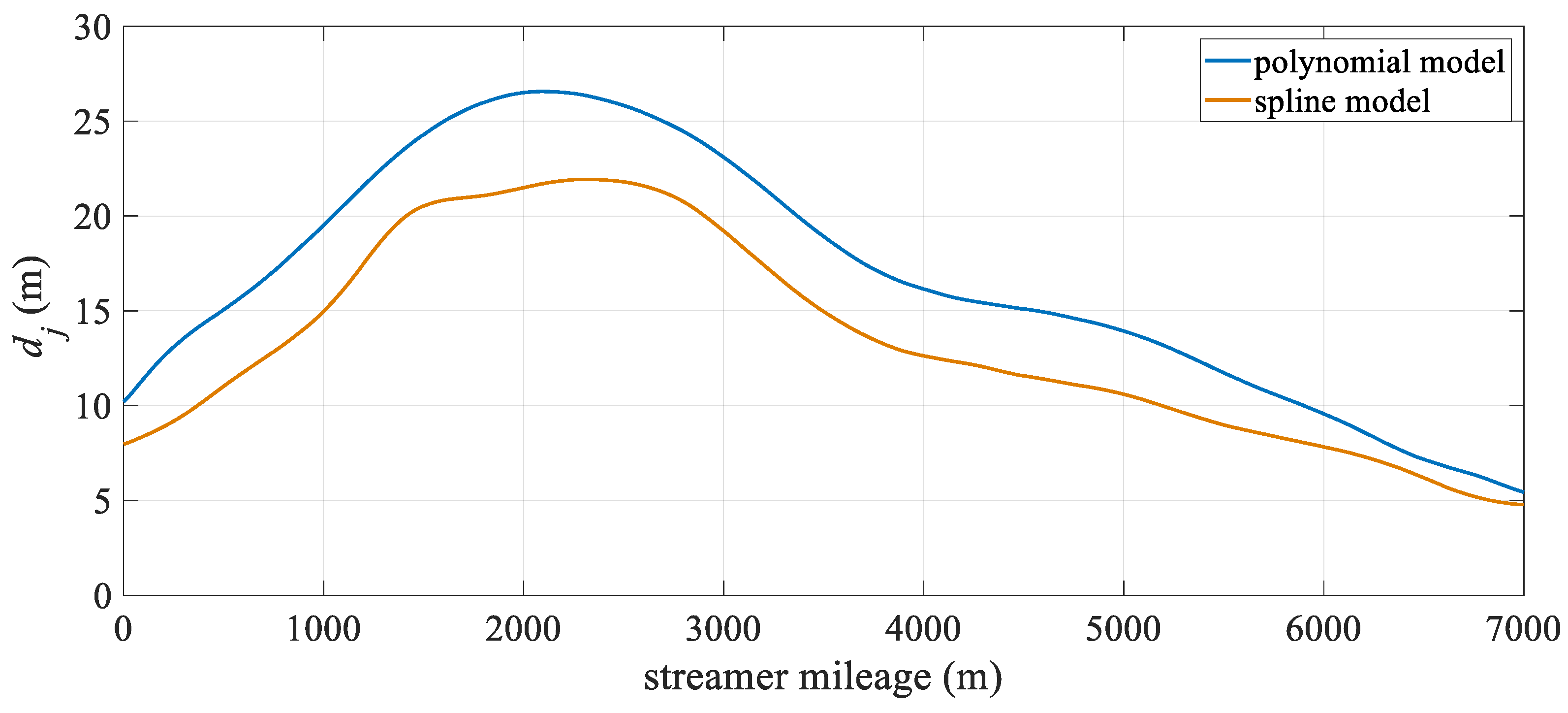
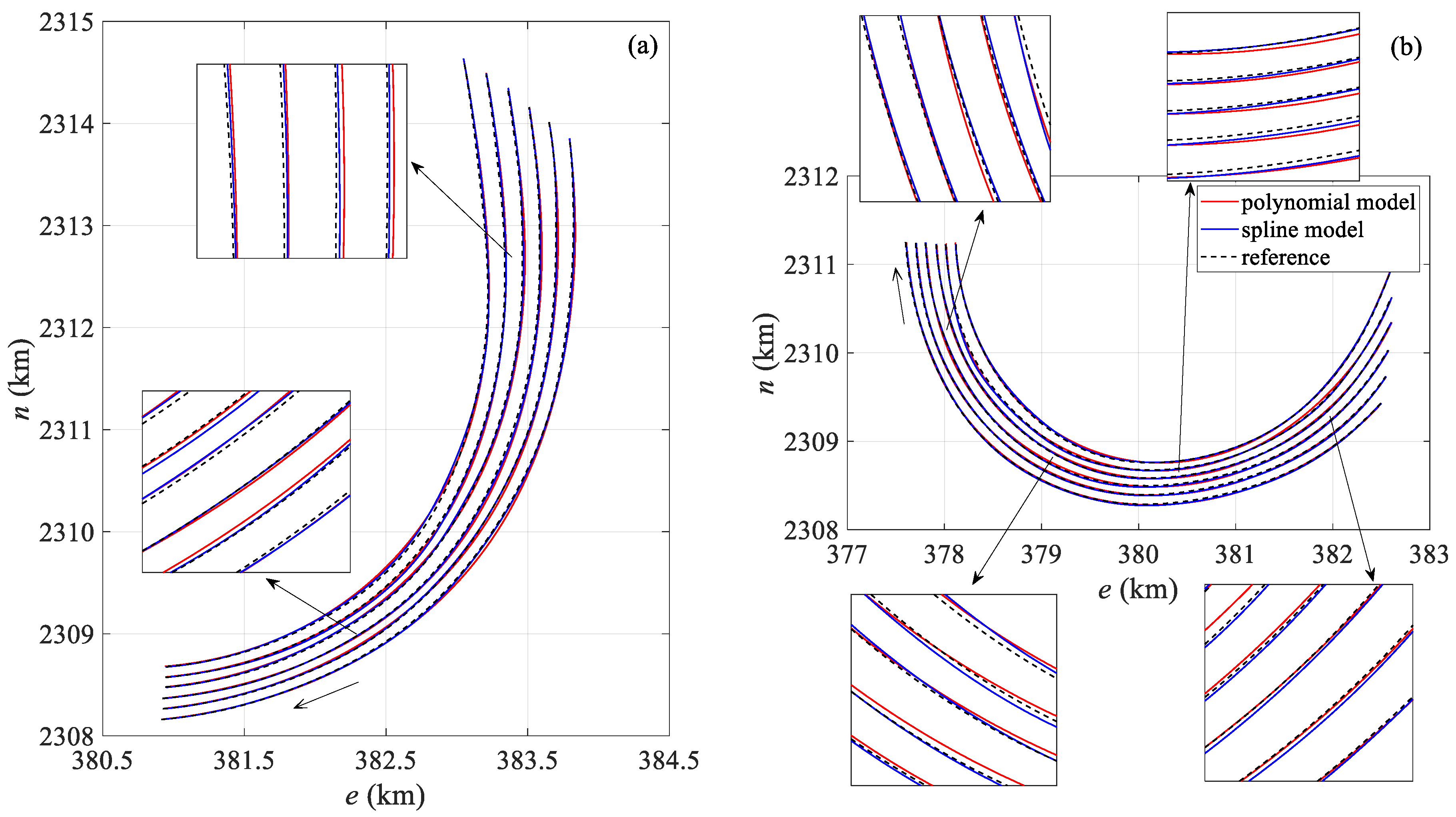
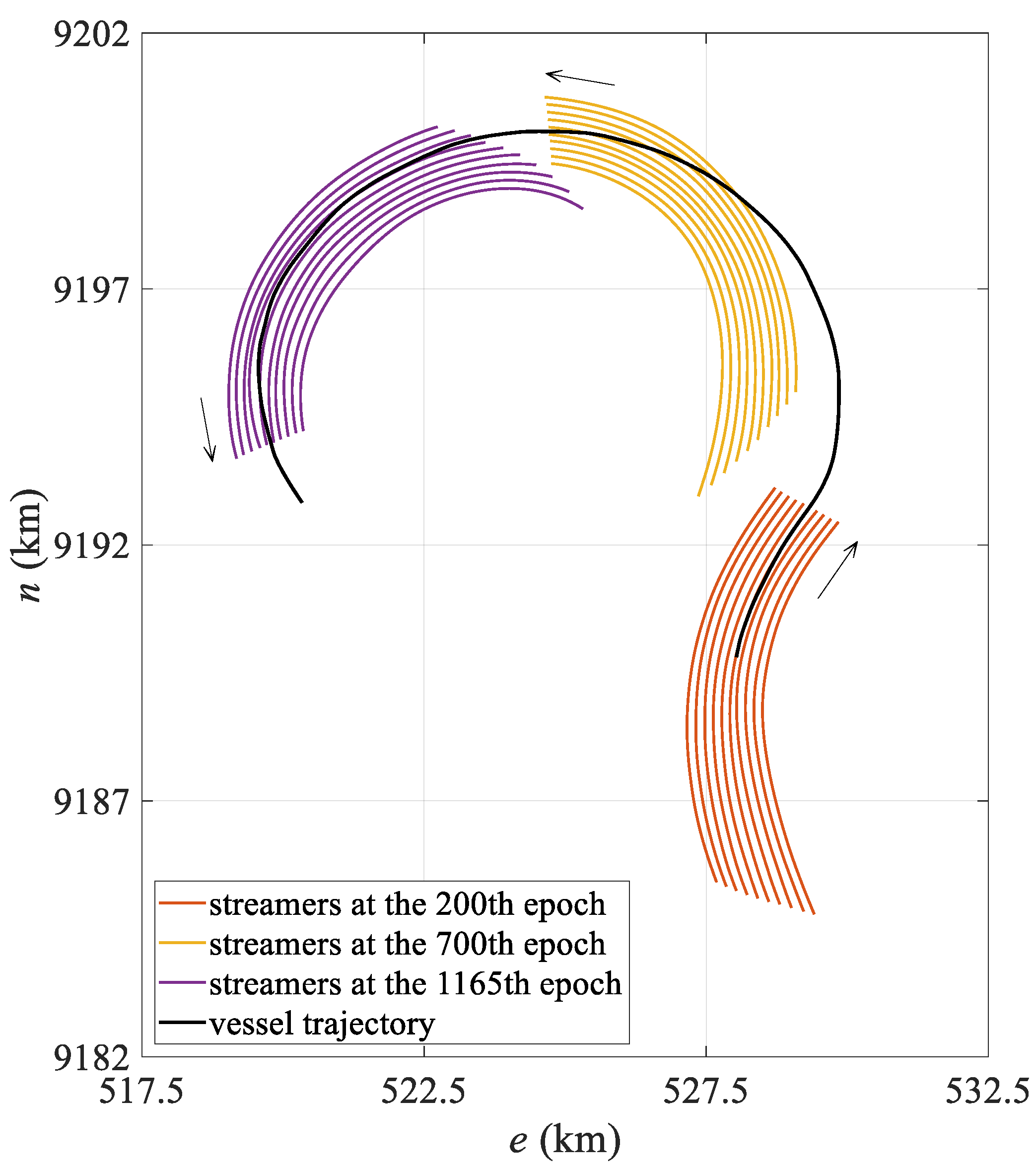
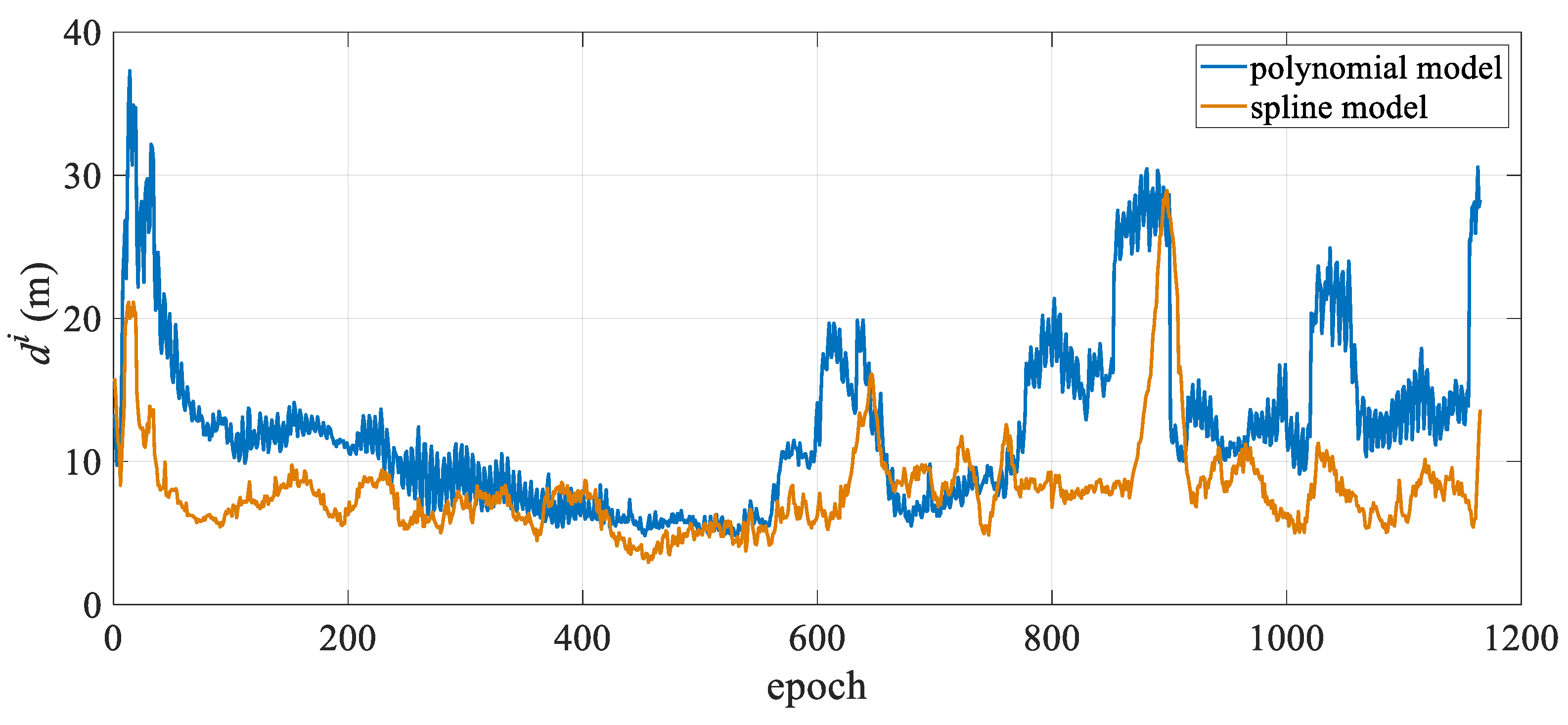
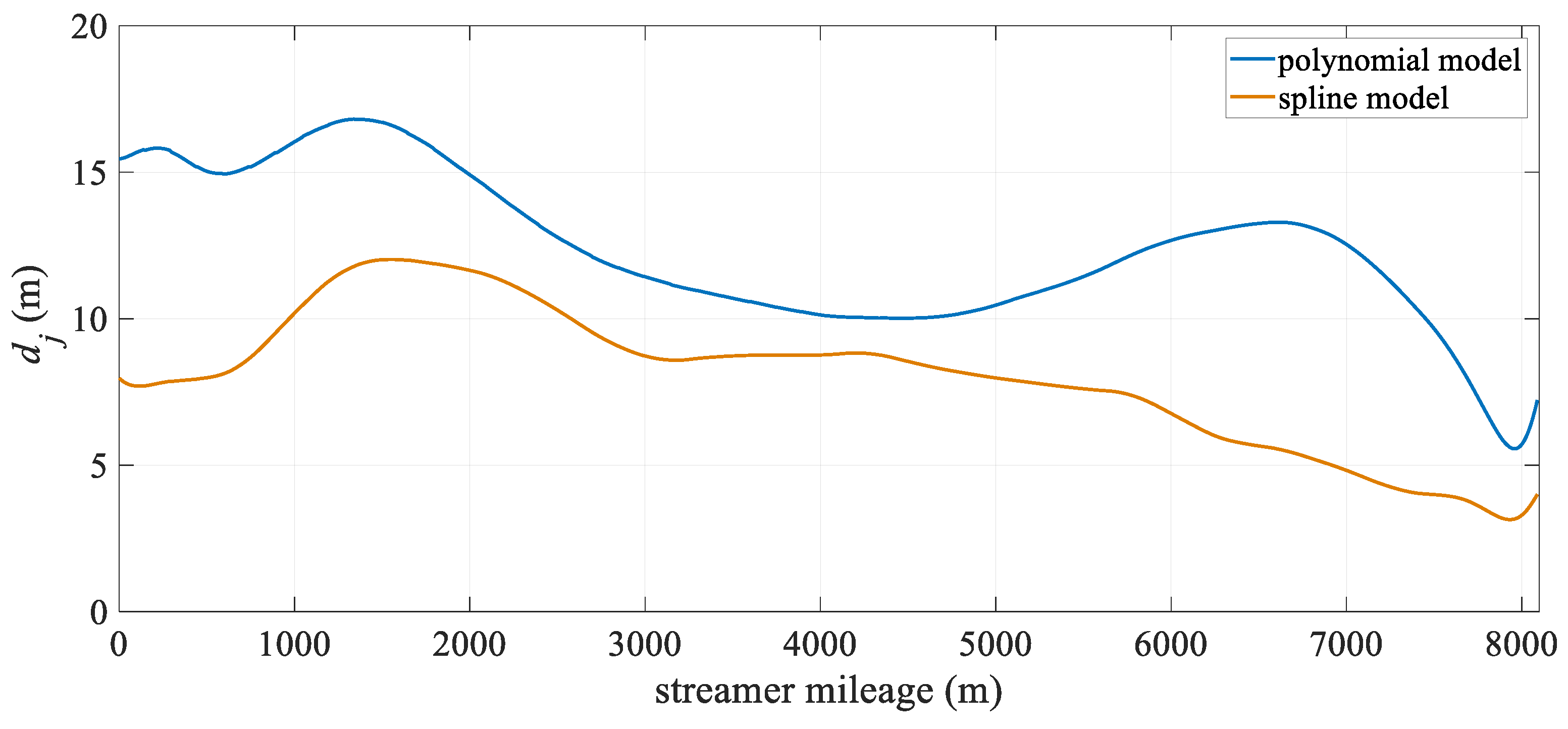
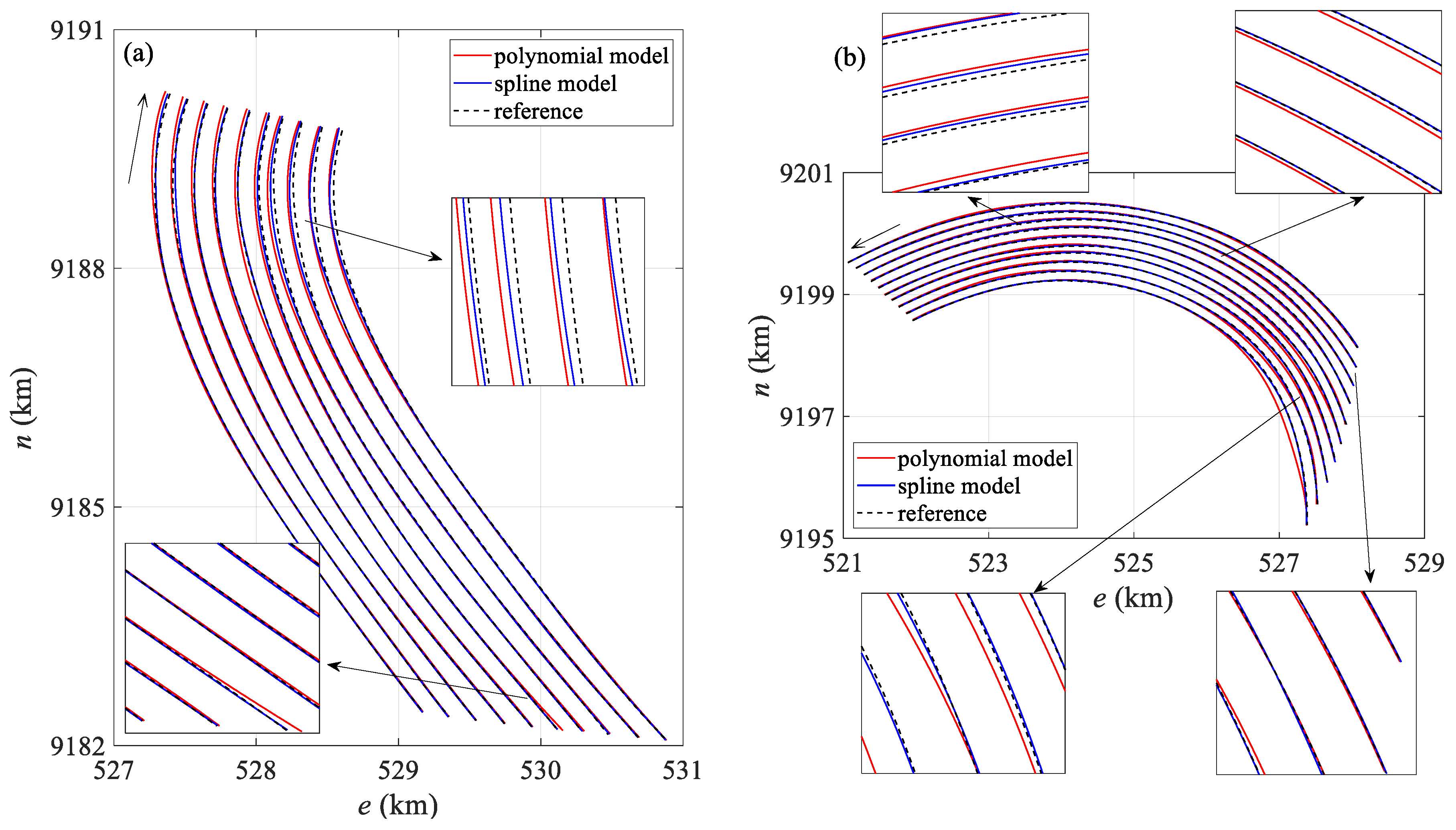
| Model | Status | Mean | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|---|
| Polynomial curve model | Turn | 10.86 | 6.23 | 30.85 | 2.54 |
| Straight | 5.09 | 1.00 | 7.83 | 2.49 | |
| Spline curve model | Turn | 5.74 | 1.10 | 10.94 | 2.88 |
| Straight | 4.66 | 1.02 | 7.84 | 2.77 |
| Model | Type | Mean | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|---|
| Polynomial curve model | Temporal | 16.74 | 6.59 | 33.81 | 5.89 |
| Spatial | 16.74 | 6.28 | 26.56 | 5.32 | |
| Spline curve model | Temporal | 13.39 | 5.05 | 28.65 | 4.82 |
| Spatial | 13.39 | 5.34 | 21.94 | 4.78 |
| Model | Type | Mean | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|---|
| Polynomial curve model | Temporal | 12.34 | 5.96 | 37.30 | 4.78 |
| Spatial | 12.34 | 2.58 | 16.81 | 5.56 | |
| Spline curve model | Temporal | 8.02 | 3.40 | 28.92 | 2.96 |
| Spatial | 8.02 | 2.36 | 12.02 | 3.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Sang, K.; Yang, B.; Duan, C.; Lv, L.; Kuang, C.; Liu, H. A Spline Curve Fitting Model for Towed Streamer Positioning in Marine Seismic Exploration. Sensors 2025, 25, 5114. https://doi.org/10.3390/s25165114
Zhang H, Sang K, Yang B, Duan C, Lv L, Kuang C, Liu H. A Spline Curve Fitting Model for Towed Streamer Positioning in Marine Seismic Exploration. Sensors. 2025; 25(16):5114. https://doi.org/10.3390/s25165114
Chicago/Turabian StyleZhang, Haonan, Kaiwei Sang, Baocai Yang, Chufeng Duan, Lingsheng Lv, Cuilin Kuang, and Heng Liu. 2025. "A Spline Curve Fitting Model for Towed Streamer Positioning in Marine Seismic Exploration" Sensors 25, no. 16: 5114. https://doi.org/10.3390/s25165114
APA StyleZhang, H., Sang, K., Yang, B., Duan, C., Lv, L., Kuang, C., & Liu, H. (2025). A Spline Curve Fitting Model for Towed Streamer Positioning in Marine Seismic Exploration. Sensors, 25(16), 5114. https://doi.org/10.3390/s25165114





