Intelligent Dynamic-Enhanced Compensation for UAV Magnetic Interference
Abstract
1. Introduction
2. Principle
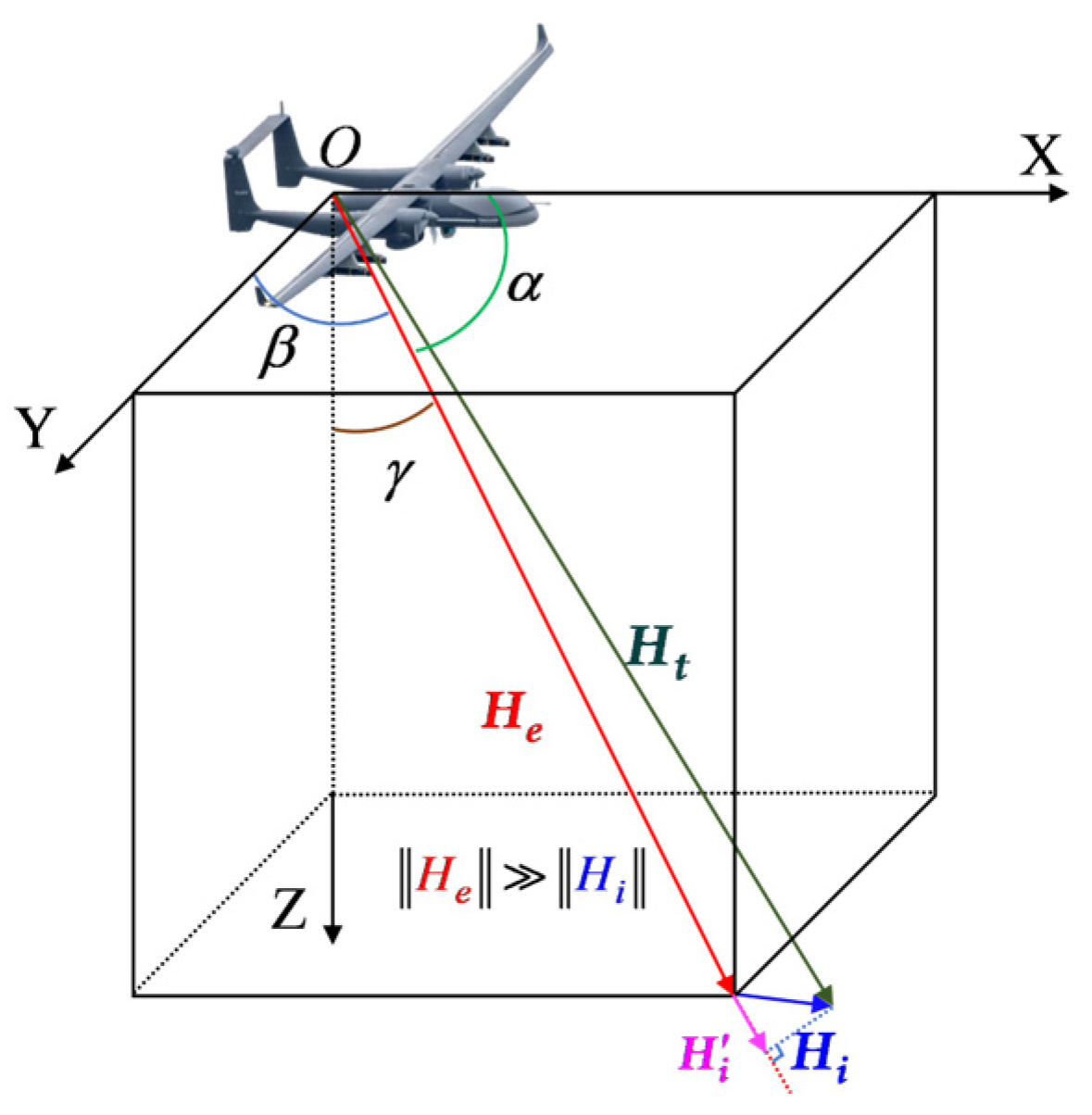
2.1. T-L Model
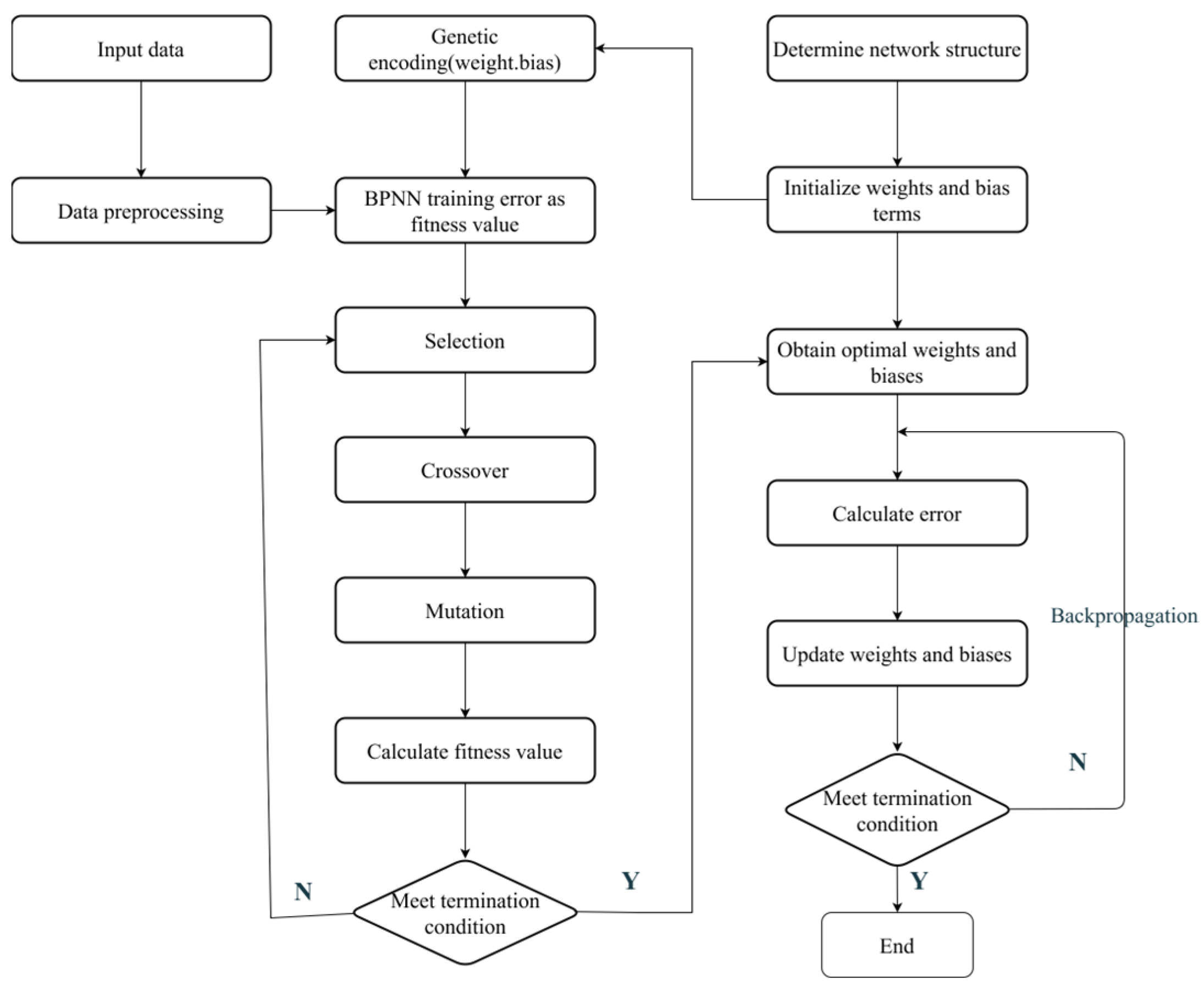
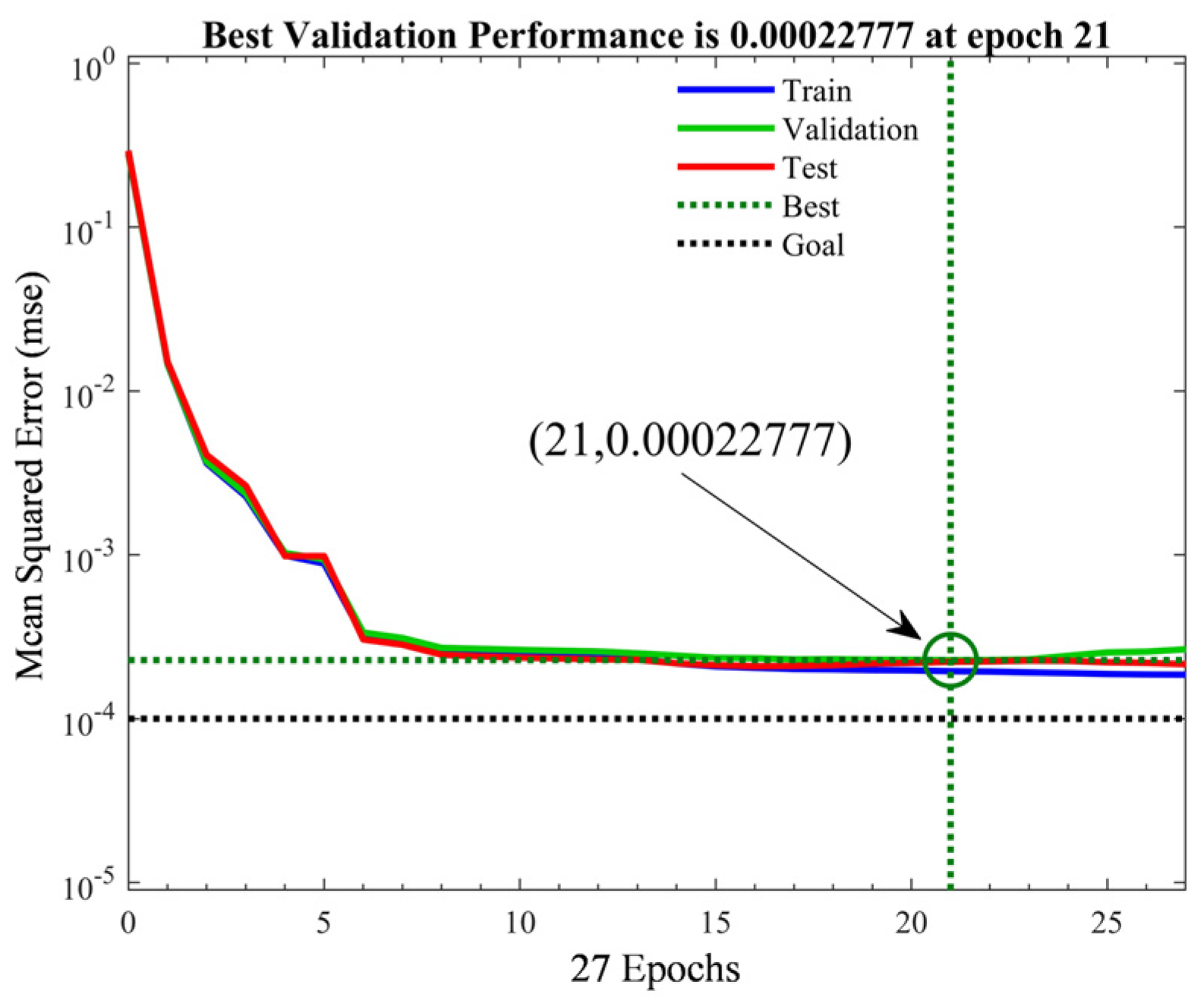
2.2. Genetic Algorithm-Optimized BP Neural Network Model
- (1)
- Data Preparation and Parameter Initialization
- (2)
- Data Feedforward Process
- (3)
- Error Backpropagation Process
- (4)
- Iterative Update Process
3. Results
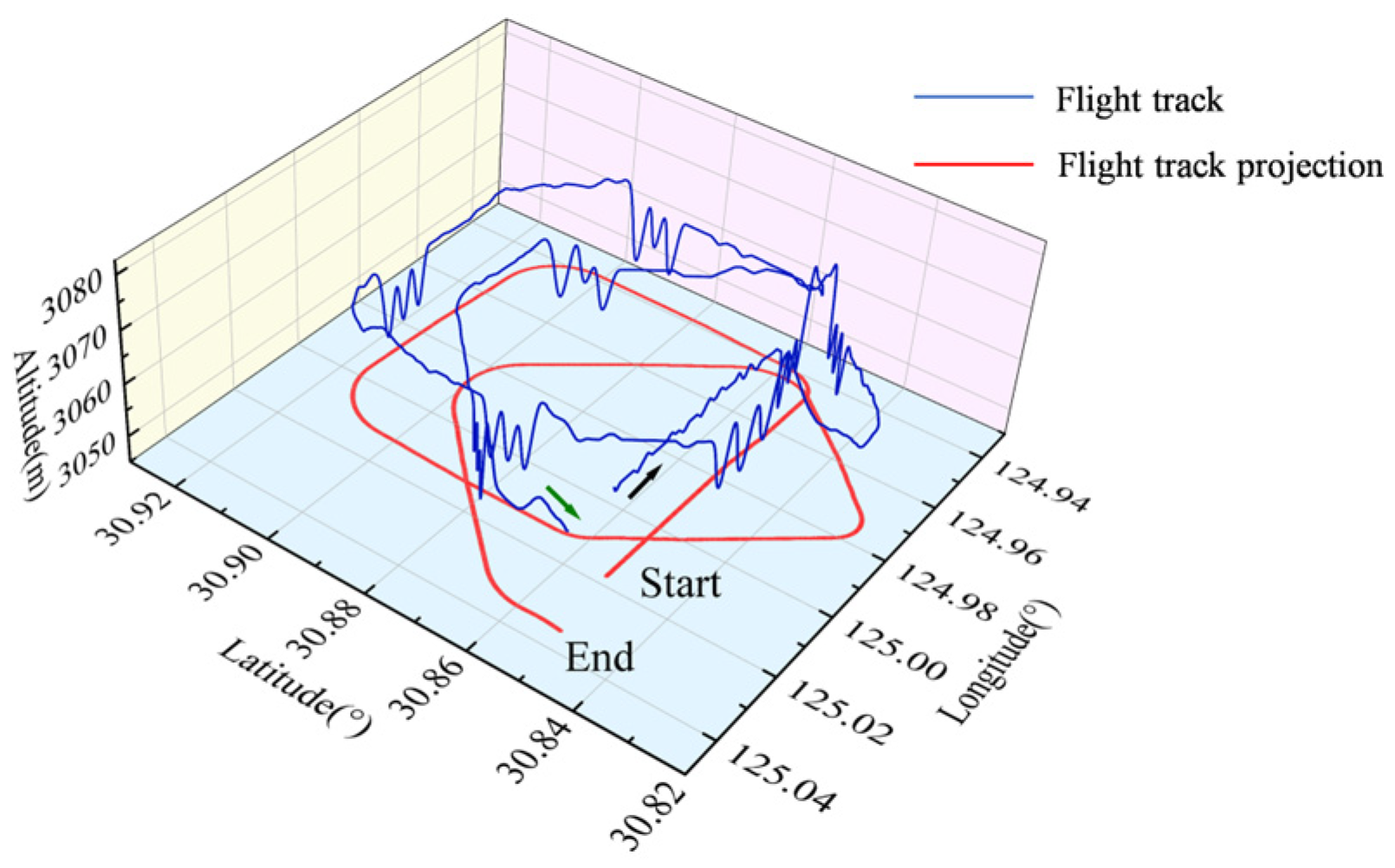
3.1. Experimental Data Acquisition and Preprocessing
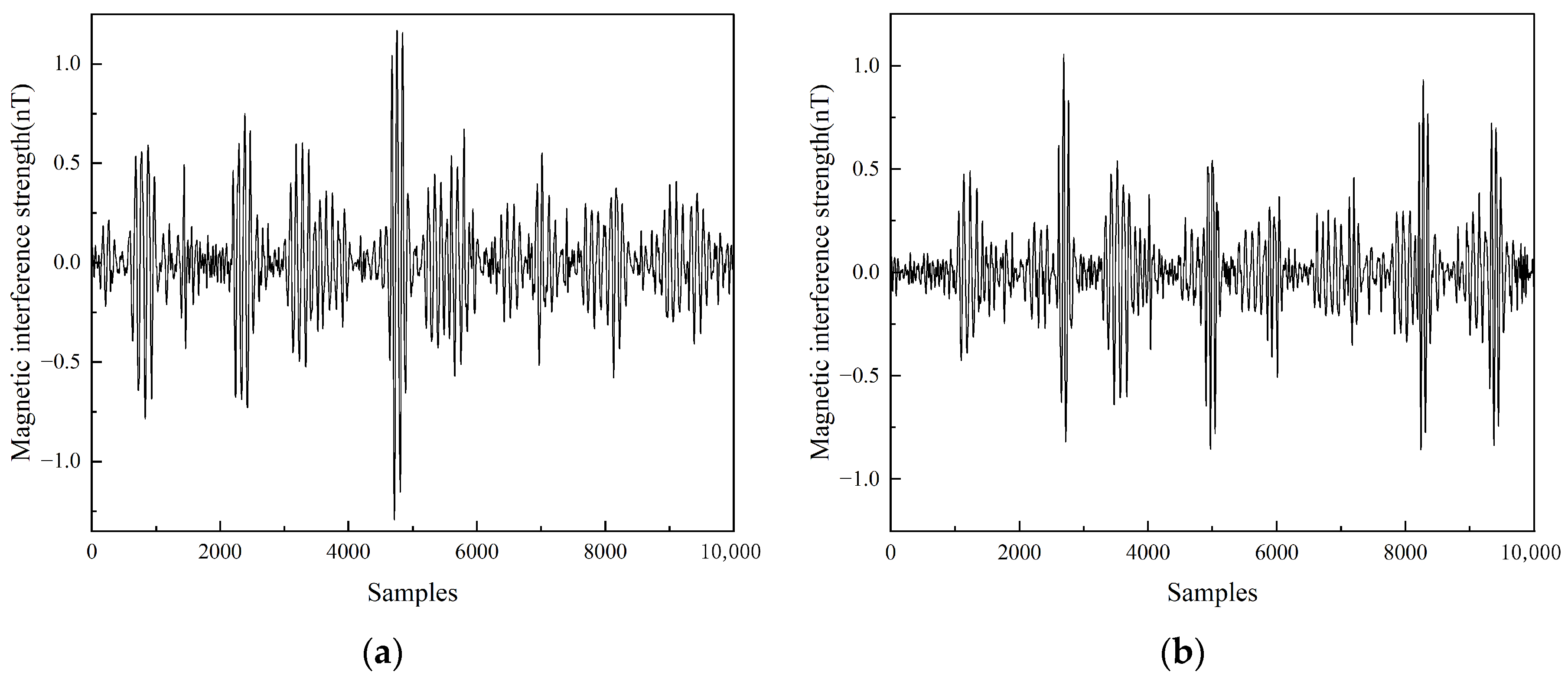
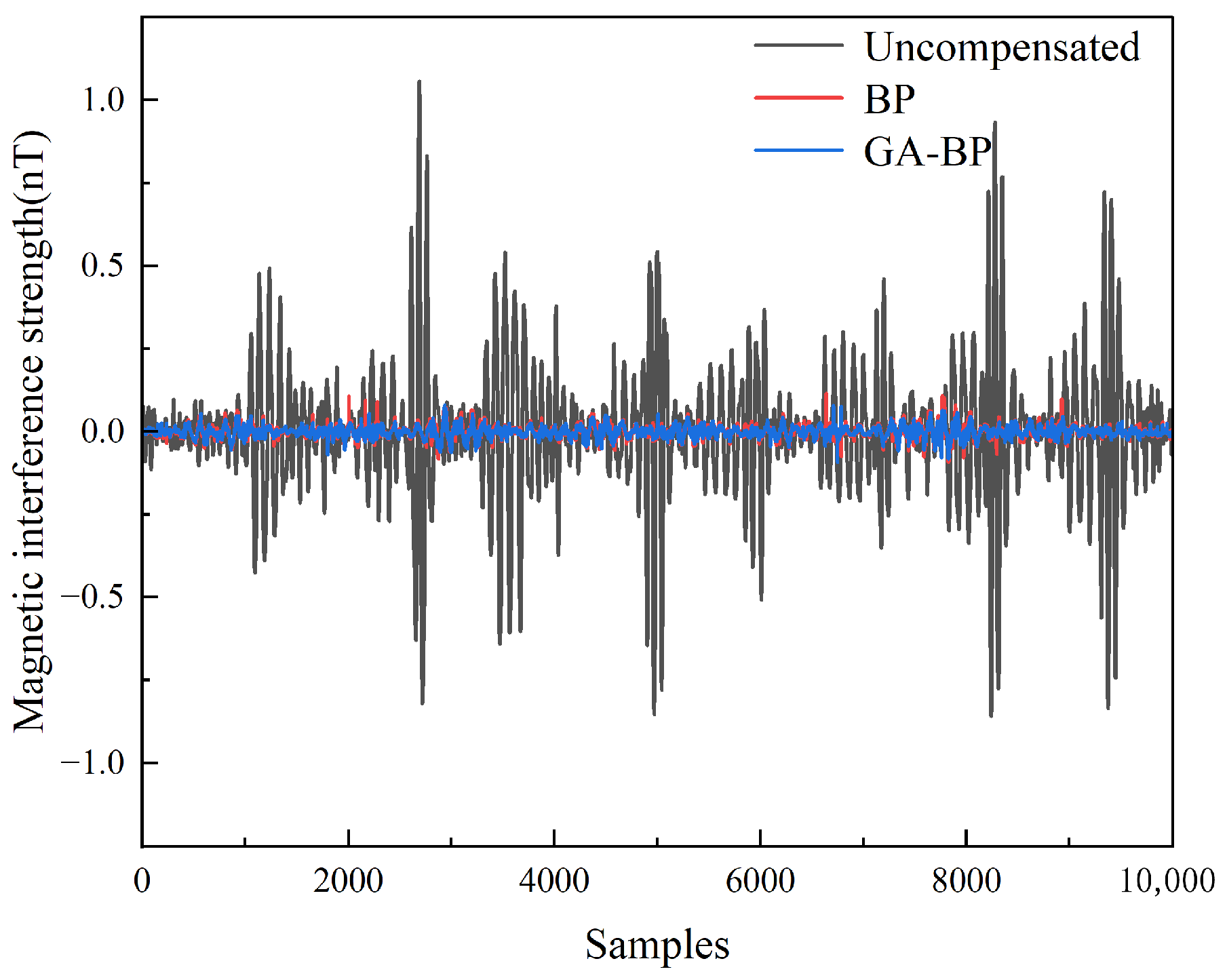
3.2. Magnetic Interference Compensation Experiment
4. Discussion
- The dynamic enhancement currently focuses exclusively on eddy-current interference through kinematic parameters. Future work should incorporate detailed coupling analyses of additional interference sources.
- The GA’s computational demands necessitate feature-rich inputs for optimal network configuration. Future studies will explore automated architecture research given sufficient data availability.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ashraf, A.; Abbas, T.; Ejaz, A. Magnetic Anamoly-Based Detection of a Submarine. In Proceedings of the 2023 International Multi-Disciplinary Conference in Emerging Research Trends (IMCERT), Karachi, Pakistan, 4–5 January 2023; Volume I, pp. 1–5. [Google Scholar]
- Rufino, G.; Conte, C.; Basso, P.; Tirri, A.E.; Donato, V. Mission Design and Validation of a Fixed-Wing Unmanned Aerial Vehicle for Environmental Monitoring. Drones 2024, 8, 641. [Google Scholar] [CrossRef]
- Matthias, G.; Barbara, K.; Anna, G. Occlusion mapping reveals the impact of flight and sensing parameters on vertical forest structure exploration with cost-effective UAV based laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2025, 139, 104493. [Google Scholar]
- Lu, S.; Guo, Y.; Long, J.; Liu, Z.; Wang, Z.; Li, Y. Dense small target detection algorithm for UAV aerial imagery. Image Vis. Comput. 2025, 156, 105485. [Google Scholar] [CrossRef]
- Tolles, W.; Lawson, J. Magnetic Compensation of MAD Equipped Aircraft; Airborne Instruments Lab. Inc.: Mineola, NY, USA, 1950; pp. 201–211. [Google Scholar]
- Leliak, P. Identification and evaluation of magnetic-field sources of magnetic airborne detector equipped aircraft. IRE Trans. Aerosp. Navig. Electron. 1961, ANE-8, 95–105. [Google Scholar] [CrossRef]
- Hardwick, C.D. Techniques For achieving stable and robust aeromagnetic compensation coefficients. In Seg Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 1986; pp. 140–141. [Google Scholar]
- Leach, B.W. Aeromagnetic compensation as a linear regression problem. In Information Linkage Between Applied Mathematics and Industry; Elsevier: Amsterdam, The Netherlands, 1980; pp. 139–161. [Google Scholar]
- Bickel, S. Small Signal Compensation of Magnetic Fields Resulting from Aircraft Maneuvers. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 518–525. [Google Scholar] [CrossRef]
- Wu, P.; Zhang, Q.; Chen, L.; Zhu, W.; Fang, Y. Aeromagnetic Compensation Algorithm Based on Principal Component Analysis. J. Sens. 2018, 2018, 5798287. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Moshe, L.; Vladimir, Y.L.; Allan, P.; Shimon, S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 1993, 6, 861–867. [Google Scholar]
- Williams, P.M. Aeromagnetic compensation using neural networks. Neural Comput. Appl. 1993, 1, 207–214. [Google Scholar] [CrossRef]
- Yu, P.; Zhao, X.; Jiao, J. An Aeromagnetic Compensation Algorithm Based on a Deep Autoencoder. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6001305. [Google Scholar] [CrossRef]
- Emery, K. Improving Aeromagnetic Calibration by Mixing Artificial Neural Networks and Tolles-Lawson—MA.NNTL. Master’s Thesis, Air Force Institute of Technology, Dayton, OH, USA, 2021. [Google Scholar]
- Yu, P.; Bi, F.; Jiao, J.; Zhao, X.; Zhou, S.; Su, Z. An Aeromagnetic Compensation Algorithm Based on a Residual Neural Network. Appl. Sci. 2022, 12, 10759. [Google Scholar] [CrossRef]
- Jiao, J.; Yu, P.; Zhao, X.; Bi, F. Real-Time Aeromagnetic Compensation with Compressed and Accelerated Neural Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8025905. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, C.; Su, Z.; Yu, P.; Jiao, J. An Aeromagnetic Compensation Algorithm Based on Radial Basis Function Artificial Neural Network. Appl. Sci. 2023, 13, 136. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, J.; Liao, S.; Li, T.; Li, Z. An Aeromagnetic Compensation Method Based on Attention Mechanism. IEEE Geosci. Remote Sens. Lett. 2025, 22, 7502005. [Google Scholar] [CrossRef]
- Nerrise, F.; Sosanya, A.S.; Neary, P. Physics-Informed Calibration of Aeromagnetic Compensation in Magnetic Navigation Systems using Liquid Time-Constant Networks. arXiv 2024, arXiv:2401.09631. [Google Scholar]
- Yu, Z.; Ye, L.; Ding, C.; Chi, C.; Liu, C.; Cheng, P. Dynamic Parameterization and Optimized Flight Paths for Enhanced Aeromagnetic Compensation in Large Unmanned Aerial Vehicles. Sensors 2025, 25, 2954. [Google Scholar] [CrossRef] [PubMed]
- Hardwick, C.D. Important design considerations for inboard airborne magnetic gradiometers. Geophysics 1984, 49, 2004–2018. [Google Scholar] [CrossRef]




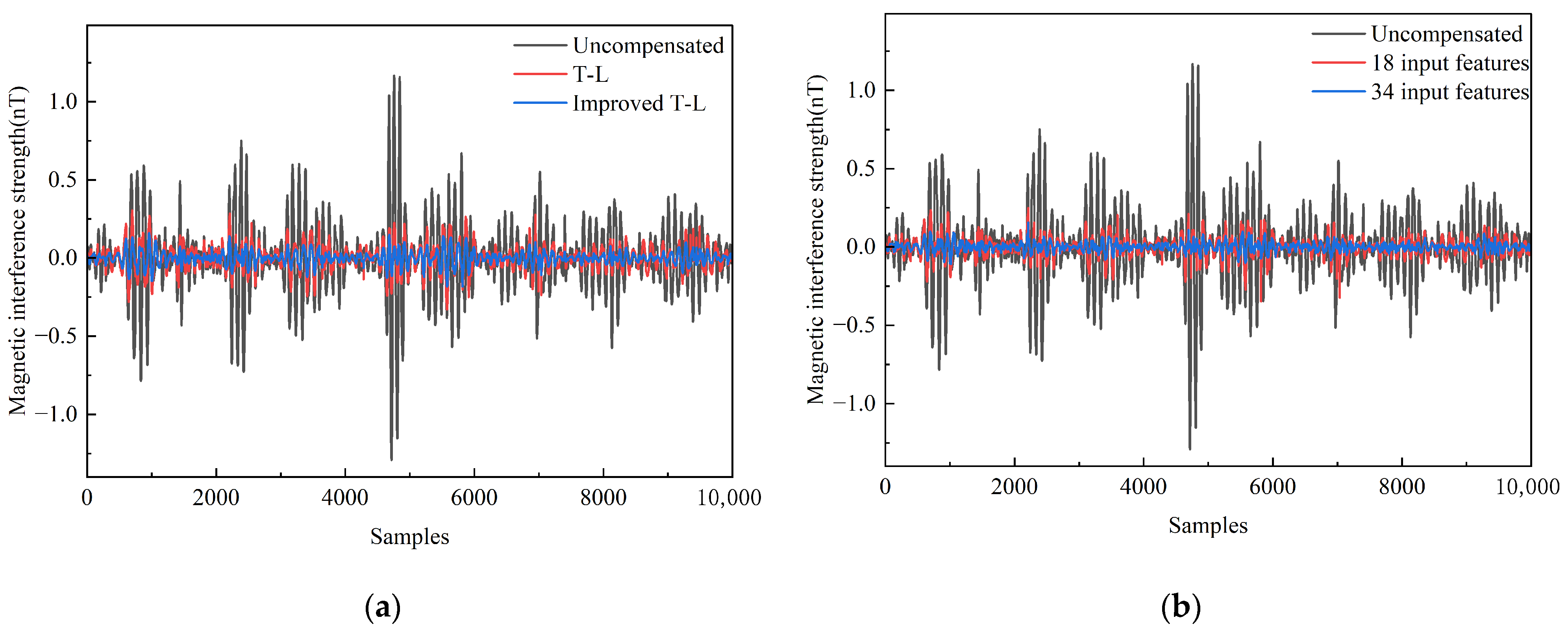





| Verification Method | Model | STDu (nT) | STDc (nT) | IR |
|---|---|---|---|---|
| Linear regression | T-L model | 0.2355 | 0.0806 | 2.9195 |
| Improved T-L model | 0.0430 | 5.4739 | ||
| Neural networks | 18 input features | 0.2355 | 0.0429 | 5.4893 |
| 34 input features | 0.0259 | 9.0657 |
| Hidden Layers | 12 | 12-6 | 12-6-12 |
|---|---|---|---|
| IR | 7.8155 | 6.7678 | 7.6022 |
| MSE | 0.0345 | 0.0392 | 0.0348 |
| R | 0.98920 | 0.98609 | 0.98902 |
| Number of Nodes | 7 | 9 | 11 | 13 | 15 |
|---|---|---|---|---|---|
| IR | 7.274 | 9.0657 | 8.0988 | 7.8082 | 7.6728 |
| MSE | 0.0376 | 0.0301 | 0.0332 | 0.0346 | 0.0353 |
| R | 0.98722 | 0.99115 | 0.98943 | 0.98915 | 0.98871 |
| Model | STDu (nT) | STDc (nT) | IR |
|---|---|---|---|
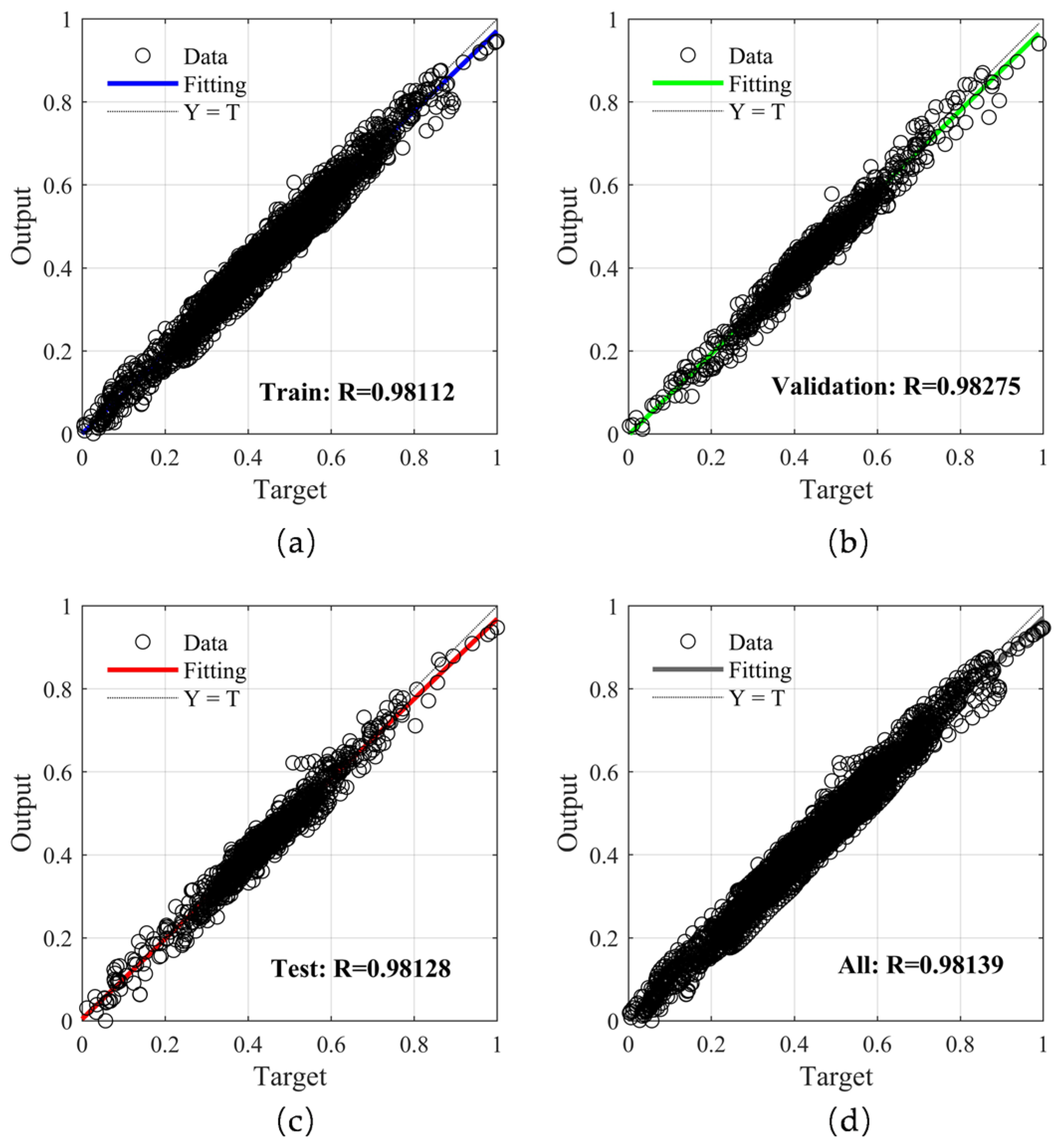
| Improved T-L model | 0.2013 | 0.0368 | 5.4739 |
| BP | 0.0186 | 11.7547 |
| Model | STDu (nT) | STDc (nT) | IR |
|---|---|---|---|
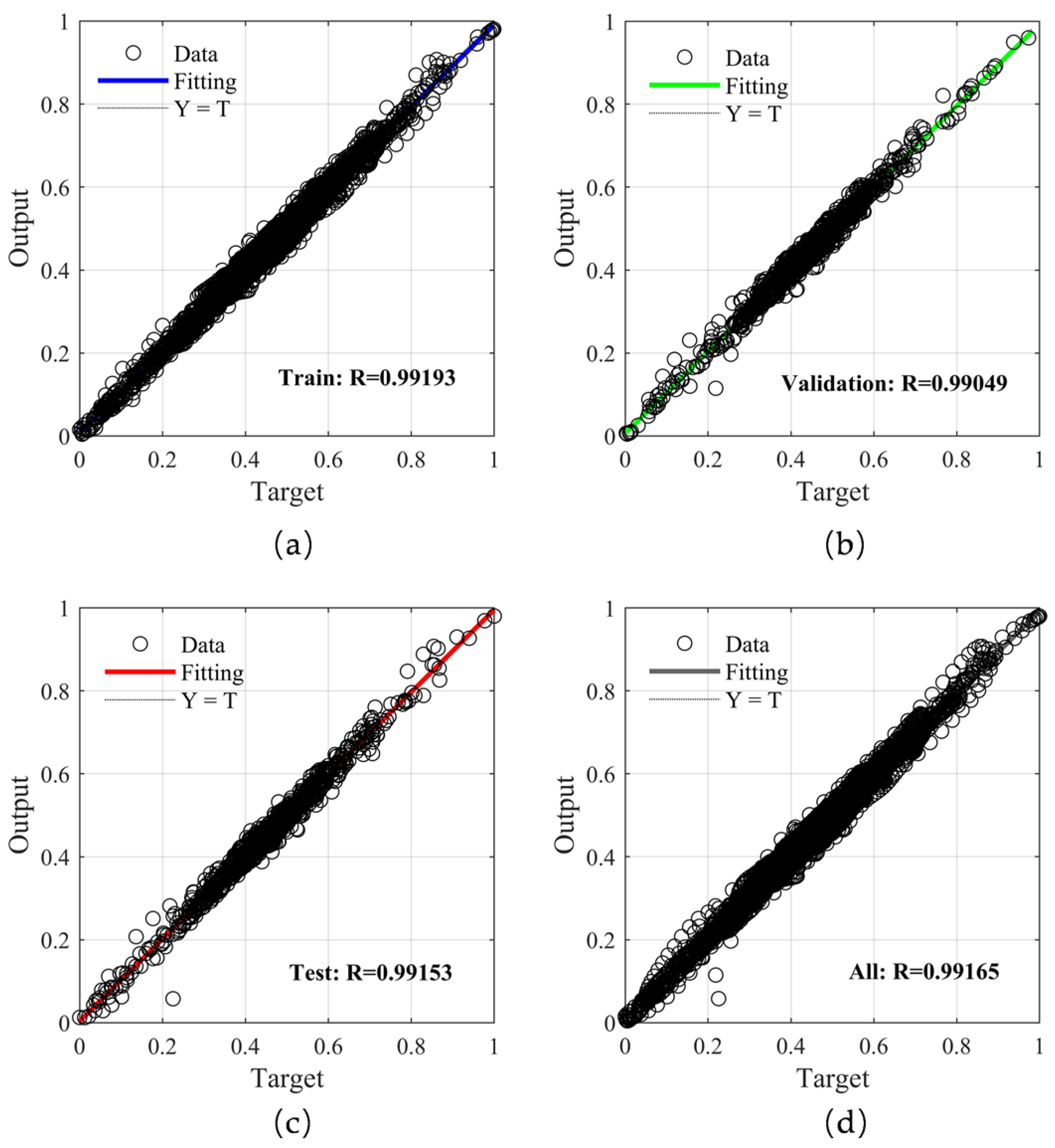
| BP | 0.2013 | 0.0186 | 11.7547 |
| GA-BP | 0.0164 | 13.3129 |
| Flight | Model | STDu (nT) | STDc (nT) | IR |
|---|---|---|---|---|
| Level Flight 1 | T-L | 0.0357 | 0.0122 | 2.9260 |
| Improved T-L | 0.0109 | 3.2672 | ||
| BP | 0.0079 | 4.4715 | ||
| GA-BP | 0.0060 | 5.9122 | ||
| Level Flight 2 | T-L | 0.0558 | 0.0235 | 2.3771 |
| Improved T-L | 0.0160 | 3.4801 | ||
| BP | 0.0133 | 4.2703 | ||
| GA-BP | 0.0102 | 5.4967 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Yu, Z.; Liu, C.; Wu, G.; Li, J.; Wang, D.; Wang, Y.; Zhang, Y. Intelligent Dynamic-Enhanced Compensation for UAV Magnetic Interference. Sensors 2025, 25, 5059. https://doi.org/10.3390/s25165059
Chen Z, Yu Z, Liu C, Wu G, Li J, Wang D, Wang Y, Zhang Y. Intelligent Dynamic-Enhanced Compensation for UAV Magnetic Interference. Sensors. 2025; 25(16):5059. https://doi.org/10.3390/s25165059
Chicago/Turabian StyleChen, Zizhou, Zhentao Yu, Cong Liu, Guozheng Wu, Jianwei Li, Dan Wang, Ye Wang, and Yaxun Zhang. 2025. "Intelligent Dynamic-Enhanced Compensation for UAV Magnetic Interference" Sensors 25, no. 16: 5059. https://doi.org/10.3390/s25165059
APA StyleChen, Z., Yu, Z., Liu, C., Wu, G., Li, J., Wang, D., Wang, Y., & Zhang, Y. (2025). Intelligent Dynamic-Enhanced Compensation for UAV Magnetic Interference. Sensors, 25(16), 5059. https://doi.org/10.3390/s25165059






