Temperature Control Method for Electric Heating Furnaces Based on Auto-Encoder and Fuzzy PI Control
Abstract
Highlights
- A discrete mathematical model of an electric heating furnace was established, and unsupervised dynamic modelling was achieved through an auto-encoder.
- A control structure combining predictive compensation and fuzzy regulation was designed to achieve stable low-overshoot control under complex interference.
- Improved the stability, accuracy, and robustness of the electric heating furnace temperature control system.
- Provided a new modelling and control framework for solving control problems in nonlinear, time-varying, and large-time-delay industrial heating systems, with good application prospects.
Abstract
1. Introduction
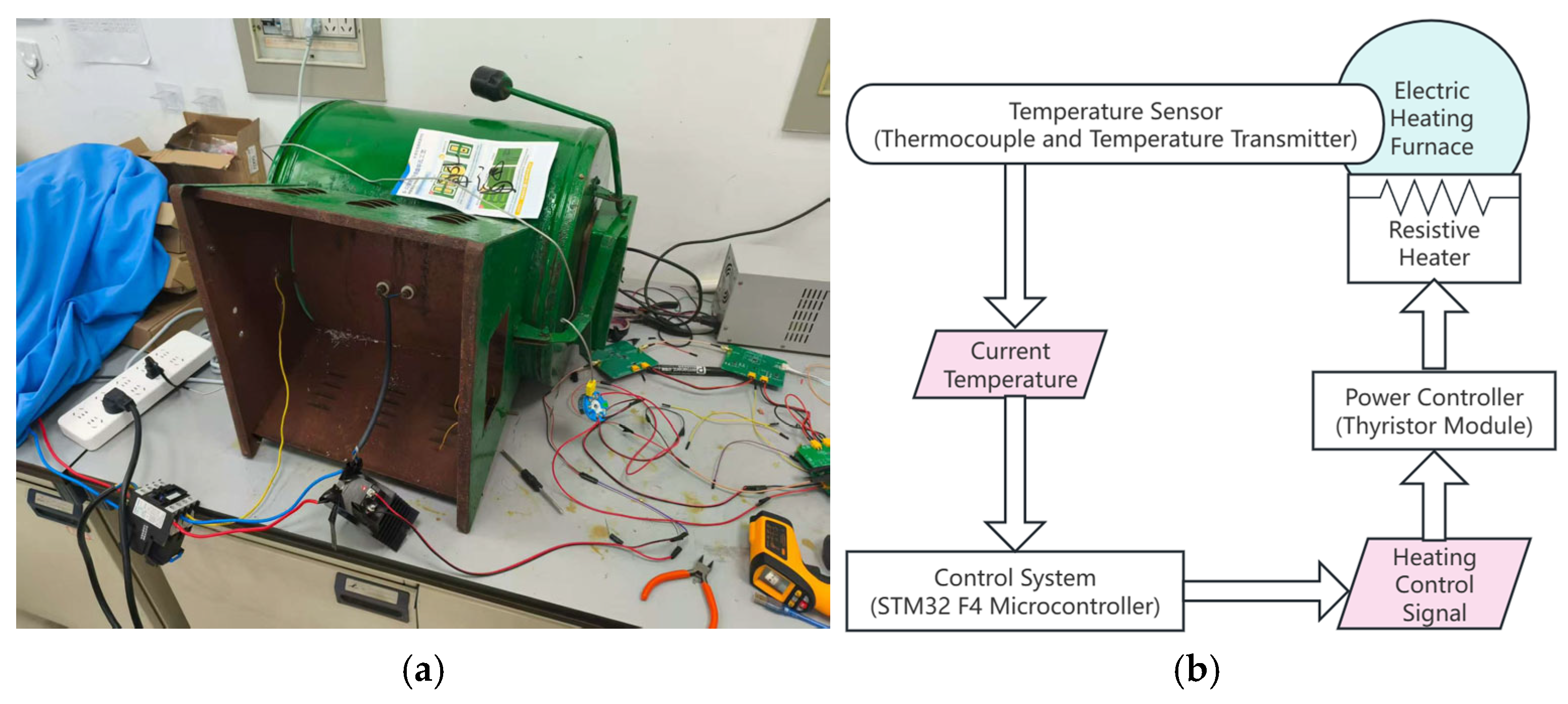
2. Materials and Methods
2.1. Establishment and Identification of Electric Heating Furnace Models
2.1.1. Model Establishment
2.1.2. Model Identification
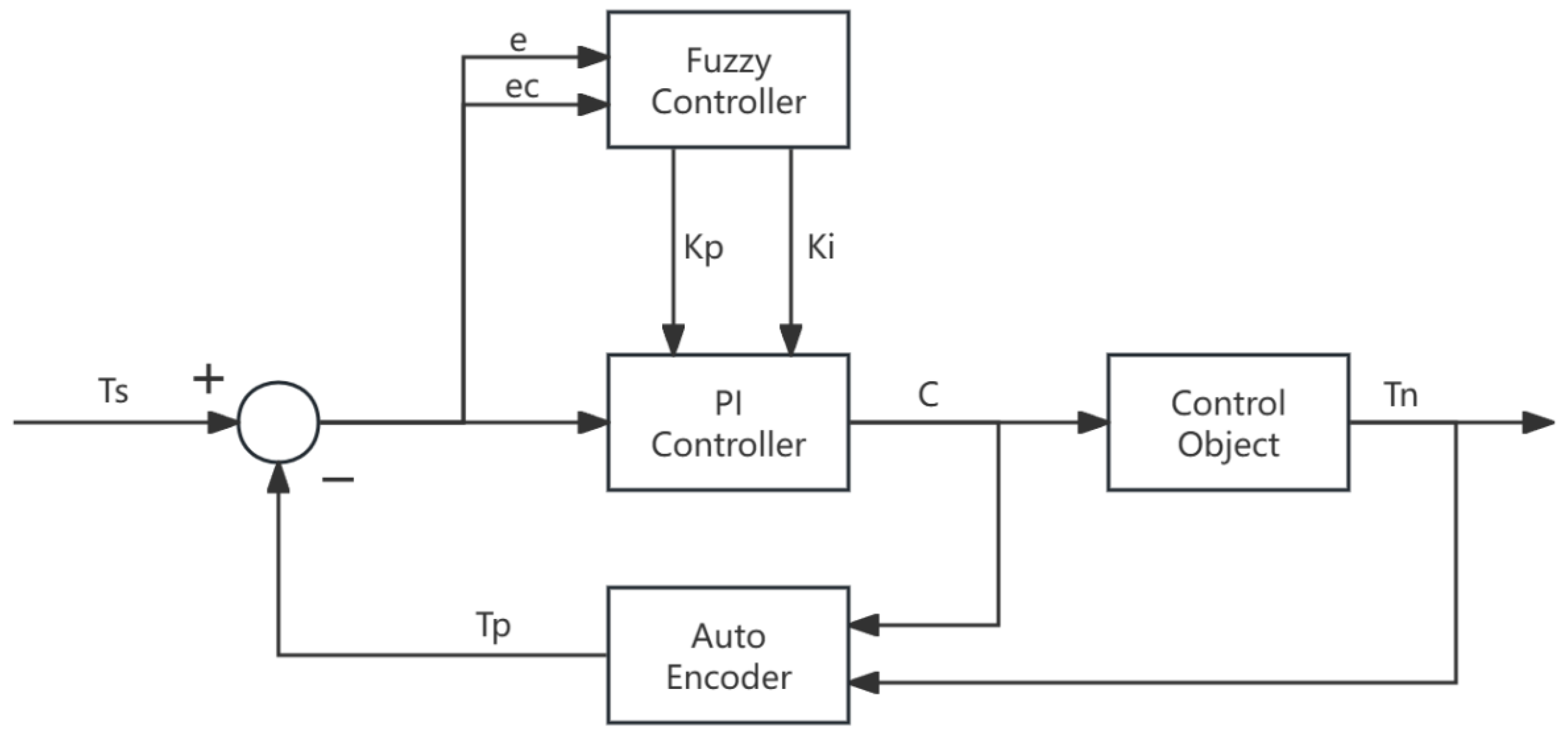
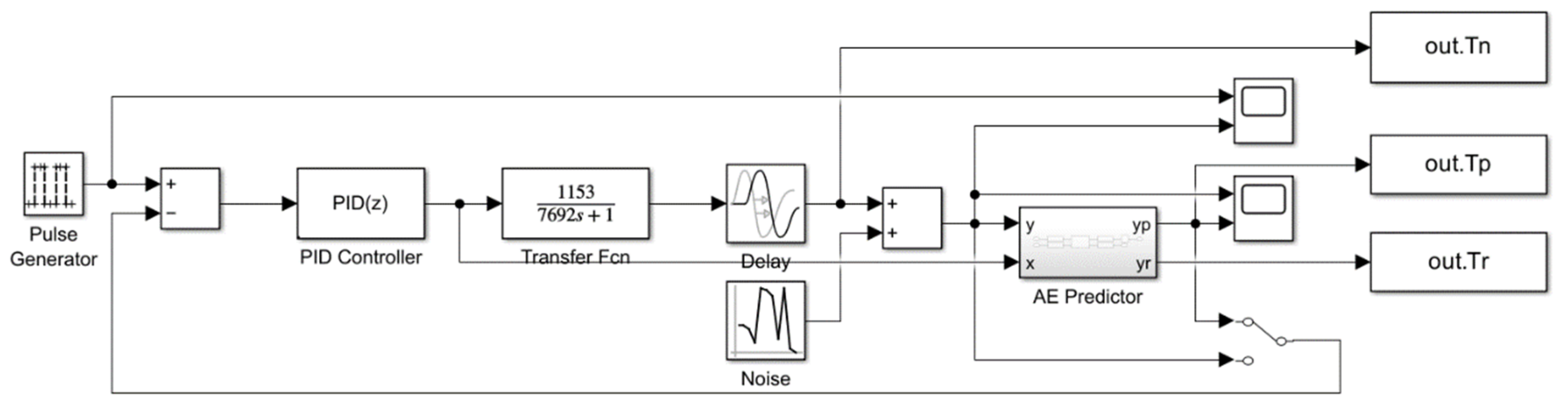
2.2. Design of Electric Heating Control Algorithm
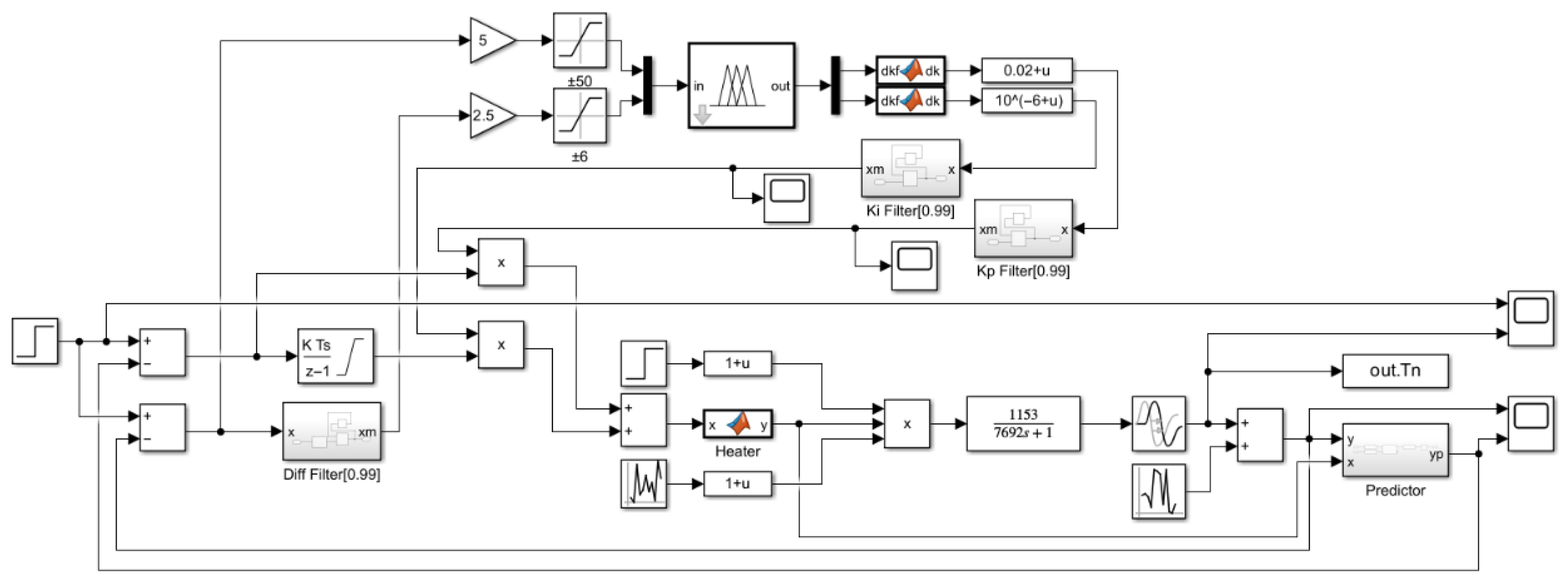
2.2.1. Logical Structure of the Controller
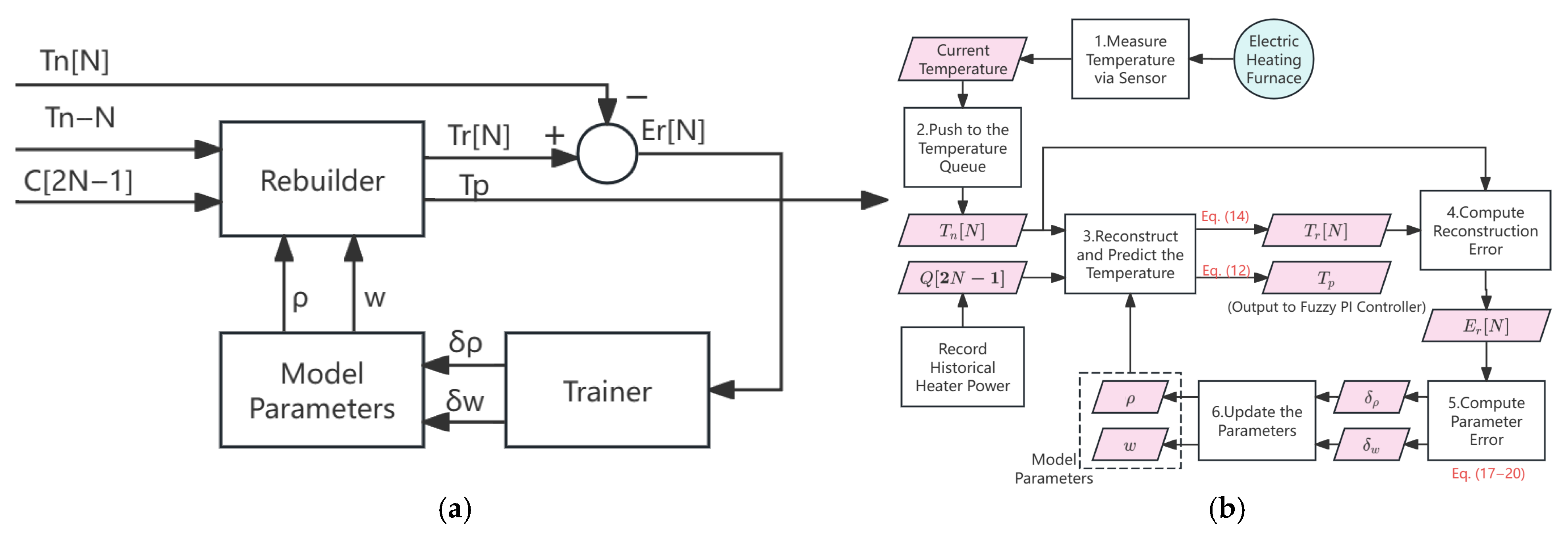
2.2.2. Auto-Encoder Design
- Temperature Acquisition and Enqueueing: The current furnace temperature is measured via sensors and pushed into a historical temperature queue that maintains the most recent temperature samples. At the same time, the historical power input to the heater is recorded to support accurate temperature reconstruction and model training.
- Temperature Reconstruction and Prediction: The reconstructor uses the furnace temperature reconstruction equation (Equation (14)) to calculate reconstructed temperatures for the most recent N sampling points. The difference between the reconstructed temperature and the true measured temperature gives the reconstruction error. Based on this reconstructed state, the auto-encoder model performs M-step iterative prediction (Equation (12)) to estimate the future furnace temperature, which is then forwarded to the fuzzy PI controller for control decision making.
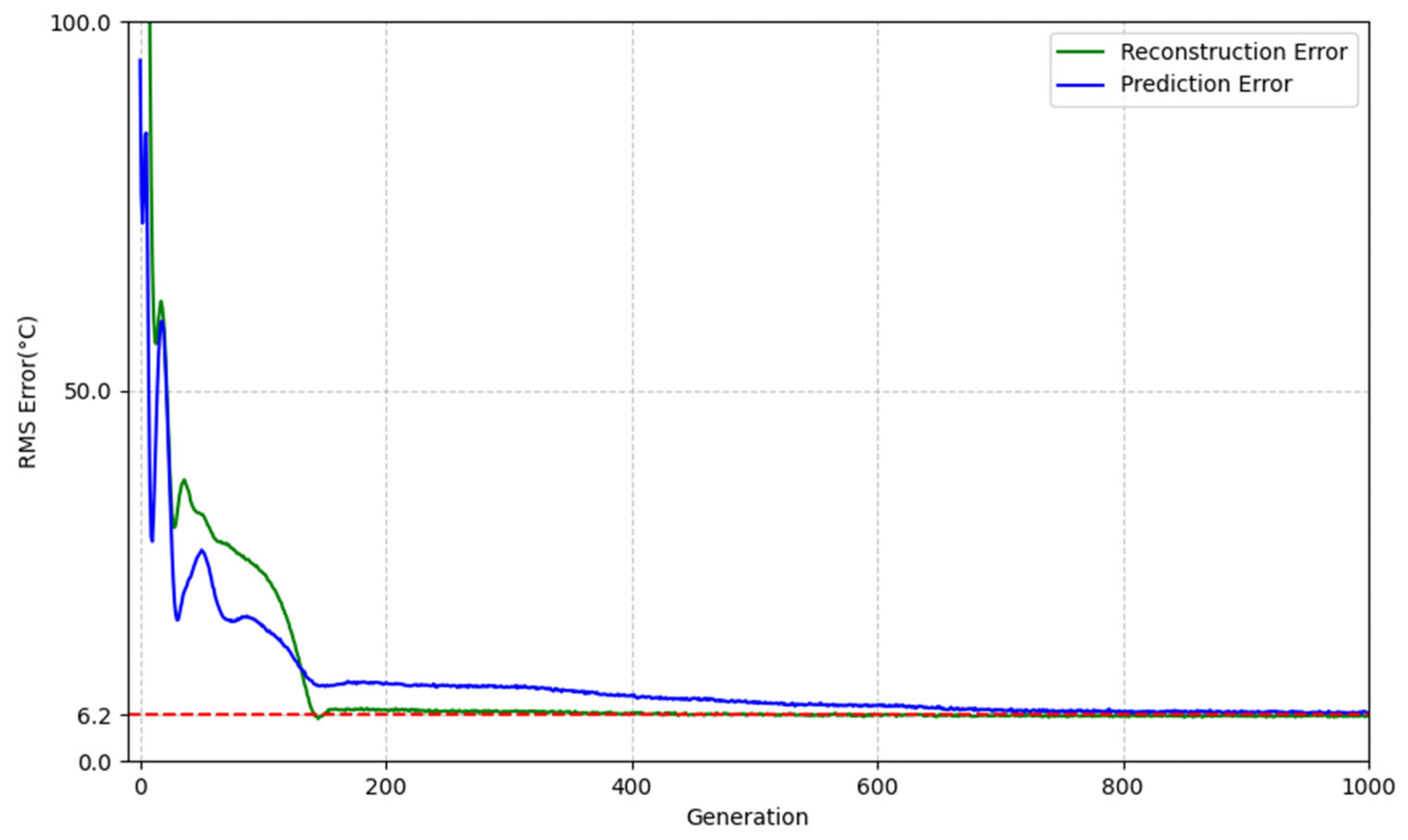
- Error Computation and Parameter Update: The trainer computes the parameter error based on Equations (17)–(20), which quantify the deviation between the predicted behaviour and actual measurements. These errors are backpropagated to update the internal model parameters using gradient descent. This online training ensures that the model can adapt to evolving furnace conditions.
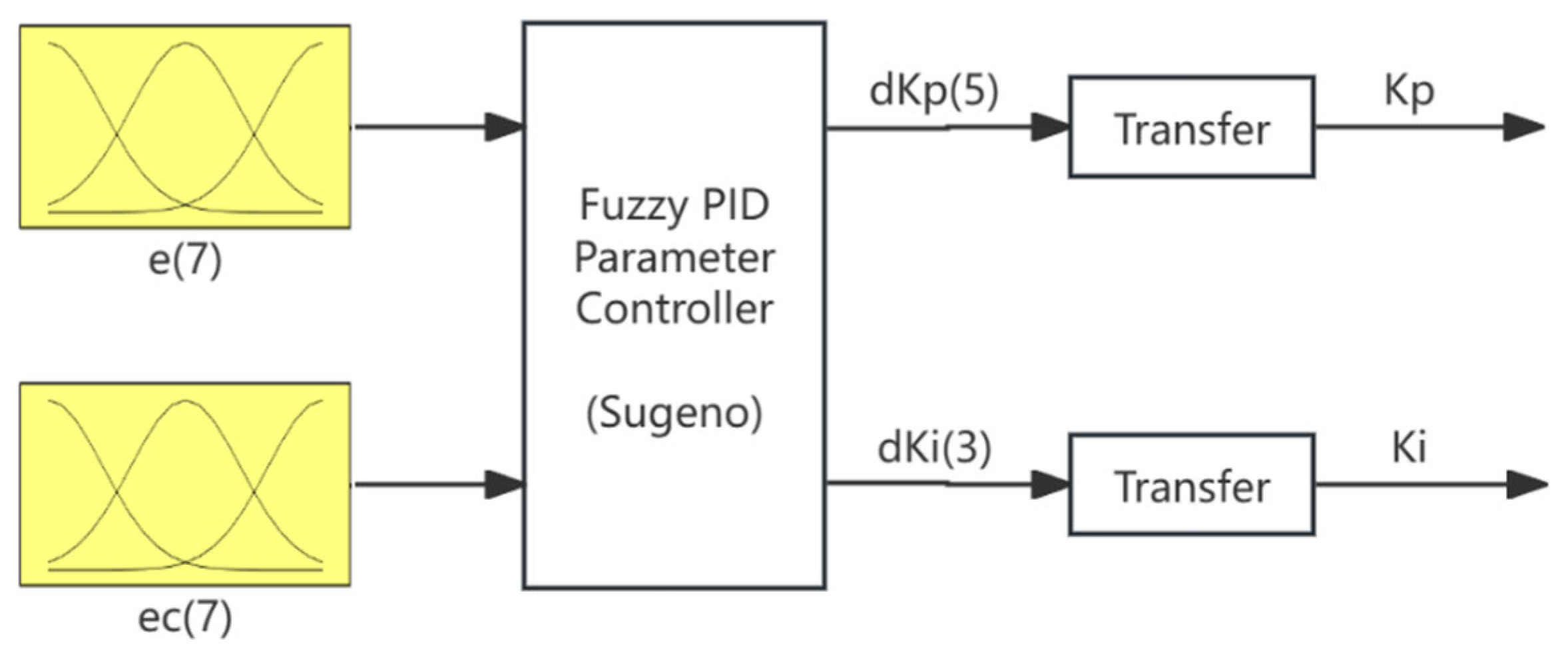
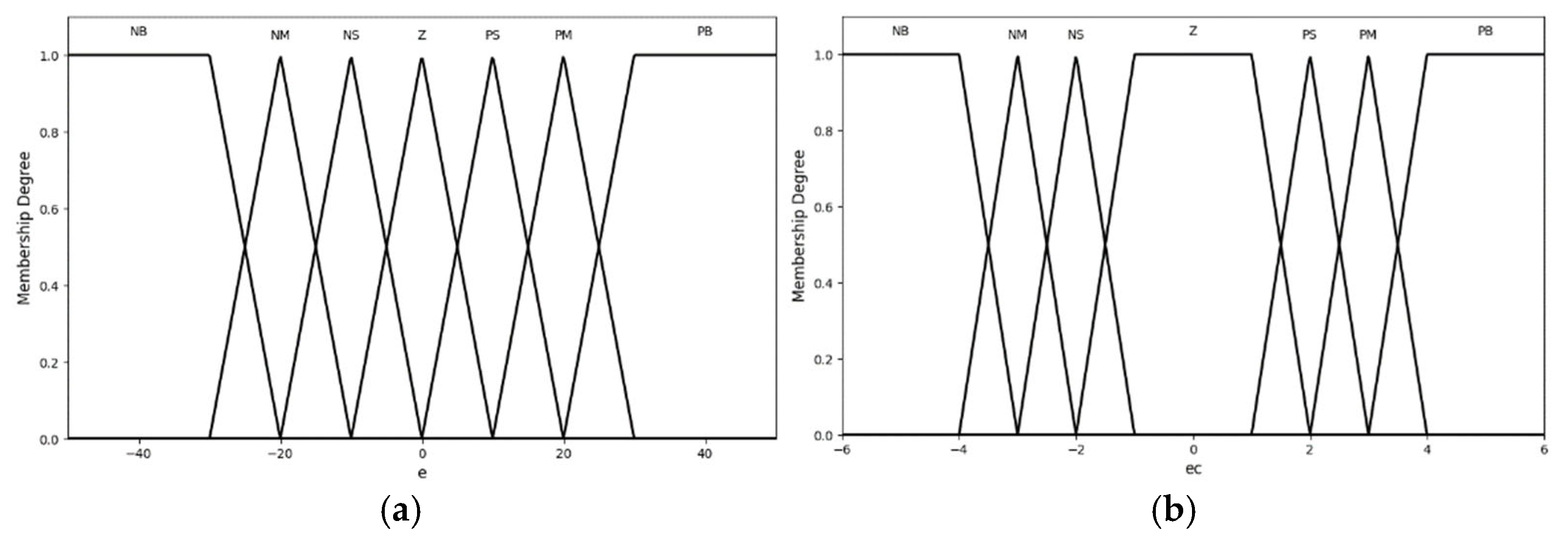
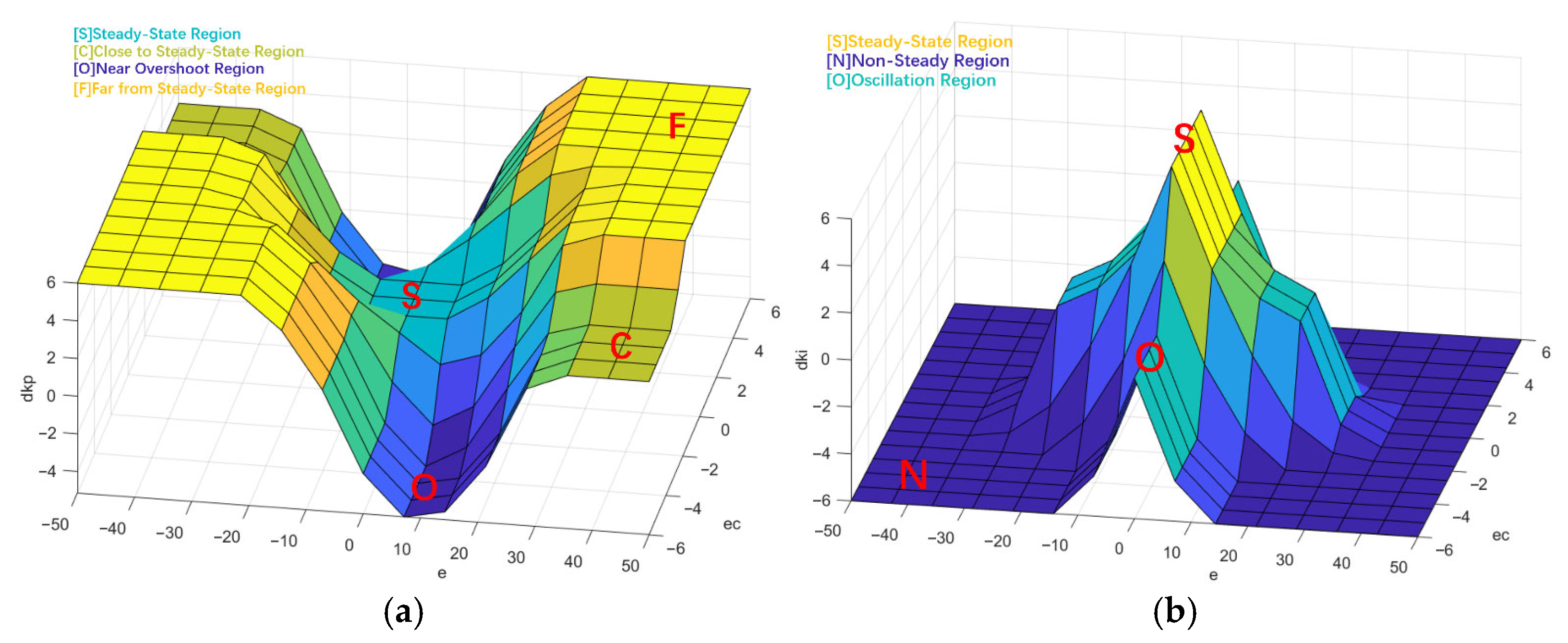
2.2.3. Fuzzy PI Parameter Controller Design
3. Results and Discussion
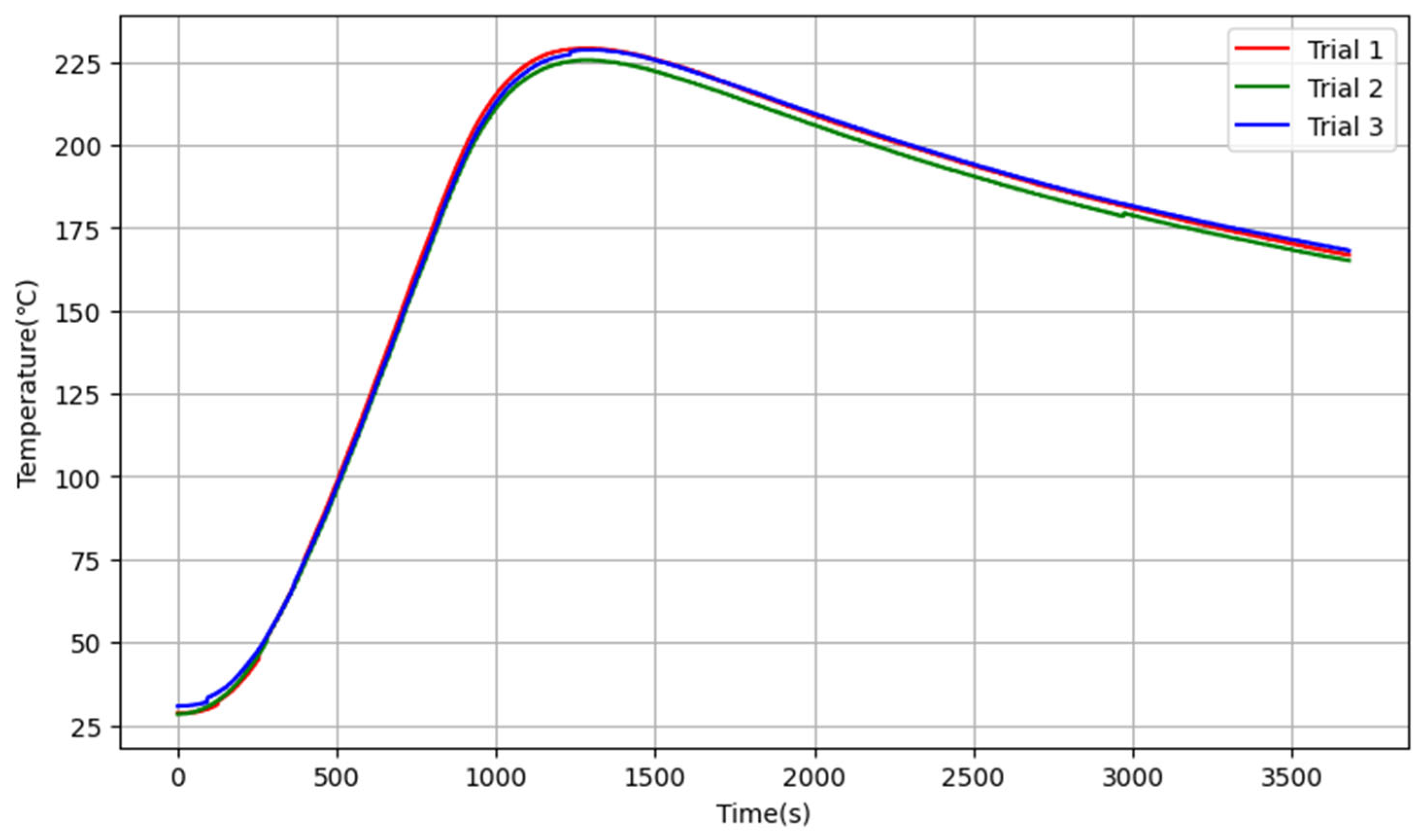
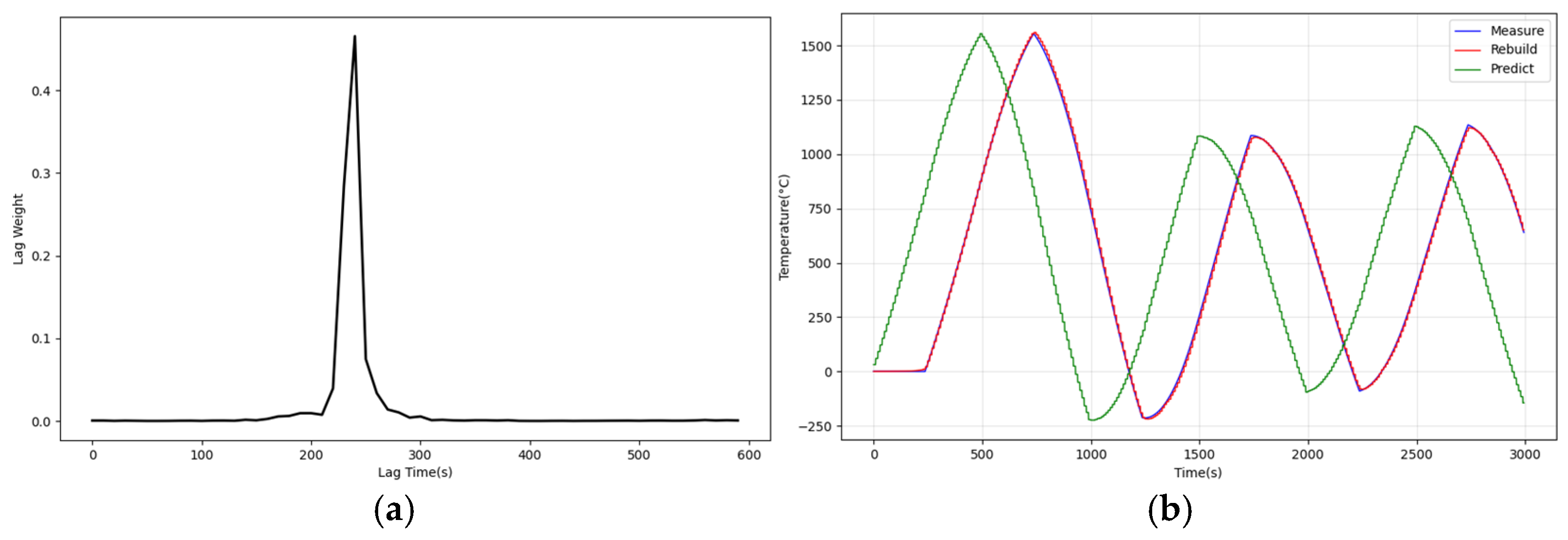
3.1. Model Estimation
3.2. Dynamic Modelling Simulation
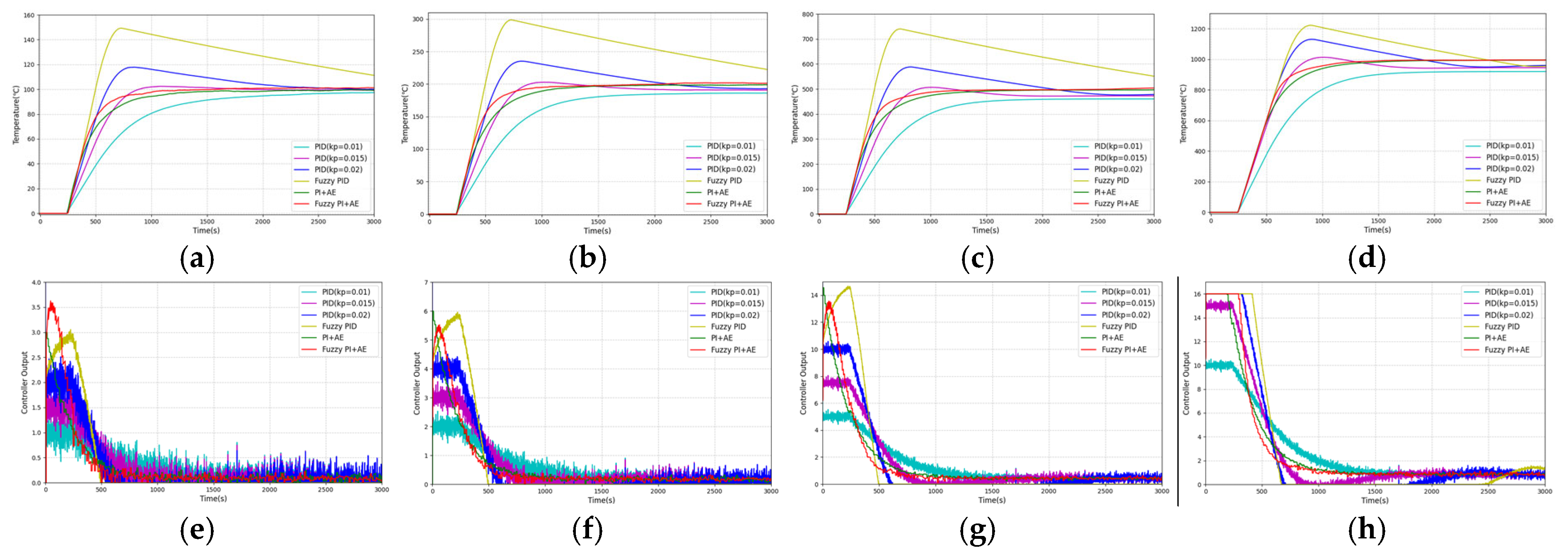
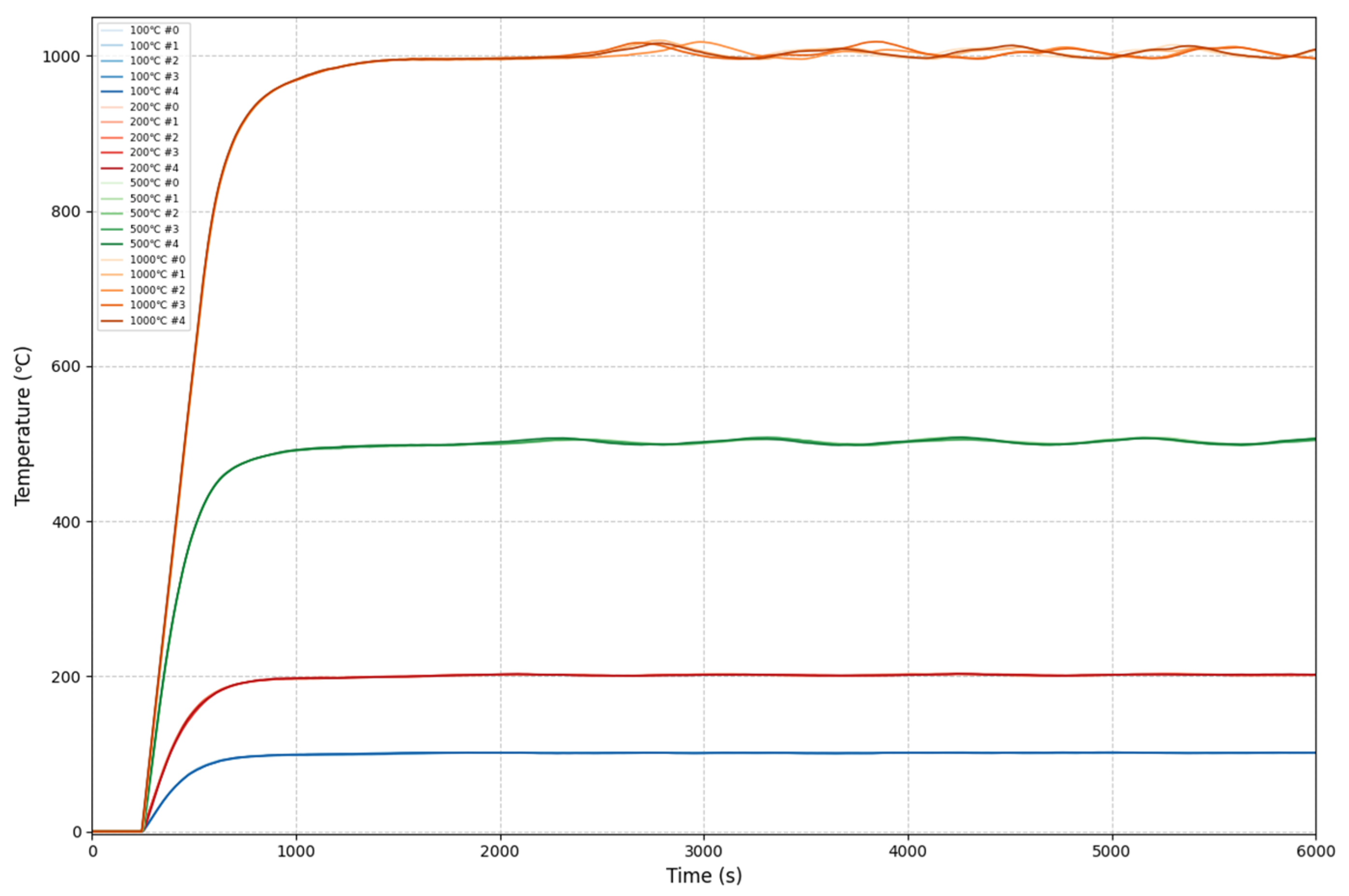
3.3. Control System Step Simulation
3.4. Disturbance-Resistant Simulation
4. Conclusions
5. Limitations and Future Work
- Experimental validation of real electric heating furnaces;
- Comparison with advanced control strategies such as MPC and robust control;
- Implementation of lightweight variants for real-time deployment, and extension to multivariable, fault-tolerant, and dynamically uncertain systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PID | Proportional–Integral–Derivative Control |
| PI | Proportional–Integral Control |
| AE | Auto-Encoder |
| ITAE | Integral of Time-Weighted Absolute Error |
References
- Xu, F. Advanced Control Research on Temperature Control System of Electric Heating Furnace. Master’s Thesis, Jilin Institute of Chemical Technology, Jilin, China, 2024. [Google Scholar]
- Basu, A.; Mohanty, S.; Sharma, R. Designing of FOPID Controller for Heating Furnace Using Different Optimization Techniques. In Proceedings of the 2017 11th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 5–6 January 2017; pp. 318–322. [Google Scholar]
- Li, X.; Zhao, Y.; Lei, M. High Precision and Stability Temperature Control System for the Immersion Liquid in Immersion Lithography. Flow Meas. Instrum. 2017, 53, 317–325. [Google Scholar] [CrossRef]
- Zong, Z.; Wei, G.; Gao, C.; Long, X. Precision Temperature Control for the Laser Gyro Inertial Navigation System in Long-Endurance Marine Navigation. Sensors 2021, 21, 4119. [Google Scholar] [CrossRef] [PubMed]
- López-Palenzuela, A.; Berenguel, M.; Gil, J.D.; Roca, L.; Guzmán, J.L.; Rodríguez, J. Temperature Control in Solar Furnaces Using Nonlinear PID-Based Control Approaches. Int. J. Control Autom. Syst. 2024, 22, 2419–2427. [Google Scholar] [CrossRef]
- Mao, D.; Li, P.; Ai, M.; Wu, J.; Yang, C.; Wang, H. Temperature Control Method for Batch Reactors Based on Adaptive Delay Compensation. In Proceedings of the 2024 China Automation Congress (CAC), Nanjing, China, 22–24 November 2024; pp. 1272–1277. [Google Scholar]
- Shi, H.; Li, P.; Cao, J.; Su, C.; Yu, J. Robust Fuzzy Predictive Control for Discrete-Time Systems with Interval Time-Varying Delays and Unknown Disturbances. IEEE Trans. Fuzzy Syst. 2019, 28, 1504–1516. [Google Scholar] [CrossRef]
- Bai, J.; Wang, S.; Zhang, X. Development of an Adaptive Smith Predictor-Based Self-Tuning PI Controller for an HVAC System in a Test Room. Energy Build. 2008, 40, 2244–2252. [Google Scholar] [CrossRef]
- Thompson, R.; Dexter, A. A Fuzzy Decision-Making Approach to Temperature Control in Air-Conditioning Systems. Control Eng. Pract. 2005, 13, 689–698. [Google Scholar] [CrossRef]
- Radakovic, Z.R.; Milosevic, V.M.; Radakovic, S.B. Application of Temperature Fuzzy Controller in an Indirect Resistance Furnace. Appl. Energy 2002, 73, 167–182. [Google Scholar] [CrossRef]
- Cheng, P.; He, S.; Stojanovic, V.; Luan, X.; Liu, F. Fuzzy Fault Detection for Markov Jump Systems with Partly Accessible Hidden Information: An Event-Triggered Approach. IEEE Trans. Cybern. 2022, 52, 7352–7361. [Google Scholar] [CrossRef]
- Fang, H.; Tu, Y.; Wang, H.; He, S.; Liu, F.; Ding, Z.; Cheng, S.S. Fuzzy-Based Adaptive Optimization of Unknown Discrete-Time Nonlinear Markov Jump Systems with Off-Policy Reinforcement Learning. IEEE Trans. Fuzzy Syst. 2022, 30, 5276–5290. [Google Scholar] [CrossRef]
- Nahlovsky, T. Optimization of Fuzzy Controller Parameters for the Temperature Control of Superheated Steam. Procedia Eng. 2015, 100, 1547–1555. [Google Scholar] [CrossRef]
- Li, Y. A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree for the Master of Engineering. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2017. [Google Scholar]
- Yu, J.-Q.; Zhou, J.; Liu, Y.-F.; Ai, T. Study on Fuzzy Self-Tuning PID Cascade Control Algorithm for Temperature of Active Solar House Heating System. In Proceedings of the 2010 Chinese Control and Decision Conference (CCDC), Xuzhou, China, 26–28 May 2010; pp. 2439–2443. [Google Scholar]
- Hu, D.; Liu, H.; Zhu, Y.; Li, Q.; Wang, J.; Zhang, Z.; Sun, J.; Yang, L.; Zhang, Z.; Yuan, J. A Temperature Control Method of Electric Heating Furnace Based on Fuzzy PID. J. Phys. Conf. Ser. 2023, 2503, 012101. [Google Scholar] [CrossRef]
- Jin, P.; Zheng, M.; Qi, B.; Feng, D. Heating Speed Control Method Based on Adaptive Fuzzy PID Algorithm. In Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 471–475. [Google Scholar]
- Pei, Z. Design of Resistance Furnace Temperature-Control System Based on Fuzzy Algorithm. Master’s Thesis, Dalian University of Technology, Dalian, China, 2015. [Google Scholar]
- Soyguder, S.; Karakose, M.; Alli, H. Design and Simulation of Self-Tuning PID-Type Fuzzy Adaptive Control for an Expert HVAC System. Expert Syst. Appl. 2009, 36, 4566–4573. [Google Scholar] [CrossRef]
- Zhou, X. Design on Temperature Control System of Heating Furnace Based on Fuzzy RBF Neural Network PID. Master’s Thesis, University of Science and Technology Liaoning, Anshan, China, 2020. [Google Scholar]
- Alzakari, S.A.; Izci, D.; Ekinci, S.; Alhussan, A.A.; Hashim, F.A. A New Control Scheme for Temperature Adjustment of Electric Furnaces Using a Novel Modified Electric Eel Foraging Optimizer. AIMS Math. 2024, 9, 13410–13438. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, H.; Lin, C. Observer-Based Adaptive Neural Network Control for Nonlinear Systems in Nonstrict-Feedback Form. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W. Research on PID Control Based on Improved Smith Prediction in Electromagnetic Induction Heating System. Master’s Thesis, Southwest University of Science and Technology, Mianyang, China, 2021. [Google Scholar]
- Karan, S.; Dey, C. IMC-Based Modified Smith Predictor for Second Order Delay Dominated Processes with RHP. ISA Trans. 2023, 142, 254–269. [Google Scholar] [CrossRef]
- Zhou, G.; Luo, H. Research on Heating Temperature Control Method of Electric Heating Furnace Based on PID Self Tuning. Ind. Heating 2023, 52, 22–25+29. [Google Scholar]
- Lusenko, D. Waste Heat Boiler Control System Based on Neural Network Technology and Fuzzy Logic. In Proceedings of the 2022 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 5–10 September 2022; pp. 772–776. [Google Scholar]
- Lan, Z.; Chen, J.; Xue, C.; Lan, J.; Wang, B.; Wang, Y.; Yang, Y. A Temperature Control Algorithm for Lithography Machine Based on Generalized Predictive Control and BP Neural Network PI Control. Meas. Control 2024, 57, 903–918. [Google Scholar] [CrossRef]
- Chen, J.; Lu, Q.; Bai, J.; Xu, X.; Yao, Y.; Fang, W. A Temperature Control Method for Microaccelerometer Chips Based on Genetic Algorithm and Fuzzy PID Control. Micromachines 2021, 12, 1511. [Google Scholar] [CrossRef]
- Pergantis, E.N.; Priyadarshan; Al Theeb, N.; Dhillon, P.; Ore, J.P.; Ziviani, D.; Groll, E.A.; Kircher, K.J. Field Demonstration of Predictive Heating Control for an All-Electric House in a Cold Climate. Appl. Energy, 2024; to appear. [Google Scholar] [CrossRef]
- Charkoutsis, S.; Kara-Mohamed, M. A Particle Swarm Optimization Tuned Nonlinear PID Controller with Improved Performance and Robustness for First Order Plus Time Delay Systems. Results Control Optim. 2023, 12, 100289. [Google Scholar] [CrossRef]
- Liao, Y.X.; She, J.H.; Wu, M. Integrated Hybrid-PSO and Fuzzy-NN Decoupling Control for Temperature of Reheating Furnace. IEEE Trans. Ind. Electron. 2009, 56, 2704–2714. [Google Scholar] [CrossRef]
- Tang, Y.; Du, F.; Cui, Y.; Zhang, Y. New Smith Predictive Fuzzy Immune PID Control Algorithm for MIMO Networked Control Systems. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 212. [Google Scholar] [CrossRef]
- Badshah, S.; Atif, M.; Ul Haq, I.; Malik, S.A.; Badshah, M.; Jan, S. Thermal Analysis of Vacuum Resistance Furnace. Processes 2019, 7, 907. [Google Scholar] [CrossRef]
- GB/T 12325-2008; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China; National Standardization Administration (China). Power Quality-Deviation of Supply Voltage. Standards Press of China: Beijing, China, 2008.


| NB | NM | NS | Z | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| e | NB | PB | PB | PB | PB | PB | PS | PS |
| NM | PB | PB | PB | PS | Z | Z | NS | |
| NS | PS | PS | PS | Z | NS | NB | NB | |
| Z | NS | NS | Z | Z | Z | NS | NS | |
| PS | NB | NB | NS | Z | PS | PS | PS | |
| PM | NS | Z | Z | PS | PB | PB | PB | |
| PB | PS | PS | PB | PB | PB | PB | PB | |
| NB | NM | NS | Z | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| NB | N | N | N | N | N | N | N | |
| NM | N | N | N | Z | N | N | N | |
| NS | N | N | Z | Z | Z | N | N | |
| Z | Z | Z | P | P | P | Z | Z | |
| PS | N | N | Z | Z | Z | N | N | |
| PM | N | N | N | Z | N | N | N | |
| PB | N | N | N | N | N | N | N | |
| Temperature (°C) | Controller | Rise Time 1 (s) | Settle Time 2 (s) | Overshoot (%) | ITAE 3 () |
|---|---|---|---|---|---|
| 100 | PID ( = 0.01) | 1094 | 2063 | 0.0 | |
| PID ( = 0.015) | 433 | 779 | 2.4 | ||
| PID ( = 0.02) | 282 | 2231 | 17.8 | ||
| Fuzzy PID | 200 | 3443 | 49.3 | ||
| PI+AE | 528 | 1061 | 0.0 | ||
| Fuzz PI+AE | 357 | 789 | 1.3 | ||
| 200 | PID ( = 0.01) | 1167 | >5000 | 0.0 | |
| PID ( = 0.015) | 433 | 779 | 1.4 | ||
| PID ( = 0.02) | 282 | 1722 | 17.6 | ||
| Fuzzy PID | 200 | 3445 | 49.4 | ||
| PI + AE | 546 | 1022 | 0.0 | ||
| Fuzz PI + AE | 362 | 789 | 1.0 | ||
| 500 | PID ( = 0.01) | 1183 | >5000 | 0.0 | |
| PID ( = 0.015) | 432 | >5000 | 1.3 | ||
| PID ( = 0.02) | 282 | 1710 | 17.6 | ||
| Fuzzy PID | 200 | 3374 | 48.0 | ||
| PI + AE | 529 | 1012 | 0.0 | ||
| Fuzz PI + AE | 375 | 837 | 0.8 | ||
| 1000 | PID ( = 0.01) | 1184 | >5000 | 0.0 | |
| PID ( = 0.015) | 432 | >5000 | 1.3 | ||
| PID ( = 0.02) | 350 | 2518 | 13.1 | ||
| Fuzzy PID | 343 | 2702 | 22.2 | ||
| PI + AE | 566 | 1060 | 0.0 | ||
| Fuzz PI + AE | 452 | 947 | 0.0 |
| Temperature (°C) | Rise Time 1 (s) | Settle Time 2 (s) | Overshoot (%) | ITAE 3 () |
|---|---|---|---|---|
| 100 | 336 ± 6 | 711 ± 9 | 1.9 ± 0.1 | |
| 200 | 339 ± 5 | 716 ± 6 | 1.6 ± 0.2 | |
| 500 | 336 ± 2 | 742 ± 2 | 1.6 ± 0.1 | |
| 1000 | 424 ± 1 | 862 ± 2 | 1.8 ± 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Luo, Y.; Zhao, C.; Suo, H. Temperature Control Method for Electric Heating Furnaces Based on Auto-Encoder and Fuzzy PI Control. Sensors 2025, 25, 5020. https://doi.org/10.3390/s25165020
Huang H, Luo Y, Zhao C, Suo H. Temperature Control Method for Electric Heating Furnaces Based on Auto-Encoder and Fuzzy PI Control. Sensors. 2025; 25(16):5020. https://doi.org/10.3390/s25165020
Chicago/Turabian StyleHuang, Haiyang, Yingmao Luo, Chun Zhao, and Hui Suo. 2025. "Temperature Control Method for Electric Heating Furnaces Based on Auto-Encoder and Fuzzy PI Control" Sensors 25, no. 16: 5020. https://doi.org/10.3390/s25165020
APA StyleHuang, H., Luo, Y., Zhao, C., & Suo, H. (2025). Temperature Control Method for Electric Heating Furnaces Based on Auto-Encoder and Fuzzy PI Control. Sensors, 25(16), 5020. https://doi.org/10.3390/s25165020






