Asymmetries of Force and Power During Single-Leg Counter Movement Jump in Young Adult Females and Males
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Data Collection
2.3. Data Analysis
2.4. Statistical Analysis
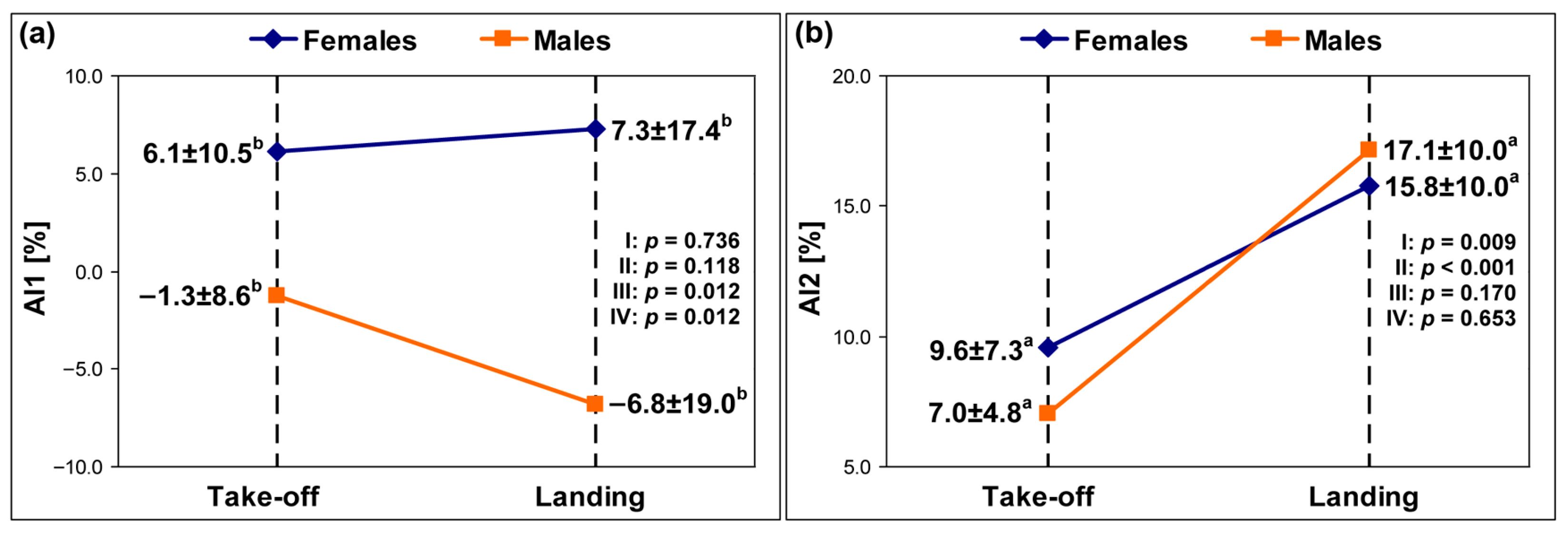
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ganguli, S.; Mukherji, P.; Bose, K.S. Gait evaluation of unilateral below-knee amputees fitted with patellar-tendon-bearing prostheses. J. Indian Med. Assoc. 1974, 63, 256–259. [Google Scholar]
- Schiltz, M.; Lehance, C.; Maquet, D.; Bury, T.; Crielaard, J.M.; Croisier, J.L. Explosive strength imbalances in professional basketball players. J. Athl. Train. 2009, 44, 39–47. [Google Scholar] [CrossRef]
- Robinson, R.O.; Herzog, W.; Nigg, B.M. Use of force platform variables to quantify the effects of chiropractic manipulation on gait symmetry. J. Manip. Physiol. Ther. 1987, 10, 172–176. [Google Scholar]
- Wong, P.L.; Chamari, K.; Chaouachi, A.; Mao, D.W.; Wisløff, U.; Hong, Y. Difference in plantar pressure between the preferred and non-preferred feet in four soccer-related movements. Br. J. Sports Med. 2007, 41, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Bell, D.R.; Sanfilippo, J.L.; Binkley, N.; Heiderscheit, B.C. Lean mass asymmetry influences force and power asymmetry during jumping in collegiate athletes. J. Strength Cond. Res. 2014, 28, 884–891. [Google Scholar] [CrossRef]
- Sugiyama, T.; Kameda, M.; Kageyama, M.; Kiba, K.; Kanehisa, H.; Maeda, A. Asymmetry between the dominant and non-dominant legs in the kinematics of the lower extremities during a running single leg jump in collegiate basketball players. J. Sports Sci. Med. 2014, 13, 951–957. [Google Scholar] [PubMed]
- Marshall, B.; Franklyn-Miller, A.; Moran, K.; King, E.; Richter, C.; Gore, S.; Strike, S.; Falvey, É. Biomechanical symmetry in elite rugby union players during dynamic tasks: An investigation using discrete and continuous data analysis techniques. BMC Sports Sci. Med. Rehabil. 2015, 7, 13. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.; Read, P.; Lake, J.; Chavda, S.; Turner, A. Interlimb asymmetries: Understanding how to calculate differences from bilateral and unilateral tests. Strength Cond. J. 2018, 40, 1–6. [Google Scholar] [CrossRef]
- Impellizzeri, F.M.; Rampinini, E.; Maffiuletti, N.; Marcora, S.M. A vertical jump force test for assessing bilateral strength asymmetry in athletes. Med. Sci. Sports Exerc. 2007, 39, 2044–2050. [Google Scholar] [CrossRef]
- Vagenas, G.; Hoshizaki, B. A multivariable analysis of lower-extremity kinematic asymmetry in running. Int. J. Sport Biomech. 1992, 8, 11–29. [Google Scholar] [CrossRef]
- Plotnik, M.; Giladi, N.; Balash, Y.; Peretz, C.; Hausdorff, J.M. Is freezing of gait in Parkinson’s disease related to asymmetric motor function? Ann. Neurol. 2005, 57, 656–663. [Google Scholar] [CrossRef]
- Brumitt, J.; Heiderscheit, B.C.; Manske, R.C.; Niemuth, P.E.; Rauh, M.J. Lower extremity functional tests and risk of injury in division III collegiate athletes. Int. J. Sports Phys. Ther. 2013, 8, 216–227. [Google Scholar]
- Vaisman, A.; Guiloff, R.; Rojas, J.; Delgado, I.; Figueroa, D.; Calvo, R. Lower limb symmetry: Comparison of muscular power between dominant and nondominant legs in healthy young adults associated with single-leg-dominant sports. Orthop. J. Sports Med. 2017, 5, 2325967117744240. [Google Scholar] [CrossRef]
- Helme, M.; Tee, J.; Emmonds, S.; Low, C. Does lower-limb asymmetry increase injury risk in sport? A systematic review. Phys. Ther. Sport. 2021, 49, 204–213. [Google Scholar] [CrossRef] [PubMed]
- Markou, S.; Vagenas, G. Multivariate isokinetic asymmetry of the knee and shoulder in elite volleyball players. Eur. J. Sport Sci. 2006, 6, 71–80. [Google Scholar] [CrossRef]
- Michailidis, Y.; Stafylidis, A.; Mandroukas, A.; Kyranoudis, A.E.; Antoniou, G.; Kollias, R.; Kanaras, V.; Bamplekis, C.; Vardakis, L.; Semaltianou, E.; et al. Correlation of the asymmetry index from the single-leg countermovement jump with the asymmetry index from isokinetic strength in elite youth football players. Appl. Sci. 2025, 15, 2779. [Google Scholar] [CrossRef]
- Jordan, M.J.; Aagaard, P.; Herzog, W. Lower limb asymmetry in mechanical muscle function: A comparison between ski racers with and without ACL reconstruction. Scand. J. Med. Sci. Sports. 2015, 25, e301–e309. [Google Scholar] [CrossRef]
- Wiggins, A.J.; Grandhi, R.K.; Schneider, D.K.; Stanfield, D.; Webster, K.E.; Myer, G.D. Risk of secondary injury in younger athletes after anterior cruciate ligament reconstruction: A systematic review and meta-analysis. Am. J. Sports Med. 2016, 44, 1861–1876. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Wang, L.; Dong, S.; Ding, Y.; Jia, S.; Zheng, C. Can symmetry of single-leg vertical jump height represent normal lower limb biomechanics of athletes after anterior cruciate ligament reconstruction? Sports Health 2024, 16, 596–605. [Google Scholar] [CrossRef]
- Chmielewski, T.L.; George, S.Z.; Tillman, S.M.; Moser, M.W.; Lentz, T.A.; Indelicato, P.A.; Trumble, T.N.; Shuster, J.J.; Cicuttini, F.M.; Leeuwenburgh, C. Low- versus high-intensity plyometric exercise during rehabilitation after anterior cruciate ligament reconstruction. Am. J. Sports Med. 2016, 44, 609–617. [Google Scholar] [CrossRef]
- Cone, S.M.; Lee, S. Lower limb force asymmetries during landing and jumping exercises: A pilot study. Int. J. Exerc. Sci. 2021, 14, 544–551. [Google Scholar] [CrossRef] [PubMed]
- Stephens, T.M.; Lawson, B.R.; Reiser, R.F. Bilateral asymmetries in max effort single-leg vertical jumps. Biomed. Sci. Instrum. 2005, 41, 317–322. [Google Scholar]
- Stephens, T.M.; Lawson, B.R.; DeVoe, D.E.; Reiser, R.F. Gender and bilateral differences in single-leg countermovement jump performance with comparison to a double-leg jump. J. Appl. Biomech. 2007, 23, 190–202. [Google Scholar] [CrossRef]
- Hewett, T.E.; Ford, K.R.; Hoogenboom, B.J.; Myer, G.D. Understanding and preventing acl injuries: Current biomechanical and epidemiologic considerations—Update 2010. N. Am. J. Sports Phys. Ther. 2010, 5, 234–251. [Google Scholar]
- Bishop, C.; Coratella, G.; Beato, M. Intra- and inter-limb strength asymmetry in soccer: A comparison of professional and under-18 players. Sports 2021, 9, 129. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.; Read, P.; McCubbine, J.; Turner, A. Vertical and horizontal asymmetries are related to slower sprinting and jump performance in elite youth female soccer players. J. Strength Cond. Res. 2021, 35, 56–63. [Google Scholar] [CrossRef]
- Lin, J.; Shen, J.; Zhou, A.; Badicu, G.; Grosz, W.R. The effects of inter-limb asymmetry on change of direction performance: A systematic review. Symmetry 2022, 14, 2177. [Google Scholar] [CrossRef]
- Michailidis, Y. Relation of jump and change of direction inter-limb asymmetries with fitness in youth male soccer players. Medicina 2023, 59, 1749. [Google Scholar] [CrossRef]
- Buckthorpe, M.; Della Villa, F. Recommendations for plyometric training after ACL reconstruction—A clinical commentary. Int. J. Sports Phys. Ther. 2021, 16, 879–895. [Google Scholar] [CrossRef]
- Hewit, J.K.; Cronin, J.B.; Hume, P.A. Asymmetry in multi-directional jumping tasks. Phys. Ther. Sport. 2012, 13, 238–242. [Google Scholar] [CrossRef] [PubMed]
- Paterno, M.V.; Ford, K.R.; Myer, G.D.; Heyl, R.; Hewett, T.E. Limb asymmetries in landing and jumping 2 years following anterior cruciate ligament reconstruction. Clin. J. Sport Med. 2007, 17, 258–262. [Google Scholar] [CrossRef]
- Ebben, W.P.; Flanagan, E.; Jensen, R.L. Bilateral facilitation and laterality during the countermovement jump. Percept. Mot. Skills 2009, 108, 251–258. [Google Scholar] [CrossRef]
- McElveen, M.T.; Riemann, B.L.; Davies, G.J. Bilateral comparison of propulsion mechanics during single-leg vertical jumping. J. Strength Cond. Res. 2010, 24, 375–381. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Kubo, J.; Matsubayashi, T.; Matsuo, A.; Kobayashi, K.; Ishii, N. Relationship between bilateral differences in single-leg jumps and asymmetry in isokinetic knee strength. J. Appl. Biomech. 2013, 29, 61–67. [Google Scholar] [CrossRef]
- Bishop, C.; de Keijzer, K.L.; Turner, A.N.; Beato, M. Measuring interlimb asymmetry for strength and power: A brief review of assessment methods, data analysis, current evidence, and practical recommendations. J. Strength Cond. Res. 2023, 37, 745–750. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Qin, Z.; Zhang, M. Association between pre-season lower limb interlimb asymmetry and non-contact lower limb injuries in elite male volleyball players. Sci. Rep. 2025, 15, 14481. [Google Scholar] [CrossRef]
- Taylor, J.B.; Westbrook, A.E.; Head, P.L.; Glover, K.M.; Paquette, M.R.; Ford, K.R. The single-leg vertical hop provides unique asymmetry information in individuals after anterior cruciate ligament reconstruction. Clin. Biomech. 2020, 80, 105107. [Google Scholar] [CrossRef] [PubMed]
- Ciccodicola, E.M.; Hanson, A.M.; Roberts, S.E.; Katzel, M.J.; Wren, T.A.L. Biomechanics and performance of single-leg vertical and horizontal hop in adolescents post-anterior cruciate ligament reconstruction. Biomechanics 2025, 5, 5. [Google Scholar] [CrossRef]
- Craig, C.L.; Marshall, A.L.; Sjöström, M.; Bauman, A.E.; Booth, M.L.; Ainsworth, B.E.; Pratt, M.; Ekelund, U.; Yngve, A.; Sallis, J.F.; et al. International physical activity questionnaire: 12-country reliability and validity. Med. Sci. Sports Exerc. 2003, 35, 1381–1395. [Google Scholar] [CrossRef] [PubMed]
- Cheung, R.T.; Smith, A.W.; Wong, D.P. H:Q ratios and bilateral leg strength in college field and court sports players. J. Hum. Kinet. 2012, 33, 63–71. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1988. [Google Scholar]
- Paterno, M.V.; Schmitt, L.C.; Ford, K.R.; Rauh, M.J.; Myer, G.D.; Huang, B.; Hewett, T.E. Biomechanical measures during landing and postural stability predict second anterior cruciate ligament injury after anterior cruciate ligament reconstruction and return to sport. Am. J. Sport Med. 2010, 38, 1968–1978. [Google Scholar] [CrossRef] [PubMed]
- Griffin, L.Y.; Agel, J.; Albohm, M.J.; Arendt, E.A.; Dick, R.W.; Garrett, W.E.; Garrick, J.G.; Hewett, T.E.; Huston, L.; Ireland, M.L.; et al. Noncontact anterior cruciate ligament injuries: Risk factors and prevention strategies. J. Am. Acad. Orthop. Surg. 2000, 8, 141–150. [Google Scholar] [CrossRef]
- Myer, G.D.; Brent, J.L.; Ford, K.R.; Hewett, T.E. Real-time assessment and neuromuscular training feedback techniques to prevent ACL injury in female athletes. Strength Cond. J. 2011, 33, 21–35. [Google Scholar] [CrossRef]
- Colby, S.; Francisco, A.; Yu, B.; Kirkendall, D.; Finch, M.; Garrett, W., Jr. Electromyographic and kinematic analysis of cutting maneuvers. Implications for anterior cruciate ligament injury. Am. J. Sports Med. 2000, 28, 234–240. [Google Scholar] [CrossRef]
- Salci, Y.; Kentel, B.B.; Heycan, C.; Akin, S.; Korkusuz, F. Comparison of landing maneuvers between male and female college volleyball players. Clin. Biomech. 2004, 19, 622–628. [Google Scholar] [CrossRef]
- Reeser, J.C.; Verhagen, E.; Briner, W.W.; Askeland, T.I.; Bahr, R. Strategies for the prevention of volleyball related injuries. Br. J. Sports Med. 2006, 40, 594–600. [Google Scholar] [CrossRef] [PubMed]
- Blackburn, J.T.; Padua, D.A. Sagittal-plane trunk position, landing forces, and quadriceps electromyographic activity. J. Athl. Train. 2009, 44, 174–179. [Google Scholar] [CrossRef] [PubMed]
- Kasmi, S.; Zouhal, H.; Hammami, R.; Clark, C.C.T.; Hackney, A.C.; Hammami, A.; Chtara, M.; Chortane, S.G.; Salah, F.Z.B.; Granacher, U.; et al. The effects of eccentric and plyometric training programs and their combination on stability and the functional performance in the post-ACL-surgical rehabilitation eriod of elite female athletes. Front. Physiol. 2021, 12, 688385. [Google Scholar] [CrossRef]

| Variable | Phase | Females | Males | ||
|---|---|---|---|---|---|
| Non-Dominant | Dominant | Non-Dominant | Dominant | ||
| PVGRF (N) | Take-off | 1163.9 ± 129.8 | 1217.8 ± 134.9 | 1572.4 ± 161.6 | 1597.0 ± 112.8 |
| Landing | 2033.7 ± 432.1 | 2149.5 ± 367.8 | 2737.4 ± 463.1 | 2705.7 ± 401.8 | |
| MP (W) | Take-off | 1733.0 ± 223.2 | 1853.1 ± 236.6 | 2580.3 ± 290.6 | 2548.7 ± 290.3 |
| Landing | 2948.0 ± 514.0 | 3206.3 ± 502.3 | 4311.3 ± 711.6 | 4053.8 ± 1016.6 | |
| Factor | PVGRF | MP | ||
|---|---|---|---|---|
| η2 | p | η2 | p | |
| Phase | 0.003 | 0.717 | 0.018 | 0.379 |
| Gender | 0.058 | 0.108 | 0.175 | 0.004 * |
| Phase × Gender | 0.012 | 0.467 | 0.041 | 0.178 |
| Factor | PVGRF | MP | ||
|---|---|---|---|---|
| η2 | p | η2 | p | |
| Phase | 0.336 | <0.001 * | 0.367 | <0.001 * |
| Gender | 0.008 | 0.547 | 0.002 | 0.743 |
| Phase × Gender | 0.005 | 0.656 | 0.032 | 0.236 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabaciński, J.; Gorwa, J.; Krakowiak, W.; Murawa, M. Asymmetries of Force and Power During Single-Leg Counter Movement Jump in Young Adult Females and Males. Sensors 2025, 25, 4995. https://doi.org/10.3390/s25164995
Kabaciński J, Gorwa J, Krakowiak W, Murawa M. Asymmetries of Force and Power During Single-Leg Counter Movement Jump in Young Adult Females and Males. Sensors. 2025; 25(16):4995. https://doi.org/10.3390/s25164995
Chicago/Turabian StyleKabaciński, Jarosław, Joanna Gorwa, Waldemar Krakowiak, and Michał Murawa. 2025. "Asymmetries of Force and Power During Single-Leg Counter Movement Jump in Young Adult Females and Males" Sensors 25, no. 16: 4995. https://doi.org/10.3390/s25164995
APA StyleKabaciński, J., Gorwa, J., Krakowiak, W., & Murawa, M. (2025). Asymmetries of Force and Power During Single-Leg Counter Movement Jump in Young Adult Females and Males. Sensors, 25(16), 4995. https://doi.org/10.3390/s25164995







