Numerical Iterative Design and Analysis of Double Freeform Surface Telecentric F-Theta Lens
Abstract
Highlights
- A numerical iterative design method of a double freeform surface telecentric f-theta lens is proposed.
- The two freeform surfaces of this f-theta lens can be obtained directly and simultaneously.
- The designed f-theta lens has a controllable distortion and high transmittance.
- It provides a new design concept for lens design.
Abstract
1. Introduction
2. Design Methodology
3. Simulation Analysis Results
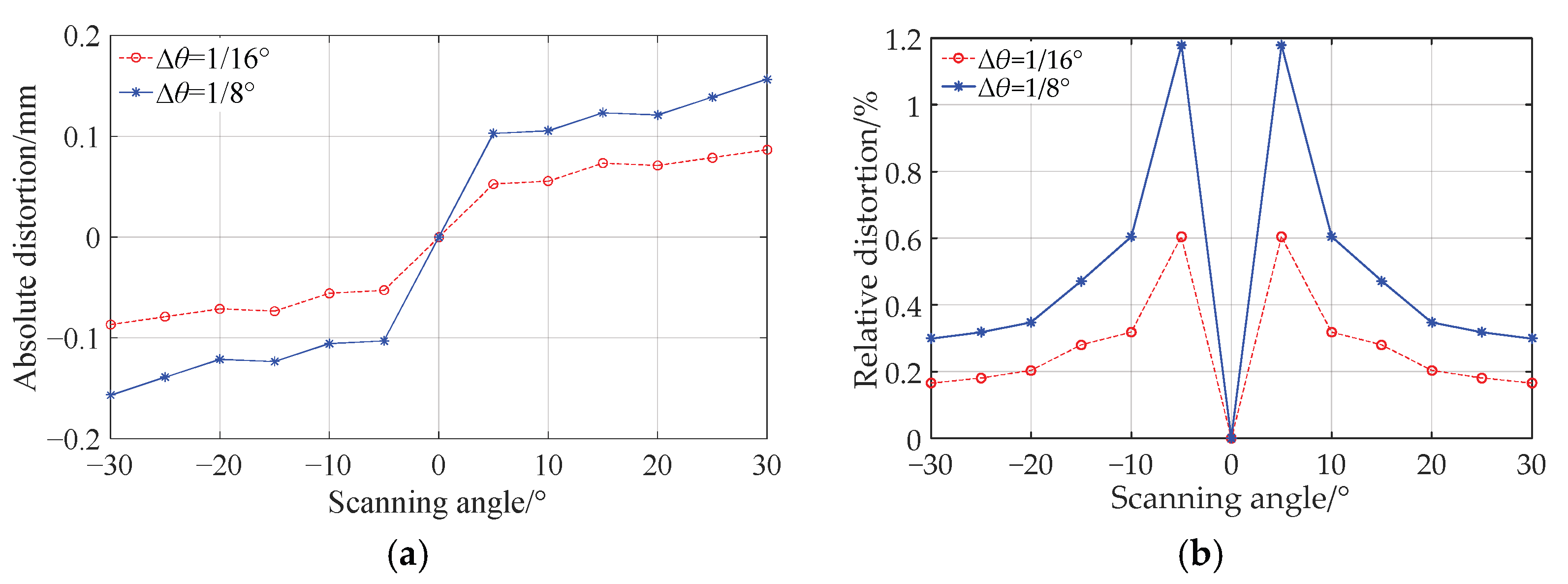
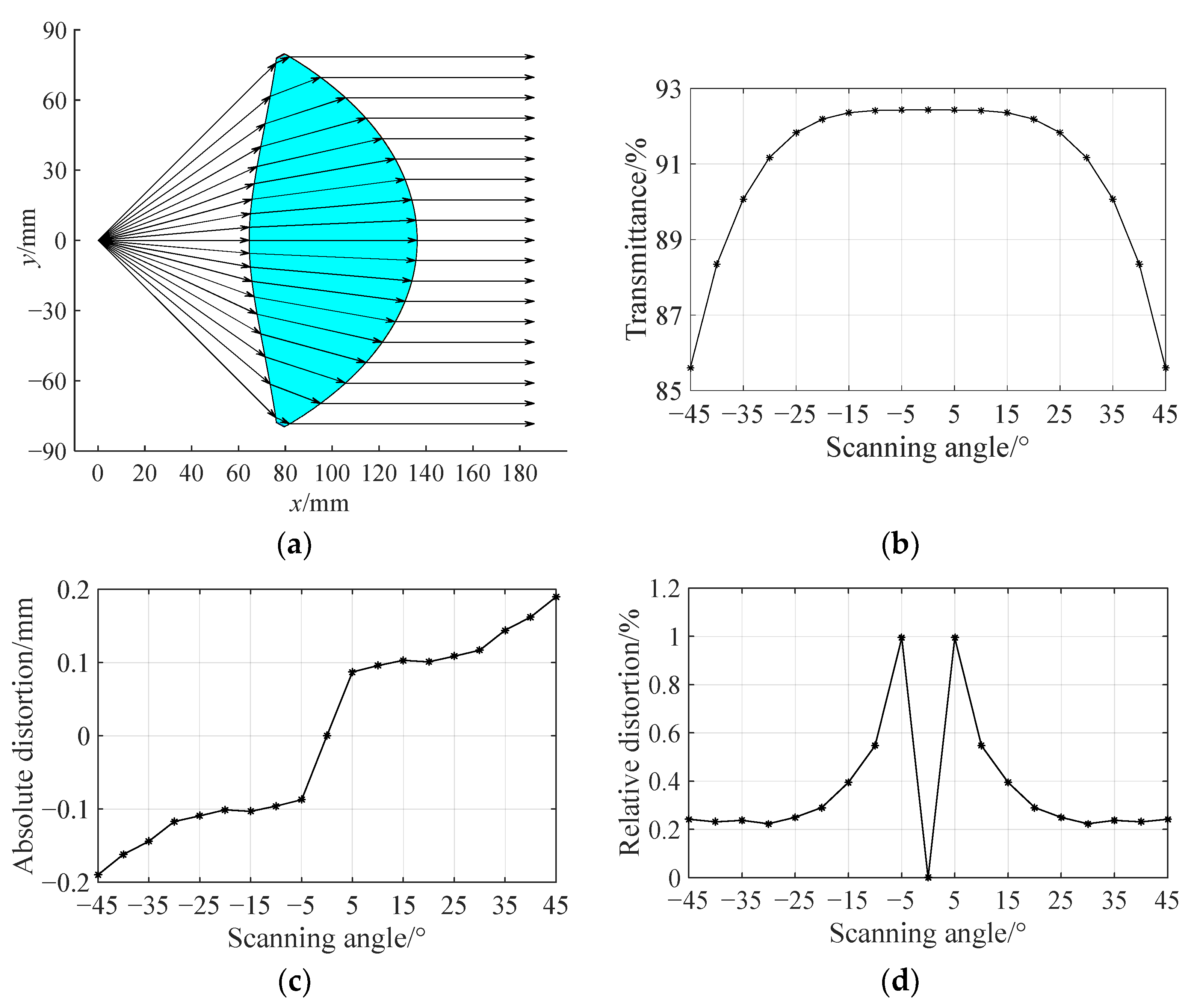
3.1. Design and Simulation Analysis of F-θ Lens with Angle of Field of 60°
3.1.1. Lens Design
3.1.2. Simulation Analysis of Thin Lens
3.1.3. Simulation Analysis of Thick Lens
3.2. Design and Simulation Analysis of F-θ Lens with Angle of Field of 90°
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marshall, G.F.; Stutz, G.E. Handbook of Optical and Laser Scanning, 2nd ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2012; pp. 70–132. Available online: http://www.taylorfrancis.com (accessed on 26 July 2025).
- May, K.H.; Mohammadzadeh, S.; Keil, A.; von Freymann, G.; Friederich, F. Coherent Off-Axis Terahertz Tomography with a Multi-Channel Array and f-theta Optics. Sensors 2024, 24, 529. [Google Scholar] [CrossRef] [PubMed]
- Mohammadzadeh, S.; Hussung, R.; Keil, A.; Leuchs, S.; Krebs, C.; Nüßler, D.; Seewig, J.; von Freymann, G.; Friederich, F. Compact hand-guided 3D scanning terahertz sensor platforms with 3D-printed aspherical telecentric f-θ lens. Int. J. Microw. Wirel. Technol. 2023, 15, 1027–1037. [Google Scholar] [CrossRef]
- Pernechele, C.; Consolaro, L.; Jones, G.H.; Brydon, G.; Da Deppo, V. Telecentric F-theta fisheye lens for space applications. OSA Contin. 2021, 4, 783–789. [Google Scholar] [CrossRef]
- Zhou, Q.; Tian, Y.; Wang, J.; Xu, M. Design and implementation of a high-performance panoramic annular lens. Appl. Opt. 2020, 59, 11246–11253. [Google Scholar] [CrossRef]
- Novák, J.; Mikš, A. Method for algebraic calculation of initial design parameters of a two-element telecentric f-theta lens. Appl. Opt. 2023, 62, 6113–6119. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Schmidt, K.; Wapler, M.C.; Wallrabe, U.; Czarske, J.W.; Koukourakis, N. Fully refractive telecentric f-theta microscope based on adaptive elements for 3D raster scanning of biological tissues. Opt. Express 2023, 31, 29703–29715. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Pu, Y.; Shi, W. Low-cost spectrometer design for ultra-high resolution spectral domain optical coherence tomography. Chin. Opt. Lett. 2023, 21, 101101. [Google Scholar] [CrossRef]
- Park, S.-H.; Kim, S.-D.; Lee, D.-H. Design of Telecentric F-theta Lens for 532 nm Wavelength Laser. J. Korean Ophthalmic Opt. Soc. 2019, 24, 447–454. (In Korean) [Google Scholar] [CrossRef]
- Hu, X.; Hua, H. High-resolution optical see-through multi-focal-plane head-mounted display using freeform optics. Opt. Express 2014, 22, 13896–13903. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, J.; Jin, G. Design of freeform imaging systems with linear field-of-view using a construction and iteration process. Opt. Express 2014, 22, 3362–3374. [Google Scholar] [CrossRef]
- Ok, G.; Park, K.; Chun, H.S.; Chang, H.-J.; Lee, N.; Choi, S.-W. High-performance sub-terahertz transmission imaging system for food inspection. Biomed. Opt. Express 2015, 6, 1929–1941. [Google Scholar] [CrossRef]
- Zhu, Z.; To, S.; Zhang, S. Active control of residual tool marks for freeform optics functionalization by novel biaxial servo assisted fly cutting. Appl. Opt. 2015, 54, 7656–7662. [Google Scholar] [CrossRef]
- Kumar, S.; Tong, Z.; Jiang, X. Advances in the design and manufacturing of novel freeform optics. Int. J. Extrem. Manuf. 2022, 4, 032004. [Google Scholar] [CrossRef]
- Aguirre-Aguirre, D.; Villalobos-Mendoza, B.; Díaz-Uribe, R.; Campos-García, M. Null-screen design for highly freeform surface testing. Opt. Express 2020, 28, 36706–36722. [Google Scholar] [CrossRef]
- Gonzalez-Utrera, D.; Villalobos-Mendoza, B.; Diaz-Uribe, R.; Aguirre-Aguirre, D. Modeling, fabrication, and metrology of 3D printed Alvarez lenses prototypes. Opt. Express 2024, 32, 3512–3527. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Li, C.; Ding, Y.; Yang, C.; Zhao, Y.; Xue, C. Precision glass molding technology for XY polynomial freeform optical elements with simulations and experiments. Opt. Express 2024, 32, 22905–22927. [Google Scholar] [CrossRef]
- Chang, X.; Hu, Y.; Wang, J.; Liu, X.; Hao, Q. Dynamic Interferometry for Freeform Surface Measurement Based on Machine Learning-Configured Deformable Mirror. Sensors 2025, 25, 490. [Google Scholar] [CrossRef]
- Wang, K.; Han, Y.; Li, H.; Luo, Y. Overlapping-based optical freeform surface construction for extended lighting source. Opt. Express 2013, 21, 19750–19761. [Google Scholar] [CrossRef] [PubMed]
- Kang, X.L.; Yao, H.B.; Liu, Q.L.; Wang, L.; Zhang, B.; Chen, K. Secondary optical design of diffused illumination of extended light source based on refractive index precompensation method. Laser Optoelectron. Prog. 2019, 56, 152202. (In Chinese) [Google Scholar] [CrossRef]
- Gao, Z.; Yuan, Q.; Li, X.; Chen, L.; Ye, J. Review of optical freeform surface representation technique and its application. Opt. Eng. 2017, 56, 110901. [Google Scholar] [CrossRef]
- Chen, C.; Hao, Q.; Liu, L.; Cao, J.; Zhang, Y.; Cheng, Y. 10× continuous optical zoom imaging using Alvarez lenses actuated by dielectric elastomers. Opt. Express 2024, 32, 1246–1256. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Li, Y.; Bai, J. Design of a panoramic annular lens system with an ultra-wide angle via an annular Gaussian radial basis function freeform surface. Appl. Opt. 2023, 62, 3941–3947. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Tang, Z.; Gross, H. Correction of 2D-telecentric scan systems with freeform surfaces. Opt. Express 2020, 2, 3041–3056. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, H.; Luo, W.; Du, H.; Cheng, D.; Wang, Y.; Wu, R.; Wang, Y.; Kidger, T.E. Optical design of a wide linear field-of-view, high resolution, and compact f-theta laser scanning system. In Proceedings of the SPIE Optical Design and Testing XII, Online, 20 December 2022; Volume 123151, p. 123151J. [Google Scholar] [CrossRef]
- Park, Y.-W.; Qin, Z.; Lyu, S.-K. Study on design and processing performance verification of a 600 dpi f-theta lens. J. Mech. Sci. Technol. 2021, 35, 5643–5653. [Google Scholar] [CrossRef]
- Harris, Z.B.; Katletz, S.; Khani, M.E.; Virk, A.; Arbab, M.H. Design and characterization of telecentric f-θ scanning lenses for broadband terahertz frequency systems. AIP Adv. 2020, 10, 125313. [Google Scholar] [CrossRef]
- Xu, C.; Ye, D.J.; Liu, H.Z.; Cheng, Z.X.; Lin, H.Z.; Song, W.T. Optical design of a freeform f-θ lens for the 405 nm laser scanning unit. Appl. Opt. 2025, 64, 2515–2524. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, T.; Jin, G. Design method of surface contour for a freeform lens with wide linear field-of-view. Opt. Express 2013, 21, 26080–26092. [Google Scholar] [CrossRef]
- Ghasemi, S.H.; Hantehzadeh, M.R.; Sabbaghzadeh, J.; Dorranian, D.; Vatani, V.; Babazadeh, A.; Hejaz, K.; Hemmati, A.; Lafouti, M. Designing a plano-convex aspheric lens for fiber optics collimator. Opt. Lasers Eng. 2012, 50, 293–296. [Google Scholar] [CrossRef]
- Syu, Y.-S.; Wu, C.-Y.; Lee, Y.-C. Double-Sided Freeform Lens for Light Collimation of Light Emitting Diodes. Appl. Sci. 2019, 9, 5452. [Google Scholar] [CrossRef]
- Gong, C.; Xu, H.; Xu, C.; Liang, J.; Mu, Y. Design and prototyping of highly-collimated long-distance optical systems with an LED light source. Appl. Opt. 2020, 59, 8724–8732. [Google Scholar] [CrossRef]
- Liu, C.; Liu, J.; Xing, Y.; Ao, X.; Shen, H.; Yang, C. An Iterative Deflectometry Method of Reconstruction of Separate Specular Surfaces. Sensors 2025, 25, 1549. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.-B.; Moon, S.-D.; Kim, H.-S.; Yoo, J.-H.; Kim, H.-C. Optical Design and Manufacturing Technology for High Resolution Laser Scanning Unit. Int. J. Precis. Eng. Manuf. 2009, 10, 141–146. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Chen, K.; Kang, X.; Zheng, H. Numerical Iterative Design and Analysis of Double Freeform Surface Telecentric F-Theta Lens. Sensors 2025, 25, 4949. https://doi.org/10.3390/s25164949
Wang L, Chen K, Kang X, Zheng H. Numerical Iterative Design and Analysis of Double Freeform Surface Telecentric F-Theta Lens. Sensors. 2025; 25(16):4949. https://doi.org/10.3390/s25164949
Chicago/Turabian StyleWang, Li, Ke Chen, Xueliang Kang, and Hongmei Zheng. 2025. "Numerical Iterative Design and Analysis of Double Freeform Surface Telecentric F-Theta Lens" Sensors 25, no. 16: 4949. https://doi.org/10.3390/s25164949
APA StyleWang, L., Chen, K., Kang, X., & Zheng, H. (2025). Numerical Iterative Design and Analysis of Double Freeform Surface Telecentric F-Theta Lens. Sensors, 25(16), 4949. https://doi.org/10.3390/s25164949





