Non-Destructive Permittivity and Moisture Analysis in Wooden Heritage Conservation Using Split Ring Resonators and Coaxial Probe
Abstract
1. Introduction
2. Methods and Models
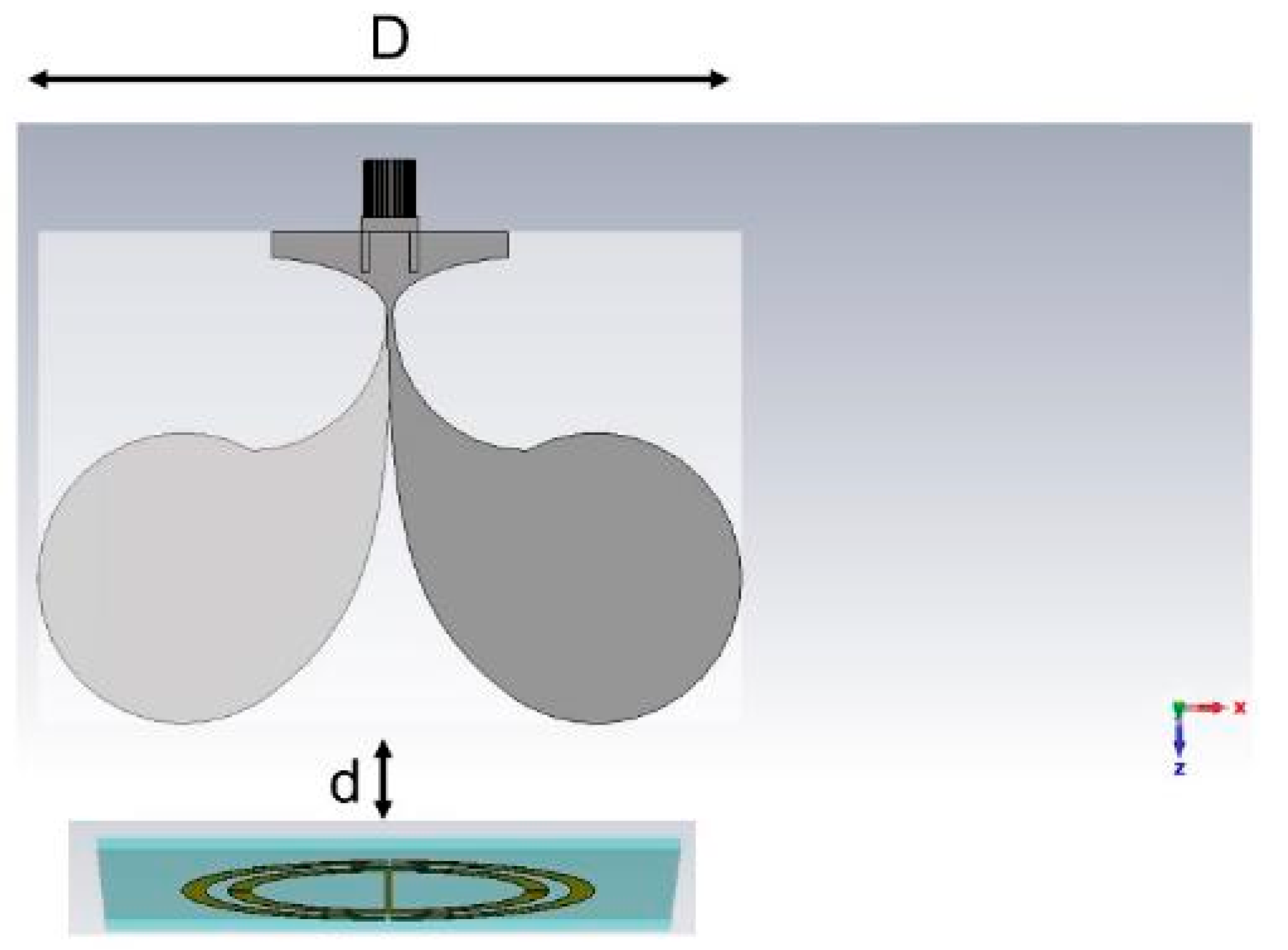
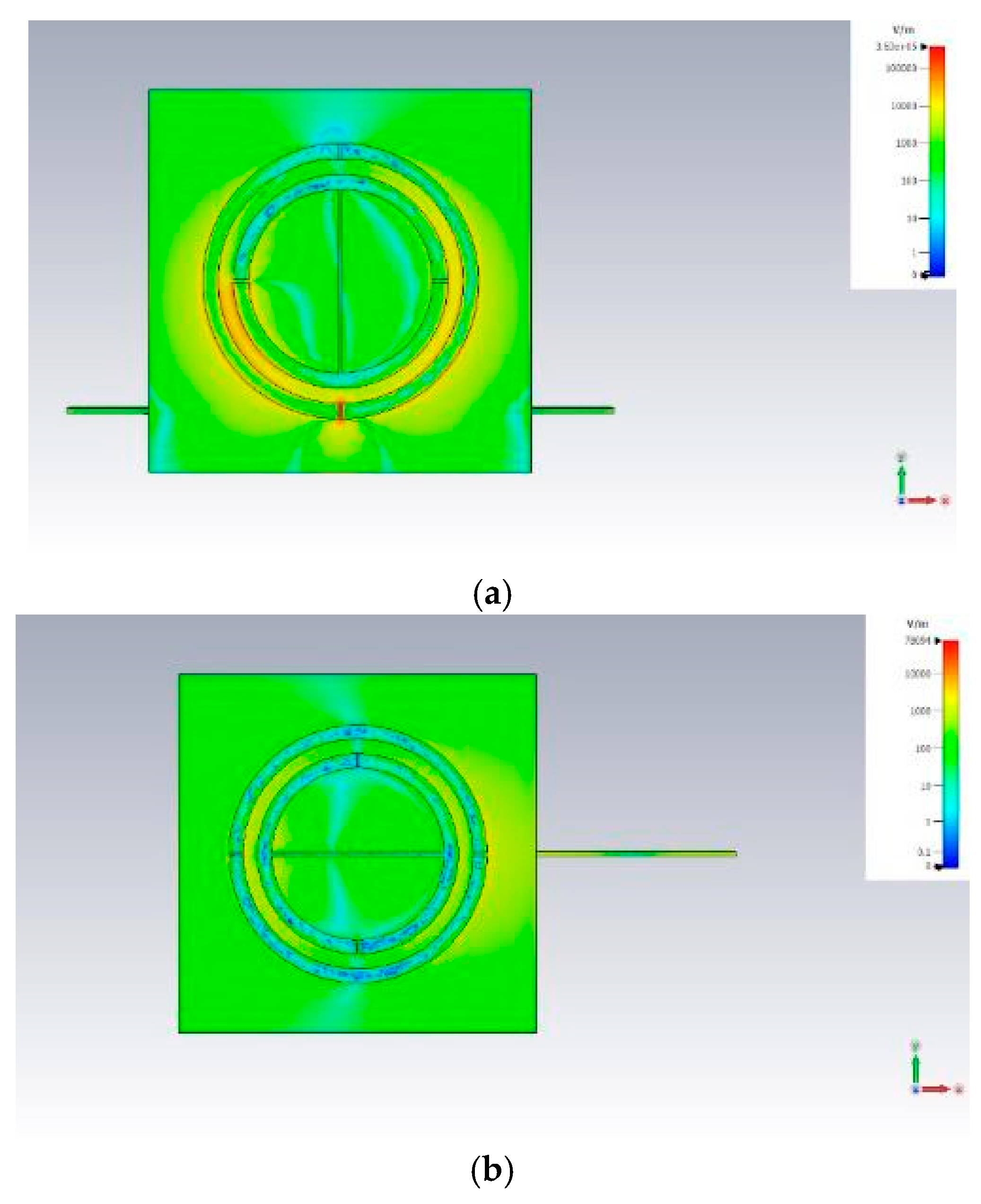
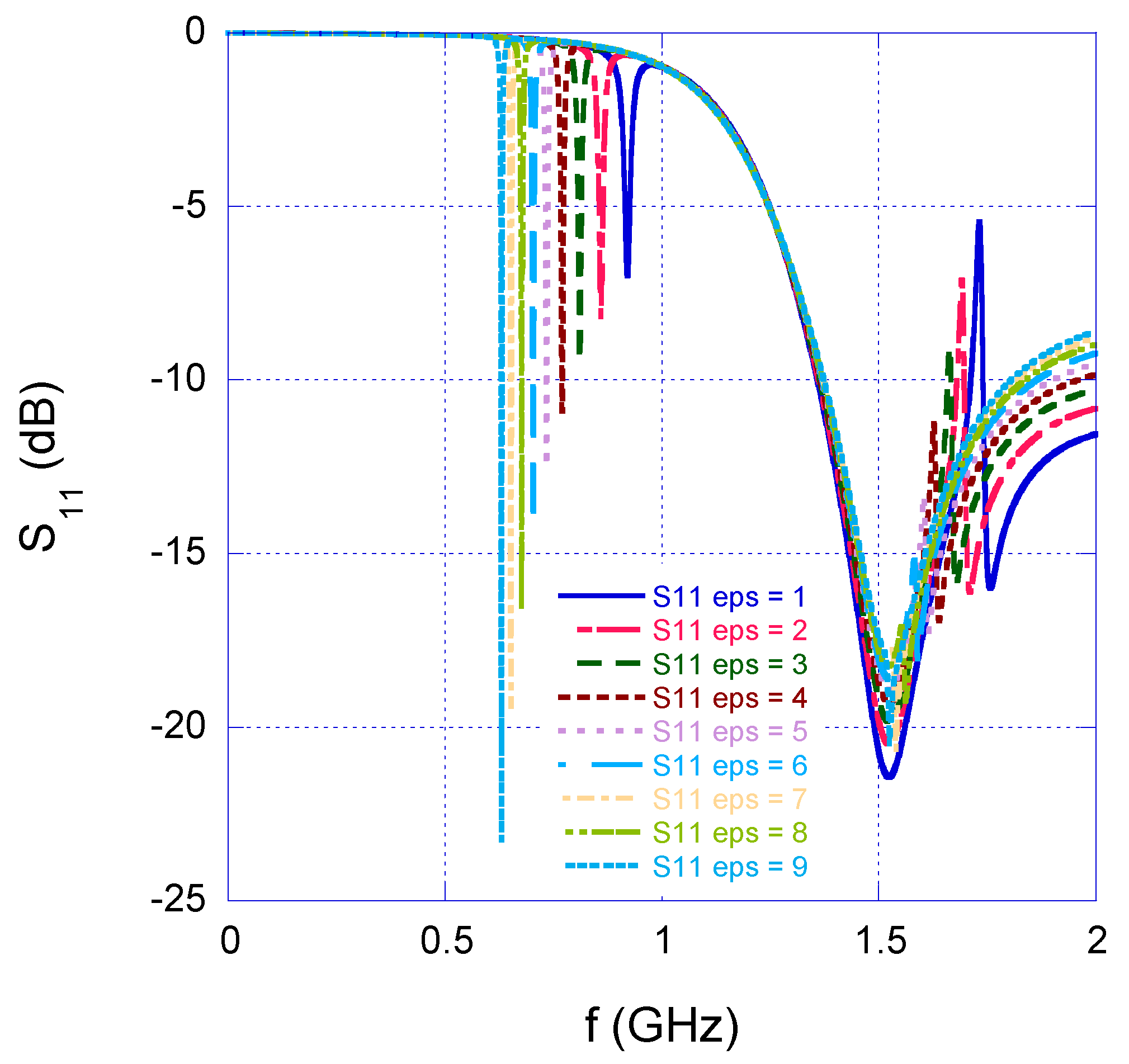
2.1. Operational Concepts and Simulations
2.2. Reference Materials
2.3. Combined Uncertainty Evaluation
2.4. Complementary Portable Sensing System
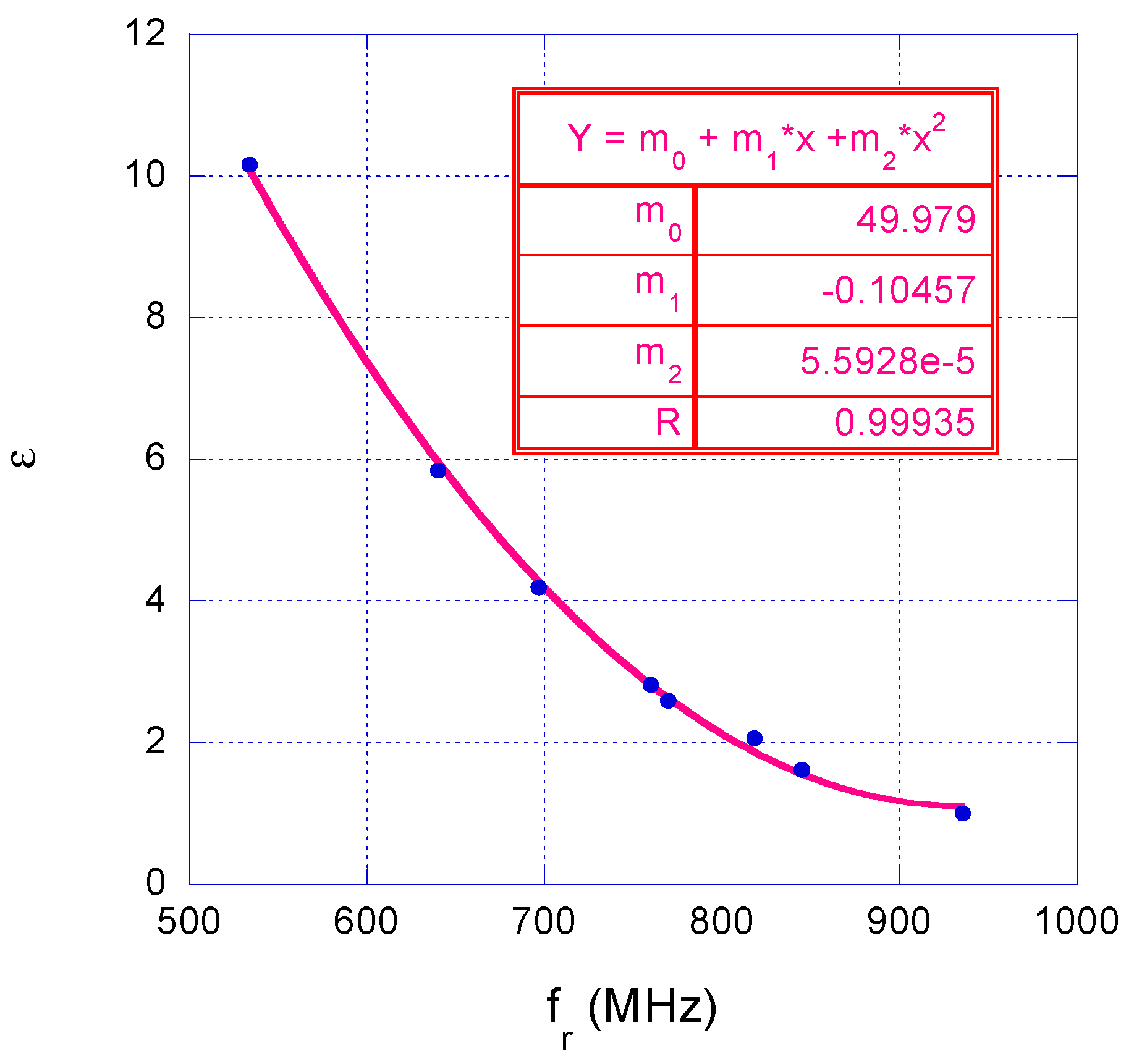
3. Experimental Calibration Curve
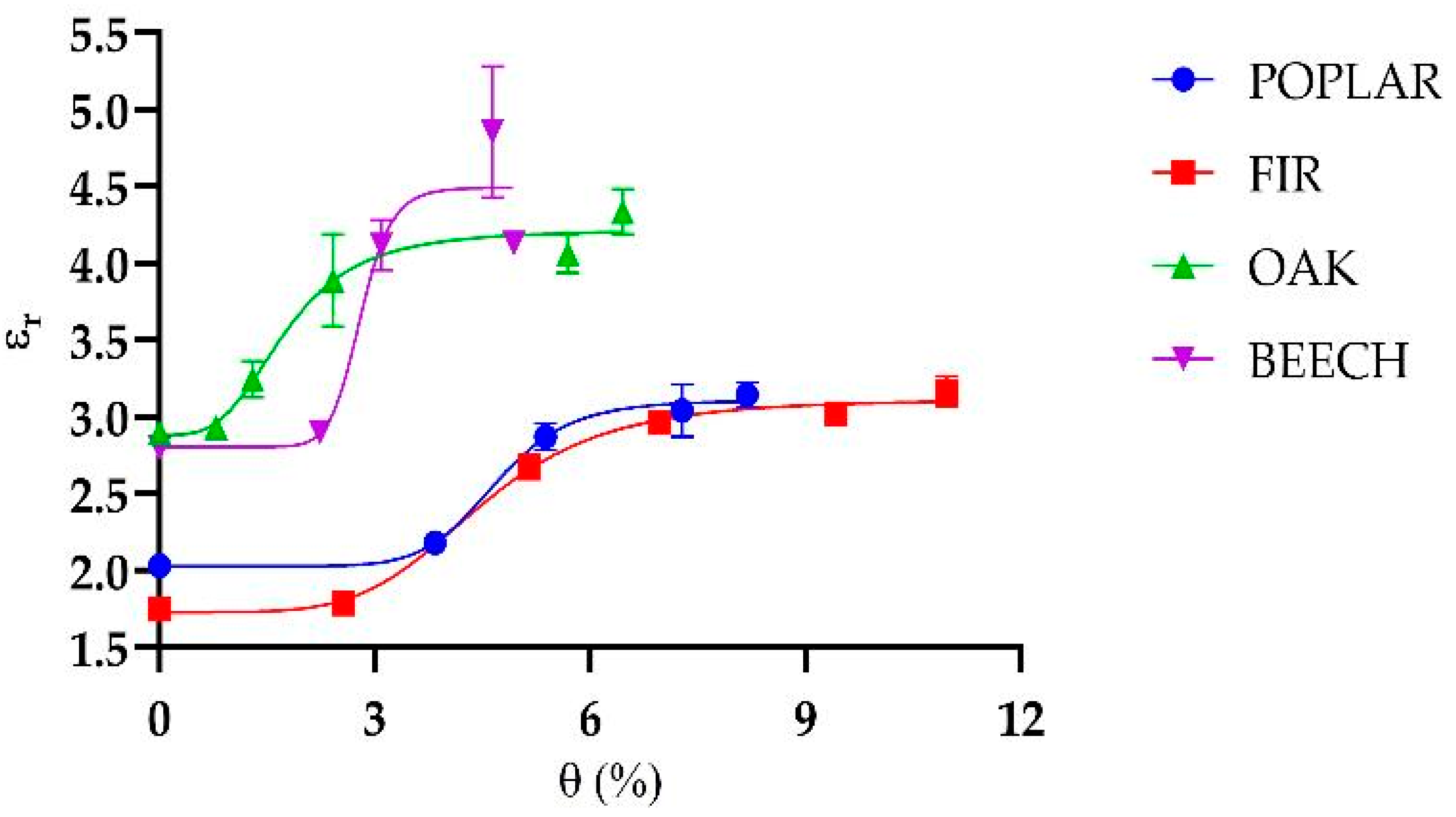
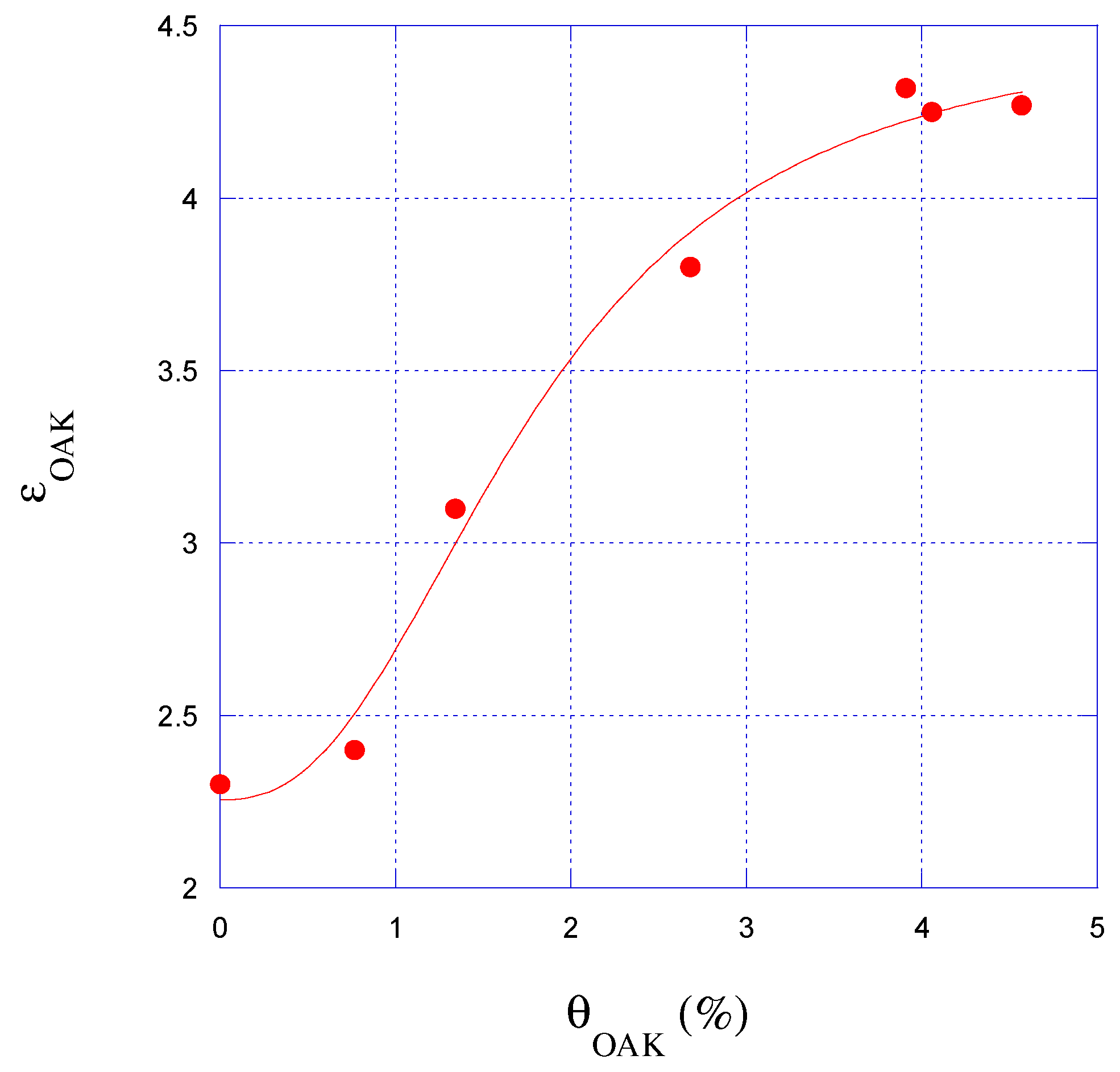
4. Measurements on Wood Samples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pavlogeorgatos, G. Environmental Parameters in Museums. Build. Environ. 2003, 38, 1457–1462. [Google Scholar] [CrossRef]
- Stovel, H. Risk Preparedness: A Management Manual for World Cultural Heritage; ICCROM: Rome, Italy, 1998; ISBN 9290771526. [Google Scholar]
- Rodriguez-Sanchez, M.C.; Borromeo, S.; Hernández-Tamames, J.A. Wireless Sensor Networks for Conservation and Monitoring Cultural Assets. IEEE Sens. J. 2011, 11, 1382–1389. [Google Scholar] [CrossRef]
- Camuffo, D. Measuring Time of Wetness and Moisture in Materials. In Microclimate for Cultural Heritage; Elsevier: Amsterdam, The Netherlands, 2019; pp. 459–482. [Google Scholar]
- D’Alvia, L.; Pittella, E.; Rizzuto, E.; Piuzzi, E.; Del Prete, Z. A Portable Low-Cost Reflectometric Setup for Moisture Measurement in Cultural Heritage Masonry Unit. Measurement 2022, 189, 110438. [Google Scholar] [CrossRef]
- D’Alvia, L.; Piuzzi, E.; Cataldo, A.; Del Prete, Z. Permittivity-Based Water Content Calibration Measurement in Wood-Based Cultural Heritage: A Preliminary Study. Sensors 2022, 22, 2148. [Google Scholar] [CrossRef]
- Dietsch, P.; Franke, S.; Franke, B.; Gamper, A.; Winter, S. Methods to Determine Wood Moisture Content and Their Applicability in Monitoring Concepts. J. Civ. Struct. Health Monit. 2015, 5, 115–127. [Google Scholar] [CrossRef]
- Niemz, P.; Mannes, D. Non-Destructive Testing of Wood and Wood-Based Materials. J. Cult. Herit. 2012, 13, S26–S34. [Google Scholar] [CrossRef]
- Aichholzer, A.; Arthaber, H.; Schuberth, C.; Mayer, H. Non-Destructive Evaluation of Grain Angle, Moisture Content and Density of Spruce with Microwaves. Eur. J. Wood Wood Prod. 2013, 71, 779–786. [Google Scholar] [CrossRef]
- Aguilar-Castro, K.M.; Flores-Prieto, J.J.; Macías-Melo, E.V. Near Infrared Reflectance Spectroscopy: Moisture Content Measurement for Ceramic Plaster. J. Mech. Sci. Technol. 2014, 28, 293–300. [Google Scholar] [CrossRef]
- Barreira, E.; Almeida, R.M.S.F.; Moreira, M. An Infrared Thermography Passive Approach to Assess the Effect of Leakage Points in Buildings. Energy Build. 2017, 140, 224–235. [Google Scholar] [CrossRef]
- Marynowicz, A.; Kucharczyk, A. Determination of the Water Absorption and Water Diffusion Coefficients by Means of Infrared Thermography Measurements. Measurement 2021, 185, 110054. [Google Scholar] [CrossRef]
- Casieri, C.; Senni, L.; Romagnoli, M.; Santamaria, U.; De Luca, F. Determination of Moisture Fraction in Wood by Mobile NMR Device. J. Magn. Reson. 2004, 171, 364–372. [Google Scholar] [CrossRef]
- Güneyli, H.; Karahan, S.; Güneyli, A.; Yapιcι, N. Water Content and Temperature Effect on Ultrasonic Pulse Velocity of Concrete. Russ. J. Nondestruct. Test. 2017, 53, 159–166. [Google Scholar] [CrossRef]
- Lencis, U.; Udris, A.; Korjakins, A. Moisture Effect on the Ultrasonic Pulse Velocity in Concrete Cured under Normal Conditions and at Elevated Temperature. Constr. Sci. 2013, 14, 71–78. [Google Scholar] [CrossRef]
- Luo, D.; Wang, S.; Du, X.; Zhao, P.; Lu, T.; Yang, H.; Frank Chen, Y. Health Detection Techniques for Historic Structures. Mater. Test. 2021, 63, 855–864. [Google Scholar] [CrossRef]
- Běťák, A.; Zach, J.; Misák, P.; Vaněrek, J. Comparison of Wood Moisture Meters Operating on Different Principles of Measurement. Buildings 2023, 13, 531. [Google Scholar] [CrossRef]
- Aichholzer, A.; Schuberth, C.; Mayer, H.; Arthaber, H. Microwave Testing of Moist and Oven-Dry Wood to Evaluate Grain Angle, Density, Moisture Content and the Dielectric Constant of Spruce from 8 GHz to 12 GHz. Eur. J. Wood Wood Prod. 2018, 76, 89–103. [Google Scholar] [CrossRef]
- Łukawski, D.; Dudkowiak, A.; Janczak, D.; Lekawa-Raus, A. Preparation and Applications of Electrically Conductive Wood Layered Composites. Compos. Part A Appl. Sci. Manuf. 2019, 127, 105656. [Google Scholar] [CrossRef]
- Larsen, P.K. Determination of Water Content in Brick Masonry Walls Using a Dielectric Probe. J. Archit. Conserv. 2012, 18, 47–62. [Google Scholar] [CrossRef]
- Razafindratsima, S.; Sbartaï, Z.M.; Demontoux, F. Permittivity Measurement of Wood Material over a Wide Range of Moisture Content. Wood Sci. Technol. 2017, 51, 1421–1431. [Google Scholar] [CrossRef]
- Moron, C.; Garcia-Fuentevilla, L.; Garcia, A.; Moron, A. Measurement of Moisture in Wood for Application in the Restoration of Old Buildings. Sensors 2016, 16, 697. [Google Scholar] [CrossRef]
- Jang, C.; Park, J.-K.; Lee, H.-J.; Yun, G.-H.; Yook, J.-G. Sensitivity-Enhanced Fluidic Glucose Sensor Based on a Microwave Resonator Coupled with an Interferometric System for Noninvasive and Continuous Detection. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 1017–1026. [Google Scholar] [CrossRef]
- Pittella, E.; Schiavoni, R.; Monti, G.; Masciullo, A.; Scarpetta, M.; Cataldo, A.; Piuzzi, E. Split Ring Resonator Network and Diffused Sensing Element Embedded in a Concrete Beam for Structural Health Monitoring. Sensors 2022, 22, 6398. [Google Scholar] [CrossRef] [PubMed]
- Pittella, E.; Angrisani, L.; Cataldo, A.; Piuzzi, E.; Fabbrocino, F. Embedded Split Ring Resonator Network for Health Monitoring in Concrete Structures. IEEE Instrum. Meas. Mag. 2020, 23, 14–20. [Google Scholar] [CrossRef]
- Velez, P.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Highly-Sensitive Microwave Sensors Based on Open Complementary Split Ring Resonators (OCSRRs) for Dielectric Characterization and Solute Concentration Measurement in Liquids. IEEE Access 2018, 6, 48324–48338. [Google Scholar] [CrossRef]
- Kilani, D.; Niknahad, F.; Shah, A.; Olsen, S.; Meaker, M.; Zarifi, M.H. Wireless Microwave Sensor Network Using Split Ring Resonators for Ice Monitoring Applications. IEEE Internet Things J. 2024, 11, 25316–25325. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, X.; Xiao, H.; Wang, Y. A Split-Ring Resonator Probe for Assessing Subsurface Wood Defects. Rev. Sci. Instrum. 2019, 90, 125004. [Google Scholar] [CrossRef]
- Mohammadi, S.; Zarifi, M.H. Differential Microwave Resonator Sensor for Real-Time Monitoring of Volatile Organic Compounds. IEEE Sens. J. 2021, 21, 6105–6114. [Google Scholar] [CrossRef]
- Alimenti, A.; Pittella, E.; Torokhtii, K.; Pompeo, N.; Piuzzi, E.; Silva, E. A Dielectric Loaded Resonator for the Measurement of the Complex Permittivity of Dielectric Substrates. IEEE Trans. Instrum. Meas. 2023, 72, 1–9. [Google Scholar] [CrossRef]
- Pittella, E.; Cataldo, A.; Cavagnaro, M.; D’Alvia, L.; Fabbrocino, F.; Piuzzi, E. Wireless Sensing of Permittivity for Cultural Heritage Monitoring Using a Passive SRR. In Proceedings of the IMEKO TC4 International Conference on Metrology for Archaeology and Cultural Heritage, Rome, Italy, 19–21 October 2023. [Google Scholar]
- Wiltshire, B.D.; Zarifi, T.; Zarifi, M.H. Passive Split Ring Resonator Tag Configuration for RFID-Based Wireless Permittivity Sensing. IEEE Sens. J. 2020, 20, 1904–1911. [Google Scholar] [CrossRef]
- Alahnomi, R.A.; Zakaria, Z.; Ruslan, E.; Ab Rashid, S.R.; Mohd Bahar, A.A. High-Q Sensor Based on Symmetrical Split Ring Resonator with Spurlines for Solids Material Detection. IEEE Sens. J. 2017, 17, 2766–2775. [Google Scholar] [CrossRef]
- Schiavoni, R.; Monti, G.; Piuzzi, E.; Tarricone, L.; Tedesco, A.; De Benedetto, E.; Cataldo, A. Feasibility of a Wearable Reflectometric System for Sensing Skin Hydration. Sensors 2020, 20, 2833. [Google Scholar] [CrossRef] [PubMed]
- Selvan, K.T.; Janaswamy, R. Fraunhofer and Fresnel Distances: Unified Derivation for Aperture Antennas. IEEE Antennas Propag. Mag. 2017, 59, 12–15. [Google Scholar] [CrossRef]
- Capozzoli, A.; Curcio, C.; D’Agostino, F.; Liseno, A. A Review of the Antenna Field Regions. Electronics 2024, 13, 2194. [Google Scholar] [CrossRef]
- Pittella, E.; Piuzzi, E.; Russo, P.; Fabbrocino, F. Microwave Characterization and Modelling of PA6/GNPs Composites. Math. Comput. Appl. 2022, 27, 41. [Google Scholar] [CrossRef]
- Agilent Technologies Agilent Technologies PNA Series Network Analyzers E8362B, E8363B, and E8364B. Available online: https://www.keysight.com/us/en/assets/9018-02435/service-manuals/9018-02435.pdf (accessed on 7 August 2025).
- Schiavoni, R.; Maietta, G.; Filieri, E.; Masciullo, A.; Cataldo, A. Microwave Reflectometry Sensing System for Low-Cost in-Vivo Skin Cancer Diagnostics. IEEE Access 2023, 11, 13918–13928. [Google Scholar] [CrossRef]
- UNI EN 13755 Natural Stone Test Methods. Determination of Water Absorption at Atmospheric Pressure. Available online: https://standards.globalspec.com/std/1146483/uni-en-13755 (accessed on 8 August 2025).
- Cataldo, A.; De Benedetto, E.; Cannazza, G.; Piuzzi, E.; Pittella, E. TDR-Based Measurements of Water Content in Construction Materials for In-the-Field Use and Calibration. IEEE Trans. Instrum. Meas. 2018, 67, 1230–1237. [Google Scholar] [CrossRef]
- Chauhan, P.D.; Gadani, D.H.; Rana, V.A. Effect of Moisture Content Variation on Dielectric Properties of Various Plant Leaves at Microwave Frequencies. Sci. Rep. 2024, 14, 13204. [Google Scholar] [CrossRef]
- Henry, F.; Gaudillat, M.; Costa, L.C.; Lakkis, F. Free and/or Bound Water by Dielectric Measurements. Food Chem. 2003, 82, 29–34. [Google Scholar] [CrossRef]
- Pico Technology Ltd. PicoVNA Specifications. Available online: https://www.picotech.com/vector-network-analyzer/picovna/picovna-specifications (accessed on 9 October 2023).



| Material Samples | ||
| Air | 1.00 | - |
| LD-PVC | 1.620 | 0.003 |
| PTFE | 2.060 | 0.004 |
| PMMA | 2.590 | 0.005 |
| PC | 2.820 | 0.006 |
| PA6-GNP 1% | 4.195 | 0.019 |
| PA6-GNP 3% | 5.846 | 0.004 |
| PA6-GNP 5% | 10.172 | 0.069 |
| FIR | ϑ1 = 0.00% | ϑ2 = 2.56% | ϑ3 = 5.15% | ϑ4 = 6.97% | ϑ5 = 9.49% | ϑ6 = 10.96 % | ||||||
| fmean | σf | fmean | σf | fmean | σf | fmean | σf | fmean | σf | fmean | σf | |
| 827.3 | 2.4 | 824.0 | 3.6 | 767.1 | 4.4 | 752.5 | 3.6 | 749.5 | 3.3 | 742.6 | 4.5 | |
| POPLAR | ϑ1 = 0.00% | ϑ2 = 3.83% | ϑ3 = 5.31% | ϑ4 = 7.23% | ϑ5 = 8.18% | |||||||
| fmean | σf | fmean | σf | fmean | σf | fmean | σf | fmean | σf | |||
| 805.89 | 1.50 | 795.86 | 1.28 | 756.86 | 4.37 | 748.71 | 8.14 | 743.74 | 3.89 | |||
| BEECH | ϑ1 = 0.00% | ϑ2 = 2.24% | ϑ3 = 3.09% | ϑ4 = 4.64% | ϑ5 = 4.94% | |||||||
| fmean | σf | fmean | σf | fmean | σf | fmean | σf | fmean | σf | |||
| 760.53 | 1.79 | 755.37 | 1.49 | 702.605 | 6.37 | 643.84 | 13.32 | 702.015 | 2.04 | |||
| OAK | ϑ1 = 0.00% | ϑ2 = 0.79% | ϑ3 = 1.29% | ϑ4 = 2.42% | ϑ5 = 5.69% | ϑ6 = 6.45% | ||||||
| fmean | σf | fmean | σf | fmean | σf | fmean | σf | fmean | σf | fmean | σf | |
| 755.30 | 2.08 | 753.86 | 1.92 | 739.13 | 5.48 | 711.87 | 12.03 | 704.78 | 4.90 | 694.42 | 5.51 | |
| FIR | ϑ1 = 0% | ϑ2 = 2.56% | ϑ3 = 5.153% | ϑ4 = 6.966% | ϑ5 = 9.4854% | ϑ6 = 10.96% | ||||||
| mean | mean | mean | mean | mean | mean | |||||||
| 1.747 | 0.057 | 1.787 | 0.0593 | 2.676 | 0.073 | 2.960 | 0.072 | 3.022 | 0.0719 | 3.169 | 0.079 | |
| POPLAR | ϑ1 = 0% | ϑ2 = 3.838% | ϑ3 = 5.3137% | ϑ4 = 7.2752% | ϑ5 = 8.1861% | |||||||
| mean | mean | mean | mean | mean | ||||||||
| 2.030 | 0.056 | 2.181 | 0.056 | 2.873 | 0.069 | 3.041 | 0.100 | 3.143 | 0.075 | |||
| BEECH | ϑ1 = 0% | ϑ2 = 2.2396% | ϑ3 = 3.0885% | ϑ4 = 4.6372% | ϑ5 = 4.9352% | |||||||
| mean | mean | mean | mean | mean | ||||||||
| 2.780 | 0.058 | 2.902 | 0.057 | 4.119 | 0.097 | 4.855 | 0.202 | 4.132 | 0.069 | |||
| OAK | ϑ1 = 0% | ϑ2 = 0.7915% | ϑ3 = 1.2939% | ϑ4 = 2.4189% | ϑ5 = 5.6914% | ϑ6 = 6.4473% | ||||||
| mean | mean | mean | mean | mean | mean | |||||||
| 2.903 | 0.059 | 2.932 | 0.059 | 3.244 | 0.082 | 3.889 | 0.149 | 4.062 | 0.086 | 4.335 | 0.094 | |
| y = a1 + (a2 − a1)/(1 + (a3/x)^a4) | ||||
| Sigmoid Coefficients | Poplar | Fir | Oak | Beech |
| a1 | 2.028 | 1.730 | 2.882 | 2.805 |
| a2 | 3.114 | 4.218 | 4.494 | 4.514 |
| a3 | 4.677 | 4.472 | 1.751 | 2.800 |
| a4 | 8.990 | 5.050 | 3.436 | 12.90 |
| R2 | 0.97 | 0.98 | 0.98 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pittella, E.; Cannazza, G.; Cataldo, A.; Cavagnaro, M.; D’Alvia, L.; Masciullo, A.; Schiavoni, R.; Piuzzi, E. Non-Destructive Permittivity and Moisture Analysis in Wooden Heritage Conservation Using Split Ring Resonators and Coaxial Probe. Sensors 2025, 25, 4947. https://doi.org/10.3390/s25164947
Pittella E, Cannazza G, Cataldo A, Cavagnaro M, D’Alvia L, Masciullo A, Schiavoni R, Piuzzi E. Non-Destructive Permittivity and Moisture Analysis in Wooden Heritage Conservation Using Split Ring Resonators and Coaxial Probe. Sensors. 2025; 25(16):4947. https://doi.org/10.3390/s25164947
Chicago/Turabian StylePittella, Erika, Giuseppe Cannazza, Andrea Cataldo, Marta Cavagnaro, Livio D’Alvia, Antonio Masciullo, Raissa Schiavoni, and Emanuele Piuzzi. 2025. "Non-Destructive Permittivity and Moisture Analysis in Wooden Heritage Conservation Using Split Ring Resonators and Coaxial Probe" Sensors 25, no. 16: 4947. https://doi.org/10.3390/s25164947
APA StylePittella, E., Cannazza, G., Cataldo, A., Cavagnaro, M., D’Alvia, L., Masciullo, A., Schiavoni, R., & Piuzzi, E. (2025). Non-Destructive Permittivity and Moisture Analysis in Wooden Heritage Conservation Using Split Ring Resonators and Coaxial Probe. Sensors, 25(16), 4947. https://doi.org/10.3390/s25164947











