Compression of 3D Optical Encryption Using Singular Value Decomposition
Abstract
1. Introduction
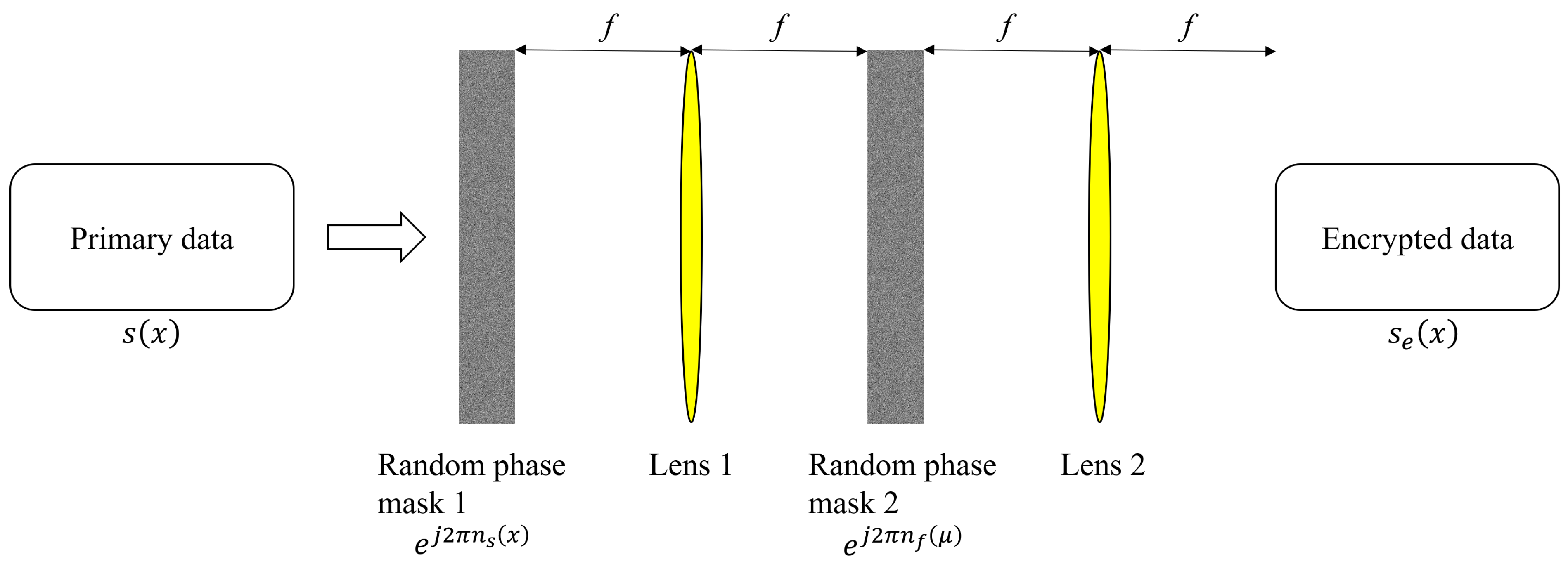
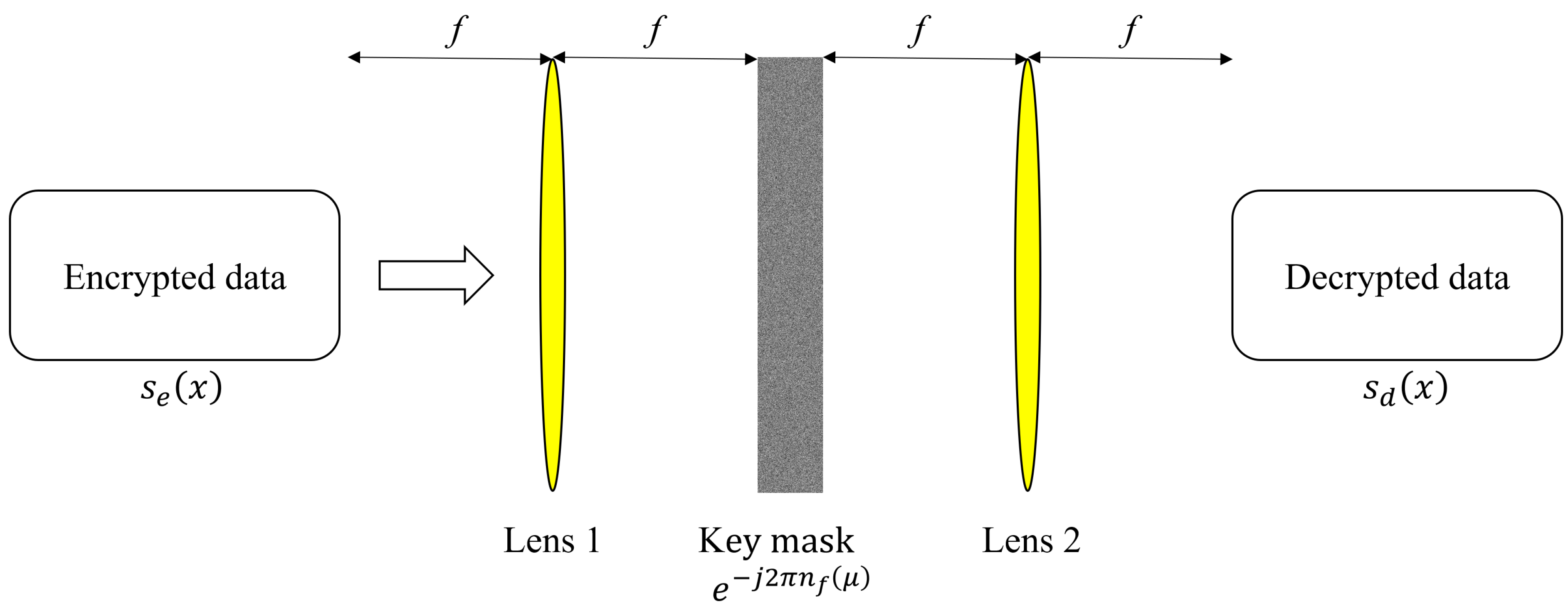
2. Double Random Phase Encryption
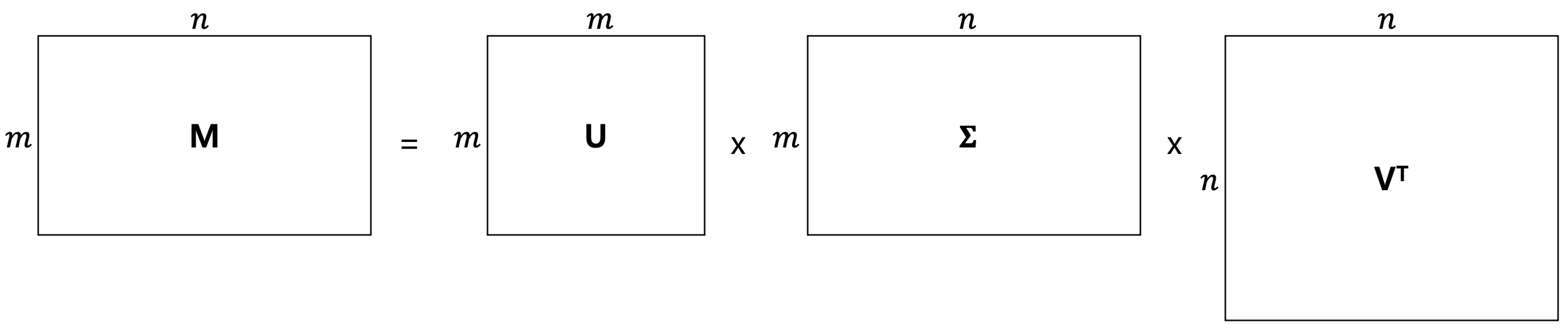
3. Singular Value Decomposition for DRPE
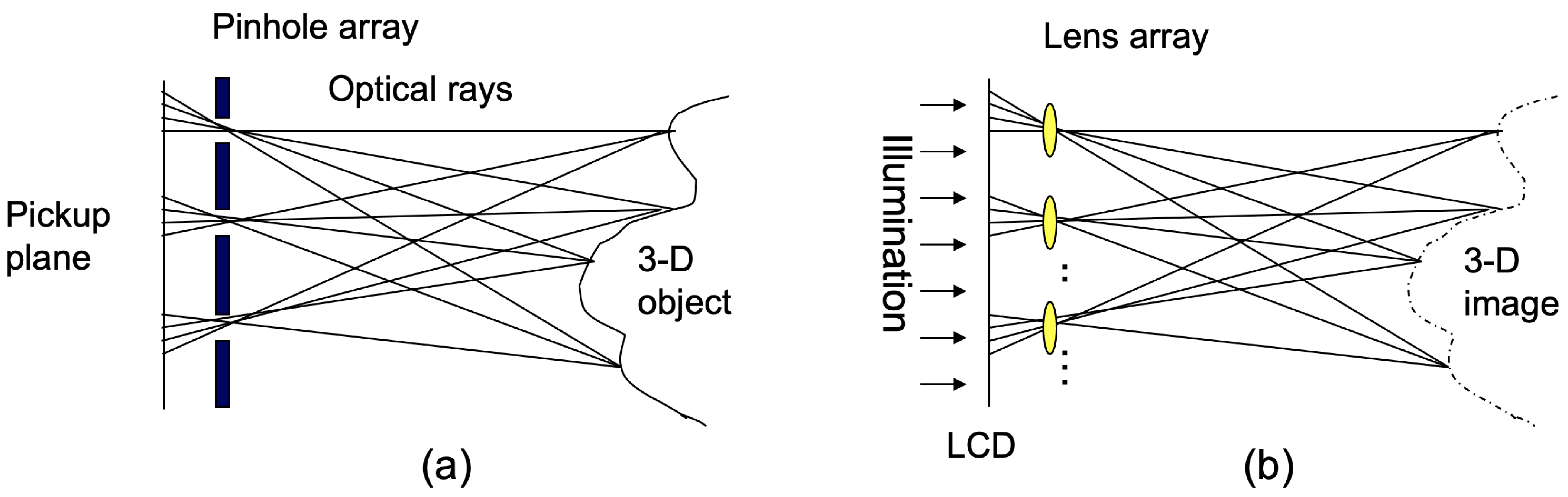
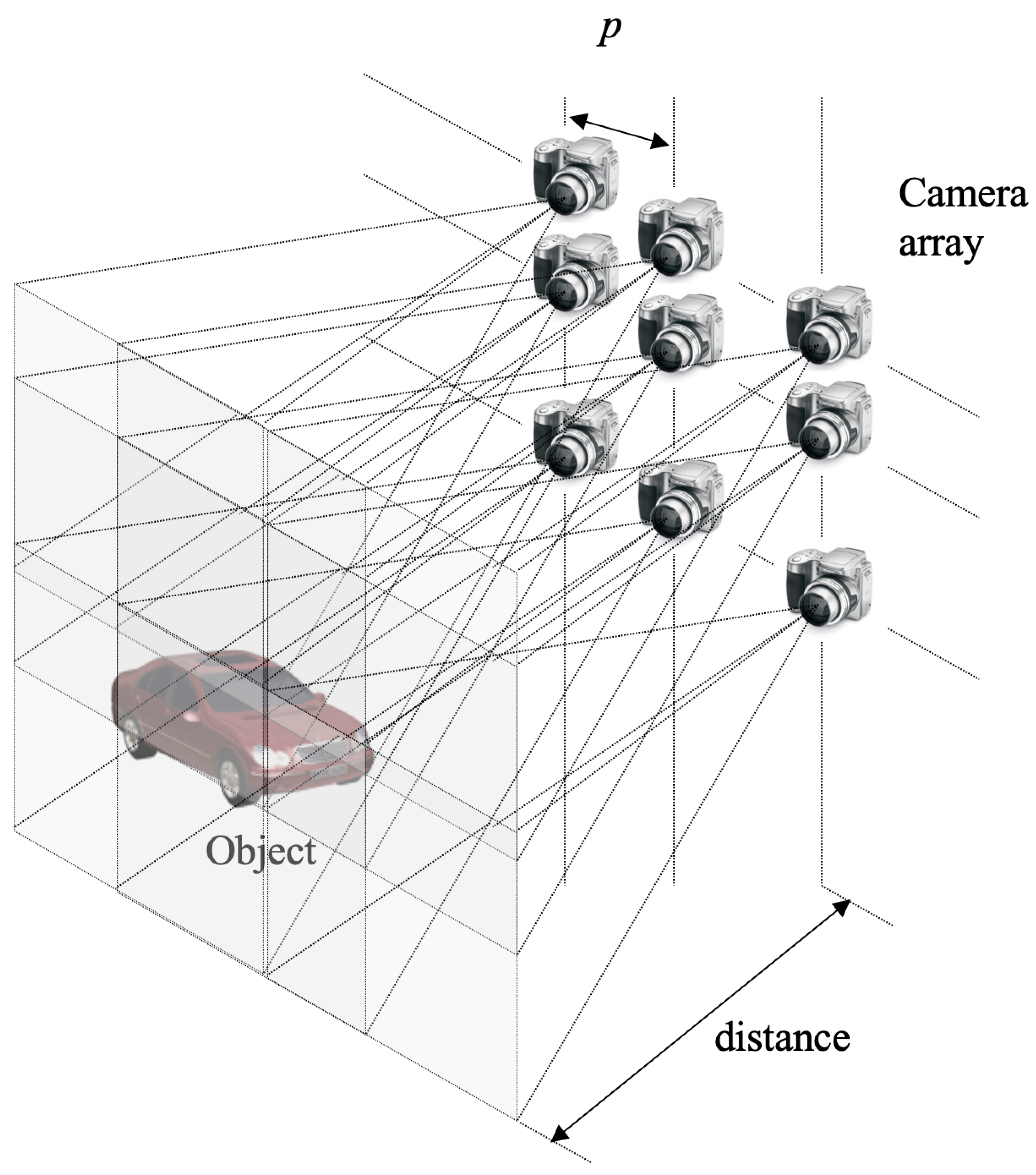
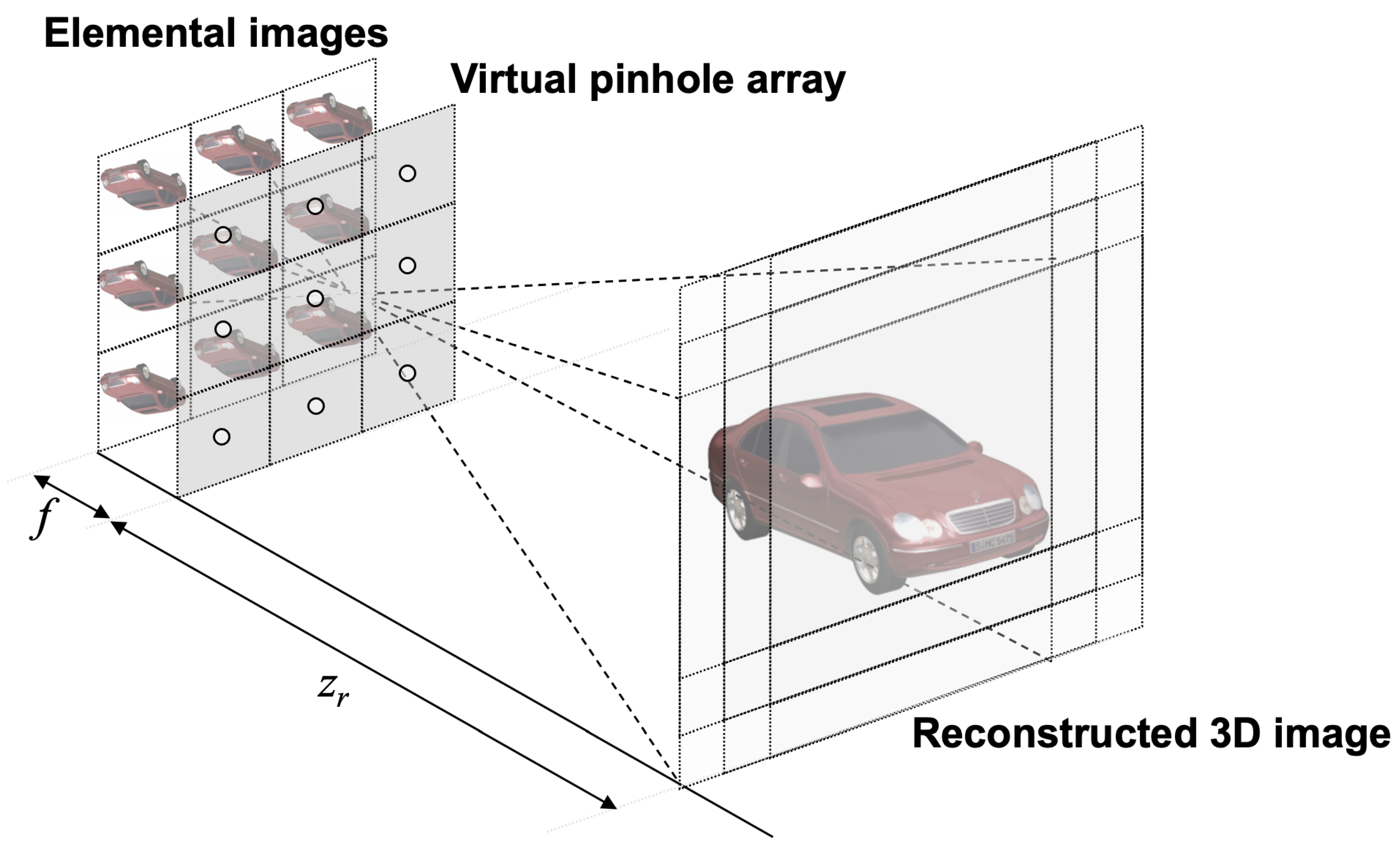
4. Volumetric Computational Reconstruction for 3D DRPE with SVD
5. Experimental Results
5.1. Experimental Setup
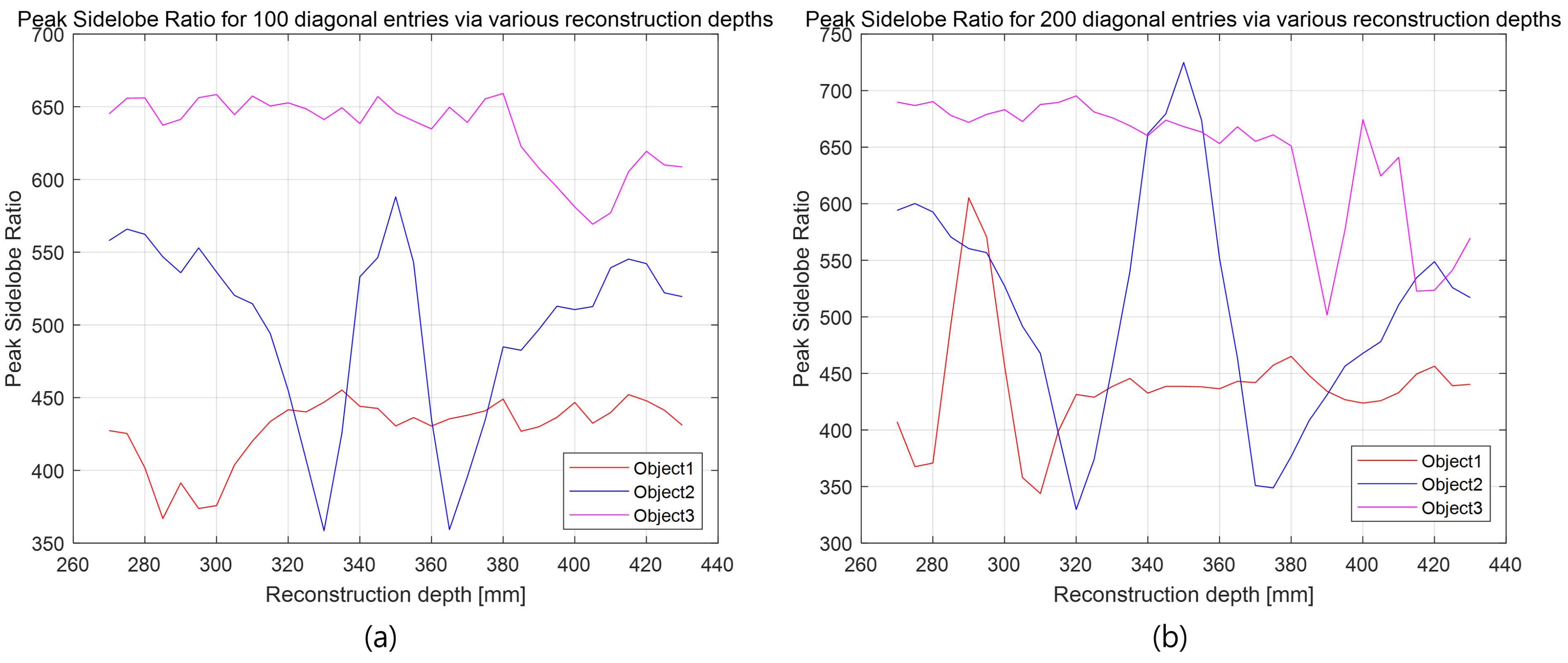
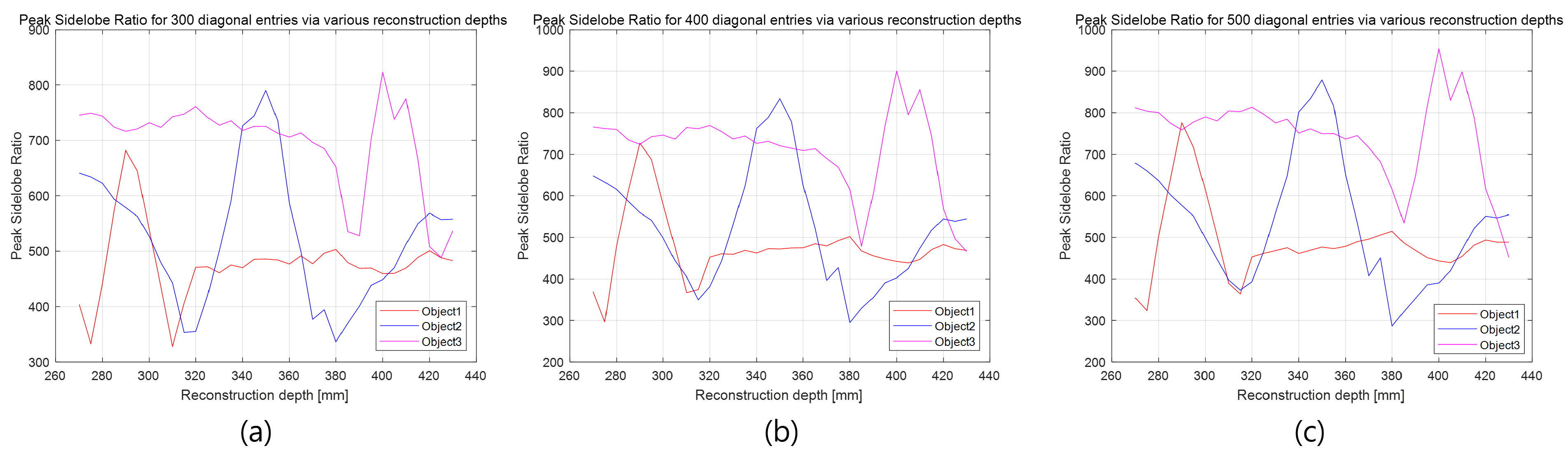
5.2. Results and Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DRPE | Double random phase encryption |
| PSNR | Peak signal-to-noise ratio |
| PSR | Peak sidelobe ratio |
| SSIM | Structural similarity index measure |
| SVD | Singular value decomposition |
| VCR | Volumetric computational reconstruction |
References
- Javidi, B.; Horner, J.L. Optical pattern recognition for validation and security verification. Opt. Eng. 1994, 33, 1752–1756. [Google Scholar] [CrossRef]
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar] [CrossRef]
- Matoba, O.; Javidi, B. Encrypted optical memory system using three-dimensional keys in the Fresnel domain. Opt. Lett. 1999, 24, 762–764. [Google Scholar] [CrossRef]
- Tan, X.; Matoba, O.; Okada-Sudo, Y.; Ide, M.; Shimura, T.; Kuroda, K. Secure optical memory system with polarization encryption. Appl. Opt. 2001, 40, 2310–2315. [Google Scholar] [CrossRef]
- Javidi, B.; Nomura, T. Securing information by use of digital holography. Opt. Lett. 2000, 25, 28–30. [Google Scholar] [CrossRef] [PubMed]
- Mogensen, P.C.; Gluckstad, J. Phase-only optical encryption. Opt. Lett. 2000, 25, 566–568. [Google Scholar] [CrossRef] [PubMed]
- Goudail, F.; Bollaro, F.; Javidi, B.; Refregier, P. Influence of a perturbation in a double random phase encoding system. J. Opt. Soc. Am. A 1998, 15, 2629–2638. [Google Scholar] [CrossRef]
- Matoba, O.; Nomura, T.; Perez-Cabre, E.; Millan, M.S.; Javidi, B. Optical techniques for information security. Proc. IEEE 2009, 97, 1128–1148. [Google Scholar] [CrossRef]
- Carnicer, A.; Montes-Usategui, M.; Arcos, S.; Juvells, I. Vulnerability to chosen-cyphertext attacks of optical encryption schemes based on double random phase keys. Opt. Lett. 2005, 30, 1644–1646. [Google Scholar] [CrossRef]
- Clemente, P.; Duran, V.; Torres-Company, V.; Tajahuerce, E.; Lancis, J. Optical encryption based on computational ghost imaging. Opt. Lett. 2010, 35, 2391–2393. [Google Scholar] [CrossRef]
- Frauel, Y.; Castro, A.; Naughton, T.J.; Javidi, B. Resistance of the double random phase encryption against various attacks. Opt. Exp. 2007, 15, 10253–10265. [Google Scholar] [CrossRef]
- Jiao, S.; Gao, Y.; Lei, T.; Yuan, X. Known-plaintext attack to optical encryption systems with space and polarization encoding. Opt. Exp. 2020, 28, 8085–8097. [Google Scholar] [CrossRef] [PubMed]
- Lee, I.-H.; Cho, M. Double random phase encryption based orthogonal encoding technique for color images. J. Opt. Soc. Korea 2014, 18, 129–133. [Google Scholar] [CrossRef]
- Markman, A.; Javidi, B.; Tehranipoor, M. Photon-counting security tagging and verification using optically encoded QR codes. IEEE Photonics J. 2013, 6, 1–9. [Google Scholar] [CrossRef]
- Markman, A.; Javidi, B. Full-phase photon-counting double-random-phase encryption. J. Opt. Soc. Am. A 2014, 31, 394–403. [Google Scholar] [CrossRef]
- Cho, M.; Javidi, B. Three-dimensional photon counting double-random-phase encryption. Opt. Lett. 2013, 38, 3198–3201. [Google Scholar] [CrossRef]
- Lippmann, G. La Photographie Integrale. C. R. Acad. Sci. 1908, 146, 446–451. [Google Scholar]
- Stern, A.; Javidi, B. Three-dimensional image sensing, visualization, and processing using integral imaging. Proc. IEEE 2006, 94, 591–607. [Google Scholar] [CrossRef]
- Levoy, M. Light fields and computational imaging. Computer 2006, 39, 46–55. [Google Scholar] [CrossRef]
- Martinez-Cuenca, R.; Saavedra, G.; Martinez-Corral, M.; Javidi, B. Progress in 3-D multiperspective display by integral imaging. Proc. IEEE 2009, 97, 1067–1077. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Improved viewing resolution of three-dimensional integral imaging by use of nonstationary micro-optics. Opt. Lett. 2002, 27, 324–326. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Three-dimensional synthetic aperture integral imaging. Opt. Lett. 2002, 27, 1144–1146. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Improvement of viewing angle in integral imaging by use of moving lenslet arrays with low fill factor. Appl. Opt. 2003, 42, 1996–2002. [Google Scholar] [CrossRef]
- Jang, J.-S.; Javidi, B. Large depth-of-focus time-multiplexed three-dimensional integral imaging by use of lenslets with nonuniform focal lengths and aperture sizes. Opt. Lett. 2003, 28, 1924–1926. [Google Scholar] [CrossRef]
- Schulein, R.; DaneshPanah, M.; Javidi, B. 3D imaging with axially distributed sensing. Opt. Lett. 2009, 34, 2012–2014. [Google Scholar] [CrossRef]
- Cho, M.; Shin, D. 3D integral imaging display using axially recorded multiple images. J. Opt. Soc. Korea 2013, 17, 410–414. [Google Scholar] [CrossRef]
- Hong, S.-H.; Jang, J.-S.; Javidi, B. Three-dimensional volumetric object reconstruction using computational integral imaging. Opt. Exp. 2004, 12, 483–491. [Google Scholar] [CrossRef] [PubMed]
- Cho, B.; Kopycki, P.; Martinez-Corral, M.; Cho, M. Computational volumetric reconstruction of integral imaging with improved depth resolution considering continuously non-uniform shifting pixels. Opt. Laser Eng. 2018, 111, 114–121. [Google Scholar] [CrossRef]
- Jang, J.-Y.; Cho, M. Three-dimensional double random phase encryption for simultaneous two-primary data. Electronics 2024, 13, 823. [Google Scholar] [CrossRef]
- Andrews, H.; Patterson, C. Singular value decomposition (SVD) image coding. IEEE Trans. Commun. 2003, 24, 425–432. [Google Scholar] [CrossRef]
- Rufai, A.M.; Anbarjafari, G.; Demirel, H. Lossy image compression using singular value decomposition and wavelet difference reduction. Digit. Signal Process. 2014, 24, 117–123. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, J.; Bo, L.; Li, H.; Zhang, H.; Zhong, Z.; Yuan, D. Singular vector sparse reconstruction for image compression. Comput. Electr. Eng. 2021, 91, 107069. [Google Scholar] [CrossRef]
- Strang, G. Introduction to Linear Algebra; Wellesley-Cambridge Press: Cambridge, MA, USA, 2016; pp. 364–392. [Google Scholar]
- Javidi, B. Nonlinear joint power spectrum based optical correlation. Appl. Opt. 1989, 28, 2358–2367. [Google Scholar] [CrossRef] [PubMed]






















| Diagonal Entries | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|
| Simulation | 13.8468 | 14.0089 | 14.1714 | 14.3333 | 14.4963 |
| Optical experiment | 8.7043 | 8.9966 | 9.2637 | 9.5104 | 9.7394 |
| Diagonal entries | 100 | 200 | 300 | 400 | 500 |
| Simulation | 14.6598 | 16.3579 | 18.2157 | 20.3167 | 22.7630 |
| Optical experiment | 9.9537 | 11.6613 | 13.0951 | 14.6158 | 16.3871 |
| Diagonal Entries | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|
| Simulation | 0.0148 | 0.0156 | 0.0168 | 0.0182 | 0.0198 |
| Optical experiment | 0.0639 | 0.0613 | 0.0596 | 0.0585 | 0.0578 |
| Diagonal entries | 100 | 200 | 300 | 400 | 500 |
| Simulation | 0.0215 | 0.0376 | 0.0490 | 0.0585 | 0.0705 |
| Optical experiment | 0.0573 | 0.0631 | 0.0786 | 0.1019 | 0.1356 |
| Compression Ratio | 4.9975 | 2.4988 | 1.6658 | 1.2494 | 0.9995 |
|---|---|---|---|---|---|
| Simulation (2D) | 14.6598 | 16.3579 | 18.2157 | 20.3167 | 22.7630 |
| Simulation (500 mm) | 17.6660 | 18.8990 | 20.3792 | 22.1842 | 24.4060 |
| Simulation (1250 mm) | 16.4376 | 18.0563 | 19.8175 | 21.8214 | 24.1811 |
| Optical experiment (2D) | 9.9537 | 11.6613 | 13.0951 | 14.6158 | 16.3871 |
| Optical experiment (290 mm) | 11.3219 | 13.9279 | 16.6633 | 19.6083 | 22.9250 |
| Optical experiment (350 mm) | 11.2243 | 13.8011 | 16.5139 | 19.4433 | 22.7514 |
| Optical experiment (400 mm) | 11.2108 | 13.7836 | 16.4958 | 19.4259 | 22.7368 |
| Compression Ratio | 4.9975 | 2.4988 | 1.6658 | 1.2494 | 0.9995 |
|---|---|---|---|---|---|
| Simulation (2D) | 0.0215 | 0.0376 | 0.0490 | 0.0585 | 0.0705 |
| Simulation (500 mm) | 0.0890 | 0.1127 | 0.1267 | 0.1372 | 0.1495 |
| Simulation (1250 mm) | 0.0775 | 0.1010 | 0.1152 | 0.1258 | 0.1382 |
| Optical experiment (2D) | 0.0573 | 0.0631 | 0.0786 | 0.1019 | 0.1356 |
| Optical experiment (290 mm) | 0.5240 | 0.6058 | 0.6728 | 0.7350 | 0.7947 |
| Optical experiment (350 mm) | 0.5176 | 0.6053 | 0.6760 | 0.7405 | 0.8020 |
| Optical experiment (400 mm) | 0.5216 | 0.6094 | 0.6809 | 0.7455 | 0.8062 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, K.; Lee, M.-C.; Cho, M. Compression of 3D Optical Encryption Using Singular Value Decomposition. Sensors 2025, 25, 4742. https://doi.org/10.3390/s25154742
Park K, Lee M-C, Cho M. Compression of 3D Optical Encryption Using Singular Value Decomposition. Sensors. 2025; 25(15):4742. https://doi.org/10.3390/s25154742
Chicago/Turabian StylePark, Kyungtae, Min-Chul Lee, and Myungjin Cho. 2025. "Compression of 3D Optical Encryption Using Singular Value Decomposition" Sensors 25, no. 15: 4742. https://doi.org/10.3390/s25154742
APA StylePark, K., Lee, M.-C., & Cho, M. (2025). Compression of 3D Optical Encryption Using Singular Value Decomposition. Sensors, 25(15), 4742. https://doi.org/10.3390/s25154742








