Figure 1.
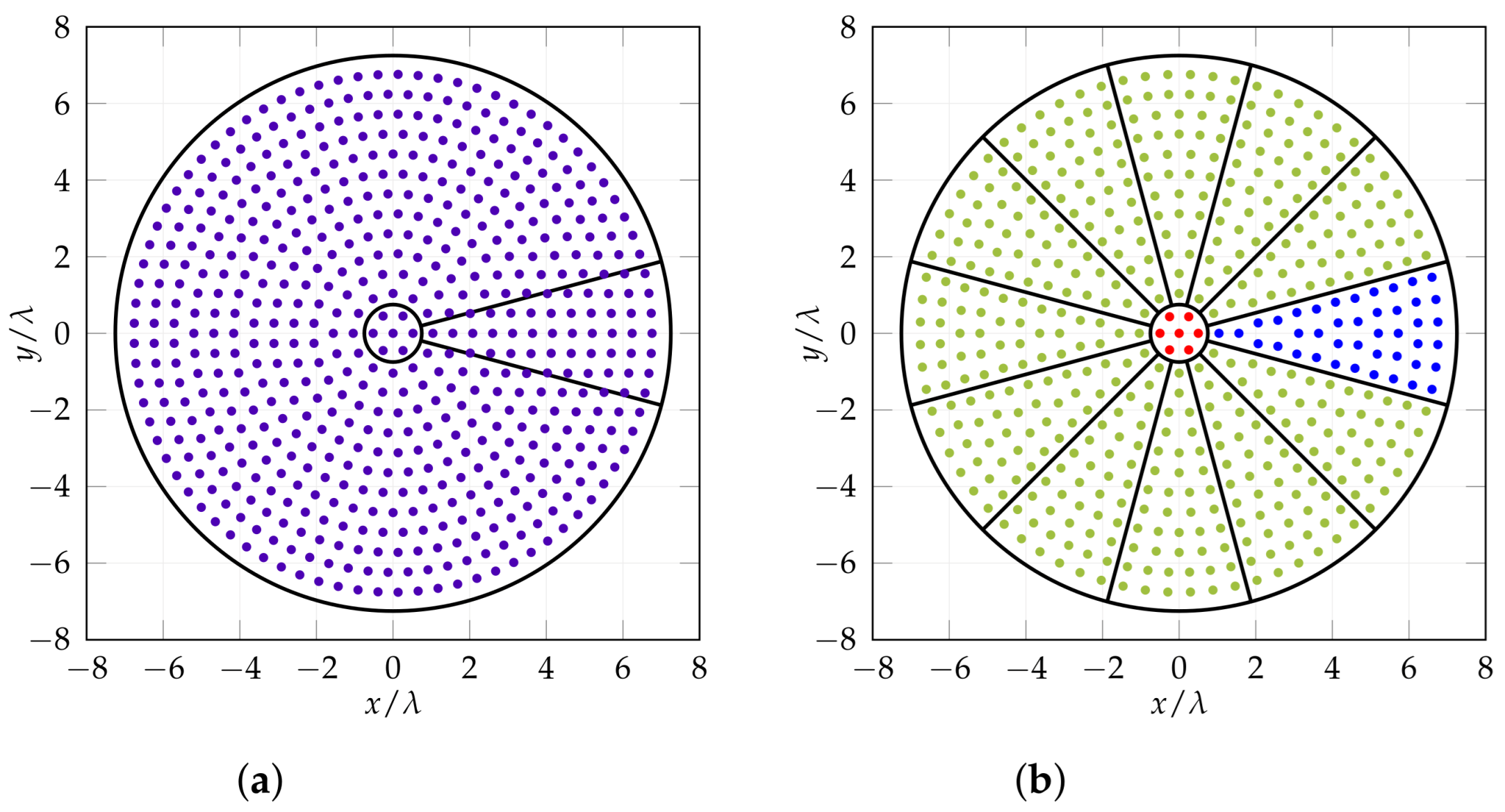
The full regular circular array composed of 13 rings and elements (a); and the sectored array of elements. (a) Circular regular array; (b) circular sectored array; red shows central sector , blue shows sector, green ones are duplicate sectors.
Figure 1.
The full regular circular array composed of 13 rings and elements (a); and the sectored array of elements. (a) Circular regular array; (b) circular sectored array; red shows central sector , blue shows sector, green ones are duplicate sectors.
Figure 2.
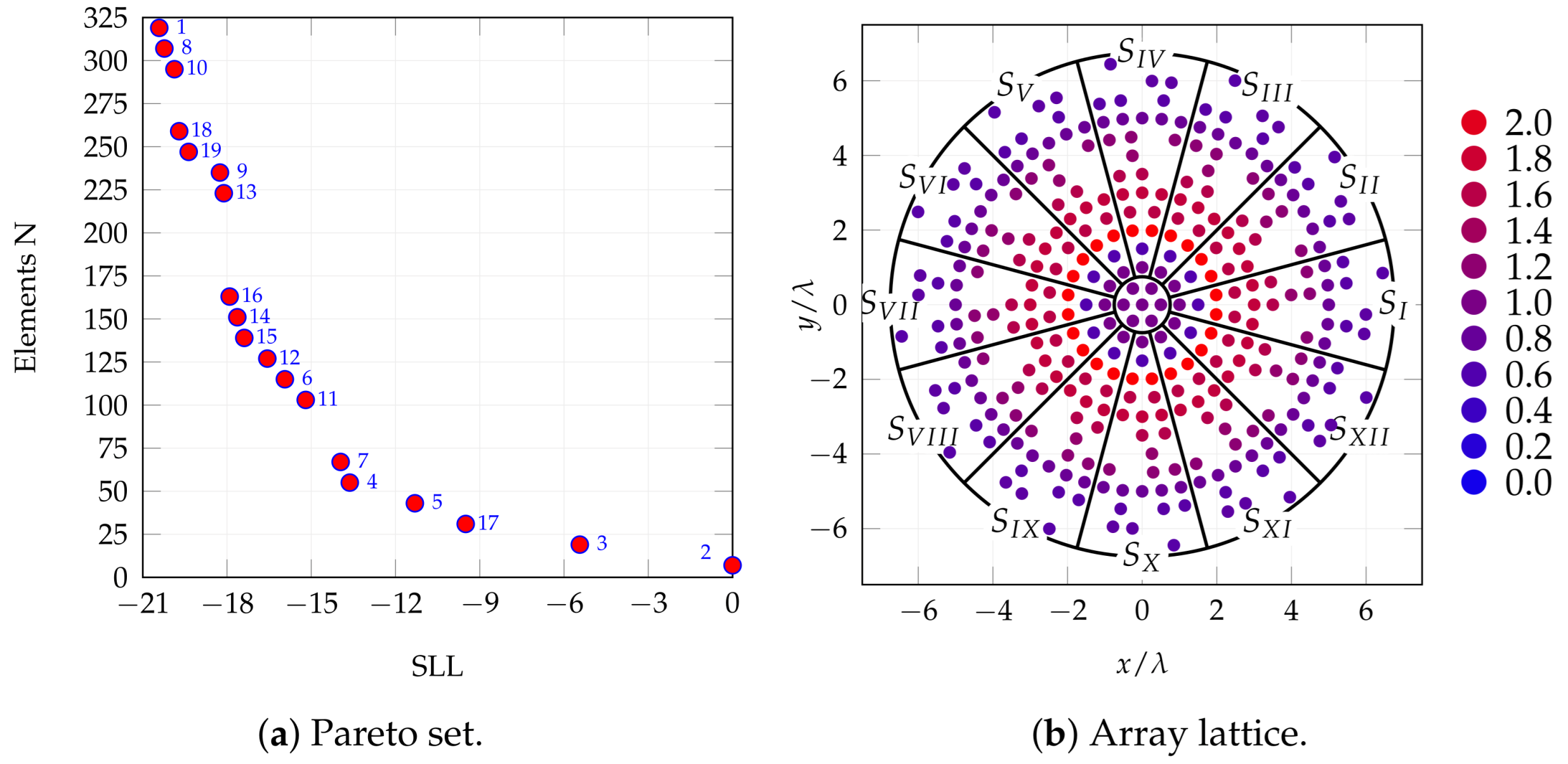
Optimization results. (a) A Pareto set derived from one of the many optimization runs with highlighted configuration 1, chosen for subsequent SO optimization; (b) geometry, with color-highlighted tapering (red: higher amplitude, blue: lower amplitude).
Figure 2.
Optimization results. (a) A Pareto set derived from one of the many optimization runs with highlighted configuration 1, chosen for subsequent SO optimization; (b) geometry, with color-highlighted tapering (red: higher amplitude, blue: lower amplitude).
Figure 3.
Attained broadside pattern. (a) Pattern drawn in polar coordinates; yellow crosshair shows the location of maximum-level side lobe; a small inset with a zoomed area shows a close-up of the broadside region of the radiation pattern. (b) plane, (c) plane. Due to the symmetry of the array lattice, the cuts , , … are identical to the cut , while the cuts , , … are identical to the cut .
Figure 3.
Attained broadside pattern. (a) Pattern drawn in polar coordinates; yellow crosshair shows the location of maximum-level side lobe; a small inset with a zoomed area shows a close-up of the broadside region of the radiation pattern. (b) plane, (c) plane. Due to the symmetry of the array lattice, the cuts , , … are identical to the cut , while the cuts , , … are identical to the cut .
Figure 4.
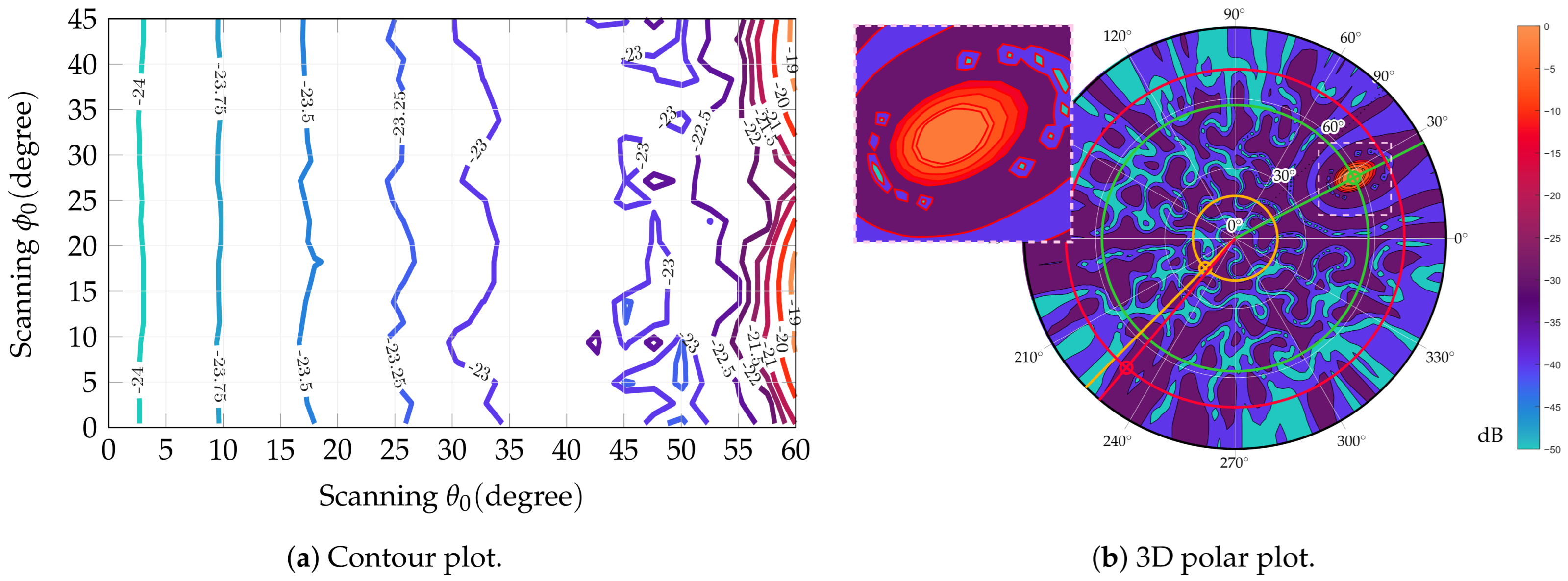
Capability of scanning of the proposed architecture. (a) Contour plot showing SLL in scanning for the optimized antenna; SLL computation is limited to a scan angle from broadside since eventual higher lobes out of this scan would fall outside Earth’s surface. (b) 3D polar plot for a scan angle , ; yellow crosshair indicates highest SLL position within antenna footprint, red crosshair highest SLL outside footprint.
Figure 4.
Capability of scanning of the proposed architecture. (a) Contour plot showing SLL in scanning for the optimized antenna; SLL computation is limited to a scan angle from broadside since eventual higher lobes out of this scan would fall outside Earth’s surface. (b) 3D polar plot for a scan angle , ; yellow crosshair indicates highest SLL position within antenna footprint, red crosshair highest SLL outside footprint.
Figure 5.
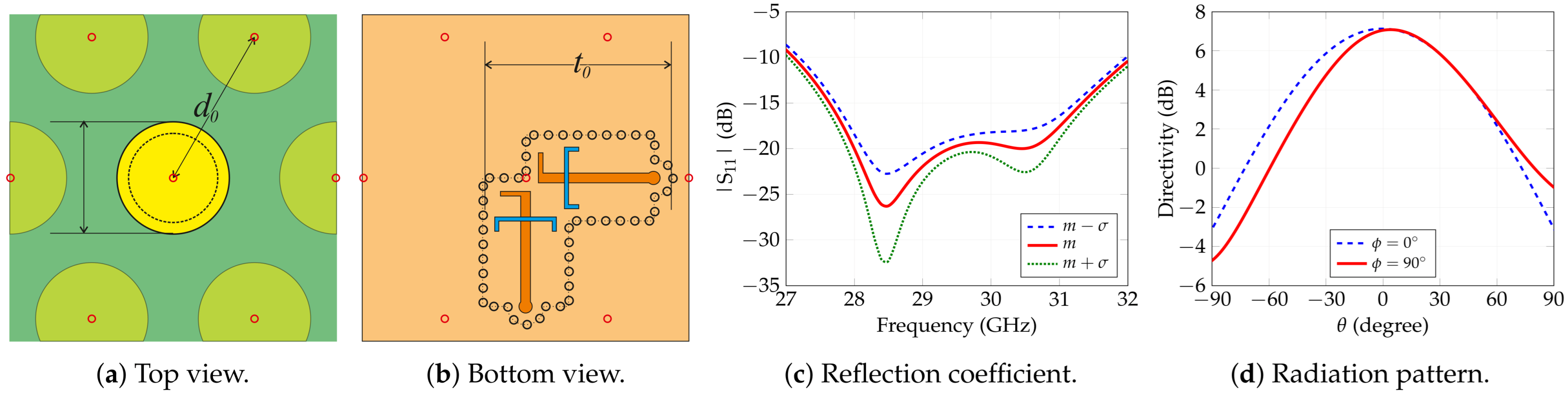
Radiating element design and performance. (a) Top view of the element showing the stacked structure. (b) Feeding network of the element. (c) Mean reflection-coefficient and standard deviation envelopes. (d) Gain pattern at center frequency (29.25 GHz).
Figure 5.
Radiating element design and performance. (a) Top view of the element showing the stacked structure. (b) Feeding network of the element. (c) Mean reflection-coefficient and standard deviation envelopes. (d) Gain pattern at center frequency (29.25 GHz).
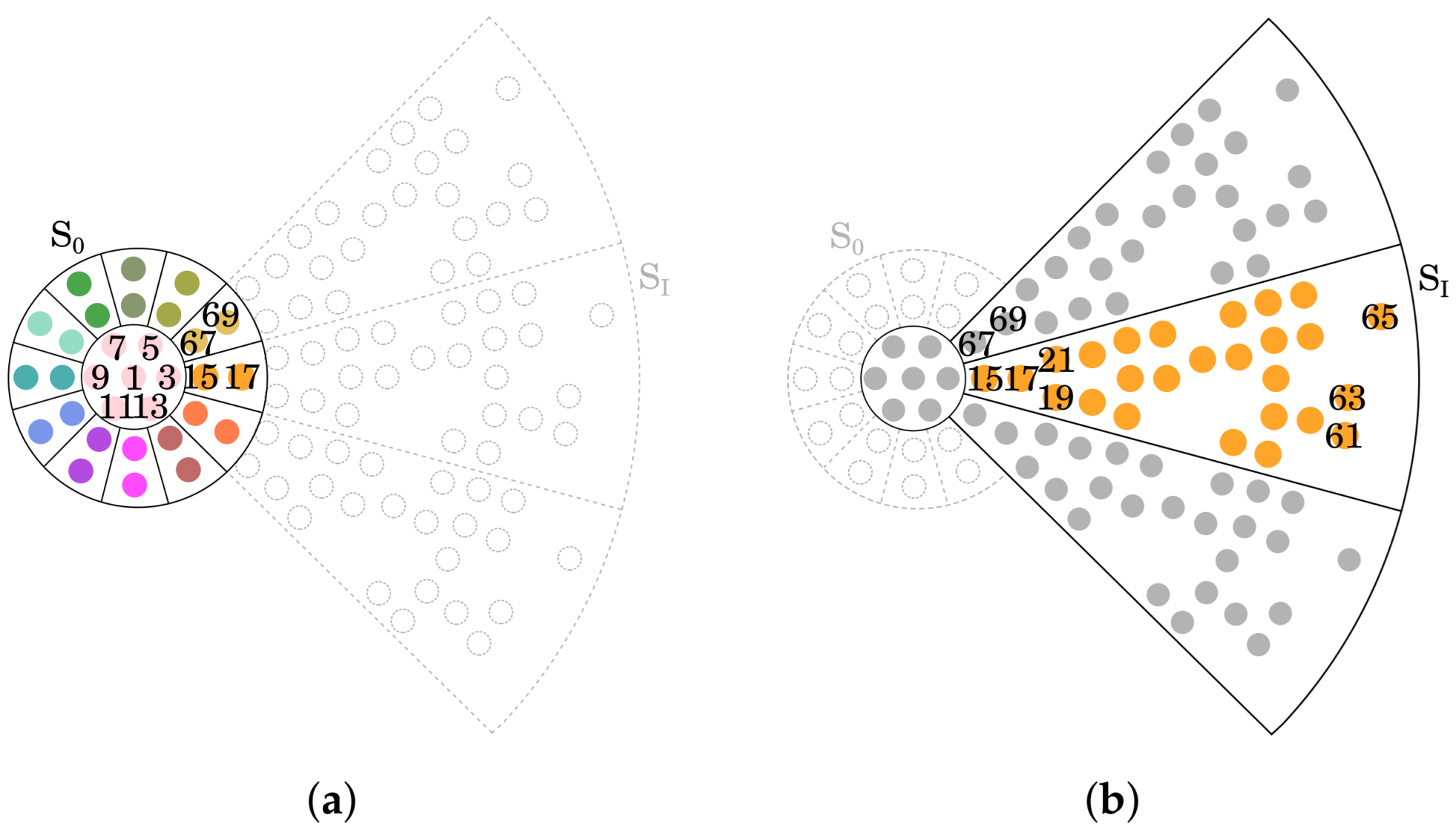
Figure 6.
Elements considered for the mutual coupling analysis; not all numbers of feeding ports are reported in the figure. (a) Tile and immediate neighbors numeration. (b) , but for symmetry, results apply to any outer tile, numeration.
Figure 6.
Elements considered for the mutual coupling analysis; not all numbers of feeding ports are reported in the figure. (a) Tile and immediate neighbors numeration. (b) , but for symmetry, results apply to any outer tile, numeration.
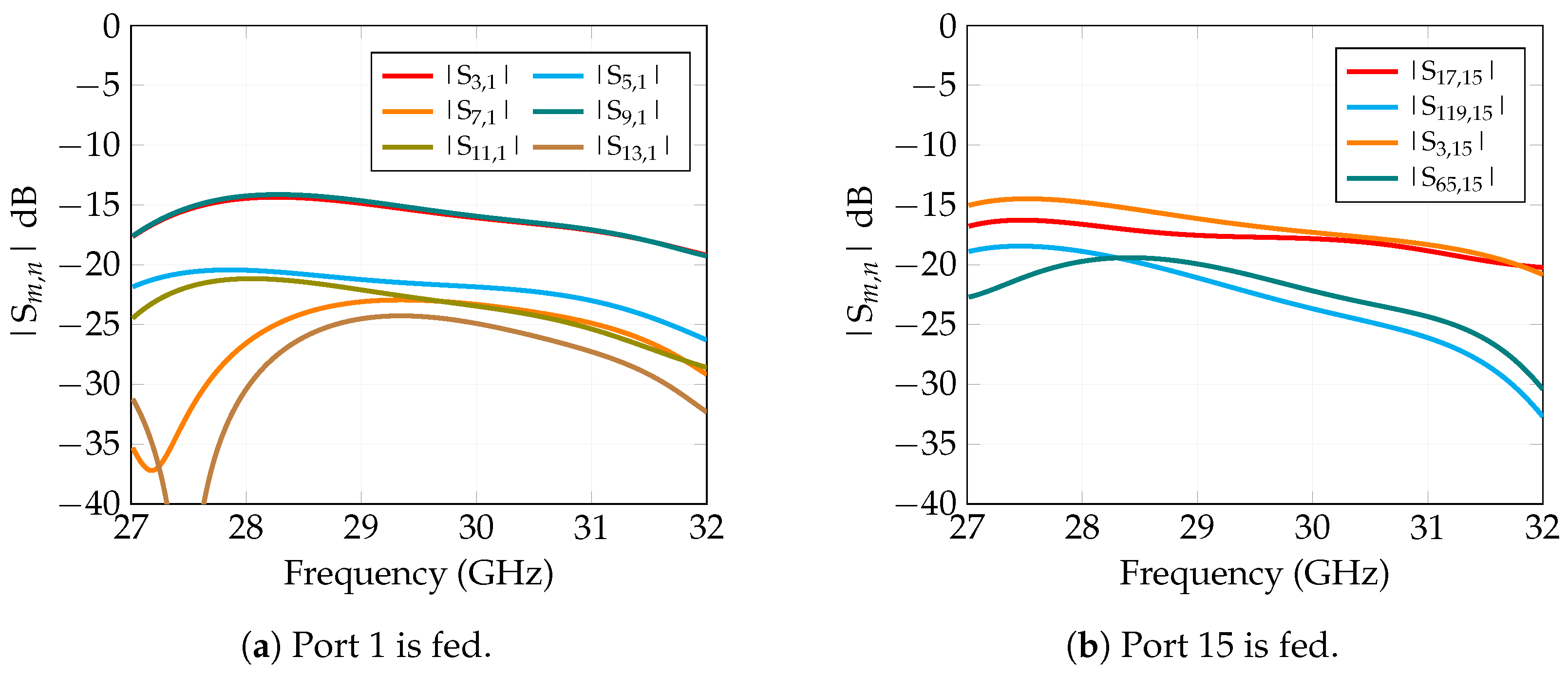
Figure 7.
Behavior of the mutual coupling for both: the central sector when port 1 is fed (a) and the peripherical sector when port 15 is fed (b).
Figure 7.
Behavior of the mutual coupling for both: the central sector when port 1 is fed (a) and the peripherical sector when port 15 is fed (b).
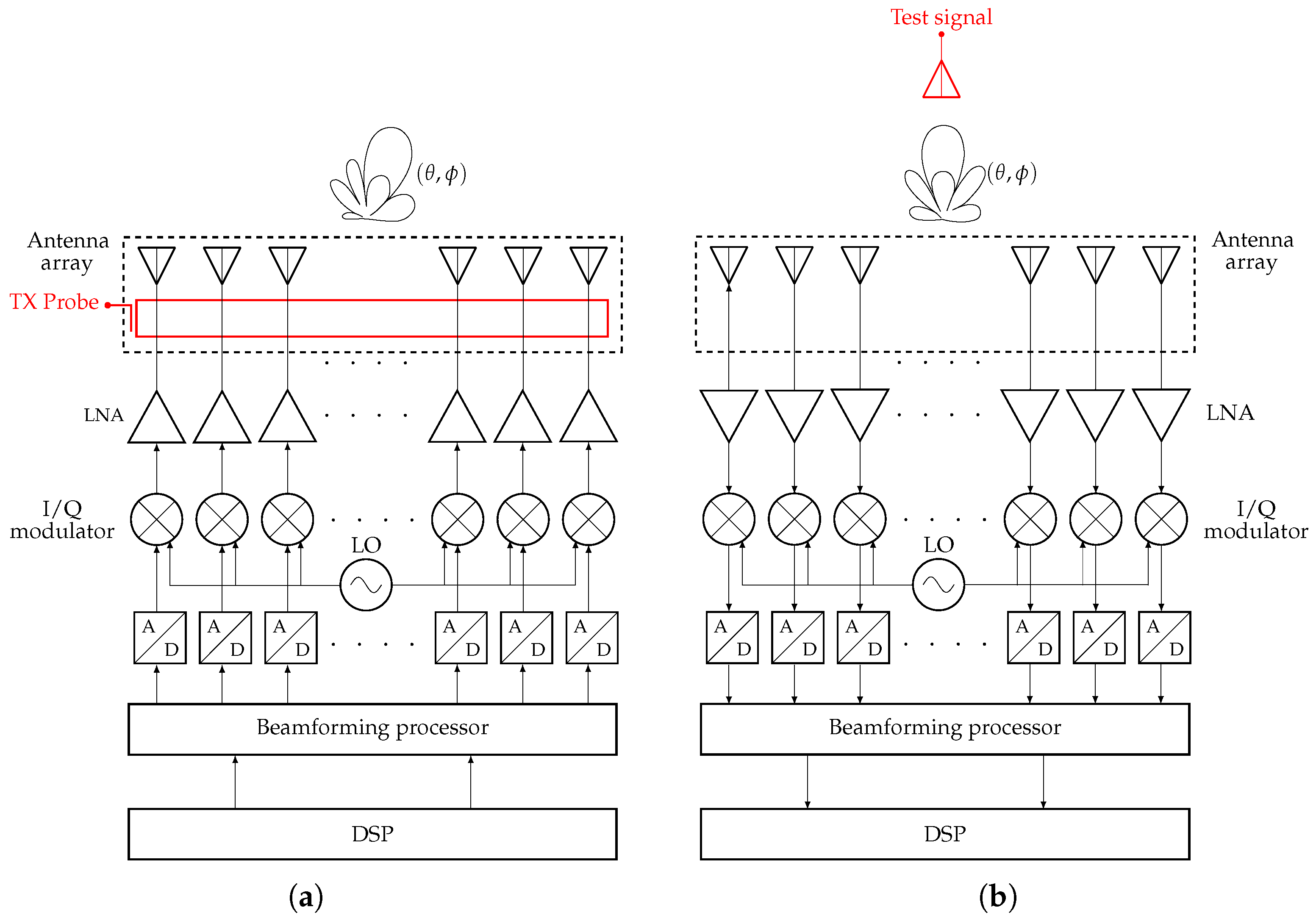
Figure 8.
Block diagram of the digital beamforming system implemented in the CAD for the system-level analysis; suitable probe and test signal are highlighted in the picture. (a) Transmitter: a probe at the antenna array element section is highlighted. (b) Receiver: a test signal illuminating the antenna array is highlighted.
Figure 8.
Block diagram of the digital beamforming system implemented in the CAD for the system-level analysis; suitable probe and test signal are highlighted in the picture. (a) Transmitter: a probe at the antenna array element section is highlighted. (b) Receiver: a test signal illuminating the antenna array is highlighted.
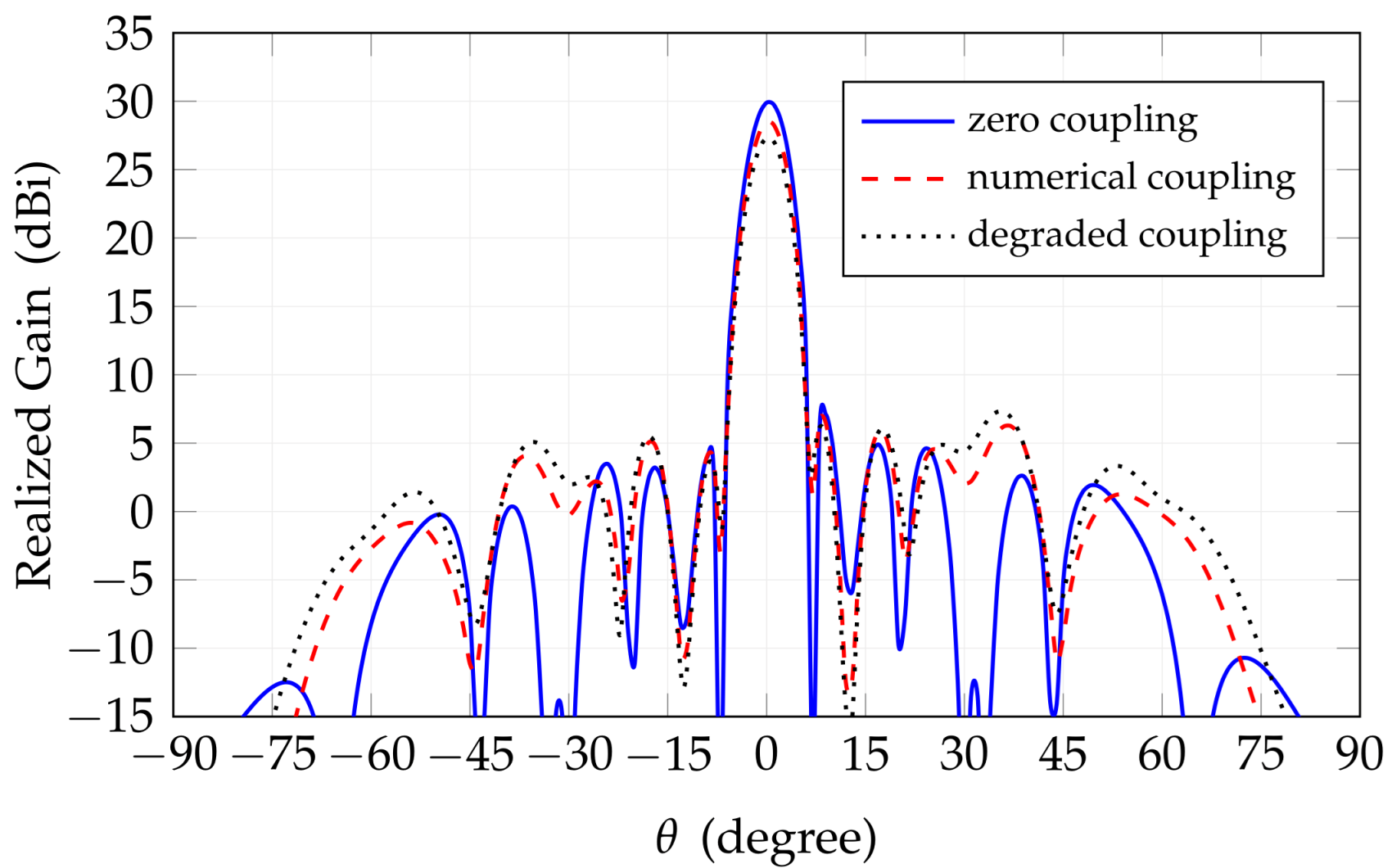
Figure 9.
Effect of coupling between array elements in the array radiation.
Figure 9.
Effect of coupling between array elements in the array radiation.
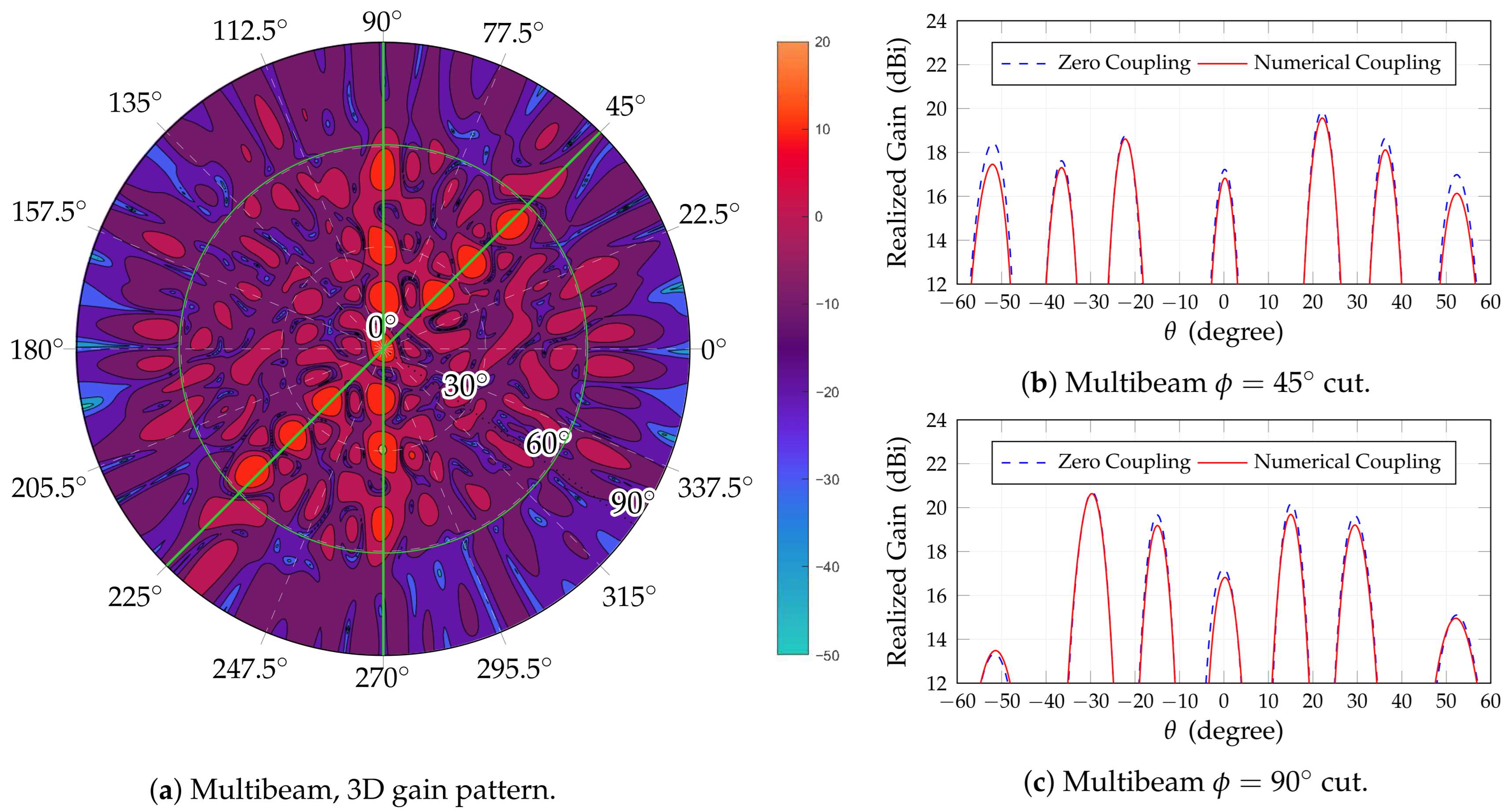
Figure 10.
Multibeam performances for 13 beams. (a) Contour polar plot; (b) cut aligned along ; (c) cut aligned along . Only the cases of no coupling and numerical coupling are considered for the cuts.
Figure 10.
Multibeam performances for 13 beams. (a) Contour polar plot; (b) cut aligned along ; (c) cut aligned along . Only the cases of no coupling and numerical coupling are considered for the cuts.
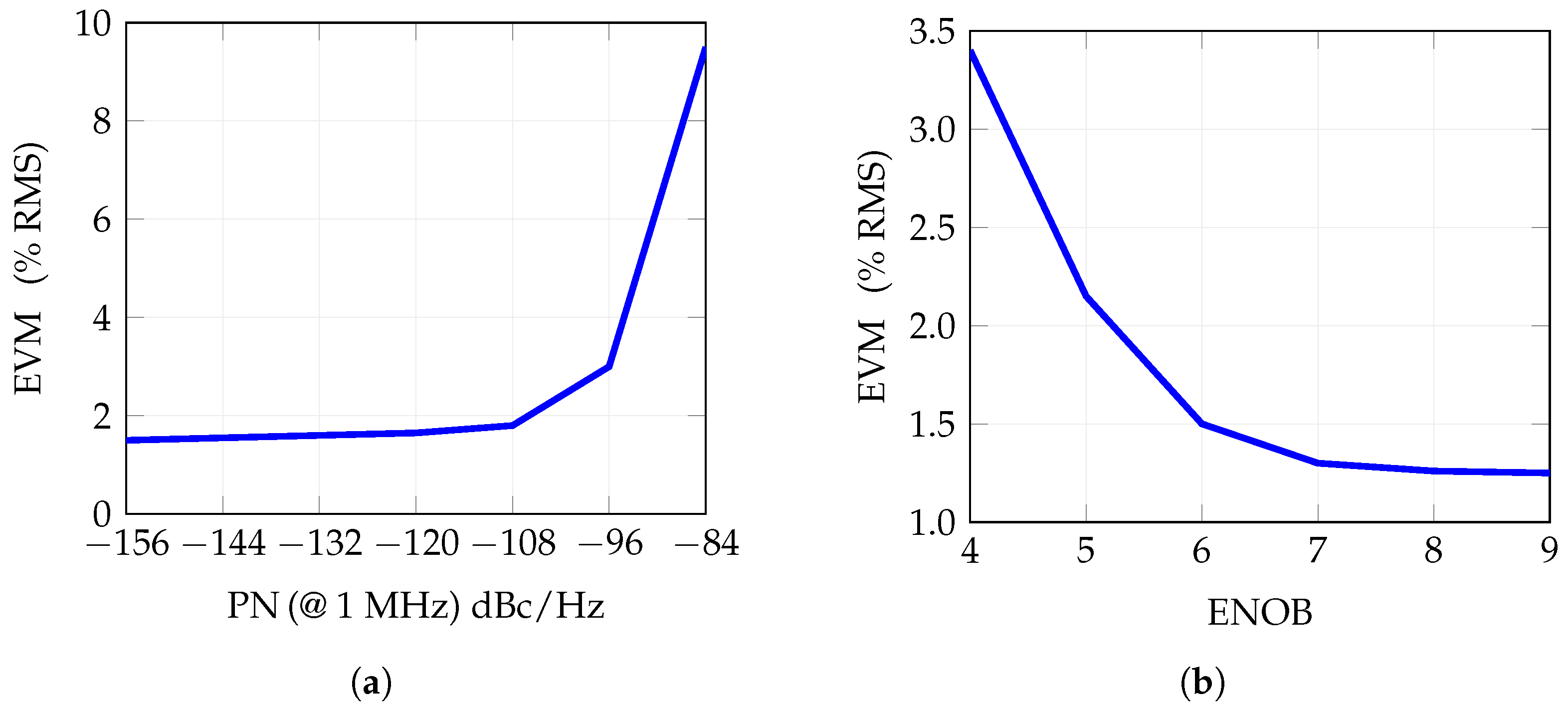
Figure 11.
Influence of the EVM of phase noise and ENOB. (a) Influence of the phase noise—nominal condition considers phase noise = −120 dBc/Hz at 1 MHz offset from the carrier. (b) Influence of ENOB—nominal value is ENOB = 6.
Figure 11.
Influence of the EVM of phase noise and ENOB. (a) Influence of the phase noise—nominal condition considers phase noise = −120 dBc/Hz at 1 MHz offset from the carrier. (b) Influence of ENOB—nominal value is ENOB = 6.
Figure 12.
EVM, expressed as a percentage, obtained by varying both the imbalances of the upconverter.
Figure 12.
EVM, expressed as a percentage, obtained by varying both the imbalances of the upconverter.
Figure 13.
EVM versus output power at PA, in in nominal conditions and degraded.
Figure 13.
EVM versus output power at PA, in in nominal conditions and degraded.
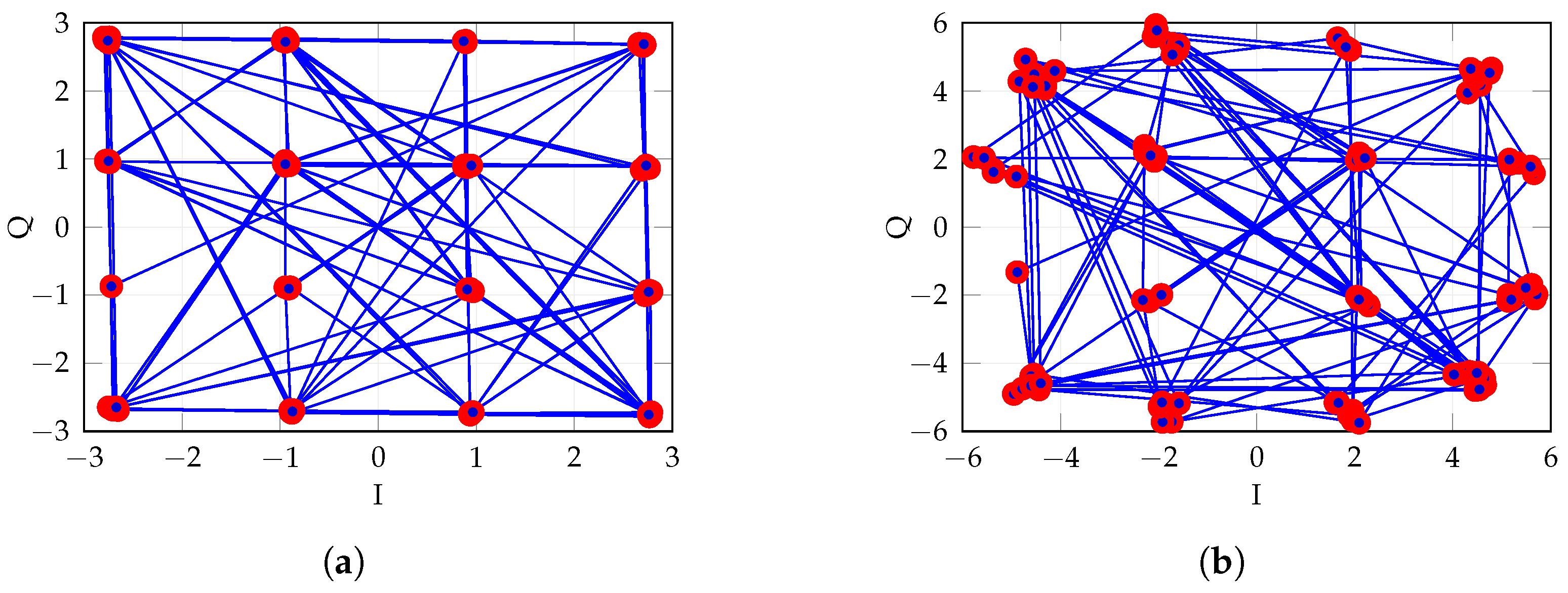
Figure 14.
Constellations comparing different transmitting power levels. (a) Transmitting power 10 dBm (Nominal), EVM = 1.35%. (b) Transmitting power 18 dBm, EVM = 4.3%.
Figure 14.
Constellations comparing different transmitting power levels. (a) Transmitting power 10 dBm (Nominal), EVM = 1.35%. (b) Transmitting power 18 dBm, EVM = 4.3%.
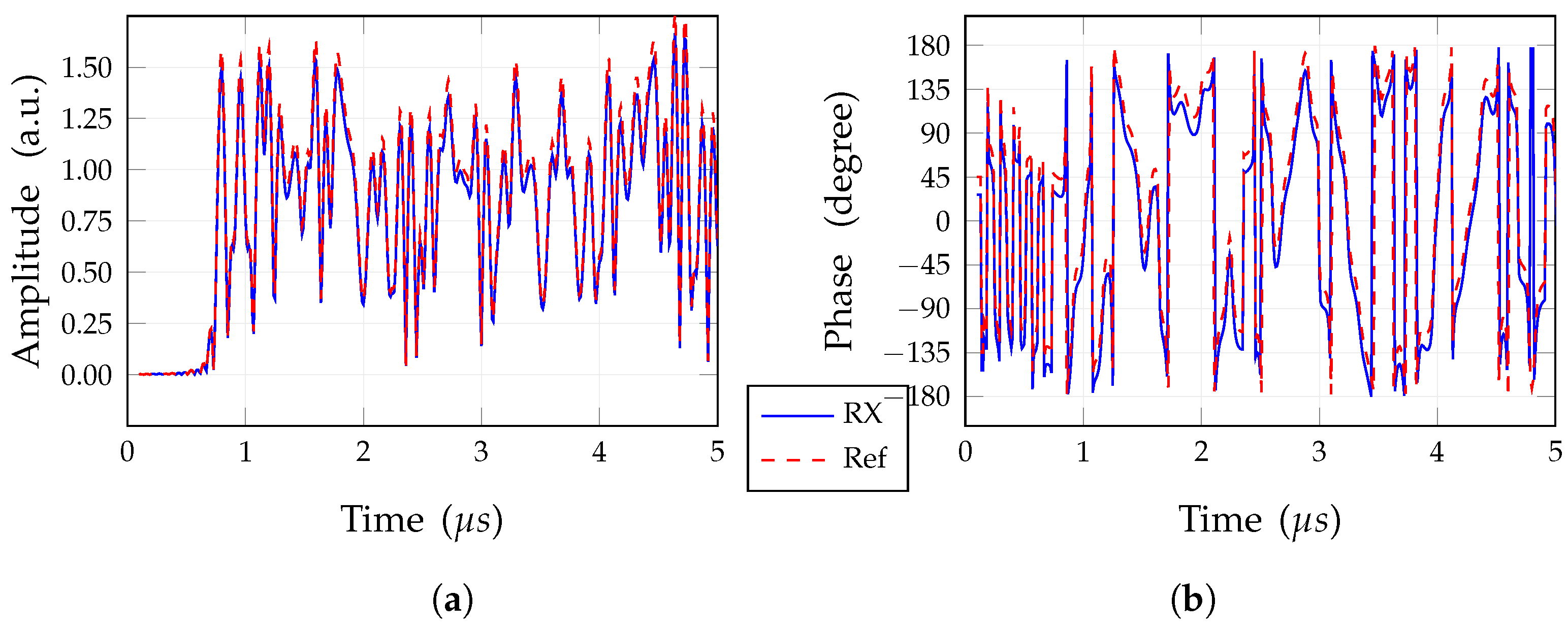
Figure 15.
Waveforms of the ideal received signal (RX), with coupling, compared to the ideal received nominal signal (nominal). (a) Magnitude; (b) phase.
Figure 15.
Waveforms of the ideal received signal (RX), with coupling, compared to the ideal received nominal signal (nominal). (a) Magnitude; (b) phase.
Figure 16.
Influence of the phase noise on the BER, nominal conditions consider phase noise = −120 dBc/Hz at 1 MHz offset from the carrier.
Figure 16.
Influence of the phase noise on the BER, nominal conditions consider phase noise = −120 dBc/Hz at 1 MHz offset from the carrier.
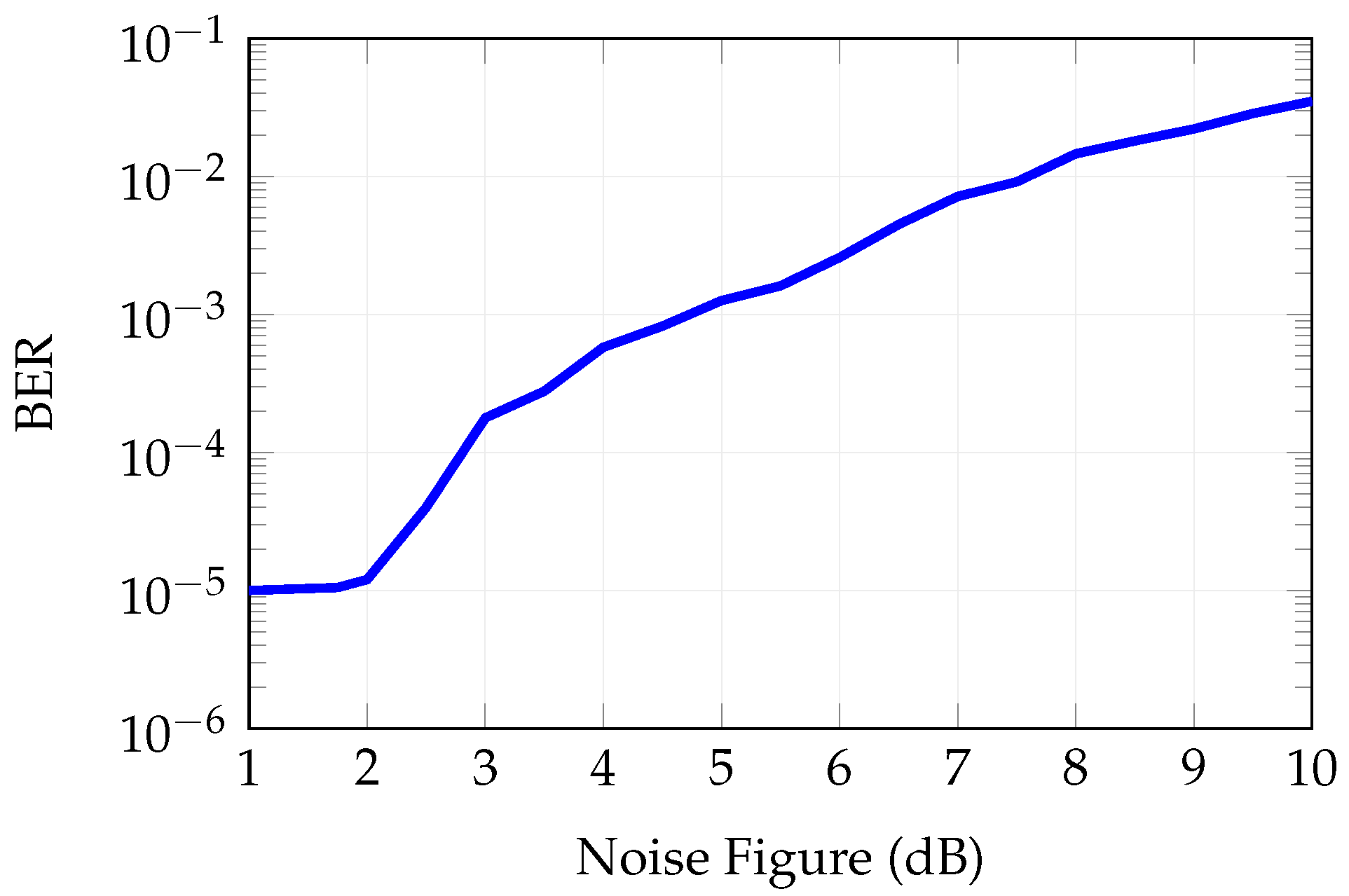
Figure 17.
Bit error rate as a function of noise figure.
Figure 17.
Bit error rate as a function of noise figure.
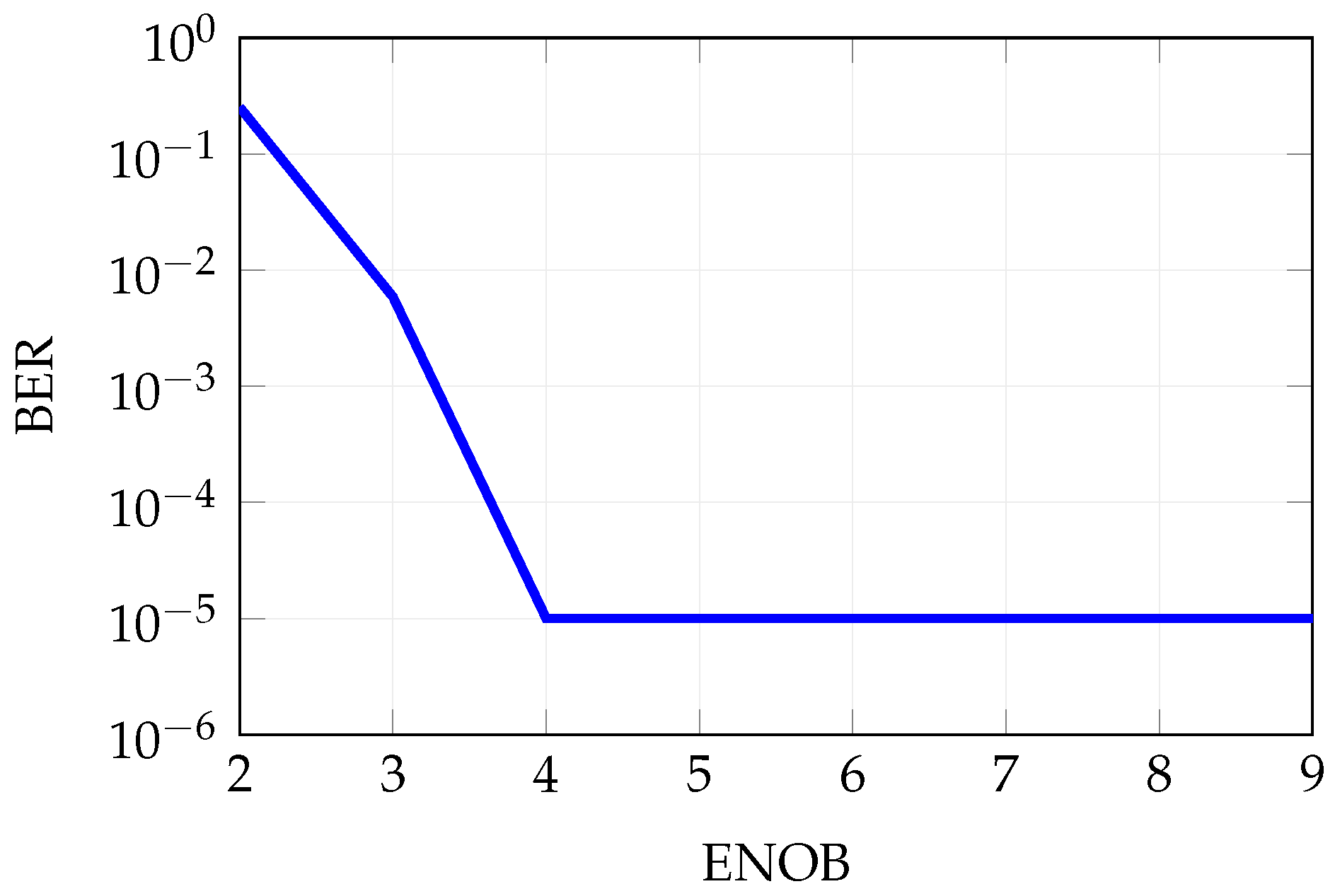
Figure 18.
Influence of the ENOB on the BER, nominal condition is ENOB = 6.
Figure 18.
Influence of the ENOB on the BER, nominal condition is ENOB = 6.
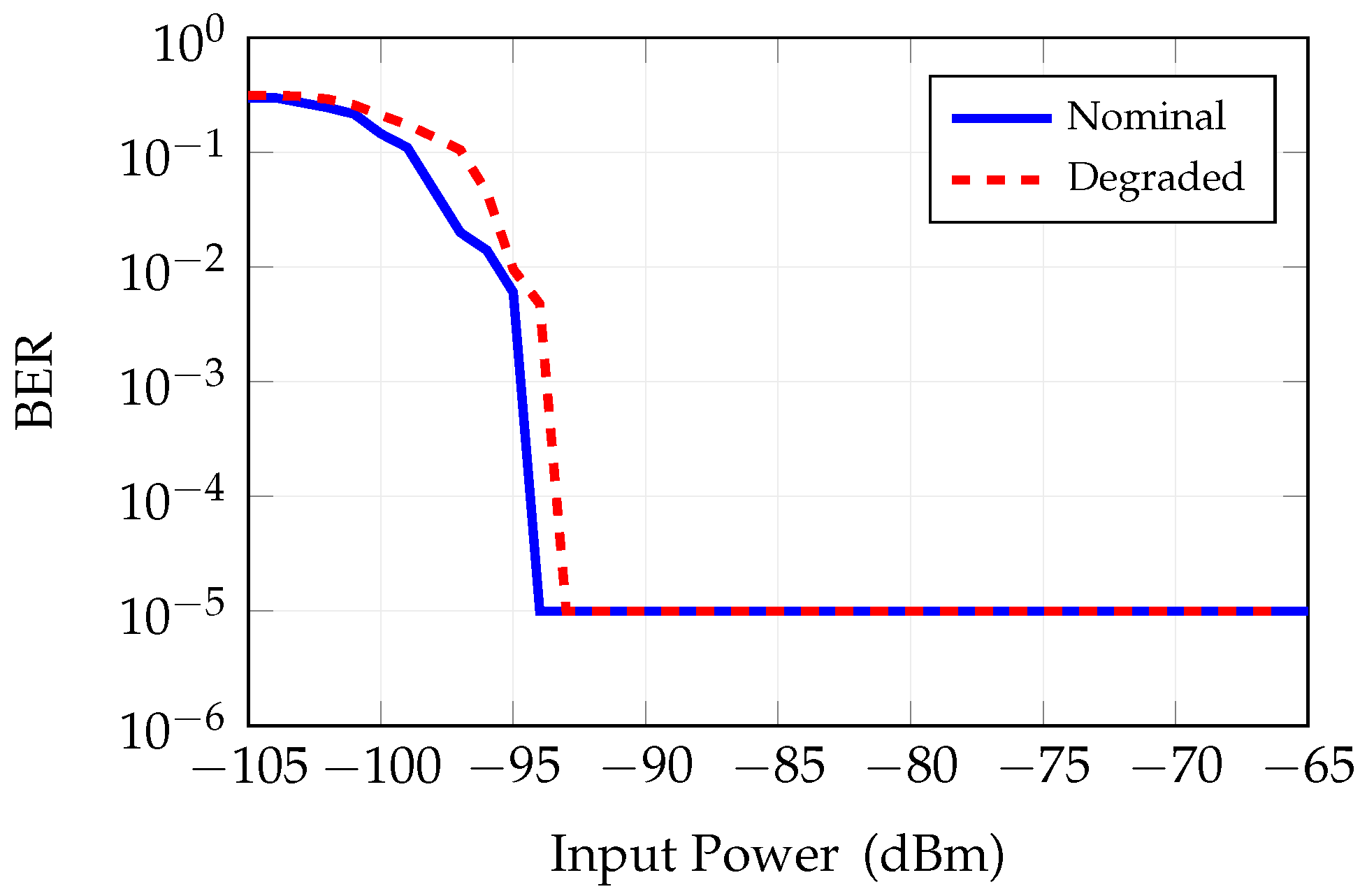
Figure 19.
BER vs. input power in the RX chain (with nominal front-end parameter settings).
Figure 19.
BER vs. input power in the RX chain (with nominal front-end parameter settings).
Table 1.
Summary of actual and scheduled satellite services for IoT.
Table 1.
Summary of actual and scheduled satellite services for IoT.
| Operator | Satellites (Deployed) | Spectrum | Services | Operational |
|---|
| Starlink | 12,000 LEO (6078) | Ku-band | Broadband | Yes |
| Kuiper | 3236 LEO (2) | Ka-band | Broadband | Scheduled |
| Viasat | 4 GEO (4) | Ka-band | Broadband | Yes |
| Hughenesat | 3 GEO (2) | Ka-band | Broadband | Yes |
| Iridium | 66 LEO (66) | L-band | messaging | Yes |
| One Web | 648 LEO (648) | Ku-band | Broadband | Scheduled |
| Telesat | 198 LEO (2) | Ka-band | Broadband | Scheduled |
Table 2.
Summary of requirements and constraints of the RX/TX antenna.
Table 2.
Summary of requirements and constraints of the RX/TX antenna.
| Requirements | Value |
|---|
| Operation frequency range | –31 GHz |
| Coverage | |
| SLL | < dB |
| Grating lobes | Out of Earth |
| Directivity | >30 |
Table 3.
Antenna optimization results. All cases are considered for 319 “on” elements. Bold line highlights the case selected for further analysis. SLL value is the worst SLL case computed while the main beam scans the whole range.
Table 3.
Antenna optimization results. All cases are considered for 319 “on” elements. Bold line highlights the case selected for further analysis. SLL value is the worst SLL case computed while the main beam scans the whole range.
| Concentric Rings | Tapered Elements | SLL (dB) | Dynamic |
|---|
| 5 | 168 (53%) | −20.85 | 2.55 |
| 8 | 240 (75%) | −20.94 | 2.12 |
| 10 | 288 (90%) | −21.61 | 4.21 |
| 12 | 312 (98%) | −21.79 | 3.06 |
Table 4.
Amplitude tapering for the selected case of
Table 3.
Table 4.
Amplitude tapering for the selected case of
Table 3.
| Ring | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Amp. | 1 | 1 | 0.93 | 0.64 | 1.96 | 1.45 | 1.52 | 1.41 | 1.15 | 1.10 | 0.83 | 0.70 | 0.73 | 0.69 |
| | Fixed | Tapered |
Table 5.
Nominal parameters adopted in simulations. Abbreviations: Param. = Parameter, Val. = Value, PN = Phase Noise, ENOB = Effective Number of Bits, I/Q AM and PH = I/Q Amplitude and Phase Imbalance. Units: Gains, noise figures, and imbalances are in dB; output powers (OP1dB, OIP3) are in dBm; PN values are in dBc/Hz. Frequency is in Hz (as specified).
Table 5.
Nominal parameters adopted in simulations. Abbreviations: Param. = Parameter, Val. = Value, PN = Phase Noise, ENOB = Effective Number of Bits, I/Q AM and PH = I/Q Amplitude and Phase Imbalance. Units: Gains, noise figures, and imbalances are in dB; output powers (OP1dB, OIP3) are in dBm; PN values are in dBc/Hz. Frequency is in Hz (as specified).
| PA | LO | ADC/DAC | IQ Mod. | LNA |
|---|
| Param. | Val. | Param. | Val. | Param. | Val. | Param. | Val. | Param. | Val. |
|---|
| Gain | 12 | PN @ 10 kHz | | ENOB | 6 | I/Q PH | | Gain | 29 |
| OP1dB | 27 | PN @ 100 kHz | | | | I/Q AM | 0.07 | NF | 1.4 |
| OIP3 | 40 | PN @ 1 MHz | | | | | | OP1dB | 6 |
| | | | | | | | | OIP3 | 11 |
Table 6.
Antenna gain (G) and the side-lobe level (SLL) comparison.
Table 6.
Antenna gain (G) and the side-lobe level (SLL) comparison.
| Cases | | | |
|---|
| | G (dB) | SLL (dB) | G (dB) | SLL (dB) | G (dB) | SLL (dB) |
|---|
| zero coupling | 29.98 | 22.48 | 29.68 | 24.68 | 27.69 | 21.57 |
| numerical coupling | 28.55 | 22.25 | 29.28 | 21.42 | 27.15 | 19.45 |
| degraded coupling | 27.32 | 21.11 | 28.83 | 18.87 | 26.45 | 19.52 |
Table 7.
Directions used for multibeam analysis.
Table 7.
Directions used for multibeam analysis.
| | | | 0 | | | |
| | | | N.A. | | | |
Table 8.
Characteristics of the transmitted signal, versus nominal and ideal transmitting chain.
Table 8.
Characteristics of the transmitted signal, versus nominal and ideal transmitting chain.
| Parameter | Nominal State | Ideal State |
|---|
| EVM (% RMS) | 1.54 | 1.54 |
| EVM (peak) | 3.36 | 2.54 |
Table 9.
Antenna gain (G) and side-lobe level (SLL) for the full TX chain, considering all components with nominal parameters, compared with the previous results given in
Table 6 (pertinent row is duplicated for easier comparison).
Table 9.
Antenna gain (G) and side-lobe level (SLL) for the full TX chain, considering all components with nominal parameters, compared with the previous results given in
Table 6 (pertinent row is duplicated for easier comparison).
| Cases | | | |
|---|
| | G (dB) | SLL (dB) | G (dB) | SLL (dB) | G (dB) | SLL (dB) |
|---|
| Nominal conditions | 28.86 | 21.11 | 29.17 | 18.17 | 26.63 | 15.63 |
| Numerical coupling | 28.55 | 22.25 | 29.28 | 21.42 | 27.15 | 19.45 |