A New Device for Measuring Trunk Diameter Variations Using Magnetic Amorphous Wires
Abstract
1. Introduction
- Contact dendrometers–variations in the trunk diameter or circumference are transformed into linear or angular displacements usually measured with an inductive, capacitive or resistive displacement transducer.
2. Operation Principle of the Dendrometer
- the slope (sensitivity) and the linearity of the characteristic (1) depend on the a/b ratio, the X1/a ratio and the mounting position of the device;
- the maximum linearity is obtained when the tree section is circular; yet, if the tree has eccentricity, the sensitivity increases with the increase in the a/b ratio, but the linearity is reduced to the same extent. It is therefore necessary to measure first the two axes, and the device should be mounted along the major axis, when the contact angle of the strip with the trunk leads to the best contact of the strip to the tree bark;
- increasing the initial distance X1 of the moving part from the trunk surface, relative to the major axis, decreases the sensitivity, but improves the linearity of the characteristic.
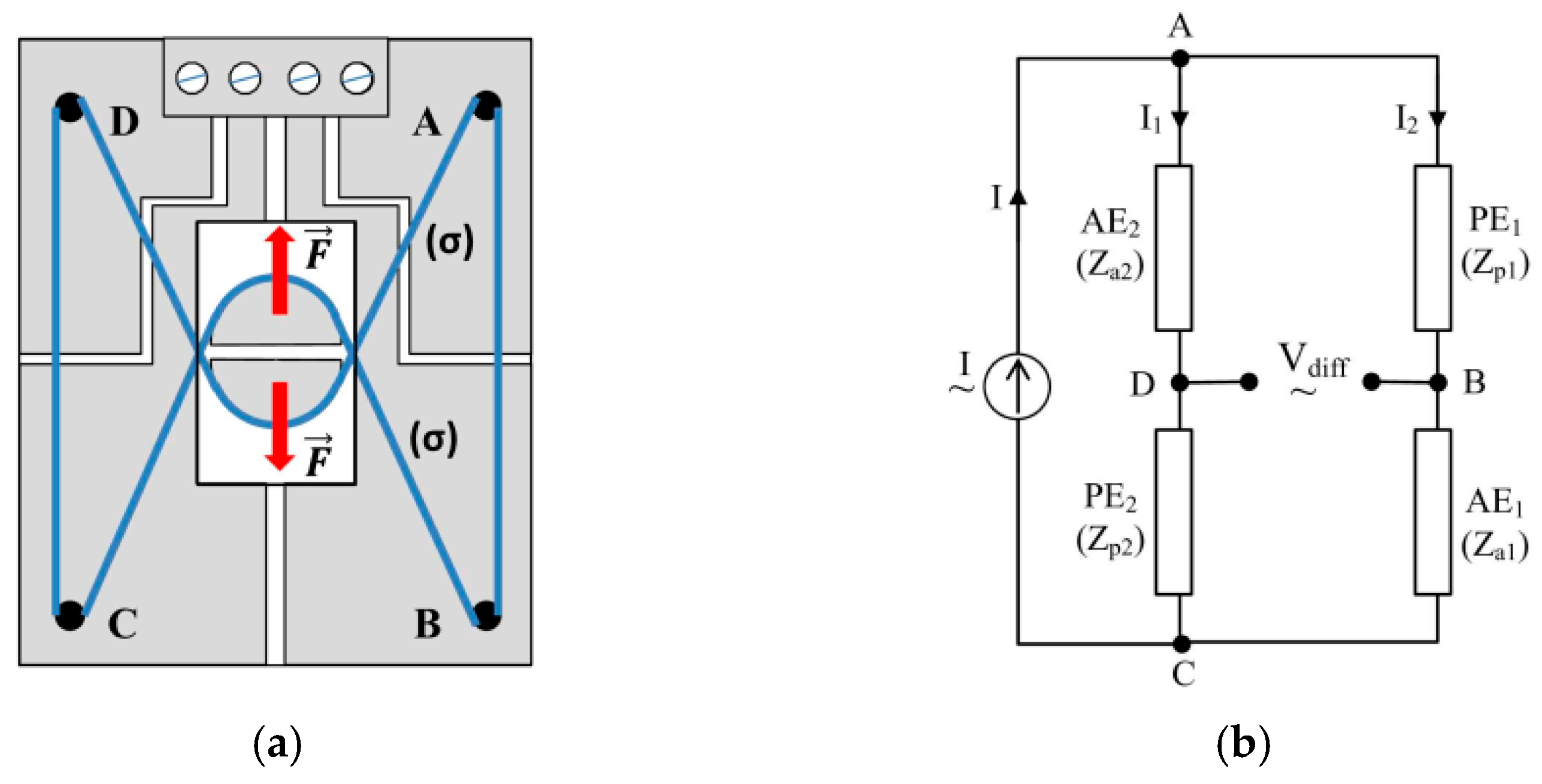
3. The Sensitive Element
3.1. About Magnetic Amorphous Wires (MAWs)
3.2. The Sensitive Element Characteristics
- The current intensity influences the shape of the characteristics to a very small extent. Therefore, the current of approximately 1 mA was considered optimal, a compromise between consumption, signal-to-noise ratio and the amount of heat released in the SE. The value of 1 mA is not critical.
- The impedance of the wire increases with its length and frequency.
- Shorter wires have more linear characteristics but are less sensitive to the GSI effect than longer wires.
4. The Dendrometer Construction
4.1. Mechanical Structure
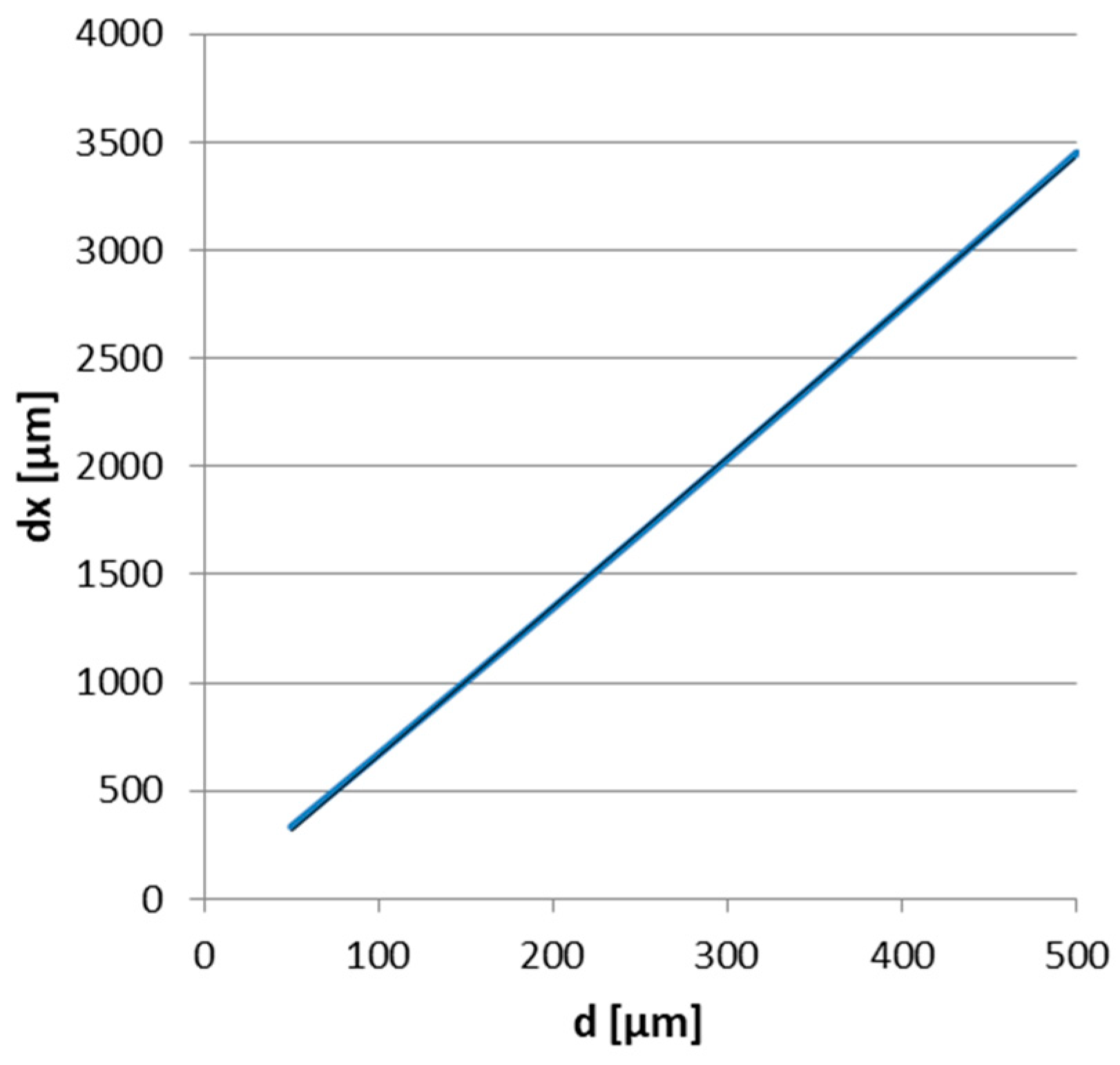
4.2. Mathematical Approach
4.3. Electronic Readout Circuit
5. Results and Discussion
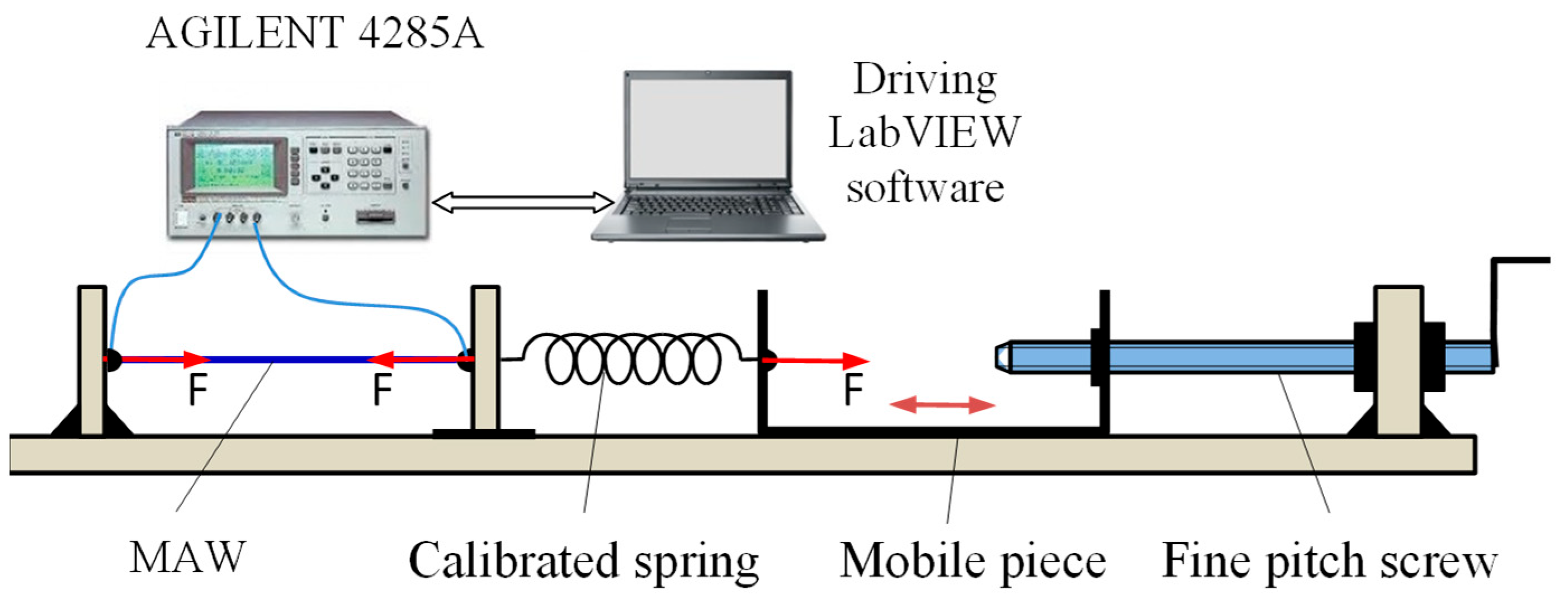
5.1. Experimental Setup
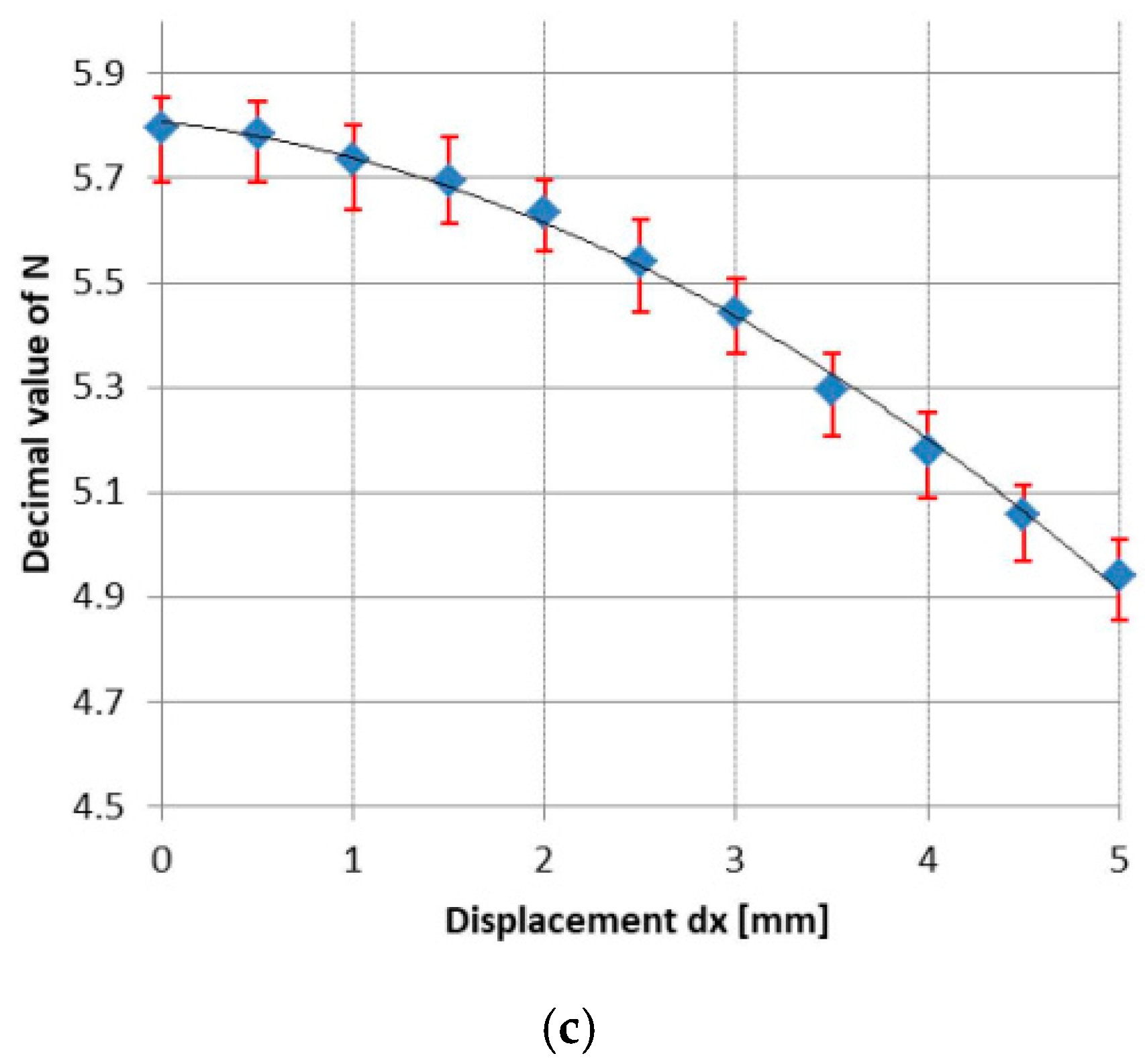
5.2. Characteristics
5.3. Error Sources and Performances
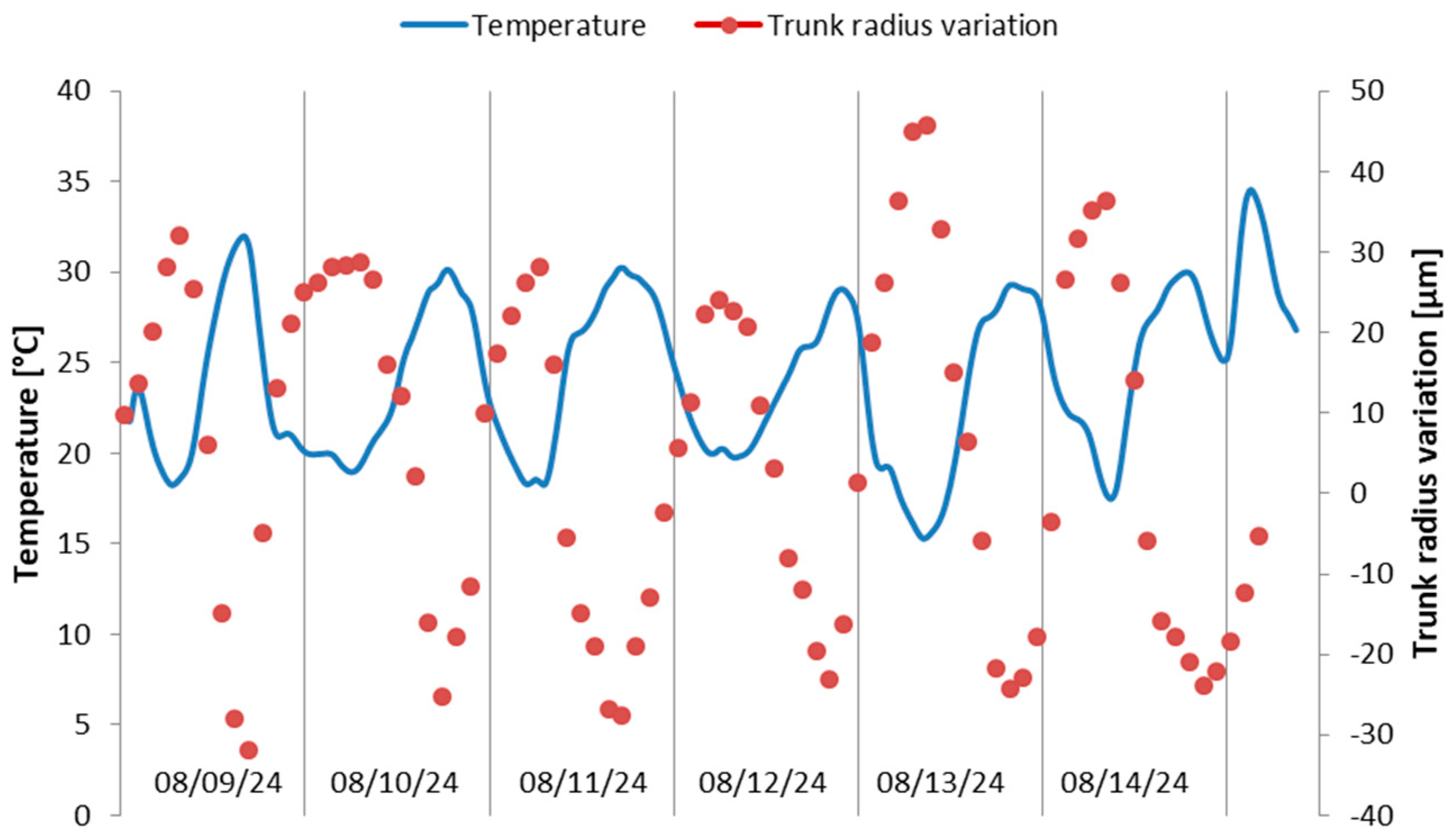
5.4. In-Field Deployment
6. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reijntjes, C.; Haverkort, B.; Waters-Bayer, A. Farming for the Future. An Introduction to Low-External-Input and Sustainable Agriculture; Macmillan Education Ltd.: London, UK, 1992. [Google Scholar]
- Raj, E.F.I.; Appadurai, M.; Athiappan, K. Precision Farming in Modern Agriculture in: Smart Agriculture Automation Using Advanced Technologies; Transactions on Computer Systems and Networks Book Series; Choudhury, A., Biswas, A., Singh, T.P., Ghosh, S.K., Eds.; Springer: Singapore, 2021; pp. 61–87. [Google Scholar]
- Suman, K.G.; Kumar, D. Role of IoT in Smart Precision Agriculture. In Handbook of Metrology and Applications; Aswal, D.K., Yadav, S., Takatsuji, T., Rachakonda, P., Kumar, H., Eds.; Springer: Singapore, 2022; pp. 1217–1238. [Google Scholar]
- McElrone, A.J.; Choat, B.; Gambetta, G.A.; Brodersen, C.R. Water Uptake and Transport in Vascular Plants. Nat. Educ. Knowl. 2013, 4, 6. [Google Scholar]
- Levesque, M.; Walthert, L.; Weber, P. Soil nutrients influence growth response of temperate tree species to drought. J. Ecol. 2016, 104, 377–387. [Google Scholar] [CrossRef]
- Brouder, S.M.; Volenec, J.J. Nutrition of Plants in a Changing Climate in Marschner’s Mineral Nutrition of Plants, 4th ed.; Academic Press: Cambridge, MA, USA, 2023; pp. 723–750. [Google Scholar]
- Linares, J.C.; Camarero, J.J.; Carreira, J.A. Influence of insect outbreaks on tree-ring growth in relict Mediterranean forests. For. Ecol. Manag. 2008, 256, 498–509. [Google Scholar]
- Kozlowski, T.T.; Pallardy, S.G. Acclimation and adaptive responses of woody plants to environmental stresses. Bot. Rev. 2002, 68, 270–334. [Google Scholar] [CrossRef]
- Fernández, J.E.; Cuevas, M.V. Irrigation scheduling from stem diameter variations: A review. Agric. For. Meteorol. 2010, 150, 135–151. [Google Scholar] [CrossRef]
- Cuevasa, M.V.; Torres-Ruiza, J.M.; Álvarezb, R.; Jiménezb, M.D.; Cuervab, J.; Fernándeza, J.E. Assessment of trunk diameter variation derived indices as water stress indicators in mature olive trees. Agric. Water Manag. 2010, 97, 1293–1302. [Google Scholar] [CrossRef]
- Electronic Caliper. Available online: https://www.infometrics.eu/en/post/developing-new-digital-caliper-forestry-stations (accessed on 15 March 2025).
- Demeyere, M.; Dereine, E.; Eugene, C.; Naydenov, V. Measurement of cylindrical objects through laser telemetry: Application to a new forest caliper. IEEE Trans. Instrum. Meas. 2002, 51, 645–649. [Google Scholar] [CrossRef]
- Bourbia, I.; Lucani, C.; Carins-Murphy, M.R.; Gracie, A.; Brodribb, T.J. In situ characterisation of whole-plant stomatal responses to VPD using leaf optical dendrometry. Plant Cell Environ. 2023, 46, 3273–3286. [Google Scholar] [CrossRef] [PubMed]
- ICT International PTY Ltd. Increment Sensor DBL60 Manual Ver. 1.3. Available online: https://ictinternational.com/product-category/b-plant/dendrometers/ (accessed on 22 February 2025).
- Gleason, S.M.; Stewart, J.; Allen, B.; Polutchko, S.K.; McMahon, J.; Spitzer, D.; Barnard, D.M. Development and application of an inexpensive open-source dendrometer for detecting xylem water potential and radial stem growth at high spatial and temporal resolution. AoB Plants 2024, 16, plae009. [Google Scholar] [CrossRef] [PubMed]
- DeLucia, E.H.; Mies, T.A. Dendrometer. US Patent No. 9.377.288B2, 28 June 2016. [Google Scholar]
- Yuan, F.; Fang, L.; Sun, L.; Zheng, S.; Zheng, X. Development of a portable measuring device for diameter at breast height and tree height. Austrian J. For. Sci. 2021, 138, 25–50. [Google Scholar]
- Beato-López, J.J.; Algueta-Miguel, J.M.; de la Cruz Blas, C.A.; Santesteban, L.G.; Pérez-Landazábal, J.I.; Gómez-Polo, C. GMI Magnetoelastic Sensor for Measuring Trunk Diameter Variations in Plants. IEEE Trans. Magn. 2017, 53, 4001105. [Google Scholar] [CrossRef]
- Li, Y.; Xin, Z.; Zhang, H.; Zhang, W.; Gu, L.; Zhang, D. Machine vision-based tree-ring image analysis for the measurement of ring width in ancient larch stem disks. Measurement 2025, 244, 116465. [Google Scholar] [CrossRef]
- Hasegawa, R. Magnetic wire fabrication and applications. J. Magn. Magn. Mater. 2002, 249, 346–350. [Google Scholar] [CrossRef]
- Ogasawara, I.; Ueno, S. Preparation and Properties of Amorphous Wires. IEEE Trans. Magn. 1995, 31, 1219–1222. [Google Scholar] [CrossRef]
- Phan, M.H.; Peng, H.X. Giant magnetoimpedance materials: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 323–420. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Zhukova, V. Advances in Giant Magnetoimpedance of Materials. In Handbook of Magnetic Materials; Elsevier: Amsterdam, The Netherlands, 2015; Volume 24, pp. 139–236. [Google Scholar]
- Morón, C.; Carracedo, M.T.; Zato, J.G.; Garcia, A. Stress and field dependence of the giant magnetoimpedance effect in Co-rich amorphous wires. Sens. Actuators A Phys. 2003, 106, 217–220. [Google Scholar] [CrossRef]
- Chiriac, H.; Ovari, T.A. Giant magnetoimpedance effect in soft magnetic wire families. IEEE Trans. Magn. 2002, 38, 3057. [Google Scholar] [CrossRef]
- Herzer, G. Modern soft magnets: Amorphous and nanocrystalline materials. Acta Mater. 2013, 61, 718–734. [Google Scholar] [CrossRef]
- Van Stan, J.T.; Jarvis, M.T.; Levia, D.F. An Automated Instrument for the Measurement of Bark Microrelief. IEEE Trans. Instrum. Meas. 2010, 59, 491–493. [Google Scholar] [CrossRef]








| θ [°C] | dx [mm] | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|
| 5 | N | 5.162 | 4.872 | 4.576 | 4.281 | 3.898 |
| 25 | N | 5.176 | 4.882 | 4.588 | 4.294 | 4.000 |
| 45 | N | 5.192 | 4.890 | 4.600 | 4.305 | 4.012 |
| Parameter | Value |
|---|---|
| Measurement range | 0–5 mm |
| Linearity | 1.4% |
| Accuracy | 5.3% of full scale |
| Resolution | 1.6 × 10−6 m |
| Repeatability | 2.8% |
| Temperature coefficient | 0.012%/°C |
| Power demand in active state | Less than 100 mW |
| Response time | Less than 1 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fosalau, C. A New Device for Measuring Trunk Diameter Variations Using Magnetic Amorphous Wires. Sensors 2025, 25, 4449. https://doi.org/10.3390/s25144449
Fosalau C. A New Device for Measuring Trunk Diameter Variations Using Magnetic Amorphous Wires. Sensors. 2025; 25(14):4449. https://doi.org/10.3390/s25144449
Chicago/Turabian StyleFosalau, Cristian. 2025. "A New Device for Measuring Trunk Diameter Variations Using Magnetic Amorphous Wires" Sensors 25, no. 14: 4449. https://doi.org/10.3390/s25144449
APA StyleFosalau, C. (2025). A New Device for Measuring Trunk Diameter Variations Using Magnetic Amorphous Wires. Sensors, 25(14), 4449. https://doi.org/10.3390/s25144449







