Research on the Bearing Remaining Useful Life Prediction Method Based on Optimized BiLSTM
Abstract
1. Introduction
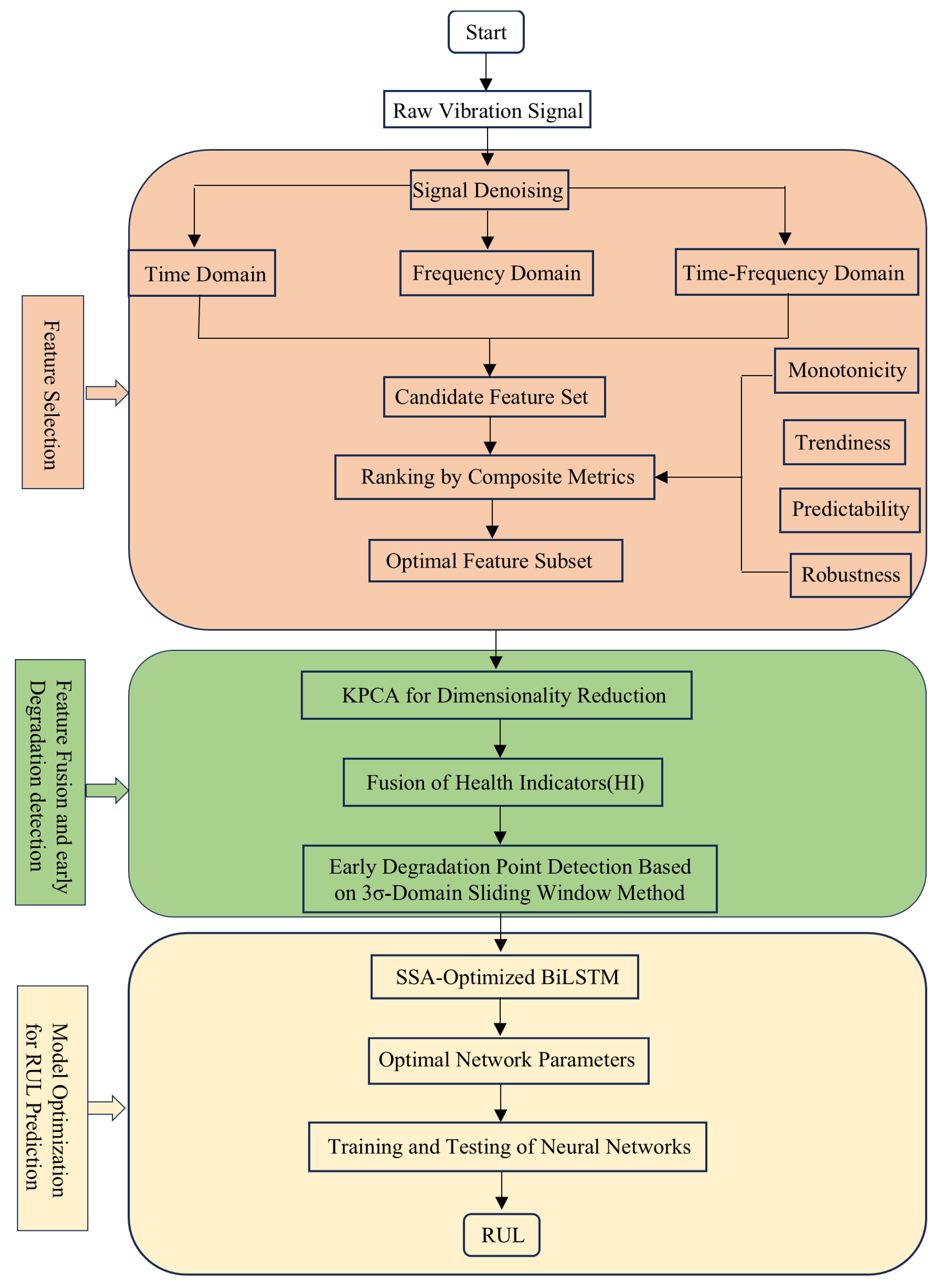
2. Preprocessing Methods for Bearing Vibration Signals
2.1. Signal Denoising Methods
2.1.1. Variational Mode Decomposition (VMD) Algorithm
2.1.2. Optimizing Variational Mode Decomposition (VMD) Using the Northern Goshawk Optimization (NGO) Algorithm
2.1.3. Pearson Correlation Coefficient
2.1.4. Denoising Evaluation Metrics
2.2. Multi-Domain Feature Extraction and Domain Selection Method
2.2.1. Multi-Domain Feature Extraction
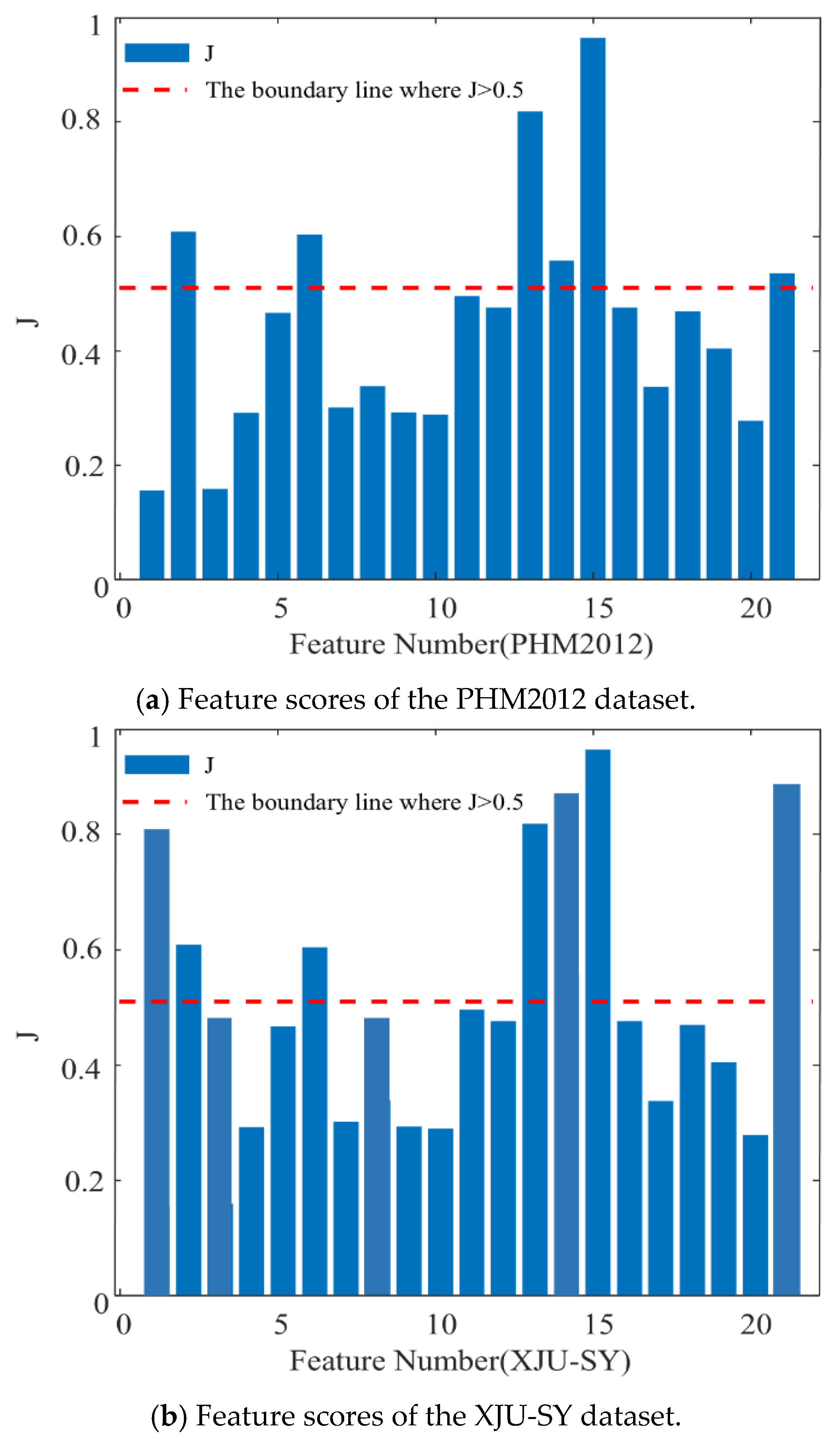
2.2.2. Feature Selection Method
3. Method for Establishing RUL Prediction Model Based on Optimized BiLSTM Networks
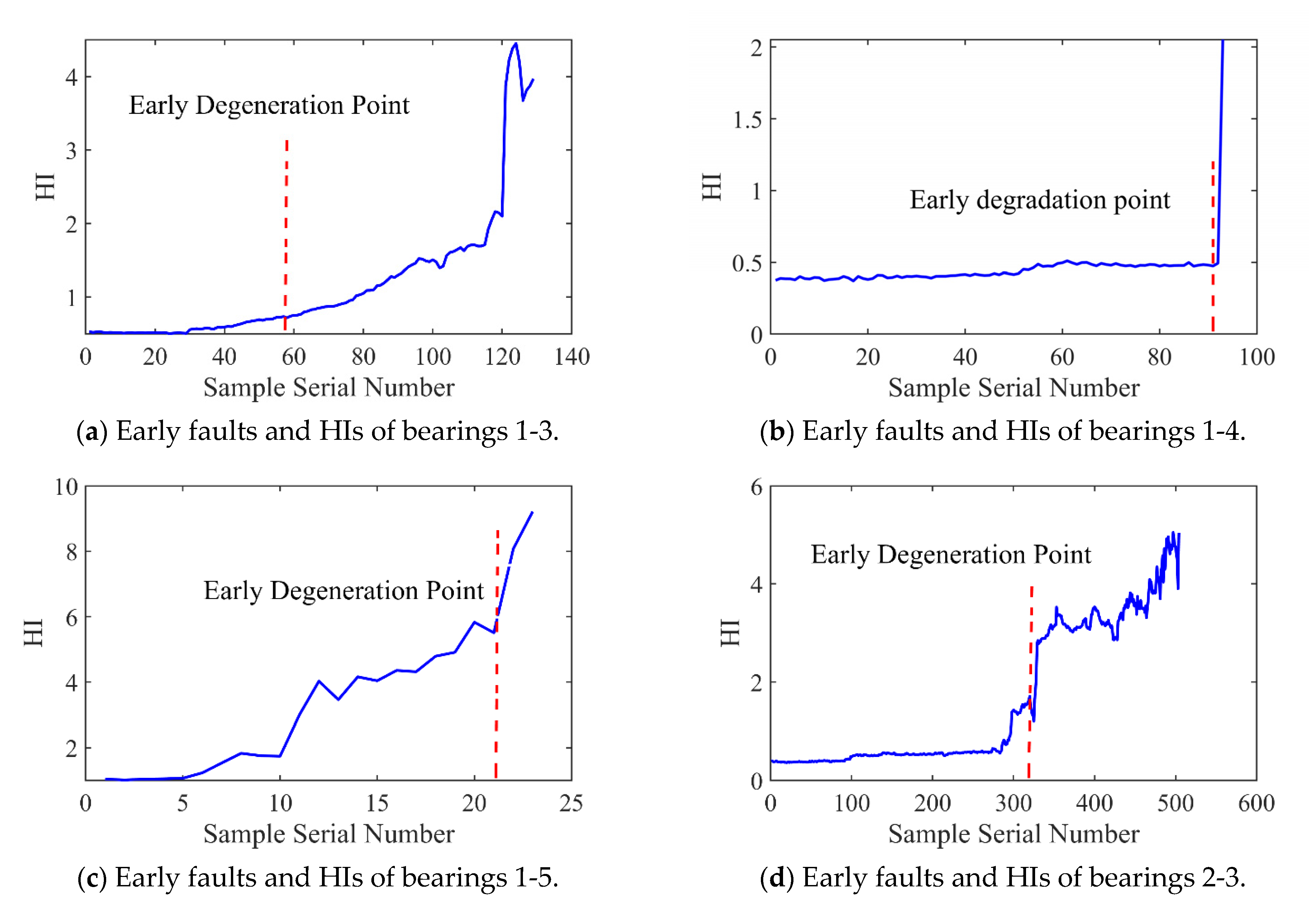
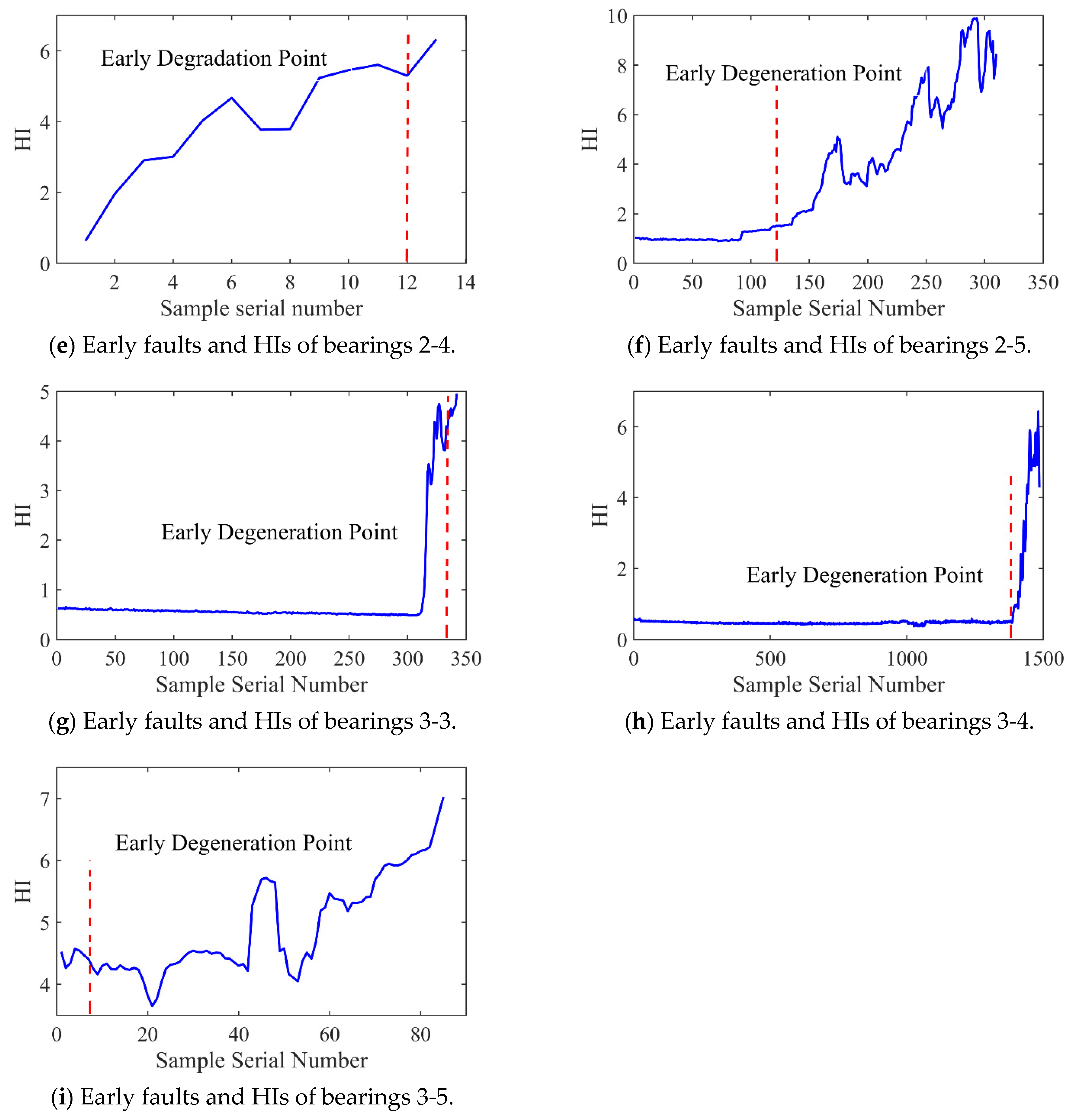
3.1. Construction of Health Indicators and Determination of Failure Thresholds
3.1.1. Construction of Health Indicators (HIs)
- (1)
- The sensitive feature subset is standardized, and the resultant feature vector matrix undergoes a nonlinear mapping using the function Φ, projecting to a higher-dimensional feature space . The samples in the input space are transformed via Φ, denoted as , and become sample points within the high-dimensional feature space , where , satisfying the centrality condition [27,38]:
- (2)
- Calculate the eigenvalues and eigenvectors of the covariance matrix [36,38]. The eigenvectors thus obtained represent the principal component directions of the original sample space in the feature space [37,38] :where represents the eigenvalue of , and v denotes the corresponding eigenvector in the feature space [37,38].
- (3)
- Given the computational challenge of directly solving , a kernel function is introduced, resulting in an symmetric positive definite matrix K, where K is the kernel matrix corresponding to , denoted as [23].
- (4)
- Centering the kernel matrix K yields the standardized kernel matrix, represented by the following formula [23]:where I is an matrix where each element is 1/n.
- (5)
- The eigenvalues and eigenvectors of , denoted as , , are calculated and arranged in descending order, represented by the following formula [23]:
- (6)
- The eigenvectors undergo Schmidt orthogonal normalization to produce the feature component matrix .
- (7)
- Extract the eigenvalue of the first principal component that accounts for more than 85% [23] of the variance, along with its corresponding eigenvector to form the projection matrix Y, where [23], and Y represents the fused feature derived from the original feature matrix X through Kernel Principal Component Analysis (KPCA) for dimensionality reduction, serving as a health indicator (HI).
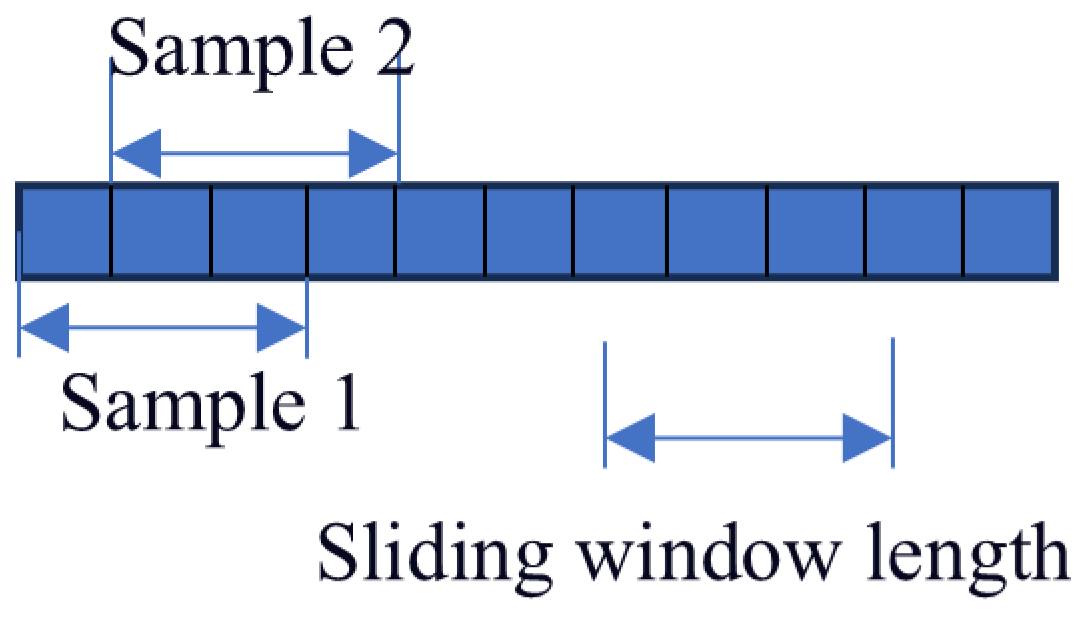
3.1.2. Determination of Failure Thresholds
- (1)
- Calculate the mean and standard deviation for each window [32]:where Z is the length of the sampling window, and denotes the sampled data points.
- (2)
- If a certain point satisfies condition , according to the 3σ principle, the data point is considered anomalous [32].
- (3)
- Sort the nh data points within the window in ascending order to obtain the ordered set {}. Calculate the first quartile (fQ1) and the third quartile (fQ3) [25]:In the above formula, if f is an integer, directly take the value at the corresponding position. If f is a decimal, compute the value using linear interpolation [25]:Q = x⌊f⌋ + (f − ⌊f⌋) (x⌊f⌋+1 + x⌊f⌋)If the condition or the condition is satisfied, the data point is considered anomalous.
- (4)
- If data anomalies are detected in either Step (2) or Step (3), the bearing is considered to have failed.
3.2. Method for Optimizing BiLSTM Networks Using the Sparrow Search Algorithm (SSA)
3.2.1. Sparrow Search Algorithm (SSA)
- (1)
- The SSA objective function is considered as the prediction error on the test set, the reciprocal of the MSE is used as the fitness value. The MSE is expressed as [36]where ny represents the number of test samples, and y represents the serial number of the data point [38].The fitness value is given by [36]
- (2)
- The position update rule for discoverers in the SSA algorithm is expressed as [36]where d represents the current iteration number, V represents the total number of iterations, represents the position information of the ath sparrow in the bth dimension at the dth iteration, represents a random number in the range of 0–1, represents the warning value in the range of 0–1, represents the safety value in the range of 0.5–1, Z0 represents a random number following normal distribution, and A0 represents a multi-dimensional row matrix of all ones.
- (3)
- The position update formula for followers is given by [36]where represents the best position occupied by discoverers, represents the global worst position, represents a matrix of all ones comprising elements randomly set to 0 or 1, and . Note that, for , half of the following sparrows cannot share the optimal position of the discoverer, and they should search on their own.
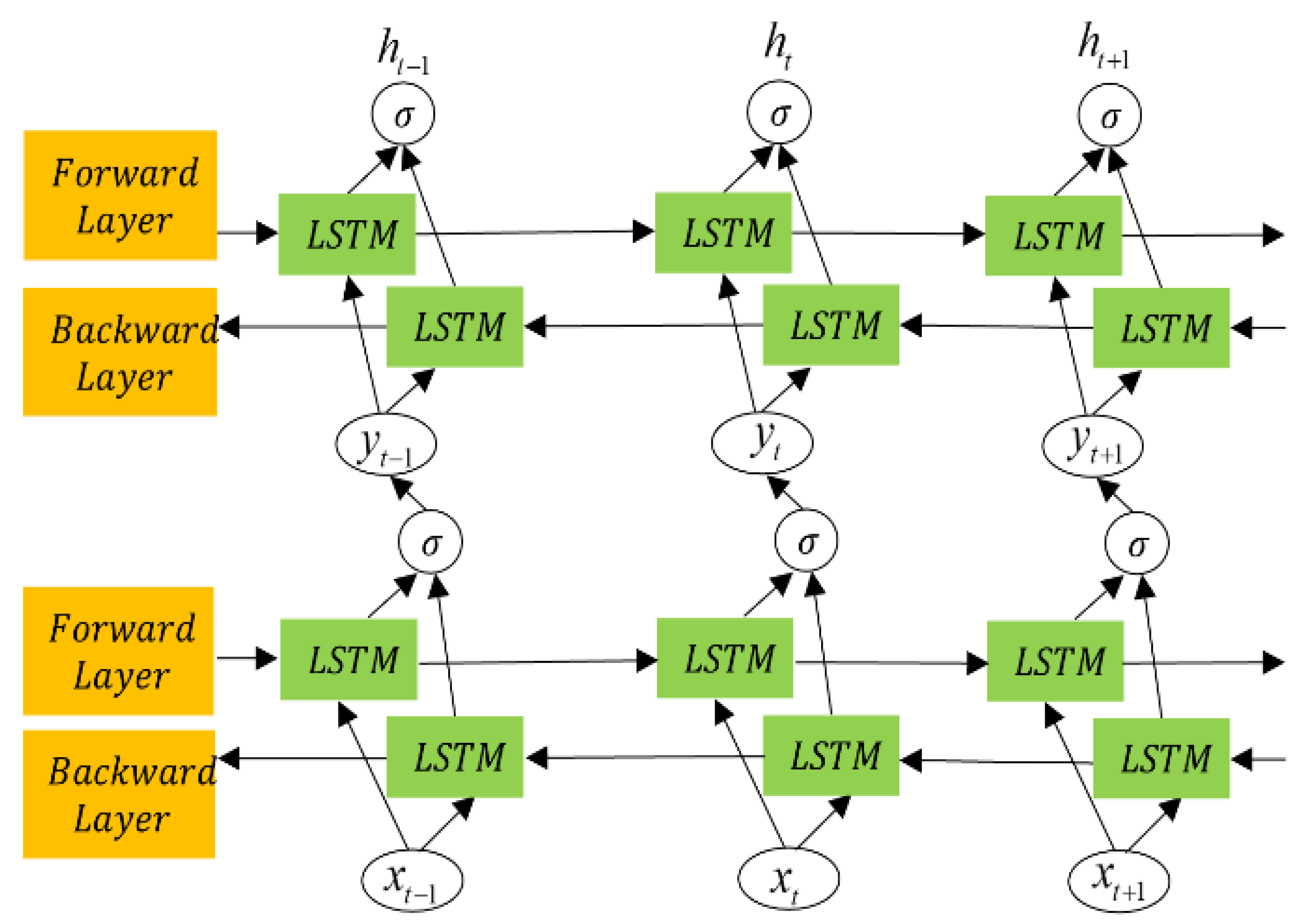
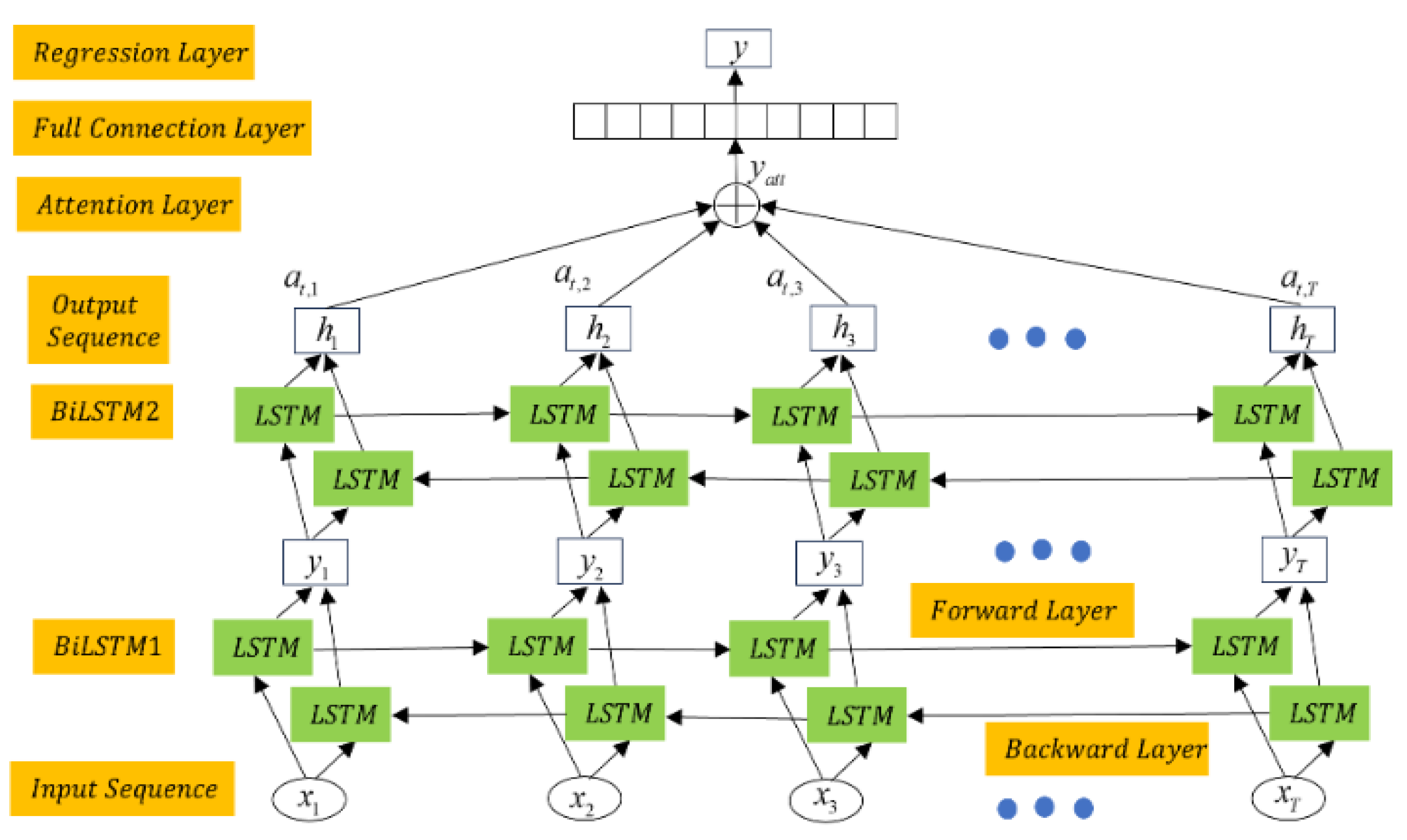
3.2.2. BiLSTM Network Algorithm
3.3. RUL Prediction Model
4. Experimental Validation and Result Analysis
4.1. Introduction to the Experimental Platform
4.2. Analysis of Data Preprocessing Results
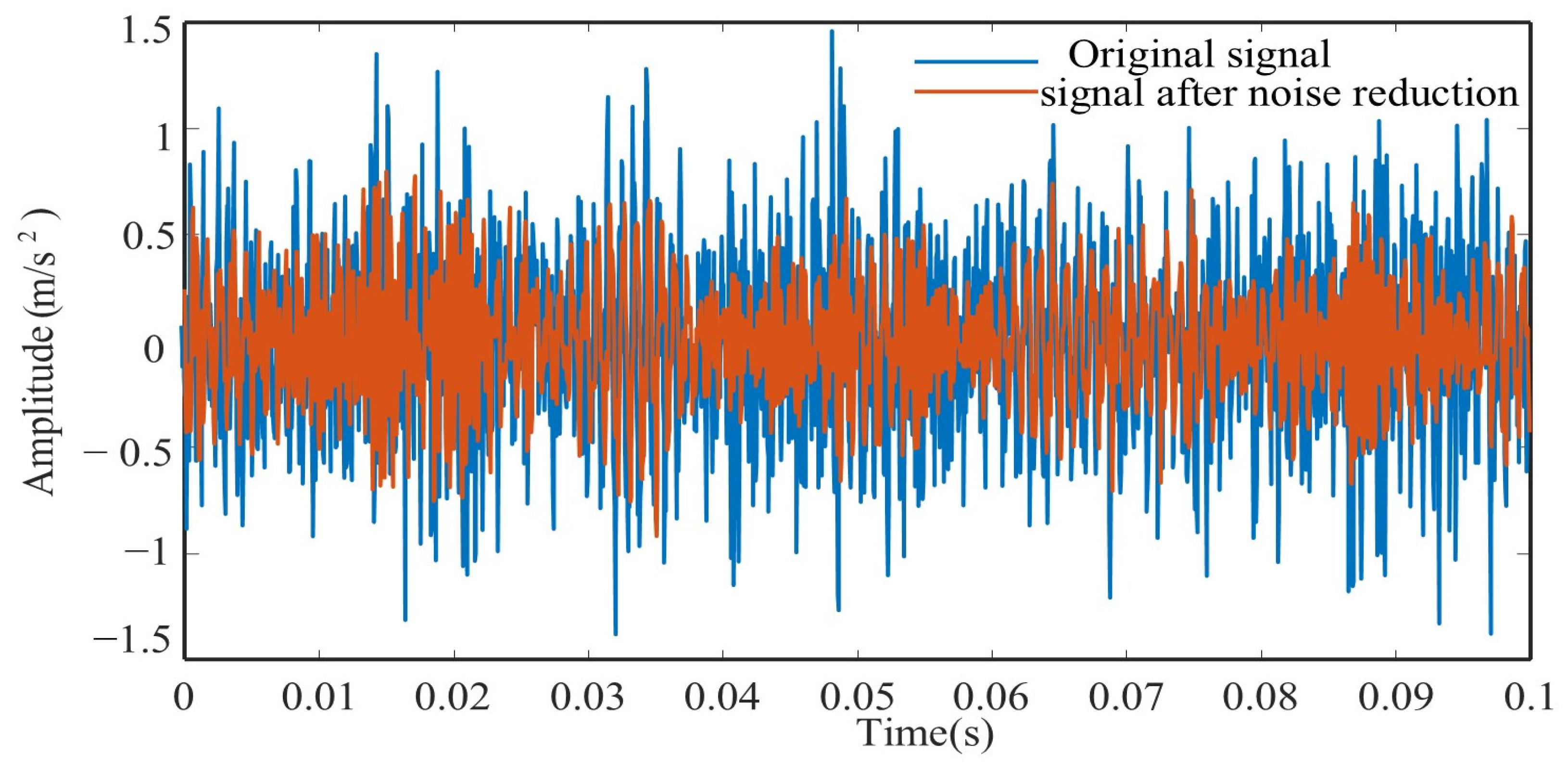
4.2.1. Analysis of Denoising Results
4.2.2. Analysis of Feature Selection Results
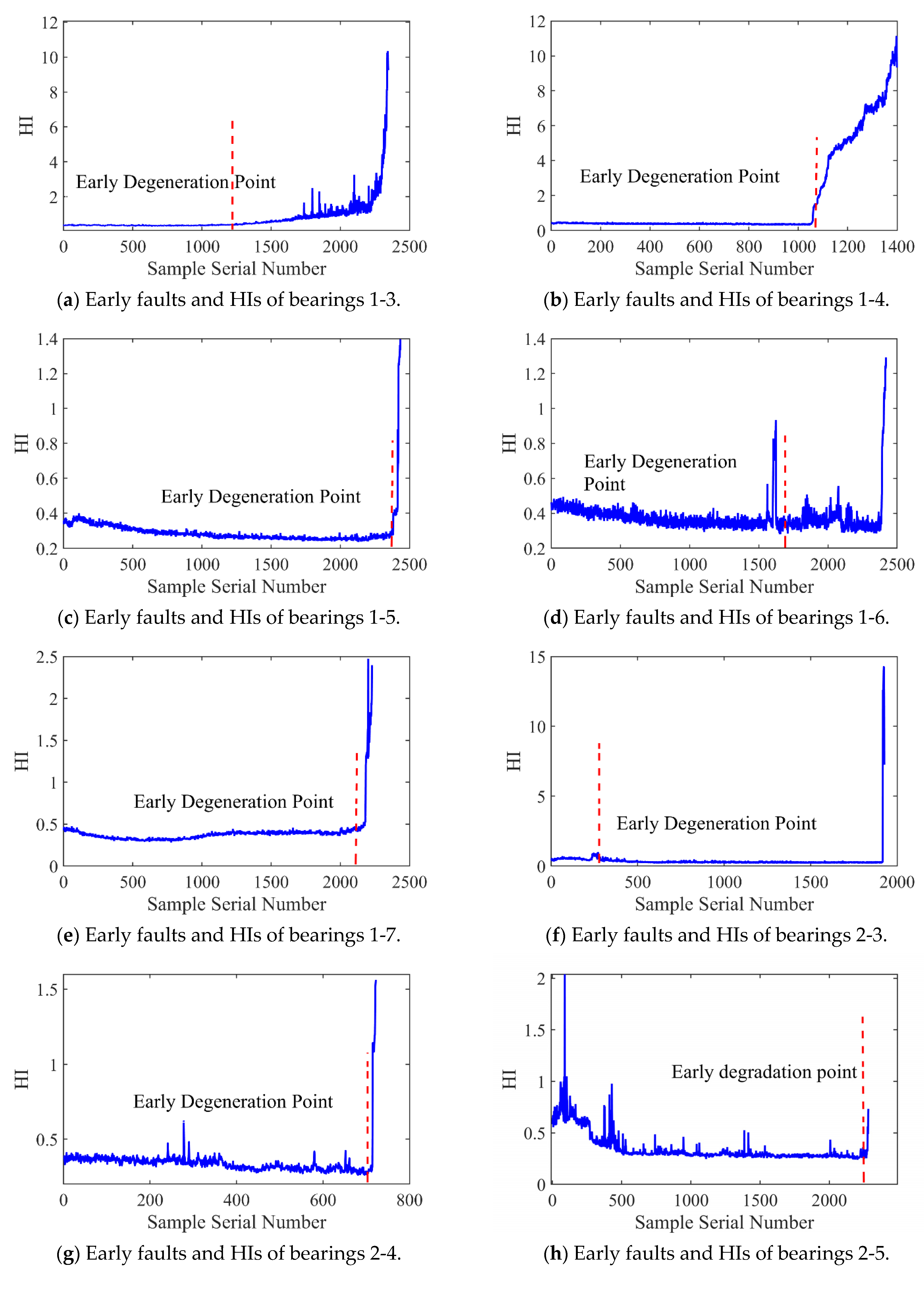
4.3. HI and Failure Threshold Results
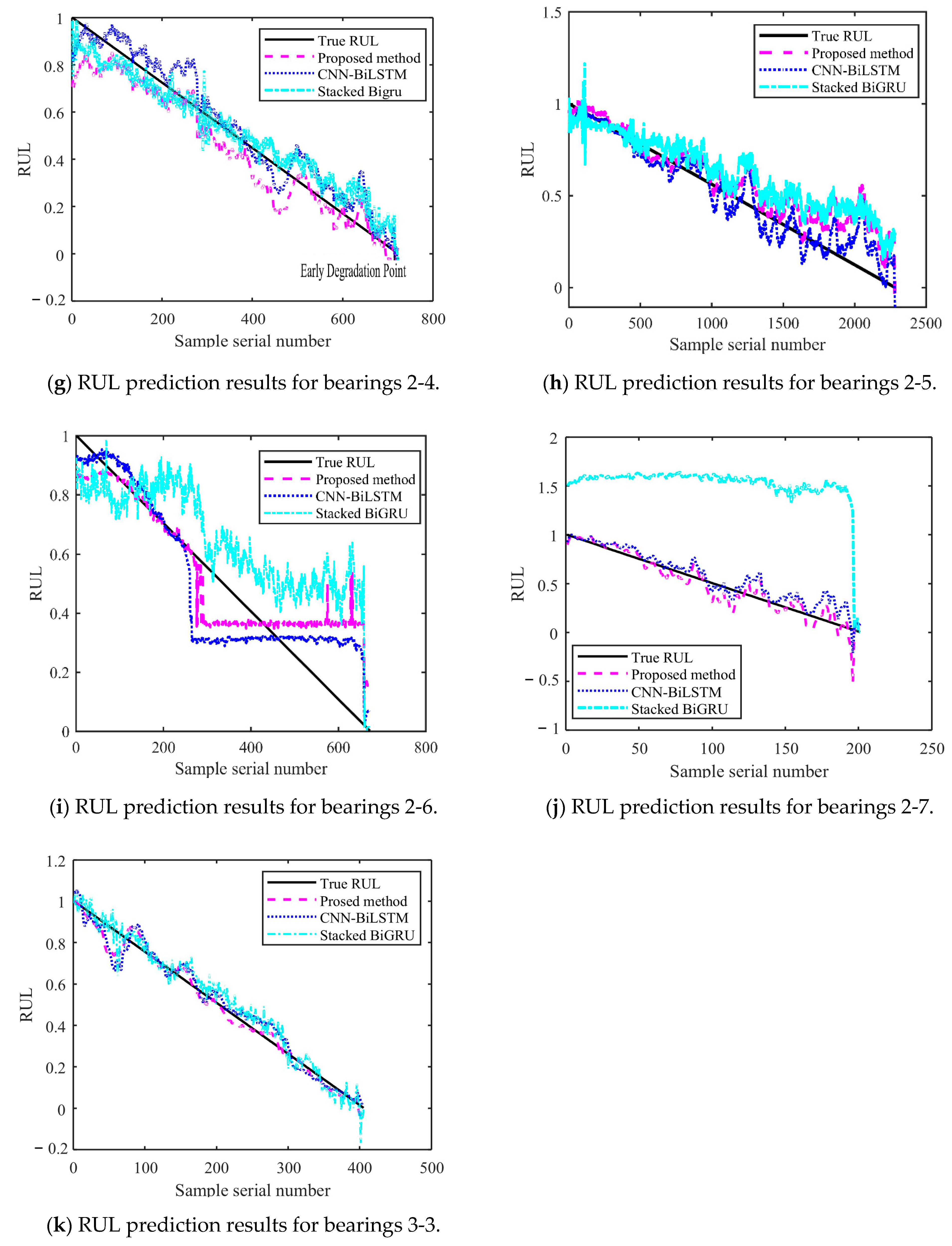
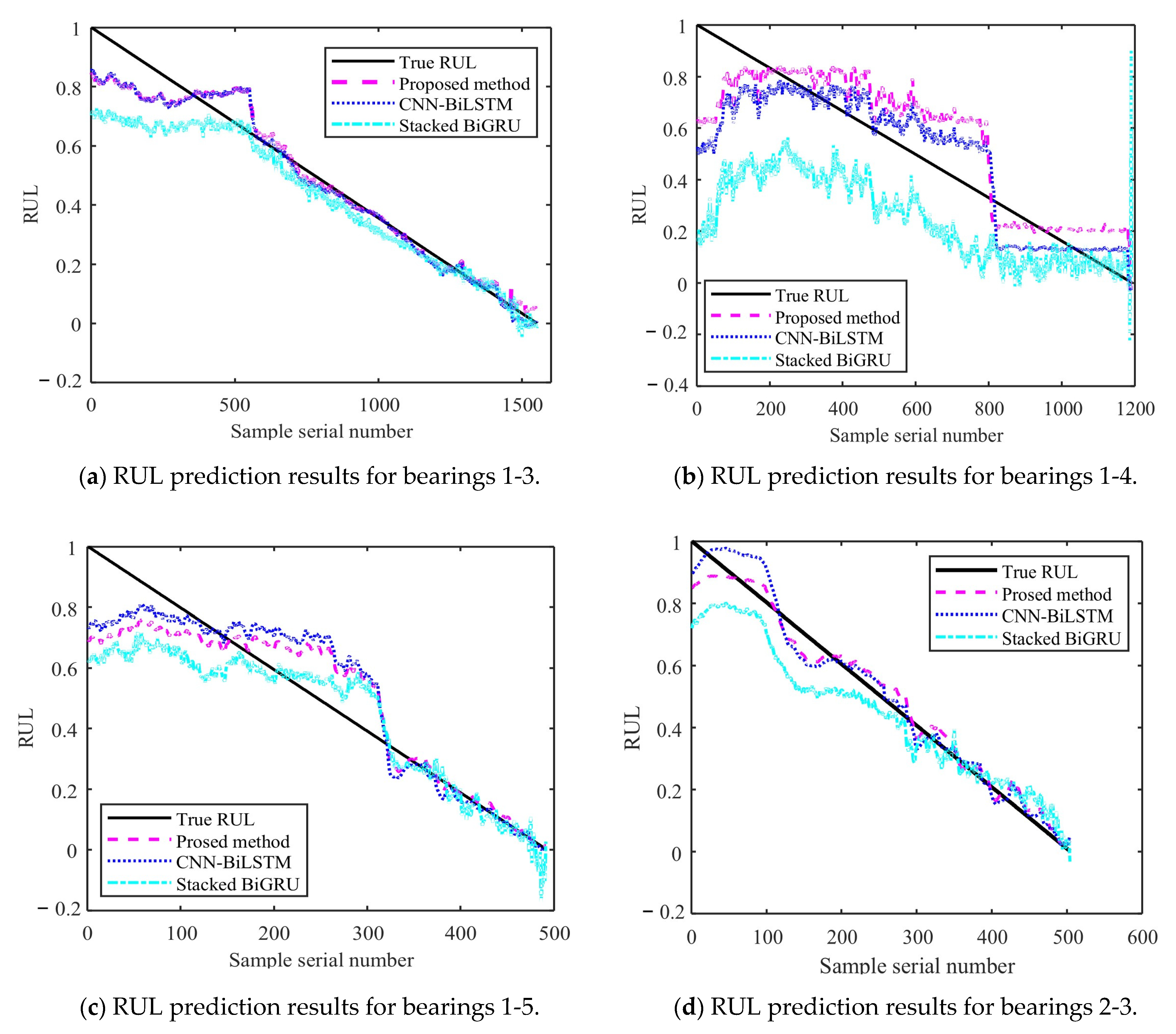
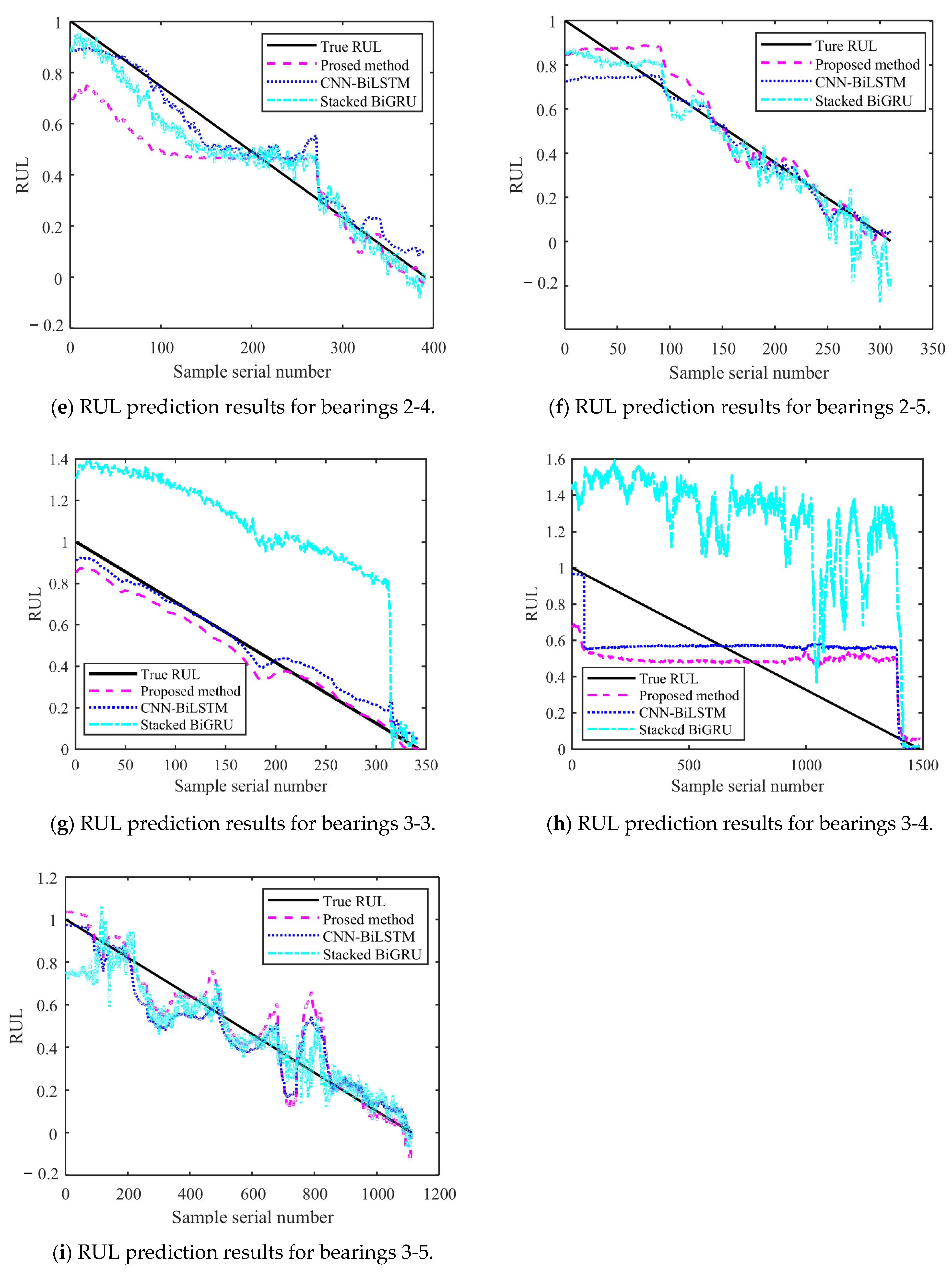
4.4. Analysis of RUL Prediction Results
5. Conclusions
- (1)
- The proposed method exhibits high denoising capability. The denoising capability significantly affects the quality of the results of bearing RUL prediction. After filtering using the NVMD method, the bearing signal becomes purer, which improves its quality for the subsequent bearing signal feature extraction, early degradation detection, and life prediction.
- (2)
- Different bearing features encapsulate degradation information from various aspects. During feature selection, it is necessary to comprehensively consider multiple features. Based on the ablation experiment results across different features, the features extracted using the proposed method contain richer degradation information. By fusing only these sensitive features, accurate prediction can be performed for RUL prediction.
- (3)
- Early degradation time detection is a crucial parameter in the evaluation of the bearing performance. Since the characteristics of bearing vibration signals change in real time, the degradation threshold of the signal also varies over time. Using a dynamic threshold setting method to determine the degradation threshold of bearing vibration signals, real-time updates of the mean and standard deviation can be performed. This allows us to update the failure threshold in real time. Compared with the fixed threshold method, the dynamic threshold method can detect the bearing degradation time earlier, enabling the preventive maintenance of bearings.
- (4)
- A comparison was conducted among the RUL, CNN-BiLSTM, and stacked BiGRU prediction performances. The obtained results showed that the proposed RUL prediction method demonstrates higher performance and stronger fitting ability. This demonstrates that it has higher effectiveness in predicting RUL. The proposed model was then applied on the PHM2012 and XJU-SY datasets, demonstrating its high generalization ability and performance. The use of the proposed method for RUL prediction allows for timely detection of potential bearing faults. This provides sufficient time for performing timely bearing repair, guiding staff in formulating complete maintenance measures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, H.; Jiang, G.; Tian, W.; Mei, X.; Nee, A.Y.C.; Ong, S.K. Microservice-based digital twin system towards smart manufacturing. Robot. Comput. Integr. Manuf. 2025, 91, 102858. [Google Scholar] [CrossRef]
- Yuan, X.; Shi, D.; Shi, N.; Li, Y.; Liang, P.; Zhang, L.; Zheng, Z. Intelligent fault diagnosis of rolling bearing based on an active federated local subdomain adaptation method. Adv. Eng. Inform. 2024, 62, 102807. [Google Scholar] [CrossRef]
- He, D.; Zhang, Z.; Jin, Z.; Zhang, F.; Yi, C.; Liao, S. RTSMFFDE-HKRR: A fault diagnosis method for train bearing in noise environment. Measurement 2025, 239, 115417. [Google Scholar] [CrossRef]
- He, D.; Zhao, J.; Jin, Z.; Huang, C.; Zhang, F.; Wu, J. Prediction of bearing remaining useful life based on a two-stage updated digital twin. Adv. Eng. Inform. 2025, 65, 103123. [Google Scholar] [CrossRef]
- Liu, S.; Fan, L. An adaptive prediction approach for rolling bearing remaining useful life based on multistage model with three-source variability. Reliab. Eng. Syst. Saf. 2022, 218, 108182. [Google Scholar] [CrossRef]
- Zimmermann, N.; Lang, S.; Blaser, P.; Mayr, J. Adaptive input selection for thermal error compensation models. CIRP Ann. 2020, 69, 485–488. [Google Scholar] [CrossRef]
- Sheng, Y.; Liu, H.; Li, J. Bearing performance degradation assessment and remaining useful life prediction based on data-driven and physical model. Meas. Sci. Technol. 2023, 34, 055002. [Google Scholar] [CrossRef]
- Shuang, L.; Shen, X.; Zhou, J.; Miao, H.; Qiao, Y.; Lei, G. Bearings remaining useful life prediction across equipment-operating conditions based on multisource-multitarget domain adaptation. Measurement 2024, 236, 115026. [Google Scholar] [CrossRef]
- Wu, J.; He, D.; Li, J.; Miao, J.; Li, X.; Li, H.; Shan, S. Temporal multi-resolution hypergraph attention network for remaining useful life prediction of rolling bearings. Reliab. Eng. Syst. Saf. 2024, 247, 110143. [Google Scholar] [CrossRef]
- Wu, C.; He, J.; Shen, W.; Xu, W.; Lv, J.; Liu, S. Remaining useful life prediction across operating conditions based on deep subdomain adaptation network considering the weighted multi-source domain. Knowl.-Based Syst. 2024, 301, 112291. [Google Scholar] [CrossRef]
- Qiu, H.; Niu, Y.; Shang, J.; Gao, L.; Xu, D. A piecewise method for bearing remaining useful life estimation using temporal convolutional networks. J. Manuf. Syst. 2023, 68, 227–241. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, B.; Feng, B.; Liu, L.; Gao, Z. A hybrid method for cutting tool RUL prediction based on CNN and multistage Wiener process using small sample data. Measurement 2023, 213, 112739. [Google Scholar] [CrossRef]
- Yousuf, S.; Khan, S.A.; Khursheed, S. Remaining useful life (RUL) regression using long–short term memory (LSTM) networks. Microelectron. Reliab. 2022, 139, 114772. [Google Scholar] [CrossRef]
- Xiang, S.; Li, P.; Huang, Y.; Luo, J.; Qin, Y. Single gated RNN with differential weighted information storage mechanism and its application to machine RUL prediction. Reliab. Eng. Syst. Saf. 2024, 242, 109741. [Google Scholar] [CrossRef]
- Kebede, G.A.; Lo, S.-C.; Wang, F.-K.; Chou, J.-H. Transfer learning-based deep learning models for proton exchange membrane fuel remaining useful life prediction. Fuel 2024, 367, 131461. [Google Scholar] [CrossRef]
- Chen, X.; Li, K.; Wang, S.; Liu, H. A hybrid prognostic approach combined with deep Bayesian transformer and enhanced particle filter for remaining useful life prediction of bearings. Measurement 2025, 252, 117184. [Google Scholar] [CrossRef]
- Zhang, G.; Jiang, D. Research on the Remaining Life Prediction Method of Rolling Bearings Based on Multi-Feature Fusion. Appl. Sci. 2024, 14, 1294. [Google Scholar] [CrossRef]
- Liu, Y.; Song, J.; Zhao, Z.; Ye, G.; Liu, Z.; Zhou, Y. Adaptive Residual Life Prediction for Small Samples of Mechanical Products Based on Feature Matching Preprocessor-LSTM. Appl. Sci. 2022, 12, 8236. [Google Scholar] [CrossRef]
- Li, J.; Huang, F.; Qin, H.; Pan, J. Research on Remaining Useful Life Prediction of Bearings Based on MBCNN-BiLSTM. Appl. Sci. 2023, 13, 7706. [Google Scholar] [CrossRef]
- Mi, J.H.; Liu, L.L.; Zhuang, Y.H. A Synthetic Feature Processing Method for Remaining Useful Life Prediction of Rolling Bearings. IEEE Trans. Reliab. 2023, 72, 110123. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Y.; Huang, Q.; Fu, Q.; Wang, R.; Wang, L. Rolling bearing remaining useful life prediction method based on vibration signal and mechanism model. Appl. Acoust. 2025, 228, 110334. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, E.; Zhang, B.; Miao, Q. RUL prediction and uncertainty management for multisensor system using an integrated data-level fusion and UPF approach. IEEE Trans. Ind. Inform. 2021, 17, 4692–4701. [Google Scholar] [CrossRef]
- Tai, Y.F.; Yan, X.Y.; Geng, X.Y.; Mu, L.; Jiang, M.S.; Zhang, F.Y. Data-driven method for predicting remaining useful life of bearings based on multi-layer perceptron neural network and bidirectional long short-term memory network. Struct. Durab. Health Monit. 2025, 19, 365–383. [Google Scholar] [CrossRef]
- Yang, L.; Li, T.; Dong, Y.; Duan, R.; Liao, Y. A knowledge-data integration framework for rolling element bearing RUL prediction across its life cycle. ISA Trans. 2024, 152, 27. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Z.; Mrad, N. A probabilistic framework for remaining useful life prediction of bearings. IEEE Trans. Instrum. Meas. 2021, 70, 3503412. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, T.; Li, Y.; Pan, E. A hybrid prognostic method based on gated recurrent unit network and an adaptive Wiener process model considering measurement errors. Mech. Syst. Signal Process. 2021, 158, e107785. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Li, F.; Li, Y.; Zhang, X.; Shi, H.; Dong, L.; Ren, W. An ensembled remaining useful life prediction method with data fusion and stage division. Reliab. Eng. Syst. Saf. 2024, 242, 109804. [Google Scholar] [CrossRef]
- Wang, G.; Xiang, J. Remain useful life prediction of rolling bearings based on exponential model optimized by gradient method. Measurement 2021, 176, 109161. [Google Scholar] [CrossRef]
- Cui, L.; Wang, X.; Wang, H.; Ma, J. Research on remaining useful life prediction of rolling element bearings based on time-varying Kalman filter. IEEE Trans. Instrum. Meas. 2019, 69, 2858–2867. [Google Scholar] [CrossRef]
- Wang, D.; Tsui, K.L. Two novel mixed effects models for prognostics of rolling element bearings. Mech. Syst. Sig. Process. 2018, 99, 1–13. [Google Scholar] [CrossRef]
- Han, T.; Pang, J.; Tan, A.C.C. Remaining useful life prediction of bearing based on stacked autoencoder and recurrent neural network. J. Manuf. Syst. 2021, 61, 576–591. [Google Scholar] [CrossRef]
- Balamurugan, R.; Takale, D.G.; Parvez, M.M.; Gnanamurugan, S. A novel prediction of remaining useful life time of rolling bearings using convolutional neural network with bidirectional long short term memory. J. Eng. Res. 2024. [Google Scholar] [CrossRef]
- Shen, Y.Z.; Tang, B.P.; Li, B.; Tan, Q.; Wu, Y.L. Remaining useful life prediction of rolling bearing based on multi-head attention embedded Bi-LSTM network. Measurement 2022, 202, 111803. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Y.; Liao, Z.; Chen, Y. A VMD-MRE bearing fault diagnosis method for parameter optimization of northern goshawk. Mech. Sci. Technol. Aerosp. Eng. 2025, 1–8. [Google Scholar] [CrossRef]
- Pan, L.; Gao, J.; Shao, X. Rolling bearing remaining life prediction model based on improved VMD and BiLSTM. Electron. Des. Eng. 2024, 32, 27–31. [Google Scholar]
- Meng, Q.Y. Research on the Tracking Method of Rolling Bearing Performance Degradation. Master’s Thesis, Anhui University of Engineering, Wuhu, China, 2024. [Google Scholar] [CrossRef]
- Shang, Y.; Tang, X.; Zhao, G.; Jiang, P.; Lin, T.R. A remaining life prediction of rolling element bearings based on a bidirectional gate recurrent unit and convolution neural network. Measurement 2022, 202, 111893. [Google Scholar] [CrossRef]
- Zou, Y.; Sun, W.; Wang, H.; Xu, T.; Wang, B. Research on Bearing Remaining Useful Life Prediction Method Based on Double Bidirectional Long Short-Term Memory. Appl. Sci. 2025, 15, 4441. [Google Scholar] [CrossRef]






| Serial Number | Name | Feature Expression |
|---|---|---|
| 1 | Mean | |
| 2 | Standard Deviation | |
| 3 | Variance | |
| 4 | Skewness | |
| 5 | Mean Square Root Value | |
| 6 | Root Mean Square Value | |
| 7 | Kurtosis | |
| 8 | Waveform | |
| 9 | Kurtosis | |
| 10 | Skewness | |
| 11 | Peak | |
| 12 | Mean Amplitude in Frequency Domain | |
| 13 | Root Mean Square Frequency |
| Data | Serial Number | Condition | Training Set | Test Set |
|---|---|---|---|---|
| PHM2012 | Condition 1 | 4 KN, 1800 rpm | Bearing 1-1 Bearing 1-2 | Bearing 1-3, Bearing 1-4 Bearing 1-5, Bearing 1-6 Bearing 1-7 |
| Condition 2 | 4.2 KN, 1650 rpm | Bearing 2-1 Bearing 2-2 | Bearing 2-3, Bearing 2-4 Bearing 2-5, Bearing 2-6 Bearing 2-7 | |
| Condition 3 | 5 KN, 1500 rpm | Bearing 3-1 Bearing 3-2 | Bearing 3-3 | |
| XJU-SY | Condition 1 | 12 KN, 2100 rpm | Bearing 1-1 Bearing 1-2 | Bearing 1-3, Bearing 1-4 Bearing 1-5 |
| Condition 2 | 11 KN, 2250 rpm | Bearing 2-1 Bearing 2-2 | Bearing 2-3, Bearing 2-4 Bearing 2-5 | |
| Condition 3 | 10 KN, 2400 rpm | Bearing 3-1 Bearing 3-2 | Bearing 3-3, Bearing 3-4 Bearing 3-5 |
| Proposed Method | Soft Thresholding | |
|---|---|---|
| NM | 2.5 | 1.9 |
| SNR | 25 | 4 |
| PHM2012 | XJU-SY | ||
|---|---|---|---|
| Feature RMSE | Feature RMSE | ||
| pall | 0.1035 | pall | 0.0642 |
| p | 0.1033 | p | 0.0630 |
| p-p2 | 0.1101 | p-p1 | 0.0710 |
| p-p6 | 0.1042 | p-p2 | 0.0644 |
| p-p13 | 0.1029 | p-p6 | 0.0649 |
| p-p14 | 0.1034 | p-p13 | 0.0890 |
| p-p15 | 0.1039 | p-p14 | 0.0798 |
| p-p21 | 0.1149 | p-p15 | 0.0644 |
| p-p2-p6 | 0.1110 | p-p21 | 0.0654 |
| p-p2-p13 | 0.1101 | p-p1-p2 | 0.0690 |
| p-p2-p14 | 0.1102 | p-p1-p6 | 0.0900 |
| p-p2-p15 | 0.1046 | p-p1-p13 | 0.0789 |
| p-p2-p21 | 0.1051 | p-p1-p14 | 0.0840 |
| p-p6-p13 | 0.1046 | p-p1-p15 | 0.0910 |
| p-p6-p14 | 0.1088 | p-p1-p21 | 0.1002 |
| p-p6-p15 | 0.1056 | p-p2-p6 | 0.0900 |
| p-p6-p21 | 0.1062 | p-p2-p13 | 0.0639 |
| p-p13-p14 | 0.1038 | p-p2-p14 | 0.0832 |
| p-p13-p15 | 0.1043 | p-p2-p15 | 0.0754 |
| p-p13-p21 | 0.1066 | p-p2-p21 | 0.0876 |
| p-p14-p15 | 0.1047 | p-p6-p13 | 0.0655 |
| p-p14-p21 | 0.1037 | p-p6-p14 | 0.0779 |
| p-p15-p21 | 0.1114 | p-p6-p15 | 0.0666 |
| p-p2-p6-p13 | 0.1117 | p-p6-p21 | 0.0977 |
| p-p2-p6-p14 | 0.1108 | p-p13-p14 | 0.0962 |
| p-p2-p6-p15 | 0.1109 | p-p13-p15 | 0.0988 |
| p-p2-p6-p21 | 0.1121 | p-p13-p21 | 0.0879 |
| p-p2-p13-p14 | 0.1089 | p-p14-p15 | 0.8567 |
| p-p2-p13-p15 | 0.1077 | p-p14-p21 | 0.9947 |
| p-p2-p13-p21 | 0.1064 | p-p15-p21 | 0.1087 |
| p-p6-p13-p14 | 0.1055 | p-p1-p2-p6 | 0.0756 |
| p-p6-p14-p15 | 0.1082 | p-p1-p2-p13 | 0.0821 |
| p-p6-p15-p21 | 0.1074 | p-p1-p2-p14 | 0.0900 |
| p-p13-p14-p15 | 0.1063 | p-p1-p2-p15 | 0.0899 |
| p-p13-p14-p21 | 0.1043 | p-p1-p2-p21 | 0.0689 |
| p-p14-p15-p21 | 0.1058 | p-p2-p6-p13 | 0.0890 |
| p-p2-p6-p13-p14 | 0.1054 | p-p2-p6-p14 | 0.0926 |
| p-p2-p6-p13-p15 | 0.1070 | p-p2-p6-p15 | 0.0920 |
| p-p2-p6-p13-p21 | 0.1044 | p-p2-p6-p21 | 0.0670 |
| p-p6-p13-p14-p15 | 0.1054 | p-p6-p13-p14 | 0.8864 |
| p-p6-p13-p14-p21 | 0.1099 | p-p6-p13-p15 | 0.1179 |
| p-p13-p14-p15-p21 | 0.1210 | p-p6-p13-p21 | 0.1123 |
| p-p2-p6-p13-p14-p15 | 0.2440 | p-p13-p14-p15 | 0.1243 |
| p-p2-p6-p13-p14-p21 | 0.1077 | p-p13-p14-p21 | 0.1104 |
| p-p2-p6-p13-p14-p15-p21 | 0.1055 | p-p14-p15-p21 | 0.1008 |
| p-p1-p2-p6-p13 | 0.0679 | ||
| p-p1-p2-p6-p14 | 0.0943 | ||
| p-p1-p2-p6-p15 | 0.0699 | ||
| p-p1-p2-p6-p21 | 0.0970 | ||
| p-p2-p6-p13-p14 | 0.0975 | ||
| p-p2-p6-p13-p15 | 0.0953 | ||
| p-p2-p6-p13-p21 | 0.0698 | ||
| p-p6-p13-p14-p15 | 0.0877 | ||
| p-p6-p13-p14-p21 | 0.0933 | ||
| p-p13-p14-p15-p21 | 0.1003 | ||
| p-p1-p2-p6-p13-p14 | 0.0999 | ||
| p-p1-p2-p6-p13-p15 | 0.1110 | ||
| p-p1-p2-p6-p13-p21 | 0.1011 | ||
| p-p2-p6-p13-p14-p15 | 0.0955 | ||
| p-p2-p6-p13-p14-p21 | 0.0987 | ||
| p-p6-p13-p14-p15-p21 | 0.1245 | ||
| p-p1-p2-p6-p13-p14-p15 | 0.1008 | ||
| p-p1-p2-p6-p13-p14-p21 | 0.0865 | ||
| p-p1-p2-p6-p13-p14-p15-p21 | 0.0954 | ||
| Bearing | Serial Number | Proposed Method | Fixed 3σ |
|---|---|---|---|
| PHM2012 | 1-3 | 1330 | 1414 |
| 1-4 | 1072 | 11,085 | |
| 1-5 | 2423 | 2428 | |
| 1-6 | 1622 | 1632 | |
| 1-7 | 2191 | 2209 | |
| 2-3 | 267 | 271 | |
| 2-4 | 744 | Not Detected | |
| 2-5 | 2244 | Not Detected | |
| 2-6 | 673 | 688 | |
| 2-7 | 199 | 222 | |
| 3-3 | 323 | 328 | |
| XJU-SY | 1-3 | 58 | 71 |
| 1-4 | 91 | Not Detected | |
| 1-5 | 21 | Not Detected | |
| 2-3 | 310 | 319 | |
| 2-4 | 12 | 12 | |
| 2-5 | 120 | 130 | |
| 3-3 | 340 | 352 | |
| 3-4 | 1411 | 1423 | |
| 3-5 | 6 | 14 |
| Model | Layer Name | Detailed Description |
|---|---|---|
| Prosed method | BiLSTM1, BiLSTM2, fully connected layer, regression layer | Number of hidden layer neurons: BiLSTM1 = 93, BiLSTM2 = 90; fully connected layer: layer1 = 45, layer2 = 20; output vector dimension: 1; learning rate: 0.0098; batch size: 128; number of iterations: 2000; dropout rate: 0.15; regression layer = 1 |
| CNN-LSTM | 1DConv1, 1DConv1, LSTM, fully connected layer, regression layer | Number of hidden layer neurons: 128; fully connected layer: layer1 = 40; layer2 = 20; output vector dimension: 1; pooling = {1 × 2}; learning rate: 0.001; batch size: 128; number of iterations: 2000; dropout rate: 0.015; regression layer = 1 |
| stacked BiGRU | GRU, Fully connected layer, regression layer | Number of hidden layer neurons: 220; fully connected layer: 45; output vector dimension: 1; learning rate: 0.001; batch size: 128; number of iterations: 2000; dropout rate: 0.15; regression layer = 1 |
| PHM2012 | XJU-SY | ||||
|---|---|---|---|---|---|
| Number | SSA Search (s) | Inference Latency (s) | Number | SSA Search (s) | Inference Latency (s) |
| 1-3 | 2101 | 4805 | 1-3 | 2207 | 3569 |
| 1-4 | 1879 | 4652 | 1-4 | 2008 | 3378 |
| 1-5 | 2221 | 4337 | 1-5 | 1995 | 3487 |
| 1-6 | 1961 | 4228 | 2-3 | 3098 | 3589 |
| 1-7 | 2004 | 3879 | 2-4 | 3209 | 2990 |
| 2-3 | 2602 | 4209 | 2-5 | 2111 | 3244 |
| 2-4 | 2507 | 3889 | 3-3 | 2033 | 3117 |
| 2-5 | 1995 | 3809 | 3-4 | 2011 | 3990 |
| 2-6 | 2117 | 4208 | 3-5 | 2207 | 3876 |
| 2-7 | 2890 | 4789 | |||
| 3-3 | 2368 | 4602 | |||
| Proposed Method | |||||||
|---|---|---|---|---|---|---|---|
| PHM2012 | XJU-SY | ||||||
| Serial Number | RMSE | MAE | R2 | Serial Number | RMSE | MAE | R2 |
| 1-3 | 0.1033 | 0.0729 | 0.8720 | 1-3 | 0.0630 | 0.0439 | 0.9755 |
| 1-4 | 0.0531 | 0.0390 | 0.9661 | 1-4 | 0.1086 | 0.1126 | 0.7320 |
| 1-5 | 0.0978 | 0.0654 | 0.7394 | 1-5 | 0.1145 | 0.0855 | 0.8427 |
| 1-6 | 0.0866 | 0.0533 | 0.9100 | 2-3 | 0.0446 | 0.0365 | 0.9721 |
| 1-7 | 0.0876 | 0.0709 | 0.9079 | 2-4 | 0.0825 | 0.0535 | 0.9432 |
| 2-3 | 0.1167 | 0.0786 | 0.8366 | 2-5 | 0.0727 | 0.0523 | 0.9366 |
| 2-4 | 0.0767 | 0.0628 | 0.9294 | 3-3 | 0.0516 | 0.0423 | 0.9680 |
| 2-5 | 0.0891 | 0.0648 | 0.9048 | 3-4 | 0.2510 | 0.2074 | 0.2437 |
| 2-6 | 0.1316 | 0.0975 | 0.7925 | 3-5 | 0.1024 | 0.0780 | 0.8742 |
| 2-7 | 0.0915 | 0.0675 | 0.89960 | ||||
| 3-3 | 0.0406 | 0.0296 | 0.9802 | ||||
| CNN-BiLSTM | |||||||
| 1-3 | 0.0503 | 0.0770 | 0.8289 | 1-3 | 0.0637 | 0.0440 | 0.9524 |
| 1-4 | 0.1919 | 0.1473 | −1.0111 | 1-4 | 0.1559 | 0.1286 | 0.7082 |
| 1-5 | 0.0978 | 0.0720 | 0.8808 | 1-5 | 0.1339 | 0.0870 | 0.8386 |
| 1-6 | 0.0871 | 0.0567 | 0.9090 | 2-3 | 0.0504 | 0.0388 | 0.9696 |
| 1-7 | 0.0876 | 0.0763 | 0.4677 | 2-4 | 0.0688 | 0.1236 | 0.7108 |
| 2-3 | 0.1186 | 0.2674 | 0.8312 | 2-5 | 0.0826 | 0.0594 | 0.9181 |
| 2-4 | 0.0917 | 0.0638 | 0.0991 | 3-3 | 0.0632 | 0.0516 | −2.788 |
| 2-5 | 0.1356 | 0.1659 | 0.6698 | 3-4 | 0.2568 | 0.2199 | 0.2089 |
| 2-6 | 0.1368 | 0.1803 | 0.7753 | 3-5 | 0.1075 | 0.0783 | 0.8613 |
| 2-7 | 0.5156 | 0.0763 | −2.189 | ||||
| 3-3 | 0.0532 | 0.0422 | 0.9660 | ||||
| Stacked BiGRU | |||||||
| 1-3 | 0.0503 | 0.1733 | 0.3007 | 1-3 | 0.1086 | 0.0747 | 0.9513 |
| 1-4 | 0.4094 | 0.3525 | 0.0579 | 1-4 | 0.1494 | 0.2607 | −0.173 |
| 1-5 | 0.1474 | 0.0654 | 0.7394 | 1-5 | 0.1160 | 0.0970 | 0.7850 |
| 1-6 | 0.1255 | 0.1054 | 0.4677 | 2-3 | 0.1025 | 0.0836 | 0.8738 |
| 1-7 | 0.2106 | 0.0157 | −6.2221 | 2-4 | 0.1552 | 0.0594 | 0.9184 |
| 2-3 | 0.3346 | 0.8544 | −0.3436 | 2-5 | 0.0780 | 0.0611 | 0.9271 |
| 2-4 | 0.0782 | 0.0730 | 0.9265 | 3-3 | 0.5619 | 0.5347 | 0.9521 |
| 2-5 | 0.1659 | 0.0979 | 0.7794 | 3-4 | 0.7627 | 0.7168 | −5.981 |
| 2-6 | 0.2166 | 0.1004 | 0.4372 | 3-5 | 0.1091 | 0.0828 | 0.8572 |
| 2-7 | 0.1192 | 1.0070 | −12.129 | ||||
| 3-3 | 0.0554 | 0.0429 | 0.9632 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Sun, W.; Xu, T.; Wang, B. Research on the Bearing Remaining Useful Life Prediction Method Based on Optimized BiLSTM. Sensors 2025, 25, 4351. https://doi.org/10.3390/s25144351
Zou Y, Sun W, Xu T, Wang B. Research on the Bearing Remaining Useful Life Prediction Method Based on Optimized BiLSTM. Sensors. 2025; 25(14):4351. https://doi.org/10.3390/s25144351
Chicago/Turabian StyleZou, Yi, Wenlei Sun, Tiantian Xu, and Bingkai Wang. 2025. "Research on the Bearing Remaining Useful Life Prediction Method Based on Optimized BiLSTM" Sensors 25, no. 14: 4351. https://doi.org/10.3390/s25144351
APA StyleZou, Y., Sun, W., Xu, T., & Wang, B. (2025). Research on the Bearing Remaining Useful Life Prediction Method Based on Optimized BiLSTM. Sensors, 25(14), 4351. https://doi.org/10.3390/s25144351






