Turbulence-Resilient Object Classification in Remote Sensing Using a Single-Pixel Image-Free Approach
Abstract
1. Introduction
2. Related Work
3. Turbulence-Resilient Classification Using SPI with Hybrid-CTNet
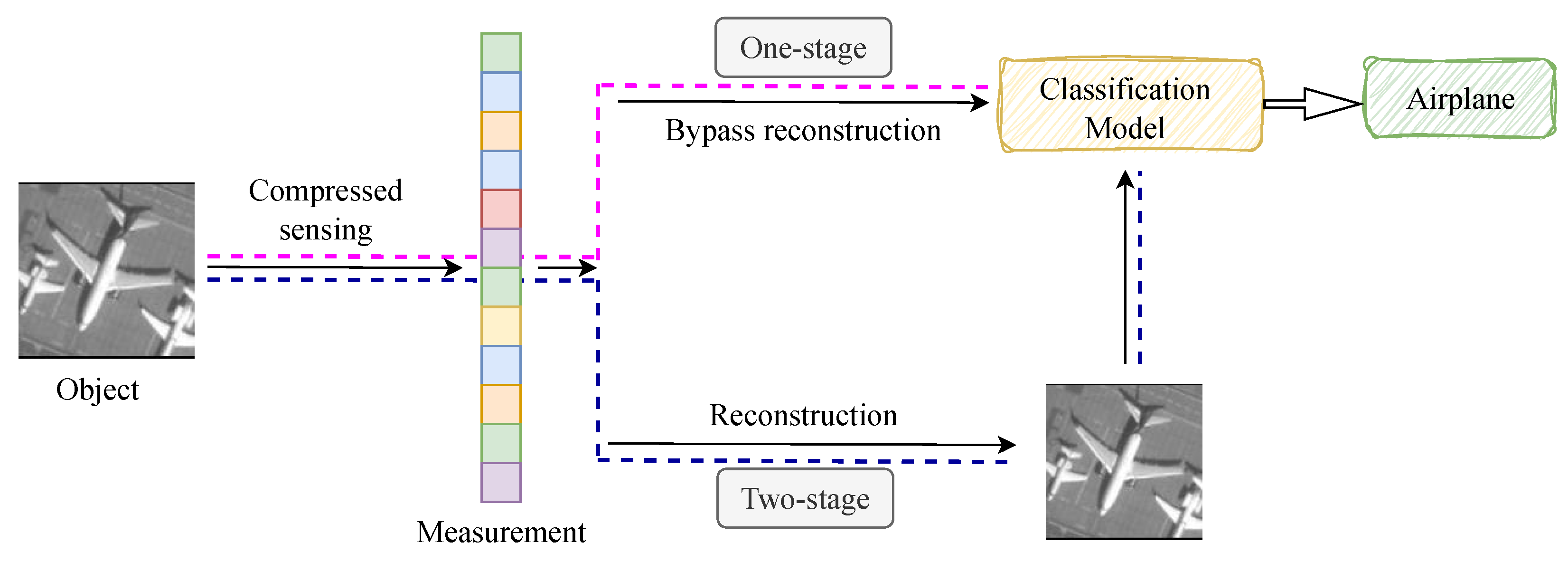
3.1. Single-Pixel Imaging for Atmospheric Turbulence
- (A)
- Learnable Measurement Matrix
- (B)
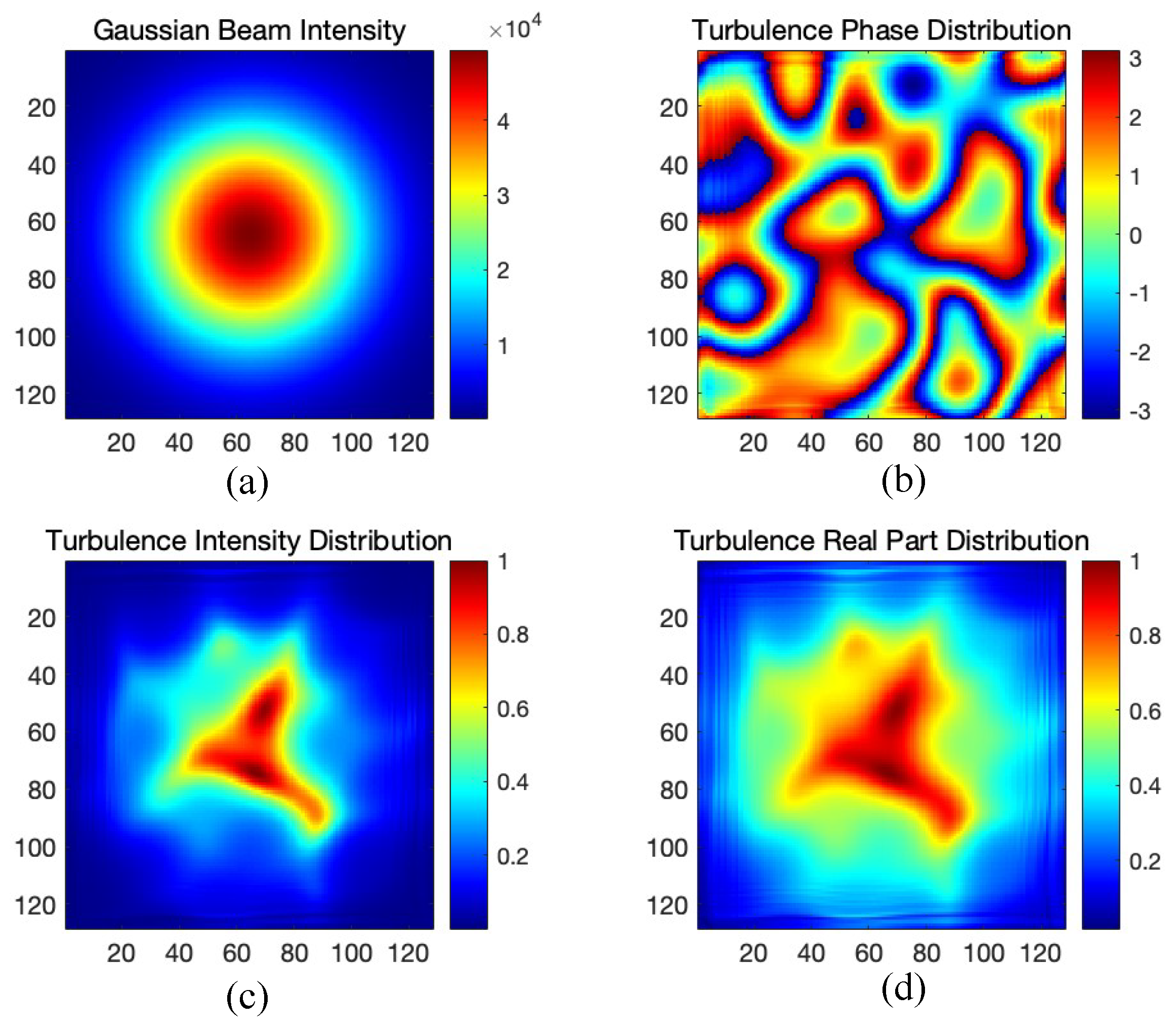
- Atmospheric turbulence
- denotes the spatial frequency (rad/m), representing the inverse of spatial scale of turbulence eddies;
- is Fried’s parameter (m), describing the effective coherent length of the turbulence (a smaller means stronger turbulence);
- is the inner scale cutoff frequency related to the smallest eddy size ;
- is the outer scale cutoff frequency corresponding to the largest turbulence eddy size .
- H is a complex Gaussian random matrix with zero mean and unit variance, representing random turbulence phase fluctuations;
- shapes the spatial frequency content according to the turbulence model;
- is the frequency sampling interval;
- denotes the inverse Fourier transform, which converts the frequency-domain representation into a spatial-domain phase screen.
3.2. Classification Network Hybrid-CTNet
- (A)
- Hybrid Strategy
- (B)
- The Convolutional block
- (B-1)
- Frequency Attention
- (B-2)
- Multi-Head Convolutional Attention (MHCA)
- (C)
- The Transformer Block
- (D)
- Loss Function
4. Simulated Experiments and Discussion
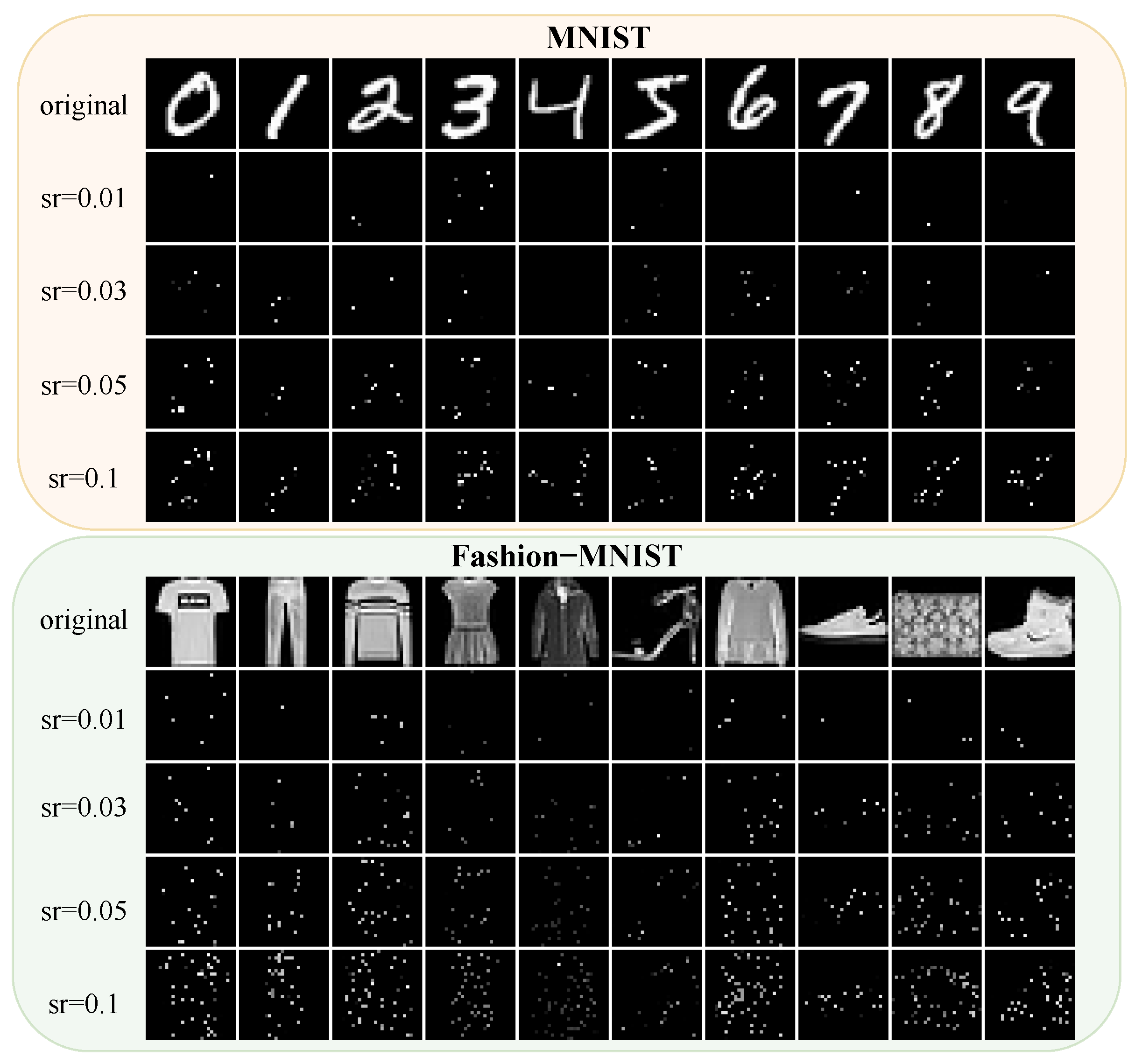
4.1. The Datasets
- (A)
- MNIST and Fashion-MNIST without turbulence
- (B)
- UCM-SPI, MWPU-SPI and DOTA-SPI with turbulence
4.2. Image-Free Classification Comparison Using MNIST and Fashion-MNIST Without Turbulence
4.3. Image-Free Classification Comparison Using UCM-SPI, MWPU-SPI, and DOTA-SPI with Turbulence
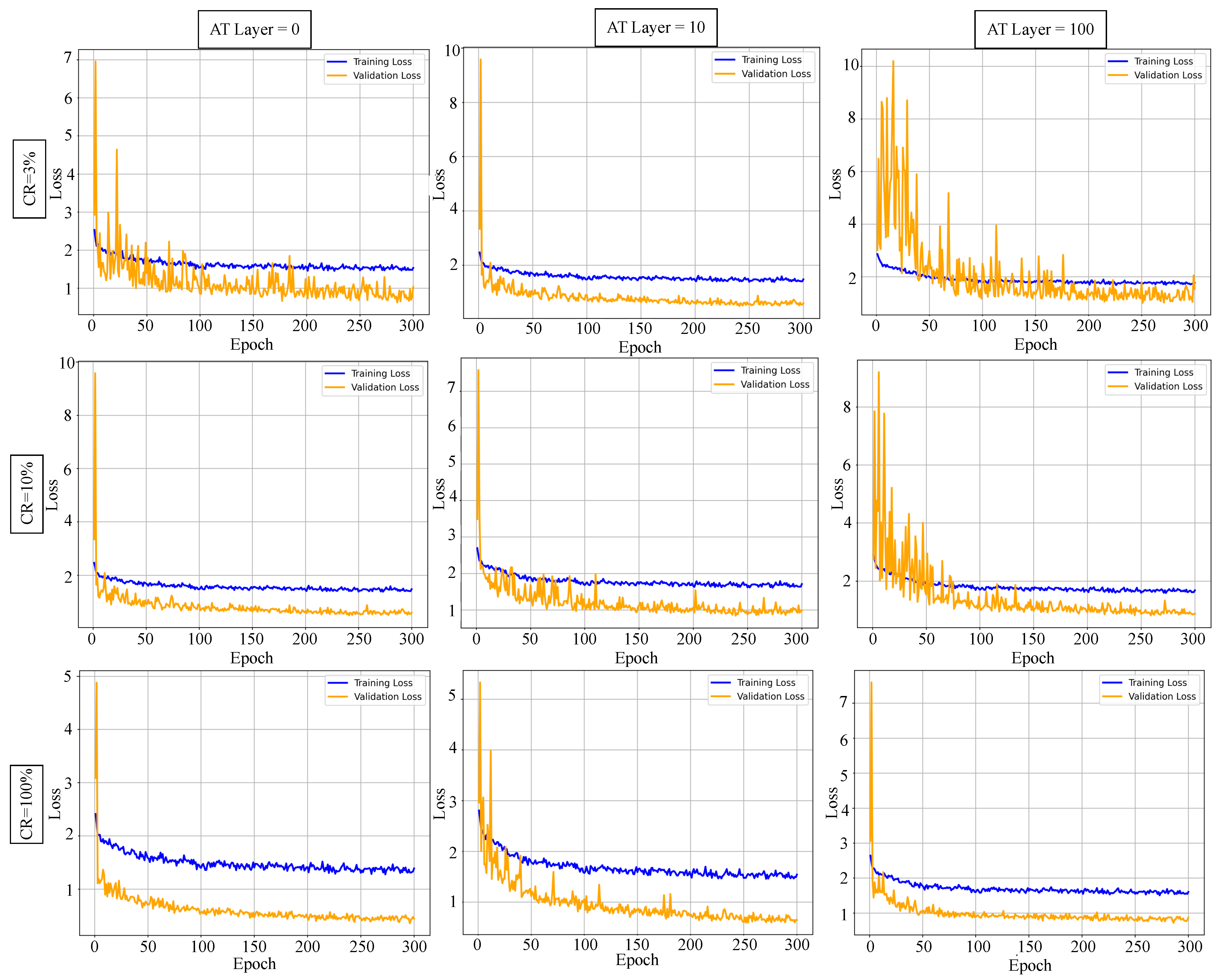
- (A)
- Training Dynamics and Convergence Analysis.
- (B)
- Image-Free Classification with ViT.
- (C)
- Ablation Study of Modules.
- (D)
- Frequency-Domain Analysis of the Learned Sampling Matrix.
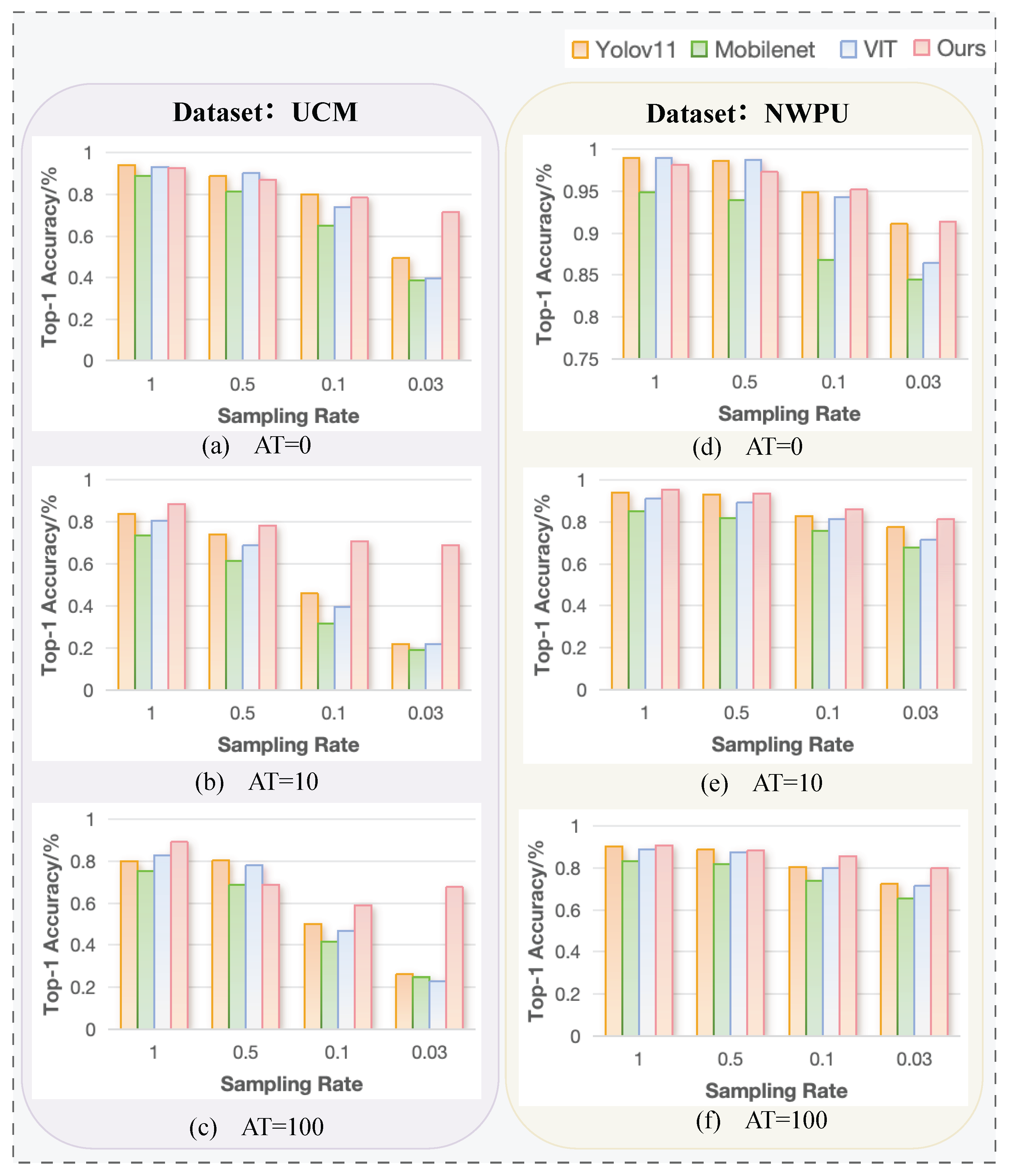
4.4. Comparisons with Reconstruction-Dependent Methods
- (A)
- Comparisons with YOLOv11, MobileNetV3, and ViT.
- (B)
- Comparisons with Ref. [34].
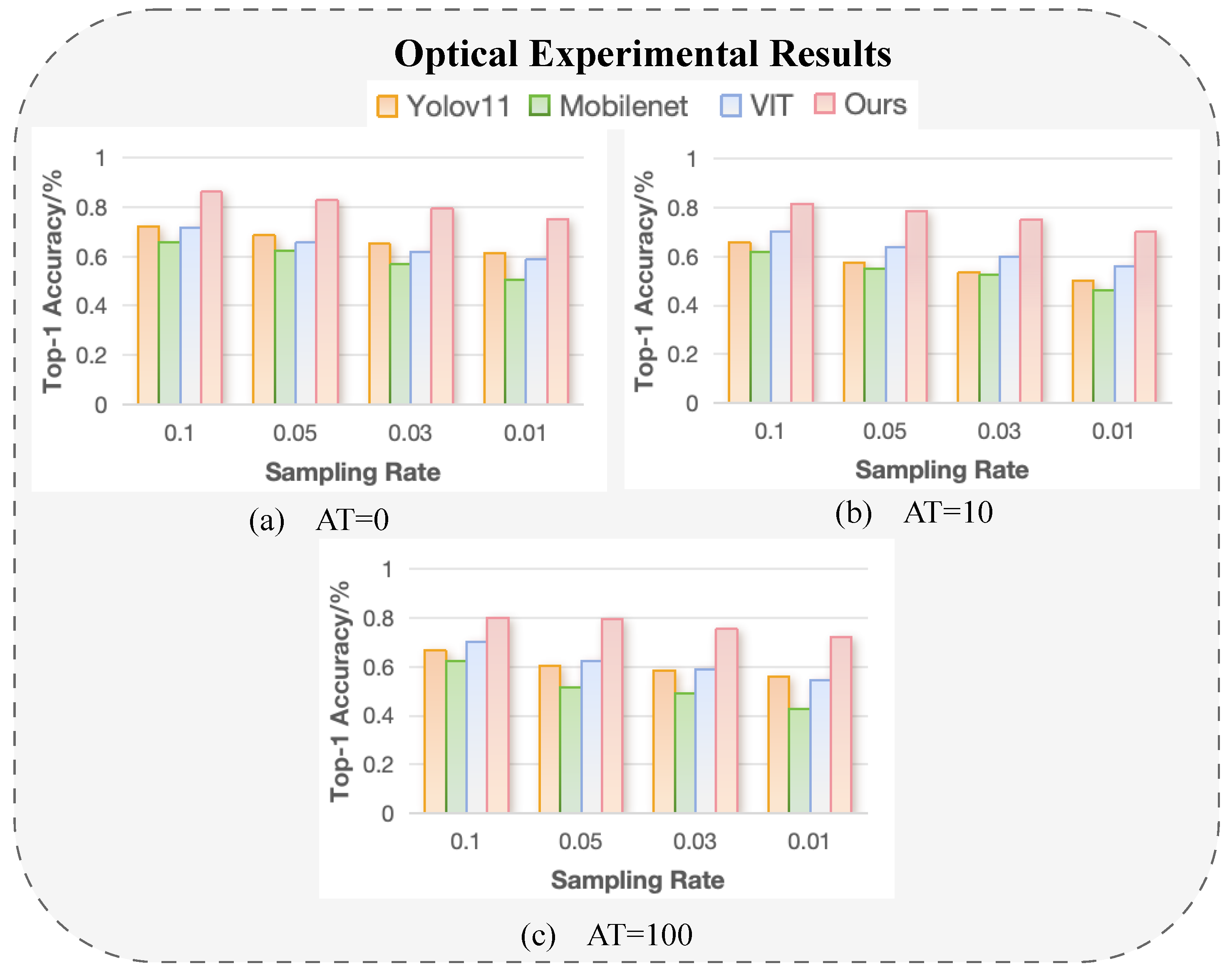
5. Optical Experiments
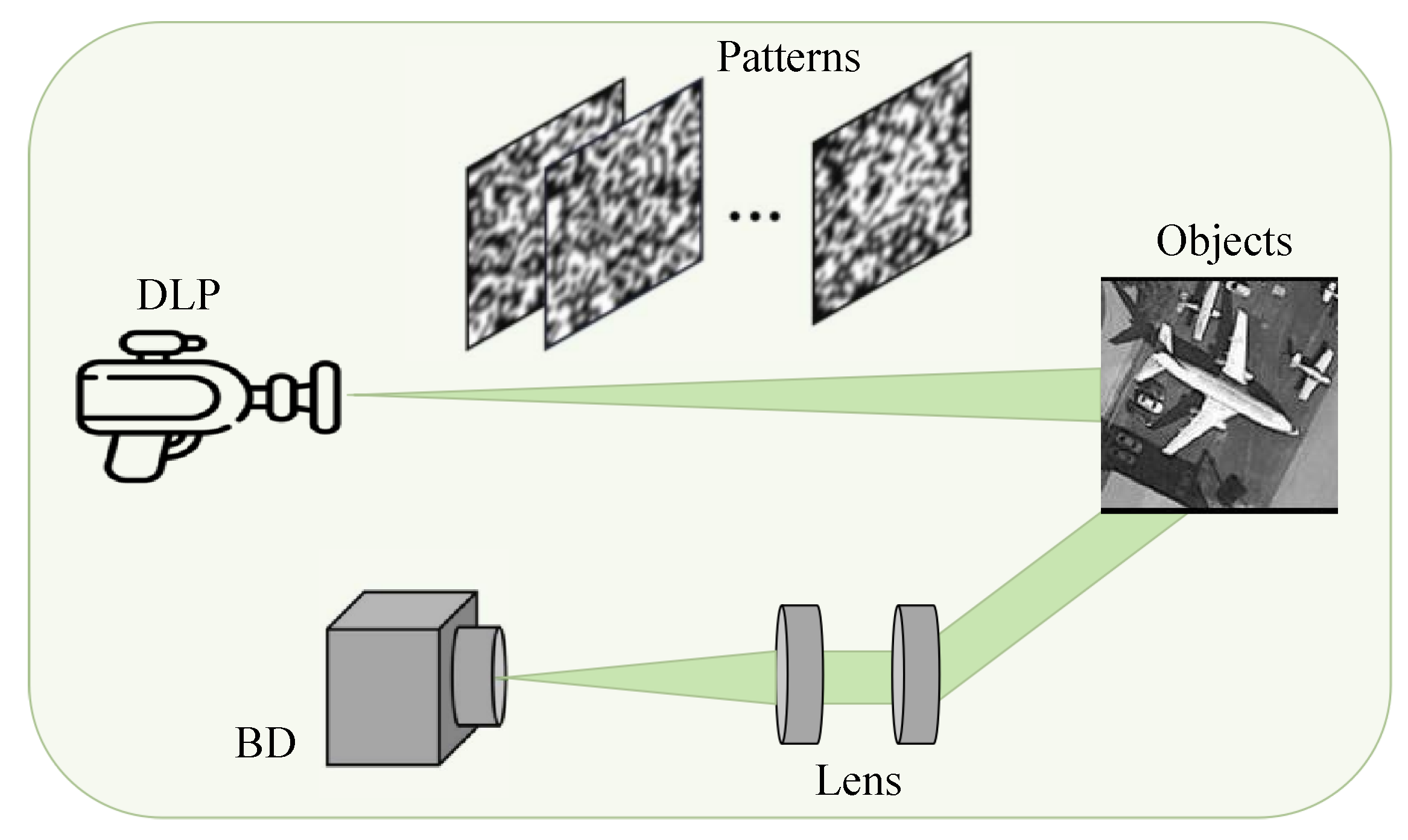
5.1. The Optical Experimental System
5.2. The Optical Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehmood, M.; Shahzad, A.; Zafar, B.; Shabbir, A.; Ali, N. Remote Sensing Image Classification: A Comprehensive Review and Applications. Math. Probl. Eng. 2022, 2022, 5880959. [Google Scholar] [CrossRef]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J. Compressive sampling. Proc. Int. Congr. Math. 2006, 3, 1433–1452. [Google Scholar]
- Calderbank, R.; Jafarpour, S.; Schapire, R. Compressed learning: Universal sparse dimensionality reduction and learning in the measurement domain. In Preprint; Citeseer: University Park, PA, USA, 2009. [Google Scholar]
- Zhang, P.; Gong, W.; Shen, X.; Han, S. Correlated imaging through atmospheric turbulence. Phys. Rev. A 2010, 82, 033817. [Google Scholar] [CrossRef]
- Erkmen, B.I. Computational ghost imaging for remote sensing. J. Opt. Soc. Am. A 2012, 29, 782–789. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, L.; Zhao, X.; Qin, W.; Li, J. Lensless ghost imaging through the strongly scattering medium. Chin. Phys. B 2015, 25, 024202. [Google Scholar] [CrossRef]
- Tang, L.; Bai, Y.; Duan, C.; Nan, S.; Shen, Q.; Fu, X. Effects of incident angles on reflective ghost imaging through atmospheric turbulence. Laser Phys. 2017, 28, 015201. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y. Computational lensless ghost imaging in a slant path non-Kolmogorov turbulent atmosphere. Optik 2012, 123, 1360–1363. [Google Scholar] [CrossRef]
- Bian, L.; Suo, J.; Dai, Q.; Chen, F. Experimental comparison of single-pixel imaging algorithms. J. Opt. Soc. Am. A 2018, 35, 78–87. [Google Scholar] [CrossRef]
- Yang, W.; Shi, D.; Han, K.; Guo, Z.; Chen, Y.; Huang, J.; Ling, H.; Wang, Y. Anti-motion blur single-pixel imaging with calibrated radon spectrum. Opt. Lett. 2022, 47, 3123–3126. [Google Scholar] [CrossRef]
- Kulkarni, K.; Turaga, P. Reconstruction-free action inference from compressive imagers. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 772–784. [Google Scholar] [CrossRef]
- Lohit, S.; Kulkarni, K.; Turaga, P.; Wang, J.; Sankaranarayanan, A.C. Reconstruction-free inference on compressive measurements. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 16–24. [Google Scholar]
- Lohit, S.; Kulkarni, K.; Turaga, P. Direct inference on compressive measurements using convolutional neural networks. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 1913–1917. [Google Scholar]
- Adler, A.; Elad, M.; Zibulevsky, M. Compressed learning: A deep neural network approach. arXiv 2016, arXiv:1610.09615. [Google Scholar]
- Xu, Y.; Liu, W.; Kelly, K.F. Compressed domain image classification using a dynamic-rate neural network. IEEE Access 2020, 8, 217711–217722. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, R.; Wang, T.; Huang, P.; Zhao, L. Attention-based interpolation network for video deblurring. Neurocomputing 2021, 453, 865–875. [Google Scholar] [CrossRef]
- Ren, W.; Nie, X.; Peng, T.; Scully, M.O. Ghost translation: An end-to-end ghost imaging approach based on the transformer network. Opt. Express 2022, 30, 47921–47932. [Google Scholar] [CrossRef]
- Lyu, M.; Wang, W.; Wang, H.; Wang, H.; Li, G.; Chen, N.; Situ, G. Deep-learning-based ghost imaging. Sci. Rep. 2017, 7, 17865. [Google Scholar] [CrossRef]
- He, Y.; Wang, G.; Dong, G.; Zhu, S.; Chen, H.; Zhang, A.; Xu, Z. Ghost imaging based on deep learning. Sci. Rep. 2018, 8, 6469. [Google Scholar] [CrossRef]
- Zhang, H.; Duan, D. Turbulence-immune computational ghost imaging based on a multi-scale generative adversarial network. Opt. Express 2021, 29, 43929–43937. [Google Scholar] [CrossRef]
- Zhang, L.; Bian, Z.; Ye, H.; Wang, Z.; Wang, K.; Zhang, D. Restoration of single pixel imaging in atmospheric turbulence by Fourier filter and CGAN. Appl. Phys. B 2021, 127, 45. [Google Scholar]
- Zhang, L.; Zhai, Y.; Xu, R.; Wang, K.; Zhang, D. End-to-end computational ghost imaging method that suppresses atmospheric turbulence. Appl. Opt. 2023, 62, 697–705. [Google Scholar] [CrossRef]
- Wang, F.; Wang, H.; Wang, H.; Li, G.; Situ, G. Learning from simulation: An end-to-end deep-learning approach for computational ghost imaging. Opt. Express 2019, 27, 25560–25572. [Google Scholar] [CrossRef]
- Li, J.; Le, M.; Wang, J.; Zhang, W.; Li, B.; Peng, J. Object identification in computational ghost imaging based on deep learning. Appl. Phys. B 2020, 126, 166. [Google Scholar] [CrossRef]
- Yang, Z.; Bai, Y.M.; Sun, L.D.; Huang, K.X.; Liu, J.; Ruan, D.; Li, J.L. SP-ILC: Concurrent single-pixel imaging, object location, and classification by deep learning. Photonics 2021, 8, 400. [Google Scholar] [CrossRef]
- Pan, X.; Chen, X.; Nakamura, T.; Yamaguchi, M. Incoherent reconstruction-free object recognition with mask-based lensless optics and the transformer. Opt. Express 2021, 29, 37962–37978. [Google Scholar] [CrossRef]
- Song, K.; Bian, Y.; Wu, K.; Liu, H.; Han, S.; Li, J.; Xiao, L. Single-pixel imaging based on deep learning. arXiv 2023, arXiv:2310.16869. [Google Scholar]
- Bian, L.; Wang, H.; Zhu, C.; Zhang, J. Image-free multi-character recognition. Opt. Lett. 2022, 47, 1343–1346. [Google Scholar] [CrossRef]
- Peng, L.; Xie, S.; Qin, T.; Cao, L.; Bian, L. Image-free single-pixel object detection. Opt. Lett. 2023, 48, 2527–2530. [Google Scholar] [CrossRef]
- He, Z.; Dai, S. Image-free single-pixel classifier using feature information measurement matrices. AIP Adv. 2024, 14, 045316. [Google Scholar] [CrossRef]
- Liao, Y.; Cheng, Y.; Ke, J. Dual-Task Learning for Long-Range Classification in Single-Pixel Imaging Under Atmospheric Turbulence. Electronics 2025, 14, 1355. [Google Scholar] [CrossRef]
- Ferri, F.; Magatti, D.; Lugiato, L.A.; Gatti, A. Differential Ghost Imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE Press: Bellingham, WA, USA, 2010. [Google Scholar] [CrossRef]
- Zhan, X.; Lu, H.; Yan, R.; Bian, L. Global-optimal semi-supervised learning for single-pixel image-free sensing. Opt. Lett. 2024, 49, 682–685. [Google Scholar] [CrossRef] [PubMed]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. arXiv 2019, arXiv:1905.02244. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Cheng, Y.; Ke, J.; Liao, Y. Single Pixel Optical Encryption in Atmospheric Turbulence. IEEE Photonics Technol. Lett. 2025; early access. [Google Scholar] [CrossRef]





| Dataset | Method | 0.01 | 0.03 | 0.05 | 0.10 |
|---|---|---|---|---|---|
| MNIST | Ref. [37] | 0.904 | 0.971 | 0.977 | 0.985 |
| Ours | 0.987 | 0.989 | 0.991 | 0.994 | |
| Fashion-MNIST | Ref. [37] | 0.818 | 0.862 | 0.876 | 0.881 |
| Ours | 0.898 | 0.901 | 0.906 | 0.913 |
| Dataset | Condition | NHDM | WSHDM | CCHDM | Our Model |
|---|---|---|---|---|---|
| MNIST | Noise-free | 0.593 | 0.818 | 0.897 | 0.982 |
| Noise-10.0% | 0.276 | 0.572 | 0.625 | 0.814 | |
| Noise-13.0% | 0.234 | 0.492 | 0.508 | 0.768 | |
| Noise-15.0% | 0.217 | 0.418 | 0.435 | 0.736 | |
| Fashion MNIST | Noise-free | 0.760 | 0.714 | 0.808 | 0.901 |
| Noise-10.0% | 0.659 | 0.640 | 0.754 | 0.763 | |
| Noise-13.0% | 0.609 | 0.602 | 0.710 | 0.722 | |
| Noise-15.0% | 0.582 | 0.574 | 0.682 | 0.676 |
| Sampling Rate (%) | 50 | 10 | 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Turbulence Layers | 0 | 10 | 100 | 0 | 10 | 100 | 0 | 10 | 100 |
| Dataset | NWPU-SPI | ||||||||
| Vit | 0.905 | 0.842 | 0.779 | 0.891 | 0.763 | 0.711 | 0.879 | 0.762 | 0.726 |
| Our Model | 0.973 | 0.938 | 0.883 | 0.952 | 0.862 | 0.857 | 0.914 | 0.815 | 0.801 |
| Dataset | UCM-SPI | ||||||||
| Vit | 0.562 | 0.445 | 0.348 | 0.446 | 0.376 | 0.25 | 0.413 | 0.357 | 0.227 |
| Our Model | 0.870 | 0.784 | 0.689 | 0.784 | 0.709 | 0.590 | 0.715 | 0.692 | 0.676 |
| Dataset | DOTA-SPI | ||||||||
| Vit | 0.909 | 0.864 | 0.837 | 0.871 | 0.826 | 0.778 | 0.863 | 0.822 | 0.768 |
| Our Model | 0.955 | 0.947 | 0.941 | 0.939 | 0.921 | 0.925 | 0.917 | 0.882 | 0.871 |
| Sampling Rate (%) | 50 | 10 | 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Turbulence Layers | 0 | 10 | 100 | 0 | 10 | 100 | 0 | 10 | 100 |
| Dataset | NWPU-SPI | ||||||||
| CNNB | 0.957 | 0.916 | 0.841 | 0.934 | 0.844 | 0.801 | 0.891 | 0.775 | 0.757 |
| TFB | 0.828 | 0.712 | 0.689 | 0.788 | 0.670 | 0.647 | 0.770 | 0.578 | 0.556 |
| CNNB + TFB | 0.955 | 0.844 | 0.810 | 0.895 | 0.795 | 0.738 | 0.796 | 0.772 | 0.634 |
| Dataset | UCM-SPI | ||||||||
| CNNB | 0.857 | 0.763 | 0.682 | 0.787 | 0.633 | 0.546 | 0.680 | 0.461 | 0.422 |
| TFB | 0.401 | 0.319 | 0.294 | 0.364 | 0.288 | 0.263 | 0.302 | 0.253 | 0.227 |
| CNNB + TFB | 0.828 | 0.641 | 0.651 | 0.638 | 0.426 | 0.401 | 0.404 | 0.223 | 0.226 |
| Dataset | DOTA-SPI | ||||||||
| CNNB | 0.948 | 0.938 | 0.923 | 0.926 | 0.921 | 0.907 | 0.903 | 0.892 | 0.883 |
| TFB | 0.849 | 0.827 | 0.819 | 0.792 | 0.768 | 0.712 | 0.765 | 0.728 | 0.670 |
| CNNB + TFB | 0.968 | 0.945 | 0.928 | 0.959 | 0.941 | 0.907 | 0.932 | 0.887 | 0.401 |
| Optimizer Condition | NT, sr = 3% | NT, sr = 1 | AT, sr = 3% | AT, sr = 1 |
|---|---|---|---|---|
| SGD | 0.909 | 0.962 | 0.878 | 0.947 |
| AdamW | 0.916 | 0.967 | 0.882 | 0.955 |
| Network | Parameter Count | FLOPs | Restoration |
|---|---|---|---|
| YOLOv11n | ✓ | ||
| ViT | ✓ | ||
| MobileNetV3 | ✓ | ||
| Ours | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Liao, Y.; Ke, J. Turbulence-Resilient Object Classification in Remote Sensing Using a Single-Pixel Image-Free Approach. Sensors 2025, 25, 4137. https://doi.org/10.3390/s25134137
Cheng Y, Liao Y, Ke J. Turbulence-Resilient Object Classification in Remote Sensing Using a Single-Pixel Image-Free Approach. Sensors. 2025; 25(13):4137. https://doi.org/10.3390/s25134137
Chicago/Turabian StyleCheng, Yin, Yusen Liao, and Jun Ke. 2025. "Turbulence-Resilient Object Classification in Remote Sensing Using a Single-Pixel Image-Free Approach" Sensors 25, no. 13: 4137. https://doi.org/10.3390/s25134137
APA StyleCheng, Y., Liao, Y., & Ke, J. (2025). Turbulence-Resilient Object Classification in Remote Sensing Using a Single-Pixel Image-Free Approach. Sensors, 25(13), 4137. https://doi.org/10.3390/s25134137







