Computational Adaptive Optics for HAR Hybrid Trench Array Topography Measurement by Utilizing Coherence Scanning Interferometry
Abstract
1. Introduction
2. Methods
2.1. Influence of Sample-Induced Aberrations on PSF
2.2. Modeling of Derived Aberrations Caused by HAR Hybrid Trench Array
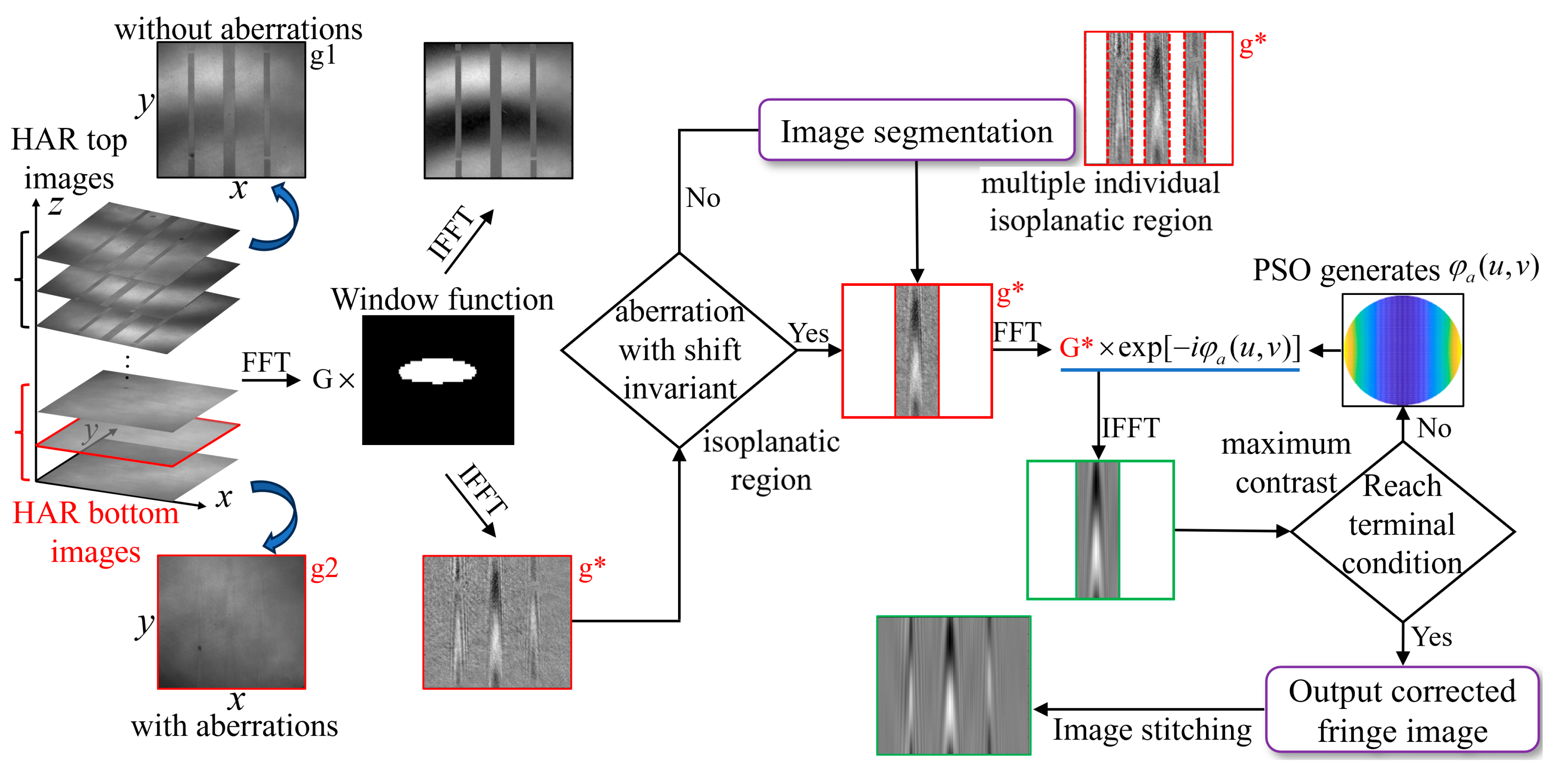
2.3. Principle of CAO
2.4. PSO Algorithm
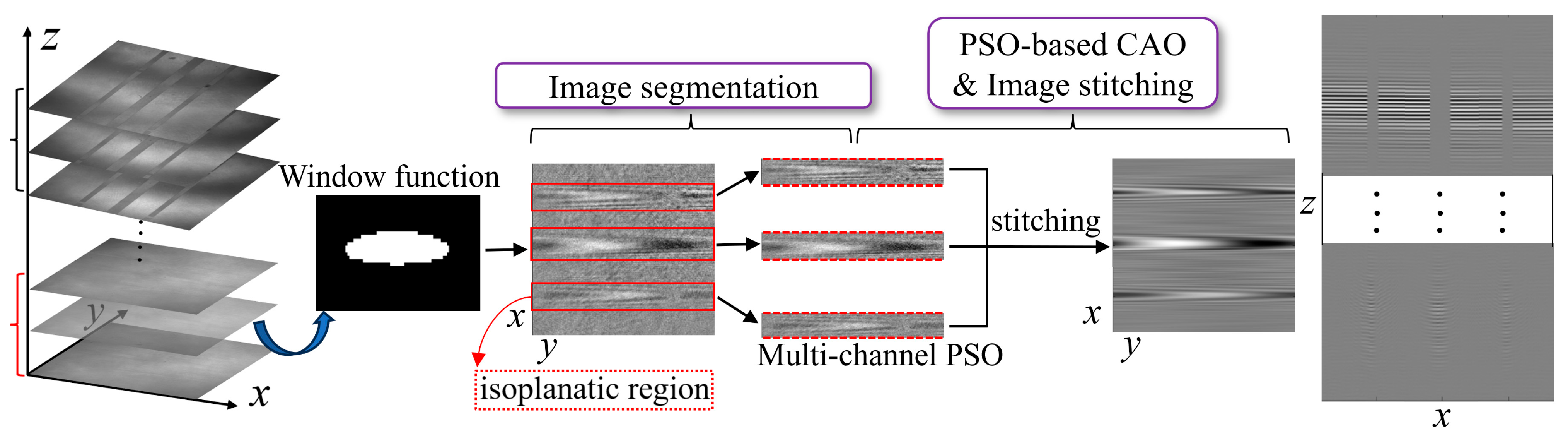
2.5. Separated the Interference Signal by a Window Function
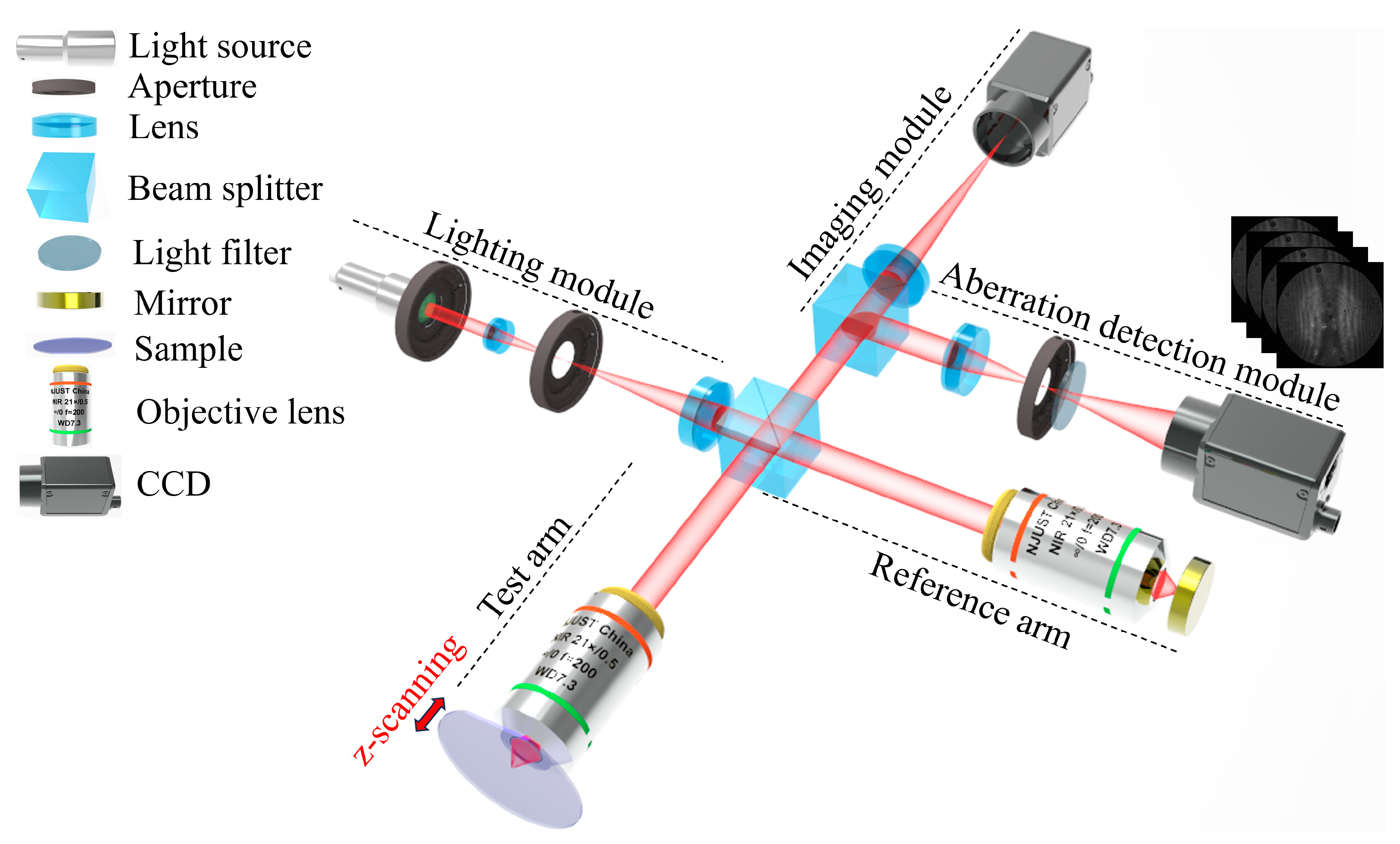
3. Experimental Results and Discussions
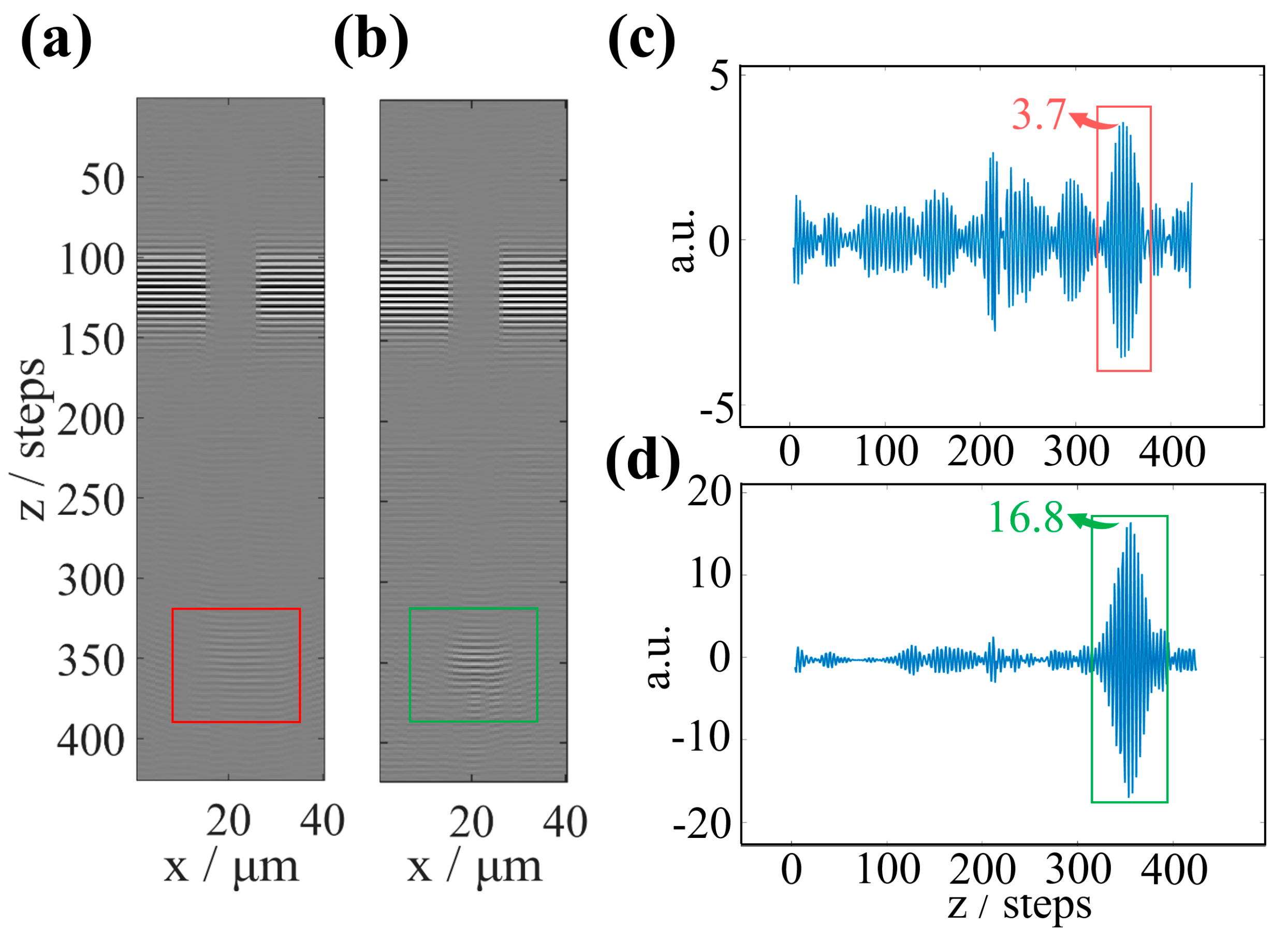
3.1. Aberration Correction for HAR Single Trench
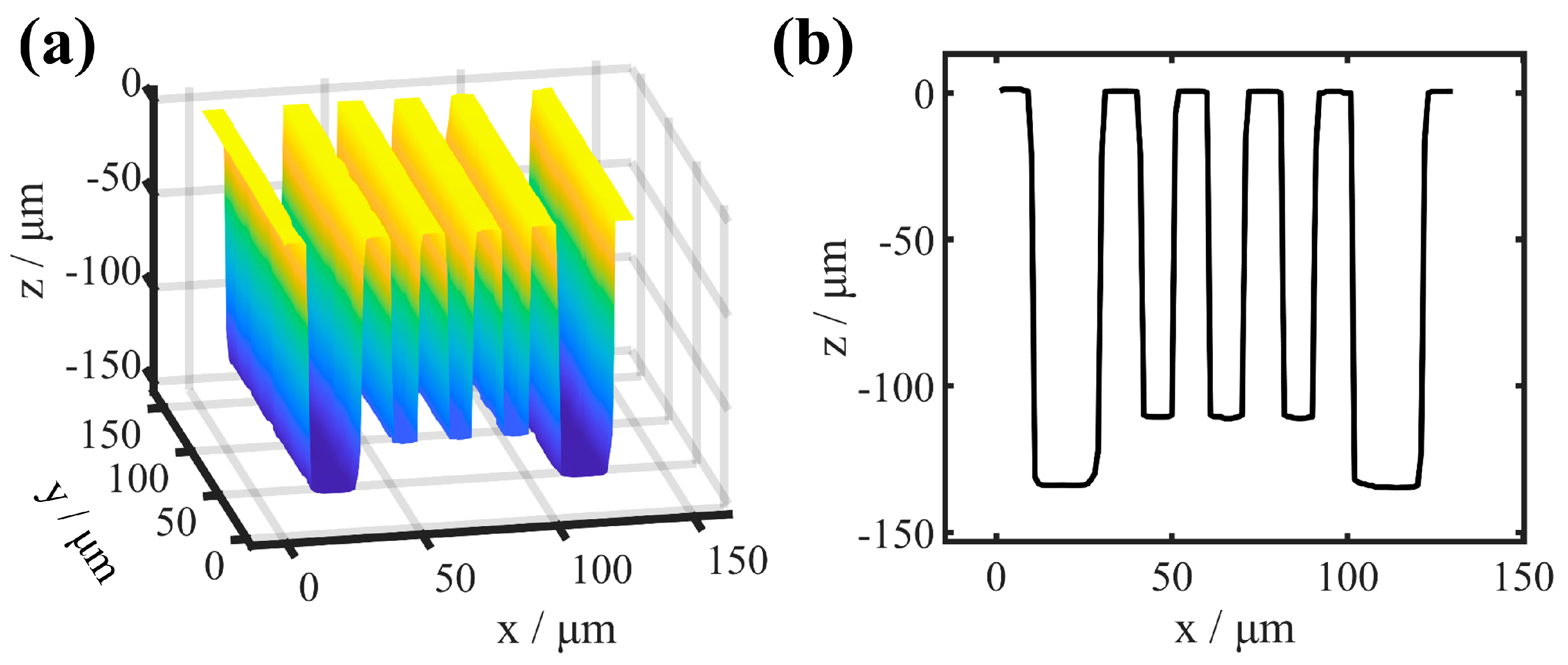
3.2. Aberration Correction for HAR Hybrid Trench Array
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HAR | High aspect ratio |
| CSI | Coherence scanning interferometry |
| PSO | Particle swarm optimization |
| 3D-TF | 3D transfer function |
| CAO | Computational adaptive optics |
| PSF | Point-spread function |
| ASM | Angular spectrum method |
| NA | Numerical aperture |
| FDTD | Finite-difference time-domain |
| CTF | Coherent transfer function |
| DC | Direct current |
| AC | Alternating current |
| RMS | Root mean square |
References
- Gambino, J.P.; Adderly, S.A.; Knickerbocker, J.U. An overview of through-silicon-via technology and manufacturing challenges. Microelectron. Eng. 2015, 135, 73–106. [Google Scholar] [CrossRef]
- Lee, S.W.; Park, S.J.; Campbell, E.E.B.; Park, Y.W. A fast and low-power microelectromechanical system-based non-volatile memory device. Nat. Commun. 2011, 2, 220. [Google Scholar] [CrossRef]
- Li, S.; Feng, H.; Lou, W.; Zhao, Y.; Lv, S.; Kan, W. Design and Testing of MEMS Component for Electromagnetic Pulse Protection. Sensors 2025, 25, 221. [Google Scholar] [CrossRef] [PubMed]
- Presutti, F.; Monticone, F. Focusing on bandwidth: Achromatic metalens limits. Optica 2020, 7, 624–631. [Google Scholar] [CrossRef]
- Kim, J.H. High precision signal processing algorithm for white light interferometry. Sensors 2008, 8, 7609–7635. [Google Scholar] [CrossRef] [PubMed]
- Marbach, S.; Claveau, R.; Wang, F.; Schiffler, J.; Montgomery, P.; Flury, M. Wide-field parallel mapping of local spectral and topographic information with white light interference microscopy. Opt. Lett. 2021, 46, 809–812. [Google Scholar] [CrossRef]
- Jo, T.; Kim, S.; Pahk, H. 3D measurement of TSVs using low numerical aperture white-light scanning interferometry. J. Opt. Soc. Korea 2013, 17, 317–322. [Google Scholar] [CrossRef]
- Sun, Y.F.; Gao, Z.S.; Ma, J.Q.; Zhou, J.; Xie, P.; Wang, L.; Lei, L.; Fu, Y.; Guo, Z.; Yuan, Q. Surface topography measurement of microstructures near the lateral resolution limit via coherence scanning interferometry. Opt. Lasers Eng. 2022, 152, 106949. [Google Scholar] [CrossRef]
- Ji, N. Adaptive optical fluorescence microscopy. Nat. Methods 2017, 14, 374–380. [Google Scholar] [CrossRef]
- Fuh, Y.K.; Fan, J.R.; Huang, C.Y.; Jang, S.C. In-process surface roughness measurement of bulk metallic glass using an adaptive optics system for aberration correction. Measurement 2013, 46, 4200–4205. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, Q.I.; Berlage, C.; Kner, P.; Judkewitz, B.; Booth, M.; Ji, N. Adaptive optics for optical microscopy. Biomed. Opt. Express 2023, 14, 1732–1756. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.Q.; Yuan, Q.; Gao, Z.S.; Huo, X.; Xu, Z.; Zhang, J.; Fan, X.; Zhu, D.; Guo, Z.; Lei, L.; et al. Three-dimensional topography of high-aspect ratio trenches by sample-induced aberration-compensable coherence scanning interferometry. ACS Photonics 2024, 11, 1068–1077. [Google Scholar] [CrossRef]
- Iyer, R.R.; Liu, Y.Z.; Boppart, S.A. Automated sensorless single-shot closed-loop adaptive optics microscopy with feedback from computational adaptive optics. Opt. Express 2019, 27, 12998–13014. [Google Scholar] [CrossRef] [PubMed]
- Saathof, R.; Schutten, G.J.; Spronck, J.W.; Schmidt, R.H.M. Design and characterisation of an active mirror for EUV-lithography. Precis. Eng. 2015, 41, 102–110. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, R.; Žurauskas, M.; Pande, P.; Bi, J.; Yuan, Q.; Wang, L.; Gao, Z.; Boppart, S.A. Automated fast computational adaptive optics for optical coherence tomography based on a stochastic parallel gradient descent algorithm. Opt. Express 2020, 28, 23306–23319. [Google Scholar] [CrossRef]
- Qiao, W.Y.; Gao, Z.S.; Zhu, D.; Chen, L.; Guo, Z.; Jianqiu, M.; Huo, X.; Xiaoxin, F.; Zhang, J.; Li, Y.; et al. Research on the modulation aberration numerical correction method of interference signals for high aspect ratio samples utilizing coherence scanning interferometry. Opt. Express 2025, 33, 330–343. [Google Scholar] [CrossRef]
- Adie, S.G.; Graf, B.W.; Ahmad, A.; Carney, P.S.; Boppart, S.A. Computational adaptive optics for broadband optical interferometric tomography of biological tissue. Proc. Natl. Acad. Sci. USA 2012, 109, 7175–7180. [Google Scholar] [CrossRef]
- Pande, P.; Liu, Y.Z.; South, F.A.; Boppart, S.A. Automated computational aberration correction method for broadband interferometric imaging techniques. Opt. Lett. 2016, 41, 3324–3327. [Google Scholar] [CrossRef]
- Bonora, S.; Zawadzki, R.J. Wavefront sensorless modal deformable mirror correction in adaptive optics: Optical coherence tomography. Opt. Lett. 2013, 38, 4801–4804. [Google Scholar] [CrossRef]
- Polans, J.; Cunefare, D.; Cole, E.; Keller, B.; Mettu, P.S.; Cousins, S.W.; Allingham, M.J.; Izatt, J.A.; Farsiu, S. Enhanced visualization of peripheral retinal vasculature with wavefront sensorless adaptive optics optical coherence tomography angiography in diabetic patients. Opt. Lett. 2016, 42, 17–20. [Google Scholar] [CrossRef]
- Li, L.J.; Liu, T.F.; Sun, M.J. Phase retrieval utilizing particle swarm optimization. IEEE Photonics J. 2017, 10, 7800109. [Google Scholar] [CrossRef]
- Boga, Z.; Sándor, C.; Kovács, P. A Multidimensional Particle Swarm Optimization-Based Algorithm for Brain MRI Tumor Segmentation. Sensors 2025, 25, 2800. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.G.; Yang, C.L.; Xu, Z.H.; Cao, Z.L.; Mu, Q.Q.; Xuan, L. Hybrid particle swarm global optimization algorithm for phase diversity phase retrieval. Opt. Express 2016, 24, 25704–25717. [Google Scholar] [CrossRef] [PubMed]
- Liang, M.; Wang, Y.; Wang, C. Multi-objective fractional-order particle swarm optimization algorithms for data processing of multi-wavelength pyrometer. Opt. Express 2023, 31, 33638–33654. [Google Scholar] [CrossRef]
- Coupland, J.; Mandal, R.; Palodhi, K.; Leach, R. Coherence scanning interferometry: Linear theory of surface measurement. Appl. Opt. 2013, 52, 3662–3670. [Google Scholar] [CrossRef]
- Su, R.; Coupland, J.; Sheppard, C.; Leach, R. Scattering and three-dimensional imaging in surface topography measuring interference microscopy. J. Opt. Soc. Am. A 2021, 38, 27–42. [Google Scholar] [CrossRef]
- Su, R.; Wang, Y.; Coupland, J.; Leach, R. On tilt and curvature dependent errors and the calibration of coherence scanning interferometry. Opt. Express 2017, 25, 3297–3310. [Google Scholar] [CrossRef]
- Su, R.; Thomas, M.; Leach, R.; Coupland, J. Effects of defocus on the transfer function of coherence scanning interferometry. Opt. Lett. 2017, 43, 82–85. [Google Scholar] [CrossRef]
- McCutchen, C.W. Generalized aperture and the three-dimensional diffraction image. J. Opt. Soc. Am. 1964, 54, 240–244. [Google Scholar] [CrossRef]
- Ma, J.Q.; Huo, X.; Zhang, J.L.; Fan, X.; Xu, Z.; Qiao, W.; Li, Y.; Wang, Y.; Zhu, D.; Guo, Z.; et al. Topography reconstruction of high aspect ratio silicon trench array via near-infrared coherence scanning interferometry. Opt. Express 2024, 32, 22493–22507. [Google Scholar] [CrossRef]
- Liu, J.; Hooshmand, H.; Piano, S.; Leach, R.; Coupland, J.; Ren, M.; Zhu, L.; Su, R. Extracing focus varalion data from coherence scaning intererometic measurementsy. Precis. Eng. 2024, 88, 699–706. [Google Scholar] [CrossRef]
- Sheppard, C.J.; Kou, S.S.; Lin, J. The Green-function transform and wave propagation. Front. Phys. 2014, 2, 67. [Google Scholar] [CrossRef]
- Wang, Z.; Ziou, D.; Armenakis, C.; Li, D.; Li, Q. A comparative analysis of image fusion methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1391–1402. [Google Scholar] [CrossRef]
- Wu, H.; Bao, C.; Hao, Q.; Cao, J.; Zhang, L. Improved Unsupervised Stitching Algorithm for Multiple Environments SuperUDIS. Sensors 2024, 24, 5352. [Google Scholar] [CrossRef]
- Kulkarni, S.C.; Rege, P.P. Pixel level fusion techniques for SAR and optical images: A review. Inf. Fusion 2020, 59, 13–29. [Google Scholar] [CrossRef]
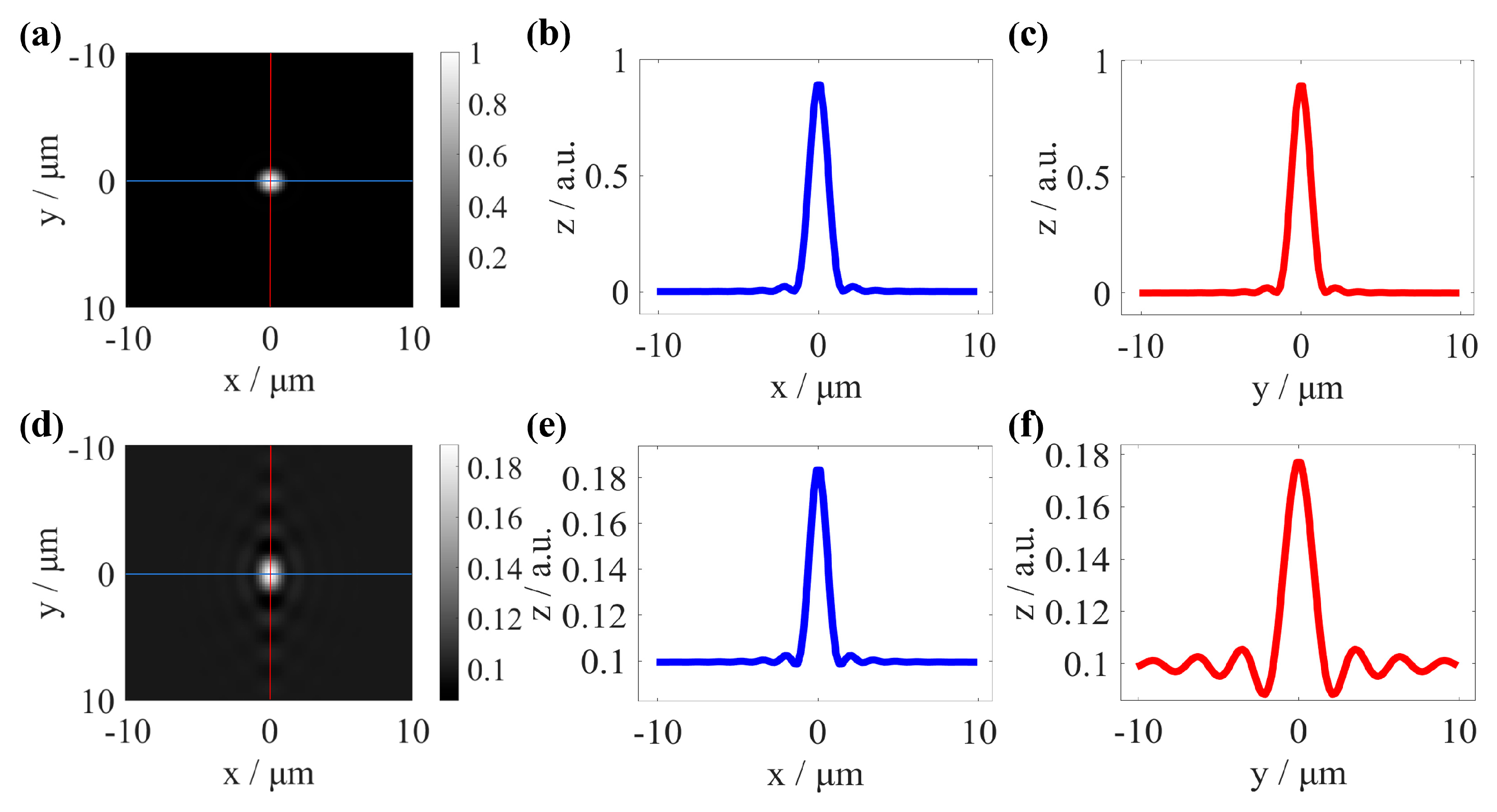
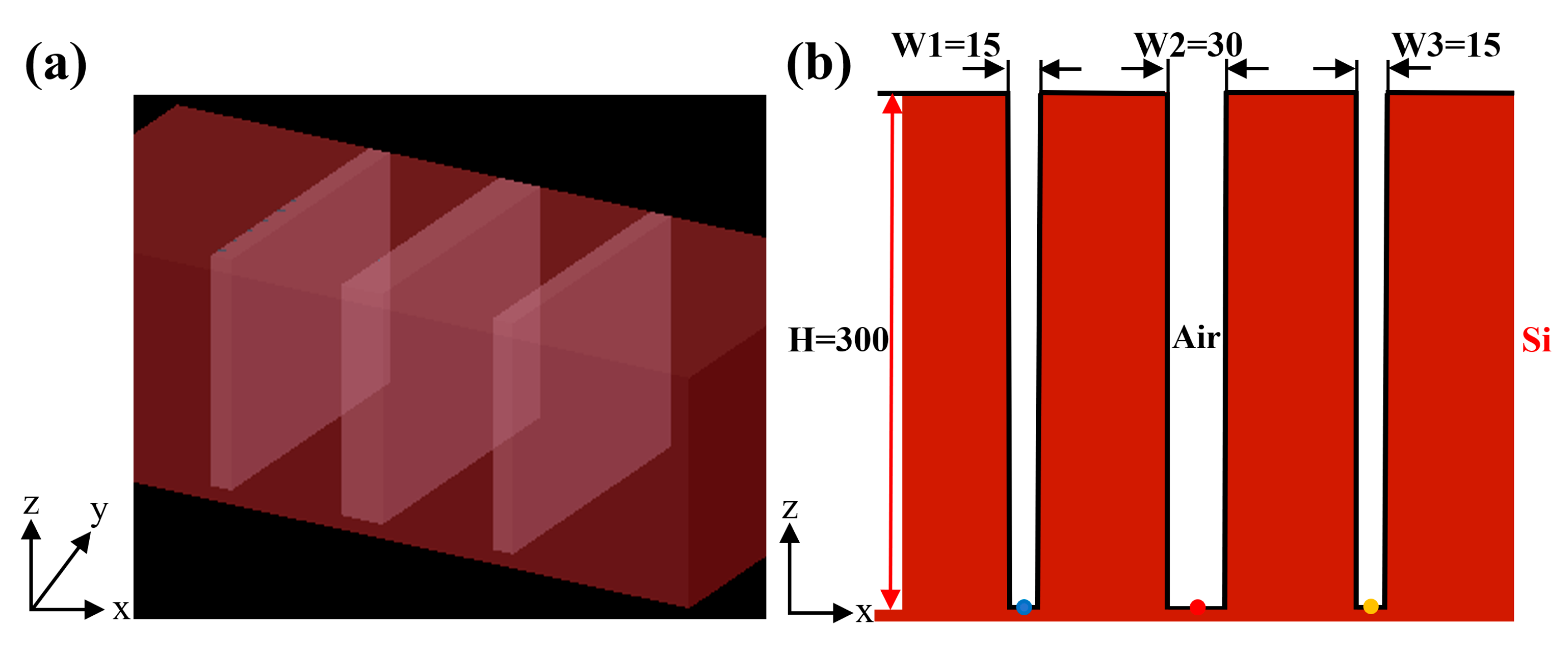
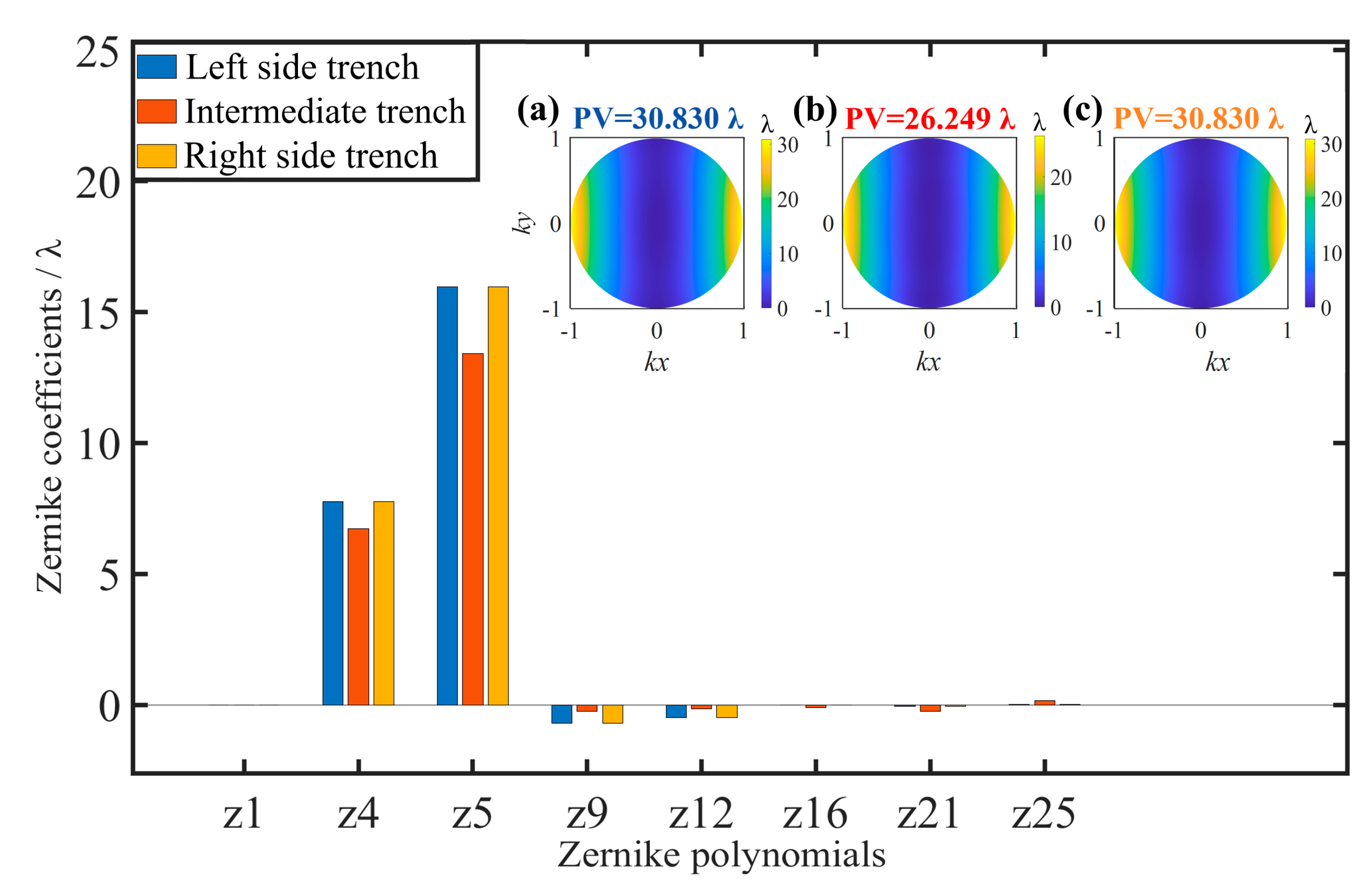

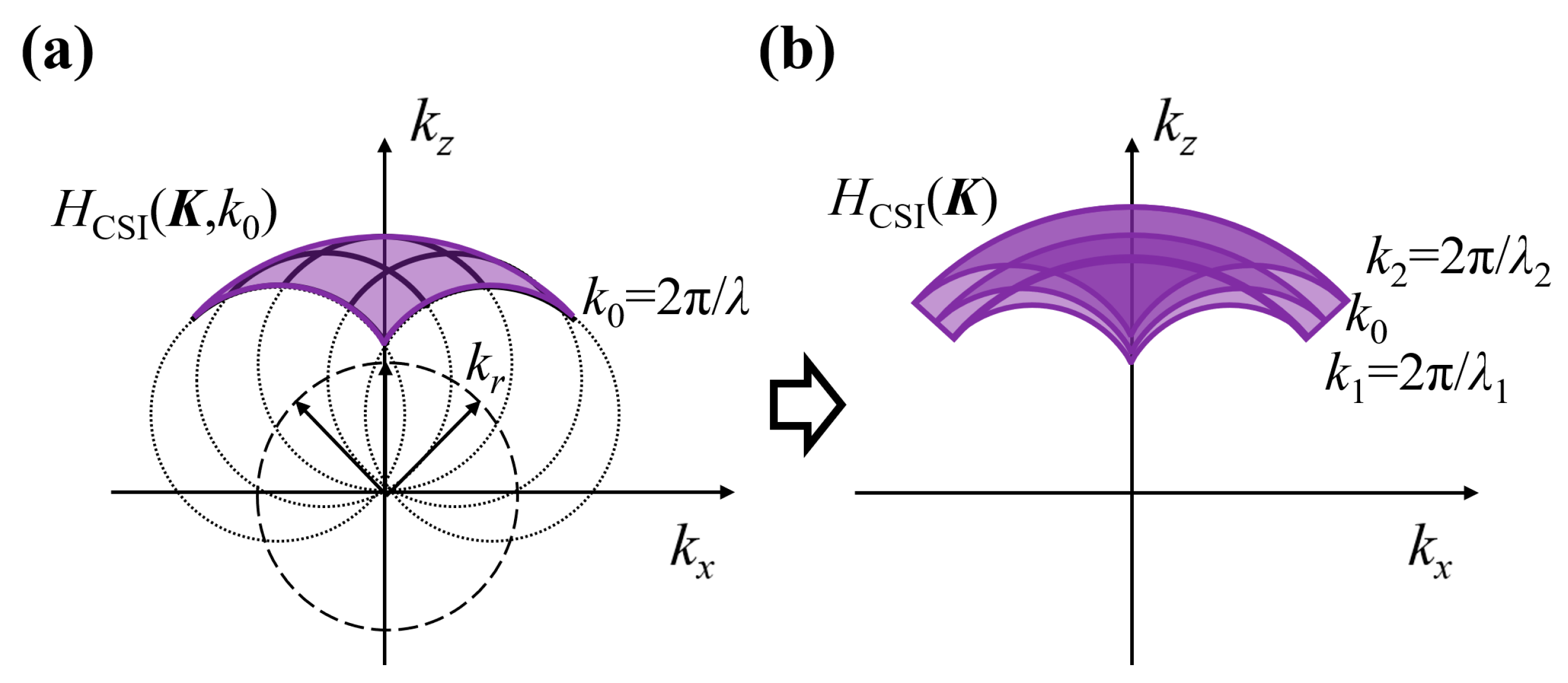




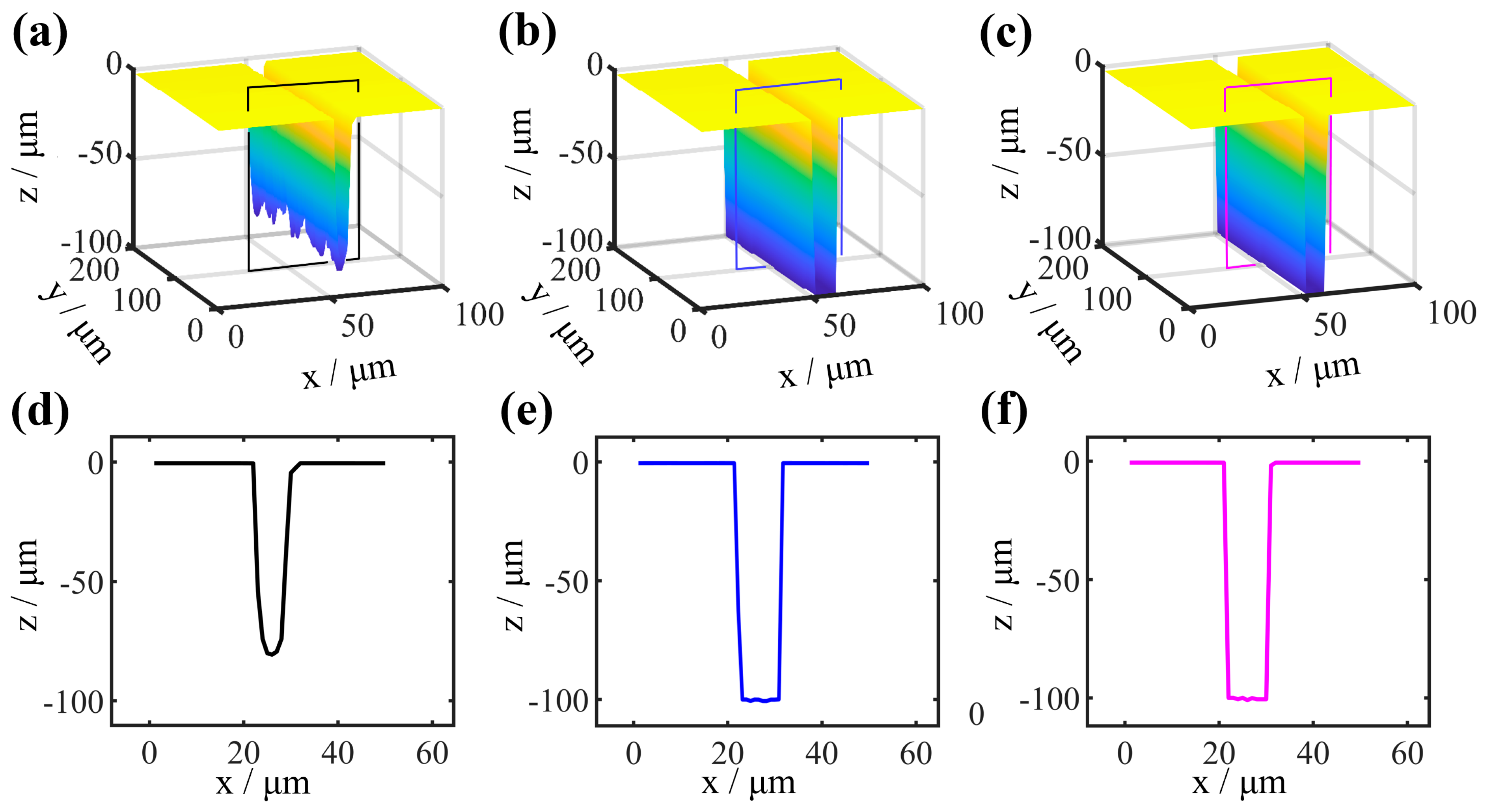

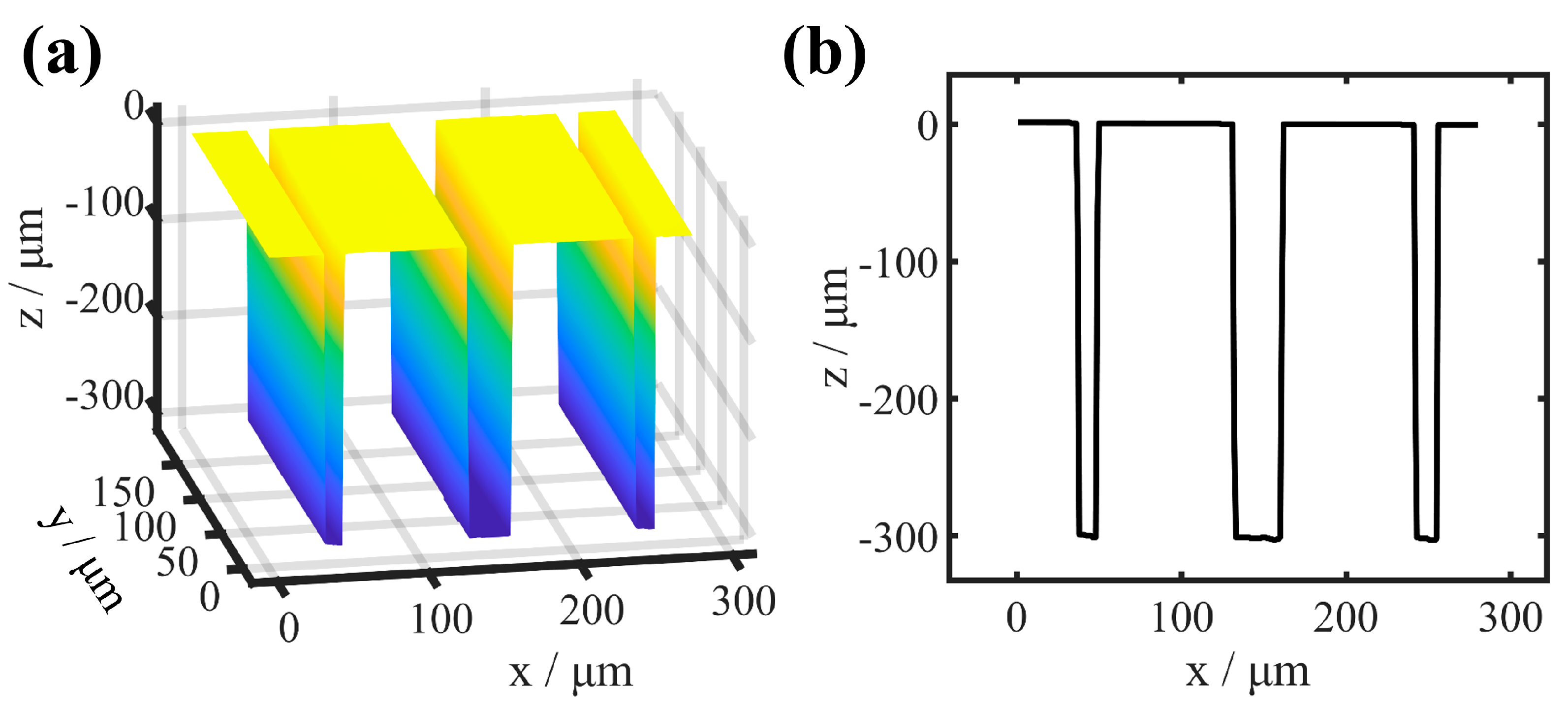
| Single Trench (Sample 1) | Trench | ||
|---|---|---|---|
| Depth/μm | 101.77 | ||
| Width/μm | 10.97 | ||
| HAR | 10:1 | ||
| Hybrid trench array (sample 2) | Trench 1 | Trench 2 | Trench 3 |
| Depth/μm | 15.00 | 30.16 | 15.01 |
| Width/μm | 299.96 | 300.02 | 300.05 |
| HAR | 20:1 | 10:1 | 20:1 |
| Hybrid trench array (sample 3) | Trench 1 | Trenches 2/3/4 (mean value) | Trench 5 |
| Depth/μm | 21.35 | 10.61 | 20.80 |
| Width/μm | 127.30 | 109.25 | 127.00 |
| HAR | 6:1 | 10:1 | 6:1 |
| Type of Interferogram | Pixel Size | Number of Iteration | Processing Time/s |
|---|---|---|---|
| Interferogram (Figure 9a) | 200 × 200 | 40 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, W.; Gao, Z.; Yuan, Q.; Chen, L.; Guo, Z.; Huo, X.; Wang, Q. Computational Adaptive Optics for HAR Hybrid Trench Array Topography Measurement by Utilizing Coherence Scanning Interferometry. Sensors 2025, 25, 4085. https://doi.org/10.3390/s25134085
Qiao W, Gao Z, Yuan Q, Chen L, Guo Z, Huo X, Wang Q. Computational Adaptive Optics for HAR Hybrid Trench Array Topography Measurement by Utilizing Coherence Scanning Interferometry. Sensors. 2025; 25(13):4085. https://doi.org/10.3390/s25134085
Chicago/Turabian StyleQiao, Wenyou, Zhishan Gao, Qun Yuan, Lu Chen, Zhenyan Guo, Xiao Huo, and Qian Wang. 2025. "Computational Adaptive Optics for HAR Hybrid Trench Array Topography Measurement by Utilizing Coherence Scanning Interferometry" Sensors 25, no. 13: 4085. https://doi.org/10.3390/s25134085
APA StyleQiao, W., Gao, Z., Yuan, Q., Chen, L., Guo, Z., Huo, X., & Wang, Q. (2025). Computational Adaptive Optics for HAR Hybrid Trench Array Topography Measurement by Utilizing Coherence Scanning Interferometry. Sensors, 25(13), 4085. https://doi.org/10.3390/s25134085







