U-Net Inspired Transformer Architecture for Multivariate Time Series Synthesis
Abstract
1. Introduction
- Dual-attention (DA) Mechanisms in U-Net Framework: The proposed TS-MSDA U-Net model integrates a hierarchical encoder–decoder structure for multiscale temporal feature extraction with DA mechanisms, comprising both sequence attention (SA) and channel attention (CA), effectively capturing complex temporal dynamics in multivariate time series data.
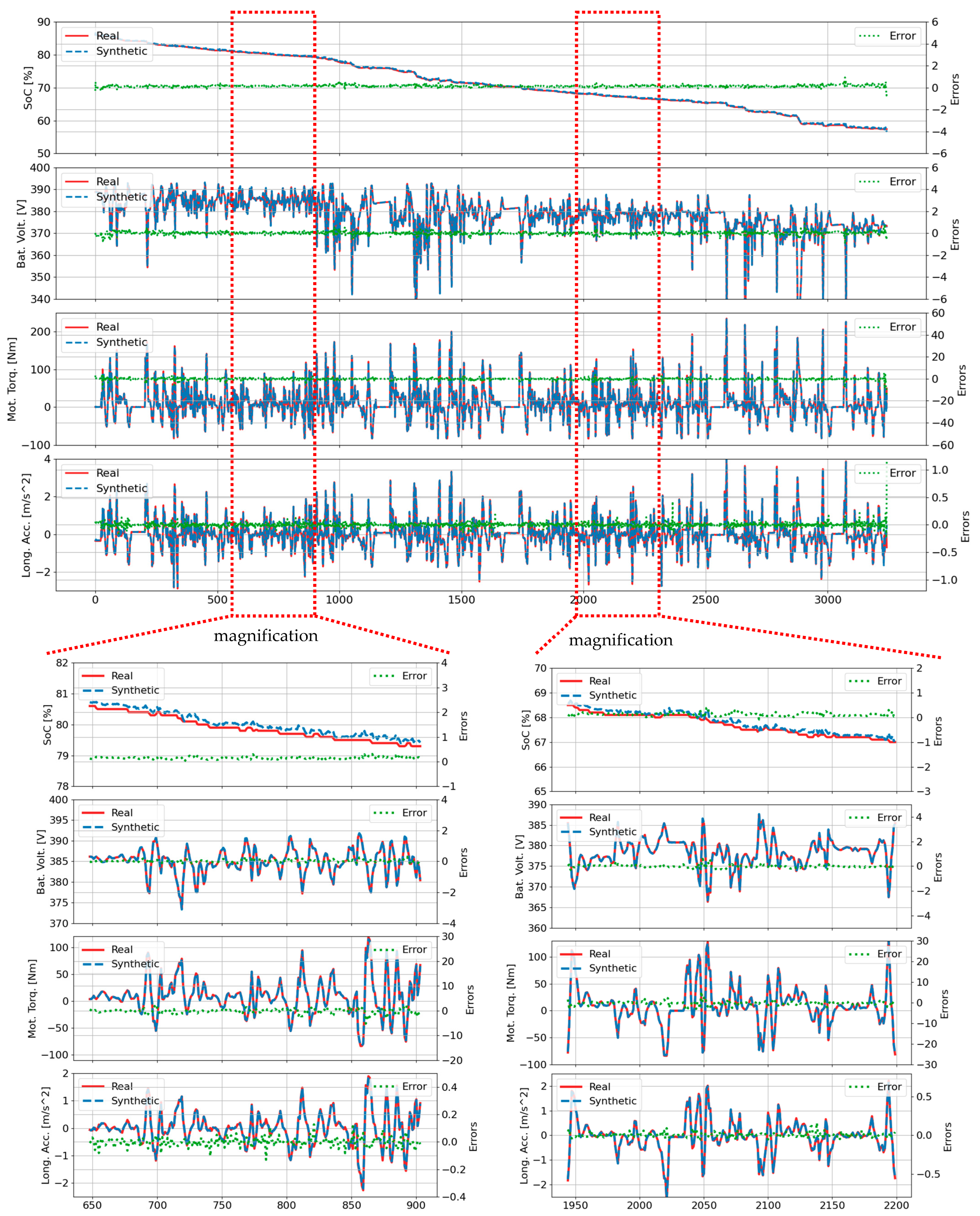
- Enhanced TSS for EVs: The proposed model achieves low mean absolute errors (MAEs), all within 1% of ground truth values, across key EV parameters (battery SOC, voltage, acceleration, and torque) using an open-source dataset from 70 real-world trips. Compared to the baseline TS-p2pGAN model, it yields a two-fold reduction in MAE.
- High-Resolution Signal Reconstruction: The TS-MSDA U-Net achieves a 36× enhancement in signal resolution from low-speed ADC data of a resonant CLLC half-bridge converter, successfully capturing complex nonlinear mappings where the basic U-Net models failed.
- Cross-Domain Validation and Attention Mechanism Analysis: The model is validated across two distinct engineering domains: automotive and power electronics, demonstrating generalizability. In the automotive domain, the baseline U-Net already achieves strong performance over TS-p2pGAN, and the addition of the DA mechanism yields a modest improvement of approximately 0.2–0.3% in MAE and RMSE metrics. Conversely, for high-frequency signal reconstruction in the resonant CLLC converter, the DA module is essential: The basic U-Net fails to capture waveform details, while the DA-enhanced model achieves successful reconstruction. This contrast highlights the DA module’s critical role in tasks requiring fine-grained temporal–spatial representation and provides insight into its domain-dependent effectiveness.
2. Materials and Methods
2.1. Hierarchical Encoder–Decoder Network
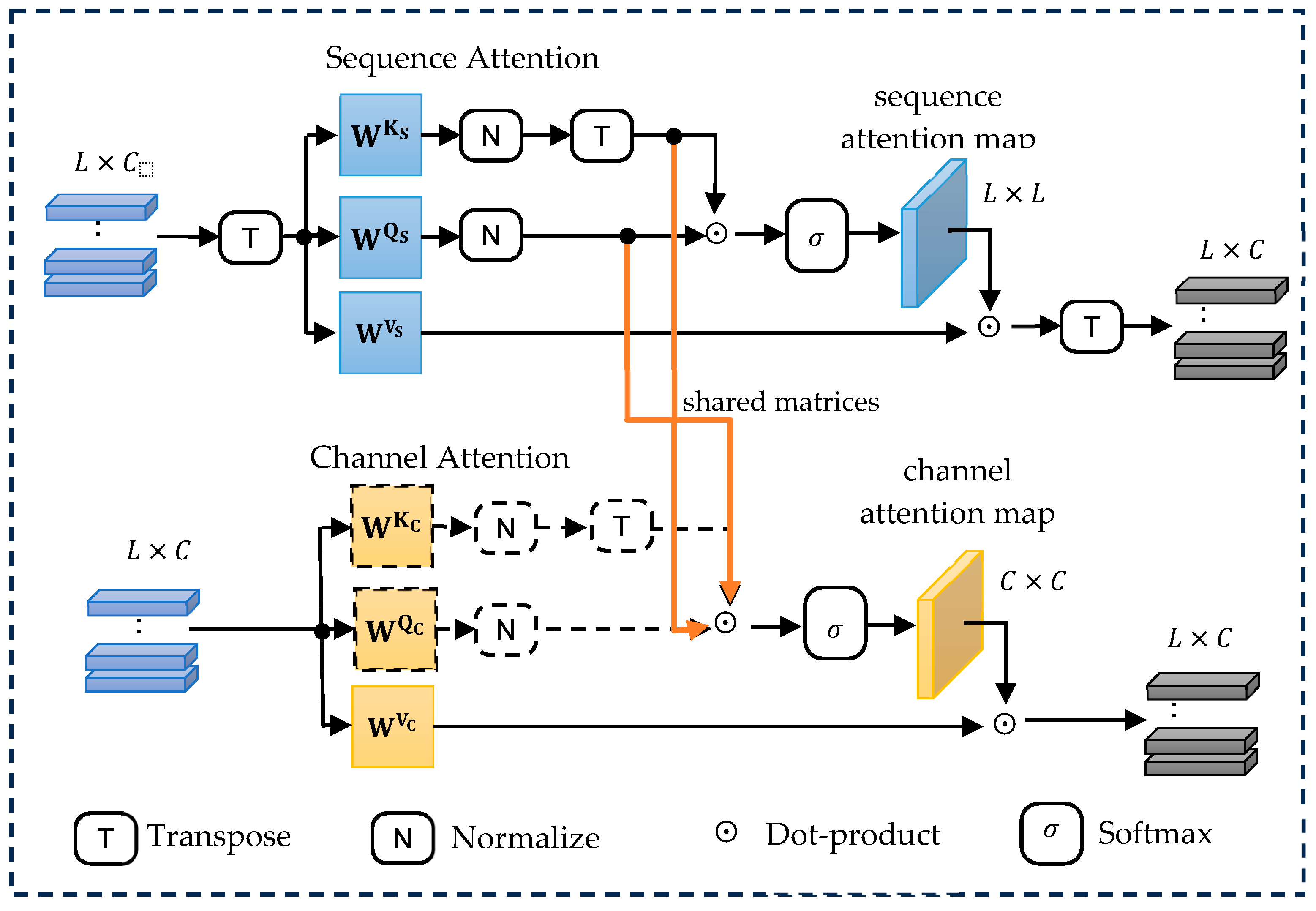
2.2. Dual-Attention Block
2.2.1. Learned Positional Embedding
2.2.2. Sequence Attention Module
2.2.3. Channel Attention Module
2.2.4. Shared Query/Key Projections and Feature Fusion
3. Experimental Setup and Results
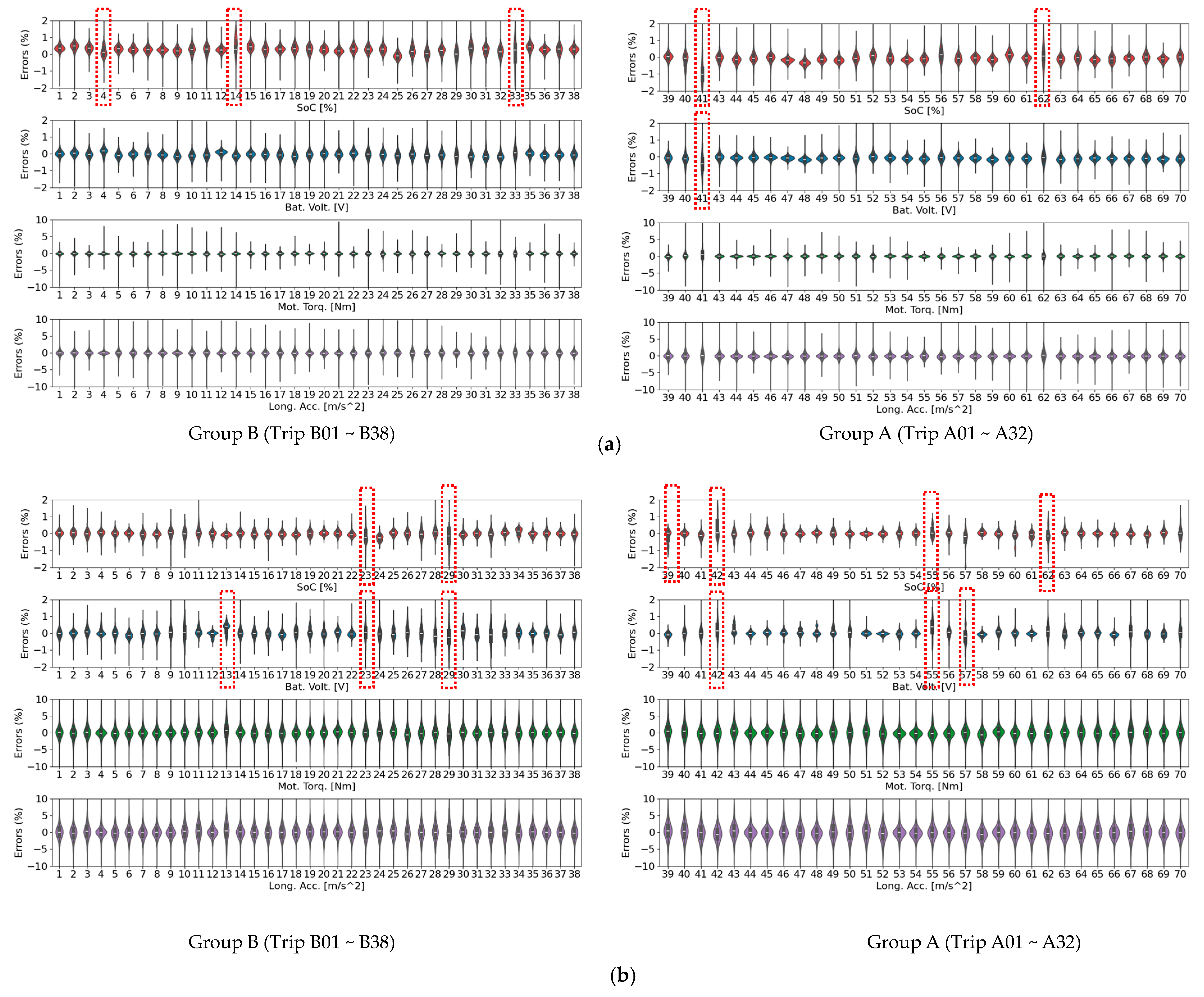
3.1. Vehcile Trip Dataset
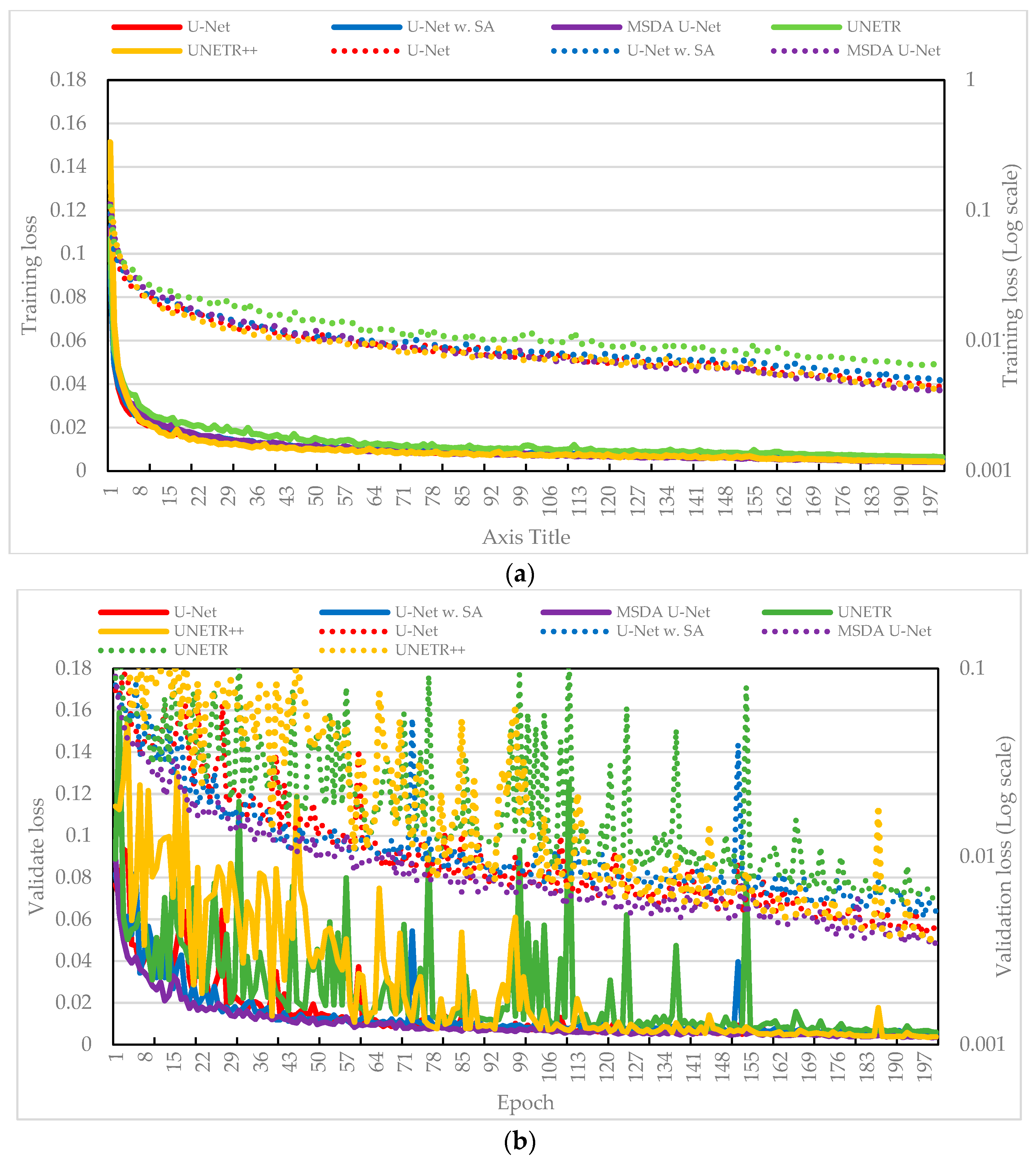
Baseline Comparison
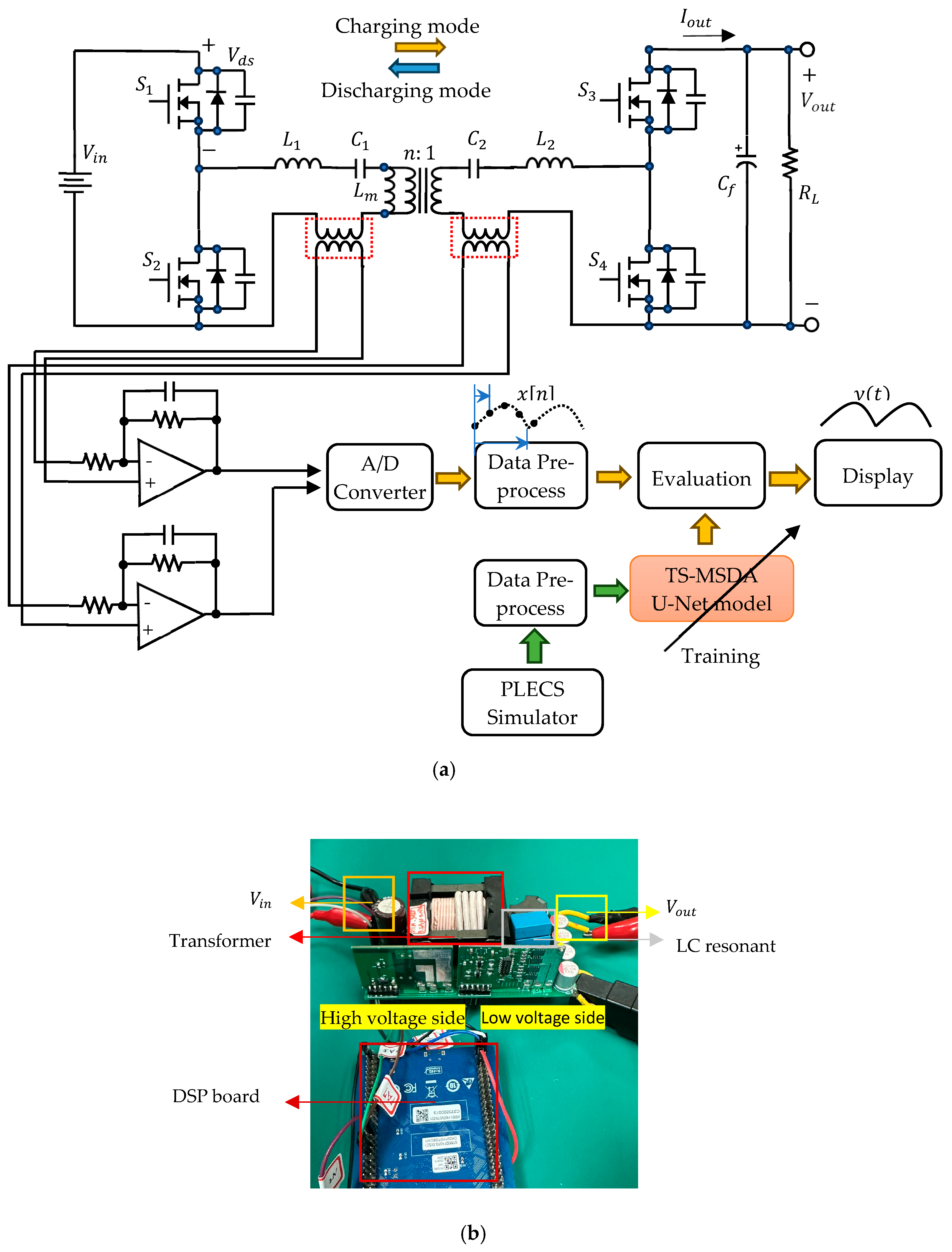
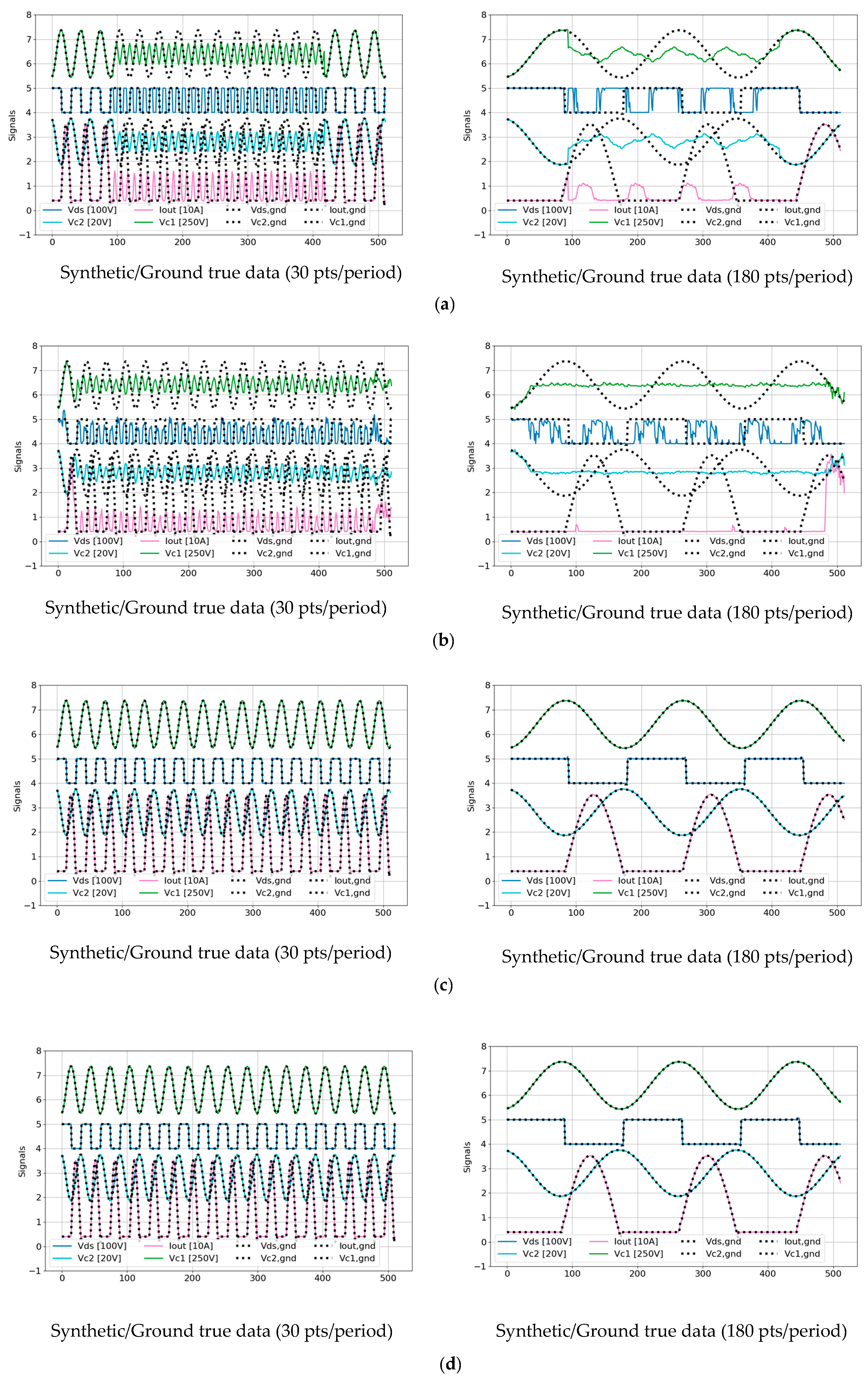
3.2. Reconstruction of Periodic Signals for Resonant CLLC Half-Bridge Converters
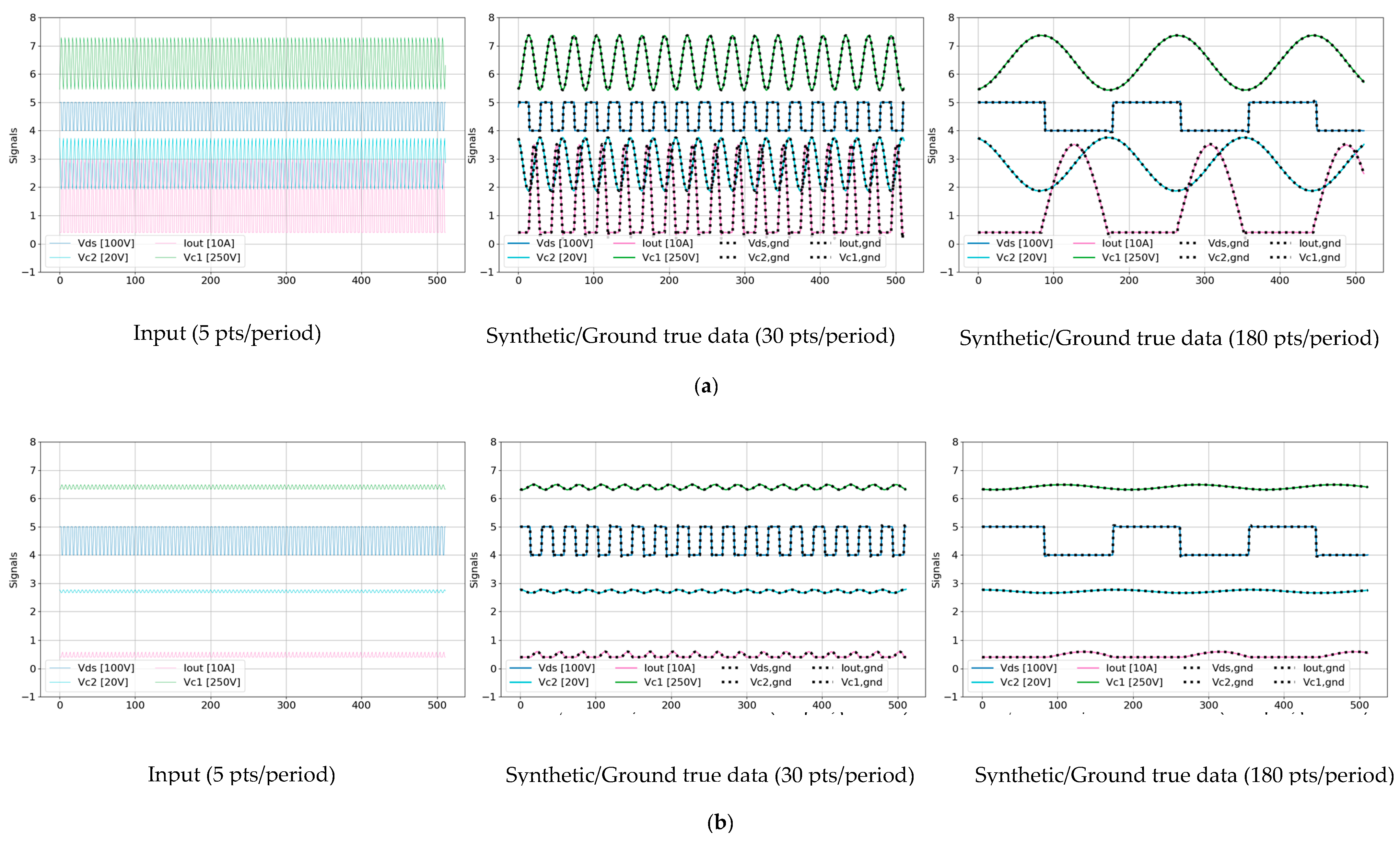
3.2.1. Generation of Training Time Series Data Using the PLECS Simulator
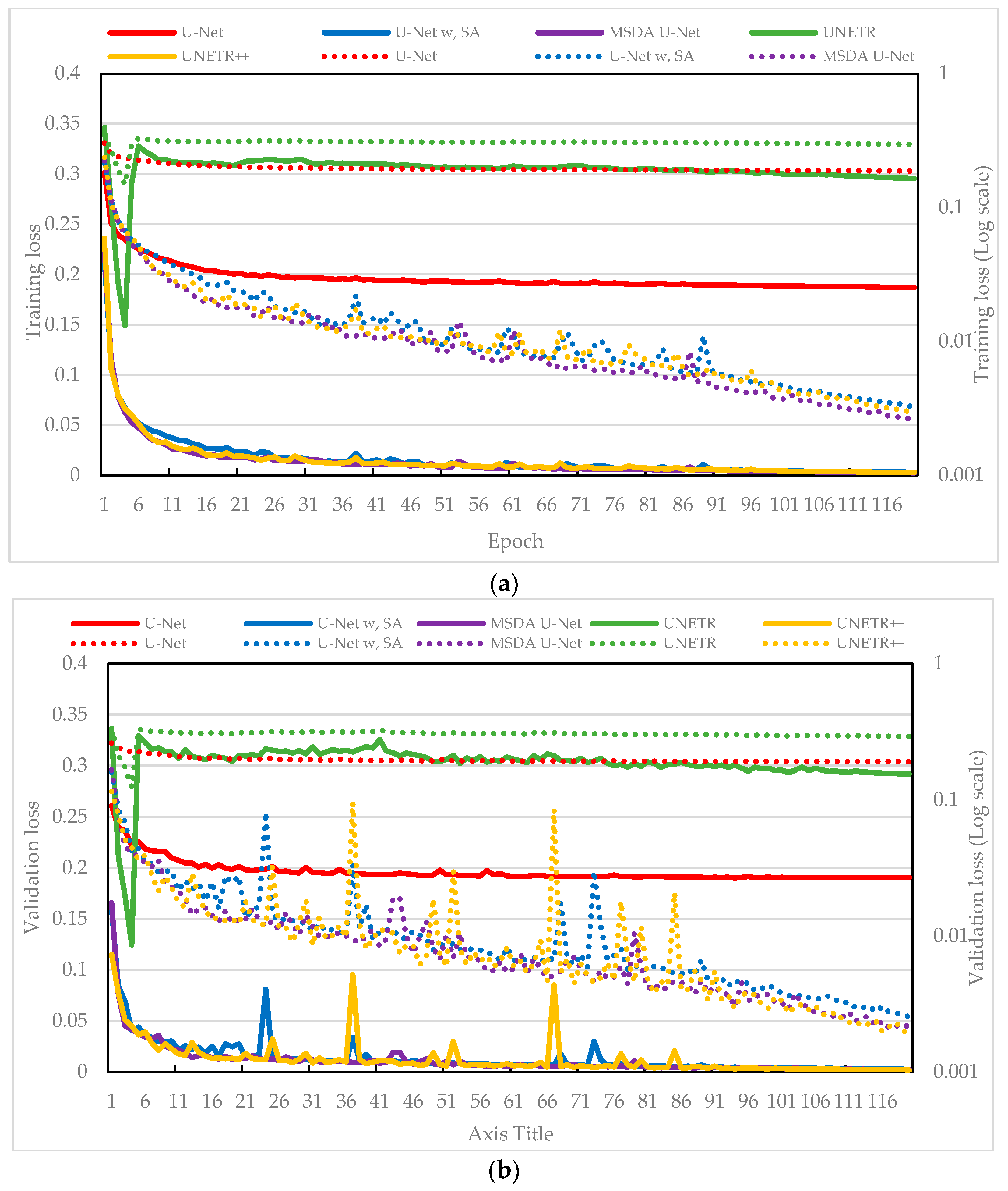
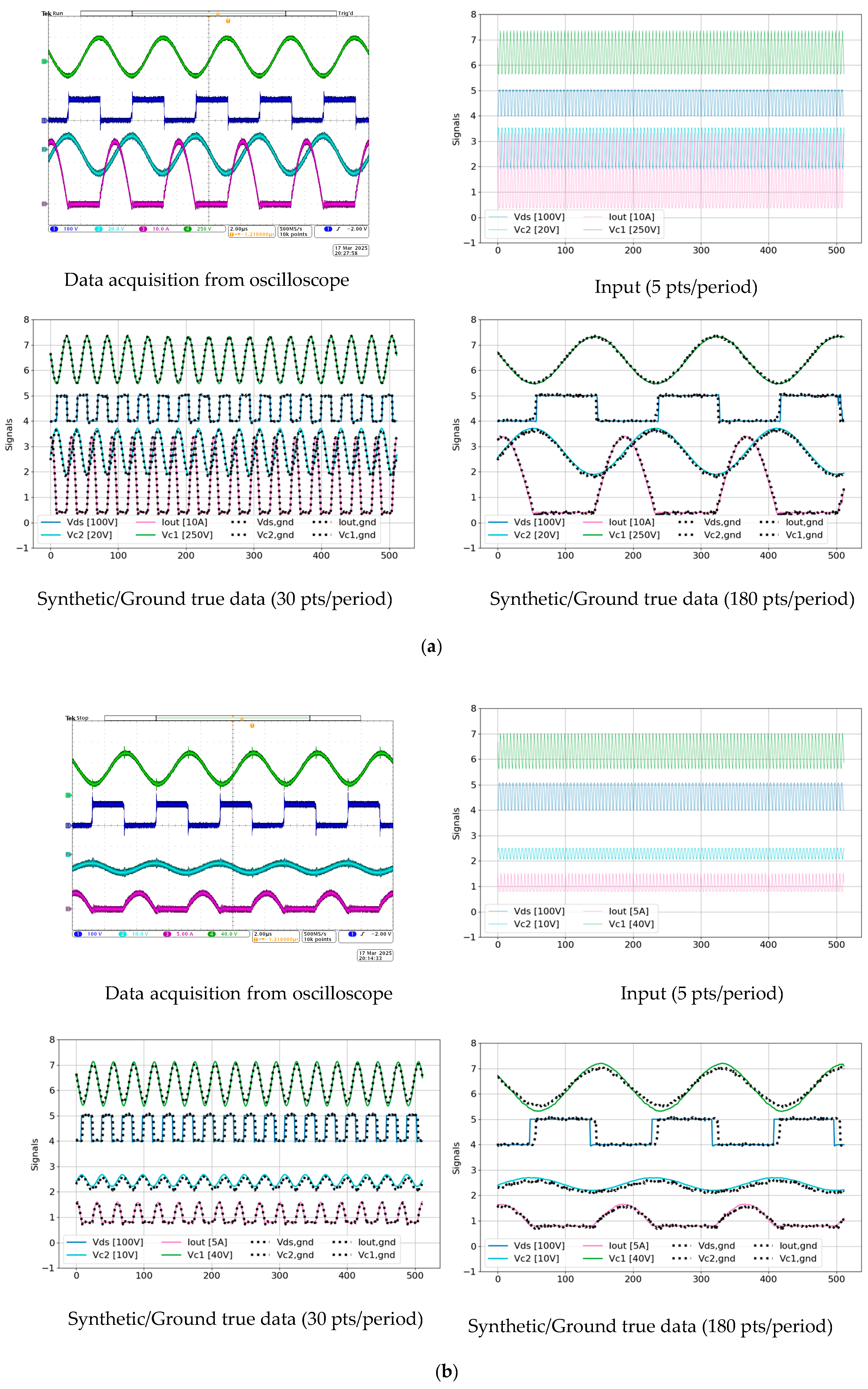
3.2.2. Analysis of Training Experimental Results
3.2.3. Testing Experimental Results Using the Prototype Converters
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iglesias, G.; Talavera, E.; González-Prieto, Á.; Mozo, A.; Gómez-Canaval, S. Data Augmentation Techniques in Time Series Domain: A Survey and Taxonomy. Neural Comput. Appl. 2023, 35, 10123–10145. [Google Scholar] [CrossRef]
- Sommers, A.; Ramezani, S.B.; Cummins, L.; Mittal, S.; Rahimi, S.; Seale, M.; Jaboure, J. Generating Synthetic Time Series Data for Cyber-Physical Systems. In Proceedings of the 2024 IEEE 10th World Forum on Internet of Things (WF-IoT), Boston, MA, USA, 1–7 November 2024; pp. 1–7. [Google Scholar]
- Brophy, E.; Wang, Z.; She, Q.; Ward, T. Generative Adversarial Networks in Time Series: A Systematic Literature Review. ACM Comput. Surv. 2023, 55, 199. [Google Scholar] [CrossRef]
- Tang, P.; Li, Z.; Wang, X.; Liu, X.; Mou, P. Time Series Data Augmentation for Energy Consumption Data Based on Improved TimeGAN. Sensors 2025, 25, 493. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Peng, X.; Zhao, L.; Zhang, S.; Metaxas, D.N. CR-GAN: Learning Complete Representations for Multi-View Generation. arXiv 2018, arXiv:1806.11191. [Google Scholar]
- El Fallah, S.; Kharbach, J.; Hammouch, Z.; Rezzouk, A.; Jamil, M.O. State of Charge Estimation of an Electric Vehicle’s Battery Using Deep Neural Networks: Simulation and Experimental Results. J. Energy Storage 2023, 62, 106904. [Google Scholar] [CrossRef]
- Jeng, S.L. Generative Adversarial Network for Synthesizing Multivariate Time-Series Data in Electric Vehicle Driving Scenarios. Sensors 2025, 25, 749. [Google Scholar] [CrossRef] [PubMed]
- Rotem, Y.; Shimoni, N.; Rokach, L.; Shapira, B. Transfer Learning for Time Series Classification Using Synthetic Data Generation. In International Symposium on Cyber Security, Cryptology, and Machine Learning; Springer: Cham, Switzerland, 2022; pp. 232–246. [Google Scholar]
- Wang, H.; Zhang, G.; Cao, H.; Hu, K.; Wang, Q.; Deng, Y.; Tang, Y. Geometry-Aware 3D Point Cloud Learning for Precise Cutting-Point Detection in Unstructured Field Environments. J. Field Robot. 2025. online version of record. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Jie, Y.; Zhao, C.; Zhang, Z. Dual-Frequency LiDAR for Compressed Sensing 3D Imaging Based on All-Phase Fast Fourier Transform. J. Opt. Photonics Res. 2024, 1, 74–81. [Google Scholar] [CrossRef]
- Lian, X.; Pang, Y.; Han, J.; Pan, J. Cascaded Hierarchical Atrous Spatial Pyramid Pooling Module for Semantic Segmentation. Pattern Recognit. 2021, 110, 107622. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Springer: Cham, Switzerland, 2015; Volume 9351. [Google Scholar]
- Tang, H.; Li, Z.; Zhang, D.; He, S.; Tang, J. Divide-and-Conquer: Confluent Triple-Flow Network for RGB-T Salient Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 47, 1958–1974. [Google Scholar] [CrossRef] [PubMed]
- Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-Net and Its Variants for Medical Image Segmentation: A Review of Theory and Applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Azad, R.; Aghdam, E.K.; Rauland, A.; Jia, Y.; Avval, A.H.; Bozorgpour, A.; Merhof, D. Medical Image Segmentation Review: The Success of U-Net. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 10076–10095. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Xu, L.; Qin, J.; Sun, D.; Liao, Y.; Zheng, J. Pfformer: A Time-Series Forecasting Model for Short-Term Precipitation Forecasting. IEEE Access 2024. [Google Scholar] [CrossRef]
- Zhu, H.; Xie, C.; Fei, Y.; Tao, H. Attention Mechanisms in CNN-Based Single Image Super-Resolution: A Brief Review and a New Perspective. Electronics 2021, 10, 1187. [Google Scholar] [CrossRef]
- Wan, A.; Chang, Q.; Khalil, A.B.; He, J. Short-Term Power Load Forecasting for Combined Heat and Power Using CNN-LSTM Enhanced by Attention Mechanism. Energy 2023, 282, 128274. [Google Scholar] [CrossRef]
- Abdel-Sater, R.; Ben Hamza, A. Abdel-Sater, R.; Ben Hamza, A. A Federated Large Language Model for Long-Term Time Series Forecasting. In ECAI 2024; IOS Press: Amsterdam, The Netherlands, 2024; pp. 2452–2459. [Google Scholar]
- Chen, J.; Mei, J.; Li, X.; Lu, Y.; Yu, Q.; Wei, Q.; Zhou, Y. TransUNet: Rethinking the U-Net Architecture Design for Medical Image Segmentation Through the Lens of Transformers. Med. Image Anal. 2024, 97, 103280. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-Unet: Unet-like Pure Transformer for Medical Image Segmentation. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2022; pp. 205–218. [Google Scholar]
- Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Xu, D. Unetr: Transformers for 3D Medical Image Segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–8 January 2022; pp. 574–584. [Google Scholar]
- Shaker, A.; Maaz, M.; Rasheed, H.; Khan, S.; Yang, M.H.; Khan, F.S. UNETR++: Delving into Efficient and Accurate 3D Medical Image Segmentation. IEEE Trans. Med. Imaging 2024, 43, 3377–3390. [Google Scholar] [CrossRef] [PubMed]
- Senin, P. Dynamic Time Warping Algorithm Review. Inf. Comput. Sci. Dep. Univ. Hawaii Manoa Honolulu USA 2008, 855, 40. [Google Scholar]
- Battery and Heating Data for Real Driving Cycles. IEEE DataPort, 2022. Available online: https://ieee-dataport.org/open-access/battery-and-heating-data-real-driving-cycles (accessed on 17 November 2024).
- Shieh, Y.T.; Wu, C.C.; Jeng, S.L.; Liu, C.Y.; Hsieh, S.Y.; Haung, C.C.; Chang, E.Y. A Turn-Ratio-Changing Half-Bridge CLLC DC–DC Bidirectional Battery Charger Using a GaN HEMT. Energies 2023, 16, 5928. [Google Scholar] [CrossRef]
- Tang, H.C.; Shieh, Y.T.; Roy, R.; Jeng, S.L.; Chieng, W.H. Coprime Reconstruction of Super-Nyquist Periodic Signal and Sampling Moiré Effect. IEEE Trans. Ind. Electron. 2025, 72, 8429–8439. [Google Scholar] [CrossRef]
- Asadi, F.; Eguchi, K. Simulation of Power Electronics Converters Using PLECS®; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
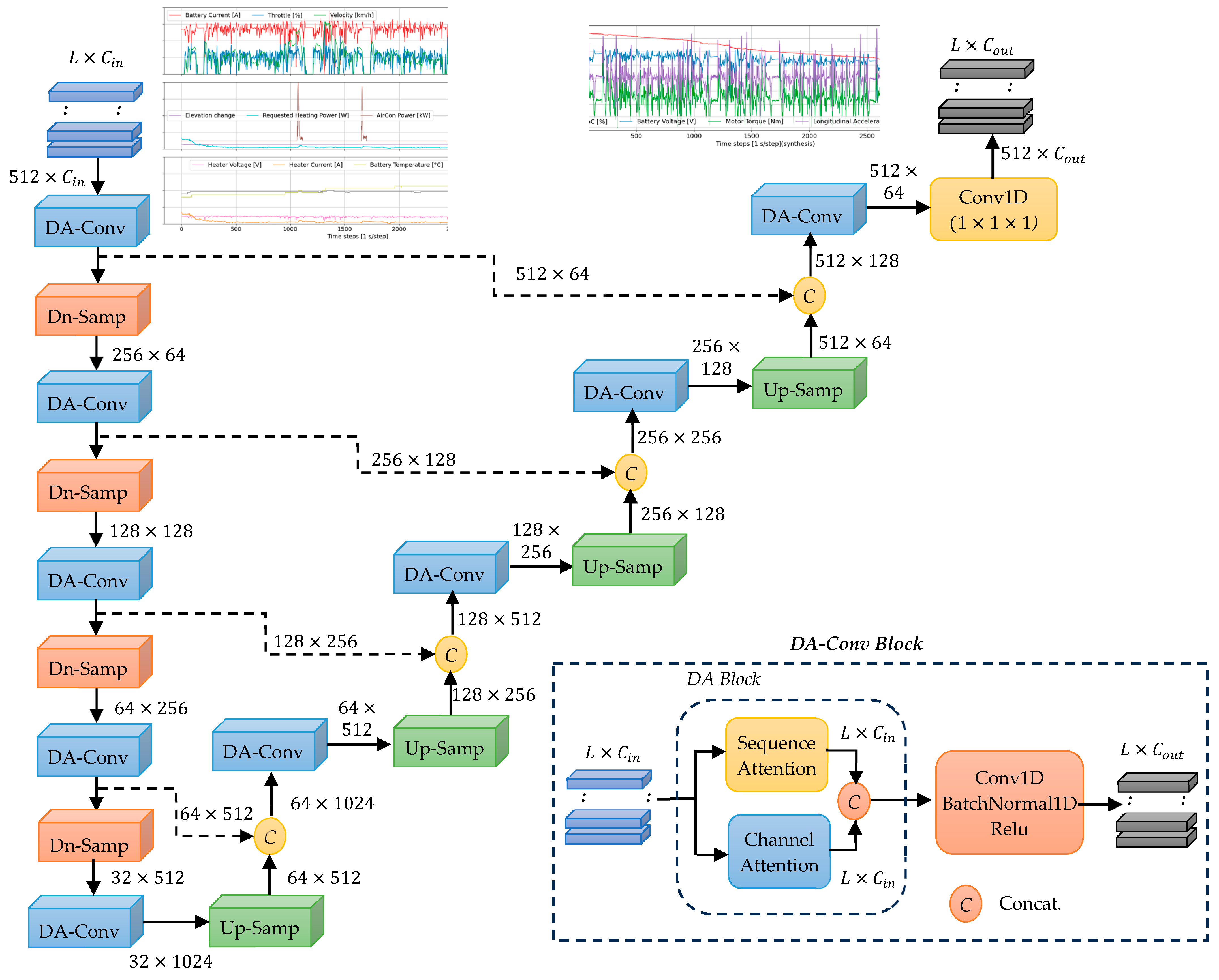
| Name | Layer | (k, s, p) | Module | ||
|---|---|---|---|---|---|
| Input | 512 | Encoder section | |||
| DA-Conv_1 | DA block | (-, -, -) | 512 | ||
| Conv1dN+R | (3, 1, 1) | 512 | 64 | ||
| Dn-Sample_1 | MaxPool1D | (2, 2, 1) | 256 | 64 | |
| DA-Conv-2 | DA block | (-, -, -) | 256 | 128 | |
| Conv1dN+R | (3, 1, 1) | 256 | 128 | ||
| Dn-Sample-2 | MaxPool1D | (2, 2, 1) | 128 | 128 | |
| DA-Conv-3 | DA block | (-, -, -) | 128 | 256 | |
| Conv1dN+R | (3, 1, 1) | 128 | 256 | ||
| Dn-Sample-3 | MaxPool1D | (2, 2, 1) | 64 | 512 | |
| DA-Conv-4 | DA block | (-, -, -) | 64 | 512 | |
| Conv1dN+R | (3, 1, 1) | 64 | 512 | ||
| Dn-Sample-4 | MaxPool1D | (2, 2, 1) | 32 | 512 | |
| DA-Conv-5 | DA block | (-, -, -) | 32 | 1024 | Bottleneck |
| Conv1dN+R | (3, 1, 1) | 32 | 1024 | ||
| Up-Sample-1 | ConvTranspose1d | (2, 2, 1) | 64 | 512 | Decoder section |
| DA-Conv-5 | DA block | (-, -, -) | 64 | 1024 | |
| Conv1dN+R | (3, 1, 1) | 64 | 512 | ||
| Up-Sample-2 | ConvTranspose1d | (2, 2, 1) | 128 | 256 | |
| DA-Conv-6 | DA block | (-, -, -) | 128 | 512 | |
| Conv1dN+R | (3, 1, 1) | 128 | 256 | ||
| Up-Sample-3 | ConvTranspose1d | (2, 2, 1) | 256 | 128 | |
| DA-Conv-7 | DA block | (-, -, -) | 256 | 256 | |
| Conv1dN+R | (3, 1, 1) | 256 | 128 | ||
| Up-Sample-4 | ConvTranspose1d | (2, 2, 1) | 512 | 64 | |
| DA-Conv-8 | DA block | (-, -, -) | 512 | 128 | |
| Conv1dN+R | (3, 1, 1) | 512 | 64 | ||
| Output | Conv1D | (1,1,1) | 512 | Output Layer |
| Trip No | U-Net | U-Net with SA | TS-MSDA-U-Net | UNETR | UNETR++ | TS-p2pGAN | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | DTW | RMSE | MAE | DTW | RMSE | MAE | DTW | RMSE | MAE | DTW | RMSE | MAE | DTW | RMSE | MAE | DTW | |
| 1 | 0.96 | 0.45 | 0.54 | 1.05 | 0.52 | 0.63 | 0.68 | 0.39 | 0.47 | 1.25 | 0.61 | 0.76 | 0.75 | 0.37 | 0.47 | 1.96 | 0.97 | 1.19 |
| 2 | 0.71 | 0.46 | 0.53 | 0.80 | 0.49 | 0.57 | 0.65 | 0.42 | 0.51 | 1.10 | 0.63 | 0.69 | 0.68 | 0.36 | 0.46 | 2.02 | 1.01 | 1.12 |
| 3 | 0.72 | 0.45 | 0.53 | 0.83 | 0.47 | 0.58 | 0.59 | 0.39 | 0.47 | 1.17 | 0.60 | 0.73 | 0.65 | 0.38 | 0.47 | 1.91 | 1.02 | 1.21 |
| 4 | 1.07 | 0.42 | 0.48 | 1.21 | 0.47 | 0.53 | 0.66 | 0.35 | 0.36 | 1.40 | 0.51 | 0.58 | 0.75 | 0.35 | 0.39 | 1.79 | 0.77 | 0.84 |
| 5 | 1.34 | 0.54 | 0.65 | 1.43 | 0.60 | 0.74 | 0.92 | 0.45 | 0.55 | 1.72 | 0.67 | 0.83 | 1.09 | 0.46 | 0.59 | 1.91 | 0.92 | 1.09 |
| 6 | 0.81 | 0.46 | 0.55 | 1.01 | 0.49 | 0.61 | 0.65 | 0.38 | 0.47 | 1.11 | 0.57 | 0.70 | 0.78 | 0.39 | 0.51 | 1.62 | 0.84 | 1.03 |
| 7 | 0.76 | 0.42 | 0.50 | 0.83 | 0.44 | 0.54 | 0.67 | 0.39 | 0.46 | 1.00 | 0.54 | 0.65 | 0.71 | 0.38 | 0.48 | 1.56 | 0.84 | 1.01 |
| 8 | 0.74 | 0.40 | 0.47 | 0.81 | 0.41 | 0.50 | 0.60 | 0.34 | 0.41 | 0.93 | 0.47 | 0.56 | 0.64 | 0.32 | 0.40 | 1.51 | 0.78 | 0.92 |
| 9 | 0.77 | 0.43 | 0.48 | 0.86 | 0.44 | 0.50 | 0.54 | 0.32 | 0.37 | 1.08 | 0.48 | 0.55 | 0.62 | 0.32 | 0.39 | 1.73 | 0.85 | 0.95 |
| 10 | 1.02 | 0.51 | 0.62 | 1.19 | 0.53 | 0.67 | 0.74 | 0.41 | 0.51 | 1.40 | 0.63 | 0.78 | 0.92 | 0.42 | 0.54 | 2.03 | 1.06 | 1.26 |
| 11 | 1.14 | 0.54 | 0.61 | 1.14 | 0.46 | 0.55 | 0.81 | 0.42 | 0.49 | 1.69 | 0.65 | 0.74 | 0.86 | 0.39 | 0.47 | 2.08 | 1.01 | 1.15 |
| 12 | 0.72 | 0.36 | 0.43 | 0.78 | 0.39 | 0.46 | 0.56 | 0.35 | 0.40 | 0.96 | 0.44 | 0.51 | 0.62 | 0.32 | 0.39 | 1.26 | 0.66 | 0.72 |
| 13 | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | 2.69 | 1.46 | 1.56 |
| 14 | 1.28 | 0.44 | 0.51 | 1.36 | 0.45 | 0.53 | 1.19 | 0.39 | 0.46 | 1.54 | 0.55 | 0.64 | 1.08 | 0.34 | 0.43 | 1.48 | 0.80 | 0.91 |
| 15 | 0.90 | 0.47 | 0.56 | 1.15 | 0.50 | 0.60 | 0.67 | 0.42 | 0.50 | 1.31 | 0.62 | 0.76 | 0.66 | 0.38 | 0.49 | 1.83 | 0.96 | 1.17 |
| 16 | 0.73 | 0.43 | 0.52 | 0.82 | 0.46 | 0.57 | 0.62 | 0.39 | 0.48 | 1.04 | 0.59 | 0.74 | 0.69 | 0.38 | 0.49 | 1.92 | 1.02 | 1.21 |
| 17 | 0.79 | 0.48 | 0.59 | 0.83 | 0.44 | 0.57 | 0.64 | 0.41 | 0.50 | 1.06 | 0.58 | 0.74 | 0.67 | 0.39 | 0.50 | 2.11 | 1.07 | 1.28 |
| 18 | 1.16 | 0.53 | 0.63 | 1.26 | 0.52 | 0.63 | 0.68 | 0.43 | 0.52 | 1.50 | 0.63 | 0.73 | 0.78 | 0.41 | 0.52 | 1.66 | 0.87 | 1.01 |
| 19 | 0.84 | 0.47 | 0.56 | 0.97 | 0.52 | 0.62 | 0.66 | 0.39 | 0.48 | 1.24 | 0.60 | 0.72 | 0.71 | 0.38 | 0.48 | 1.80 | 0.92 | 1.09 |
| 20 | 0.76 | 0.43 | 0.51 | 0.94 | 0.49 | 0.59 | 0.58 | 0.37 | 0.45 | 1.25 | 0.62 | 0.76 | 0.80 | 0.38 | 0.48 | 1.91 | 0.96 | 1.11 |
| 21 | 0.97 | 0.45 | 0.55 | 1.20 | 0.46 | 0.57 | 0.68 | 0.36 | 0.44 | 1.51 | 0.58 | 0.71 | 0.83 | 0.37 | 0.47 | 1.56 | 0.80 | 0.97 |
| 22 | 1.00 | 0.47 | 0.57 | 1.15 | 0.49 | 0.61 | 0.68 | 0.39 | 0.49 | 1.25 | 0.60 | 0.73 | 0.82 | 0.41 | 0.53 | 2.05 | 0.97 | 1.20 |
| 23 | 1.07 | 0.54 | 0.66 | 1.37 | 0.59 | 0.74 | 0.86 | 0.46 | 0.57 | 1.76 | 0.73 | 0.90 | 1.09 | 0.49 | 0.63 | 2.65 | 1.31 | 1.52 |
| 24 | 1.46 | 0.59 | 0.73 | 1.98 | 0.67 | 0.88 | 0.81 | 0.48 | 0.60 | 2.34 | 0.90 | 1.14 | 1.07 | 0.50 | 0.66 | 2.36 | 1.25 | 1.42 |
| 25 | 0.78 | 0.49 | 0.60 | 0.80 | 0.45 | 0.56 | 0.60 | 0.37 | 0.46 | 1.03 | 0.56 | 0.68 | 0.66 | 0.37 | 0.48 | 2.23 | 1.09 | 1.26 |
| 26 | 1.53 | 0.64 | 0.76 | 1.56 | 0.64 | 0.77 | 1.09 | 0.46 | 0.56 | 2.55 | 0.90 | 1.07 | 1.22 | 0.46 | 0.60 | 2.75 | 1.30 | 1.51 |
| 27 | 1.22 | 0.59 | 0.70 | 1.47 | 0.60 | 0.72 | 0.89 | 0.43 | 0.52 | 1.68 | 0.71 | 0.86 | 0.89 | 0.48 | 0.58 | 2.04 | 1.11 | 1.30 |
| 28 | 0.96 | 0.64 | 0.74 | 0.98 | 0.62 | 0.72 | 0.70 | 0.43 | 0.53 | 1.30 | 0.65 | 0.79 | 0.75 | 0.42 | 0.54 | 2.21 | 1.23 | 1.40 |
| 29 | 0.92 | 0.59 | 0.68 | 1.04 | 0.61 | 0.70 | 0.69 | 0.45 | 0.53 | 1.20 | 0.67 | 0.79 | 0.77 | 0.51 | 0.60 | 2.90 | 1.67 | 1.77 |
| 30 | 1.54 | 0.65 | 0.76 | 1.89 | 0.66 | 0.77 | 0.87 | 0.49 | 0.58 | 1.85 | 0.75 | 0.89 | 0.97 | 0.54 | 0.64 | 2.25 | 1.02 | 1.22 |
| 31 | 1.15 | 0.54 | 0.67 | 1.29 | 0.56 | 0.70 | 0.64 | 0.42 | 0.51 | 1.54 | 0.65 | 0.82 | 0.74 | 0.41 | 0.54 | 1.86 | 0.87 | 1.06 |
| 32 | 1.15 | 0.56 | 0.67 | 1.49 | 0.60 | 0.75 | 0.92 | 0.51 | 0.61 | 1.90 | 0.73 | 0.88 | 0.99 | 0.48 | 0.60 | 2.70 | 1.30 | 1.52 |
| 33 | 1.89 | 0.89 | 1.04 | 2.34 | 0.91 | 1.08 | 1.52 | 0.76 | 0.91 | 2.15 | 0.99 | 1.17 | 1.47 | 0.74 | 0.91 | 2.45 | 1.24 | 1.60 |
| 34 | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | 2.32 | 1.12 | 1.32 |
| 35 | 1.02 | 0.51 | 0.62 | 1.15 | 0.56 | 0.67 | 0.71 | 0.44 | 0.54 | 1.46 | 0.64 | 0.79 | 0.79 | 0.40 | 0.53 | 1.95 | 0.93 | 1.08 |
| 36 | 0.90 | 0.43 | 0.52 | 1.08 | 0.45 | 0.56 | 0.71 | 0.37 | 0.46 | 1.26 | 0.55 | 0.67 | 0.84 | 0.36 | 0.46 | 1.75 | 0.86 | 1.00 |
| 37 | 1.19 | 0.53 | 0.62 | 1.44 | 0.60 | 0.71 | 0.79 | 0.42 | 0.52 | 1.84 | 0.73 | 0.90 | 0.87 | 0.43 | 0.53 | 1.89 | 0.93 | 1.13 |
| 38 | 0.94 | 0.51 | 0.63 | 1.14 | 0.55 | 0.69 | 0.70 | 0.41 | 0.50 | 1.52 | 0.66 | 0.83 | 0.81 | 0.43 | 0.55 | 2.30 | 1.13 | 1.36 |
| 39 | 1.04 | 0.53 | 0.66 | 1.21 | 0.57 | 0.70 | 0.80 | 0.41 | 0.52 | 1.28 | 0.65 | 0.80 | 0.87 | 0.44 | 0.57 | 2.17 | 1.18 | 1.40 |
| 40 | 1.36 | 0.81 | 0.95 | 1.78 | 1.10 | 1.35 | 1.05 | 0.60 | 0.72 | 2.22 | 1.40 | 1.66 | 0.97 | 0.57 | 0.71 | 2.45 | 1.33 | 1.67 |
| 41 | 2.42 | 1.26 | 1.41 | 4.71 | 2.10 | 2.34 | 2.81 | 1.42 | 1.52 | 5.57 | 2.94 | 3.34 | 2.45 | 1.03 | 1.17 | 2.40 | 1.19 | 1.48 |
| 42 | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | 2.71 | 1.26 | 1.40 |
| 43 | 0.87 | 0.45 | 0.58 | 1.12 | 0.58 | 0.73 | 0.76 | 0.39 | 0.51 | 1.40 | 0.68 | 0.84 | 0.91 | 0.45 | 0.60 | 2.33 | 1.22 | 1.48 |
| 44 | 0.81 | 0.37 | 0.47 | 1.01 | 0.49 | 0.59 | 0.60 | 0.32 | 0.40 | 1.19 | 0.50 | 0.63 | 0.72 | 0.34 | 0.45 | 1.47 | 0.77 | 0.90 |
| 45 | 0.60 | 0.38 | 0.47 | 0.74 | 0.46 | 0.56 | 0.53 | 0.33 | 0.41 | 0.86 | 0.52 | 0.64 | 0.61 | 0.35 | 0.45 | 1.58 | 0.79 | 0.93 |
| 46 | 0.89 | 0.43 | 0.52 | 1.13 | 0.58 | 0.66 | 0.62 | 0.32 | 0.40 | 1.13 | 0.54 | 0.66 | 0.70 | 0.37 | 0.47 | 2.41 | 1.20 | 1.39 |
| 47 | 1.06 | 0.46 | 0.57 | 1.58 | 0.62 | 0.78 | 0.72 | 0.36 | 0.45 | 1.78 | 0.65 | 0.84 | 0.87 | 0.42 | 0.56 | 2.28 | 1.08 | 1.30 |
| 48 | 1.21 | 0.49 | 0.63 | 1.40 | 0.60 | 0.75 | 0.90 | 0.44 | 0.54 | 1.57 | 0.67 | 0.84 | 1.05 | 0.47 | 0.61 | 1.72 | 0.85 | 1.00 |
| 49 | 0.76 | 0.40 | 0.48 | 0.93 | 0.49 | 0.58 | 0.58 | 0.34 | 0.41 | 0.98 | 0.51 | 0.63 | 0.70 | 0.36 | 0.46 | 2.58 | 1.24 | 1.45 |
| 50 | 1.14 | 0.49 | 0.62 | 1.65 | 0.63 | 0.80 | 0.72 | 0.38 | 0.47 | 2.14 | 0.78 | 0.98 | 0.95 | 0.46 | 0.60 | 3.29 | 1.46 | 1.75 |
| 51 | 1.24 | 0.57 | 0.73 | 1.60 | 0.67 | 0.86 | 0.92 | 0.47 | 0.60 | 2.47 | 0.79 | 1.01 | 1.12 | 0.52 | 0.68 | 2.19 | 1.15 | 1.39 |
| 52 | 1.13 | 0.55 | 0.68 | 1.37 | 0.68 | 0.83 | 0.79 | 0.44 | 0.55 | 1.52 | 0.73 | 0.92 | 0.95 | 0.52 | 0.67 | 2.21 | 1.09 | 1.30 |
| 53 | 0.67 | 0.37 | 0.47 | 0.85 | 0.49 | 0.60 | 0.58 | 0.33 | 0.42 | 1.04 | 0.52 | 0.66 | 0.69 | 0.36 | 0.47 | 1.58 | 0.79 | 0.94 |
| 54 | 0.86 | 0.40 | 0.48 | 1.05 | 0.51 | 0.60 | 0.55 | 0.33 | 0.40 | 1.39 | 0.56 | 0.66 | 0.84 | 0.35 | 0.44 | 1.45 | 0.73 | 0.87 |
| 55 | 0.56 | 0.38 | 0.45 | 0.61 | 0.41 | 0.49 | 0.54 | 0.35 | 0.43 | 0.65 | 0.44 | 0.52 | 0.52 | 0.31 | 0.40 | 2.31 | 1.14 | 1.27 |
| 56 | 1.01 | 0.48 | 0.58 | 1.32 | 0.61 | 0.73 | 0.75 | 0.45 | 0.55 | 1.41 | 0.71 | 0.84 | 0.73 | 0.45 | 0.56 | 1.48 | 0.84 | 0.99 |
| 57 | 0.99 | 0.40 | 0.50 | 1.22 | 0.54 | 0.64 | 0.74 | 0.34 | 0.42 | 1.45 | 0.58 | 0.72 | 0.72 | 0.35 | 0.45 | 2.54 | 1.24 | 1.45 |
| 58 | 0.88 | 0.40 | 0.51 | 1.55 | 0.54 | 0.67 | 0.56 | 0.32 | 0.41 | 1.91 | 0.60 | 0.76 | 0.71 | 0.38 | 0.49 | 1.75 | 0.94 | 1.15 |
| 59 | 0.81 | 0.46 | 0.57 | 1.01 | 0.56 | 0.69 | 0.76 | 0.42 | 0.53 | 1.02 | 0.57 | 0.71 | 0.80 | 0.44 | 0.57 | 1.55 | 0.79 | 0.97 |
| 60 | 0.99 | 0.45 | 0.55 | 1.24 | 0.55 | 0.66 | 0.76 | 0.36 | 0.45 | 1.54 | 0.63 | 0.77 | 1.14 | 0.46 | 0.57 | 2.05 | 1.00 | 1.19 |
| 61 | 0.83 | 0.39 | 0.49 | 1.21 | 0.54 | 0.65 | 0.80 | 0.36 | 0.45 | 1.57 | 0.57 | 0.71 | 0.87 | 0.37 | 0.50 | 2.05 | 1.03 | 1.27 |
| 62 | 1.72 | 0.91 | 1.04 | 1.84 | 1.09 | 1.24 | 1.84 | 0.85 | 1.01 | 1.80 | 0.95 | 1.12 | 1.45 | 0.76 | 0.94 | 2.78 | 1.27 | 1.43 |
| 63 | 0.88 | 0.55 | 0.65 | 0.99 | 0.70 | 0.80 | 0.65 | 0.40 | 0.50 | 1.07 | 0.65 | 0.80 | 0.78 | 0.42 | 0.55 | 1.87 | 0.99 | 1.21 |
| 64 | 0.84 | 0.47 | 0.58 | 0.99 | 0.56 | 0.67 | 0.64 | 0.37 | 0.46 | 1.15 | 0.62 | 0.77 | 0.75 | 0.40 | 0.53 | 2.04 | 1.06 | 1.35 |
| 65 | 0.86 | 0.46 | 0.58 | 1.05 | 0.59 | 0.71 | 0.61 | 0.35 | 0.45 | 1.38 | 0.62 | 0.80 | 0.75 | 0.40 | 0.53 | 2.52 | 1.16 | 1.45 |
| 66 | 1.28 | 0.52 | 0.66 | 1.44 | 0.66 | 0.80 | 0.74 | 0.40 | 0.51 | 1.79 | 0.67 | 0.85 | 0.93 | 0.44 | 0.58 | 1.63 | 0.87 | 1.09 |
| 67 | 0.77 | 0.44 | 0.55 | 0.93 | 0.51 | 0.62 | 0.57 | 0.34 | 0.43 | 1.49 | 0.58 | 0.72 | 0.92 | 0.39 | 0.50 | 2.74 | 1.37 | 1.69 |
| 68 | 1.13 | 0.55 | 0.67 | 1.40 | 0.64 | 0.79 | 0.81 | 0.41 | 0.53 | 1.69 | 0.74 | 0.93 | 0.94 | 0.47 | 0.62 | 2.16 | 1.10 | 1.35 |
| 69 | 0.81 | 0.47 | 0.59 | 0.98 | 0.65 | 0.76 | 0.65 | 0.38 | 0.49 | 1.09 | 0.58 | 0.75 | 0.79 | 0.42 | 0.56 | 1.88 | 0.96 | 1.22 |
| 70 | 1.07 | 0.51 | 0.62 | 1.25 | 0.60 | 0.73 | 0.82 | 0.38 | 0.48 | 2.02 | 0.73 | 0.91 | 0.85 | 0.41 | 0.54 | 2.37 | 1.13 | 1.34 |
| Model | RMSE | MAE | DTW | Interpretation |
|---|---|---|---|---|
| U-Net | Significant difference (p < 0.05) | |||
| U-Net with SA | Significant difference (p < 0.05) | |||
| UNETR | Significant difference (p < 0.05) | |||
| UNETR++ | Mixed results; MAE not significant | |||
| Ts-p2pGAN | Significant difference (p < 0.05) |
| Case No | U-Net | U-Net with SA | TS-MSDA-UNet | UNETR | UNETR++ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (%) | MAE (%) | DTW (%) | RMSE (%) | MAE (%) | DTW (%) | RMSE (%) | MAE (%) | DTW (%) | RMSE (%) | MAE (%) | DTW (%) | RMSE (%) | MAE (%) | DTW (%) | |
| 1 | 52.60 | 30.19 | 20.17 | 1.34 | 0.44 | 0.47 | 0.84 | 0.40 | 0.41 | 63.37 | 45.57 | 31.28 | 1.05 | 0.43 | 0.47 |
| 2 | 49.11 | 28.04 | 18.80 | 1.15 | 0.31 | 0.34 | 0.90 | 0.33 | 0.35 | 59.09 | 42.35 | 29.26 | 0.89 | 0.37 | 0.37 |
| 3 | 46.20 | 26.28 | 17.59 | 1.36 | 0.29 | 0.33 | 0.82 | 0.30 | 0.32 | 55.48 | 39.57 | 27.30 | 1.04 | 0.33 | 0.33 |
| 4 | 43.30 | 24.49 | 16.09 | 1.41 | 0.29 | 0.32 | 0.67 | 0.26 | 0.28 | 52.14 | 37.12 | 25.38 | 0.65 | 0.28 | 0.29 |
| 5 | 39.79 | 22.32 | 14.85 | 1.35 | 0.26 | 0.28 | 0.65 | 0.24 | 0.25 | 48.45 | 34.49 | 23.23 | 0.48 | 0.24 | 0.24 |
| 6 | 37.20 | 20.60 | 13.65 | 1.24 | 0.24 | 0.27 | 0.81 | 0.22 | 0.24 | 45.25 | 31.98 | 21.45 | 0.69 | 0.22 | 0.22 |
| 7 | 34.74 | 18.90 | 12.41 | 1.30 | 0.24 | 0.27 | 0.72 | 0.20 | 0.22 | 42.21 | 29.49 | 19.63 | 0.74 | 0.20 | 0.20 |
| 8 | 31.68 | 16.60 | 10.70 | 1.36 | 0.25 | 0.29 | 0.53 | 0.18 | 0.19 | 38.54 | 26.28 | 17.18 | 0.51 | 0.18 | 0.18 |
| 9 | 29.62 | 14.86 | 9.40 | 1.48 | 0.23 | 0.27 | 0.54 | 0.17 | 0.18 | 35.65 | 23.49 | 15.33 | 0.63 | 0.17 | 0.17 |
| 10 | 27.76 | 13.10 | 8.11 | 1.07 | 0.22 | 0.25 | 0.55 | 0.16 | 0.18 | 33.62 | 21.14 | 13.49 | 0.68 | 0.18 | 0.18 |
| 11 | 26.24 | 11.34 | 6.85 | 0.51 | 0.18 | 0.19 | 0.30 | 0.14 | 0.14 | 32.09 | 18.74 | 11.65 | 0.28 | 0.16 | 0.15 |
| 12 | 25.12 | 9.56 | 5.56 | 0.39 | 0.16 | 0.16 | 0.27 | 0.12 | 0.12 | 30.92 | 16.18 | 9.80 | 0.27 | 0.15 | 0.14 |
| 13 | 24.47 | 7.89 | 4.32 | 0.41 | 0.13 | 0.14 | 0.25 | 0.10 | 0.10 | 30.16 | 13.62 | 8.09 | 0.28 | 0.16 | 0.15 |
| Model | RMSE | MAE | DTW | Interpretation |
|---|---|---|---|---|
| U-Net | Significant difference (p < 0.05) | |||
| U-Net with SA | Significant difference (p < 0.05) | |||
| UNETR | Significant difference (p < 0.05) | |||
| UNETR++ | Mixed results; RMSE and DTW not significant |
| Case No | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (%) | MAE (%) | DTW (%) | RMSE (%) | MAE (%) | DTW (%) | RMSE (%) | MAE (%) | DTW (%) | RMSE (%) | MAE (%) | DTW (%) | |
| 1 | 0.71 | 0.17 | 0.20 | 0.54 | 0.38 | 0.60 | 1.27 | 0.62 | 0.95 | 0.61 | 0.43 | 0.68 |
| 2 | 1.41 | 0.16 | 0.22 | 0.43 | 0.31 | 0.49 | 0.93 | 0.51 | 0.80 | 0.48 | 0.34 | 0.54 |
| 3 | 1.32 | 0.15 | 0.22 | 0.37 | 0.27 | 0.42 | 0.81 | 0.46 | 0.72 | 0.41 | 0.30 | 0.48 |
| 4 | 1.05 | 0.14 | 0.20 | 0.34 | 0.25 | 0.39 | 0.68 | 0.38 | 0.61 | 0.36 | 0.27 | 0.43 |
| 5 | 1.07 | 0.14 | 0.20 | 0.29 | 0.22 | 0.35 | 0.59 | 0.35 | 0.55 | 0.31 | 0.23 | 0.37 |
| 6 | 1.49 | 0.16 | 0.24 | 0.26 | 0.20 | 0.31 | 0.52 | 0.31 | 0.49 | 0.29 | 0.22 | 0.35 |
| 7 | 1.32 | 0.15 | 0.22 | 0.24 | 0.18 | 0.29 | 0.45 | 0.26 | 0.41 | 0.27 | 0.20 | 0.33 |
| 8 | 0.92 | 0.13 | 0.21 | 0.21 | 0.16 | 0.26 | 0.40 | 0.23 | 0.36 | 0.24 | 0.18 | 0.29 |
| 9 | 0.96 | 0.13 | 0.21 | 0.20 | 0.15 | 0.24 | 0.40 | 0.22 | 0.34 | 0.23 | 0.17 | 0.27 |
| 10 | 0.97 | 0.14 | 0.22 | 0.21 | 0.15 | 0.25 | 0.43 | 0.20 | 0.31 | 0.22 | 0.16 | 0.26 |
| 11 | 0.48 | 0.11 | 0.15 | 0.18 | 0.13 | 0.21 | 0.24 | 0.16 | 0.23 | 0.20 | 0.15 | 0.24 |
| 12 | 0.46 | 0.11 | 0.15 | 0.14 | 0.11 | 0.17 | 0.20 | 0.13 | 0.19 | 0.16 | 0.12 | 0.19 |
| 13 | 0.45 | 0.11 | 0.15 | 0.11 | 0.08 | 0.12 | 0.14 | 0.10 | 0.14 | 0.12 | 0.09 | 0.14 |
| Model | Parameter Count | Training Time (s/Epoch) | Inference Speed (s/Sample) |
|---|---|---|---|
| U-Net | 10,825,544 | 49.5 | 0.216 |
| U-Net with SA | 8,010,673 | 50 | 0.116 |
| TS-MSDA U-Net | 37,984,700 | 104 | 0.035 |
| UNETR | 57,424,712 | 59 | 0.032 |
| UNETR++ | 8,783,600 | 105 | 0.111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeng, S.-L. U-Net Inspired Transformer Architecture for Multivariate Time Series Synthesis. Sensors 2025, 25, 4073. https://doi.org/10.3390/s25134073
Jeng S-L. U-Net Inspired Transformer Architecture for Multivariate Time Series Synthesis. Sensors. 2025; 25(13):4073. https://doi.org/10.3390/s25134073
Chicago/Turabian StyleJeng, Shyr-Long. 2025. "U-Net Inspired Transformer Architecture for Multivariate Time Series Synthesis" Sensors 25, no. 13: 4073. https://doi.org/10.3390/s25134073
APA StyleJeng, S.-L. (2025). U-Net Inspired Transformer Architecture for Multivariate Time Series Synthesis. Sensors, 25(13), 4073. https://doi.org/10.3390/s25134073





