Fault Diagnosis Method for Shearer Arm Gear Based on Improved S-Transform and Depthwise Separable Convolution
Abstract
1. Introduction
- (1)
- A diagnostic framework combining adaptive window S-transform and depthwise separable convolutional networks is proposed. Compared with existing methods using fixed-window S-transform or complex convolutional architectures, the proposed approach can dynamically adapt to energy variations in different fault signals while effectively reducing model complexity.
- (2)
- A window-width adjustment mechanism based on the energy distribution of the signal is designed, enabling more accurate time–frequency decomposition of transient fault signals and enhancing diagnostic robustness.
- (3)
- A lightweight diagnostic network architecture is developed, which, compared to deep models such as ResNet, achieves a reduction of approximately 66% in parameter count and nearly 12% in inference latency per prediction, while maintaining comparable diagnostic accuracy—demonstrating its potential for deployment in edge computing scenarios.
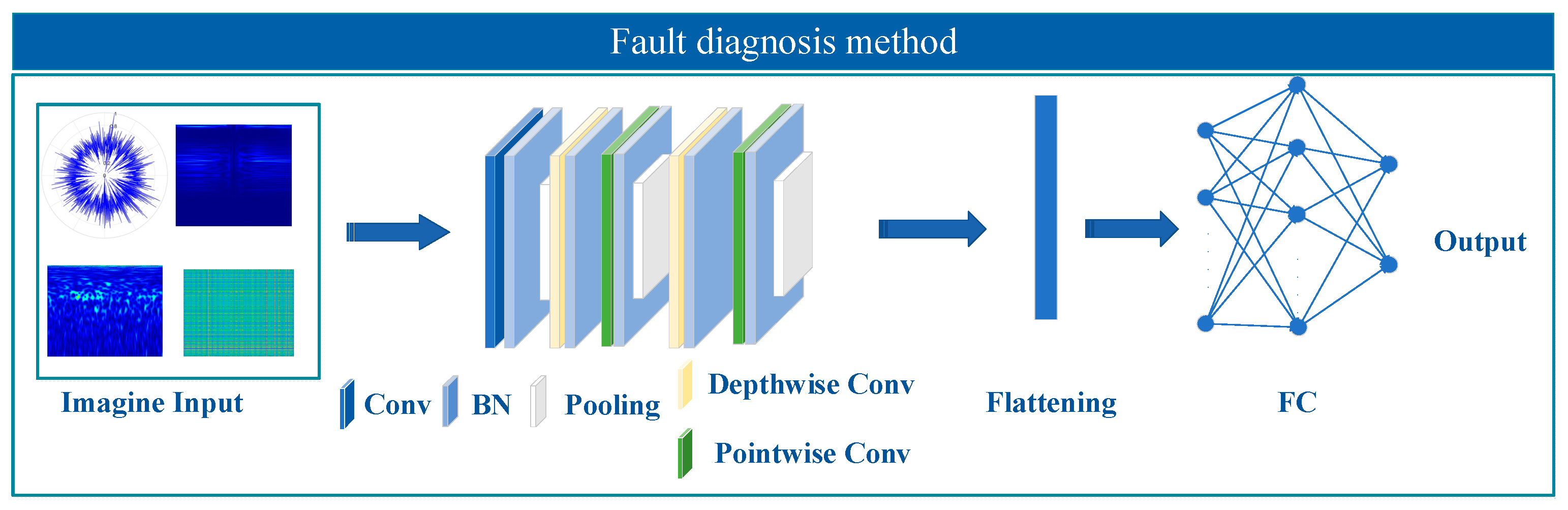
2. Method for Fault Diagnosis
2.1. Theory of the Improved S-Transform
2.2. Depthwise Separable Convolution
2.3. Construction of the Diagnostic Model
2.4. Fault Diagnosis Process
3. Experimental Data Acquisition
4. Experimental Analysis
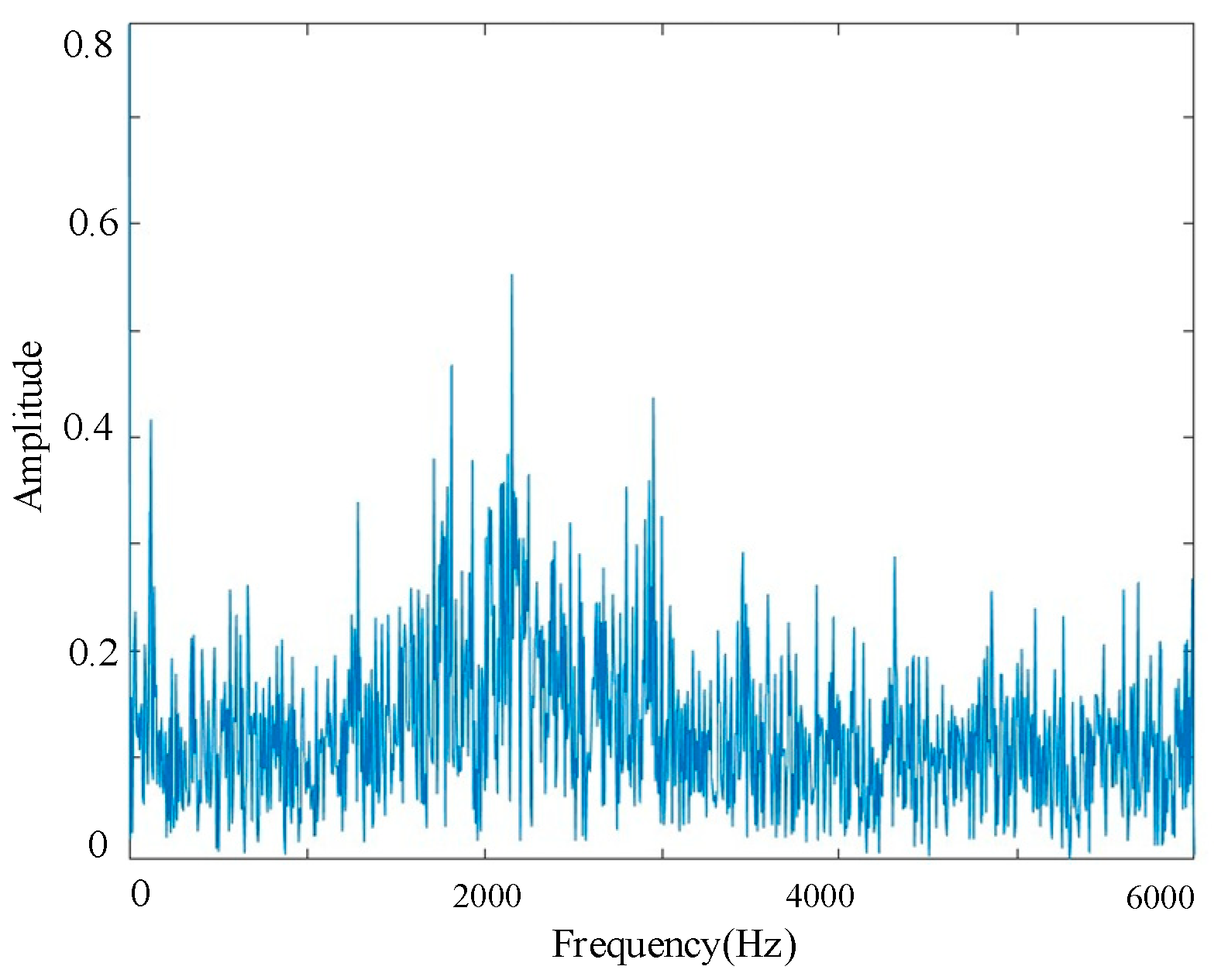
4.1. Preprocessing Analysis
4.2. Fault Diagnosis Analysis
4.2.1. Dataset Construction
4.2.2. Model Parameter Settings
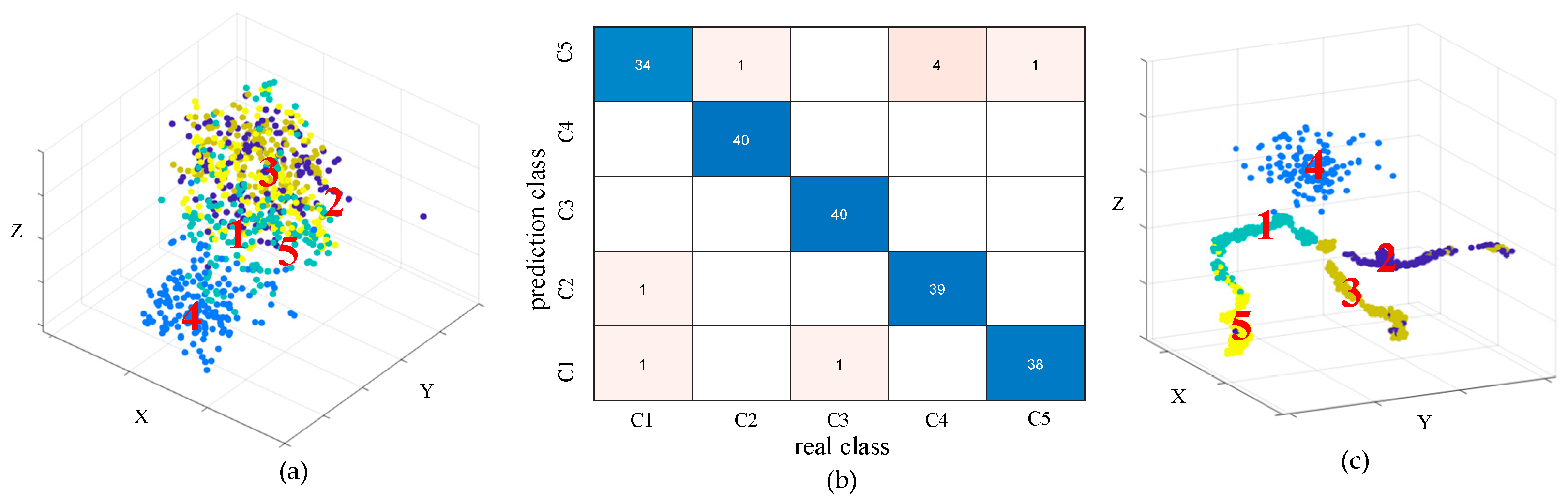
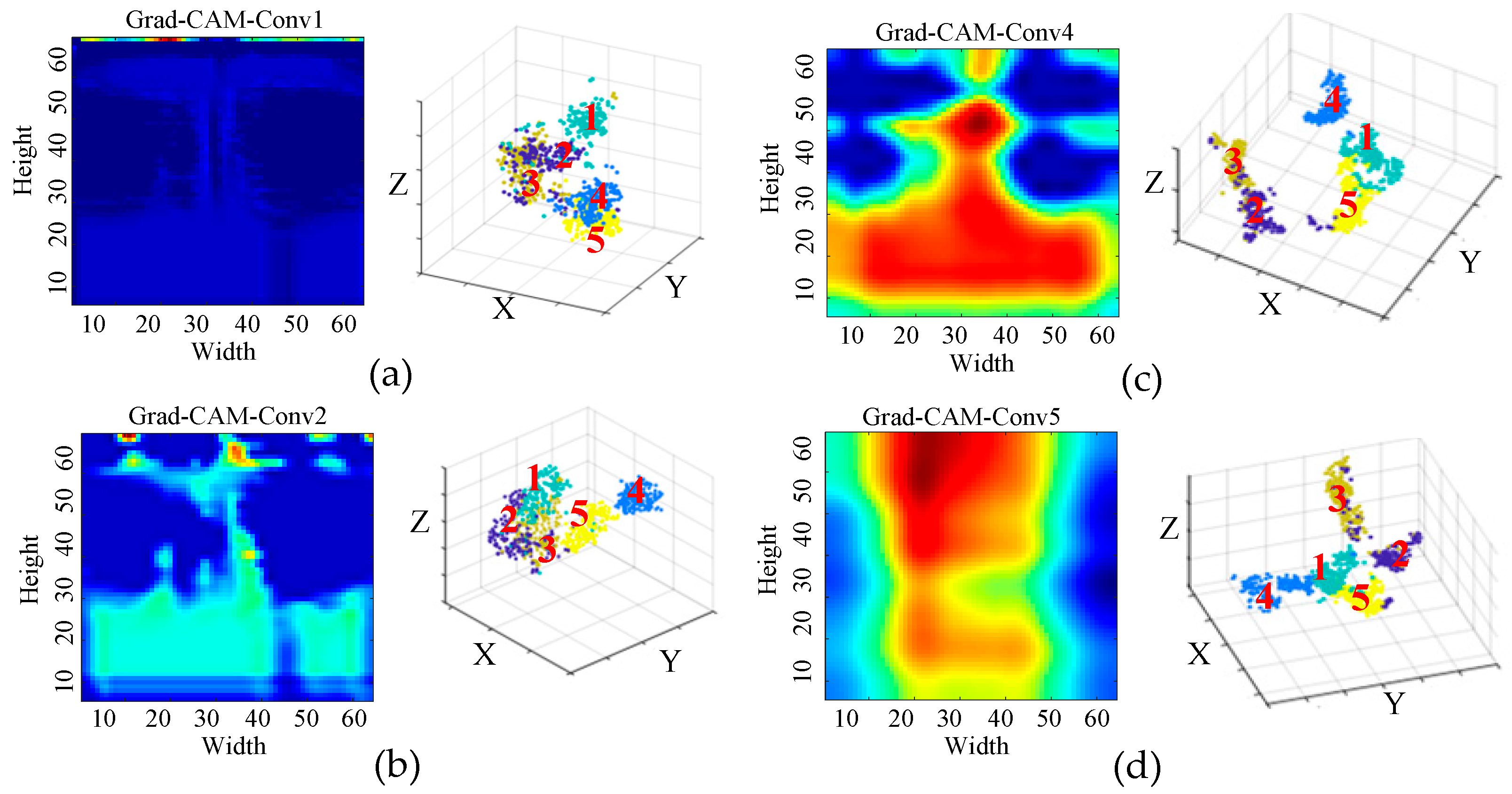
4.2.3. Diagnostic Results Analysis
4.2.4. Imbalanced Class Experiment and Analysis
4.3. Comparative Experiment
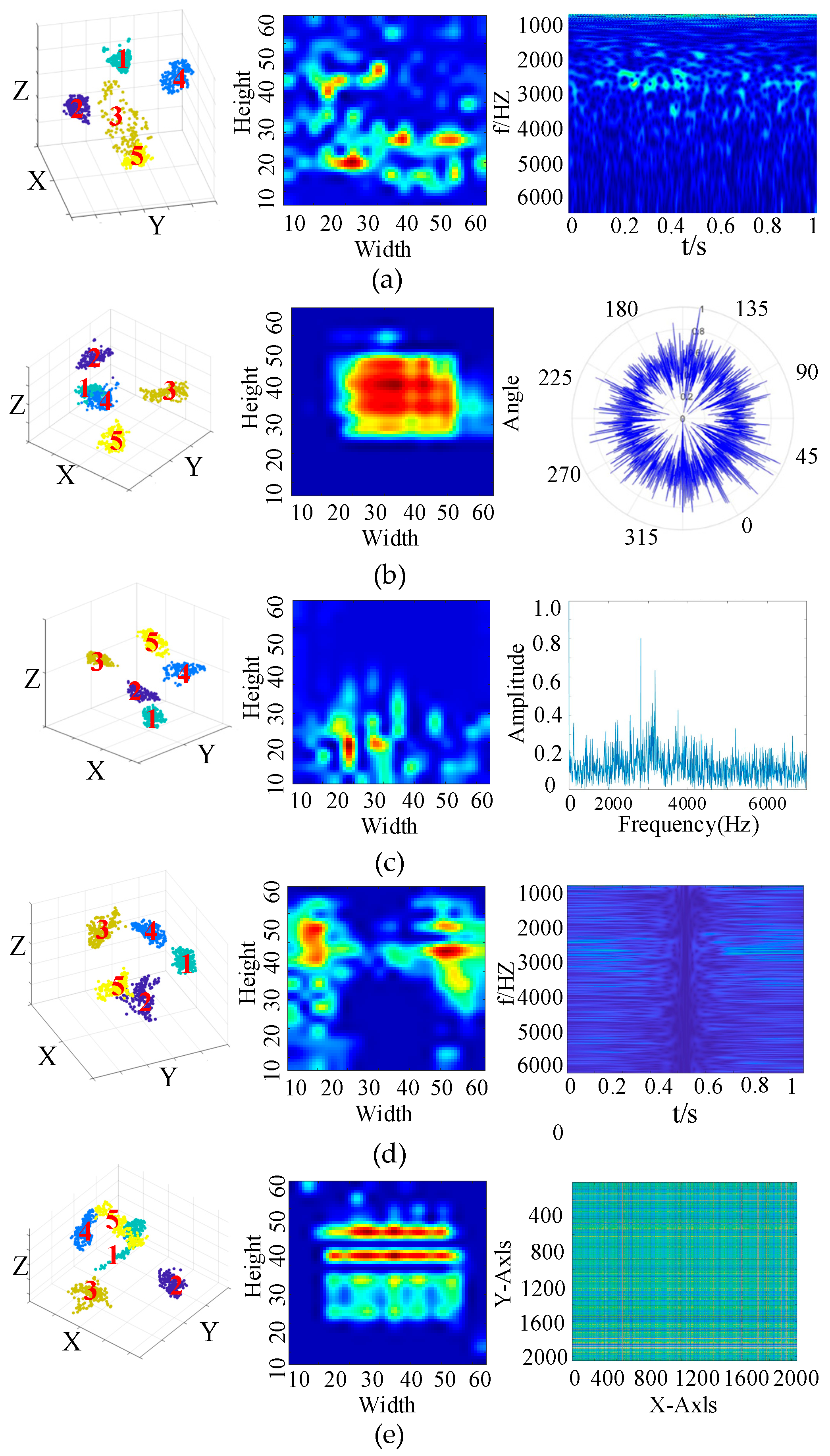
4.3.1. Analysis of Recognition Results Using Different Transformation Methods
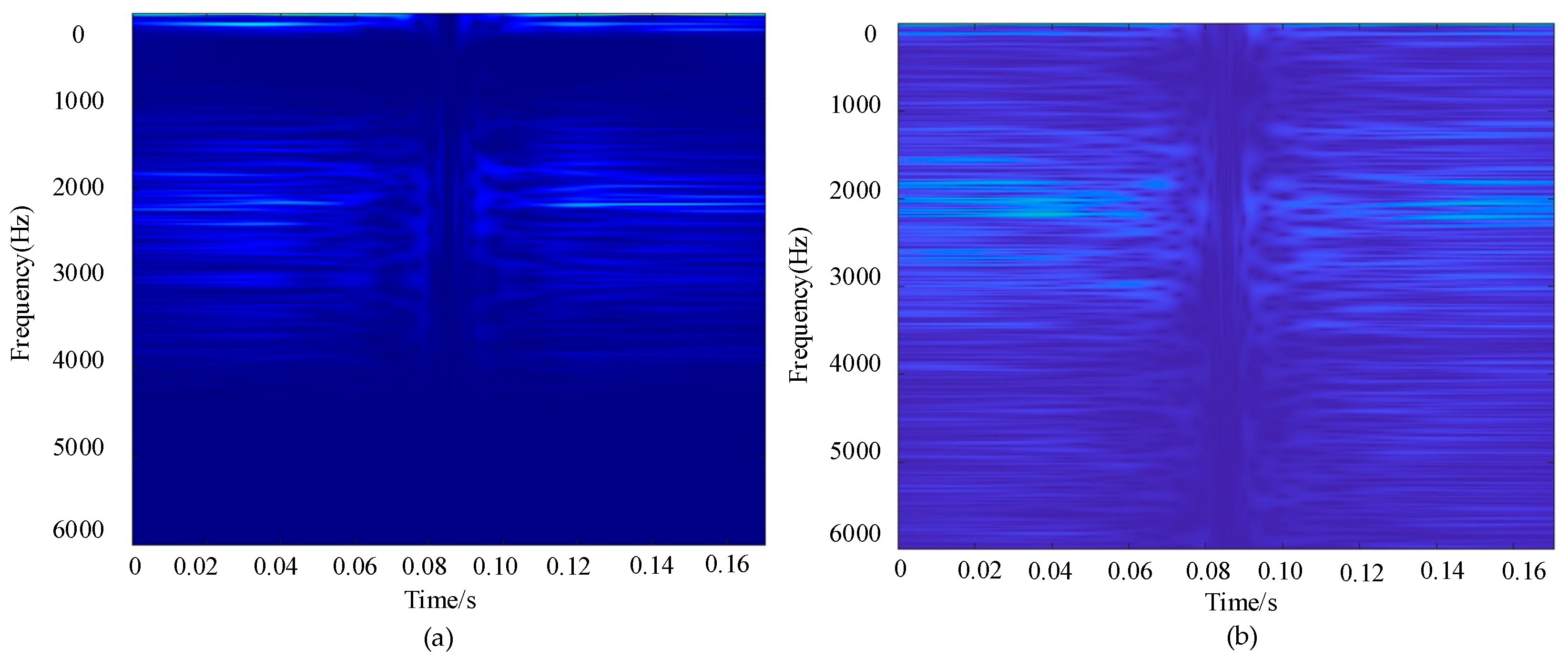
4.3.2. Visualization-Based Comparison of Time–Frequency Transformation Methods
4.3.3. Comparison of Diagnostic Performance Among Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mao, Q.; Zhang, Y.; Zhang, X.; Liu, Z.; Wang, H.; Wang, Z. Accurate fault location method of the mechanical transmission system of shearer ranging arm. IEEE Access 2020, 8, 202260–202273. [Google Scholar] [CrossRef]
- Rybak, G.; Strzecha, K. Short-time fourier transform based on metaprogramming and the stockham optimization method. Sensors 2021, 21, 4123. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, Y.; Wu, Z.; Qin, Y.; Yang, J. Ramanujan fourier mode decomposition and its application in gear fault diagnosis. IEEE Trans. Ind. Inform. 2021, 18, 6079–6088. [Google Scholar] [CrossRef]
- Deng, M.; Deng, A.; Zhu, J.; Zeng, X. Resonance-based bandwidth fourier decomposition method for gearbox fault diagnosis. Meas. Sci. Technol. 2020, 32, 035003. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M. Fault diagnosis of wind turbine planetary gearbox under nonstationary conditions via adaptive optimal kernel time–frequency analysis. Renew. Energy 2014, 66, 468–477. [Google Scholar] [CrossRef]
- Saravanan, N.; Ramachandran, K.I. Fault diagnosis of spur bevel gear box using discrete wavelet features and decision tree classification. Expert Syst. Appl. 2009, 36, 9564–9573. [Google Scholar] [CrossRef]
- Mao, Q.; Fang, X.; Hu, Y.; Tang, J.; Chen, S. Chiller sensor fault detection based on empirical mode decomposition threshold denoising and principal component analysis. Appl. Therm. Eng. 2018, 144, 21–30. [Google Scholar] [CrossRef]
- Qi, B.; Li, Y.; Yao, W.; Xu, B.; Tang, J. Application of emd combined with deep learning and knowledge graph in bearing fault. J. Signal Process. Syst. 2023, 95, 935–954. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, S.; Cao, R.; He, D.; Liu, H. A rolling bearing fault diagnosis method based on the woa-vmd and the gat. Entropy 2023, 25, 889. [Google Scholar] [CrossRef]
- Luo, J.; Wen, G.; Lei, Z.; Deng, Y.; Shi, Y. Weak signal enhancement for rolling bearing fault diagnosis based on adaptive optimized vmd and sr under strong noise background. Meas. Sci. Technol. 2023, 34, 064001. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Qian, J. Fault diagnosis of hydro-turbine via the incorporation of bayesian algorithm optimized cnn-lstm neural network. Energy 2024, 290, 130326. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, W.A.; Guo, F.; Lin, Y. Wavelet packet decomposition-based multiscale cnn for fault diagnosis of wind turbine gearbox. IEEE Trans. Cybern. 2021, 53, 443–453. [Google Scholar] [CrossRef] [PubMed]
- Yin, A.; Yan, Y.; Zhang, Z.; Cao, Y. Fault diagnosis of wind turbine gearbox based on the optimized lstm neural network with cosine loss. Sensors 2020, 20, 2339. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Jiang, J.; Guo, X.; Lin, Z.; Yu, Y. An efficient cnn with tunable input-size for bearing fault diagnosis. Int. J. Comput. Intell. Syst. 2021, 14, 625–634. [Google Scholar] [CrossRef]
- Qiu, G.; Nie, Y.; Peng, Y.; Wu, B.; Zhu, L. A variable-speed-condition fault diagnosis method for crankshaft bearing in the rv reducer with wso-vmd and resnet-swin. Qual. Reliab. Eng. Int. 2024, 40, 2321–2347. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning (ICML), 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 6105–6114. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017. [Google Scholar] [CrossRef]
- Li, C.; Sánchez, R.V.; Zurita, G.; Cerrada, M.; Cabrera, D. Fault Diagnosis for Rotating Machinery Using Vibration Measurement Deep Statistical Feature Learning. Sensors 2016, 16, 895. [Google Scholar] [CrossRef]
- Ren, L.; Li, X.; Ma, H.; Zhang, G.; Huang, S.; Chen, K.; Wang, X.; Yue, W. Lightweight Intelligent Fault Diagnosis Method Based on a Multi-Stage Pruning Distillation Interleaving Network. Adv. Mech. Eng. 2024, 16, 16878132241281470. [Google Scholar] [CrossRef]
- Chen, R.; Chen, S.; He, M.; Zhu, X.; Yang, J. Rolling bearing fault severity identification using deep sparse auto-encoder network with noise added sample expansion. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2017, 231, 666–679. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z.; Yan, Y.; Sun, T.; Wang, Q. Research on diesel engine fault status identification method based on synchro squeezing s-transform and vision transformer. Sensors 2023, 23, 6447. [Google Scholar] [CrossRef]
- Kazemi, K.; Amirian, M.; Dehghani, M.J. The s-transform using a new window to improve frequency and time resolutions. Signal Image Video Process. 2014, 8, 533–541. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Cai, G. The multiclass fault diagnosis of wind turbine bearing based on multisource signal fusion and deep learning generative model. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Yi, J.; Tan, H.; Yan, J.; Ma, F.; Zhou, L. Adaptive rotating machinery fault diagnosis method using mkist. Meas. Sci. Technol. 2024, 35, 045010. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, X.; Liao, S.; Zhou, L.; Wang, X. Probabilistic prognosis of wind turbine faults with feature selection and confidence calibration. IEEE Trans. Sustain. Energy 2023, 15, 52–67. [Google Scholar] [CrossRef]
- Li, G.; Deng, C.; Wu, J.; Zhao, J.; Chen, X. Sensor data-driven bearing fault diagnosis based on deep convolutional neural networks and s-transform. Sensors 2019, 19, 2750. [Google Scholar] [CrossRef]
- Li, X.; Yuan, P.; Wang, X.; Tang, W.; Zhang, M. An unsupervised transfer learning bearing fault diagnosis method based on depthwise separable convolution. Meas. Sci. Technol. 2023, 34, 095401. [Google Scholar] [CrossRef]
- Ling, L.; Wu, Q.; Huang, K.; Yang, C.; Luo, Y. A lightweight bearing fault diagnosis method based on multi-channel depthwise separable convolutional neural network. Electronics 2022, 11, 4110. [Google Scholar] [CrossRef]

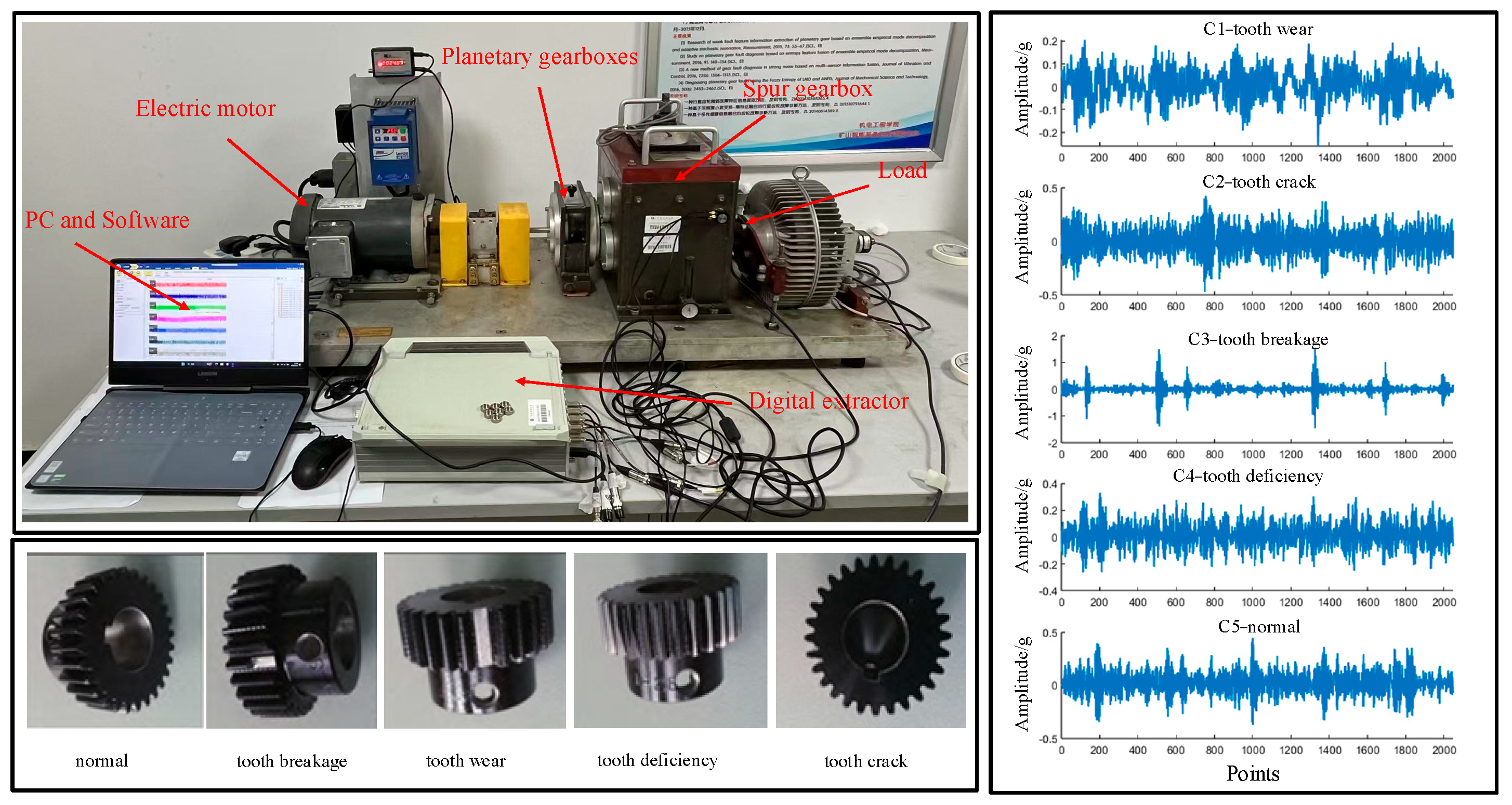


| Fault ID | Fault Type | Speed (HZ) | Training Set | Test Set | Total Samples | Label |
|---|---|---|---|---|---|---|
| C1 | tooth wear | 30 | 160 | 40 | 200 | 1 |
| C2 | tooth crack | 30 | 160 | 40 | 200 | 2 |
| C3 | tooth breakage | 30 | 160 | 40 | 200 | 3 |
| C4 | tooth deficiency | 30 | 160 | 40 | 200 | 4 |
| C5 | normal | 30 | 160 | 40 | 200 | 5 |
| —— | sum | —— | 800 | 200 | 1000 | —— |
| Fault ID | Fault Type | Precision | Recall | F1-Score |
|---|---|---|---|---|
| C1 | tooth wear | 0.9645 | 0.8579 | 0.9081 |
| C2 | tooth crack | 0.9912 | 0.9932 | 0.9897 |
| C3 | tooth breakage | 0.8600 | 0.9297 | 0.8935 |
| C4 | tooth deficiency | 0.9355 | 0.7713 | 0.8455 |
| C5 | normal | 0.5063 | 1.0000 | 0.6723 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhou, H.; Liu, C.; Cheng, G.; Pang, Y. Fault Diagnosis Method for Shearer Arm Gear Based on Improved S-Transform and Depthwise Separable Convolution. Sensors 2025, 25, 4067. https://doi.org/10.3390/s25134067
Wu H, Zhou H, Liu C, Cheng G, Pang Y. Fault Diagnosis Method for Shearer Arm Gear Based on Improved S-Transform and Depthwise Separable Convolution. Sensors. 2025; 25(13):4067. https://doi.org/10.3390/s25134067
Chicago/Turabian StyleWu, Haiyang, Hui Zhou, Chang Liu, Gang Cheng, and Yusong Pang. 2025. "Fault Diagnosis Method for Shearer Arm Gear Based on Improved S-Transform and Depthwise Separable Convolution" Sensors 25, no. 13: 4067. https://doi.org/10.3390/s25134067
APA StyleWu, H., Zhou, H., Liu, C., Cheng, G., & Pang, Y. (2025). Fault Diagnosis Method for Shearer Arm Gear Based on Improved S-Transform and Depthwise Separable Convolution. Sensors, 25(13), 4067. https://doi.org/10.3390/s25134067






