Abstract
The Fit for 55 and Euro 7 regulations significantly reduce CO2 emissions from combustion sources. This will be reflected in the regulations governing the approval of in-service vehicles, including those using alternative fuels. The present study focused on the rapid diagnostics of the technical condition of gas injectors. The test method was a modification of the Gaussian characteristic fields method using the Szpica–Warakomski rectilinear trend. The flow tests resulted in average volumetric intensities of 111 NL/min and 124 NL/min, depending on the operating conditions. The opening and closing times were in the range of (1.3…3.5) ms. The directional parameter of the rectilinear trend, which is important from the point of view of the analyses, was 0.97 for brand new (BN) injectors and 1.00 for in-service (IO) injectors. The intersection parameters were 0.64 and 0.24, respectively. The qualitative evaluation yielded coefficients of determination of 95.01 and 94.07. The values of the trend parameters were strongly dependent on the design solution and model/type of injector. Inferring the effect of operating condition on the trend parameter values, a one-factor analysis of variance was performed, which showed the significance of only the directional coefficient. A comparison of the same BN and IO injector model showed an apparent change in the value of the intercept only. No significant relationships between the injector opening and closing times and the trend parameters were shown. Thus, the usefulness of using the Szpica–Warakomski rectilinear trend in the functional evaluation of gas injectors of different designs and under different operating conditions was demonstrated.
1. Introduction
Modern legislation related to climate and energy policy mandates a reduction in CO2 emissions [1]. The largest emitters are listed as follows: EU, CN and US. They total about 50% of global emissions [2]. Globally, transportation accounts for 16% of global emissions and road transport for 12% [3], with the EU accounting for 27% and 19%, respectively [4,5]. New legislation being created for future years, such as Euro 7, LEV 4 and Low NOx, and is expected to reduce the permissible emission levels of NH3, N2O, CO, HC, NOx, and PM not only for engines powered by classical fuels but also hydrogen [6] in successive steps. Regulations relating to new species and particulate matter are also planned [7]. The climate agreement that was signed in Paris set a rise in the annual average temperature to just 1.5 °C by 2050. In addition to the widespread introduction of renewables, efforts are also focusing on CCTs [8]. The EU has recently introduced ‘Fit for 55′ regulations, significantly affecting the emissions performance of cars and vans [9,10]. As early as 1988, it was noted that the number of cars in the world exceeded 400 million and was 10 times higher than in 1950 [11], hence the increased legislative action on emissions. The year 2020 marks the 50th anniversary of the US Clean Air Act (EPA and NAAQS) for air pollutant criteria. Tackling increased emissions in transportation has resulted in various design and organizational solutions: EGR; TWC, SCR, DPF/FAP [7], S&S [12,13], ‘free-wheeling’ [14], car sharing and alternative means of transport [15,16], and ‘eco-driving’ [7]. There has been a steady increase in interest in alternative fuels, which must comply with CAFÉ and AMFA regulations [17,18]. New energy sources in vehicles (H2, FCV, BEV, MHEV, and PHEV) have not ruled out the use of ICE for the time being [19]. In particular, ICE’s GDIs using alternative fuels combined with assistance in hybrid systems have not exhausted their potential as sources of energy in transportation [20]. The use of oxygenated fuels, such as alcohols and their blends, can enhance combustion efficiency and reduce harmful exhaust emissions due to improved oxygen availability and cleaner burning characteristics [21]. Intensive research is being conducted on ethanol, butanol, and methanol for these benefits [21,22,23]. As a substitute, or in the form of mixtures, carbon-reduced fuels can be used in ICEs with different combustion organizations [24]. The most popular of this group are H2 [25], LPG [26,27], CNG [28,29], and LNG [30]. HVO [31], FAME [32], NH3 [33], and OME e-fuels [34] are also gaining popularity. A separate group includes fuels made from various types of waste or food products: biogas [35], syngas [25], PVO [36], GTL [37], biomass-gasifiers [38], POMDME [39], and TPO [40].
The most popular alternative fuels, which undoubtedly include LPG and CNG, today require low-pressure gas-phase injectors in their supply systems. Injectors of this type are normally closed solenoid valves that open for a specified period of time when electrical power is applied. Electromagnetic injectors are the most common in this field, although piezoelectric-driven injector concepts are being developed [41]. The injector is the last component of the power system and its role in the fuel system is decisive regarding the power supply and the formation of the combustible mixture.
In [42], the test methods applicable to the testing of injectors of various fuels in the main liquid fuels are presented in great detail, but the study of the issue of gas injectors and diagnostic methods is not exhaustive. For any power system, tests can be carried out on an engine dynamometer or chassis dynamometer using an exhaust gas analyzer [43,44], where a preliminary diagnosis of the fuel system will be possible. Among the most extensive and costly test methods are the Zeuch method [45]; Schlieren imaging method [46,47,48]; shadow classification and particle image accelerometry method [49]; high-speed cameras [50]; light fluorescence absorption [51]; optical lasers and laser absorption scattering techniques [52,53]; a combination of high-speed cameras and optical lasers [54]; X-ray [55]; heat flow sensors [56]; and long-range microscopy [57]. They allow a very detailed process evaluation but require a sophisticated apparatus and appropriate inference procedures. They are applicable to developmental research and the creation of new technical studies. As an alternative to these methods, there are simplified methods that allow the evaluation of basic functional parameters of importance in the initial diagnosis of the operating condition. Mainly, these are methods using lift sensors [58] and optical sensors [59].
The primary test method for diagnosing the operating condition of gas injectors is the determination of the volumetric flow rate using a flow meter [60]. Based on this, it is possible to evaluate the flow rate at fixed values of supply pressure and outlet nozzle diameter [61]. Using a surrogate fluid, the flow characteristics of a gas injector can also be determined, but the state of aggregation of the test medium can make the inference difficult [62]. An innovative approach in gas injector testing is presented in [63]. The ‘fuel tank refill’ method took into account the use of tanks and the test medium as air (often practiced for safety reasons). With this method, it was possible to simultaneously determine the flow characteristics of several injectors included in the array. As a result, the dosage irregularity of the gas rail was calculated. Some of the simplest diagnostic methods that can be used in the study of gas injectors are current and voltage in the power line [64]. These are indirect methods to determine the opening and closing times of injectors using waveforms from the power line (their curvature). Complementing this with acceleration sensors [65,66], the effectiveness of electrical measurements can be confirmed in a non-intrusive manner. An alternative to in-line electrical testing is presented in [67], where an injector nozzle outlet pressure sensor was used. The effectiveness of this method was confirmed for the lift sensor mounted in the injector under test. Tests using the pressure sensor allowed the evaluation of opening and closing times and the determination of dosing uniqueness, which is an obvious novelty in injector testing [67]. Condition verification using the methods presented earlier should be complemented by measurements of the electrical parameters of coils and circuits [68]. It should be noted at this point that the low-pressure gas-phase injectors do not have defined legal legislations, like, for example, gasoline injectors in SAE J1832 and J2715 [69].
One of the main problems in studying the low-pressure gas-phase injectors is access to comparative data. Manufacturers’ technical materials provide the maximum flow rate of continuously open injectors [70,71] and occasionally the flow characteristics of selected pressure values and outlet nozzle diameters [72,73]. Information on opening and closing times can also be found, but without specifying the method of determining them.
A literature analysis of the study of the low-pressure gas-phase injectors revealed a research gap in the area of rapid condition diagnostics. The research presented in this paper is a continuation of the analyses contained in [74]. The innovative Szpica–Warakomski (S-W) method presented there complemented the Gaussian characteristic area method used in diagnostics.
The main objective of this work was to determine the parameters of the rectilinear trend constituting the basis for inference in the S-W method for gas injectors of different designs and at different stages of operation.
The research question of this study was whether different designs and different operating conditions affect the indicators relevant for analyses using the Szpica–Warakomski method. In view of the research question formulated in this way, the determination of the rectilinear trend parameters underlying the S-W method for gas injectors of different designs and at different stages of operation was identified as the main objective. In addition, consistency, or the lack thereof, was sought in inferring the technical condition of gas injectors using the Gaussian characteristic figure area method and the Szpica–Warakomski rectilinear trend. The results obtained will be used in the future to determine the tolerance limits of the pattern.
The rest of the study is organized as follows: Section 2 presents the research objects. Section 3 describes the research methodology, equipment, and analysis methods. The research results and their discussion are included in Section 4, which was divided into the determination of the volumetric flow rate, opening and closing times, areas formed from measurements at significant points, and parameters of the rectilinear trend of the S-W method. The applicability of the results was also highlighted (Section 5). The entire study was summarized in Section 6, and future research in the subject area is finally described in Section 7.
The activities described in this manuscript revolve around the diagnosis of the condition of gas injectors, which is very important in the context of green transformation and the use of alternative fuels in internal combustion engines.
2. Subjects of This Research
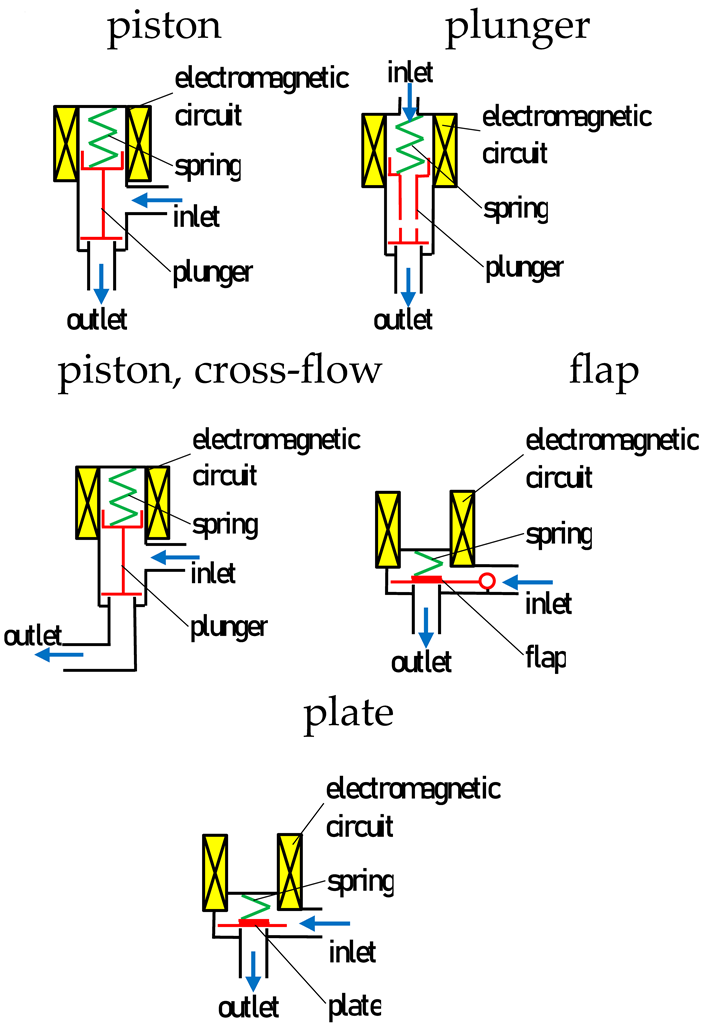
The objects of this study were the low-pressure gas-phase injectors applicable to LPG and CNG vapor-phase supply systems. Injectors using a solenoid coil and movable opening elements in operation were selected for this study. Injectors of this type are normally closed solenoid injectors, in which, after the appearance of electrical power, the magnetic field of the coil causes them to open. In the analysis, different design solutions of injector valve actuators were considered in order to broaden the scope of inference. The objects of this study were injectors with valves opened by a piston, plunger, flap, and plate, as included in Table 1. In the plunger group, ‘c-f’ (cross-flow) was distinguished, in which the working medium, after passing through the control valve, does not flow in the axis of the valve, but bends at an angle of 90 deg.

Table 1.
Technical data of the injectors.
3. Research Methods, Equipment, and Processing of Results
3.1. Research Methods
The research methods used in this study were aimed at determining the parameters of the rectilinear trend using the S-W method [74]. In order to look for possible reasons for the differences between the values obtained for different gas injectors, the scope of this study was extended to include the determination of functional parameters. In addition, the Gaussian half-surface method was included in the analysis of the results, which was juxtaposed with the S-W method. The scope of the research included
- Preliminary tests—a determination of the maximum volumetric flow rate Q and opening to and closing tc times of injectors;
- Preliminary tests—a determination of Gaussian methods of the areas of the resulting geometric figures A built from the values Q obtained at different supply pressures p and injector opening times timp;
- Main research—a determination of the parameters of the rectilinear trend of the S-W method on the basis of Q obtained at different p and timp.
The first part of this study (preliminary research) was aimed at determining the basic functional characteristics of the injectors. Opening and closing times affect the volumetric flow rate when the injector is cycled. The maximum volumetric flow rate values given by injector manufacturers in technical documents [71,73,75] are determined with the injector constantly open. This does not directly translate into the flow characteristics of the injectors due to the different opening and closing times and the associated geometric characteristics of the valve elements. Therefore, it was considered important, in addition to determining the maximum volumetric flow rate, to determine these times. This was supported by their possible usefulness in further analyses when looking for sources of differences in the results of the main study.
The second part of the preliminary study is based on the descriptions presented in [76], where the half-Gaussian method was adapted to the functional evaluation of common-rail diesel injectors. A comparison of the fields of the resulting geometric figures determined at different supply pressures and opening times made it possible to predict the causes of injector failures. In the case of the low-pressure gas-phase injectors, as a novelty, the adoption of test points was necessary, bearing in mind that gas injectors basically operate at a single, stabilized fuel operating pressure.
The third stage of this research (the main research) is an original method developed by one of the authors of the study [74]. The method differs in its method of inference relative to the second part, while leaving the same research points. The innovation in this case is the replacement of the air field of the resulting geometric figure built from the research points by the parameters of the rectilinear trend obtained by linear regression. The parameters of the rectilinear trend, such as the directional parameter and the intersection parameter, are considered sufficient for evaluating the differences between injectors. In addition, the coefficient of determination shows the scatter of points with respect to the determined rectilinear trend.
3.2. Research Equipment
The original test stand, shown in Figure 1a, was used to carry out the study. It is dedicated to flow testing of gas injectors, but can be used to test other solenoid valves at a specific differential pressure. Due to the danger of using the vapor phase of LPG or CNG, the tests were conducted on compressed air. This is a common procedure in gas injector testing [72,73,75]. Compressed air from air supply 1 flowed to air preparation system 2, where it was subjected to cleaning and its pressure was established in the measuring system. Furthermore, the air went to buffer tank 3 with a volume of 40 L, which, in addition to accumulating the air supply, had the task of suppressing pulsations resulting from the cyclic operation of the injector. From buffer tank 3, the air flowed through mass flow meter 4 to the injector 5 under test. In this case, a BRONKHORST F-113AC-M50-ABD-00-V flow meter using a thermal sensor and microprocessor-based signal conversion board in operation was used (response time 0.5 s; range (0…300) LN/min; output signal range (0…5) V; accuracy 0.5%). The control of the parameters of the tested injector was carried out using the injector control system (based on the STAG controller), allowing the control of the operating frequency, opening time, and PWM signal parameters responsible for sustained opening. The electrical voltage signal from the flow meter was read using an AXIOMET AX 102 voltage meter (range (200 m…600) V; accuracy ± 0.5%). With this bench configuration, it was possible to determine the maximum volumetric flow rate and conduct the second part of the preliminary and main tests. For the determination of the opening and closing times, the stand was supplemented with pressure sensor 8. This sensor was the author’s solution described in [65,68], and the method of measurement and inference should be considered indirect, since it does not interfere with the actuator element of the injector valve. In operation, it used the MPXH6400A pressure transducer (response time <1 ms, range (20…400) kPa, output signal range (0…5) V, accuracy 0.25%) into which the air jet flowing out of the injector nozzle hit. Furthermore, the air jet left sensor 8 through the outlet holes into the atmosphere. Electrical signals from sensor 8 as well as from the injector’s electrical power line were transmitted to oscilloscope 9. The oscilloscope used in the study was a RIGOL MSO4014 (bandwidth 100 MHz; real time sample rate up to 4 GSa/s; real time waveform record, replay, and analysis up to 200,000 frames; vertical resolution 8 bit).
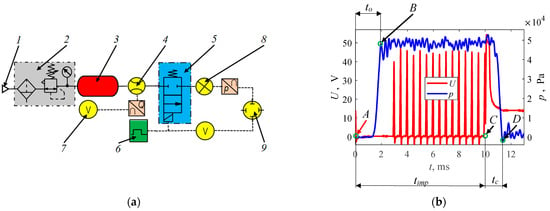
Figure 1.
Schematic of the test stand: (a) 1—air supply; 2—air preparation system; 3—buffer tank; 4—mass flow meter; 5—tested injector; 6—injector control system; 7—voltage meter; 8—pressure sensor; and 9—oscilloscope. Examples of the waveforms of electric supply voltage and pressure at the outlet of the injector nozzle (b).
3.3. Processing of Results
When measuring the maximum volumetric flow rate on the test stand (Figure 1a), a constant pressure was set in air preparation system 2 (1 × 105 Pa) and the opening time of injector 5 was set large enough to cause continuous opening. At an operating frequency of 2000 imp/min, this was 30 ms, with a 95% filled PWM signal appearing after 3.5 ms to prevent overheating of the injector coil. The electrical voltage signal from flow meter 4 indicated on voltage meter 7 was converted according to the manufacturer’s data. In order to reduce noise during the measurement, a flexible tube with an inner diameter of 12 mm and a length of 5 m was installed at the outlet of the injector nozzle, thus taking the air out of the room in which the tests were conducted. It should be noted here that the gas injector was controlled by a short circuit to ground.
In determining the opening and closing times of the injectors, the test stand was supplemented with a pressure sensor 8 and an oscilloscope 9. The pressure in the air preparation system 2 was set at (1 × 105 Pa), the injection time at 10 ms, and the operating frequency at 1000 imp/min (corresponding to 2000 r./min for a 4-stroke engine). Having the waveforms of supply voltage and pressure at the outlet of the injector nozzle recorded with an oscilloscope, further data processing was performed using MATLAB 2023 software. The signals were limited with a 2nd-order Butterworth low-pass filter at a frequency of 0.25. Example waveforms are shown in Figure 1b. The opening time to was determined from the onset of the control pulse A (in this case, shorted to ground) until the pressure at the injector nozzle outlet reached the first peak, indicating the maximum value B. The slight drop in pressure after the first maximum was reached was due to the reflection of the control element from the valve body. The closing time was determined from the disappearance of the control pulse timp marked C to the pressure drop D. The correctness of this method has been confirmed in a number of publications, including [64,65,77]. Sometimes manufacturers specify the closing time only for the pressure drop phase after the disappearance of the electric pulse, which is not correct, since it is not referred to the beginning of the process C.
In the second part of the preliminary tests as well as in the main tests, the primary issue was to determine the test points for the supply pressure p and injection time timp. For this purpose, the results of standardized [78,79] and non-standardized [80] tests of gas-fueled engines available in the literature were analyzed. In addition, a number of previous results of our own tests of engines with different power systems in daily use (data recorder AC STAG) were analyzed with a special emphasis on transients. Based on this, 5 test points were proposed, as shown in Table 2. Initially, the first test point defined the injection time at 2.0 ms, but preliminary tests on the test bench showed that a large proportion of the tested injectors were unable to overcome the supply pressure in this case, resulting in no flow (no injector opening).

Table 2.
Test point supply pressures and opening times.
The test points, in addition to their reference to the operating conditions of the supply system, have their rationale in diagnosing the condition of the injector. High pressure and short opening time (points 1 and 2) assess the operation of the electromagnetic system and changes in the characteristics of the compression spring (increase in stiffness caused by the presence of debris between the coils). A low pressure and long opening time (points 4 and 5) are diagnostics of the compression spring (increase in stiffness). Normal operation (point 3) provides diagnostics of changes in the stiffness of the compression spring and the presence of debris on the injector actuator. Details of the selection of test points (injection feed conditions) are presented in [74]. The case described in this study relates to LPG vapor-phase injectors. Based on this and using Table 2 in the second part of this study based on the results at the test points at each time, a geometric figure was created (Figure 2a). Test conditions at each point were established using air preparation system 3 and injector control system 6.
Figure 2.
Determining the area of the characteristic figure (a) and a rectilinear trend from the measurement points (b).
The areas of the resulting geometric figures in the Cartesian coordinate system Q = f (timp) based on its vertices were determined analytically using the Gaussian method [81]. Assuming that the vertices of each geometric figure in number i…n (timp1, Q1), (timp2, Q2),…, (timpn, Qn) were marked clockwise, the area was determined by the ‘shoelace method’ [82,83] of the general form
while taking into account the timp coordination
and Qi coordination
The areas of A1 and A2 should give the same values.
In the main study, based on the results of measurements at points according to Table 2, a rectilinear trend was determined according to the S-W method using linear regression and the least squares method of deviations (Figure 2b).
The rectilinear trend was written as follows:
where its parameters were calculated from the relationship
A coefficient of determination was used to qualitatively assess the fit of the rectilinear trend to the points:
where and are the arithmetic averages.
It was important from the cognitive point of view of this study to analyze the parameters of the rectilinear trend, such as the directional parameter and the intersection parameter in relation to the injectors, which are structurally different. An additional analysis was also aimed at confronting the values of the areas of the resulting geometric figures obtained from the measurement points with the values of the coefficients of determination. The novelty of the S-W method lies in its innovative inference of the state of the gas injector. As shown in [74], the use of the rectilinear trend of the S-W method has advantages over the Gaussian area field method. The area fields calculated according to the Gaussian method for injectors in different operating wear states can be similar, which does not allow for correct fault identification. It is particularly evident when the characteristic figures determined using this method were rotated. Using the rectilinear trend S-W method, it is possible to accurately identify the faults present using three parameters, such as the directional coefficient, the intercept, and the coefficient of determination.
4. Results and Discussion
4.1. Determination of the Maximum Volumetric Flow Rate and Injector Opening and Closing Times
In determining the volumetric flow rate Q, a constant air pressure of 1 × 105 Pa was maintained in the measurement line. The injector was opened to the maximum with its opening sustained for 3.0 s, and the measurements were repeated five times. Due to the fact that the measurements concerned maximum values, nozzles with a maximum bore diameter (3 mm) were installed in the injectors, depending on their design, or they were tested without nozzles. In determining the opening and closing times, the air pressure in the measuring line did not change (1 × 105 Pa), the opening pulse time was set at 10 ms, and the pulse frequency was set at 1000 imp/min. Figure 3 summarizes the results as average values from five times.
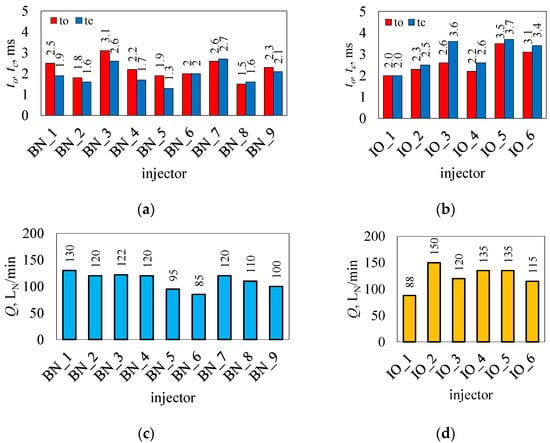
Figure 3.
Opening (to) and closing times (tc) of the tested injectors, brand new (a) and in operation (b), and maximum values of the volumetric flow rate of the tested injectors: brand new (c) and in operation (d).
Of all the injectors tested (Figure 3a,b), as many as six showed an opening time to equal to or greater than 2.5 ms (BN_1, BN_3, BN_7, IO_3, IO_5, and IO_6). This is important in the context of the first test point, according to Table 2. This can result in a worst-case scenario of no opening or reduced flow. The average opening time to for brand new injectors was 2.2 ms, and that for injectors in operation was 2.6 ms. The closing times tc were 1.9 ms and 3.0 ms, respectively. The shortest opening time was shown by BN_8 (flap), it was 1.5 ms, while the longest time for IO_5 (piston) was 3.5 ms. The shortest closing time was recorded for BN_5 (plunger) at 1.3 ms, and the longest time for IO_5 (piston) was 3.7 ms. In the case of injectors labeled c-f (cross-flow), the indirect method test may be subject to error due to the collapse of the jet leaving the injector valve in the body. It was required for technical reasons that the opening and closing times be equal (to = tc), which was noted for injectors BN_6 and IO_1. In such cases, there was a relationship between the time of the control pulse timp and the response of the injector in the form Q. The worst in the relationship to/tc was the IO_3 injector, and it was 2.6 ms/3.6 ms.
In the control systems for the operation of the gas engine supply system, in terms of the injectors used, very often manufacturers offer the possibility of selecting the type of injector from the level of the diagnostics and calibration program. The selection results in a change in the time after which the PWM signal appears. As the measurements showed, only the IO_5 injector with an opening time of 3.5 ms approached the limit of switching on the PWM signal in the adopted configuration of the injector control system used in the test bench. The other injectors tested showed opening times lower than 3.5 ms.
The results for Q are shown in Figure 3c, d. Due to the small scatter of results for the repetitions of each injector, the whiskers on the graph are not visible. The average value Q for brand new injectors was 111 LN/min, while for in-operation injectors, it was 124 LN/min. The higher average value for injectors in operation was due to the flow capacity of IO_2, which is an injector with increased output. The lowest value of Q was shown by injector BN_6 and was 85 LN/min. In contrast, the highest value of Q was that of the aforementioned IO_2, 150 LN/min. Depending on the needs of the required fuel supply conditions, the value of Q for a given engine type can be limited by the diameter of the nozzle mounted on the outlet of the injector (calibration nozzle). Nozzle diameters for the most part are nominally 1.5 mm; furthermore, in the machining process, they can be increased to about 3.0 mm. Not all injectors had the outlet nozzle fused to the body, in some cases it was necessary to mount them to the body. In the case of injectors with composite stubs, calibration nozzles were mounted internally. The name ‘calibration nozzle’ is associated with the process of calibrating the gas supply system to a particular engine type using dedicated computer software. In the case of calibration problems, a message in the form of ‘injector nozzle too small’ or ‘injector nozzle too large’ was often displayed. Analyzing Table 2 and Figure 3, there were no fundamental differences in Q depending on the design solution of the injector valve. The reason for the differences was the geometric parameters of the valve components, such as the diameters of the valve seats and the stroke of the injector moving element.
4.2. Determination of the Areas of Geometric Figures Constructed from Measuring Points
For the purpose of determining the areas of the resulting geometric figures using the Gaussian method, the tests were repeated five times at each of the measurement points specified in Table 2. Table A1 shows the average values of volumetric flow rate. Due to the scatter not exceeding 0.5 LN/min, the posting of deviations was abandoned. Despite an increase in the control pulse time at the shortest time tested from 2.0 ms to 2.5 ms at 2 × 105 Pa, three of the injectors tested did not show flow at this point. Of the brand new injectors, it was BN_9, while of the injectors in operation, they were IO_5 and IO_6. In these cases, the electromagnetic force generated by the coil was unable to lift the flow control element. This was due to the significant pressure difference below and above the actuator and the associated hydraulic drag force. In these three cases, additional tests were carried out to demonstrate the maximum in-line pressure at which the injector would begin to open. The pressure was gradually lowered and the flow meter readings were observed. Tests with an opening pulse duration of 2.5 ms showed that injector BN_9 opened at 1.2 × 105 Pa, while IO_5 opened at 1.1 × 105 Pa and IO_6 opened at 0.7 × 105 Pa.
The resulting geometric figures from the measurement results contained in Table A1 are shown in Figure 4. The differences between the results at the different measurement points were so significant that the scatter whiskers at the test points were not visible.
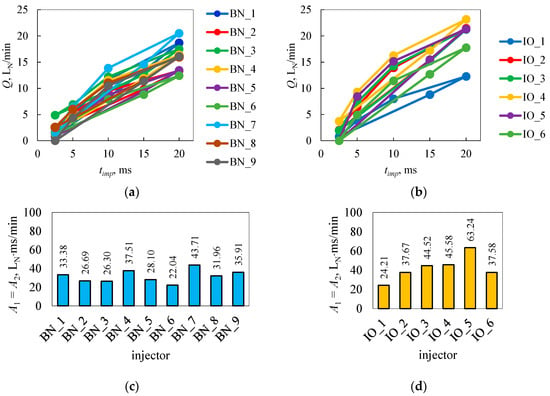
Figure 4.
Geometric figures built from the research results of brand new (a) and in operation (b) injectors and surface areas of geometric figures of brand new (c) and in operation (d) injectors.
Based on Table A1, the surface areas of the resulting figures were calculated using Equations (1) and (2), as shown in Figure 4a,b. The results of calculating the areas contained in Figure 4c,d showed variation in the values for individual injectors. The smallest area of the resulting geometric figure (22.04 LN × ms/min) was calculated for injector BN_6, while the largest (63.24 LN × ms/min) was calculated for IO_5. The average values of the areas of the resulting geometric figures are 36.73 LN × ms/min for brand new injectors and 42.13 LN × ms/min for injectors in operation. As can be seen in Figure 4c,d, brand new injectors show less variation in figure areas than those in operation.
The results in Figure 4a,b showed that the resulting figure could be similar in shape and therefore area, but was located above or below another figure being compared or rotated in some way relative to it. Therefore, the method using only the determination of the areas of the constructed figures did not give a clear result when making comparisons or searching for the source of injector defects. As an example here, BN_2 (26.69 LN × ms/min) and BN_3 (26.30 LN × ms/min) (Figure 4c,d) were rotated relative to each other. Hence, the idea of using another methodology in the inference came, which was the rectilinear trend. The parameters of the rectilinear trend are able to indicate the direction and position of the approximating line. In addition, the coefficient of determination evaluates the degree of clustering of points relative to the rectilinear trend. It was considered important to compare the values of the areas with the values of the coefficient of determination.
4.3. Determination of Rectilinear Trend Parameters Using the Szpica–Warakomski Method
Having the results presented in Table A1, rectilinear trends were determined using Equations (4)–(6) according to the S-W method (Figure 5). The location of the rectilinear trend for each injector varied, being more concentrated for brand new injectors than for injectors in operation. As shown in the previous section of this paper, the determination of the area created from the results of the geometric figure does not allow a precise assessment of the differences between injectors.
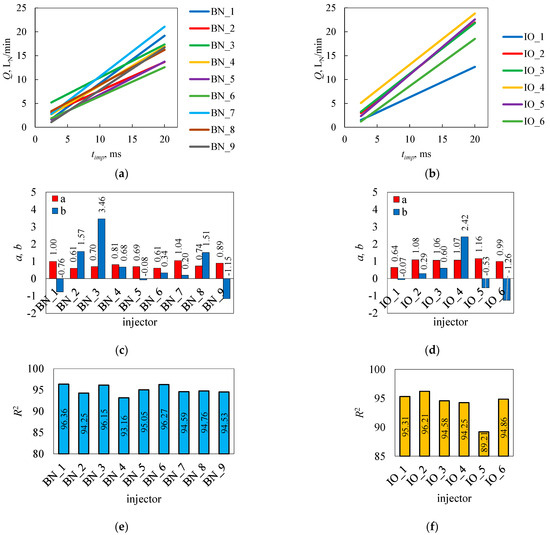
Figure 5.
S-W method for the rectilinear trends for the tested injectors: brand new (a) and in operation (b). Parameters of the rectilinear trend: brand new (c) and in operation (d). Determination coefficients: brand new (e) and in operation (f).
The values of the directional parameter of the rectilinear trend a for all tested injectors were in the range of (0.61…1.08) (Figure 5c,d). The average value a for brand new injectors was 0.79, and for injectors in operation, it was 1.00. The rectilinear trend intersection parameter b took both positive and negative values in the range (−1.26…+3.46). The average value b for brand new injectors was 0.64, while for those in operation, it was 0.24. For this rectilinear trend parameter, the differences may be due to the volumetric flow rate in cyclic operation, which does not necessarily relate to the value of maximum volumetric flow rate in continuous opening, which are shown in Figure 3c. The geometric parameters of the injector’s valve elements are important in this case. The coefficient of determination of the rectilinear trend R2 was in the range of (89.21…96.36). The spread R2, according to the assumptions of the S-W method, evaluated the clustering of the measurement points relative to the approximating rectilinear trend and could be reflected in the area of the geometric figure built from the measurement results.
Negative values of the intersection parameter b of the rectilinear trend were shown for BN_1, BN_5, BN_9, IO_1, IO_5, and IO_6. In the case of BN_9, IO_5, and IO_6, this may have been a consequence of the lack of flow at the first test point according to Table 2. Similarly, injectors BN_1, BN_5, and IO_1 showed a flow of less than 1 LN/min at this point, well below the measured values for the others that showed flow. The lack of opening at the first test point, according to Table 2 (2.5 ms), in addition to lowering the value b, can also cause changes in the value a. It was found that no or limited flow at the first test point can result in a value of parameter b below zero. The opposite situation was found for injector BN_3, which responded well to a high system pressure and short control pulse times. On the other hand, in the range of longer times, it had a problem with sustained opening. Injector IO_4 showed a highly localized rectilinear trend, with some of the highest index values.
The values of the coefficient of determination oscillated at 95.00 (Figure 5e,f). For brand new injectors, the average value R2 was 95.00. For injectors in operation, it was 94.00, with the IO_5 injector dominating this average result (89.21).
Correlations between the values of the areas of the figures formed from the test results of the points with the values of the coefficients of determination of the rectilinear trend of the S-W method were determined. As can be seen in Figure 6a, there was a correlation between the area fields and the coefficients of determination. A decrease in the value of the area field resulted in an increase in the coefficient of determination and vice versa, but this was not clear for the two groups compared (different directional parameters). Further work in this area is needed to confirm the assumption made.
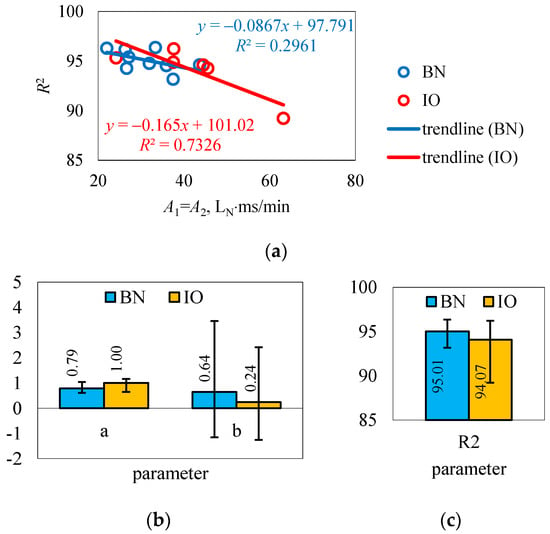
Figure 6.
Correlation of determination coefficients with the areas of constructed figures (a) and values of the parameters of the rectilinear trend S-W method (b,c).
In response to the main objective of this study, concerning the values of the parameters of the rectilinear trend S-W method, Figure 6b,c were created. In the studied group of brand new injectors, the value of the directional parameter was on average a = 0.79, with upper (+0.26) and lower (−0.18) deviations. This seems to correctly illustrate the average slope of the rectilinear trend of the survey and inference method in question. In the in operation group, the directional parameter a = 1.00 and is characterized by a slightly larger scatter relative to brand new injectors, amounting in the upper level of +0.16 and lower level of −0.36. The interval of the directional parameter (0.8…1.00) should be considered the reference for injector comparisons. The second significant parameter, which was the intersection parameter b, showed a very large variation, taking both positive and negative values. Brand new injectors gave an average value of b = 0.64, with upper (+2.82) and lower (−1.79) deviations, while injectors in operation had b = 0.24, with upper (+2.18) and lower (−1.50) deviations. In both cases, the deviations were multiples of the mean value. Such large discrepancies were due to the fact that the geometric parameters of the valve elements varied. This was not reflected in the maximum volumetric flow rate at continuous opening, and in cyclic flow, it turned out to be dominant. Therefore, the value of the parameter b should be determined in each case for a given type of injector, taking into account various factors, such as the diameter of the outlet nozzle, which limits the flow rate and, as a result, lowers the position of the rectilinear trend. The clustering of points with respect to the trend line assessed in the method in question by the coefficient of determination took average values for brand new injectors of R2 = 95.01 and for injectors in operation of R2 = 94.07. Deviations in this parameter were small, for brand new injectors the upper deviation was +1.35 and lower deviation was −1.85, and for injectors in operation, they were slightly larger, with an upper deviation of +2.14 and lower deviation of −4.85, but still represented a small percentage of the average value. In summary, the range of the coefficient of determination (94.00…95.00) should be considered representative at this stage of the study.
In response to the research question of this study, small differences in the mean values of the analyzed parameters of the rectilinear trend of the S-W method for injectors of different designs in both study groups were indicated (Figure 6b,c). It should be emphasized that this study was preliminary and conducted on small representative groups. On this basis, it was suggested to consider an individual approach to each design solution in comparative studies. With a view to assess the variability of the analyzed parameters of the S-W method during the operation of the injectors, it was decided to statistically assess the differences in the mean values based on the results from Figure 5c–f, taking into account the different numbers in the groups. A one-way ANOVA (Excel) was carried out, with the null hypothesis H0 stating the equality of mean values of the analyzed parameters and the alternative hypothesis H1 rejecting this equality. The results are presented in Table 3.

Table 3.
Results of one-way ANOVA.
The variance values (Table 3) confirm the variation in each of the analyzed parameters (a, b, and R2), depending on the BN and IO groups. The table also includes values for the sum of squares of deviations SS, the number of degrees of freedom df, and the mean square error MS within groups (columns) and between groups (error).
The F value was the value of the statistic that we refer to Test F, while p was the probability. Assuming a confidence level of 0.05, was found that only for parameter a a probability p of 0.033 confirmed the rejection of hypothesis H0 in favor of hypothesis H1 in the analysis of the influence of operating conditions. In this case, the mean values differed significantly. This was confirmed by the F value of 5.66, which was above the 4.67 resulting from the Test F. In the case of the other two parameters, b and R2, the values of the statistics were above 0.05 and were 0.58 and 0.31, respectively. This indicates that there was no basis for rejecting the H0 hypothesis of the equality of mean values. With this in mind, it was concluded that the decisive parameter for the comparative study of both injectors in the BN and IO groups and between groups would be the directional coefficient of the straight line a. Other parameters, such as the intercept b and the coefficient of determination R2, would not be statistically significantly different. In the case of R2, the variance value in the IO group was significantly influenced by injector IO_5 with a value of 89.21, where the others oscillated in the range (94…96). This confirms the need for an individual approach to the study of individual injector models. It was considered reasonable to establish the S-W rectilinear trend parameters for individual brand new models and to provide tolerance limits for injectors in service. The results of this study form the basis for determining the tolerance limits based on a group with varying conditions and technical solutions.
Due to the fact that there was some novelty in the analyses associated with the S-W method, there was a lack of data for comparisons with the results of this study. Therefore, it was decided to compile the results of this study into radar plots in order to further search for reasons for the differences between the values of the parameters of the rectilinear trend for the injectors studied. To achieve this, the coefficient of determination R2/100 was used, and the scale of the graph was set at (−2…4) (Figure 7). In the search for the relationship of the values of a, b, and R2 with the opening time to and closing time tc, a lack of correlation with respect to the parameter b in particular became apparent. Both the short opening and closing times of brand new BN_1 or BN_4 injectors gave different values of b. The variation in b was best shown by comparing BN_3 and BN_9. For injectors in operation, the opening to and closing tc times, except for IO_1, were longer than in brand new injectors. As before, this yielded different values of b. Parameters a and R2 did not have as much variation as b, but should be determined on a case-by-case basis for individual injectors. It does not directly follow from Figure 7 that the values of a and R2 depend on the design solution of the injector valve. Parameter b, on the other hand, reflects the geometric characteristics of the injector valve, and so it should be determined for comparisons on a case-by-case basis.
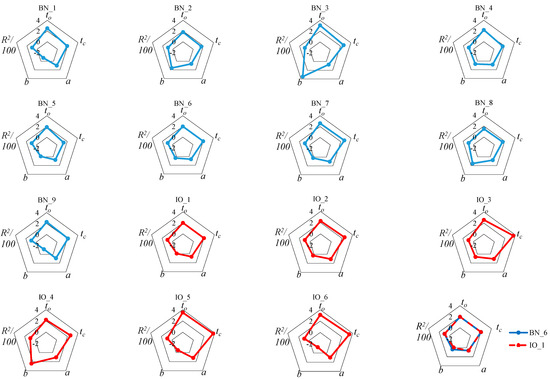
Figure 7.
Radar charts with values of the coefficients relevant to the analysis of the tested injectors.
Having established the fact that the significant parameters of the S-W method rectilinear trend can be averaged only in terms of the directional parameter and the coefficient of determination, while the intersection parameter should depend on the geometric parameters of the valve element, a comparison was made between two injectors from one manufacturer, which were BN_6 and IO_1 (Figure 7). In spite of the almost 10-year difference in production date separating them and, in the case of IO_1, a vehicle mileage of about 80,000 km, there was apparent agreement in the values of the parameters to, tc, a, and R2. There was a slight difference for parameter b, which may be due to the different designs of the injector valve system components. This once again confirms the need to determine parameter b individually for each injector.
5. Application Guidelines
The measurement and analysis results presented in this paper allowed the determination of the average values of the significant parameters of the rectilinear trend of the S-W method. The directional and determination parameters showed acceptable scatter with respect to the average, while the point of intersection resulted from the geometric parameters of the design solution of the valve elements. Therefore, it seems most authoritative to use the S-W method in the preliminary diagnosis of the technical condition of gas injectors, especially those placed in a common rail. In this way, it will be possible, having a standard, of course, to compare injectors of the same design among themselves and direct them to calibration (brand new) or regeneration (in operation).
6. Conclusions
In the course of the conducted activities, nine brand new injectors and six injectors in operation from the group of the low-pressure gas-phase injectors were analyzed using the original test stand and the adopted innovative inference, and the following conclusions were drawn:
- Of all the injectors tested, six showed an opening time to equal to or greater than 2.5 ms (BN_1, BN_3, BN_7, IO_3, IO_5, and IO_6), which affected the subsequent analysis of the results.
- The average value of volumetric flow rate Q for brand new injectors was 111 LN/min and for those in operation was 124 LN/min. The lowest value Q was obtained for injector BN_6 (85 LN/min) and the highest for IO_2 (150 LN/min).
- The average opening time to for brand new injectors was 2.2 ms and for injectors in operation was 2.6 ms. Closing times tc were 1.9 ms and 3.0 ms, respectively. The shortest opening time was shown for BN_8 (1.5 ms), while the longest was shown for IO_5 (3.5 ms). The shortest closing time was shown for BN_5 (1.3 ms) and the longest for IO_5 (3.7 ms). The worst in the relationship (to/tc) was the IO_3 injector; it was 2.6 ms/3.6 ms.
- In the proposed innovative test method (S-W), at the point characterized by the shortest opening time and highest pressure, in three cases, the injectors did not open. Gradual lowering of pressure showed opening for BN_9 at 1.2 × 105 Pa, IO_5 at 1.1 × 105 Pa, and IO_6 at 0.7 × 105 Pa.
- The smallest area of the geometric figure formed from the results of the test points (22.04 LN × ms/min) was calculated for injector BN_6 and the largest (63.24 LN × ms/min) for IO_5. The average values were 36.73 LN × ms/min for brand new injectors and 42.13 LN × ms/min for injectors in operation. The method using only the determination of the area of the constructed figures to infer the state of the injector may not give a clear result when comparing, as an example, BN_2 (26.69 LN × ms/min) and BN_3 (26.30 LN × ms/min), which are rotated relative to each other.
- The values of the directional parameter of the rectilinear trend of the S-W method averaged a = 0.79 with upper (+0.26) and lower (−0.18) deviations. In the in operation group, the parameter a = 1.00 and was characterized by a slightly larger scatter relative to brand new injectors, amounting in the upper level of +0.16 and lower level of −0.36. The interval of the directional parameter (0.8…1.00) should be considered a reference for injector comparisons.
- The parameter of the intersection of the rectilinear trend of the S-W method showed a very large variation, taking both positive and negative values. Brand new injectors gave an average value b = 0.64, with upper (+2.82) and lower (−1.79) deviations. In injectors in operation, b = 0.24, with upper (+2.18) and lower (−1.50) deviations. In both cases, the deviations were multiples of the average value. Such large differences were due to the fact that the geometric parameters of the injector’s valve elements varied. Therefore, the value of the coefficient b should be determined in each case for a given type of injector, taking into account various factors, such as the diameter of the outlet nozzle, which restricts the flow and, as a result, lowers the position of the rectilinear trend.
- The coefficient of determination of the rectilinear trend of the S-W method took average values for brand new injectors R2 = 95.01 and for injectors in operation R2 = 94.07. The deviations for this parameter were small; for brand new injections the upper deviation was +1.35 and lower deviation was −1.85, and for injectors in operation, they were slightly larger, upper (+2.14) and lower (−4.85), but still represented a small percentage of the average value. In summary, the range of the coefficient of determination 94…95 should be considered as a reference at this stage of this research.
- The one-way analysis of variance to assess the significance of differences in the mean values of the S-W rectilinear trend parameters for the BN and IO cases yielded a positive result only for the directional coefficient a. The intercept and the coefficient of determination reached probabilities well above the accepted threshold of 0.05, indicating that there were no grounds for rejecting the hypothesis that the mean values of the BN and IO groups were equal. This showed that only the directional coefficient was affected by the operating time.
- The summary of test results in radar charts showed no direct relationship of parameters a, b, and R2 with the opening time to and closing time tc. The values of a and R2 clearly did not depend on the design solution of the injector valve. Parameter b, on the other hand, reflected the geometric characteristics of the injector valve, and so it should be determined for comparisons individually.
- The research presented in this study was preliminary and needs to be gradually supplemented with analyses of injectors of the same type under different operating conditions. However, based on the results of this study, it was found that injectors of different designs and in different operating conditions gave varying values of the S-W rectilinear trend parameters. In one comparison, where the same injector model was confronted with each other, the differences for the BN and IO cases were mainly related to the intersection point b. This means that the exploitation influences the vertical shift of the trend line.
7. Further Research
In further activities, it was planned to carry out tests of injectors with the same design solutions to determine the tolerance limits of the parameters of the rectilinear trend of the S-W method for the selected manufacturer and model. It was also planned to develop a concept for the design of a test stand implementing tests in automatic mode with the possibility of comparing to a standard and inferring the potential source of injector deficiency.
Author Contributions
Conceptualization of the paper, review of the literature, preparation of the test site and test facilities, testing and preprocessing of results, analysis of the results, figures, graphs, writing the original version of the manuscript, revision of the final version, D.S.; preparation of the test site and test facilities, analysis of the results, corrections and additions, revision of the final version, J.H.; analysis of the results, review of the literature, revision of the final version, A.B.; analysis of the results, figures, graphs, revision of the final version, G.M.; analysis of the results, revision of the final version; P.W. analysis of the results, revision of the final version, B.A. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results received funding from the commissioned task entitled “VIA CARPATIA Universities of Technology Network named after the President of the Republic of Poland Lech Kaczynski” contract no. MEiN/2022/DPI/2577 action entitled “In the neighborhood—inter-university research internships and study visits”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no competing interests.
Abbreviations
The following abbreviations are used in this manuscript:
| AMFA | Alternative Motor Fuels Act |
| BEV | Battery Electric Vehicle |
| CAFÉ | Corporate Average Fuel Economy |
| car sharing | The model of car rental where people rent cars for short periods of time, often by the hour |
| CARB | California Air Resources Board |
| CCT | Carbon Credit Token |
| CN | China |
| CNG | Compressed Natural Gas |
| CO | Carbon Monoxide |
| CO2 | Carbon Dioxide |
| DPF/FAP | Diesel Particulate Filter |
| eco-driving | Driving a car that allows the lowest possible fuel consumption |
| EGR | Exhaust Gas Recirculation |
| EPA | Environmental Protection Agency |
| EU | European Union |
| EURO 7 | European Vehicle Emissions Standards |
| FAME | Fatty Acid Methyl Ester |
| FCV | Fuel-Cell Electric Hybrid Vehicle |
| free-wheeling | The mechanism that allows the vehicle’s wheels to rotate freely without the need for engine power |
| GTL | Gas to Liquid |
| H2 | Hydrogen |
| HC | Hydrocarbon |
| HVO | Hydrotreated Vegetable Oil |
| ICE | Internal Combustion Engine |
| LEV 4 | Low-Emission Vehicle |
| LNG | Liquefied Natural Gas |
| Low NOx | Key Elements of EPA’s 2027 Low-NOx Rule |
| LPG | Liquefied Petroleum Gas |
| MHEV | Mild Hybrid Electric Vehicle |
| N2O, NOx | Nitrous Oxide |
| NAAQS | National Ambient Air Quality Standards |
| NH3 | Ammonia |
| OME | Oxymethylene Ether |
| PHEV | Plug-in Hybrid Electric Vehicle |
| PM | Particulate Matter |
| POMDME | Polyoxymethylene Dimethyl Ether |
| PVO | Pure Vegetable Oil |
| S&S | Start and Stop |
| SCR | Selective Catalytic Reduction |
| S-W | Szpica–Warakomski method |
| TPO | Tire Pyrolytic Oil |
| TWC | Three-Way Catalyst; US, United States of America |
| A, A1, and A2 | Polygon surface area |
| a | Slope |
| b | Intersection |
| p | Pressure |
| Q | Volumetric flow rate |
| R2 | Coefficient of determination |
| tc | Closing time |
| tinj | Injection time |
| to | Opening time |
Appendix A

Table A1.
Volumetric flow rate values determined at the measurement points.
Table A1.
Volumetric flow rate values determined at the measurement points.
| Code | Valve Type | Injector | 2.5 ms, 2 × 105 Pa | 5 ms, 1.5 × 105 Pa | 10 ms, 1 × 105 Pa | 20 ms, 0.5 × 105 Pa | 15 ms, 0.5 × 105 Pa |
|---|---|---|---|---|---|---|---|
| brand new (BN)—LN/min | |||||||
| BN_1 | piston | AC-W01-4 | 0.78 | 5.15 | 11.65 | 18.68 | 13.27 |
| BN_2 | piston | VALTEK 39STD | 2.38 | 5.27 | 9.50 | 13.37 | 9.82 |
| BN_3 | piston | TOMASETTO Achille IT01 | 4.87 | 6.92 | 12.19 | 17.50 | 12.62 |
| BN_4 | plunger | ALEX Barracuda | 1.58 | 5.91 | 11.48 | 16.31 | 11.84 |
| BN_5 | plunger | HANA H2000 Red | 0.86 | 4.23 | 8.63 | 13.43 | 9.45 |
| BN_6 | plunger | KEIHIN Blue | 1.28 | 4.07 | 7.91 | 12.41 | 8.81 |
| BN_7 | piston, c-f | OMVL Dream XXI SL | 1.64 | 6.45 | 13.85 | 20.50 | 14.56 |
| BN_8 | flap | MATRIX HSF.211.20 | 2.56 | 5.99 | 11.02 | 15.99 | 11.47 |
| BN_9 | plate | ACON Apis Solo | 0.00 | 4.36 | 10.49 | 16.09 | 11.36 |
| in operation (IO)—LN/min | |||||||
| IO_1 | plunger | KEIHIN Blue | 0.80 | 3.88 | 8.00 | 12.28 | 8.81 |
| IO_2 | piston | MAGIC JET | 2.03 | 6.47 | 13.93 | 21.46 | 15.37 |
| IO_3 | piston, c-f | OMVL REG Fast Black | 1.96 | 7.33 | 14.26 | 21.24 | 15.22 |
| IO_4 | piston | KME IG3 Horizon | 3.71 | 9.31 | 16.26 | 23.16 | 17.21 |
| IO_5 | piston | ELPGAS IG1 Stella VERDE | 0.00 | 8.44 | 15.16 | 21.31 | 15.47 |
| IO_6 | piston | MWM FOCUS | 0.00 | 4.92 | 11.44 | 17.76 | 12.69 |
References
- Clairotte, M.; Suarez-Bertoa, R.; Zardini, A.A.; Giechaskiel, B.; Pavlovic, J.; Valverde, V.; Ciuffo, B.; Astorga, C. Exhaust emission factors of greenhouse gases (GHGs) from European road vehicles. Environ. Sci. Eur. 2020, 32, 125. [Google Scholar] [CrossRef]
- Robiou du Pont, Y.; Meinshausen, M. Warming assessment of the bottom-up Paris Agreement emissions pledges. Nat. Commun. 2018, 9, 4810. [Google Scholar] [CrossRef]
- Ritchie, H. A Global Breakdown of Greenhouse Gas Emissions by Sector. Available online: https://www.visualcapitalist.com/cp/a-global-breakdown-of-greenhouse-gas-emissions-by-sector/ (accessed on 8 March 2023).
- Tiseo, I. Distribution of Carbon Dioxide Emissions in the European Union (EU-27) in 2021, by Sector. Available online: https://www.statista.com/statistics/1240108/road-transportation-greenhouse-gas-emissions-eu/ (accessed on 8 March 2023).
- European Parliament CO2 Emissions from Cars: Facts and Figures (Infographics). Available online: https://www.europarl.europa.eu/news/en/headlines/society/20190313STO31218/co2-emissions-from-cars-facts-and-figures-infographics (accessed on 8 March 2023).
- Rezaei, R.; Kovacs, D.; Hayduk, C.; Mennig, M.; Delebinski, T. Euro VII and beyond with Hydrogen Combustion for Commercial Vehicle Applications: From Concept to Series Development. In Proceedings of the SAE Technical Papers; SAE International: Warrendale, PA, USA, 2021. [Google Scholar]
- Kalghatgi, G.; Agarwal, A.K.; Leach, L.; Senecal, L. Engines and Fuels for Future Transport; Springer: Berlin/Heidelberg, Germany, 2022; ISBN 9789811687167. [Google Scholar]
- Olabi, A.G.; Obaideen, K.; Elsaid, K.; Wilberforce, T.; Sayed, E.T.; Maghrabie, H.M.; Abdelkareem, M.A. Assessment of the pre-combustion carbon capture contribution into sustainable development goals SDGs using novel indicators. Renew. Sustain. Energy Rev. 2022, 153, 111710. [Google Scholar] [CrossRef]
- Schlacke, S.; Wentzien, H.; Thierjung, E.-M.; Köster, M. Implementing the EU Climate Law via the ‘Fit for 55’ package. Oxf. Open Energy 2022, 1, oiab002. [Google Scholar] [CrossRef]
- European Commission. CO2 Emission Performance Standards for Cars and Vans; European Commission: Brussels, Belgium, 2020; p. 2.
- Walsh, M. Global trends in motor vehicle use and emissions. Annu. Rev. Energy 1990, 15, 217–243. [Google Scholar] [CrossRef]
- Kremer, M.; Hulshorst, T. In-Market Application of Start-Stop Systems in European Market. 2011. Available online: https://doczz.net/doc/4781005/in-market-application-of-start-stop-systems-in-european-m... (accessed on 9 June 2025).
- Kropiwnicki, J.; Kneba, Z. Carbon dioxide potential reduction using Start-Stop system in a car. Key Eng. Mater. 2014, 597, 185–192. [Google Scholar] [CrossRef]
- Mueller, N.; Strauss, S.; Tumback, S.; Goh, G.C.; Christ, A. Next Generation Engine Start/Stop Systems: “Free-Wheeling”. SAE Int. J. Engines 2011, 4, 874–887. [Google Scholar] [CrossRef]
- Bucsky, P.; Juhász, M. Is car ownership reduction impact of car sharing lower than expected? A Europe wide empirical evidence. Case Stud. Transp. Policy 2022, 10, 2208–2217. [Google Scholar] [CrossRef]
- Aguilera-García, Á.; Gomez, J.; Sobrino, N. Exploring the adoption of moped scooter-sharing systems in Spanish urban areas. Cities 2020, 96, 102424. [Google Scholar] [CrossRef]
- Liu, Y.; Helfand, G.E. The Alternative Motor Fuels Act, alternative-fuel vehicles, and greenhouse gas emissions. Transp. Res. Part A Policy Pract. 2009, 43, 755–764. [Google Scholar] [CrossRef]
- Sangeeta; Moka, S.; Pande, M.; Rani, M.; Gakhar, R.; Sharma, M.; Rani, J.; Bhaskarwar, A.N. Alternative fuels: An overview of current trends and scope for future. Renew. Sustain. Energy Rev. 2014, 32, 697–712. [Google Scholar] [CrossRef]
- Shinde, B.; Karunamurthy, K. A Review on the Assessment of Injection Characteristics and Energy Levels for CNG and Hydrogen Gas Injectors. In Proceedings of the SAE Technical Papers; SAE International: Warrendale, PA, USA, 2021. [Google Scholar]
- Shuai, S.; Ma, X.; Li, Y.; Qi, Y.; Xu, H. Recent Progress in Automotive Gasoline Direct Injection Engine Technology. Automot. Innov. 2018, 1, 95–113. [Google Scholar] [CrossRef]
- Iodice, P.; Cardone, M. Ethanol/gasoline blends as alternative fuel in last generation spark-ignition engines: A review on co and hc engine out emissions. Energies 2021, 14, 4034. [Google Scholar] [CrossRef]
- Yusuf, A.A.; Inambao, F.L. Progress in alcohol-gasoline blends and their effects on the performance and emissions in SI engines under different operating conditions. Int. J. Ambient Energy 2021, 42, 465–481. [Google Scholar] [CrossRef]
- Merola, S.S.; Valentino, G.; Tornatore, C.; Marchitto, L. In-cylinder spectroscopic measurements of knocking combustion inaSI engine fuelled with butanol-gasoline blend. Energy 2013, 62, 150–161. [Google Scholar] [CrossRef]
- Hunicz, J.; Kordos, P. An experimental study of fuel injection strategies in CAI gasoline engine. Exp. Therm. Fluid Sci. 2011, 35, 243–252. [Google Scholar] [CrossRef]
- Fiore, M.; Magi, V.; Viggiano, A. Internal combustion engines powered by syngas: A review. Appl. Energy 2020, 276, 115415. [Google Scholar] [CrossRef]
- Raslavičius, L.; Keršys, A.; Mockus, S.; Keršiene, N.; Starevičius, M. Liquefied petroleum gas (LPG) as a medium-term option in the transition to sustainable fuels and transport. Renew. Sustain. Energy Rev. 2014, 32, 513–525. [Google Scholar] [CrossRef]
- Warguła, Ł.; Kukla, M.; Lijewski, P.; Dobrzyński, M.; Markiewicz, F. Influence of the use of Liquefied Petroleum Gas (LPG) systems in woodchippers powered by small engines on exhaust emissions and operating costs. Energies 2020, 13, 5773. [Google Scholar] [CrossRef]
- Frick, M.; Axhausen, K.W.; Carle, G.; Wokaun, A. Optimization of the distribution of compressed natural gas (CNG) refueling stations: Swiss case studies. Transp. Res. Part D Transp. Environ. 2007, 12, 10–22. [Google Scholar] [CrossRef]
- Warguła, Ł.; Kukla, M.; Lijewski, P.; Dobrzyński, M.; Markiewicz, F. Impact of Compressed Natural Gas (CNG) fuel systems in small engine wood chippers on exhaust emissions and fuel consumption. Energies 2020, 13, 6709. [Google Scholar] [CrossRef]
- Kumar, S.; Kwon, H.-T.; Choi, K.-H.; Lim, W.; Cho, J.H.; Tak, K.; Moon, I. LNG: An eco-friendly cryogenic fuel for sustainable development. Appl. Energy 2011, 88, 4264–4273. [Google Scholar] [CrossRef]
- Parravicini, M.; Barro, C.; Boulouchos, K. Experimental characterization of GTL, HVO, and OME based alternative fuels for diesel engines. Fuel 2021, 292, 120177. [Google Scholar] [CrossRef]
- Haryono, I.; Ma’ruf, M.; Setiapraja, H. Investigation on used oil and engine components of vehicles road test using twenty percent Fatty Acid Methyl Ester (B20). Int. J. Energy Environ. 2016, 7, 383. [Google Scholar]
- Boretti, A. Novel dual fuel diesel-ammonia combustion system in advanced TDI engines. Int. J. Hydrog. Energy 2017, 42, 7071–7076. [Google Scholar] [CrossRef]
- Novella, R.; Bracho, G.; Gomez-Soriano, J.; Fernandes, C.S.; Lucchini, T. Combustion system optimization for the integration of e-fuels (Oxymethylene Ether) in compression ignition engines. Fuel 2021, 305, 121580. [Google Scholar] [CrossRef]
- Singh, A.P.; Kumar, D.; Agarwal, A.K. Introduction to Alternative Fuels and Advanced Combustion Techniques as Sustainable Solutions for Internal Combustion Engines. In Energy, Environment, and Sustainability; Cengage: Boston, MA, USA, 2021. [Google Scholar]
- Chiaramonti, D.; Prussi, M. Pure vegetable oil for energy and transport. Int. J. Oil Gas Coal Technol. 2009, 2, 186–198. [Google Scholar] [CrossRef]
- Bassiony, M.A.; Ibrahim, A.; El-Kassaby, M.M. An experimental study on the effect of using gas-to-liquid (GTL) fuel on diesel engine performance and emissions. Alex. Eng. J. 2016, 55, 2115–2124. [Google Scholar] [CrossRef]
- Susastriawan, A.A.P.; Purwanto, Y. Purnomo Biomass gasifier–internal combustion engine system: Review of literature. Int. J. Sustain. Eng. 2021, 14, 1090–1100. [Google Scholar] [CrossRef]
- Pélerin, D.; Gaukel, K.; Härtl, M.; Jacob, E.; Wachtmeister, G. Potentials to simplify the engine system using the alternative diesel fuels oxymethylene ether OME1 and OME3–6 on a heavy-duty engine. Fuel 2020, 259, 116231. [Google Scholar] [CrossRef]
- Mikulski, M.; Ambrosewicz-Walacik, M.; Hunicz, J.; Nitkiewicz, S. Combustion engine applications of waste tyre pyrolytic oil. Prog. Energy Combust. Sci. 2021, 85, 100915. [Google Scholar] [CrossRef]
- Szpica, D.; Mieczkowski, G.; Borawski, A. Iniettore di Gas Piezoelettrico, Specialmente per i Sistemi di Alimentazione di Motori a Combustione. IT Patent 102019000005520, 24 February 2021. [Google Scholar]
- Lefebvre, A.H.; Mc Donell, V.G. Atomization and Sprays, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781498736268. [Google Scholar]
- Tang, Q.; Jiang, P.; Peng, C.; Chang, H.; Zhao, Z. Comparison and analysis of the effects of spark timing and lambda on a high-speed spark ignition engine fuelled with n-butanol/gasoline blends. Fuel 2021, 287, 119505. [Google Scholar] [CrossRef]
- Sarıkoç, S. Effect of H2 addition to methanol-gasoline blend on an SI engine at various lambda values and engine loads: A case of performance, combustion, and emission characteristics. Fuel 2021, 297, 120732. [Google Scholar] [CrossRef]
- Pearce, D.; Hardalupas, Y.; Taylor, A.M.K.P. Near Nozzle Field Conditions in Diesel Fuel Injector Testing. In Proceedings of the SAE Technical Papers; SAE International: Warrendale, PA, USA, 2015; Volume 2015. [Google Scholar]
- Dong, Q.; Yang, X.; Jia, D.; Song, E.; Yao, C. Measurement and verification of transient injection flow rate of high pressure natural gas pulse injector. Flow Meas. Instrum. 2020, 76, 101831. [Google Scholar] [CrossRef]
- Erfan, I.; Hajialimohammadi, A.; Chitsaz, I.; Ziabasharhagh, M.; Martinuzzi, R.J. Influence of chamber pressure on CNG jet characteristics of a multi-hole high pressure injector. Fuel 2017, 197, 186–193. [Google Scholar] [CrossRef]
- Rolke, P.; Broja, D.; Fink, A.; Maaß, J.; Nett, O. Pneumatic and Optical Characterization and Optimization of Hydrogen Injectors for Internal Combustion Engine Application. Front. Mech. Eng. 2022, 8, 868855. [Google Scholar] [CrossRef]
- Guerra, L.A.O.; Temer, B.O.; Loureiro, J.B.R.; Silva Freire, A.P. Experimental study of gas-lift systems with inclined gas jets. J. Pet. Sci. Eng. 2022, 216, 110749. [Google Scholar] [CrossRef]
- Aleiferis, P.G.; Serras-Pereira, J.; Augoye, A.; Davies, T.J.; Cracknell, R.F.; Richardson, D. Effect of fuel temperature on in-nozzle cavitation and spray formation of liquid hydrocarbons and alcohols from a real-size optical injector for direct-injection spark-ignition engines. Int. J. Heat Mass Transf. 2010, 53, 4588–4606. [Google Scholar] [CrossRef]
- Aleiferis, P.G.; Van Romunde, Z.R. An analysis of spray development with iso-octane, n-pentane, gasoline, ethanol and n-butanol from a multi-hole injector under hot fuel conditions. Fuel 2013, 105, 143–168. [Google Scholar] [CrossRef]
- Cavicchi, A.; Postrioti, L. Simultaneous needle lift and injection rate measurement for GDI fuel injectors by laser Doppler vibrometry and Zeuch method. Fuel 2021, 285, 119021. [Google Scholar] [CrossRef]
- Safiullah; Chandra Ray, S.; Nishida, K.; McDonell, V.; Ogata, Y. Effects of full transient Injection Rate and Initial Spray Trajectory Angle profiles on the CFD simulation of evaporating diesel sprays—Comparison between singlehole and multi hole injectors. Energy 2023, 263, 125796. [Google Scholar] [CrossRef]
- Sedarsky, D.; Idlahcen, S.; Rozé, C.; Blaisot, J.B. Velocity measurements in the near field of a diesel fuel injector by ultrafast imagery. Exp. Fluids 2013, 54, 1451. [Google Scholar] [CrossRef]
- Ramírez, A.I.; Som, S.; Aggarwal, S.K.; Kastengren, A.L.; El-Hannouny, E.M.; Longman, D.E.; Powell, C.F. Quantitative X-ray measurements of high-pressure fuel sprays from a production heavy duty diesel injector. Exp. Fluids 2009, 47, 119–134. [Google Scholar] [CrossRef]
- Serras-Pereira, J.; Aleiferis, P.G.; Walmsley, H.L.; Davies, T.J.; Cracknell, R.F. Heat flux characteristics of spray wall impingement with ethanol, butanol, iso-octane, gasoline and E10 fuels. Int. J. Heat Fluid Flow 2013, 44, 662–683. [Google Scholar] [CrossRef]
- Crua, C.; Heikal, M.R.; Gold, M.R. Microscopic imaging of the initial stage of diesel spray formation. Fuel 2015, 157, 140–150. [Google Scholar] [CrossRef]
- Ambrozik, A.; Kurczyński, D. Analysis of fast-changing quantities in the AD3.152 UR engine running of mineral fuel, plant fuel and their blends. Motrol 2008, 10, 11–22. [Google Scholar]
- Walaszyk, A.; Busz, W. Application of optical method for the analysis delay between control injector coil and beginning of the fuel injection. Combust. Engines 2013, 154, 1038–1041. [Google Scholar]
- Czarnigowski, J. The impact of supply pressure on gas injector expenditure characteristics. Silniki Spalinowe 2010, 49, 18–26. [Google Scholar] [CrossRef]
- Szpica, D.; Toczko, B.; Borawski, A.; Mieczkowski, G. Experimental Evaluation of the Influence of the Diameter of the Outlet Nozzle Bore of a Gas Injector on Its Flow Characteristic. Appl. Sci. 2023, 13, 1700. [Google Scholar] [CrossRef]
- Lim, B.C.; Lee, C.H. A comparative study of the measurement of the fuel injection rate of a diesel piezo injector with a scale and a positive displacement flow meter. ARPN J. Eng. Appl. Sci. 2021, 16, 2668–2673. [Google Scholar]
- Szpica, D.; Czaban, J. Operational assessment of selected gasoline and LPG vapour injector dosage regularity. Mechanika 2014, 20, 480–488. [Google Scholar] [CrossRef]
- Duk, M.; Czarnigowski, J. The method for indirect identification gas injector opening delay time. Prz. Elektrotech. 2012, 88, 59–63. [Google Scholar]
- Szpica, D. Validation of indirect methods used in the operational assessment of LPG vapor phase pulse injectors. Meas. J. Int. Meas. Confed. 2018, 118, 253–261. [Google Scholar] [CrossRef]
- Czarnigowski, J.; Barański, G.; Wendeker, M.; Duk, M.; Zyska, T. Method to measure injector opening and closing lag times. Combust. Engines 2011, 144, 20–28. [Google Scholar] [CrossRef]
- Szpica, D. Investigating fuel dosage non-repeatability of low-pressure gas-phase injectors. Flow Meas. Instrum. 2018, 59, 147–156. [Google Scholar] [CrossRef]
- Szpica, D. The influence of selected adjustment parameters on the operation of LPG vapor phase pulse injectors. J. Nat. Gas Sci. Eng. 2016, 34, 1127–1136. [Google Scholar] [CrossRef]
- Hung, D.L.S.; Harrington, D.L.; Gandhi, A.H.; Markle, L.E.; Parrish, S.E.; Shakal, J.S.; Sayar, H.; Cummings, S.D.; Kramer, J.L. Gasoline fuel injector spray measurement and characterization—A new SAE J2715 recommended practice. SAE Int. J. Fuels Lubr. 2009, 1, 534–548. [Google Scholar] [CrossRef]
- AC S.A. Instrukcja Obsługi. Listwa Wtryskowa AC W01 i AC W01 BFC. Available online: https://www.ac.com.pl/pl-centrum-pobran-schematy-listwy-wtryskowe (accessed on 20 December 2022).
- Alex Sp. z o.o. Barracuda LPG/SNG Injector. Available online: https://autogas-alex.com/wp-content/uploads/2019/07/Barracuda-PL.pdf (accessed on 20 December 2022).
- Alex Sp. z o.o. Tabela Przepływów Statycznych Względem Średnicy Dyszy Wtryskiwaczy RAIL-001, FLIPPER, Barracuda. Available online: https://autogas-alex.com/wp-content/uploads/2020/12/tabela-przeplywow-statycznych-względem-średnicy-dyszy.pdf (accessed on 20 December 2022).
- Vosken Valtek Injector Rail STD 3 Ohm Type 30 (4 Cyl.). Available online: https://vosken.de/Valtek-injector-rail-STD-3-ohm-type-30-4-cyl (accessed on 15 April 2022).
- Szpica, D.; Warakomski, J. Complementing the method of areas of Gaussian characteristic figures for the rapid diagnosis of the technical condition of the low-pressure gas-phase injectors. Renew. Sustain. Energy Rev. 2025, 209, 115113. [Google Scholar] [CrossRef]
- AC S.A. User’s Manual. Injection Rail AC W02 and AC W02 BFC. Available online: https://www.ac.com.pl/fr-download-manuels (accessed on 20 December 2022).
- Stoeck, T. Methodology of testing common rail fuel injectors with the use of Gauss’ s formulas. Combust. Engines 2021, 184, 11–15. [Google Scholar] [CrossRef]
- Czarnigowski, J. Teoretyczno-Empiryczne Studium Modelowania Impulsowego Wtryskiwacza Gazu; Wydawnictwo Politechniki Lubelskiej: Lublin, Poland, 2012; ISBN PL 978-83-63569-09-9. [Google Scholar]
- Beik, Y.; Dziewiątkowski, M.; Szpica, D. Exhaust emissions of an engine fuelled by petrol and Liquefied Petroleum Gas with control algorithm adjustment. SAE Int. J. Engines 2020, 13, 739–759. [Google Scholar] [CrossRef]
- Szpica, D.; Dziewiątkowski, M. Analysis of selected functional parameters of the gas supply system during NEDC and WLTC cycles. In Proceedings of the 24th International Scientific Conference, Transport Means 2020, Palanga, Lithuania, 30 September–2 October 2020. [Google Scholar]
- Szpica, D. Operation of a lpg vapor phase fuel system under the conditions of non-standardized driving. In Proceedings of the 22nd International Scientific Conference. Transport Means, Trakai, Lithuania, 3–5 October 2018; pp. 136–139. [Google Scholar]
- Baldin, N.; Firsching, M.; Cederbaum, C. Estimating the volume of a convex body. Snapshots Mod. Math. Oberwolfach 2018, 15, 1–12. [Google Scholar] [CrossRef]
- Ochilbek, R. A New Approach (Extra Vertex) and Generalization of Shoelace Algorithm Usage in Convex Polygon (Point-in-Polygon). In Proceedings of the 14th International Conference on Electronics Computer and Computation (ICECCO), Kaskelen, Kazakhstan, 29 November–1 December 2018; pp. 206–212. [Google Scholar]
- Pure, R.; Durrani, S. Computing Exact Closed-Form Distance Distributions in Arbitrarily Shaped Polygons with Arbitrary Reference Point. Math. J. 2015, 17, 1–27. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).