Research on Measurement Error Distribution and Optimization Measurement Method of Clamp-On Ultrasonic Flowmeter in Downstream Pipeline Disturbance
Abstract
1. Introduction
2. Methods
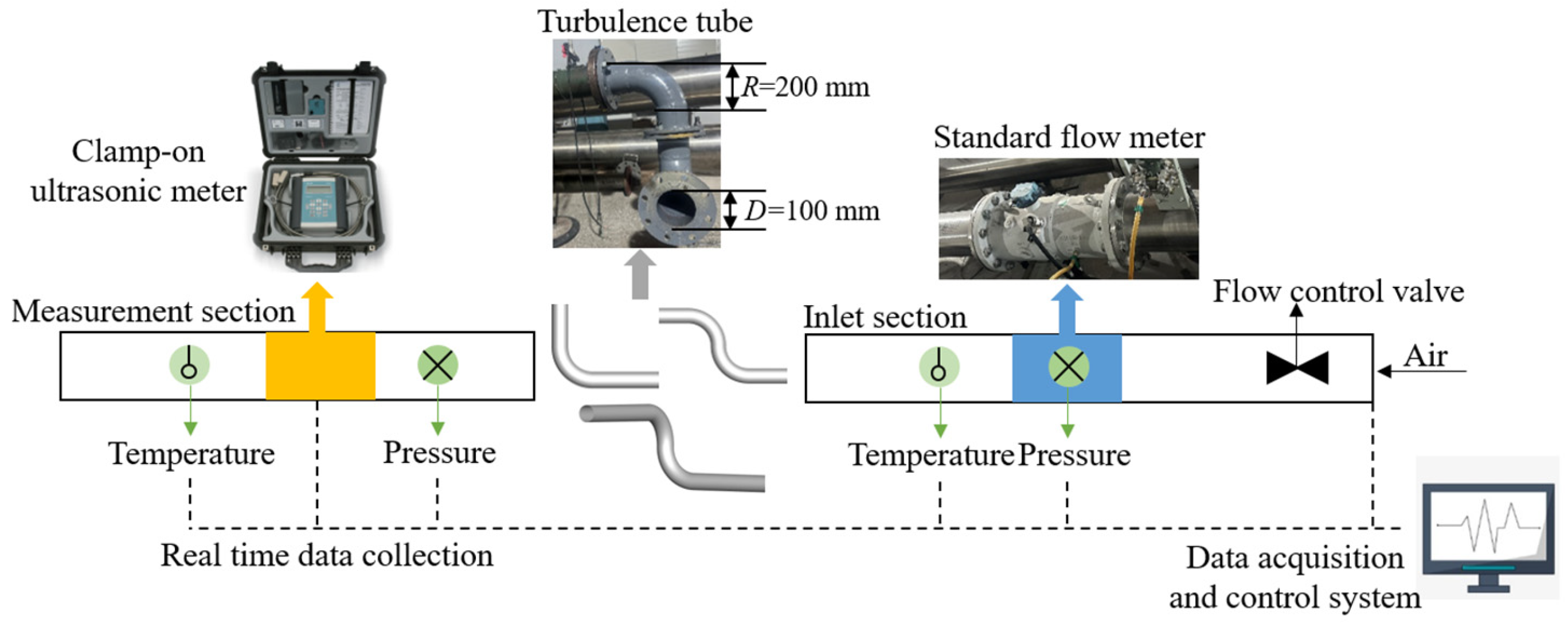
2.1. Experimental System
2.2. Numerical Simulation
3. Results and Discussion
3.1. The Influence of Disturbance Type on the Flow Velocity Distribution
3.2. The Influence of Operating Conditions on the Flow Velocity Deviation
3.3. The Influence of Measurement Methods on Flow Measurement Deviation
3.4. The Influence of Installation Angle on Flow Measurement Deviation
3.5. Comparison of Measurement Deviation of Different Flowmeters Downstream of Disturbance
3.6. Reference Correction Factors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, J.; Li, H.; Yang, R. Effects of environmental liability insurance on illegal pollutant discharge of heavy polluting enterprises: Emission reduction incentives or pollution protector? Socio-Econ. Plan. Sci. 2024, 92, 101830. [Google Scholar] [CrossRef]
- Wu, D.; Xie, Y.; Liu, D. Rethinking the complex effects of the clean energy transition on air pollution abatement: Evidence from China’s coal-to-gas policy. Energy 2023, 283, 128413. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, L. The Russia-Ukraine war, energy poverty, and social conflict: An analysis based on global liquified natural gas maritime shipping. Appl. Geogr. 2024, 166, 103263. [Google Scholar] [CrossRef]
- Levin, T.; Blaisdell-Pijuan, P.L.; Kwon, J.; Mann, W.N. High temporal resolution generation expansion planning for the clean energy transition. Renew. Sustain. Energy Transit. 2024, 5, 100072. [Google Scholar] [CrossRef]
- Baker, R.C.; Gautrey, D.P.; Mahadeva, D.V.; Sennitt, S.D.; Thorne, A.J. Case study of the electrical hardware and software for a flowmeter calibration facility. Flow Meas. Instrum. 2013, 29, 9–18. [Google Scholar] [CrossRef]
- Barateiro, C.E.R.B.; Makarovsky, C.; Rodrigues de Farias Filho, J. Fiscal liquid and gaseous hydrocarbons flow and volume measurement: Improved reliability and performance paradigms by harnessing for fourth industrial revolution. Flow Meas. Instrum. 2020, 74, 101773. [Google Scholar] [CrossRef]
- Baker, R.C.; Sorbie, I. A review of the impact of component variation in the manufacturing process on variable area (VA) flowmeter performance. Flow Meas. Instrum. 2001, 12, 101–112. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, C.; Lin, J. Effects of Velocity Profiles on Measuring Accuracy of Transit-Time Ultrasonic Flowmeter. Appl. Sci. 2019, 9, 1648. [Google Scholar] [CrossRef]
- Eisenhauer, D.E. Using Ultrasonic Flow Meters in Irrigation Applications. 2001. Available online: https://core.ac.uk/download/pdf/354401018.pdf#page=68 (accessed on 1 January 2020).
- Zhang, D.; Geng, C.; Liu, X.; Shen, Q. Research on online calibration method for large-diameter electromagnetic flow meters based on standard meter fixed-point measurement transmission. Meas. Tech. 2018, 3, 1–3. [Google Scholar]
- Murakawa, H.; Ichimura, S.; Sugimoto, K.; Asano, H.; Umezawa, S.; Sugita, K. Evaluation method of transit time difference for clamp-on ultrasonic flowmeters in two-phase flows. Exp. Therm. Fluid Sci. 2020, 112, 109957. [Google Scholar] [CrossRef]
- Papathanasiou, P.; Kissling, B.; Berberig, O.; Kumar, V.; Rohner, A.; Bezděk, M. Flow disturbance compensation calculated with flow simulations for ultrasonic clamp-on flowmeters with optimized path arrangement. Flow Meas. Instrum. 2022, 85, 102167. [Google Scholar] [CrossRef]
- Moore, P.I.; Brown, G.J.; Stimpson. Ultrasonic transit-time flowmeters modelled with theoretical velocity profiles: Methodology. Meas. Sci. Technol. 2000, 11, 1802. [Google Scholar] [CrossRef]
- Mousavi, S.F.; Hashemabadi, S.H.; Jamali, J. Calculation of geometric flow profile correction factor for ultrasonic flow meter using semi-3D simulation technique. Ultrasonics 2020, 106, 106165. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.C.; Seong, P.H. Estimation of the flow profile correction factor of a transit-time ultrasonic flow meter for the feedwater flow measurement in a nuclear power plant. IEEE Trans. Nucl. Sci. 2005, 52, 714–718. [Google Scholar] [CrossRef]
- Hilgenstock, A.; Ernst, R. Analysis of installation effects by means of computational fluid dynamics—CFD vs experiments? Flow Meas. Instrum. 1996, 7, 161–171. [Google Scholar] [CrossRef]
- Iooss, B.; Lhuillier, C.; Jeanneau, H. Numerical simulation of transit-time ultrasonic flowmeters: Uncertainties due to flow profile and fluid turbulence. Ultrasonics 2002, 40, 1009–1015. [Google Scholar] [CrossRef]
- Zhao, H.; Peng, L.; Takahashi, T.; Hayashi, T.; Shimizu, K.; Yamamoto, T. CFD-Aided Investigation of Sound Path Position and Orientation for a Dual-Path Ultrasonic Flowmeter With Square Pipe. Sens. J. IEEE 2015, 15, 128–137. [Google Scholar] [CrossRef]
- Tang, X. Simulation and Experiment Study Onmulti-Path Ultrasonic Gas Flowmeasurement. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Martins, R.S.; Andrade, J.R.; Ramos, R. On the effect of the mounting angle on single-path transit-time ultrasonic flow measurement of flare gas: A numerical analysis. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 18. [Google Scholar] [CrossRef]
- Synowiec, P.; Andruszkiewicz, A.; Wdrychowicz, W.; Piechota, P.; Wróblewska, E. Influence of Flow Disturbances behind the 90° Bend on the Indications of the Ultrasonic Flow Meter with Clamp-on Sensors on Pipelines. Sensors 2021, 21, 868. [Google Scholar] [CrossRef]
- Enayet, M.M.; Gibson, M.M.; Taylor, A.M.K.P.; Yianneskis, M. Laser-Doppler measurements of laminar and turbulent flow in a pipe bend. Int. J. Heat Fluid Flow 1982, 3, 213–219. [Google Scholar] [CrossRef]
- Lim, K.W.; Chung, M.K. Numerical investigation on the installation effects of electromagnetic flowmeter downstream of a 90° elbow–laminar flow case. Flow Meas. Instrum. 1999, 10, 167–174. [Google Scholar] [CrossRef]
- JJG1037-2008; Turbine Flow Mete. General Administration of Quality Supervision, Inspection and Quarantine of China: Beijing, China, 2008.
- Balino, J.L. Bond-graph approach for computational fluid dynamics: A comparison with other numerical methods. In Proceedings of the Systems, Man and Cybernetics, 2002 IEEE International Conference on 2002, Yasmine Hammamet, Tunisia, 6–9 October 2002. [Google Scholar]
- Papathanasiou, P.; Kissling, B.; Kumar, V.; Rohner, A.; Bezdk, M. Effect of an asymmetric flow disturber on an ultrasonic flowmeter. Tm-Tech. Mess. 2019, 87, 3–17. [Google Scholar] [CrossRef]
- Lee, S.; Ayton, L.; Bertagnolio, F.; Moreau, S.; Chong, T.P.; Joseph, P. Turbulent boundary layer trailing-edge noise: Theory, computation, experiment, and application. Prog. Aerosp. Sci. 2021, 126, 100737. [Google Scholar] [CrossRef]
- Zhang, Z. A two-point boundary value problem arising in boundary layer theory. J. Math. Anal. Appl. 2014, 417, 361–375. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Herry, T.; Raverdy, B.; Mimouni, S.; Vincent, S. Volume average of two-fluid RANS equations and a priori estimation of subgrid terms on subcooled boiling experiments. Int. J. Heat Mass Transf. 2024, 223, 125232. [Google Scholar] [CrossRef]
- Elzaabalawy, H.; Deng, G.; Eça, L.; Visonneau, M. Assessment of solving the RANS equations with two-equation eddy-viscosity models using high-order accurate discretization. J. Comput. Phys. 2023, 483, 112059. [Google Scholar] [CrossRef]
- Swanson, R.C.; Rossow, C.C. An efficient solver for the RANS equations and a one-equation turbulence model. Comput. Fluids 2011, 42, 13–25. [Google Scholar] [CrossRef]
- Marta, A.C.; Shankaran, S. On the handling of turbulence equations in RANS adjoint solvers. Comput. Fluids 2013, 74, 102–113. [Google Scholar] [CrossRef]
- Wackers, J.; Koren, B. Multigrid solution method for the steady RANS equations. J. Comput. Phys. 2007, 226, 1784–1807. [Google Scholar] [CrossRef]
- Lynnworth, L.C. 4—Flow Applications. In Ultrasonic Measurements for Process Control; Lynnworth, L.C., Ed.; Academic Press: San Diego, CA, USA, 1989; pp. 245–368. [Google Scholar] [CrossRef]
- Pernu, T.; Saarilahti, J.; Sillanpää, T. Real-time frequency matching circuit for a high sensitivity cMUT-based gas flow sensor. Sens. Actuators A Phys. 2025, 383, 116252. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Ding, H.; Sun, H.; Li, X. Vortex flowmeter with enhanced turndown ratio based on high-frequency pressure sensors and improved convection velocity estimation. Flow Meas. Instrum. 2019, 69, 101626. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, P.; Wang, R.; Niu, Z.; Zhang, K. Signal processing method of ultrasonic gas flowmeter based on transit-time mathematical characteristics. Measurement 2025, 239, 115485. [Google Scholar] [CrossRef]
- Steenbergen, W. Turbulent Pipe Flow with Swirl. 1995. Available online: https://pure.tue.nl/ws/files/1534421/430720.pdf (accessed on 1 January 2020).
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-e eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-Averaged Navier–Stokes Equations for Turbulence Modeling. Appl. Mech. Rev. 2009, 62, 933–944. [Google Scholar] [CrossRef]
- Heritage, J.E. The performance of transit time ultrasonic flowmeters under good and disturbed flow conditions. Flow Meas. Instrum. 1989, 1, 24–30. [Google Scholar] [CrossRef]
- Ruppel, C.; Peters, F. Effects of upstream installations on the reading of an ultrasonic flowmeter. Flow Meas. Instrum. 2004, 15, 167–177. [Google Scholar] [CrossRef]
- Chen, W. Study on the Influence of Flow Separation and Non-Ideal Flow Field Evolution on Gas Ultrasonic Flowmeter. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2023. [Google Scholar]
- Chen, W. Analysis and Compensation Method of Non-Ideal Flow Field for UltrasonicGas Flowmeter. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2015. [Google Scholar]
- Dell’Isola, M.; Cannizzo, M.; Diritti, M. Measurement of high-pressure natural gas flow using ultrasonic flowmeters. Measurement 1997, 20, 75–89. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, J. Research on the inherent error of ultrasonic flowmeter in non-ideal hydrogen flow fields. Int. J. Hydrogen Energy 2014, 39, 6104–6110. [Google Scholar] [CrossRef]
- Tang, Z. Research on Key Technologies for Multipath GasUltrasonic Flowmeters Flow Field Compensation. Master’s Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Kenbar, A.; Schakel, M. Influence of flow disturbances on the performance of industry-standard LNG flow meters—ScienceDirect. Flow Meas. Instrum. 2020, 77, 101871. [Google Scholar] [CrossRef]
- Salehi, S.M.; Lao, L.; Simms, N.; Drahm, W.; Lin, Y.; Rieder, A.; Güttler, A. Advancing two-phase wet gas flow measurement with Coriolis meters: Optimal sensor orientation and a new model development. Flow Meas. Instrum. 2025, 102, 102809. [Google Scholar] [CrossRef]
- Pei, X.; Zhang, X. Review and prospect of high-precision Coriolis mass flowmeters for hydrogen flow measurement. Flow Meas. Instrum. 2025, 102, 102790. [Google Scholar] [CrossRef]
- Kim, J.; Yadav, M.; Kim, S. Characteristics of Secondary Flow Induced by 90-Degree Elbow in Turbulent Pipe Flow. Eng. Appl. Comput. Fluid Mech. 2014, 8, 229–239. [Google Scholar] [CrossRef]
- Bilde, K.G.; Srensen, K.; Hrvig, J. Decay of secondary motion downstream bends in turbulent pipe flows. Phys. Fluids 2023, 35, 015102. [Google Scholar] [CrossRef]
- Tohline, J.E.; Ge, J.; Even, W.; Anderson, E. A Customized Python Module for CFD Flow Analysis within VisTrails. Comput. Sci. Eng. 2009, 11, 68–73. [Google Scholar] [CrossRef]
- Dong, Z.; Lu, Z.; Yang, Y. Fine-tuning a large language model for automating computational fluid dynamics simulations. Theor. Appl. Mech. Lett. 2025, 15, 100594. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Wang, W.; Liu, X.; Chen, X.; Li, X.; Lu, X. Research on Measurement Error Distribution and Optimization Measurement Method of Clamp-On Ultrasonic Flowmeter in Downstream Pipeline Disturbance. Sensors 2025, 25, 4011. https://doi.org/10.3390/s25134011
Yang Z, Wang W, Liu X, Chen X, Li X, Lu X. Research on Measurement Error Distribution and Optimization Measurement Method of Clamp-On Ultrasonic Flowmeter in Downstream Pipeline Disturbance. Sensors. 2025; 25(13):4011. https://doi.org/10.3390/s25134011
Chicago/Turabian StyleYang, Zhongzhi, Wei Wang, Xianjie Liu, Xin Chen, Xia Li, and Xiaofeng Lu. 2025. "Research on Measurement Error Distribution and Optimization Measurement Method of Clamp-On Ultrasonic Flowmeter in Downstream Pipeline Disturbance" Sensors 25, no. 13: 4011. https://doi.org/10.3390/s25134011
APA StyleYang, Z., Wang, W., Liu, X., Chen, X., Li, X., & Lu, X. (2025). Research on Measurement Error Distribution and Optimization Measurement Method of Clamp-On Ultrasonic Flowmeter in Downstream Pipeline Disturbance. Sensors, 25(13), 4011. https://doi.org/10.3390/s25134011





