Numerical Study of a Dual-Mode Optical Sensor for Temperature and Refractive Index Sensing with Enhanced Temperature Range
Abstract
1. Introduction
2. Materials and Methods
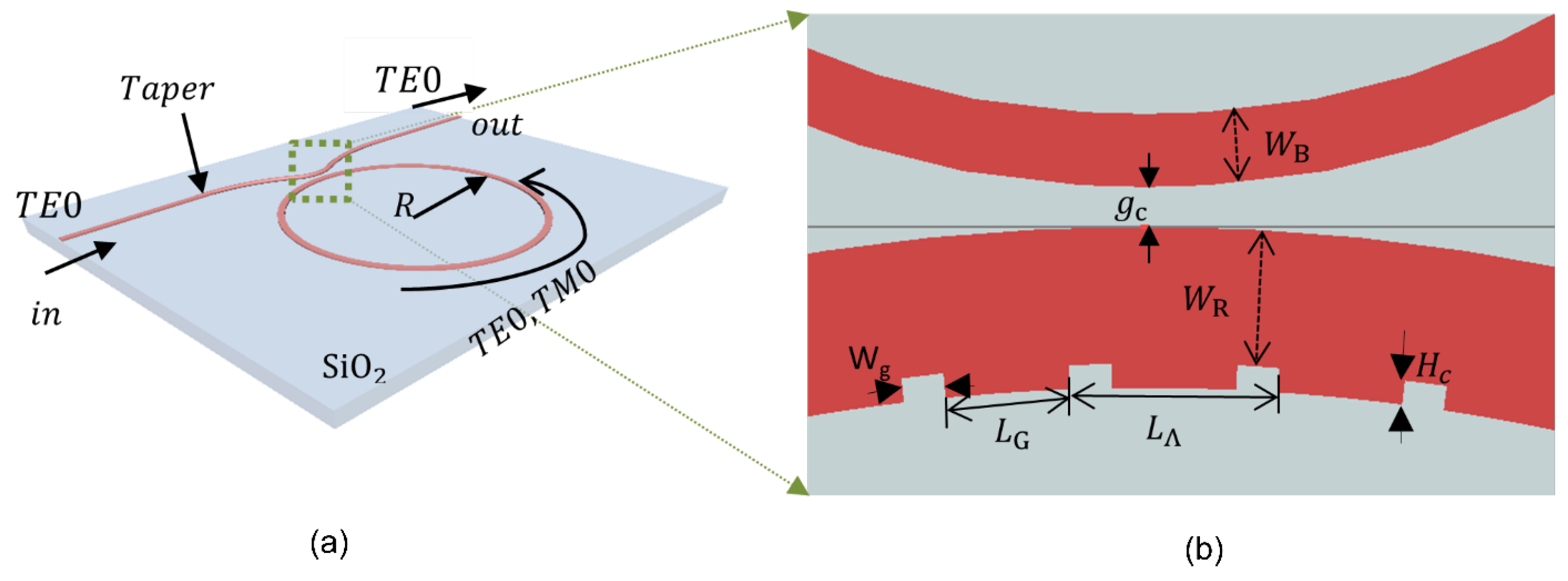
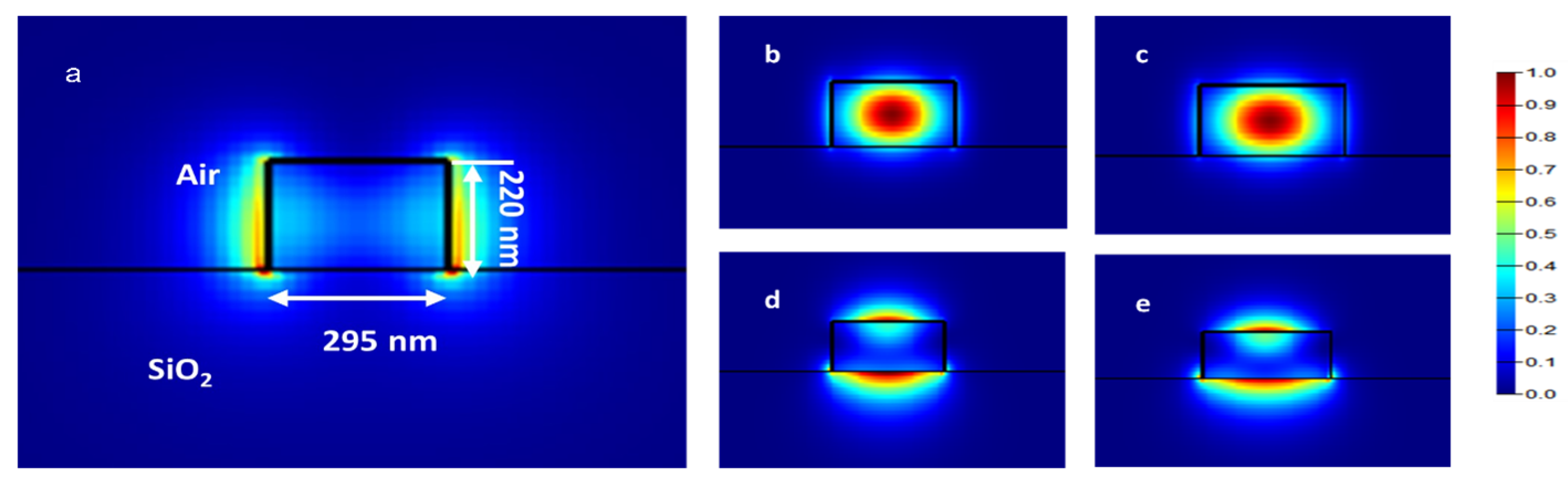
2.1. Structure Design and Working Principle
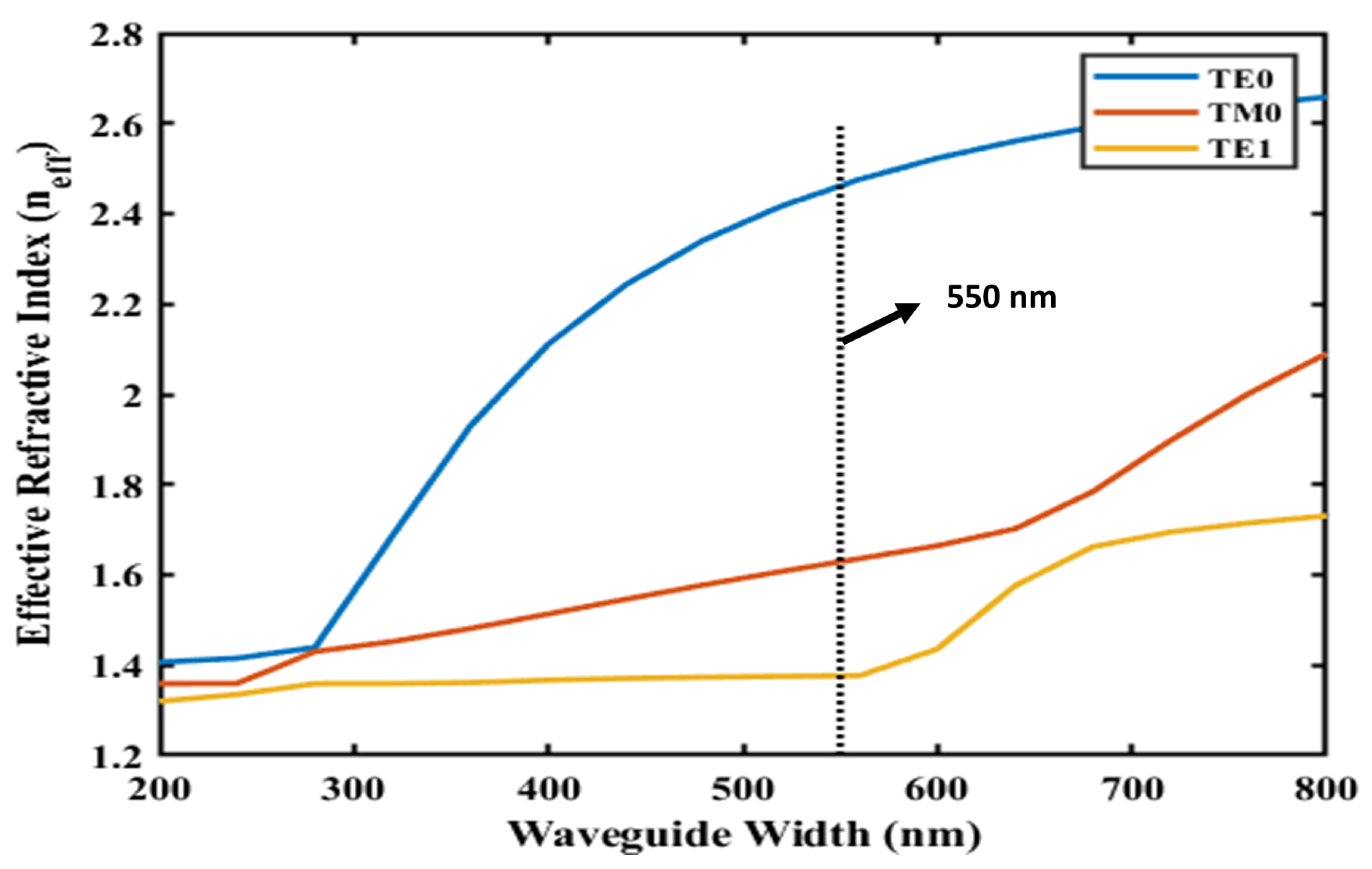
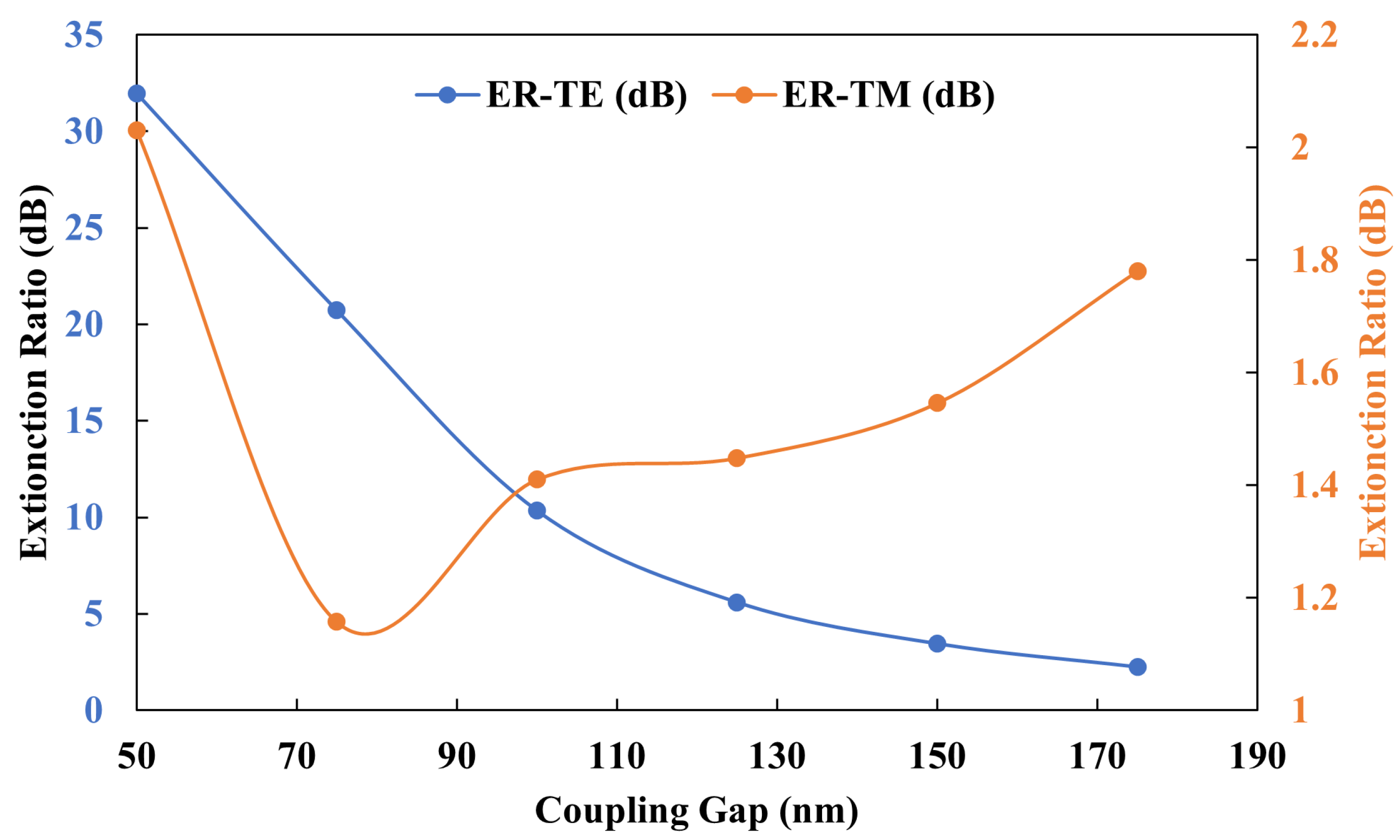
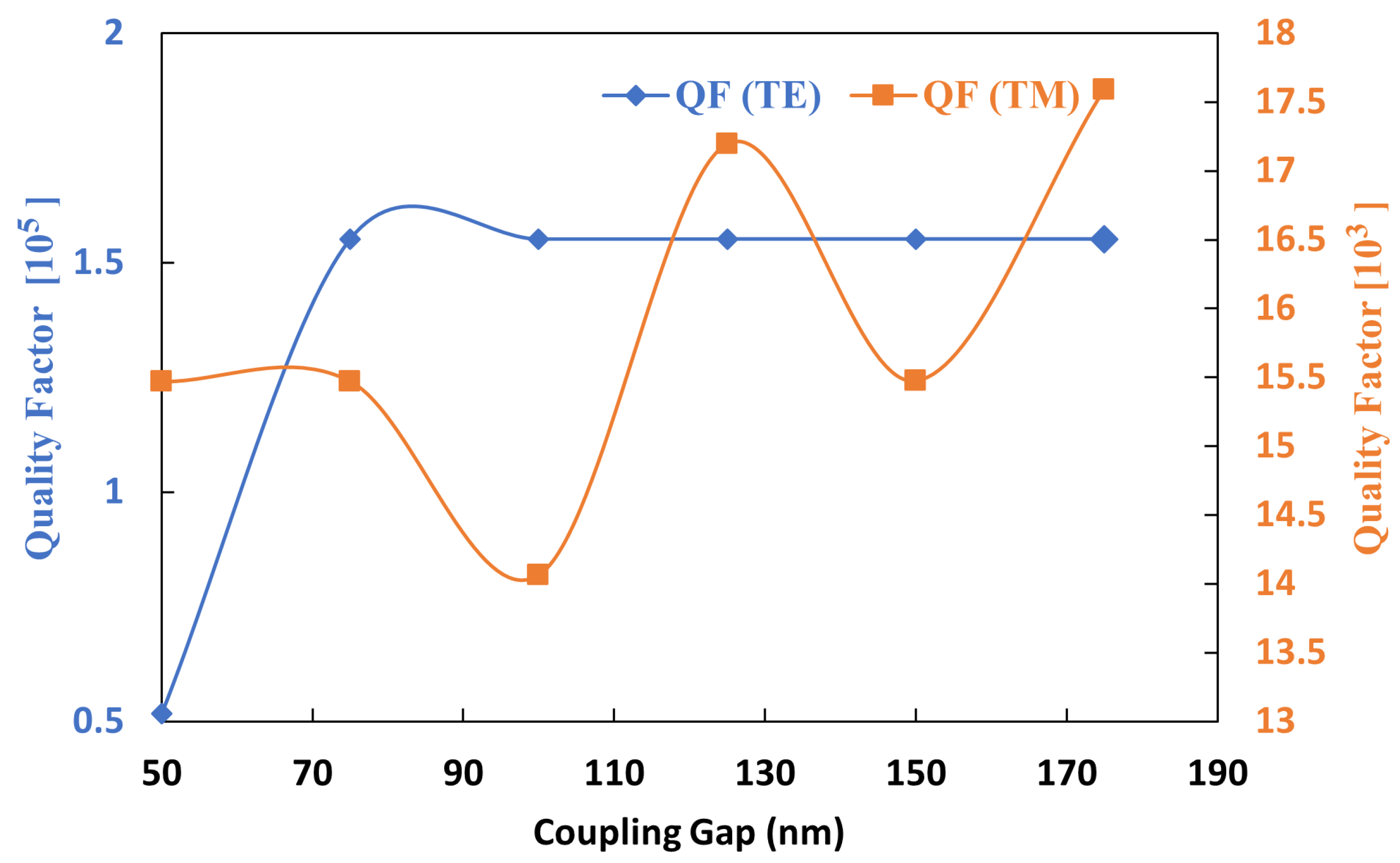
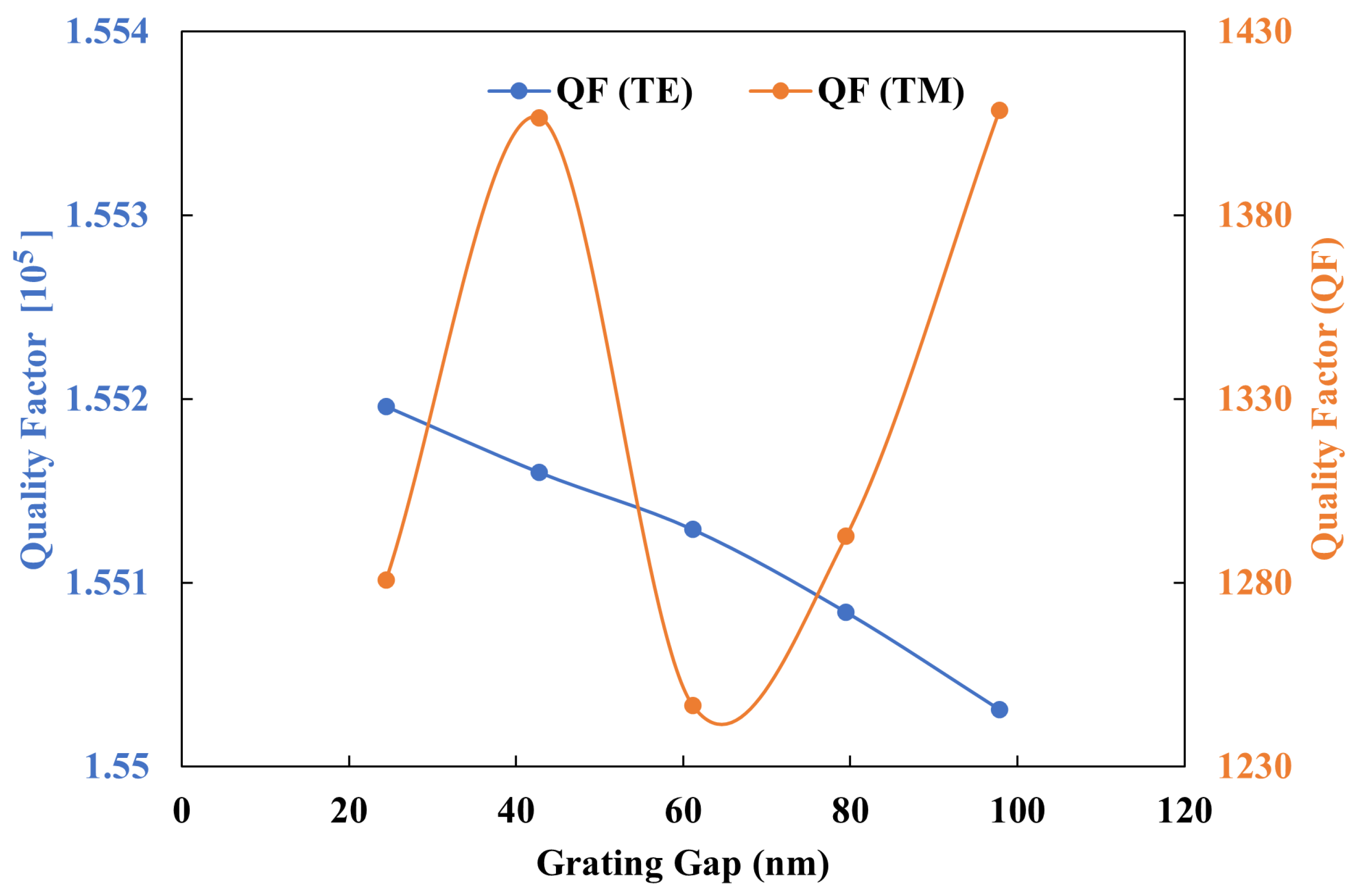
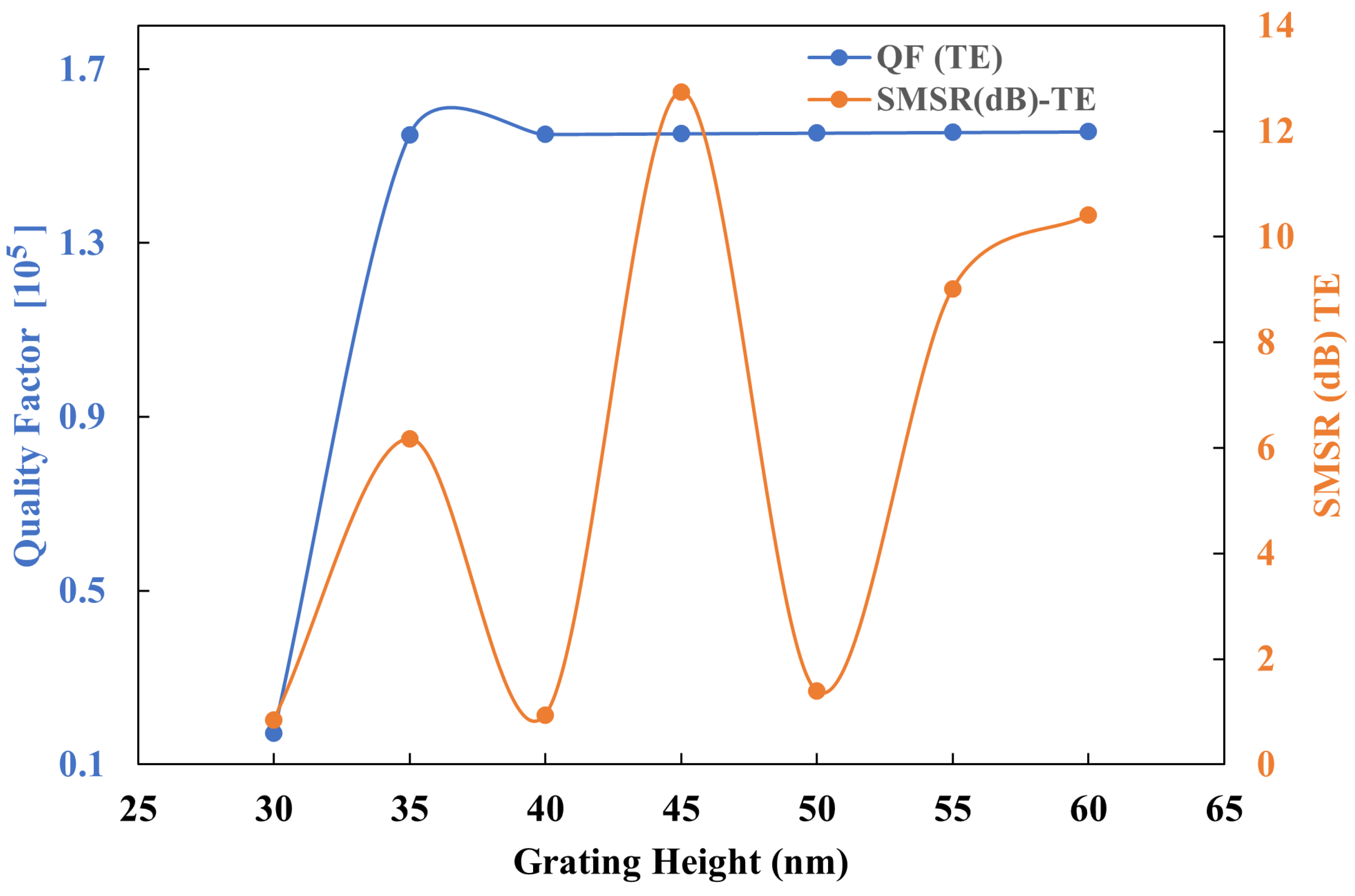
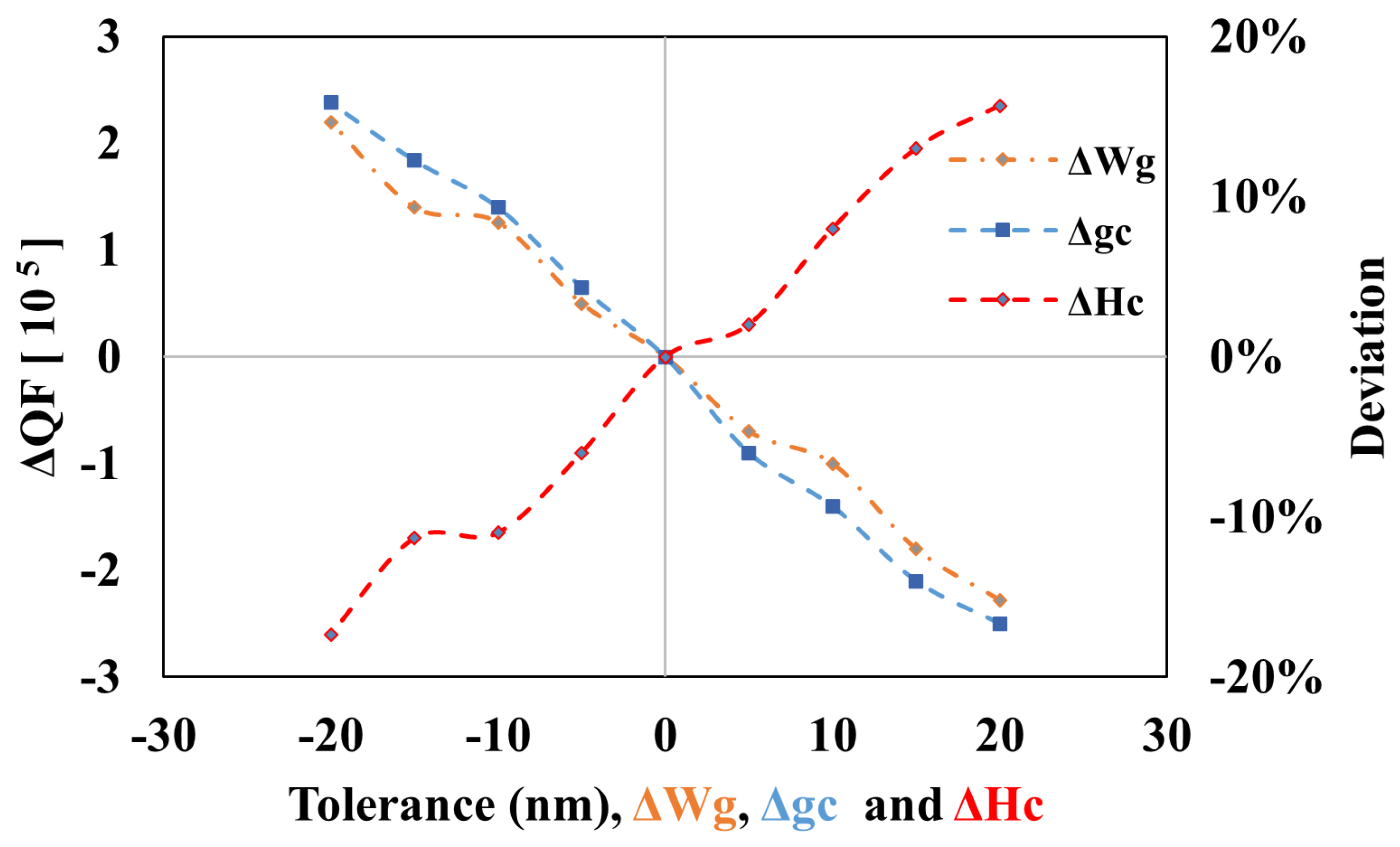
2.2. Parametric Analysis
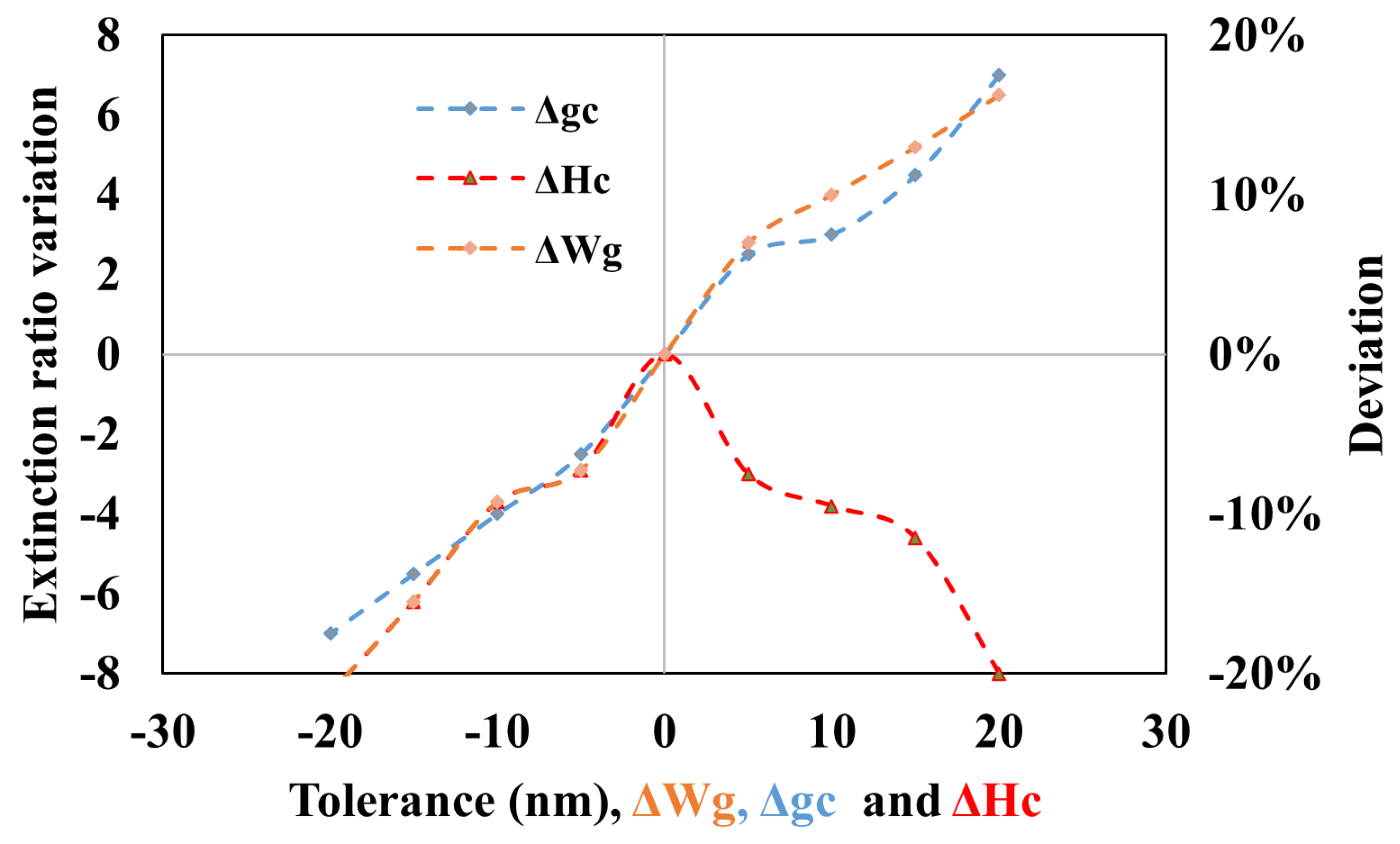
2.3. Quality Factor, Extinction Ratio, and Side-Mode Suppression
3. Results and Discussion
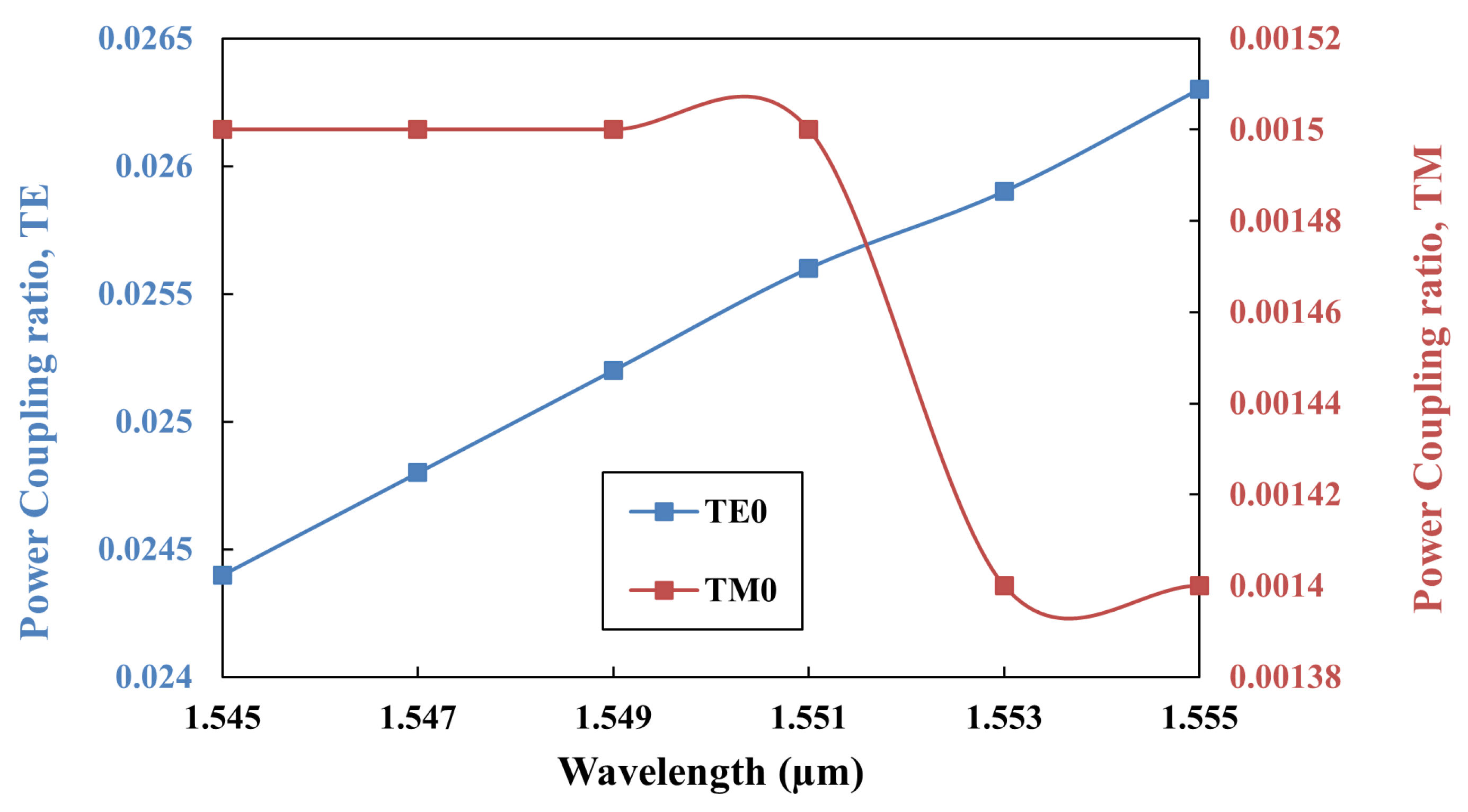
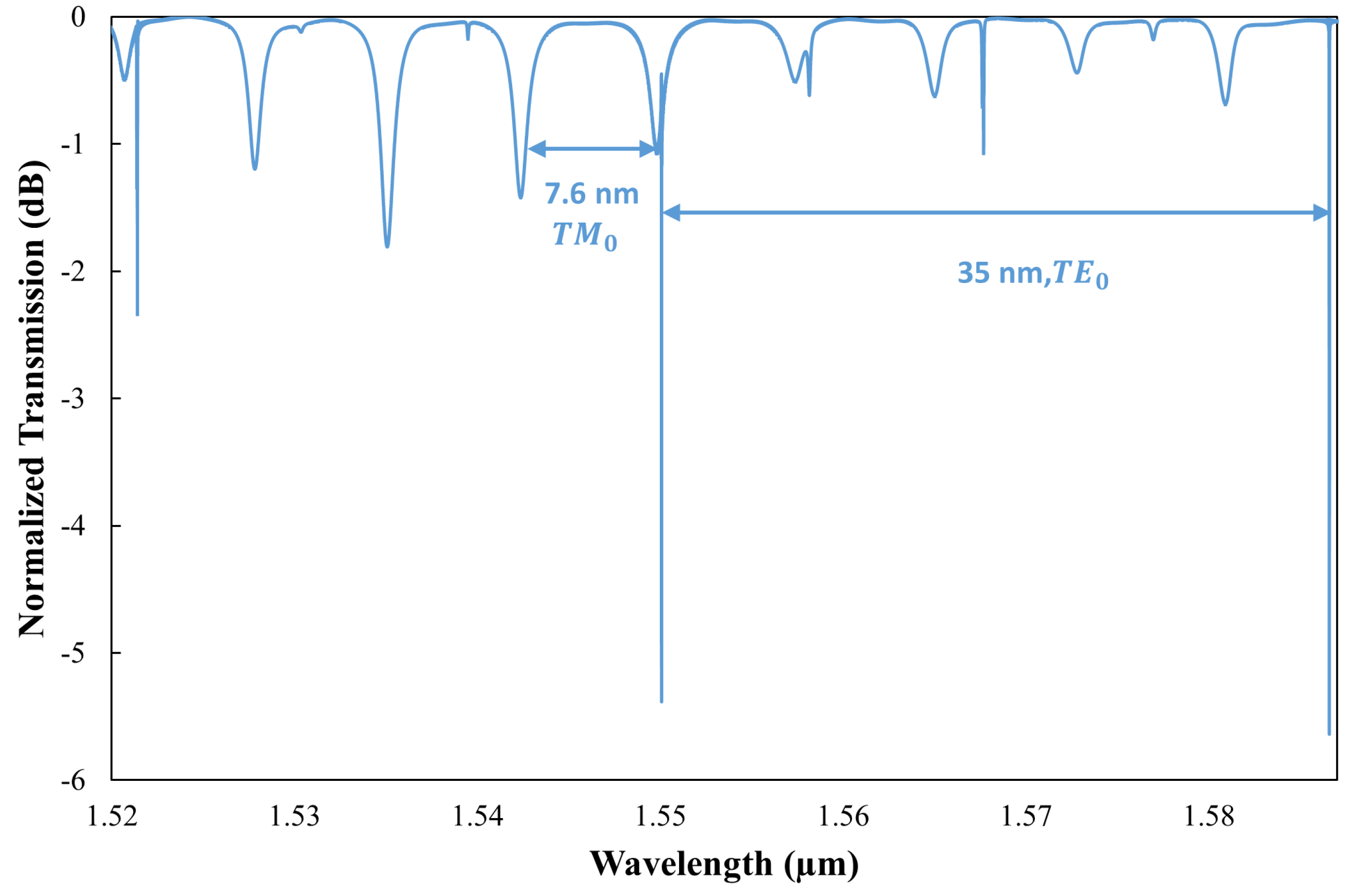
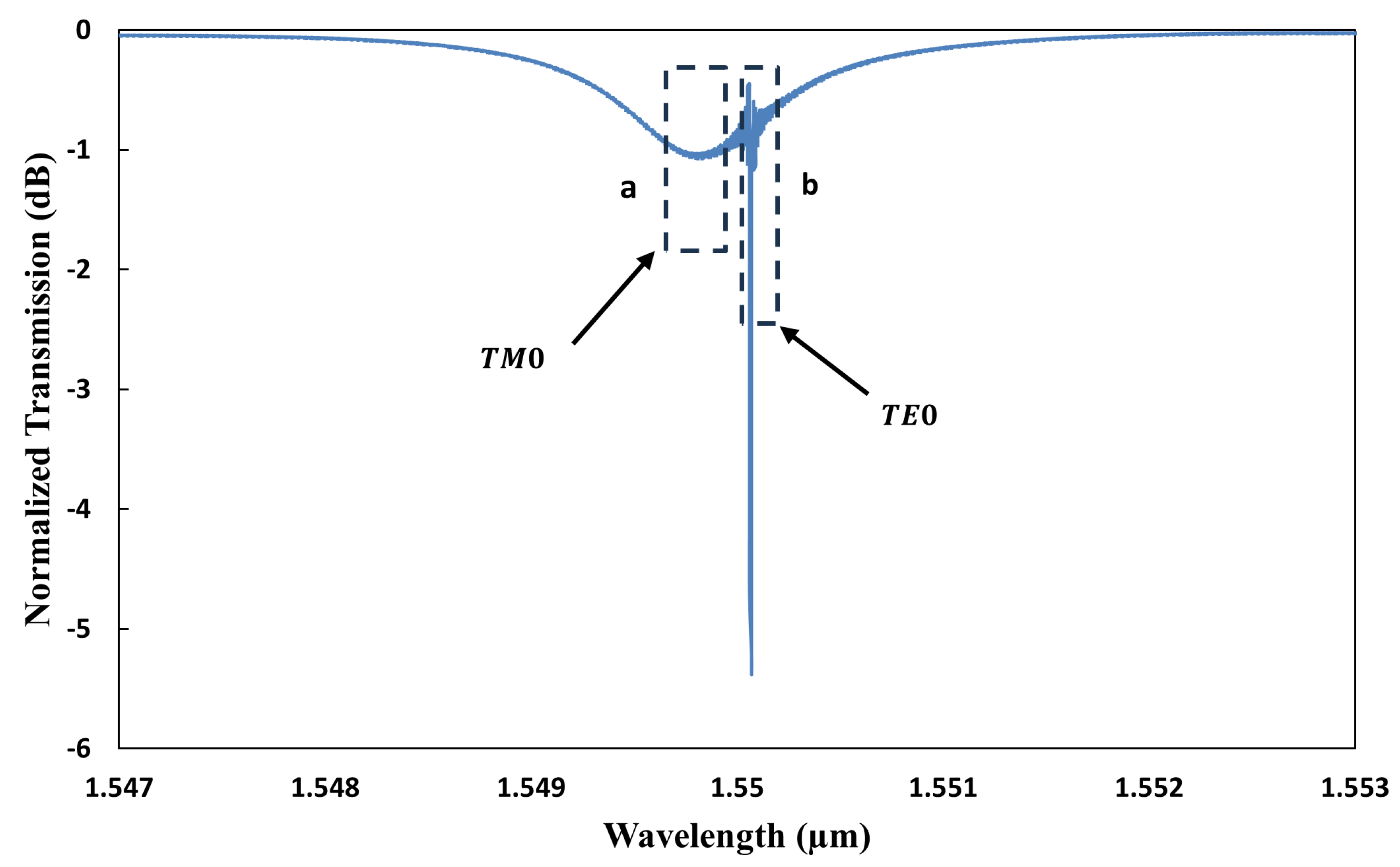
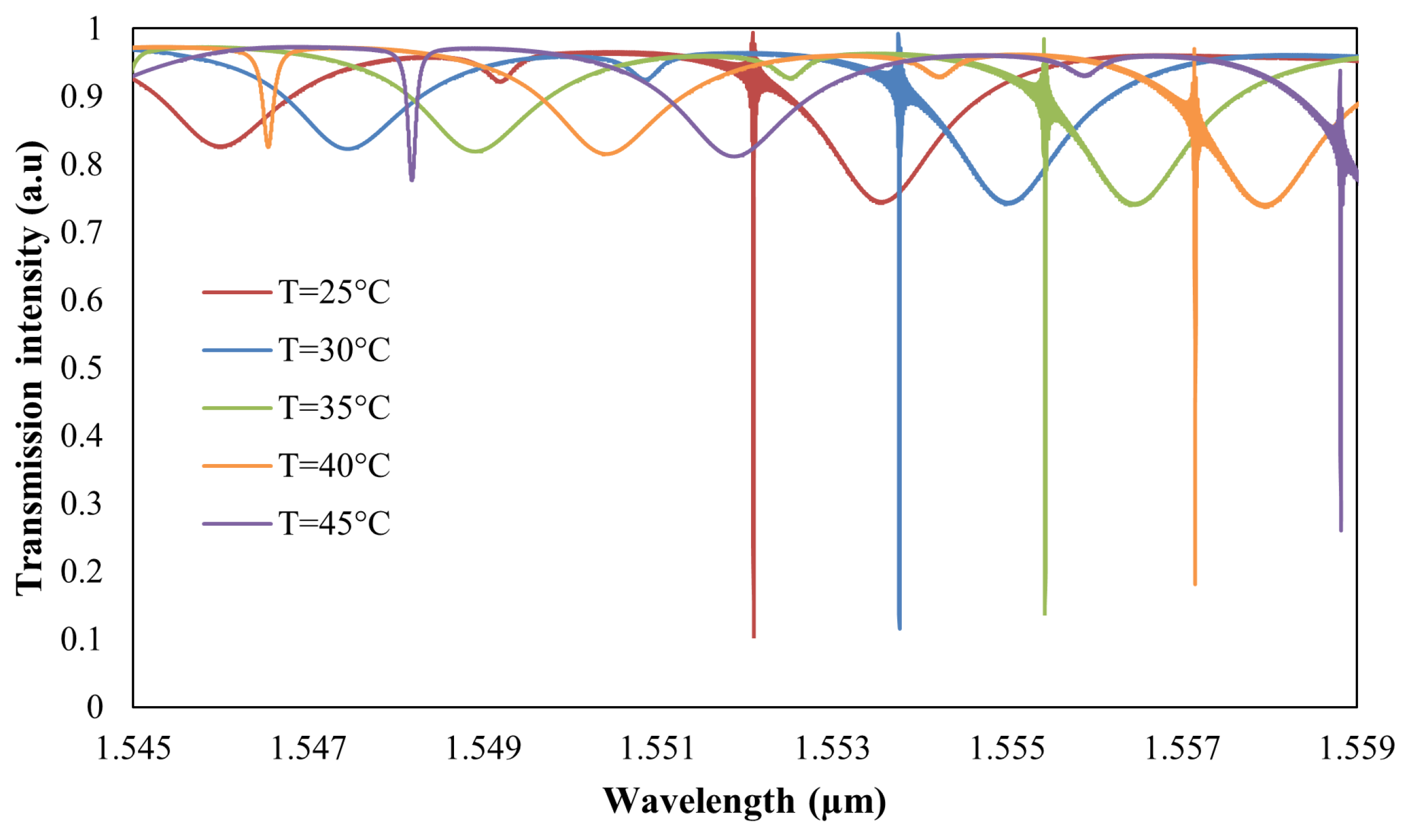
3.1. Resonant Wavelength Shift
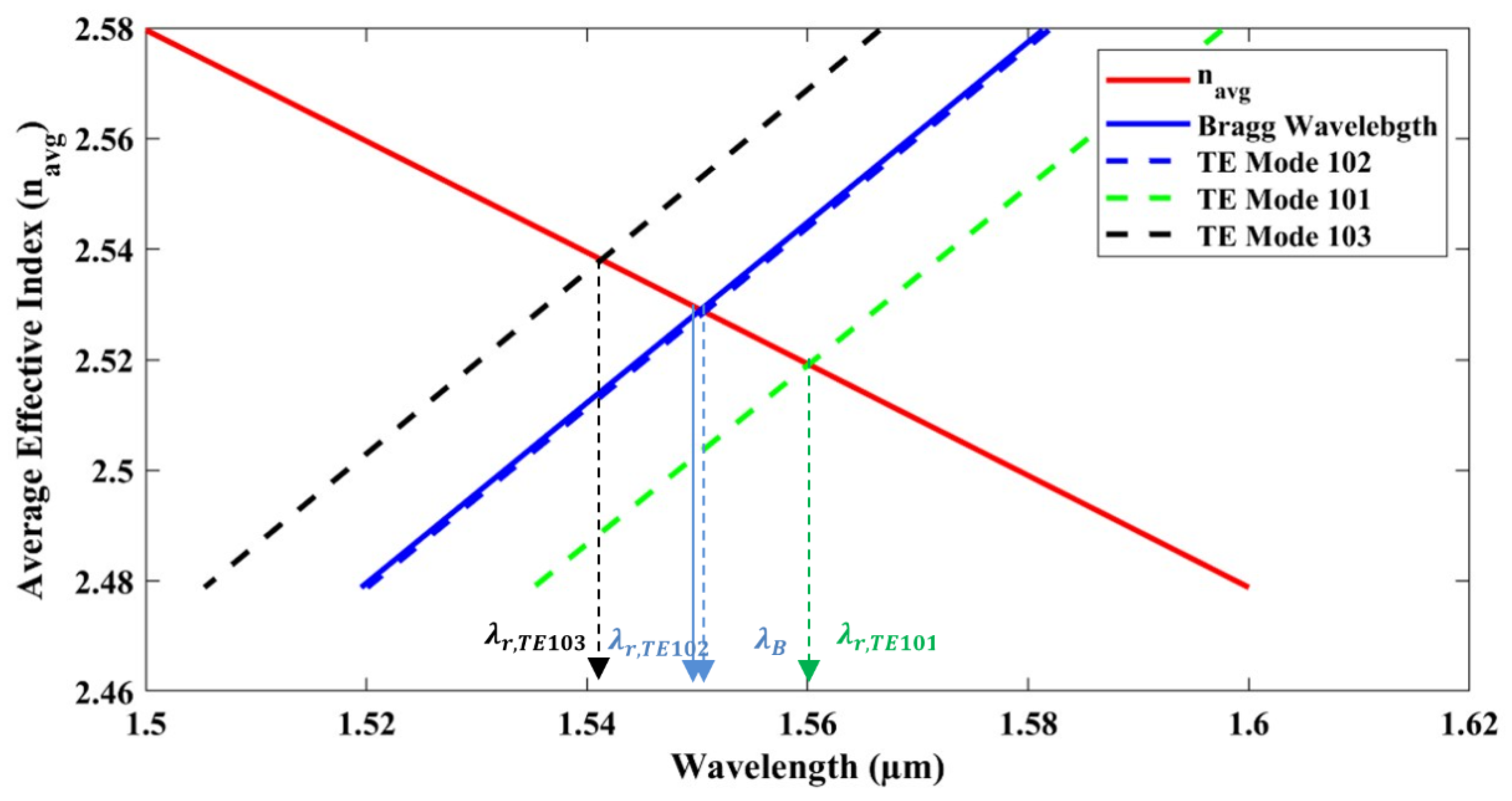
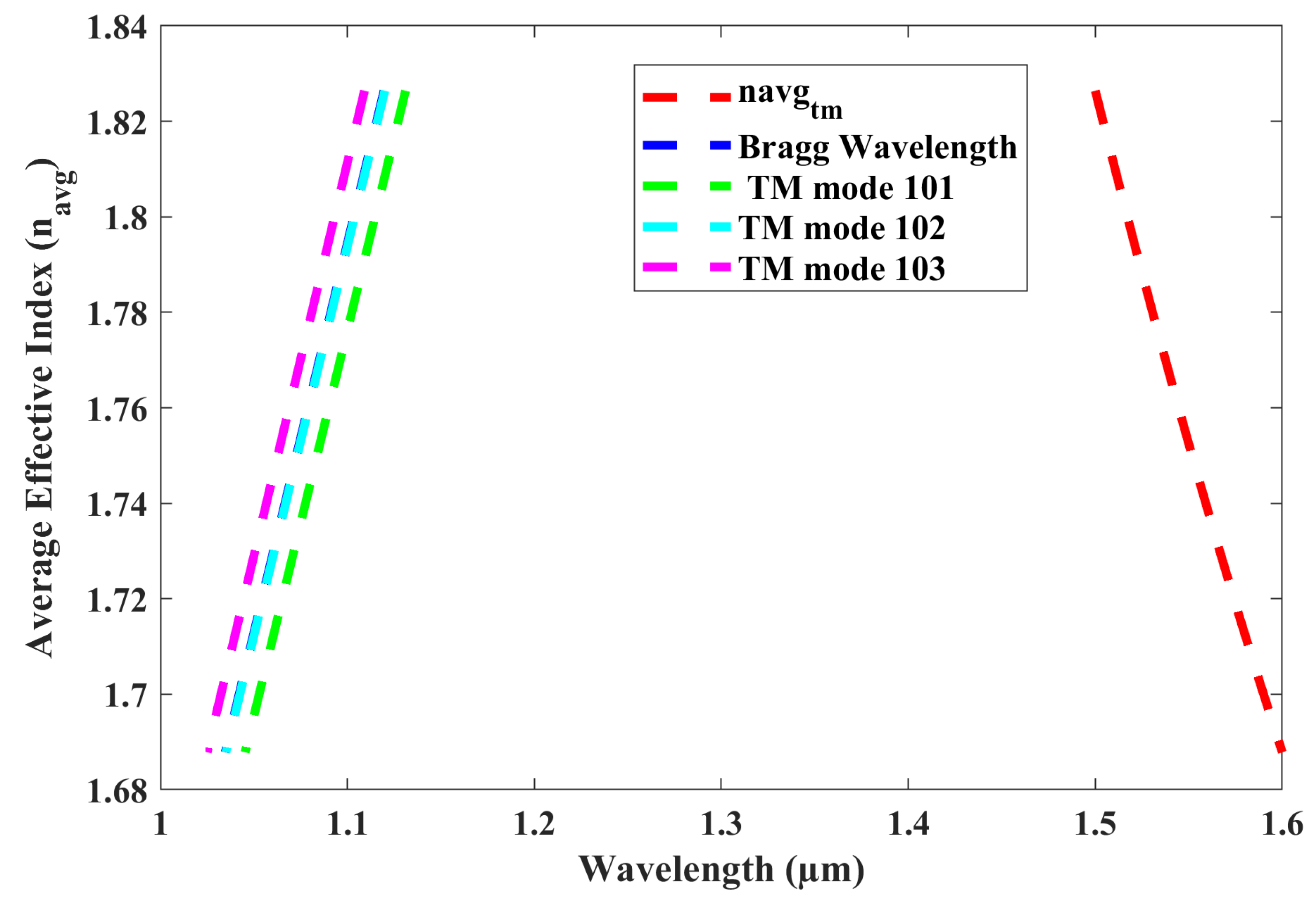
3.2. Wavelength Selection
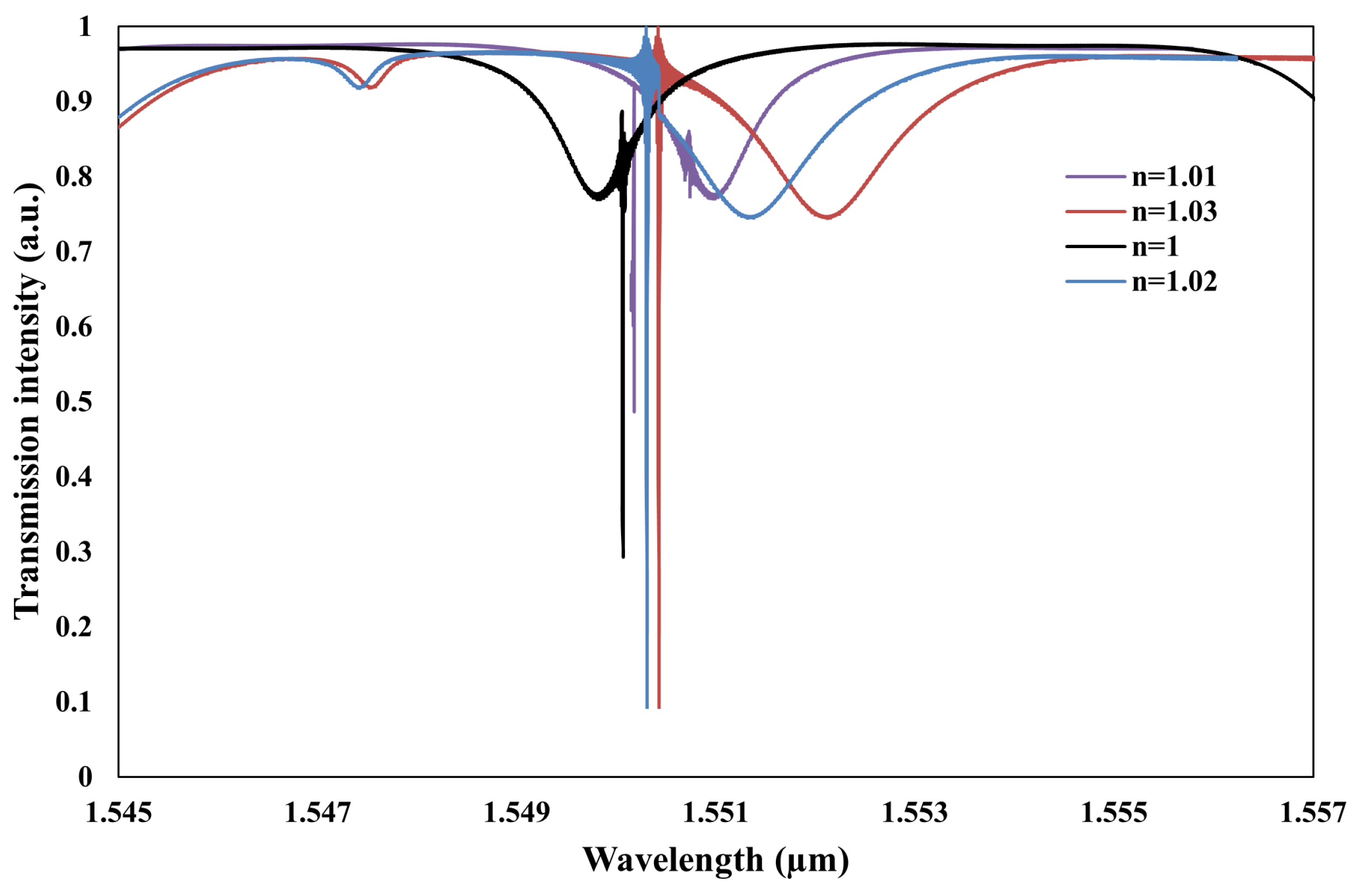
3.3. Sensing Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SOI | Silicon-On-Insulator; |
| TE | Transverse Electric; |
| TM | Transverse Magnetic; |
| RI | Refractive Index; |
| SPR | Surface Plasmon Resonance; |
| MRR | Microring Resonator; |
| FSR | Free Spectral Range; |
| MCRW | Metal-Clad Ridge Waveguide; |
| DP AG-MRR | Dual-Polarization Angular-Grating microring resonator; |
| ICP-RIE | Inductively Coupled Plasma Reactive Ion Etching; |
| CW | Continuous Wave; |
| PML | Perfectly Matched Layer; |
| ER | Extinction Ratio; |
| QF | Quality Factor; |
| LOD | Limit of Detection. |
References
- Alonso-Murias, M.d.C.; Velázquez-González, J.S.; Monzón-Hernández, D. SPR Fiber Tip Sensor for the Simultaneous Measurement of Refractive Index, Temperature, and Level of a Liquid. J. Light. Technol. 2019, 37, 4808–4814. [Google Scholar] [CrossRef]
- Liu, M.; Leng, X.; Ni, W.; Shum, P. Simultaneous and Ultrasensitive Measurement of Refractive Index and Temperature Based on SPR of Hollow-Core Anti-resonant Fibers. Plasmonics 2024, 19, 3091–3100. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Zhang, Y.; Liu, Z.; Yang, X.; Zhang, J.; Yang, J.; Yuan, L. Simultaneous measurement of temperature and refractive index based on a hybrid surface plasmon resonance multimode interference fiber sensor. Appl. Opt. 2020, 59, 1225–1229. [Google Scholar] [CrossRef]
- Yu, F.; Xue, P.; Zhao, X.; Zheng, J. Simultaneous Measurement of Refractive Index and Temperature Based on a Peanut-Shape Structure In-Line Fiber Mach–Zehnder Interferometer. IEEE Sens. J. 2019, 19, 950–955. [Google Scholar] [CrossRef]
- Freitas, A.I.; Pereira, D.; Bierlich, J.; Marques, J.C.; Ferreira, M.S. Simultaneous measurement of refractive index and temperature using a balloon-type optical fiber sensor. Optik 2024, 309, 0030–4026. [Google Scholar] [CrossRef]
- Butt, M.A. Plasmonic Sensor System Embedded with Orthogonal Mode Couplers for Simultaneous Monitoring of Temperature and Refractive Index. Plasmonics 2025, 20, 459–469. [Google Scholar] [CrossRef]
- Geetha, T.S.; Chellaswamy, C.; Kaliraja, T. Optimized convolutional neural network-based temperature and refractive index fiber optic sensor. J. Opt. 2024. [Google Scholar] [CrossRef]
- Gou, Z.; Wang, C.; Han, Z.; Nie, T.; Tian, H. Artificial neural networks assisting the design of a dual-mode photonic crystal nanobeam cavity for simultaneous sensing of the refractive index and temperature. Appl. Opt. 2022, 61, 4802–4808. [Google Scholar] [CrossRef]
- Dhara, P.; Singh, V.K.; Kumar, A.; Olivero, M.; Perrone, G. Reflection based silicon incorporated silver coated fiber optic SPR sensor for refractive index and temperature measurement. Microsyst. Technol. 2024, 30, 913–922. [Google Scholar] [CrossRef]
- Duan, C.; Li, J.; Zhang, K.; Tian, M. Optical fiber dual-parameter sensors based on different kinds of interferometers for measuring refractive index and temperature: A review. Opt. Quant. Electron. 2024, 56, 262. [Google Scholar] [CrossRef]
- Yu, X.; Zuo, S.; Zhang, Y.; Ma, Y.; Wang, R.; Yang, W.; Tian, K.; Geng, T.; Wang, P. Mach–Zehnder interferometer based on peanut structure for temperature and refractive index measurement. Opt. Quant. Electron. 2024, 56, 492–497. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, D.; Li, X.; Gao, H.; Yu, D. Simultaneous measurement of temperature and liquid refractive index based on fiber open Fabry-Pérot cavity and Bragg grating. Optoelectron. Lett. 2024, 20, 477–482. [Google Scholar] [CrossRef]
- André, R.M.; Warren-Smith, S.C.; Becker, M.; Dellith, J.; Rothhardt, M.; Zibaii, M.I.; Latifi, H.; Marques, M.B.; Bartelt, H.; Fraz, O. Simultaneous measurement of temperature and refractive index using focused ion beam milled Fabry-Perot cavities in optical fiber micro-tips. Opt. Express 2016, 24, 14053–14065. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Tang, Q.; Li, S.; Zheng, H.; Liang, D.; Xiao, H.; Du, C.; Yu, Y.; Ruan, S. Double-Cavity Fabry–Perot Interferometer Sensor Based on Polymer-Filled Hollow Core Fiber for Simultaneous Measurement of Temperature and Gas Pressure. Sensors 2025, 25, 2396. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Yu, X.; Zhou, J.; Chang, M.; Lu, D. An Ultra-Wide Range D-Shaped Fiber SPR Sensor with a Nanostructure of Gold–MoS2 and Sodium for the Simultaneous Measurement of Refractive Index and Temperature. Sensors 2025, 25, 377. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Wu, Y.; Yang, Y.; Wang, C.; Tian, H. High sensitivity and anti-external interference dual-parameter sensor based on a multimode slotted photonic crystal nanobeam cavity. J. Mod. Opt. 2021, 68, 357–364. [Google Scholar] [CrossRef]
- Liu, P.; Shi, Y. Simultaneous measurement of refractive index and temperature using cascaded side-coupled photonic crystal nanobeam cavities. Opt. Express 2017, 25, 28398–28406. [Google Scholar] [CrossRef]
- Claes, T.; Molera, J.G.; Vos, K.D.; Schacht, E.; Baets, R.; Bienstman, P. Label-Free Biosensing With a Slot-Waveguide-Based Ring Resonator in Silicon on Insulator. IEEE Photonics J. 2009, 1, 197–204. [Google Scholar] [CrossRef]
- Ma, T.; Sun, L.; Yuan, J.; Sang, X.; Yan, B.; Wang, K.; Yu, C. Integrated label-free optical biochemical sensor with a large measurement range based on an angular grating-microring resonator. Appl. Opt. 2016, 55, 4784–4790. [Google Scholar] [CrossRef]
- Kim, H.-T.; Yu, M. Cascaded ring resonator-based temperature sensor with simultaneously enhanced sensitivity and range. Opt. Express 2016, 24, 9501–9510. [Google Scholar] [CrossRef]
- Addya, S.; Dey, S.; Mandal, S. Optical Ring Resonator Based Temperature Sensor. Sens. Imaging 2017, 18, 33. [Google Scholar] [CrossRef]
- Saha, N.; Kumar, A. A novel dual resonance long period waveguide grating based highly sensitive refractive index sensor with reduced temperature sensitivity. Opt. Commun. 2020, 474, 126092. [Google Scholar] [CrossRef]
- Prinzen, A.; Waldow, M.; Kurz, H. Fabrication tolerances of SOI based directional couplers and ring resonators. Opt. Express 2013, 21, 17212–17220. [Google Scholar] [CrossRef] [PubMed]
- Selvaraja, S.K.; Sleeckx, E.; Schaekers, M.; Bogaerts, W.; Thourhout, D.V.; Dumon, P.; Baets, R. Low-loss amorphous silicon-on-insulator technology for photonic integrated circuitry. Opt. Commun. 2009, 282, 1767–1770. [Google Scholar] [CrossRef]
- Watts, M.R.; Trotter, D.C.; Young, R.W.; Lentine, A.L. Ultralow power silicon microdisk modulators and switches. In Proceedings of the 2008 5th IEEE International Conference on Group IV Photonics, Sorrento, Italy, 17–19 September 2008. [Google Scholar] [CrossRef]
- Roelkens, G.; Thourhout, D.V.; Baets, R. High efficiency grating coupler between silicon-on-insulator waveguides and perfectly vertical optical fibers. Opt. Lett. 2007, 32, 1495–1497. [Google Scholar] [CrossRef]
- Vos, K.D.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-Insulator microring resonator for sensitive and label-free biosensing. Opt. Express 2007, 15, 7610–7615. [Google Scholar] [CrossRef]
- Marcatili, E.A.J. Dielectric rectangular waveguide and directional coupler for integrated optics. Bell Syst. Tech. J. 1969, 48, 2071–2102. [Google Scholar] [CrossRef]
- Tseng, C.-W.; Tsai, C.-W.; Lin, K.-C.; Lee, M.-C.; Chen, Y.-J. Study of coupling loss on strongly-coupled, ultra compact microring resonators. Opt. Express 2013, 21, 7250–7257. [Google Scholar] [CrossRef]
- Cai, X.; Wang, J.; Strain, M.J.; Johnson-Morris, B.; Zhu, J.; Sorel, M.; O’Brien, J.L.; Thompson, M.G.; Yu, S. Integrated compact optical vortex beam emitters. Science 2012, 338, 363–366. [Google Scholar] [CrossRef]
- Selvaraja, S.K.; Jaenen, P.; Bogaerts, W.; Thourhout, D.V.; Dumon, P.; Baets, R. Fabrication of Photonic Wire and Crystal Circuits in Silicon-on-Insulator Using 193-nm Optical Lithography. J. Light. Technol 2009, 27, 4076–4083. [Google Scholar] [CrossRef]
- Bauld, R.; Choi, D.-Y.W.; Bazylewski, P.; Divigalpitiya, R.; Fanchini, G. Thermo-optical characterization and thermal properties of graphene–polymer composites: A review. J. Mater. Chem. C 2018, 6, 2901–2914. [Google Scholar] [CrossRef]
- Shi, W.; Wang, X.; Zhang, W.; Yun, H.; Lin, C.; Chrostowski, L.; Jaeger, N.A.F. Grating-coupled silicon microring resonators. Appl. Phys. Lett. 2012, 100, 121118. [Google Scholar] [CrossRef]
- Liu, W.; Lai, Z.; Guo, H.; Liu, Y. Guided-mode resonance filters with shallow grating. Opt. Lett. 2010, 35, 865–867. [Google Scholar] [CrossRef]
- Liu, P.; Shi, Y. Simultaneous measurement of refractive index and temperature using a dual polarization ring. Appl. Opt. 2016, 55, 3537–3541. [Google Scholar] [CrossRef]
- Tu, Z.; Gao, D.; Zhang, M.; Zhang, D. High-sensitivity complex refractive index sensing based on Fano resonance in the subwavelength grating waveguide micro-ring resonator. Opt. Express 2017, 25, 20911–20922. [Google Scholar] [CrossRef]
- Wu, N.; Xia, L. Side-mode suppressed filter based on an angular grating-subwavelength grating microring resonator with high flexibility in wavelength design. Appl. Opt. 2019, 58, 7174–7180. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.-w.; Zhao, H.; Qiao, X.-g.; Li, Y.; Zhao, D.-z.; Yong, Z. Study on a novel photonic crystal temperature sensor. Optoelectron. Lett. 2011, 7, 419–422. [Google Scholar] [CrossRef]
- Kamikawachi, R.C.; Abe, I.; Paterno, A.S.; Kalinowski, H.J.; Muller, M.; Pinto, J.L.; Fabris, J.L. Determination of thermo-optic coefficient in liquids with fiber Bragg grating refractometer. Opt. Commun. 2008, 281, 621–625. [Google Scholar] [CrossRef]
- Lee, C.-L.; Ho, H.-Y.; Gu, J.-H.; Yeh, T.-Y.; Tseng, C.-H. Dual hollow core fiber-based Fabry Perot interferometer for measuring the thermo-optic coefficients of liquids. Opt. Lett. 2015, 40, 459–462. [Google Scholar] [CrossRef]
- Frey, B.J.; Leviton, D.B.; Madison, T.J. Temperature-dependent refractive index of silicon and germanium. Proc. Optomech. Technol. Astron. 2006, 6273, 62732J. [Google Scholar] [CrossRef]
- Chrostowski, L.; Grist, S.; Flueckiger, J.; Shi, W.; Wang, X.; Ouellet, E.; Yun, H.; Webb, M.; Nie, B.; Liang, Z.; et al. Silicon photonic resonator sensors and devices. In Proceedings of the SPIE 8236, Laser Resonators, Microresonators, and Beam Control XIV, San Francisco, CA, USA, 6 February 2012. [Google Scholar] [CrossRef]
| References | Structure Type | Parameters | RI Sensitivities (nm/RIU) | T Sensitivities (pm/°C) | Range RI; T (nm) | LOD (/RIU); (/°C) |
|---|---|---|---|---|---|---|
| [19] | AG-MRR | Single | 95.27 pm/% | NA 1 | 50.2 (RI) | 0.0032 |
| [35] | DP-MRR | Dual | 104; 319 | 78.7; 34.1 | Limited by FSR | ; 0.5 |
| [36] | SWGMRR | Single | 366 | NA 1 | Limited by FSR | NM 2 |
| [37] | AG-SWGMRR | Single | 672.8 | NA 1 | NM 2 | |
| This Work | DP-AGMRR | Dual | 76.66; 13.33 | 260; 334 | 7.6; 35 (FSR Free for T) | ; |
| 0 | 0.03 | 0.4 | 2.3 | 0.030 | 0.001 |
| 3 | 0.01 | 1.51 | 3.24 | 0.010 | 3.33 |
| 5 | 0 | 1.4 | 1.6 | 0.003 | 5.55 |
| 8 | 0.02 | 3.5 | 7.0 | 0.028 | 8.05 |
| 12 | 0.015 | 4.6 | 6.9 | 0.025 | 11.98 |
| 13 | 0.025 | 5.33 | 9.65 | 0.044 | 12.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qadir, M.F.; Zakwan, M.; Shahid, S.; Rana, A.S.; Ali, M.M.; Bösch, W. Numerical Study of a Dual-Mode Optical Sensor for Temperature and Refractive Index Sensing with Enhanced Temperature Range. Sensors 2025, 25, 3999. https://doi.org/10.3390/s25133999
Qadir MF, Zakwan M, Shahid S, Rana AS, Ali MM, Bösch W. Numerical Study of a Dual-Mode Optical Sensor for Temperature and Refractive Index Sensing with Enhanced Temperature Range. Sensors. 2025; 25(13):3999. https://doi.org/10.3390/s25133999
Chicago/Turabian StyleQadir, Muhammad Favad, Muhammad Zakwan, Saleem Shahid, Ahsan Sarwar Rana, Muhammad Mahmood Ali, and Wolfgang Bösch. 2025. "Numerical Study of a Dual-Mode Optical Sensor for Temperature and Refractive Index Sensing with Enhanced Temperature Range" Sensors 25, no. 13: 3999. https://doi.org/10.3390/s25133999
APA StyleQadir, M. F., Zakwan, M., Shahid, S., Rana, A. S., Ali, M. M., & Bösch, W. (2025). Numerical Study of a Dual-Mode Optical Sensor for Temperature and Refractive Index Sensing with Enhanced Temperature Range. Sensors, 25(13), 3999. https://doi.org/10.3390/s25133999







