A Spatio-Temporal Joint Diagnosis Framework for Bearing Faults via Graph Convolution and Attention-Enhanced Bidirectional Gated Networks
Abstract
1. Introduction
2. Related Work
2.1. Dynamic Graph Structure Modeling
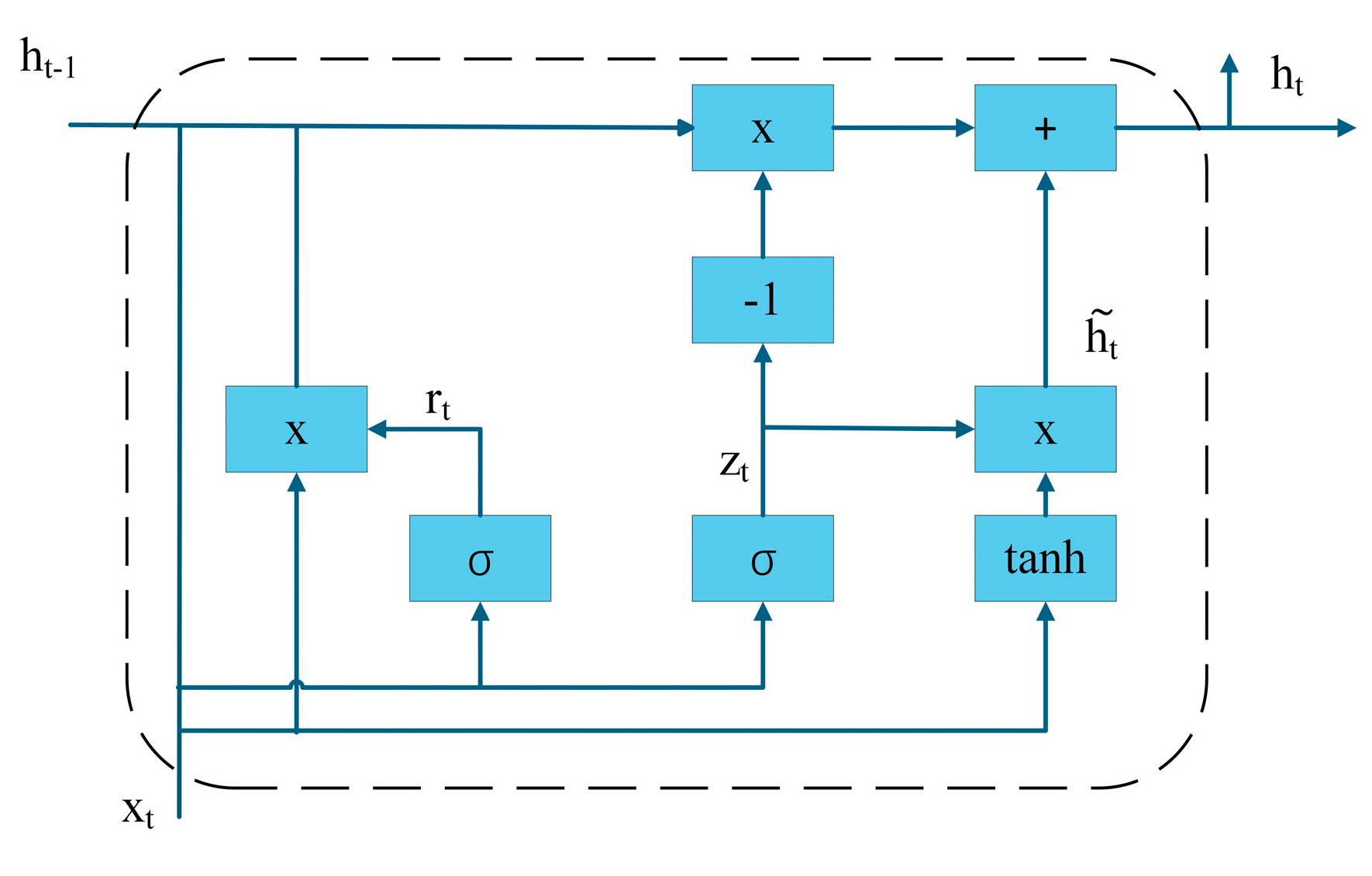
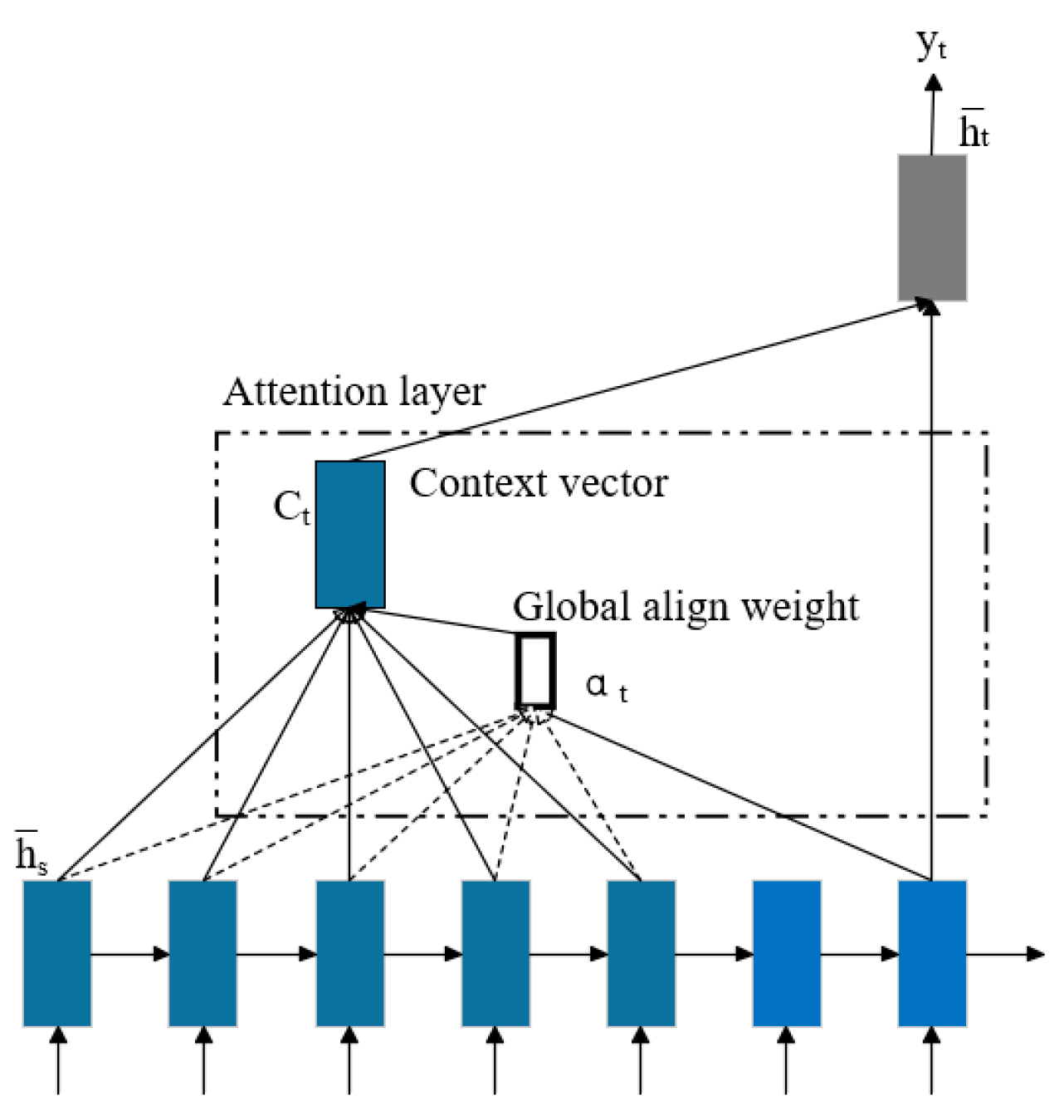
2.2. Research and Principles Related to GRU Units and Global Attention
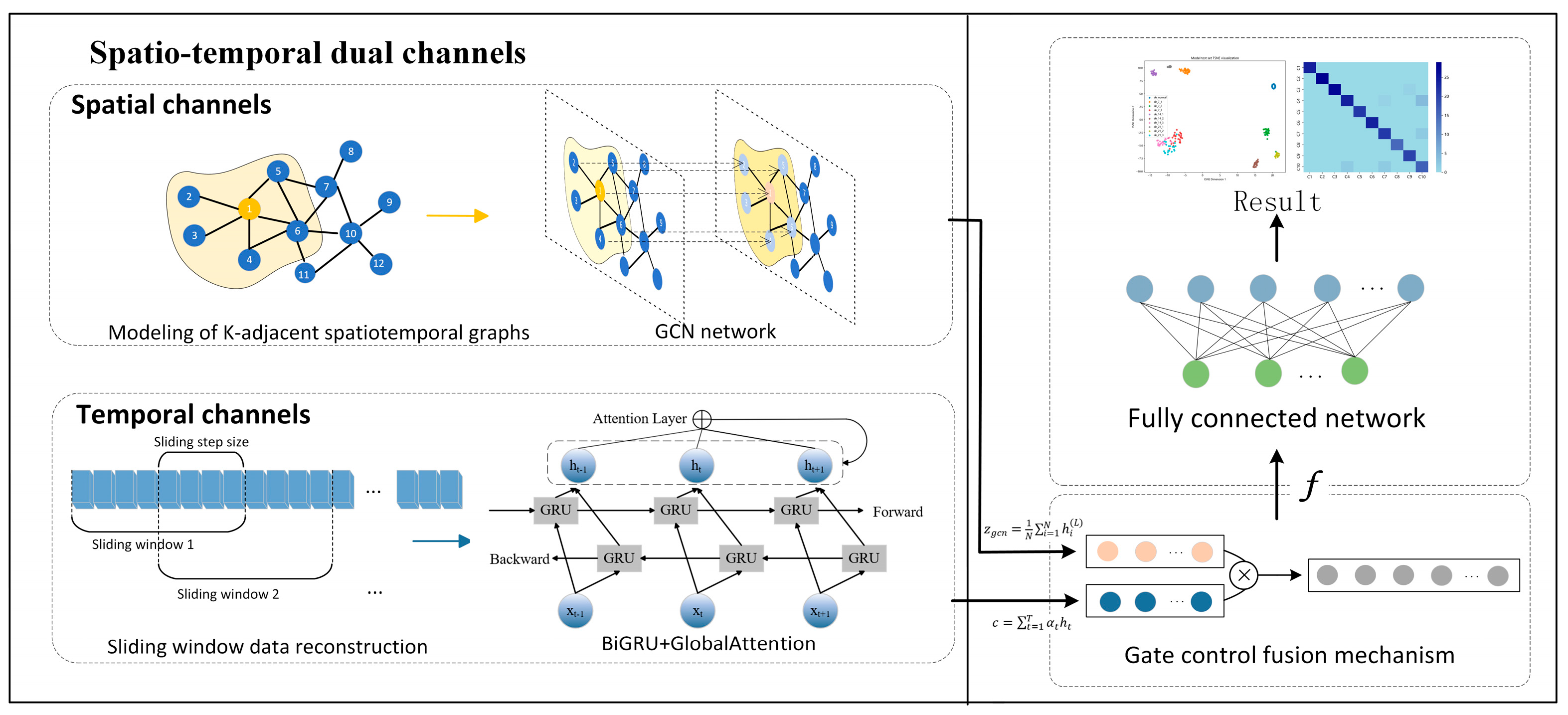
3. The Proposed Method
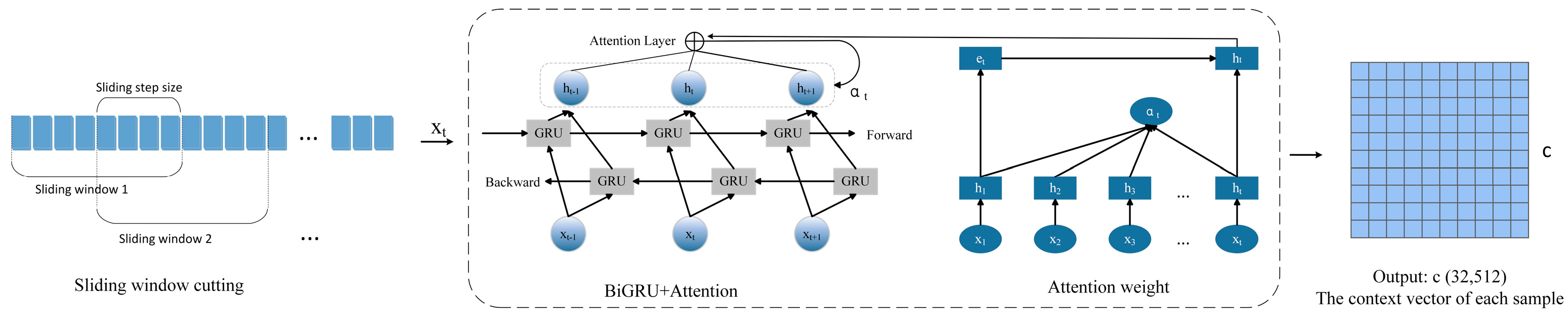
3.1. Improved KNN-Based Spatiotemporal Modeling of Rolling Bearing Data
3.2. The Main Procedure of the ST-GABG Diagnostic Model
4. Experiments
4.1. Experimental Setup and Training Evaluation Metrics
4.2. Description of Comparison Methods
4.3. The Ablation Experiments of the Proposed Method
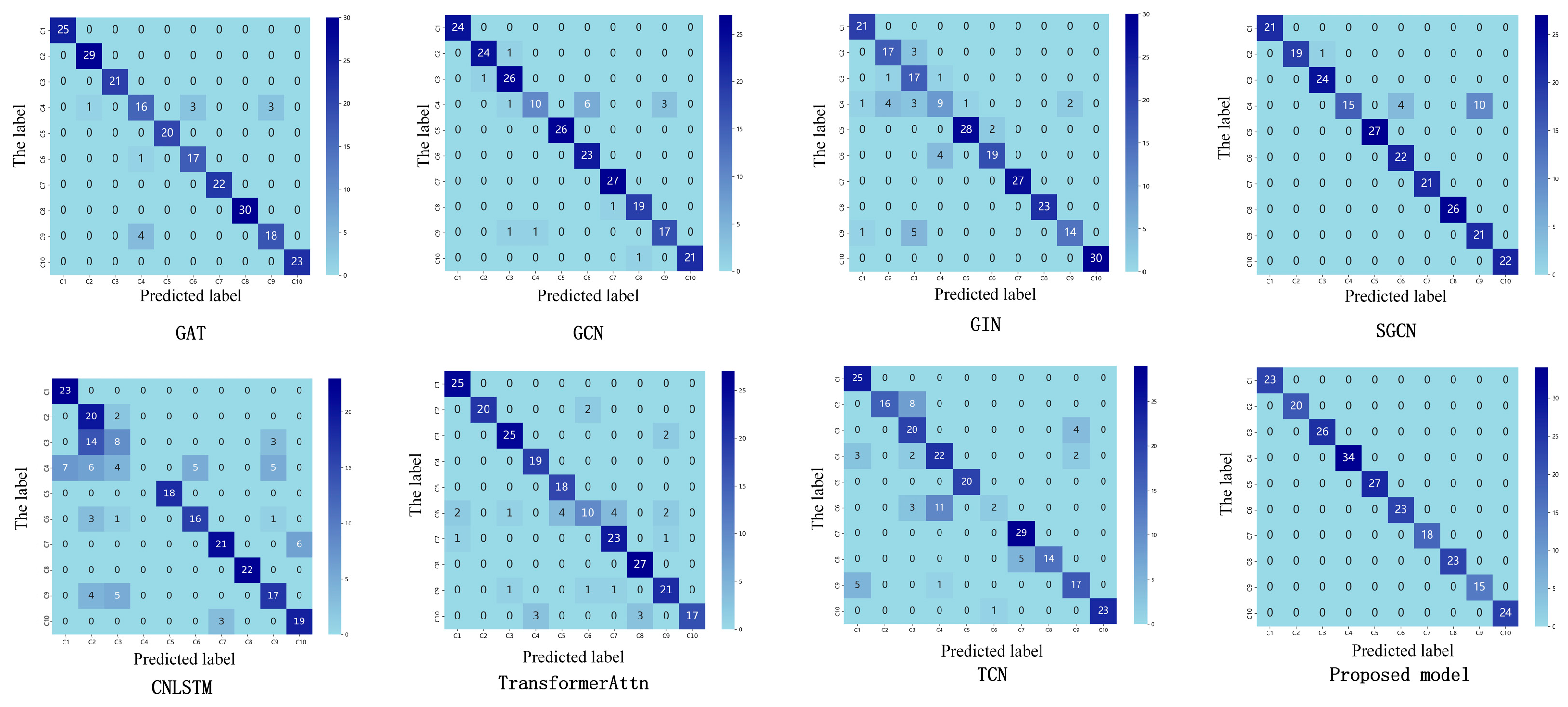
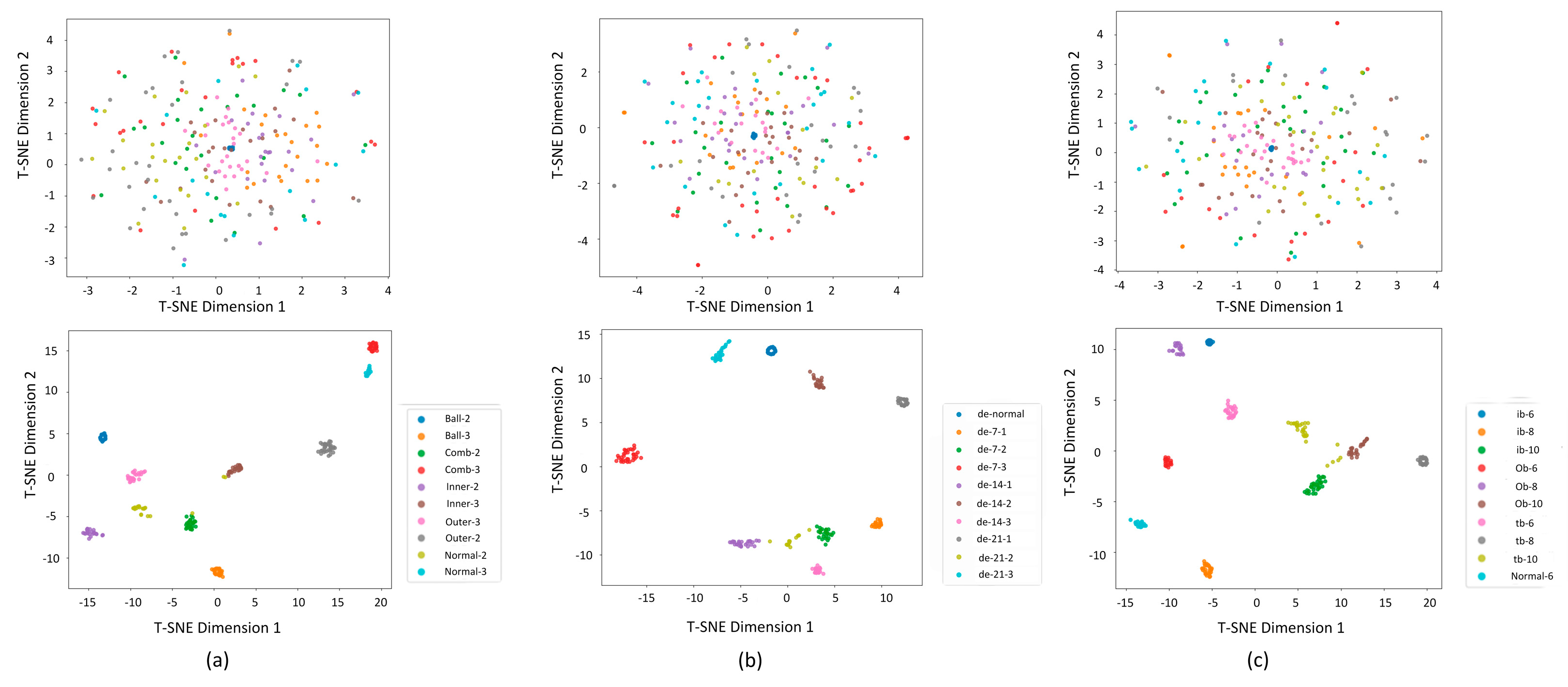
4.4. Visualization of the Feature Extraction Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Model | Learn Rate | Weight_Decay | Head/Kernel | Layer |
|---|---|---|---|---|
| GAT | 0.0003 | 1 | 3 | |
| GCN | 0.0003 | 3 | ||
| GIN | 0.0003 | 3 | ||
| SGCN | 0.0003 | 1 | 3 | |
| TCN | 0.003 | 2 | 2 | |
| CNLSTM | 0.003 | 3 | 2 | |
| TransformerAttn | 1 × 10−4 | 1 × 10−5 | 2 | 2 |
| Acronym | Fall Name |
|---|---|
| BiGRU | The Bidirectional Gated Recurrent Unit |
| GCN | Graph Convolutional Network |
| KNN | K-Nearest Neighbor |
| ST-GABG | The Proposed Spatio-Temporal Joint Diagnosis Model |
| CWRU | Case Western Reserve University |
| SEU | Southeast University |
| JU | Jiangnan University |
| TransformerAttn | Transformer Attention Fusion Architecture |
| CNLSTM | CNN and LSTM Fusion Architecture |
| T-SNE | T-Distributed Stochastic Neighbor Embedding |
References
- Shen, S.; Lu, H.; Sadoughi, M.; Hu, C.; Nemani, V.; Thelen, A.; Webster, K.; Darr, M.; Sidon, J.; Kenny, S. A Physics-Informed Deep Learning Approach for Bearing Fault Detection. Eng. Appl. Artif. Intell. 2021, 103, 104295. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, S.; Li, W. Bearing Performance Degradation Assessment Using Long Short-Term Memory Recurrent Network. Comput. Ind. 2019, 106, 14–29. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, K.; An, Y.; Luo, H.; Yin, S. An Integrated Multitasking Intelligent Bearing Fault Diagnosis Scheme Based on Representation Learning Under Imbalanced Sample Condition. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 6231–6242. [Google Scholar] [CrossRef] [PubMed]
- Ruan, D.; Wang, J.; Yan, J.; Gühmann, C. CNN Parameter Design Based on Fault Signal Analysis and Its Application in Bearing Fault Diagnosis. Adv. Eng. Inform. 2023, 55, 101877. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault Diagnosis of Rolling Bearings Using an Improved Multi-Scale Convolutional Neural Network with Feature Attention Mechanism. ISA Trans. 2021, 110, 379–393. [Google Scholar] [CrossRef] [PubMed]
- Sinitsin, V.; Ibryaeva, O.; Sakovskaya, V.; Eremeeva, V. Intelligent Bearing Fault Diagnosis Method Combining Mixed Input and Hybrid CNN-MLP Model. Mech. Syst. Signal Process. 2022, 180, 109454. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Q.; Shu, Y.; Xiao, W.; Ma, W. Remaining Useful Life Prediction for Rolling Bearings With a Novel Entropy-Based Health Indicator and Improved Particle Filter Algorithm. IEEE Access 2023, 11, 3062–3079. [Google Scholar] [CrossRef]
- Gawde, S.; Patil, S.; Kumar, S.; Kamat, P.; Kotecha, K.; Abraham, A. Multi-Fault Diagnosis of Industrial Rotating Machines Using Data-Driven Approach : A Review of Two Decades of Research. Eng. Appl. Artif. Intell. 2023, 123, 106139. [Google Scholar] [CrossRef]
- Machado, M.; Moreira, P.; Flores, P.; Lankarani, H.M. Compliant Contact Force Models in Multibody Dynamics: Evolution of the Hertz Contact Theory. Mech. Mach. Theory 2012, 53, 99–121. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, N.; Shen, C. A New Data-Driven Transferable Remaining Useful Life Prediction Approach for Bearing under Different Working Conditions. Mech. Syst. Signal Process. 2020, 139, 106602. [Google Scholar] [CrossRef]
- Fernández-Francos, D.; Martínez-Rego, D.; Fontenla-Romero, O.; Alonso-Betanzos, A. Automatic Bearing Fault Diagnosis Based on One-Class ν-SVM. Comput. Ind. Eng. 2013, 64, 357–365. [Google Scholar] [CrossRef]
- Wan, L.; Gong, K.; Zhang, G.; Yuan, X.; Li, C.; Deng, X. An Efficient Rolling Bearing Fault Diagnosis Method Based on Spark and Improved Random Forest Algorithm. IEEE Access 2021, 9, 37866–37882. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, X.; Li, H.; Yang, Z. Intelligent Fault Diagnosis of Rolling Bearings Based on Normalized CNN Considering Data Imbalance and Variable Working Conditions. Knowl. -Based Syst. 2020, 199, 105971. [Google Scholar] [CrossRef]
- Nemani, V.P.; Lu, H.; Thelen, A.; Hu, C.; Zimmerman, A.T. Ensembles of Probabilistic LSTM Predictors and Correctors for Bearing Prognostics Using Industrial Standards. Neurocomputing 2022, 491, 575–596. [Google Scholar] [CrossRef]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in Vision: A Survey. ACM Comput. Surv. 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Yeh, C.; Chen, Y.; Wu, A.; Chen, C.; Viégas, F.; Wattenberg, M. AttentionViz: A Global View of Transformer Attention; Cornell University: Ithaca, NY, USA, 2023. [Google Scholar]
- Khan, A.; Rauf, Z.; Sohail, A.; Khan, A.R.; Asif, H.; Asif, A.; Farooq, U. A Survey of the Vision Transformers and Their CNN-Transformer Based Variants. Artif. Intell. Rev. 2023, 56, 2917–2970. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, J.; Liu, S.; Feng, Y.; He, S.; Xu, E. Multi-Channel Calibrated Transformer with Shifted Windows for Few-Shot Fault Diagnosis under Sharp Speed Variation. ISA Trans. 2022, 131, 501–515. [Google Scholar] [CrossRef]
- Yin, C.; Li, Y.; Wang, Y.; Dong, Y. Physics-Guided Degradation Trajectory Modeling for Remaining Useful Life Prediction of Rolling Bearings. Mech. Syst. Signal Process. 2025, 224, 112192. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Li, X.; Shao, H.; Han, T.; Xie, M. Attention-Aware Temporal–Spatial Graph Neural Network with Multi-Sensor Information Fusion for Fault Diagnosis. Knowl. -Based Syst. 2023, 278, 110891. [Google Scholar] [CrossRef]
- Peng, B.; Bi, Y.; Xue, B.; Zhang, M.; Wan, S. A Survey on Fault Diagnosis of Rolling Bearings. Algorithms 2022, 15, 347. [Google Scholar] [CrossRef]
- Liu, M.-K.; Weng, P.-Y. Fault Diagnosis of Ball Bearing Elements: A Generic Procedure Based on Time-Frequency Analysis. Meas. Sci. Rev. 2019, 19, 185–194. [Google Scholar] [CrossRef]
- Khan, M.A.; Asad, B.; Kudelina, K.; Vaimann, T.; Kallaste, A. The Bearing Faults Detection Methods for Electrical Machines—The State of the Art. Energies 2022, 16, 296. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, C.; Zhang, J.; Gao, M.; Zhang, H.; Zhong, K. Multi-Layered Graph Convolutional Network-Based Industrial Fault Diagnosis with Multiple Relation Characterization Capability. Machines 2022, 10, 873. [Google Scholar] [CrossRef]
- Zhang, Q.; Hao, C.; Lv, Z.; Fan, Q. The Combination Model of CNN and GCN for Machine Fault Diagnosis. PLoS ONE 2023, 18, e0292381. [Google Scholar] [CrossRef] [PubMed]
- Cabrera, D.; Guamán, A.; Zhang, S.; Cerrada, M.; Sánchez, R.-V.; Cevallos, J.; Long, J.; Li, C. Bayesian Approach and Time Series Dimensionality Reduction to LSTM-Based Model-Building for Fault Diagnosis of a Reciprocating Compressor. Neurocomputing 2020, 380, 51–66. [Google Scholar] [CrossRef]
- Zhou, J.; Qin, Y.; Chen, D.; Liu, F.; Qian, Q. Remaining Useful Life Prediction of Bearings by a New Reinforced Memory GRU Network. Adv. Eng. Inform. 2022, 53, 101682. [Google Scholar] [CrossRef]
- Brauwers, G.; Frasincar, F. A General Survey on Attention Mechanisms in Deep Learning. IEEE Trans. Knowl. Data Eng. 2023, 35, 3279–3298. [Google Scholar] [CrossRef]
- de Santana Correia, A.; Colombini, E.L. Attention, Please! A Survey of Neural Attention Models in Deep Learning; Cornell University: Ithaca, NY, USA, 2021. [Google Scholar]
- He, S.; Sang, X.; Yin, J.; Zheng, Y.; Chen, H. Short-Term Runoff Prediction Optimization Method Based on BGRU-BP and BLSTM-BP Neural Networks. Water Resour. Manag. 2023, 37, 747–768. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, J.; Yu, Z.; Zhang, Y.; Liu, Z. The Bidirectional Gated Recurrent Unit Network Based on the Inception Module (Inception-BiGRU) Predicts the Missing Data by Well Logging Data. ACS Omega 2023, 8, 27710–27724. [Google Scholar] [CrossRef]
- Zhou, F.; Hu, P.; Yang, S.; Wen, C. A Multimodal Feature Fusion-Based Deep Learning Method for Online Fault Diagnosis of Rotating Machinery. Sensors 2018, 18, 3521. [Google Scholar] [CrossRef]
- Qin, Y.; Song, D.; Chen, H.; Cheng, W.; Jiang, G.; Cottrell, G. A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence Main track, Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Feng, S.; Feng, Y. A Dual-Staged Attention Based Conversion-Gated Long Short Term Memory for Multivariable Time Series Prediction. IEEE Access 2022, 10, 368–379. [Google Scholar] [CrossRef]
- Yang, S.; Chen, X.; Bai, Y. Exploiting Graph Neural Network with One-Shot Learning for Fault Diagnosis of Mechanical Equipment. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1207, 012022. [Google Scholar] [CrossRef]
- Zhang, F.; Jin, Q.; Li, D.; Zhang, Y.; Zhu, Q. Physical Graph-Based Spatiotemporal Fusion Approach for Process Fault Diagnosis. ACS Omega 2024, 9, 9486–9502. [Google Scholar] [CrossRef] [PubMed]
- Xing, J.; Li, F.; Ma, X.; Qin, Q. An Optimal Spatio-Temporal Hybrid Model Based on Wavelet Transform for Early Fault Detection. Sensors 2024, 24, 4736. [Google Scholar] [CrossRef]
- Lin, J.; Shao, H.; Zhou, X.; Cai, B.; Liu, B. Generalized MAML for Few-Shot Cross-Domain Fault Diagnosis of Bearing Driven by Heterogeneous Signals. Expert Syst. Appl. 2023, 230, 120696. [Google Scholar] [CrossRef]
- Hendriks, J.; Dumond, P.; Knox, D.A. Towards Better Benchmarking Using the CWRU Bearing Fault Dataset. Mech. Syst. Signal Process. 2022, 169, 108732. [Google Scholar] [CrossRef]
- Chatzimparmpas, A.; Martins, R.M.; Kerren, A. T-viSNE: Interactive Assessment and Interpretation of t-SNE Projections. IEEE Trans. Vis. Comput. Graph. 2020, 26, 2696–2714. [Google Scholar] [CrossRef]
- Pezzotti, N.; Thijssen, J.; Mordvintsev, A.; Hollt, T.; van Lew, B.; Lelieveldt, B.P.F.; Eisemann, E.; Vilanova, A. GPGPU Linear Complexity T-SNE Optimization; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Meng, L.; van den Elzen, S.; Pezzotti, N.; Vilanova, A. Class-Constrained t-SNE: Combining Data Features and Class Probabilities. IEEE Trans. Vis. Comput. Graph. 2024, 30, 164–174. [Google Scholar] [CrossRef]





| Dataset | Load | Fault Type |
|---|---|---|
| CWRU | 12 Hertz 0 Mach | Normal |
| 0.007 inner, 0.014 inner, 0.021 inner | ||
| 0.007 ball, 0.014 ball, 0.021 ball | ||
| 0.007 outer, 0.014 outer, 0.021 outer | ||
| SEU | 20 Hz-0V | Normal, ball, comb, inner, outer |
| 30 Hz-2V | Normal, ball, comb, inner, outer | |
| JU | 600 r/min | Normal, tb, ib, ob |
| 800 r/min | tb, ib, ob | |
| 1000 r/min | tb, ib, ob |
| Optimum Model Parameters | Value |
|---|---|
| BiGRU Hidden Layer | 3 |
| GCN Hidden Layer | 3 |
| Fully Connected Layer | 1 |
| Learning Rate | 0.003 |
| Batch | 32 |
| Dropout Rate | 0.9 |
| Methods | Precision | F1 Score | Macro Average Recall Rate |
|---|---|---|---|
| GCN | 91.25% | 0.9742 | 0.9724 |
| GIN | 83.95% | 0.8412 | 0.8212 |
| GAT | 92.08% | 0.9356 | 0.9287 |
| SGCN | 92.70% | 0.9399 | 0.9502 |
| TransformAttn | 86.91% | 0.8798 | 0.8804 |
| TCN | 57.29% | 0.5900 | 0.5800 |
| CNLSTM | 66.39% | 0.7039 | 0.7286 |
| Proposed method | 97.08% | 0.9914 | 0.9906 |
| Experiment Number | GCN | BiGRU | Attention | Precision | F1 Score | Macro Average Recall Rate |
|---|---|---|---|---|---|---|
| Ablation1 | √ | √ | 90.83% | 0.9399 | 0.9385 | |
| Ablation2 | √ | √ | 73.12% | 0.7253 | 0.7276 | |
| Ablation3 | √ | √ | 87.91% | 0.9227 | 0.9233 | |
| Ablation4 | √ | 50.62% | 0.4850 | 0.5052 | ||
| Ablation5 | √ | 89.58% | 0.9396 | 0.9337 | ||
| Ablation6 | √ | 70.00% | 0.6652 | 0.6643 | ||
| Proposed method | √ | √ | √ | 97.08% | 0.9914 | 0.9906 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Z.; Cao, X.; Hao, H.; Liang, S.; Liu, J.; Li, D. A Spatio-Temporal Joint Diagnosis Framework for Bearing Faults via Graph Convolution and Attention-Enhanced Bidirectional Gated Networks. Sensors 2025, 25, 3908. https://doi.org/10.3390/s25133908
Xiao Z, Cao X, Hao H, Liang S, Liu J, Li D. A Spatio-Temporal Joint Diagnosis Framework for Bearing Faults via Graph Convolution and Attention-Enhanced Bidirectional Gated Networks. Sensors. 2025; 25(13):3908. https://doi.org/10.3390/s25133908
Chicago/Turabian StyleXiao, Zhiguo, Xinyao Cao, Huihui Hao, Siwen Liang, Junli Liu, and Dongni Li. 2025. "A Spatio-Temporal Joint Diagnosis Framework for Bearing Faults via Graph Convolution and Attention-Enhanced Bidirectional Gated Networks" Sensors 25, no. 13: 3908. https://doi.org/10.3390/s25133908
APA StyleXiao, Z., Cao, X., Hao, H., Liang, S., Liu, J., & Li, D. (2025). A Spatio-Temporal Joint Diagnosis Framework for Bearing Faults via Graph Convolution and Attention-Enhanced Bidirectional Gated Networks. Sensors, 25(13), 3908. https://doi.org/10.3390/s25133908







