Bridge Deformation Monitoring Combining 3D Laser Scanning with Multi-Scale Algorithms
Abstract
1. Introduction
2. Theoretical Framework
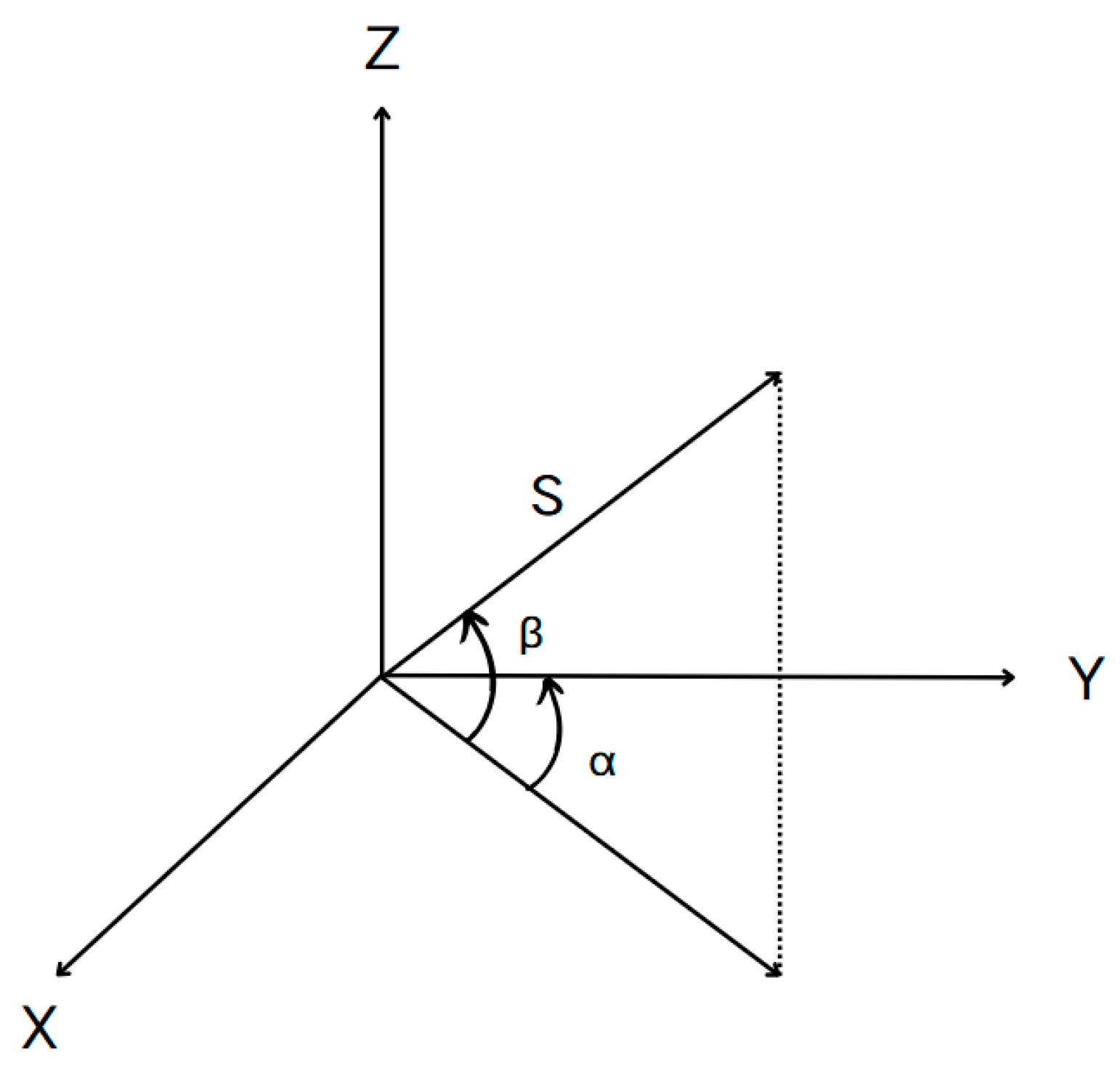
2.1. The Basic Principle of 3D Laser Scanning Technology
2.2. The Principle of Point Cloud Data Acquisition
2.3. The Principle of Statistical Filtering
- Calculate the average Euclidean distance between each point Pi in the point set and the nearest n points, as follows:
- Calculate the mean value μ and the standard value σ of the average distance of all points in the point set, as follows:where N is the total number of points in the point set.
- Determine the distance threshold dm, . Compare the sizes of di and dm. If they are greater than the threshold, eliminate the corresponding points. It is evident that this method requires the determination of two parameters to effectively remove noise: the number of neighboring points n, and the distance threshold dmax. In practical applications, these parameters should be adjusted based on the specific context.
2.4. Point Cloud Downsampling Based on the Octree Method
2.5. The Iterative Closest Point (ICP) Registration Algorithm
3. Plane Fitting Based on the Least-Squares Method
3.1. Plane Fitting
3.2. Extraction of the Center Point of the Point Cloud Slice Fitting Plane
4. The Principle of the M3C2 Algorithm
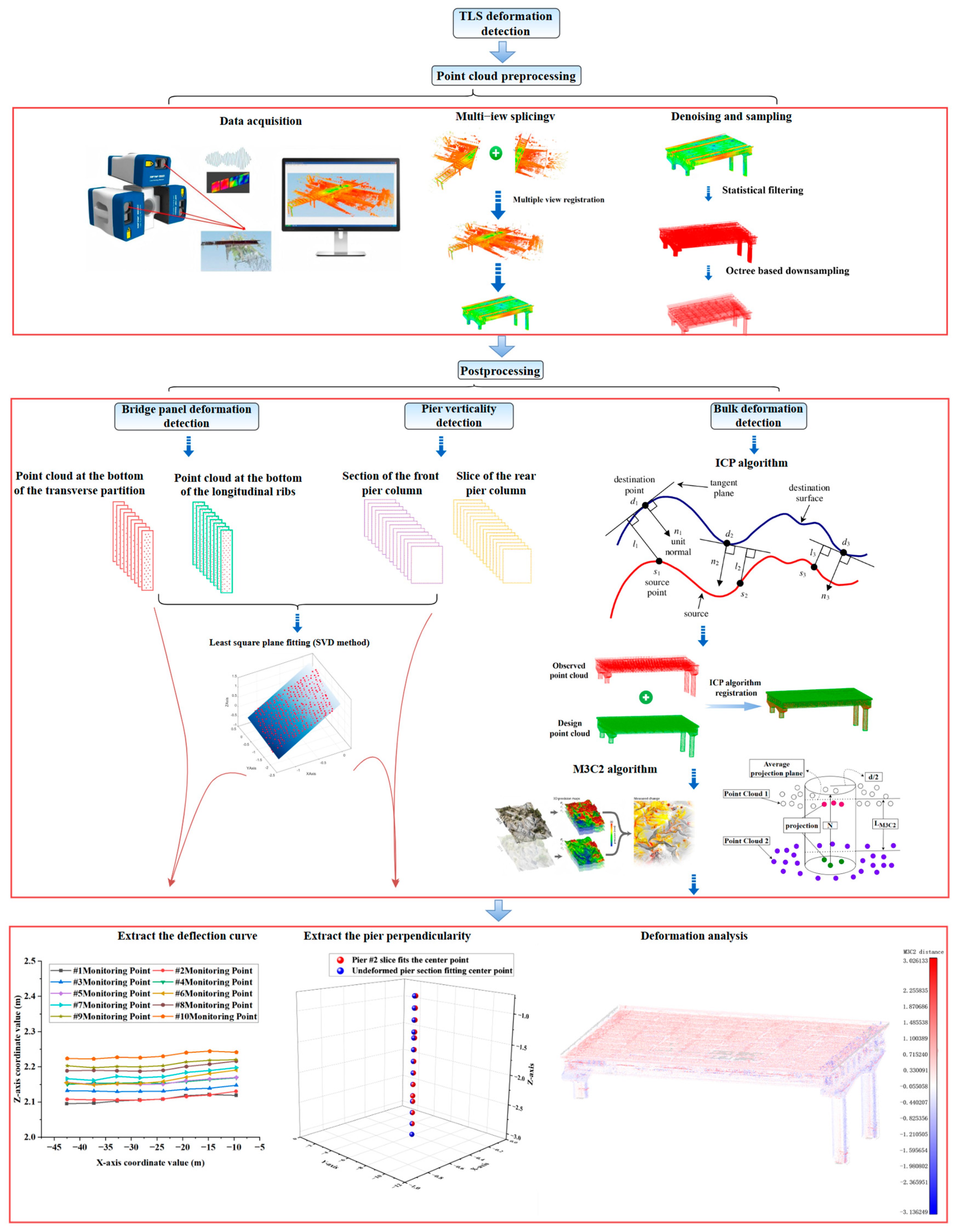
5. Applied Research on Bridge Deformation Detection
5.1. Data Collection
5.2. Data Processing
- Point Cloud Denoising: Statistical Outlier Removal (SOR) and Weighted Principal Component Analysis (WPCA) algorithms can be employed to remove unstructured noise caused by environmental interference or equipment errors.
- Point Cloud Simplification: Optimized algorithms based on octree downsampling can be employed to reduce data redundancy while preserving essential features.
- Point Cloud Registration: Enhanced 4PCS or Iterative Closest Point (ICP) algorithms can be utilized to align multi-temporal or multi-station point clouds into a unified coordinate system.
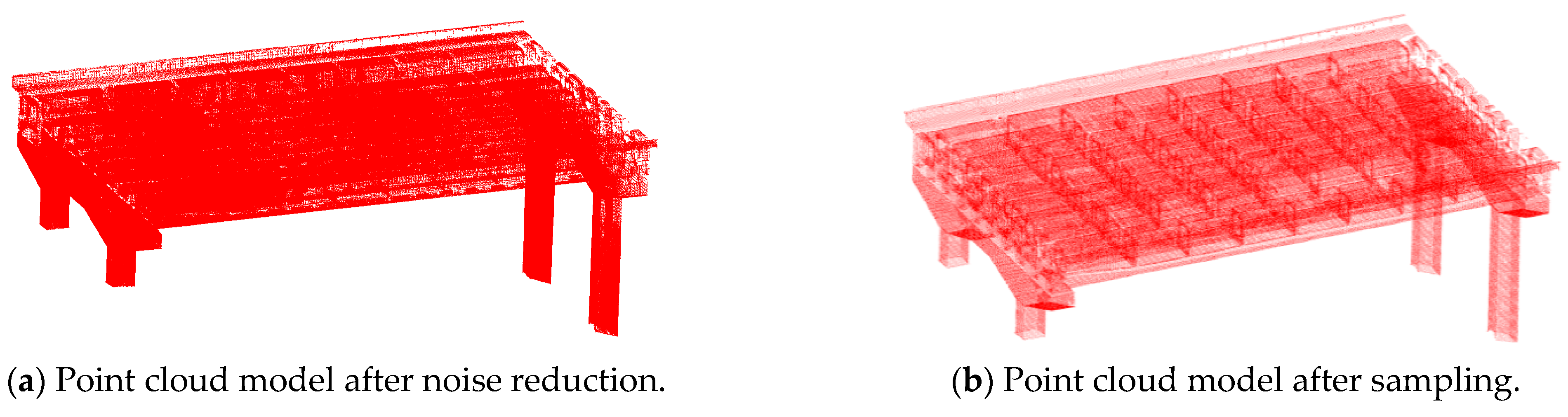
5.2.1. Point Cloud Noise Reduction
5.2.2. Point Cloud Sampling
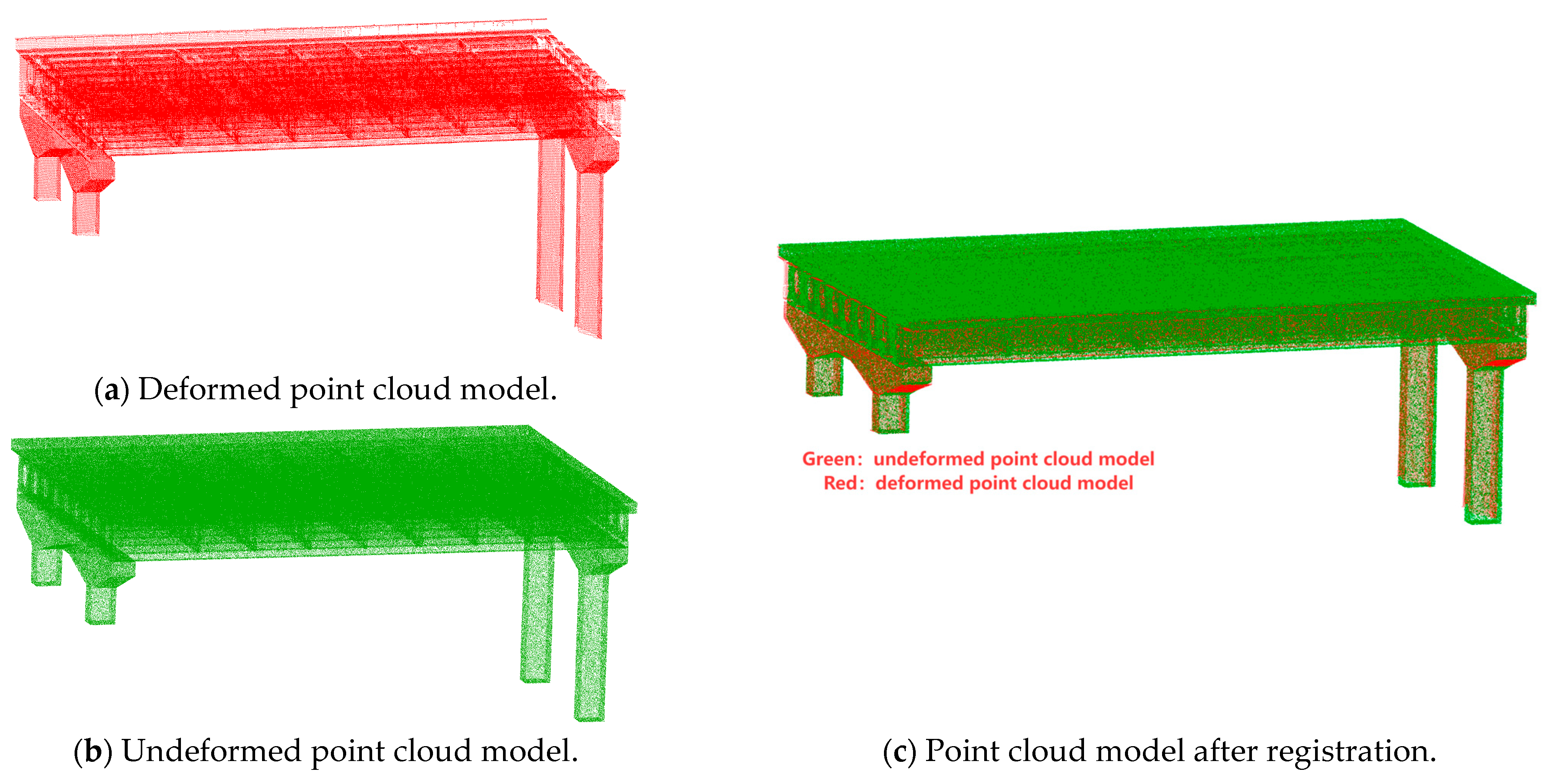
5.2.3. Point Cloud Registration
5.3. Overall Deformation Detection of Bridges
5.4. Bridge Deck Deflection Monitoring
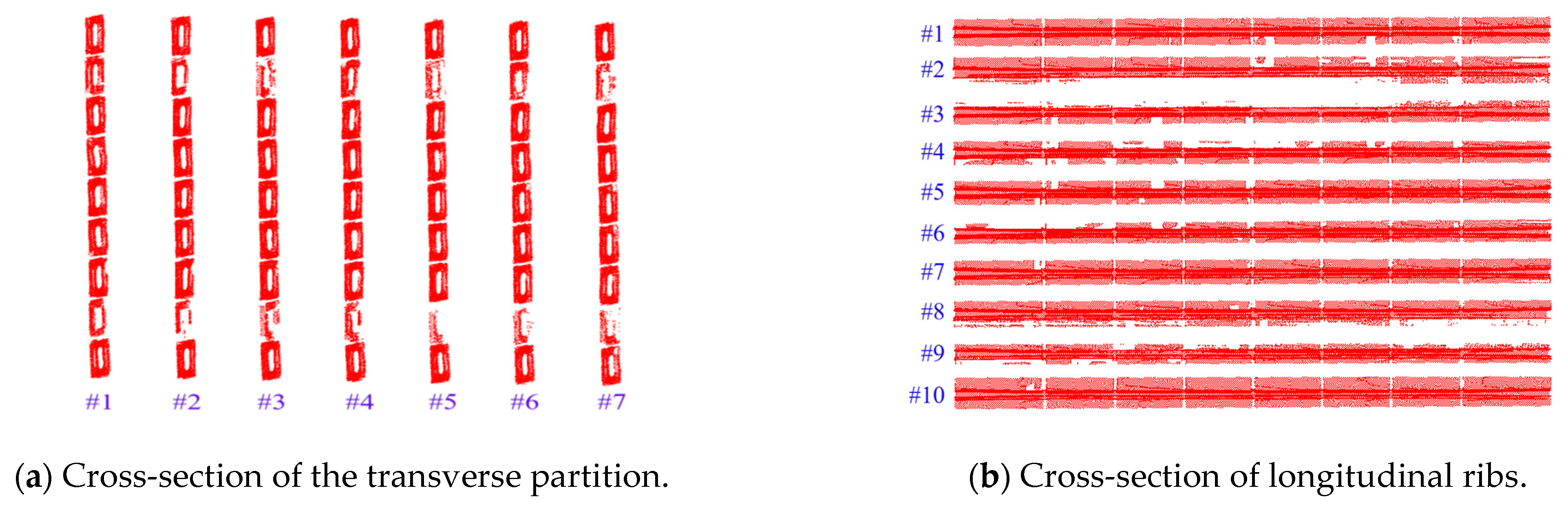
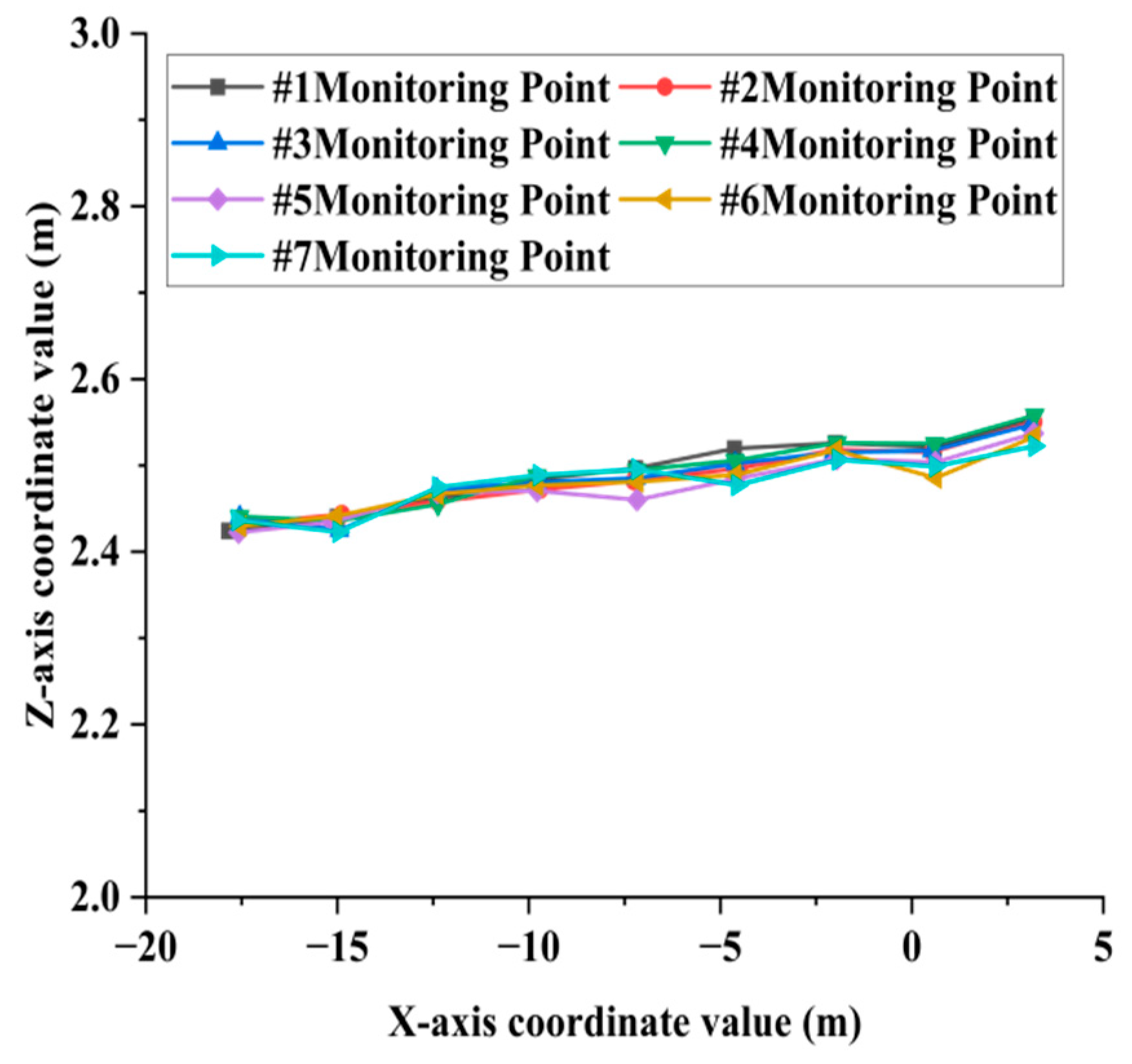
- Diaphragm Deflection Curve Extraction: Seven diaphragm cross-sections were selected, and nine monitoring points were extracted from the bottom point cloud of each diaphragm. The variation in vertical displacement (Z-direction) at the monitoring points within the X-Z plane was analyzed. The cross-sectional schematic diagram of the transverse partition is shown in Figure 9a, the cross-sections of each selected transverse partition are shown in Figure 10a, and the point cloud at the bottom of the transverse partition is shown in Figure 11a.
- Longitudinal Rib Deflection Curve Extraction: Ten longitudinal rib cross-sections were selected, and eight monitoring points were extracted from the bottom point cloud of each rib. The variation in vertical displacement (Z-direction) of the monitoring points in the Y-Z plane was analyzed. The schematic diagram of the longitudinal rib section is shown in Figure 9a, the selected longitudinal rib sections are shown in Figure 10a, and the point cloud at the bottom of the longitudinal ribs is shown in Figure 11a.
Analysis of Bridge Deck Deflection Monitoring Results
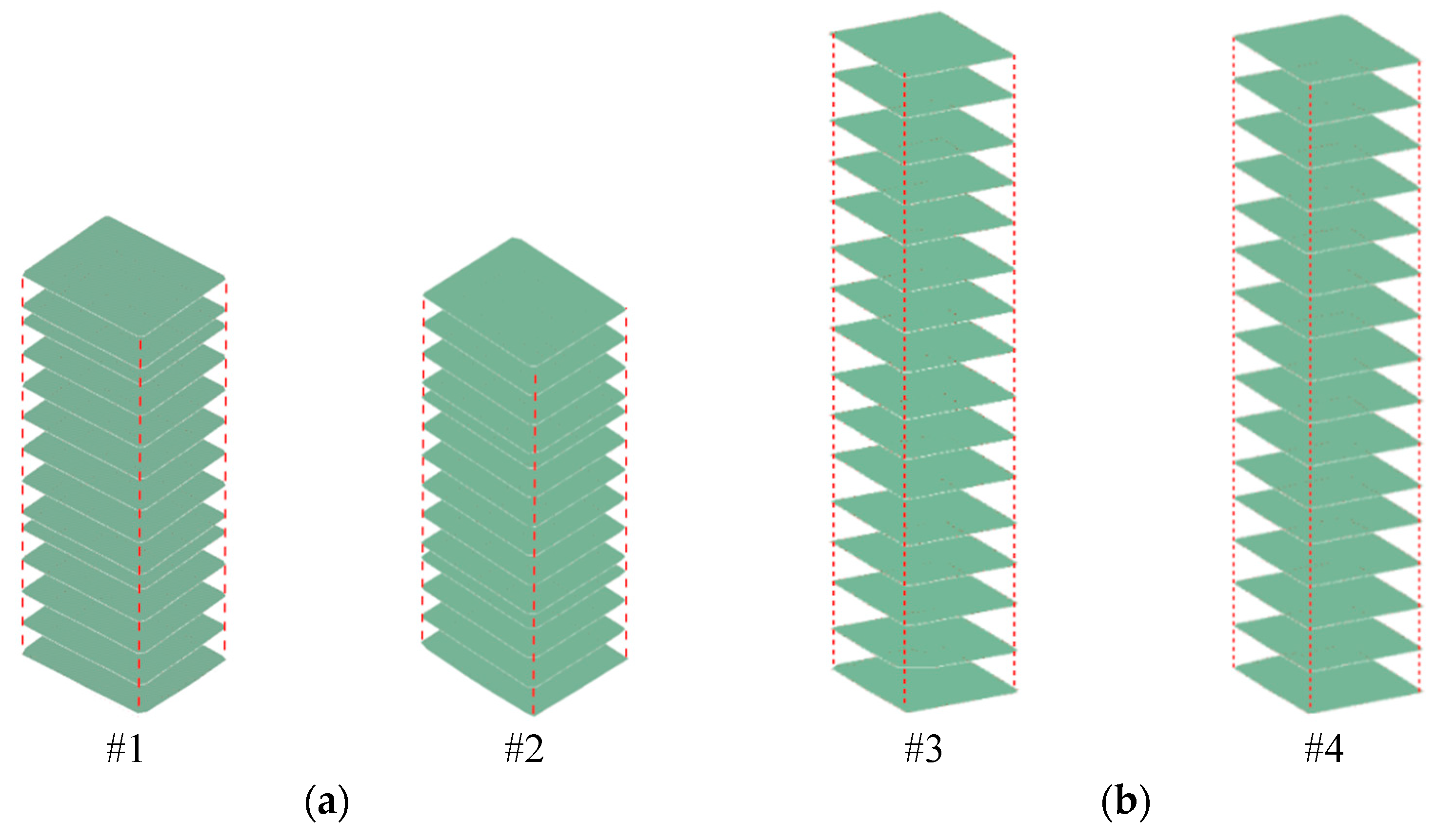
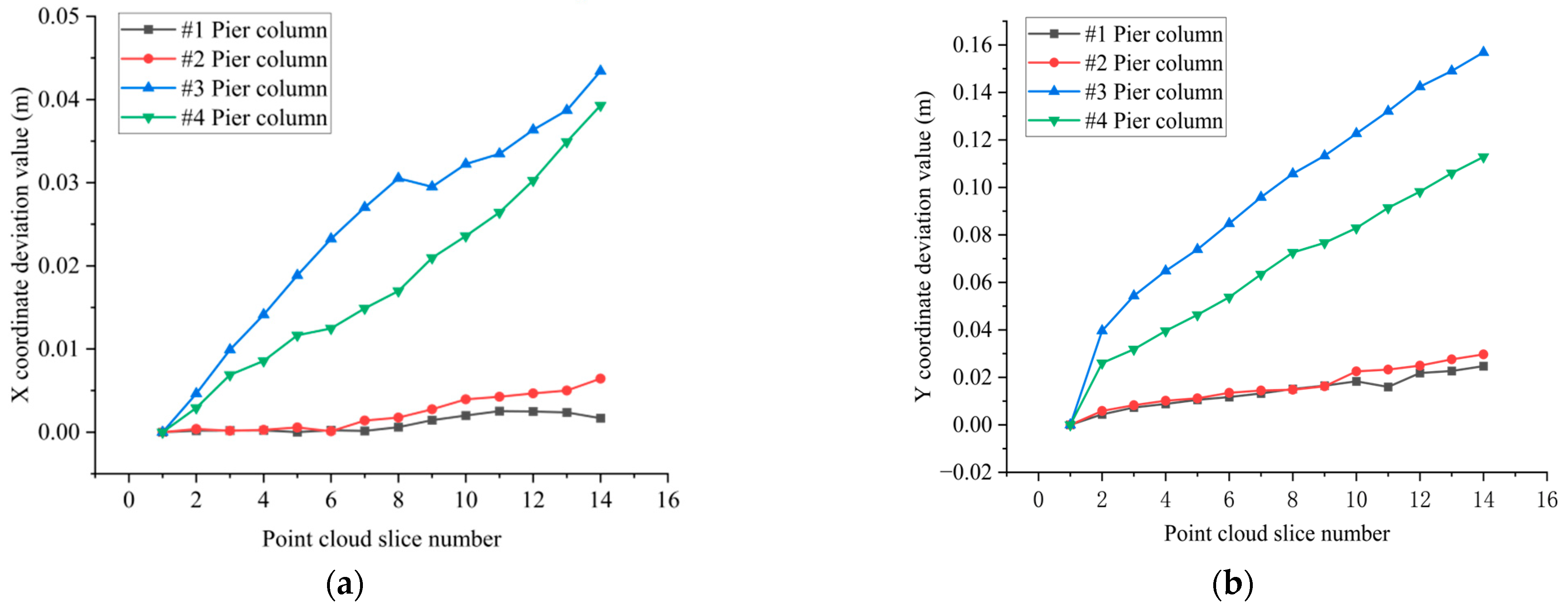
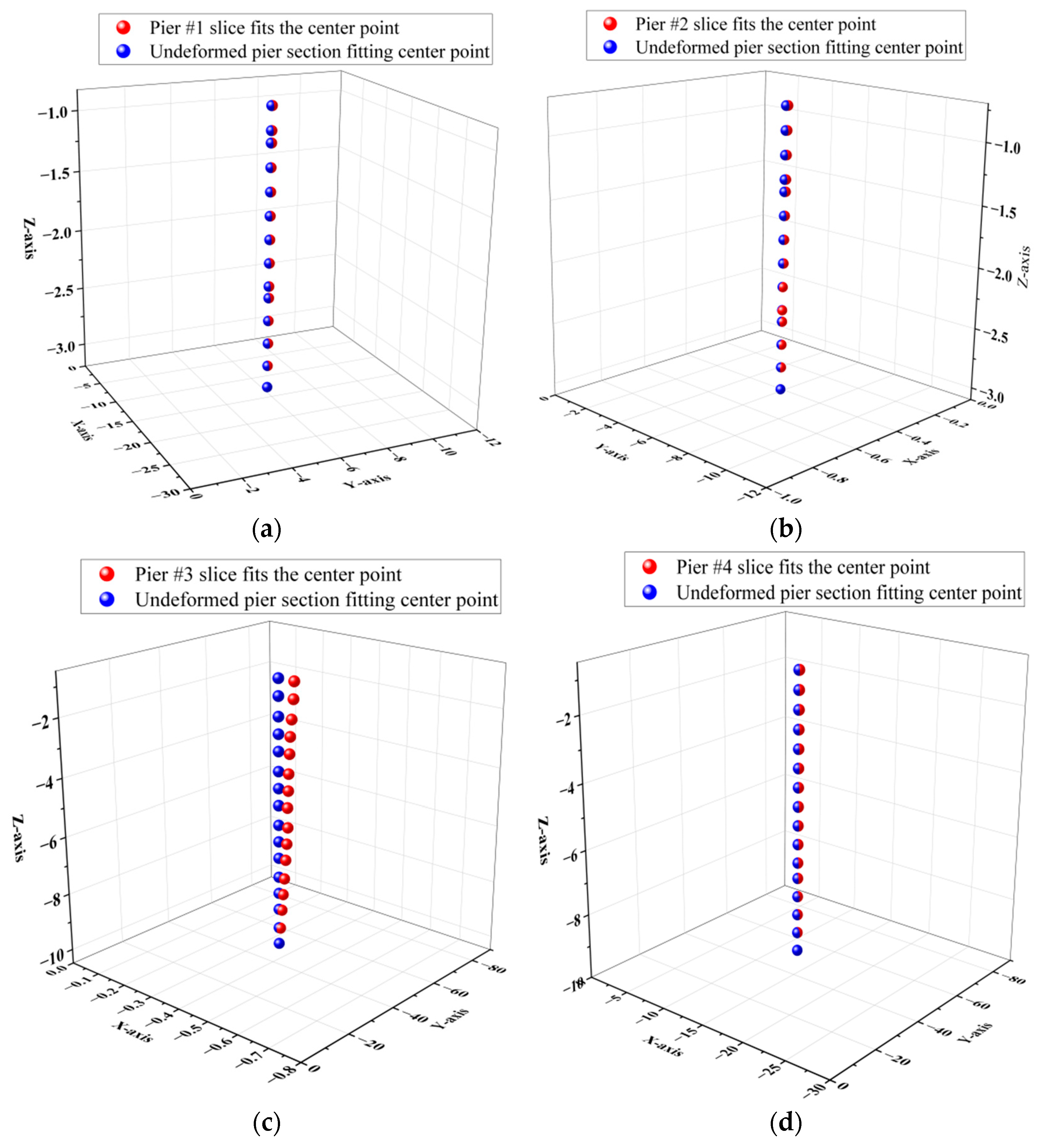
5.5. Bridge Pier Verticality Monitoring Based on Point Cloud Continuous Slice Extraction Technology
Analysis of the Verticality Detection Results of Pier Columns
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, D.A.; Zhu, G.; Lu, L.; Liao, L. Whole object deformation monitoring based on 3D laser scanning technology. Bull. Surv. Mapp. 2005, 7, 40–42. [Google Scholar]
- Fekete, S.; Diederichs, M.; Lato, M. Geotechnical and operational applications for 3-dimensional laser scanning in drill and blast tunnels. Tunn. Undergr. Space Technol. 2010, 25, 614–628. [Google Scholar] [CrossRef]
- Lovse, J.W.; Teskey, W.F.; Lachapelle, G.; Cannon, M.E. Dynamic deformation monitoring of tall structure using GPS technology. J. Surv. Eng. 1995, 121, 35–40. [Google Scholar] [CrossRef]
- Nickitopoulou, A.; Protopsalti, K.; Stiros, S. Monitoring dynamic and quasi-static deformations of large flexible engineering structures with GPS: Accuracy, limitations and promises. Eng. Struct. 2006, 28, 1471–1482. [Google Scholar] [CrossRef]
- Casciati, F.; Fuggini, C. Engineering vibration monitoring by GPS: Long duration records. Earthq. Eng. Eng. Vib. 2009, 8, 459–467. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation global navigation satellite systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 8328. [Google Scholar] [CrossRef]
- Park, H.S.; Lee, H.M.; Adeli, H.; Lee, I. A new approach for health monitoring of structures: Terrestrial laser scanning. Comput.-Aided Civ. Infrastruct. Eng. 2007, 22, 19–30. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Y. Research on 3D finite element simulation model of aluminium beam with lamination defects based on 2D Fourier transform. Int. J. Crit. Infrastruct. 2022, 18, 1–13. [Google Scholar] [CrossRef]
- Dai, K.; Li, A.; Zhang, H.; Chen, S.-E.; Pan, Y. Surface damage quantification of postearthquake building based on terrestrial laser scan data. Struct. Control. Health Monit. 2018, 25, e2210. [Google Scholar] [CrossRef]
- Jaafar, H.A.; Meng, X.; Sowter, A.; Bryan, P. New approach for monitoring historic and heritage buildings: Using terrestrial laser scanning and generalised Procrustes analysis. Struct. Control. Health Monit. 2017, 24, e1987. [Google Scholar] [CrossRef]
- Law, D.W.; Silcock, D.; Holden, L. Terrestrial laser scanner assessment of deteriorating concrete structures. Struct. Control Health Monit. 2018, 25, e2156. [Google Scholar] [CrossRef]
- Xiong, W.; Shi, Y.; Ding, X.D. Identification and analysis of geometric shape change trends of bridges based on point cloud model. Bridge Constr. 2018, 48, 35–40. [Google Scholar]
- Songlin, H.; Zhixiang, Z.; Xi, C.; Ju, X.; Xu, H. Bridge deck deformation analysis based on vehicle borne three-dimensional laser scanning results. Sci. Technol. Eng. 2019, 19, 268–276. [Google Scholar]
- Xiang, X.J.; Hou, X.; Zhou, Z.X.; Chu, X.; Jiang, T.J. The 3D laser scanning results of long-span bridge deformation are compared with the finite element simulation. Highw. Eng. 2019, 44, 103–108, 155. [Google Scholar]
- Lubowiecka, I.; Armesto, J.; Arias, P.; Lorenzo, H. Historic bridge modelling using laser scanning, ground penetrating radar and finite element methods in the context of structural dynamics. Eng. Struct. 2009, 31, 2667–2676. [Google Scholar] [CrossRef]
- Sedek, M.; Serwa, A. Development of new system for detection of bridges construction defects using terrestrial laser remote sensing technology. Egypt. J. Remote Sens. Space Sci. 2016, 19, 273–283. [Google Scholar] [CrossRef][Green Version]
- Xu, X.; Yang, H.; Neumann, I. Monotonic loads experiment for investigation of composite structure based on terrestrial laser scanner measurement. Compos. Struct. 2018, 183, 563–567. [Google Scholar] [CrossRef]
- Xu, X.; Yang, H.; Neumann, I. Deformation monitoring of typical composite structures based on terrestrial laser scanning technology. Compos. Struct. 2018, 202, 77–81. [Google Scholar] [CrossRef]
- Yang, H.; Xu, X.; Neumann, I. Deformation behavior analysis of composite structures under monotonic loads based on terrestrial laser scanning technology. Compos. Struct. 2018, 183, 594–599. [Google Scholar] [CrossRef]
- Deng, Y.; Jia, Y.; Li, Y.; Li, A. Structural parameter identification of ancient stone arch bridge via three-dimensional laser ranger scanning. J. Perform. Constr. Facil. 2022, 36, 04022041. [Google Scholar] [CrossRef]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-points congruent sets for robust pairwise surface registration. ACM Trans. Graph. 2008, 27, 1–10. [Google Scholar] [CrossRef]
- Theiler, P.W.; Wegner, J.D.; Schindler, K. Keypoint-based 4-points congruent sets–automated marker-less registration of laser scans. ISPRS J. Photogramm. Remote Sens. 2014, 96, 149–163. [Google Scholar] [CrossRef]
- Theiler, P.W.; Wegner, J.D.; Schindler, K. Markerless point cloud registration with keypoint-based 4-points congruent sets. ISPRS Annals of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2013, 2, 283–288. [Google Scholar]
- Chetverikov, D.; Svirko, D.; Stepanov, D.; Krsek, P. The trimmed iterative closest point algorithm. In Proceedings of the 2002 International Conference on Pattern Recognition, Quebec City, QC, Canada, 11–15 August 2002; IEEE: New York, NY, USA, 2002; Volume 3, pp. 545–548. [Google Scholar]
- Narváez, E.A.L.; Narváez, N.E.L. Point cloud denoising using robust principal component analysis. In Proceedings of the International Conference on Computer Graphics Theory and Applications, Setúbal, Portugal, 25–28 February 2006; SciTePress: Setúbal, Portugal, 2006; Volume 2, pp. 51–58. [Google Scholar]
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Dolha, M.; Beetz, M. Towards 3D point cloud based object maps for household environments. Robot. Auton. Syst. 2008, 56, 927–941. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, X.; Wang, C.; Yang, B. Non-iterative denoising algorithm based on a dual threshold for a 3D point cloud. Opt. Lasers Eng. 2020, 126, 105921. [Google Scholar] [CrossRef]
- Weir, D.J.; Milroy, M.J.; Bradley, C.; Vickers, G.W. Reverse engineering physical models employing wrap-around B-spline surfaces and quadrics. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 1996, 210, 147–157. [Google Scholar] [CrossRef]
- Sun, W.; Bradley, C.; Zhang, Y.; Loh, H. Cloud data modelling employing a unified, non-redundant triangular mesh. Comput.-Aided Des. 2001, 33, 183–193. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, C.H.; Levin, D. Surface simplification using a discrete curvature norm. Comput. Graph. 2002, 26, 657–663. [Google Scholar] [CrossRef]
- Qi, J.; Hu, W.; Guo, Z. Feature preserving and uniformity-controllable point cloud simplification on graph. In Proceedings of the 2019 IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 8–12 July 2019; IEEE: New York, NY, USA, 2019; pp. 284–289. [Google Scholar]
- Schürch PDensmore, A.L.; Rosser, N.J.; Lim, M.; McArdell, B.W. Detection of surface change in complex topography using terrestrial laser scanning: Application to the llgrabendebris-flow channel. Farth Surf. Process. Land Forms 2011, 36, 1847–1859. [Google Scholar] [CrossRef]
- Riouelme, A.; Soldato, M.; Tomás, R.; Cano, M.; Bordehore, L.J.; Moretti, S. Digital land form reconstruction using old and recent open access digital aerial photos. Geomorphology 2019, 329, 206–223. [Google Scholar] [CrossRef]
- Olsen, M.J.; Kuester, F.; Chang, B.J.; Hutchinson, T.C. Terrestrial laser scanning-based structural damage assessment. J. Comput. Civ. Eng. 2010, 24, 264–272. [Google Scholar] [CrossRef]
- Kanzhdan, M.; Hoppe, H. Sereened Poisson surfacere construction. ACM Trans. Graph. 2013, 32, 1–13. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial lasers canner:application to the Rangitikei canyon(N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Cook Kristen, L. An evaluation of the effectiveness of low-cost UAVs and structure from motion for geomorphic change detection. Geomorphology 2017, 278, 195–208. [Google Scholar] [CrossRef]
- Hout, R.; Maleval, V.; Mahe, G.; Rouvellac, E.; Crouzevialle, R.; Cerbelaud, F. UAV and LiDAR data in the service of bank gully erosion measurement in rambla de Algeciras lakeshore. Water 2020, 12, 2748. [Google Scholar] [CrossRef]
- Costantino, D.; Settembrini, F.; Pepe, M.; Alfio, V.S. Develop of new tools for 4D monitoring: Case study ofcliff in Apulia region (Italy). Remote Sens. 2021, 13, 1857. [Google Scholar] [CrossRef]
- Lichti, D.D.; Gordon, S.J.; Stewart, M.P.; Franke, J.; Tsakiri, M. Comparison of digital photogrammetry and laser scanning. In Proceedings of the International Society for Photogrammetr and Remote Sensing, Denver, CO, USA, 10–15 November 2002; pp. 39–44. [Google Scholar]
- Zogg, H.M.; Ingensand, H. Terrestrial laser scanning for deformation monitoring: Load tests on the Felsenau Viaduct (CH). International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2008, 37, 555–562. [Google Scholar]
- Lidu, Z.; Zhongfu, X.; Yin, Z.; Xiaping, M.; Shuangcheng, Z.; Mengyuan, S.; Maolin, C.; Chuan, H.; Jianping, P. Analysis of bridge deflection deformation based on ground three-dimensional laser scanning. Bull. Surv. Mapp. 2022, 5, 95. [Google Scholar]
- Xiaolong, D.; Shizhu, T. Bridge deformation detection and data processing based on 3D laser scanning. Laser Optoelectron. Prog. 2018, 55, 071201–071206. [Google Scholar] [CrossRef]
- Xu, J.J.; Wang, H.C.; Luo, Y.Z.; Wang, S.Q.; Yan, X.Q. Deformation monitoring and data processing of landslide based on 3D laser scanning. Rock Soil Mech. 2010, 31, 2188–2191. [Google Scholar]
- Buckley, S.J.; Howell, J.A.; Enge, H.D.; Kurz, T.H. Terrestrial laser scanning in geology: Data acquisition, processing and accuracy considerations. J. Geol. Soc. 2008, 165, 625–638. [Google Scholar] [CrossRef]
- Zhao, Q.; Gao, X.; Li, J.; Luo, L.; Liguori, R. Optimization algorithm for point cloud quality enhancement based on statistical filtering. J. Sens. 2021, 2021, 7325600. [Google Scholar] [CrossRef]
- Yang, Y.; Fan, D.; Du, S.; Wang, M.; Chen, B.; Gao, Y. Point setregistration with similarity and affine transformations based on bidirectional KMPE loss. IEEE Trans. Cybern. 2021, 51, 1678–1689. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Liu, X.; Zhang, X.; Wang, M.; Zhao, L. Building extraction from terrestrial laser scanning data with density of projected points on polar grid and adaptive threshold. Remote Sens. 2021, 13, 4392. [Google Scholar] [CrossRef]
- Rychkov, I.; Brasington, J.; Vericat, D. Computational and methodological aspects of terrestrial surface analysis based on point clouds. Comput. Geosci. 2012, 42, 64–70. [Google Scholar] [CrossRef]
- Piotr, O.; Owerko, T. Novel approach to inspections of as-built reinforcement in incrementally launched bridges by means of computer vision-based point cloud data. IEEE Sens. J. 2020, 21, 11822–11833. [Google Scholar]





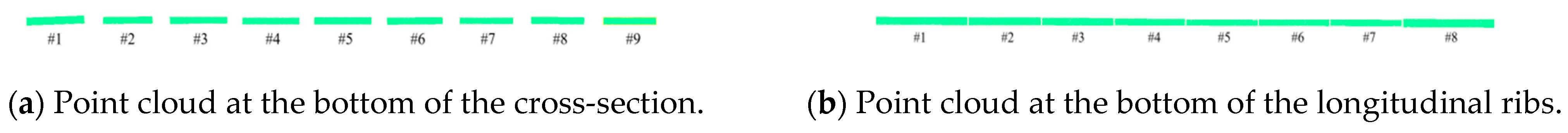



| Scanning Range | 0.5–130 m |
|---|---|
| Scanning rate | Up to 2,000,000 points per second |
| Field-of-view angle | Level: 360° Vertical: 300° |
| Resolution | 3 mm@10 m |
| 6 mm@10 m | |
| 12 mm@10 m | |
| Built-in camera | 36 million pixels |
| Range noise | 0.4 mm@10 m, 0.5 mm@20 m |
| Working temperature | −5–40 °C |
| Pier Column Number | Inclination Angle (°) | Offset (mm) | Verticality |
|---|---|---|---|
| #1 | 0.6103° | 24.8 | 0.010682 |
| #2 | 0.7499° | 30.4 | 0.013078 |
| #3 | 1.1350° | 182.2 | 0.019765 |
| #4 | 0.9050° | 136.6 | 0.015813 |
| Monitoring Location | Error in the X-Direction (mm) | Error in the Y-Direction (mm) | Error in the Z-Direction (mm) |
|---|---|---|---|
| Left bridge deck | ±0.8 | ±0.5 | ±1.2 |
| Right bridge deck | ±0.7 | ±0.4 | ±1.0 |
| Front bridge pier #1 | ±1.0 | ±1.5 | ±0.5 |
| Front bridge pier #2 | ±1.2 | ±1.8 | ±0.6 |
| Rear bridge pier #3 | ±1.5 | ±2.8 | ±0.9 |
| Rear bridge pier #4 | ±1.3 | ±2.5 | ±0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, D.; Li, W.; Tao, Y.; Ji, B. Bridge Deformation Monitoring Combining 3D Laser Scanning with Multi-Scale Algorithms. Sensors 2025, 25, 3869. https://doi.org/10.3390/s25133869
Tan D, Li W, Tao Y, Ji B. Bridge Deformation Monitoring Combining 3D Laser Scanning with Multi-Scale Algorithms. Sensors. 2025; 25(13):3869. https://doi.org/10.3390/s25133869
Chicago/Turabian StyleTan, Dongmei, Wenjie Li, Yu Tao, and Baifeng Ji. 2025. "Bridge Deformation Monitoring Combining 3D Laser Scanning with Multi-Scale Algorithms" Sensors 25, no. 13: 3869. https://doi.org/10.3390/s25133869
APA StyleTan, D., Li, W., Tao, Y., & Ji, B. (2025). Bridge Deformation Monitoring Combining 3D Laser Scanning with Multi-Scale Algorithms. Sensors, 25(13), 3869. https://doi.org/10.3390/s25133869







