Adaptive Model Predictive Control for 4WD-4WS Mobile Robot: A Multivariate Gaussian Mixture Model-Ant Colony Optimization for Robust Trajectory Tracking and Obstacle Avoidance
Abstract
1. Introduction
- Novel Optimization Framework: We introduce the MGMM-, an advanced optimization method that integrates multivariate Gaussian Mixture Models with Continuous Ant Colony Optimization to enhance the search process and to achieve superior performance in complex optimization tasks.
- Benchmark Testing and Comparative Analysis: The proposed MGMM- is rigorously tested using standard benchmark functions and its performance is compared against traditional Ant Colony Optimization (ACO) and Continuous Ant Colony Optimization () algorithms. The results demonstrate significant improvements in terms of convergence speed.
- MPC Weighting Matrix Optimization: We apply MGMM- to optimize the weighting matrices of MPC, enabling a more effective balance between path tracking accuracy and computational efficiency.
- Evaluation in Diverse Scenarios: The optimized MPC is evaluated in various scenarios, including path tracking and dynamic obstacle avoidance. The results highlight the effectiveness of the proposed method, ensuring smooth and safe trajectories.
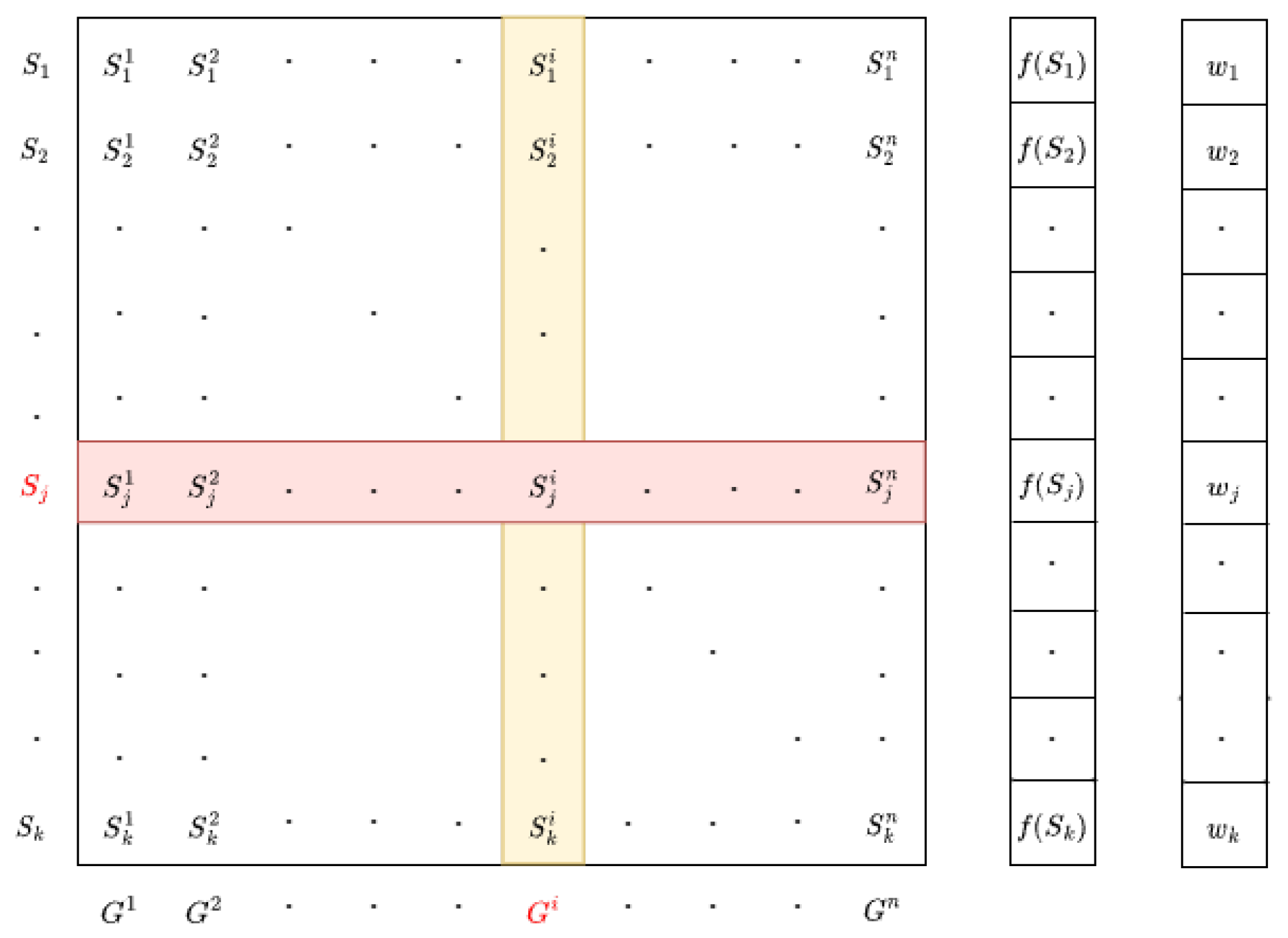
2. Classical ACOR Algorithm
- k: Represents the size of the solution archive, indicating the number of elite solutions retained at each iteration. It also determines the breadth of the weight distribution.
- q: Denotes the selection pressure parameter, which controls the rate at which weights decay with increasing solution rank, thus balancing exploration and exploitation.
- qk: Defines the standard deviation of the Gaussian function employed to assign weights.
3. The Proposed Multivariate GMM-ACOR Algorithm
3.1. Representation of Solutions
- : The mean vector of the k-th Gaussian component (cluster center).
- : The covariance matrix of the k-th Gaussian component, capturing the relationships between variables.
- : The weight (or mixture coefficient) of the k-th Gaussian component, representing the proportion of solutions in the k-th cluster.
- x is the solution vector.
- n is the dimensionality of the solution space (i.e., the number of variables).
- is the determinant of the covariance matrix.
- is the inverse of the covariance matrix.
3.2. Ant-Based Solution Construction
3.3. Update Mechanism
| Algorithm 1 MGMM- Algorithm Pseudo-Code |
|
3.4. Performance Evaluation
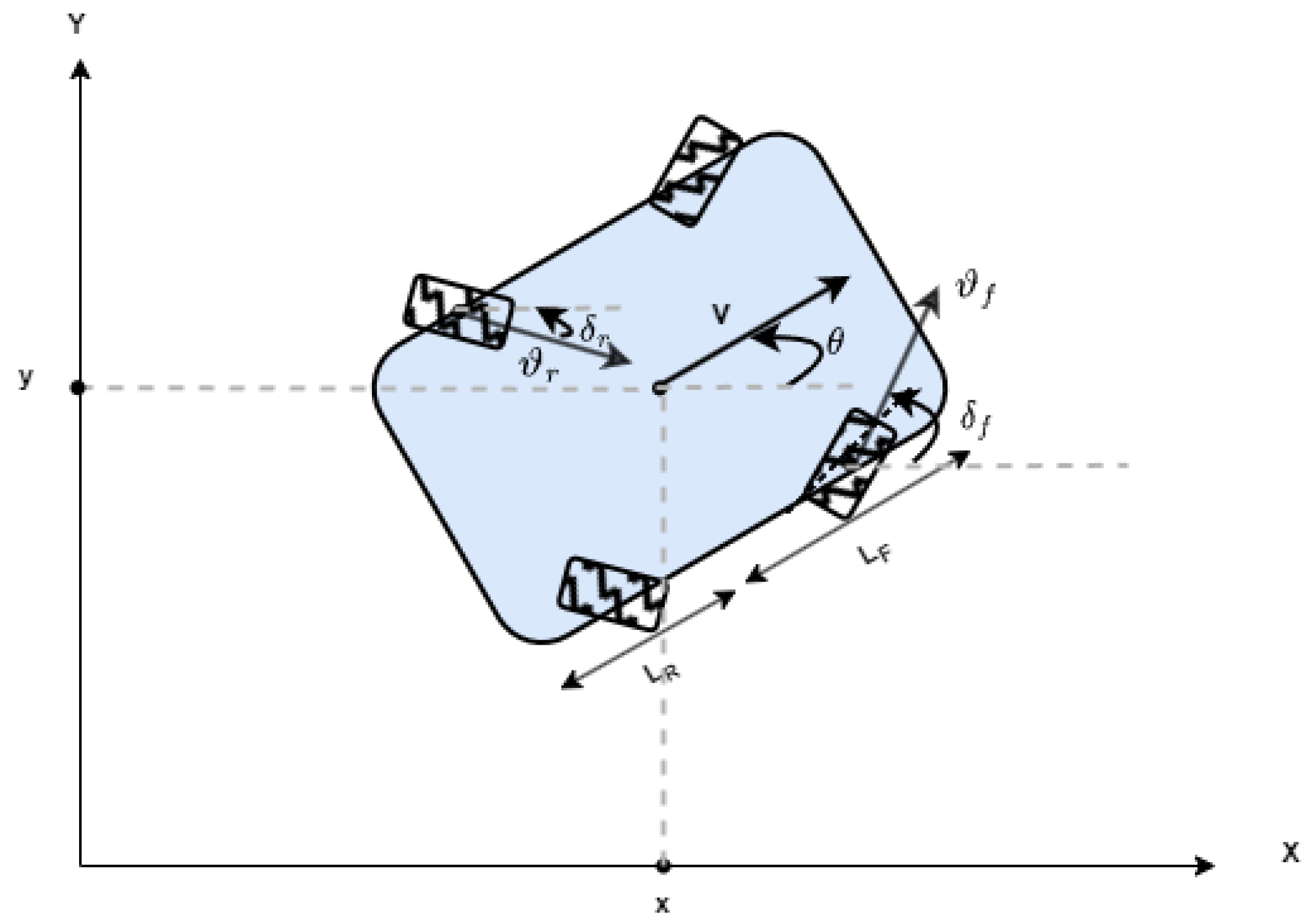
4. An NMPC Controller Implemented for a 4WD/4WS Robot
4.1. Formulation of Trajectory Tracking Using an MPC Controller
4.2. Trajectory Tracking with Obstacle Avoidance
4.3. Casadi Framework
5. Adaptative NMPC Controller Using MGMM-ACOR Algorithm
6. Simulation Results and Comparison
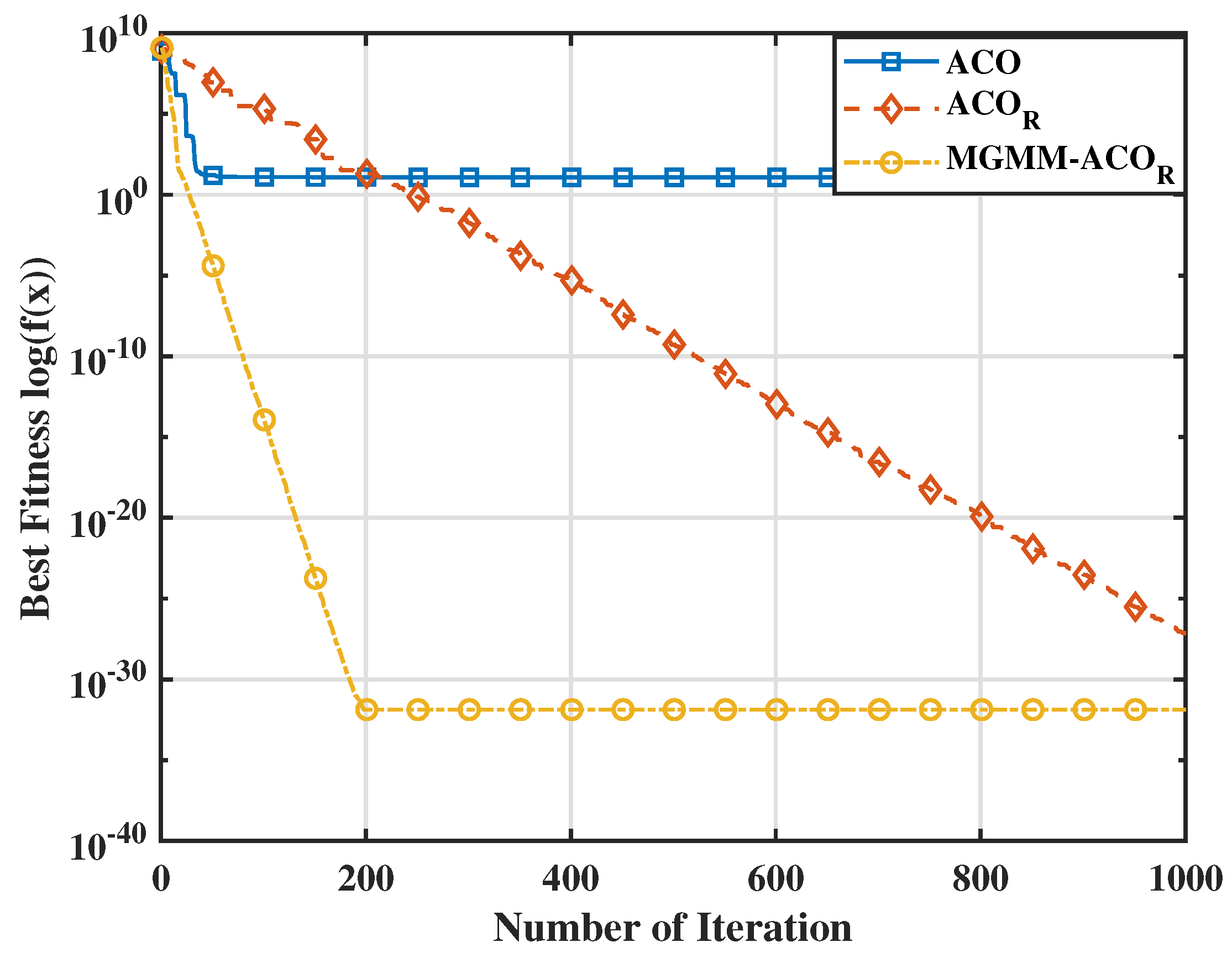
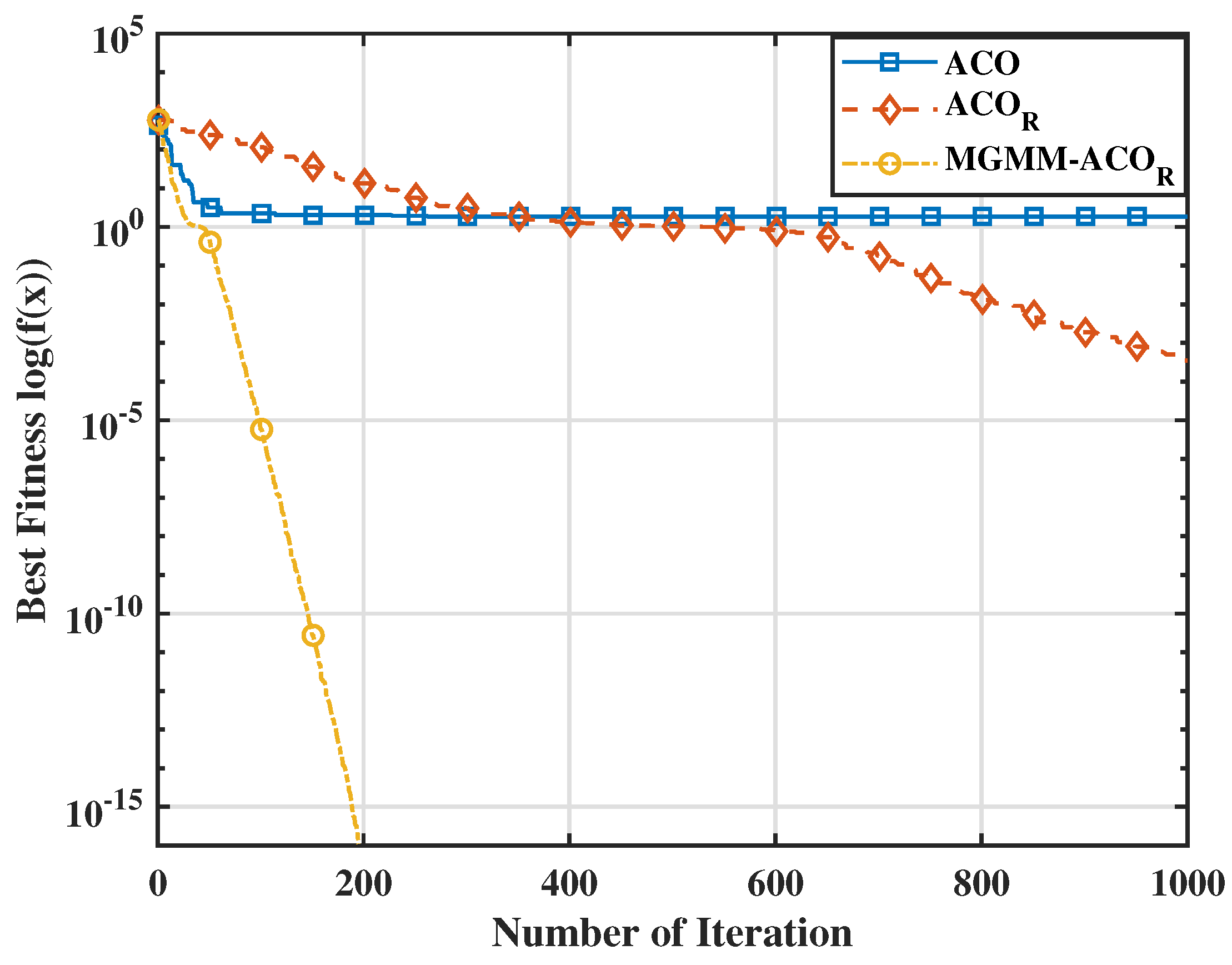
6.1. Benchmarking Evaluation
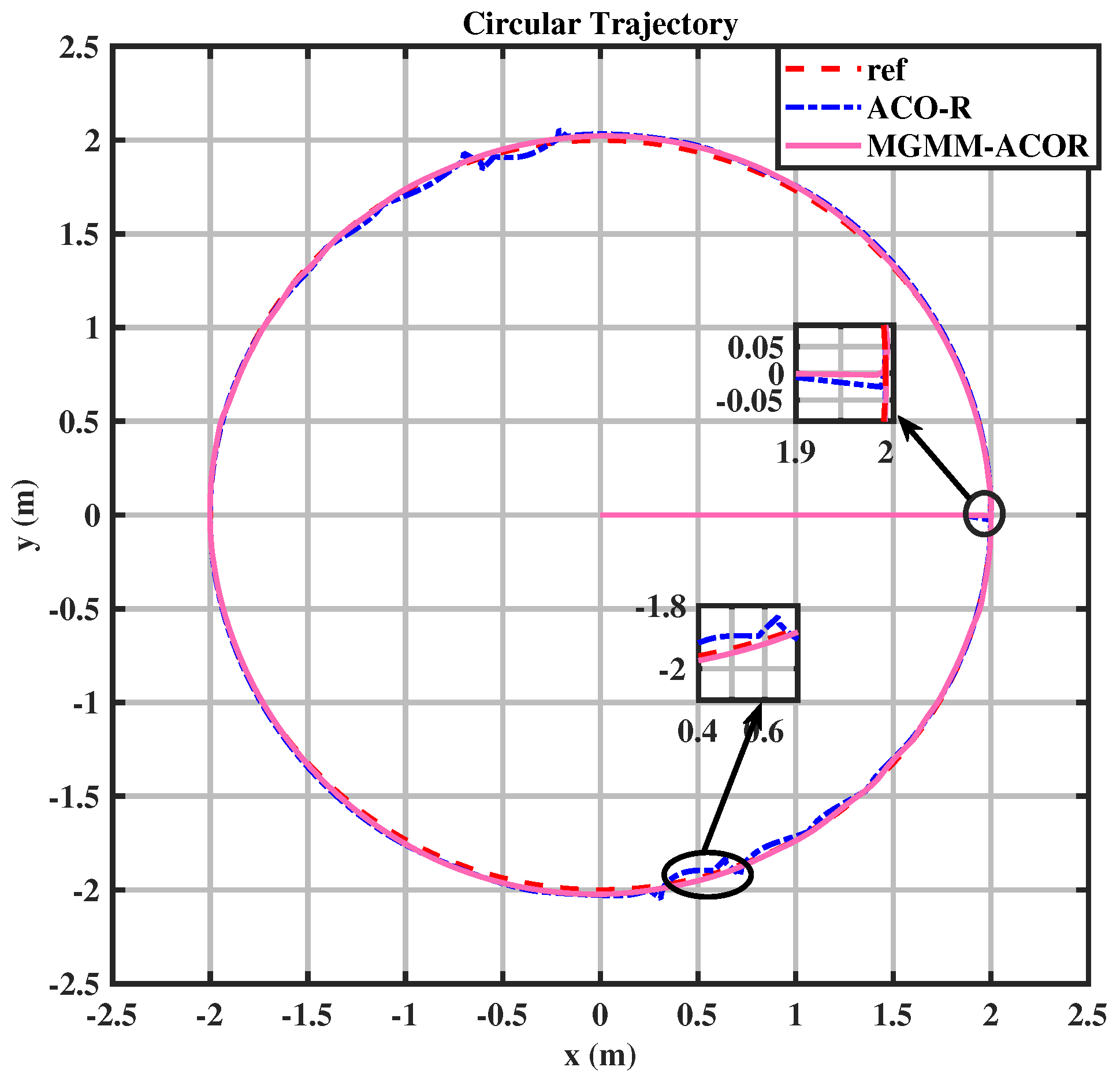
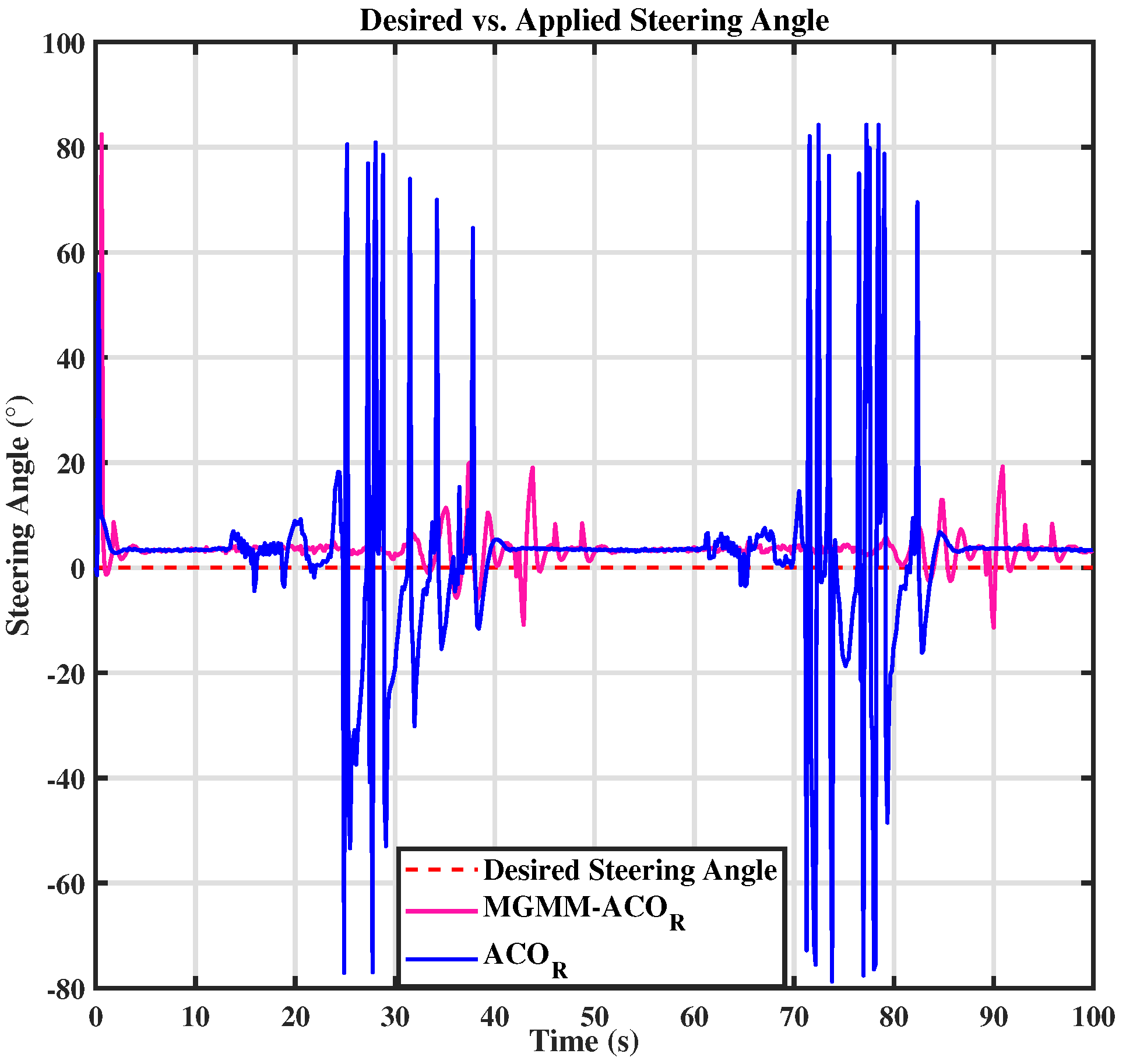
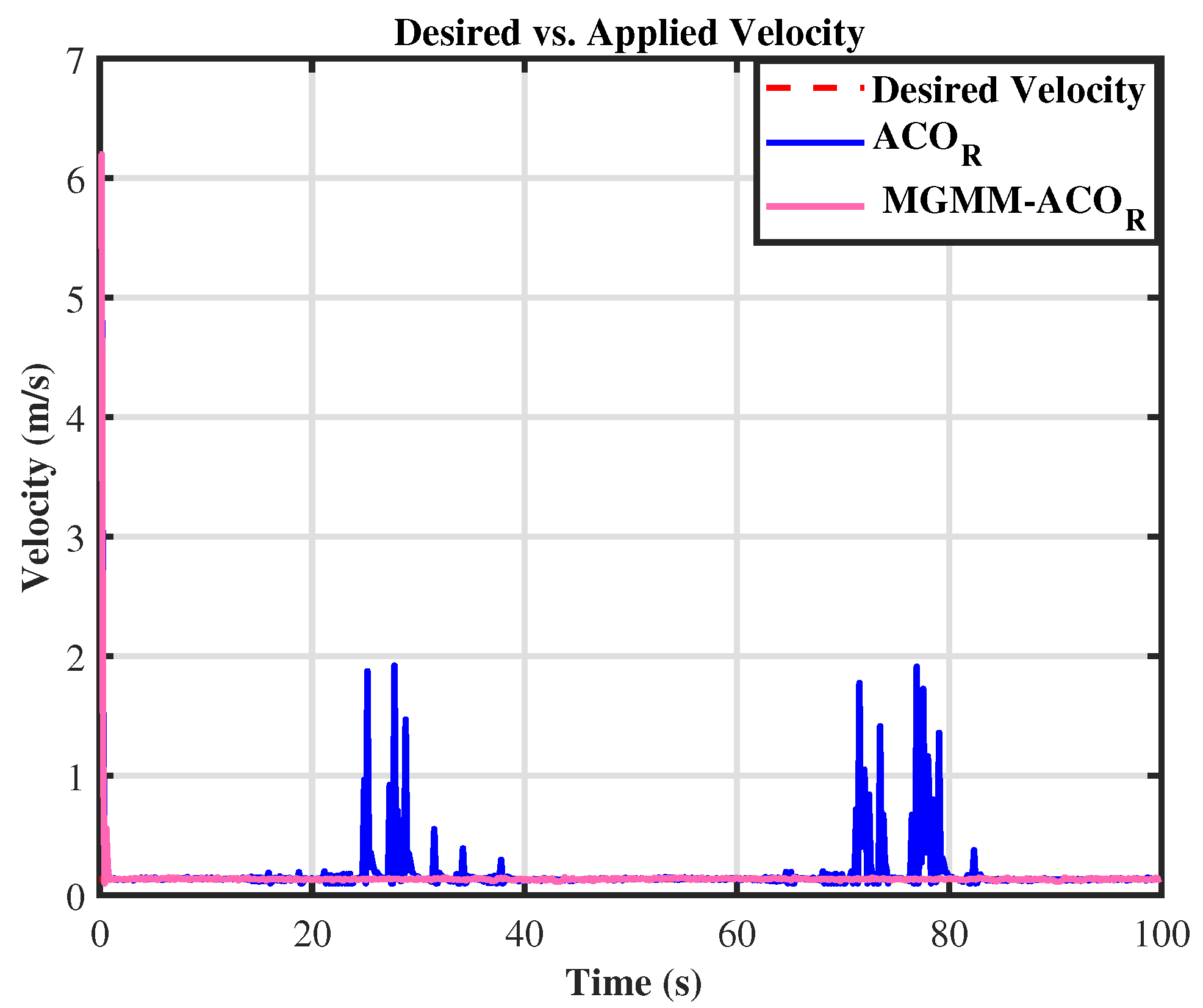
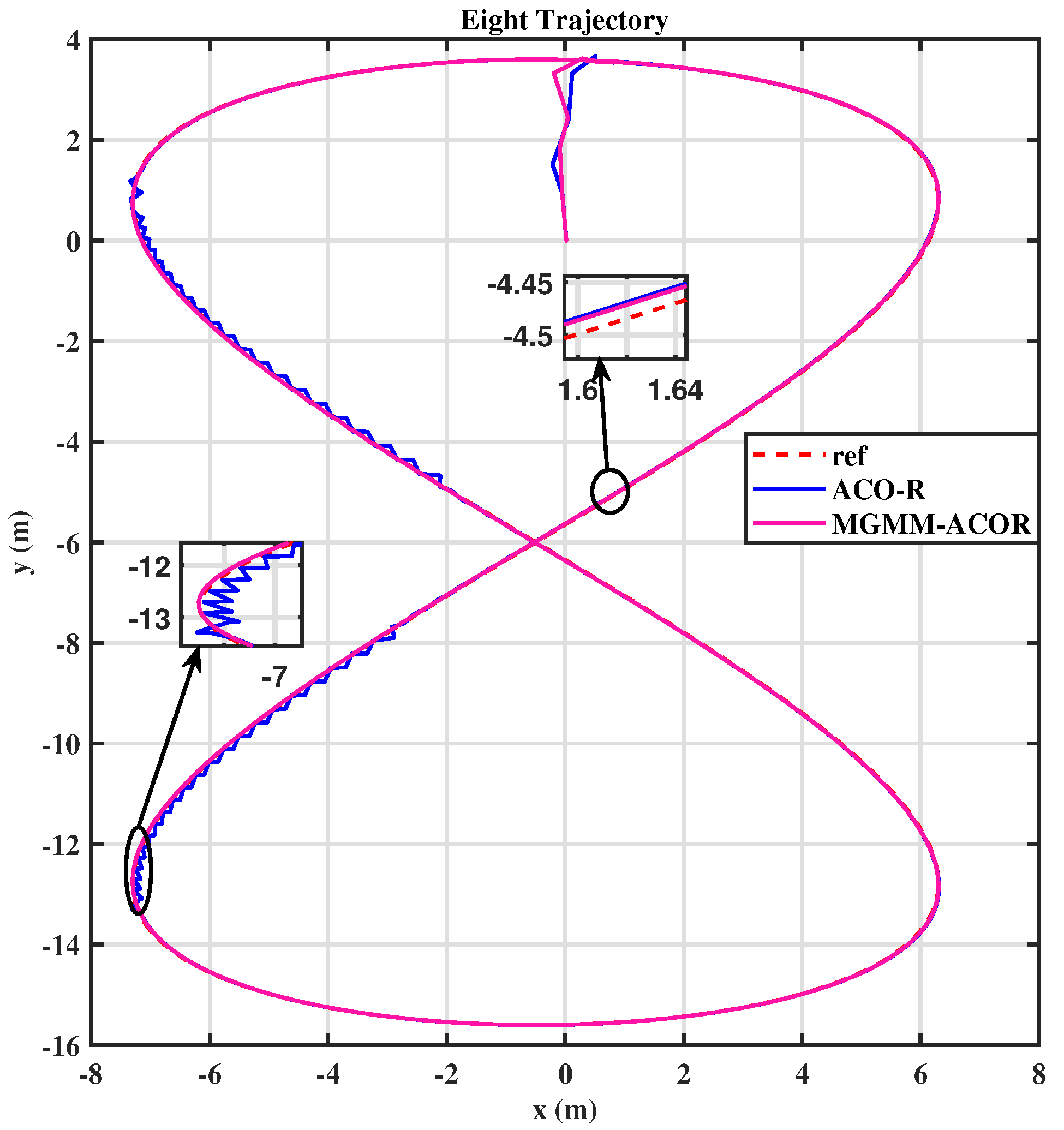
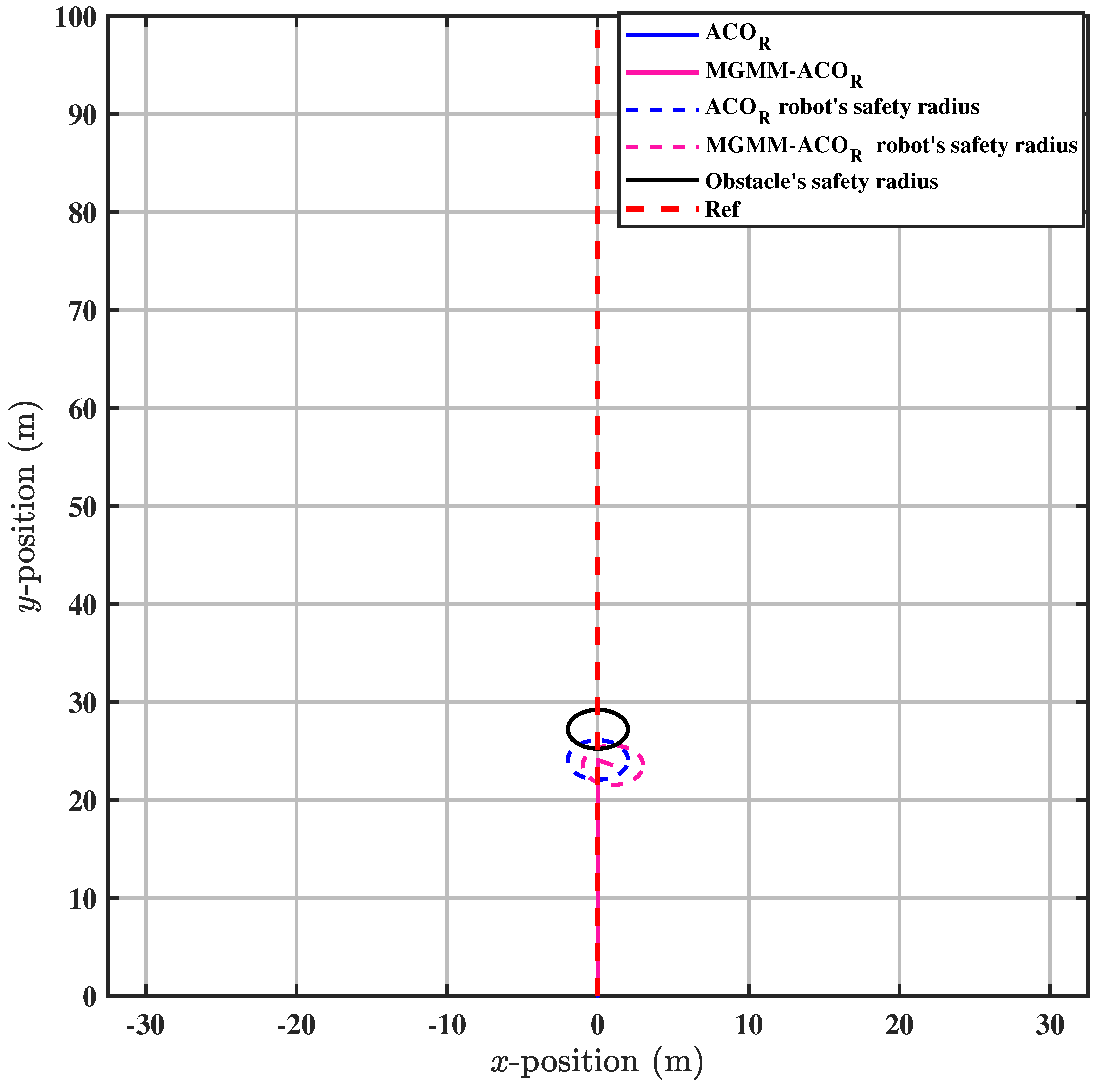
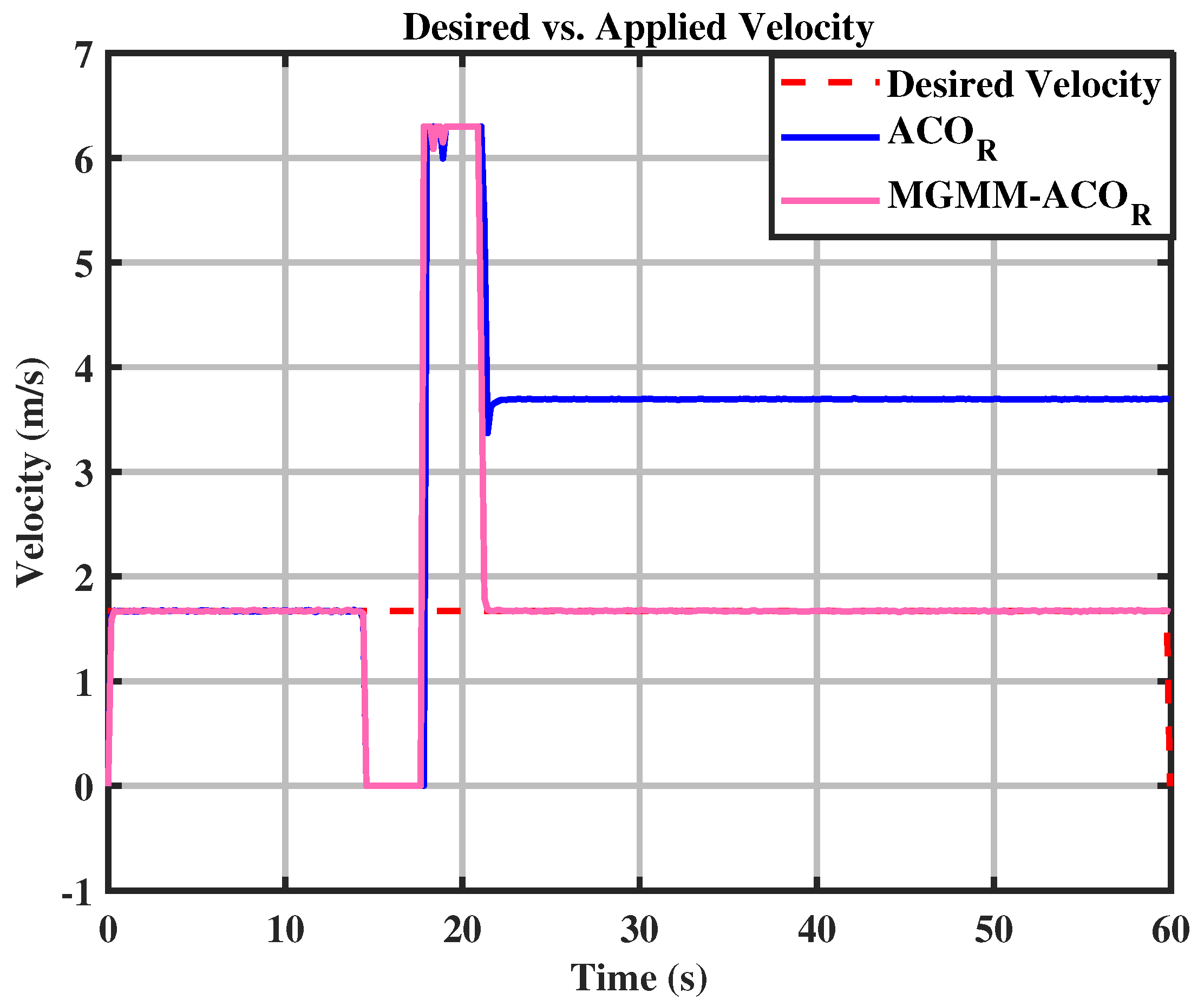
6.2. Trajectory Tracking and Dynamic Obstacle Avoidance
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paz-Delgado, G.J.; Sánchez-Ibáñez, J.R.; Domínguez, R.; Pérez-Del-Pulgar, C.J.; Kirchner, F.; García-Cerezo, A. Combined Path and Motion Planning for Workspace Restricted Mobile Manipulators in Planetary Exploration. IEEE Access 2023, 11, 78152–78169. [Google Scholar] [CrossRef]
- Li, M.; Wu, F.; Wang, F.; Zou, T.; Li, M.; Xiao, X. CNN-MLP-Based Configurable Robotic Arm for Smart Agriculture. Agriculture 2024, 14, 1624. [Google Scholar] [CrossRef]
- Morsi, N.M.; Mata, M.; Harrison, C.S.; Semple, D. Adaptive robotic system for the inspection of aerospace slat actuator mount. Front. Robot. 2024, 11, 1423319. [Google Scholar] [CrossRef]
- Mortensen, A.B.; Pedersen, E.T.; Benedicto, L.V.; Burg, L.; Madsen, M.R.; Bøgh, S. Two-Stage Reinforcement Learning for Planetary Rover Navigation: Reducing the Reality Gap with Offline Noisy Data. In Proceedings of the International Conference on Space Robotics (iSpaRo), Luxembourg, 24–27 June 2024. [Google Scholar]
- Cui, L.; Le, F.; Xue, X.; Sun, T.; Jiao, Y. Design and experiment of an agricultural field management robot and its navigation control system. Agronomy 2024, 14, 654. [Google Scholar] [CrossRef]
- Le, T.L.; Khang, N.G.; Thien, V.D. A Study on the Kalman Filter Based PID Controller for Mecanum-wheeled Mobile Robot. J. Phys. Conf. Ser. 2025, 2949, 012029. [Google Scholar] [CrossRef]
- Thai, N.H.; Ly, T.T.K.; Thien, H.; Dzung, L.Q. Trajectory tracking control for differential-drive mobile robot by a variable parameter PID controller. Int. J. Mech. Eng. Robot. Res. 2022, 11, 614–621. [Google Scholar] [CrossRef]
- Huang, H.; Gao, J. Backstepping and novel sliding mode trajectory tracking controller for wheeled mobile robots. Mathematics 2024, 12, 1458. [Google Scholar] [CrossRef]
- Pérez-Juárez, J.G.; García-Martínez, J.R.; Barra-Vázquez, O.A.; Cruz-Miguel, E.E.; Olmedo-García, L.F.; Santiago, A.M. Fuzzy logic controller for a terrestrial mobile robot based on the global positioning system. In Proceedings of the IEEE International Conference on Engineering Veracruz (ICEV), Boca del Rio, Mexico, 21–24 October 2024. [Google Scholar]
- Ait Dahmad, H.; Ayad, H.; Cerezo, A.G.; Mousannif, H. IT-2 Fuzzy Control and Behavioral Approach Navigation System for Holonomic 4WD/4WS Agricultural Robot. Int. J. Comput. Commun. Control. 2024, 19, 6420. [Google Scholar] [CrossRef]
- Kamil, F.; Moghrabiah, M.Y. Multilayer decision-based fuzzy logic model to navigate mobile robot in unknown dynamic environments. Fuzzy Inf. Eng. 2022, 14, 51–73. [Google Scholar] [CrossRef]
- Shivkumar, S.; Amudha, J.; Nippun Kumaar, A.A. Federated deep reinforcement learning for mobile robot navigation. J. Intell. Fuzzy Syst. 2024, 1–16. [Google Scholar] [CrossRef]
- Xiao, H.; Chen, C.; Zhang, G.; Chen, C.P. Reinforcement learning-driven dynamic obstacle avoidance for mobile robot trajectory tracking. Knowl.-Based Syst. 2024, 297, 111974. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, S.; Cheng, S.; Xia, Q.; Zhang, J. Path-following and obstacle avoidance control of nonholonomic wheeled mobile robot based on deep reinforcement learning. Appl. Sci. 2022, 12, 6874. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, J.; Xin, X.; Li, X.; Sun, C.; Huang, J.; Kong, W. A survey on learning-based model predictive control: Toward path tracking control of mobile platforms. Appl. Sci. 2022, 12, 1995. [Google Scholar] [CrossRef]
- Katona, K.; Neamah, H.A.; Korondi, P. Obstacle avoidance and path planning methods for autonomous navigation of mobile robot. Sensors 2024, 24, 3573. [Google Scholar] [CrossRef]
- Rybczak, M.; Popowniak, N.; Lazarowska, A. A survey of machine learning approaches for mobile robot control. Robotics 2024, 13, 12. [Google Scholar] [CrossRef]
- Quang, H.D.; Tran, T.L.; Manh, T.N.; Manh, C.N.; Nhu, T.N.; Duy, N.B. Design a nonlinear MPC controller for autonomous mobile robot navigation system based on ROS. Int. J. Mech. Eng. Robot. Res. 2022, 11, 379–388. [Google Scholar] [CrossRef]
- Aro, K.; Urvina, R.; Deniz, N.N.; Menendez, O.; Iqbal, J.; Prado, A. A nonlinear model predictive controller for trajectory planning of skid-steer mobile robots in agricultural environments. In Proceedings of the IEEE Conference on AgriFood Electronics (CAFE), Torino, Italy, 25–27 September 2023. [Google Scholar]
- Fan, Z.; Wang, L.; Meng, H.; Yang, C. RL-MPC-based anti-disturbance control method for pod-driven ship. Ocean. Eng. 2025, 325, 120791. [Google Scholar] [CrossRef]
- Outiligh, A.; Ayad, H.; El Kari, A.; Mjahed, M.; El Gmili, N.; Horváth, E.; Pozna, C. An Improved IEHO Super-Twisting Sliding Mode Control Algorithm for Trajectory Tracking of a Mobile Robot. Stud. Inform. Control. 2024, 33, 49–60. [Google Scholar] [CrossRef]
- Azegmout, M.; Mjahed, M.; El Kari, A.; Ayad, H. New Meta-heuristic-Based Approach for Identification and Control of Stable and Unstable Systems. Int. J. Comput. Control. 2023, 18, 5294. [Google Scholar] [CrossRef]
- Fayti, M.; Mjahed, M.; Ayad, H.; El Kari, A. Recent Metaheuristic-Based Optimization for System Modeling and PID Controllers Tuning. Stud. Inform. Control. 2023, 32, 57–67. [Google Scholar] [CrossRef]
- Socha, K.; Blum, C. Ant colony optimization. In Metaheuristic Procedures for Training Neutral Networks; Springer: Boston, MA, USA, 2006; pp. 153–180. [Google Scholar]
- Ojha, V.K.; Abraham, A.; Snášel, V. ACO for continuous function optimization: A performance analysis. In Proceedings of the 14th International Conference on Intelligent Systems Design and Applications, Okinawa, Japan, 28–30 November 2014. [Google Scholar]
- Yun, S.; Zanetti, R. Clustering methods for particle filters with Gaussian mixture models. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1109–1118. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Yuan, Y.; Zeng, N.; Hone, K.; Liu, X. A novel sigmoid-function-based adaptive weighted particle swarm optimizer. IEEE Trans. Cybern. 2019, 51, 1085–1093. [Google Scholar] [CrossRef]
- Ait Dahmad, H.; Ayad, H.; Mousannif, H.; El Alaoui, A. Fuzzy logic controller for 4WD/4WS autonomous agricultural robotic. In Proceedings of the IEEE 3rd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Fez, Morocco, 1–2 December 2022. [Google Scholar]
- Azizi, M.R.; Rastegarpanah, A.; Stolkin, R. Motion planning and control of an omnidirectional mobile robot in dynamic environments. Robotics 2021, 10, 48. [Google Scholar] [CrossRef]
- Nfaileh, N.; Alipour, K.; Tarvirdizadeh, B.; Hadi, A. Formation control of multiple wheeled mobile robots based on model predictive control. Robotica 2022, 40, 3178–3213. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Chen, H.; Zhang, Y.; Zhang, D.; Peng, C. Trajectory tracking control of a skid-steer mobile robot based on nonlinear model predictive control with a hydraulic motor velocity mapping. Appl. Sci. 2023, 14, 122. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, X.; Liu, Y.; Xue, G. Real-time nonlinear model predictive control of unmanned surface vehicles for trajectory tracking and collision avoidance. In Proceedings of the 7th International Conference on Mechatronics and Robotics Engineering (ICMRE), Budapest, Hungary, 3–5 February 2021. [Google Scholar]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Haris, M.; Bhatti, D.M.S.; Nam, H. A fast-convergent hyperbolic tangent PSO algorithm for UAVs path planning. IEEE Open J. Veh. Technol. 2024, 5, 681–694. [Google Scholar] [CrossRef]







| Unimodal Functions | ||
| Function Name | Mathematical Expression | Search Space |
| Sphere | ||
| Schwefel 2.21 | ||
| Schwefel 2.22 | ||
| Schwefel 1.2 | ||
| Quartic Noise | ||
| Rosenbrock | ||
| Multimodal Functions | ||
| Penalized 2 | ||
| Penalized 1 | ||
| Griewank | ||
| Rastrigin | ||
| Ackley | ||
| Salomon | ||
| Xin-She Yang | ||
| Function | ACO | MGMM- | |
|---|---|---|---|
| Algorithm’s Parameters | Best Solution | |||
|---|---|---|---|---|
| MGMM- | MGMM- | |||
| Circular trajectory | K = 3 MaxIter = 100 nvar = 5 npop = 150 Samples = 250 | q = 0.5, z = 1 MaxIter = 100 nvar = 5 npop = 150 Samples = 250 | Q = diag(800, 82.6308, 0) R = diag(0.36327, 0.0992) | Q = diag(800, 97.5706, 5.0509 × 10−7) R = diag(0.2000, 0.2973) |
| Eight trajectory | K = 3 MaxIter = 60 nvar = 5 npop = 100 Samples = 200 | q = 0.5, z = 1 MaxIter = 60 nvar = 5 npop = 100 Samples = 200 | Q = diag(10, 199.27, 0) R = diag(0.20, 0.9775) | Q = diag(57.5204, 184.03, 1.0636 × 10−5) R = diag(0.20, 0.8701) |
| Dynamic obstacle avoidance | K = 3 MaxIter = 60 nvar = 6 npop = 150 Samples = 250 | q = 0.5, z = 1 MaxIter = 60 nvar = 6 npop = 150 Samples = 250 | Q = diag(196.36, 101.40, 5.2519 × 10−5, 2.2356 × 10−7) R = diag(0.1676, 0.7030) | Q = diag(153.95, 110.81, 1 × 10−4, 1 × 10−6) R = diag(0.10, 0.8642) |
| MPC- | MPC-MGMM- | ||
|---|---|---|---|
| Circular | Control Effort | 0.31329 0.26522 0.36536 0.25973 1.6561 × 10−5 | 0.35465 0.25244 0.36538 0.06775 1.3474 × 10−5 |
| Eight | Control Effort | 0.18497 0.24437 0.49605 0.10342 1.6505 × 10−5 | 0.22567 0.23974 0.43881 0.095839 1.4086 × 10−5 |
| Dynamic Obstacle | Control Effort | 0.036835 0.073705 0.4307 0.76467 2.0863 × 10−5 | 0.028935 0.059707 0.48267 0.15837 1.8541 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ait Dahmad, H.; Ayad, H.; García Cerezo, A.; Mousannif, H. Adaptive Model Predictive Control for 4WD-4WS Mobile Robot: A Multivariate Gaussian Mixture Model-Ant Colony Optimization for Robust Trajectory Tracking and Obstacle Avoidance. Sensors 2025, 25, 3805. https://doi.org/10.3390/s25123805
Ait Dahmad H, Ayad H, García Cerezo A, Mousannif H. Adaptive Model Predictive Control for 4WD-4WS Mobile Robot: A Multivariate Gaussian Mixture Model-Ant Colony Optimization for Robust Trajectory Tracking and Obstacle Avoidance. Sensors. 2025; 25(12):3805. https://doi.org/10.3390/s25123805
Chicago/Turabian StyleAit Dahmad, Hayat, Hassan Ayad, Alfonso García Cerezo, and Hajar Mousannif. 2025. "Adaptive Model Predictive Control for 4WD-4WS Mobile Robot: A Multivariate Gaussian Mixture Model-Ant Colony Optimization for Robust Trajectory Tracking and Obstacle Avoidance" Sensors 25, no. 12: 3805. https://doi.org/10.3390/s25123805
APA StyleAit Dahmad, H., Ayad, H., García Cerezo, A., & Mousannif, H. (2025). Adaptive Model Predictive Control for 4WD-4WS Mobile Robot: A Multivariate Gaussian Mixture Model-Ant Colony Optimization for Robust Trajectory Tracking and Obstacle Avoidance. Sensors, 25(12), 3805. https://doi.org/10.3390/s25123805






