Remaining Useful Life Prediction of Bearings via Semi-Supervised Transfer Learning Based on an Anti-Self-Healing Health Indicator
Abstract
1. Introduction
2. Datasets
2.1. Benchmark Datasets
| Dataset | RPM | Load | Running Time | Bearing Size | Sampling Frequency |
|---|---|---|---|---|---|
| PHM 2012 | 1800 RPM | 4000 N | 7.7 h | 25.6 mm | 25.6 kHz |
| PHM 2012 | 1800 RPM | 4000 N | 2.5 h | 25.6 mm | 25.6 kHz |
| PHM 2012 | 1650 RPM | 4200 N | 2.5 h | 25.6 mm | 25.6 kHz |
| PHM 2012 | 1650 RPM | 4200 N | 2.1 h | 25.6 mm | 25.6 kHz |
| PHM 2012 | 1500 RPM | 5000 N | 1.5 h | 25.6 mm | 25.6 kHz |
| PHM 2012 | 1500 RPM | 5000 N | 4.5 h | 25.6 mm | 25.6 kHz |
| NASA IMS | 2000 RPM | 26,000 N | 34 days | 71.5 mm | 20 kHz |
| NASA IMS | 2000 RPM | 26,000 N | 34 days | 71.5 mm | 20 kHz |
| NASA IMS | 2000 RPM | 26,000 N | 7 days | 71.5 mm | 20 kHz |
2.2. Experimental Setup
2.2.1. Hardware Construction
| Outer Diameter | Inner Diameter | Gear Pitch Diameter | Roller Diameter | Bearing Pitch Diameter | Contact Angle | # of Rollers | # of Teeth |
|---|---|---|---|---|---|---|---|
| 320 mm | 280 mm | 312 mm | 12 mm | 234 mm | 61 | 78 |

2.2.2. Data Acquisition


3. Anti-Self-Healing Health Indicator
3.1. Data Analysis
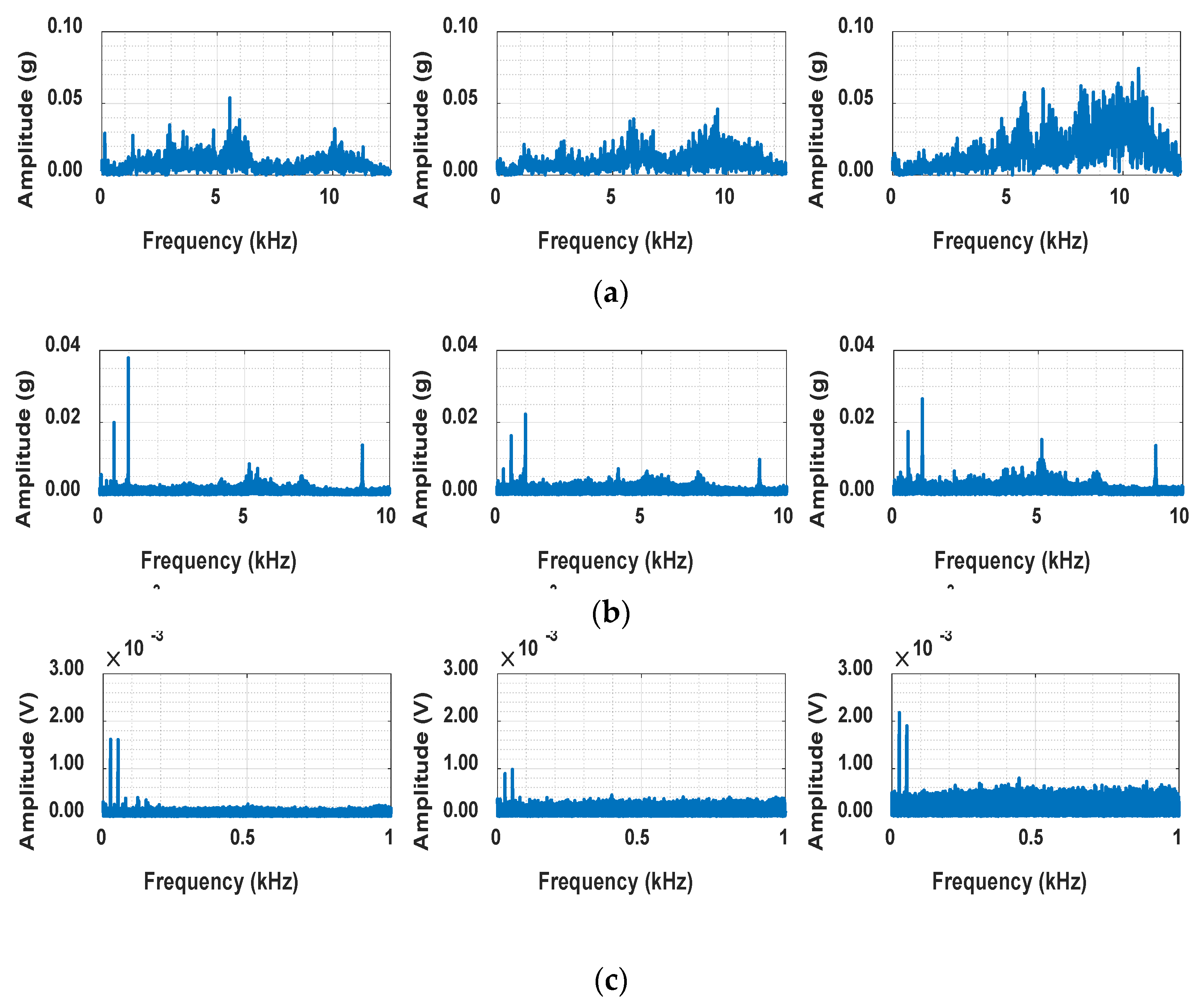
3.2. Average PSD Construction
| Algorithm 1. construction. |
| Initialize M, K, N Initialize list while true do for from 0 to do Compute end for Add to Compute Compute if then break end if Increment end while |
3.3. Skewness-Based Parameter Selection
| Algorithm 2. Skewness-Based Parameter Selection. |
| Initialize and while true do Smooth with smoothing number Compute of if then break end if Increment smoothing number end while Compute min-max normalization of for from 0 to do Segment with Compute of all Add to end for Select segmentation by |
3.4. Anti-Self-Healing Factor
| Algorithm 3. ASH-HI Calculation. |
| Define Initialize for each current PSD do Pre-process using the same parameters as for Compute mean difference across identical segments if then Update end if Compute end for |

4. Semi-Supervised Transfer Learning
4.1. RUL Labeling
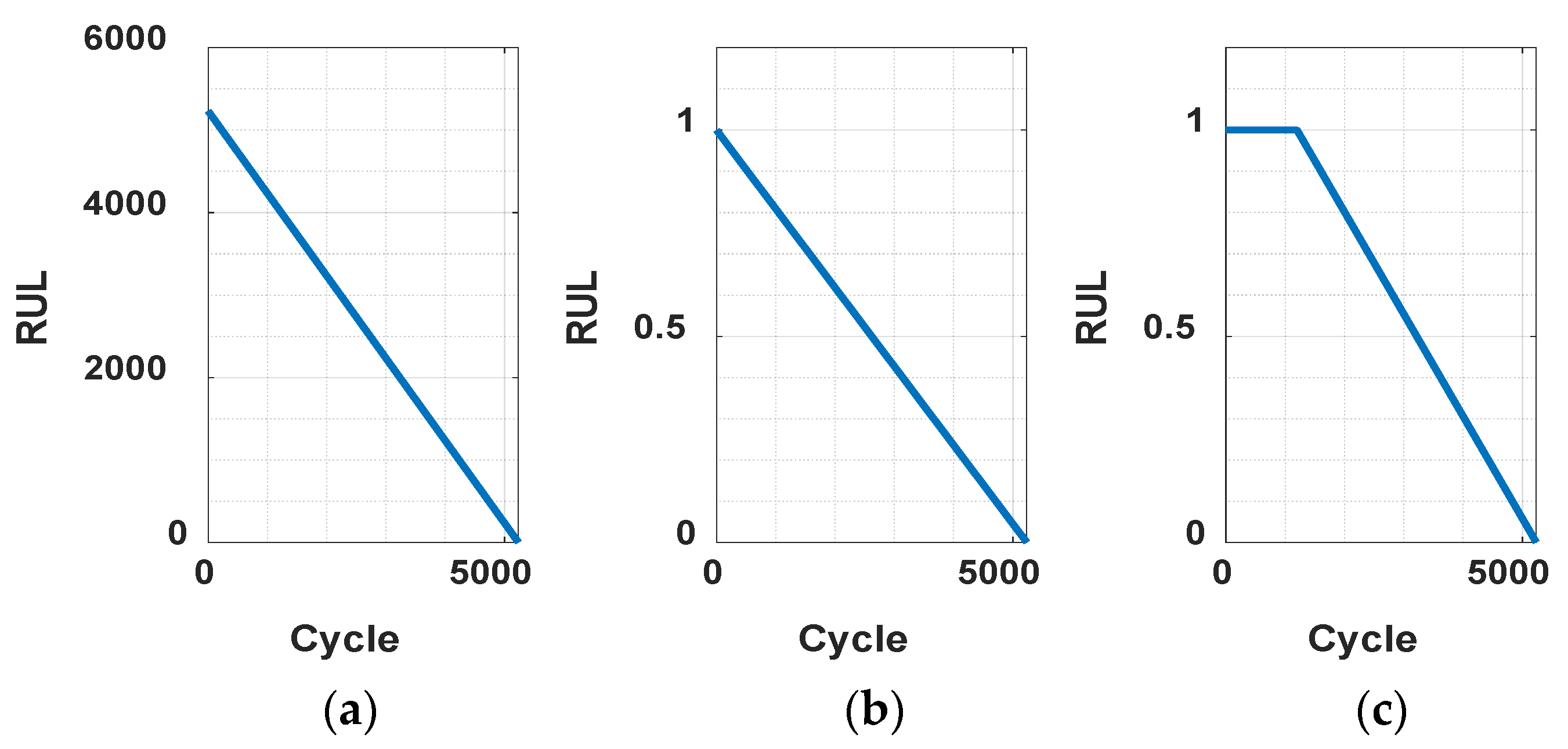
4.2. Baseline Architecture Model

5. Verification
5.1. Comparison Studies
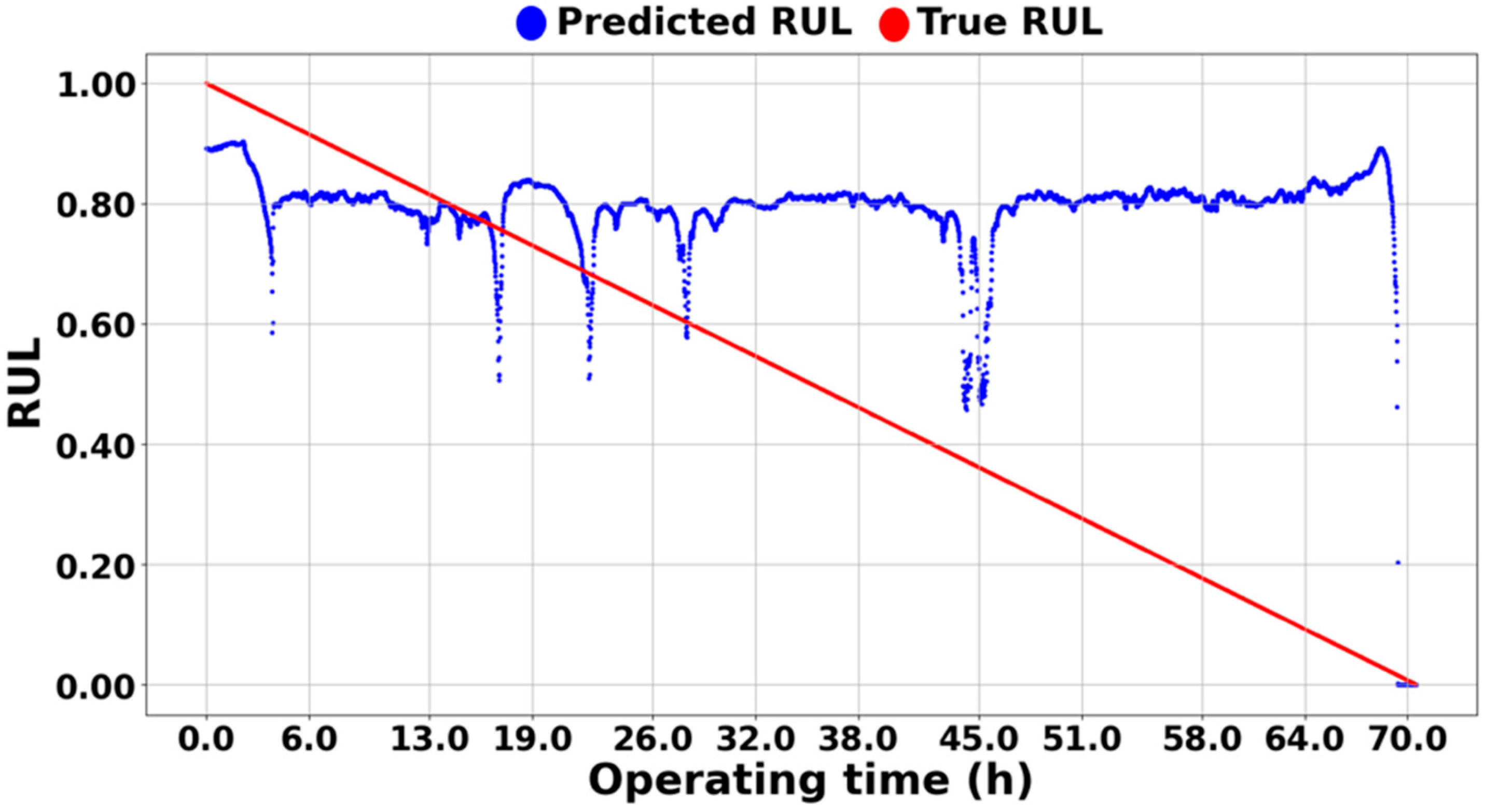
5.2. HI Verification


5.3. Mean Squared Error




| Dataset | Bearing # | ASH-HI | RMS | Variance | P2P | Skewness | Kurtosis | Maximum | Spectral Kurtosis | Wavelet Energy | [44] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PHM 2012 | 1-1 | 0.98 | 0.33 | 0.21 | 0.29 | −0.01 | 0.02 | 0.28 | 0.04 | 0.01 | −0.18 |
| PHM 2012 | 1-2 | 0.94 | 0.22 | 0.25 | 0.03 | −0.01 | −0.02 | 0.04 | −0.07 | −0.08 | 0.50 |
| PHM 2012 | 2-1 | 0.82 | 0.63 | 0.48 | 0.53 | 0.00 | 0.20 | 0.53 | 0.44 | 0.37 | 0.37 |
| PHM 2012 | 2-2 | 0.95 | 0.58 | 0.47 | 0.53 | 0.26 | 0.28 | 0.55 | 0.11 | −0.08 | 0.13 |
| PHM 2012 | 3-1 | 0.84 | 0.34 | 0.35 | 0.34 | −0.09 | 0.14 | 0.34 | −0.09 | −0.07 | 0.34 |
| PHM 2012 | 3-2 | 0.97 | 0.27 | 0.21 | 0.28 | 0.00 | 0.05 | 0.27 | −0.09 | −0.04 | 0.20 |
| NASA IMS | 1-1 | 0.93 | 0.46 | 0.45 | 0.24 | −0.28 | −0.31 | 0.19 | 0.10 | −0.01 | 0.31 |
| NASA IMS | 1-2 | 0.96 | 0.46 | 0.27 | 0.60 | −0.15 | 0.37 | 0.56 | −0.36 | −0.36 | −0.10 |
| NASA IMS | 2-1 | 0.83 | 0.46 | 0.45 | 0.24 | −0.28 | −0.31 | 0.19 | 0.10 | −0.01 | 0.14 |
| Experiment set | 1 | 0.98 | 0.34 | 0.22 | 0.42 | −0.25 | −0.33 | 0.35 | −0.47 | −0.49 | 0.47 |
| Dataset | Bearing # | ASH-HI | RMS | Variance | P2P | Skewness | Kurtosis | Maximum | Spectral Kurtosis | Wavelet Energy | [44] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PHM 2012 | 1-1 | 0.99 | 0.96 | 0.92 | 0.89 | 0.94 | 0.73 | 0.86 | 0.94 | 1.00 | 0.87 |
| PHM 2012 | 1-2 | 0.99 | 0.93 | 0.88 | 0.49 | 0.94 | 0.25 | 0.52 | 0.93 | 0.99 | 0.77 |
| PHM 2012 | 2-1 | 0.98 | 0.98 | 0.97 | 0.87 | 0.99 | 0.69 | 0.87 | 0.95 | 1.00 | 0.84 |
| PHM 2012 | 2-2 | 0.99 | 0.99 | 0.98 | 0.94 | 0.97 | 0.89 | 0.94 | 0.95 | 1.00 | 0.30 |
| PHM 2012 | 3-1 | 0.89 | 0.99 | 0.99 | 0.91 | 0.96 | 0.82 | 0.92 | 0.94 | 1.00 | 0.59 |
| PHM 2012 | 3-2 | 0.98 | 0.99 | 0.99 | 0.87 | 0.99 | 0.69 | 0.89 | 0.95 | 1.00 | 0.85 |
| NASA IMS | 1-1 | 0.99 | 0.99 | 0.98 | 0.93 | 0.99 | 0.98 | 0.93 | 0.87 | 0.84 | 0.70 |
| NASA IMS | 1-2 | 0.99 | 099 | 0.97 | 0.89 | 0.98 | 0.76 | 0.85 | 0.99 | 0.99 | 0.67 |
| NASA IMS | 2-1 | 0.98 | 0.99 | 0.98 | 0.93 | 0.99 | 0.98 | 0.93 | 0.87 | 0.76 | 0.68 |
| Experiment set | 1 | 0.99 | 1.00 | 1.00 | 0.98 | 0.89 | 0.92 | 0.98 | 0.92 | 0.89 | 0.93 |




| Target Domain | w/o Anti-Self-Healing | Proposed Model | [43] | [44] |
| PHM 2012 1-1 | 0.0518 | 0.0091 | 0.2476 | 0.1161 |
| PHM 2012 1-2 | 0.1131 | 0.0085 | 0.2400 | 0.1605 |
| PHM 2012 2-1 | 0.0857 | 0.0097 | 0.2477 | 0.2717 |
| PHM 2012 2-2 | 0.0486 | 0.0082 | 0.2670 | 0.5599 |
| PHM 2012 3-1 | 0.0347 | 0.0040 | 0.2414 | 0.1489 |
| PHM 2012 3-2 | 0.0648 | 0.0067 | 0.2450 | 0.3012 |
| NASA IMS 1-1 | 0.0421 | 0.0011 | 0.2171 | 0.1374 |
| NASA IMS 1-2 | 0.0276 | 0.0012 | 0.2353 | 0.2877 |
| NASA IMS 2 | 0.0372 | 0.0023 | 0.2549 | 0.3305 |
| Experiment | 0.2439 | 0.0078 | 0.1628 | 0.1626 |
6. Conclusions
- It significantly outperformed traditional domain adaptation techniques, which exhibited MSEs 36 to 40 times higher.
- Supervised transfer learning using raw physical values suffered from overfitting, failing to capture the decreasing RUL trend accurately.
- Semi-supervised transfer learning with normalized features remained vulnerable to the self-healing phenomenon, leading to a performance degradation.
- The inclusion of an anti-self-healing factor in the health indicator was found to be crucial, as its absence resulted in substantially lower predictive accuracy, confirming its role in mitigating misleading effects caused by self-healing.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vencl, A.; Rac, A. Diesel engine crankshaft journal bearings failures: Case study. Eng. Fail. Anal. 2014, 44, 217–228. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, H.; Fan, Y.; Shangguan, L.; Yang, Y. A review of research on wind turbine bearings’ failure analysis and fault diagnosis. Lubricants 2022, 11, 14. [Google Scholar] [CrossRef]
- Roy, M. Failure analysis of bearings of aero-engine. J. Fail. Anal. Prev. 2019, 19, 1615–1629. [Google Scholar] [CrossRef]
- Hamadache, M.; Jung, J.H.; Park, J.; Youn, B.D. A comprehensive review of artificial intelligence-based approaches for rolling element bearing PHM: Shallow and deep learning. JMST Adv. 2019, 1, 125–151. [Google Scholar] [CrossRef]
- Eftekharnejad, B.; Carrasco, M.; Charnley, B.; Mba, D. The application of spectral kurtosis on acoustic emission and vibrations from a defective bearing. Mech. Syst. Signal Process. 2011, 25, 266–284. [Google Scholar] [CrossRef]
- Caesarendra, W.; Kosasih, B.; Tieu, K.; Moodie, C.A.S. An application of nonlinear feature extraction-A case study for low speed slewing bearing condition monitoring and prognosis. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1713–1718. [Google Scholar]
- Guo, H.; Jack, L.B.; Nandi, A.K. Automated feature extraction using genetic programming for bearing condition monitoring. In Proceedings of the 2004 14th IEEE Signal Processing Society Workshop Machine Learning for Signal Processing, Sao Luis, Brazil, 29 September–1 October 2004; pp. 519–528. [Google Scholar]
- Hakim, M.; Omran, A.A.B.; Ahmed, A.N.; Al-Waily, M.; Abdellatif, A. A systematic review of rolling bearing fault diagnoses based on deep learning and transfer learning: Taxonomy, overview, application, open challenges, weaknesses and recommendations. Ain Shams Eng. J. 2023, 14, 101945. [Google Scholar] [CrossRef]
- Diaz, M.; Henriquez, P.; Ferrer, M.A.; Pirlo, G.; Alonso, J.B.; Carmona-Duarte, C.; Impedovo, D. Stability-based system for bearing fault early detection. Expert Syst. Appl. 2017, 79, 65–75. [Google Scholar] [CrossRef]
- Ding, H.; Yang, L.; Cheng, Z.; Yang, Z. A remaining useful life prediction method for bearing based on deep neural networks. Measurement 2021, 172, 108878. [Google Scholar] [CrossRef]
- Asutkar, S.; Tallur, S. Deep transfer learning strategy for efficient domain generalization in machine fault diagnosis. Sci. Rep. 2023, 13, 6607. [Google Scholar] [CrossRef]
- Huang, M.; Yin, J.; Yan, S.; Xue, P. A fault diagnosis method of bearings based on deep transfer learning. Simul. Model. Pract. Theory 2023, 122, 102659. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnostics—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Park, S.-H.; Park, K.-S. A pre-trained model selection for transfer learning of remaining useful life prediction of grinding wheel. J. Intell. Manuf. 2024, 35, 2295–2312. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, Y.; Ou, J. Transfer remaining useful life estimation of bearing using depth-wise separable convolution recurrent network. Measurement 2021, 176, 109090. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Zuo, M.J. Predicting remaining useful life of rolling bearings based on deep feature representation and transfer learning. IEEE Trans. Instrum. Meas. 2019, 69, 1594–1608. [Google Scholar] [CrossRef]
- Osterrieder, P.; Budde, L.; Friedli, T. The smart factory as a key construct of industry 4.0: A systematic literature review. Int. J. Prod. Econ. 2020, 221, 107476. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, H.; Sun, X. Residual life prediction of bearings based on SENet-TCN and transfer learning. IEEE Access 2022, 10, 123007–123019. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Hauptmann, A.G. Simultaneous bearing fault recognition and remaining useful life prediction using joint-loss convolutional neural network. IEEE Trans. Ind. Inform. 2019, 16, 87–96. [Google Scholar] [CrossRef]
- Hu, T.; Guo, Y.; Gu, L.; Zhou, Y.; Zhang, Z.; Zhou, Z. Remaining useful life estimation of bearings under different working conditions via Wasserstein distance-based weighted domain adaptation. Reliab. Eng. Syst. Saf. 2022, 224, 108526. [Google Scholar] [CrossRef]
- Cheng, H.; Kong, X.; Wang, Q.; Ma, H.; Yang, S. The two-stage RUL prediction across operation conditions using deep transfer learning and insufficient degradation data. Reliab. Eng. Syst. Saf. 2022, 225, 108581. [Google Scholar] [CrossRef]
- Berghout, T.; Mouss, L.-H.; Bentrcia, T.; Benbouzid, M. A semi-supervised deep transfer learning approach for rolling-element bearing remaining useful life prediction. IEEE Trans. Energy Convers. 2021, 37, 1200–1210. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Williams, T.; Ribadeneira, X.; Billington, S.; Kurfess, T. Rolling element bearing diagnostics in run-to-failure lifetime testing. Mech. Syst. Signal Process. 2001, 15, 979–993. [Google Scholar] [CrossRef]
- Li, C.; Zhu, X.; Li, X.; Zhu, Q.; Yu, G. The bearing health condition assessment method based on alpha-stable probability distribution model. In Proceedings of the 2016 Prognostics and System Health Management Conference (PHM-Chengdu), Chengdu, China, 19–21 October 2016; pp. 1–5. [Google Scholar]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management at Minneapolis, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]
- Gousseau, W.; Antoni, J.; Girardin, F.; Griffaton, J. Analysis of the Rolling Element Bearing data set of the Center for Intelligent Maintenance Systems of the University of Cincinnati. In Proceedings of the CM2016, Charenton, France, 10–12 October 2016. [Google Scholar]
- Chen, P. Bearing Condition Monitoring and Fault Diagnosis. Ph.D. Thesis, The University of Calgary, Calgary, AB, Canada, 2000. [Google Scholar]
- Pietrzak, P.; Wolkiewicz, M. Stator Winding Fault Detection of Permanent Magnet Synchronous Motors Based on the Short-Time Fourier Transform. Power Electron. Drives 2022, 7, 112–133. [Google Scholar] [CrossRef]
- Ruiz, J.R.R.; Rosero, J.A.; Espinosa, A.G.; Romeral, L. Detection of demagnetization faults in permanent-magnet synchronous motors under nonstationary conditions. IEEE Trans. Magn. 2009, 45, 2961–2969. [Google Scholar] [CrossRef]
- Rosero, J.; Ortega, J.; Urresty, J.; Cardenas, J.; Romeral, L. Stator short circuits detection in PMSM by means of higher order spectral analysis (HOSA). In Proceedings of the Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 964–969. [Google Scholar]
- Makhloufi, S.; Kadri, A.; Belbali, A.; Abdallah, L.; Seddik, Z. Mathematical Modelling of a 3-Phase Induction Motor; IntechOpen: London, UK, 2023. [Google Scholar]
- Amarouayache, I.I.E.; Saadi, M.N.; Guersi, N.; Boutasseta, N. Bearing fault diagnostics using EEMD processing and convolutional neural network methods. Int. J. Adv. Manuf. Technol. 2020, 107, 4077–4095. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Li, S. Research on test bench bearing fault diagnosis of improved EEMD based on improved adaptive resonance technology. Measurement 2021, 185, 109986. [Google Scholar] [CrossRef]
- Brkovic, A.; Gajic, D.; Gligorijevic, J.; Savic-Gajic, I.; Georgieva, O.; Di Gennaro, S. Early fault detection and diagnosis in bearings for more efficient operation of rotating machinery. Energy 2017, 136, 63–71. [Google Scholar] [CrossRef]
- Hu, A.; Xiang, L.; Xu, S.; Lin, J. Frequency Loss and Recovery in Rolling Bearing Fault Detection. Chin. J. Mech. Eng. 2019, 32, 35. [Google Scholar] [CrossRef]
- Patil, M.S.; Mathew, J.; RajendraKumar, P.K. Bearing Signature Analysis as a Medium for Fault Detection: A Review. J. Tribol. 2008, 103, 014001. [Google Scholar] [CrossRef]
- Li, H.; Wang, C. Combining first prediction time identification and time-series feature window for remaining useful life prediction of rolling bearings with limited data. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2024, 238, 274–290. [Google Scholar] [CrossRef]
- Suh, S.; Jang, J.; Won, S.; Jha, M.S.; Lee, Y.O. Supervised Health Stage Prediction Using Convolutional Neural Networks for Bearing Wear. Sensors 2020, 20, 5846. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hao, R.; Liu, Q.; Guo, W. Prediction of remaining useful life of rolling element bearings based on LSTM and exponential model. Int. J. Mach. Learn. Cybern. 2023, 14, 1567–1578. [Google Scholar] [CrossRef]
- Ahmad, W.; Khan, S.A.; Islam, M.M.M.; Kim, J.-M. A reliable technique for remaining useful life estimation of rolling element bearings using dynamic regression models. Reliab. Eng. Syst. Saf. 2019, 184, 67–76. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Zhang, G.; Wang, Y.; Li, X.; Qin, Y.; Tang, B. Health indicator based on signal probability distribution measures for machinery condition monitoring. Mech. Syst. Signal Process. 2023, 198, 110460. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, Y.; Lin, L.; Zhao, M.; Zhong, S.-S. Deep residual LSTM with domain-invariance for remaining useful life prediction across domains. Reliab. Eng. Syst. Saf. 2021, 216, 108012. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-W.; Park, K.-S. Remaining Useful Life Prediction of Bearings via Semi-Supervised Transfer Learning Based on an Anti-Self-Healing Health Indicator. Sensors 2025, 25, 3662. https://doi.org/10.3390/s25123662
Kim J-W, Park K-S. Remaining Useful Life Prediction of Bearings via Semi-Supervised Transfer Learning Based on an Anti-Self-Healing Health Indicator. Sensors. 2025; 25(12):3662. https://doi.org/10.3390/s25123662
Chicago/Turabian StyleKim, Jung-Woo, and Kyoung-Su Park. 2025. "Remaining Useful Life Prediction of Bearings via Semi-Supervised Transfer Learning Based on an Anti-Self-Healing Health Indicator" Sensors 25, no. 12: 3662. https://doi.org/10.3390/s25123662
APA StyleKim, J.-W., & Park, K.-S. (2025). Remaining Useful Life Prediction of Bearings via Semi-Supervised Transfer Learning Based on an Anti-Self-Healing Health Indicator. Sensors, 25(12), 3662. https://doi.org/10.3390/s25123662








