Data Quality Monitoring for the Hadron Calorimeters Using Transfer Learning for Anomaly Detection
Abstract
1. Introduction
- This study explores the potential and limitations of TL in the context of high-dimensional ST models for AD application, at scale with 3000–7000 spatial nodes.
- This study, different from existing TL studies, assesses both encoder and decoder networks of a hybrid AE—evaluated on each main building block with various configurations. Related TL studies primarily focus on the feature extraction encoder or fine-tuning the entire network, as highlighted in this study. We present deeper insights and considerations on previously underexplored angles of TL.
- We demonstrate the robustness of TL, with limited training data sets, in improving model accuracy, reducing training parameters, and better mitigation against vulnerability to training data contamination.
2. Background
2.1. Transfer Learning on Deep Learning
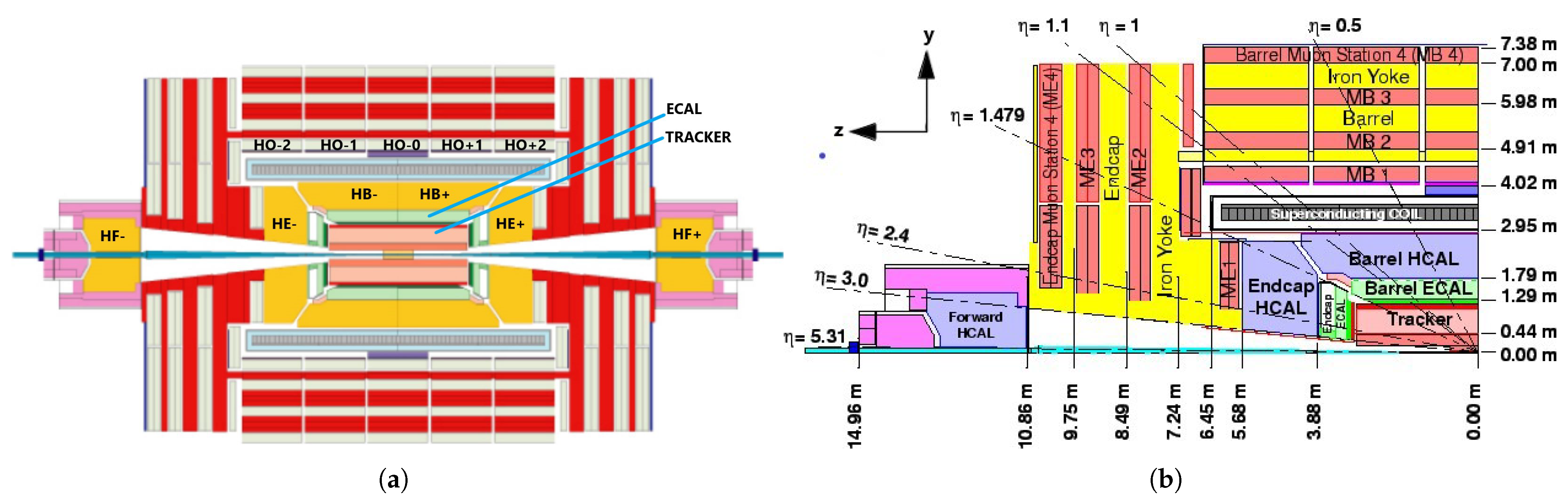
2.2. The Hadron Calorimeter of the CMS Detector
2.3. CMS Data Quality Monitoring
3. Dataset Description
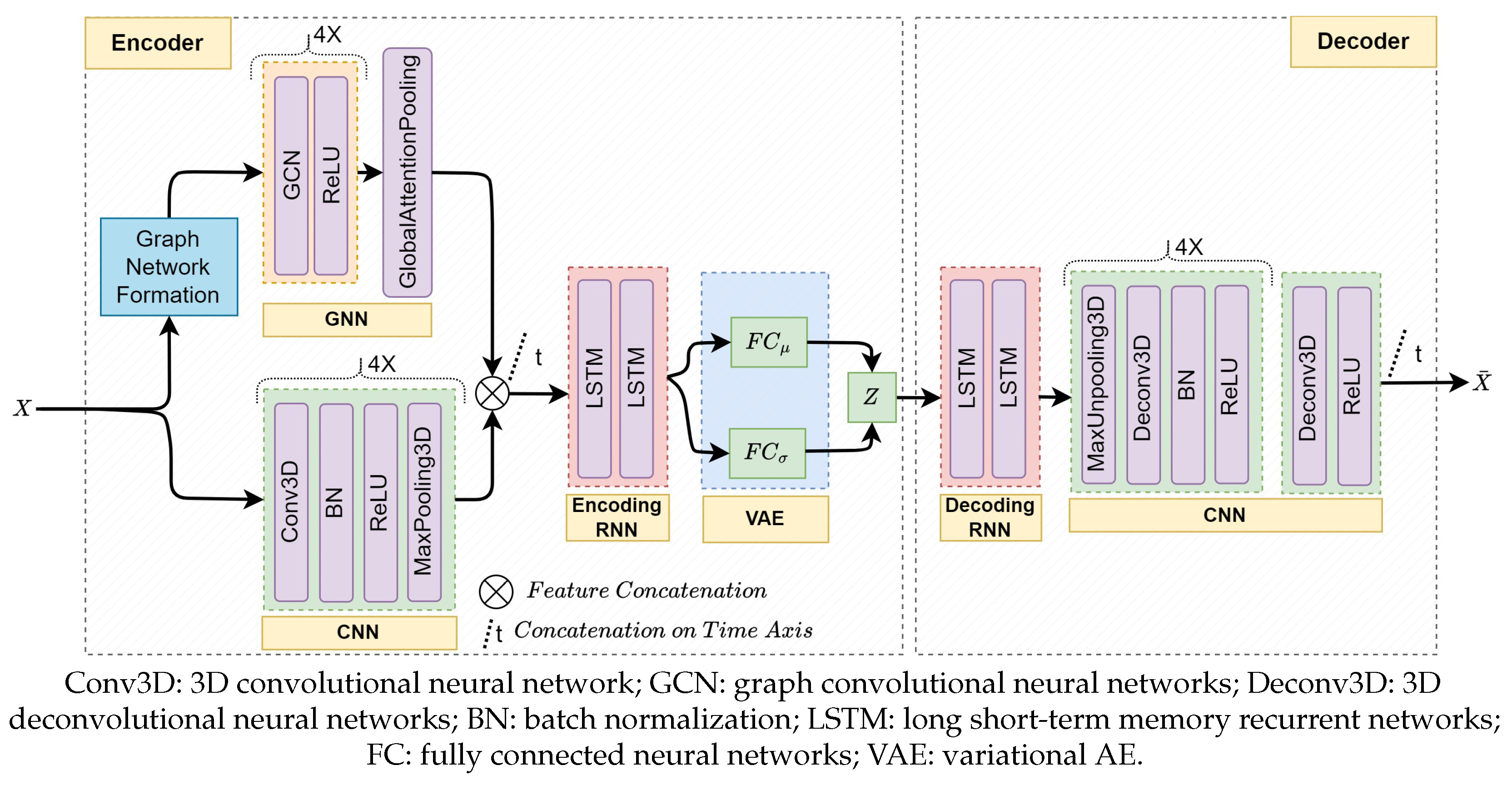
4. Methodology
4.1. Data Preprocessing
4.1.1. Digi-Occupancy Map Renormalization
4.1.2. Adjacency Matrix Generation
4.2. Anomaly Detection Mechanism
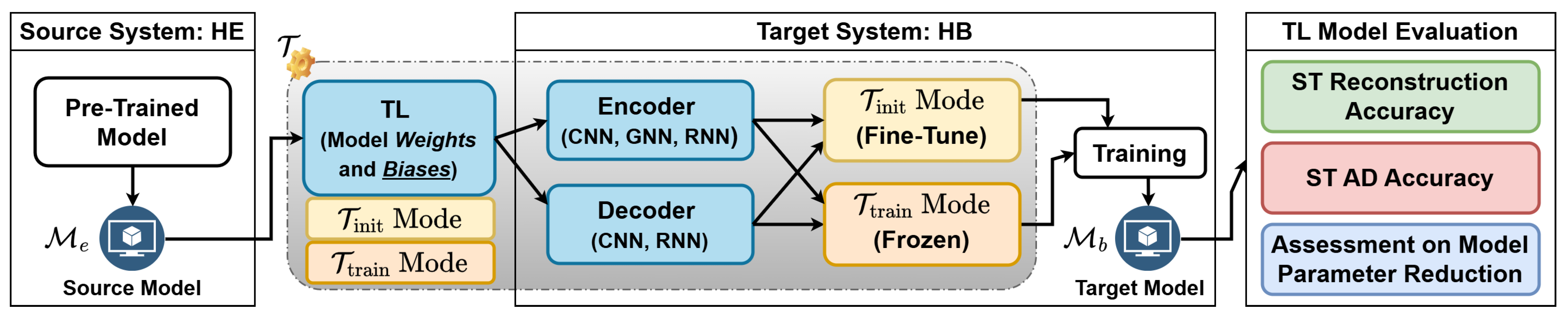
4.3. Transfer Learning Approach
- Init mode (): the trainable network parameters (weights and bias) of the source model are transferred into the target model initialization. The target model is further trained on the target HB dataset, resulting in fine-tuning.
- Train mode (): The model parameters of the source model are directly reused as the final inference parameters of the target model; the parameters are frozen and excluded from fine-tuning on the target HB dataset.
5. Results and Discussion
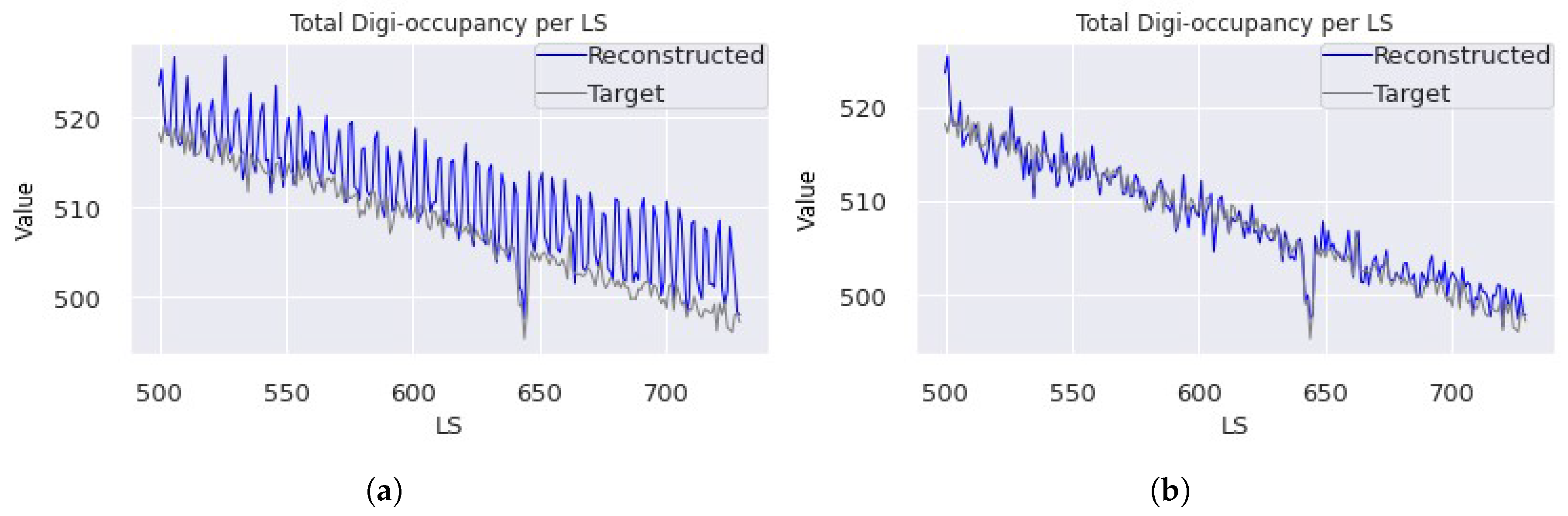
5.1. Spatio-Temporal Reconstruction Performance
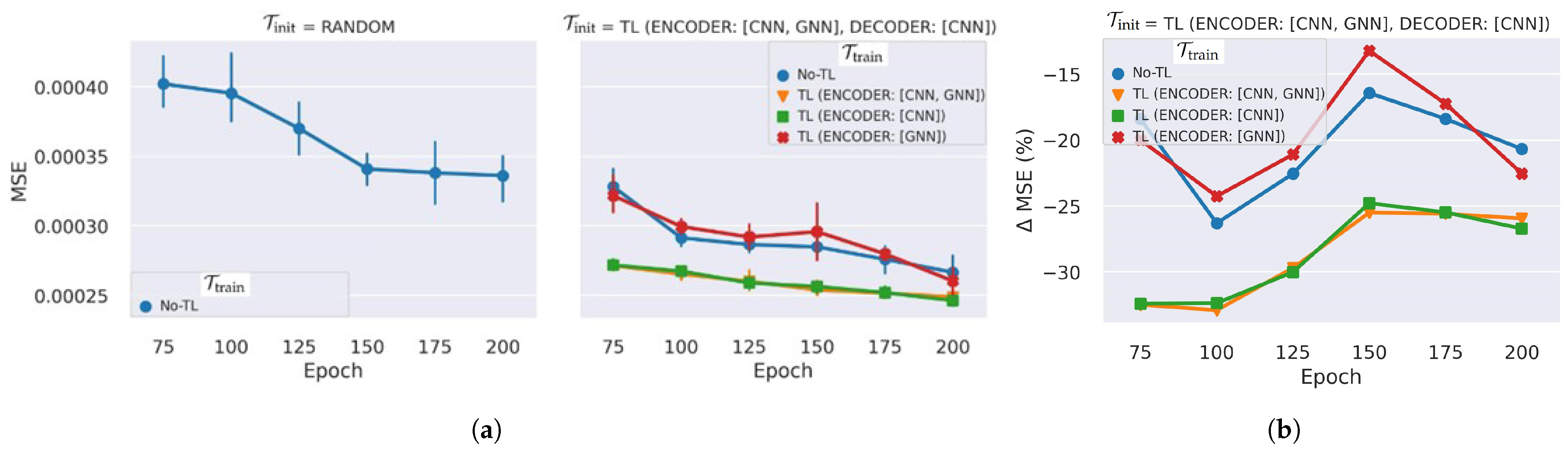
5.1.1. Transfer Learning on Spatial Learning Networks
5.1.2. Transfer Learning on Spatio-Temporal Learning Networks
5.1.3. Applying Learning Rate Scheduling
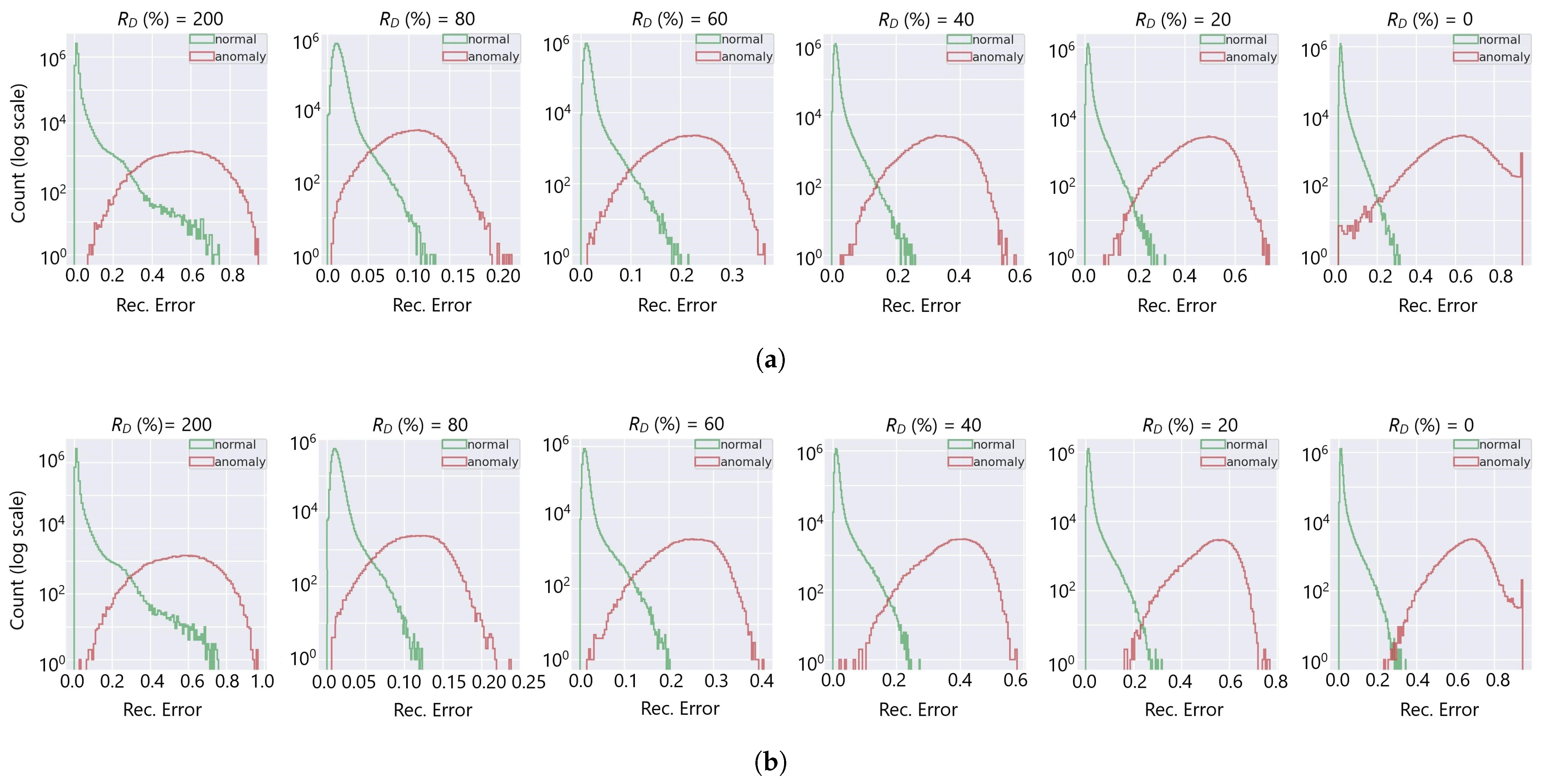
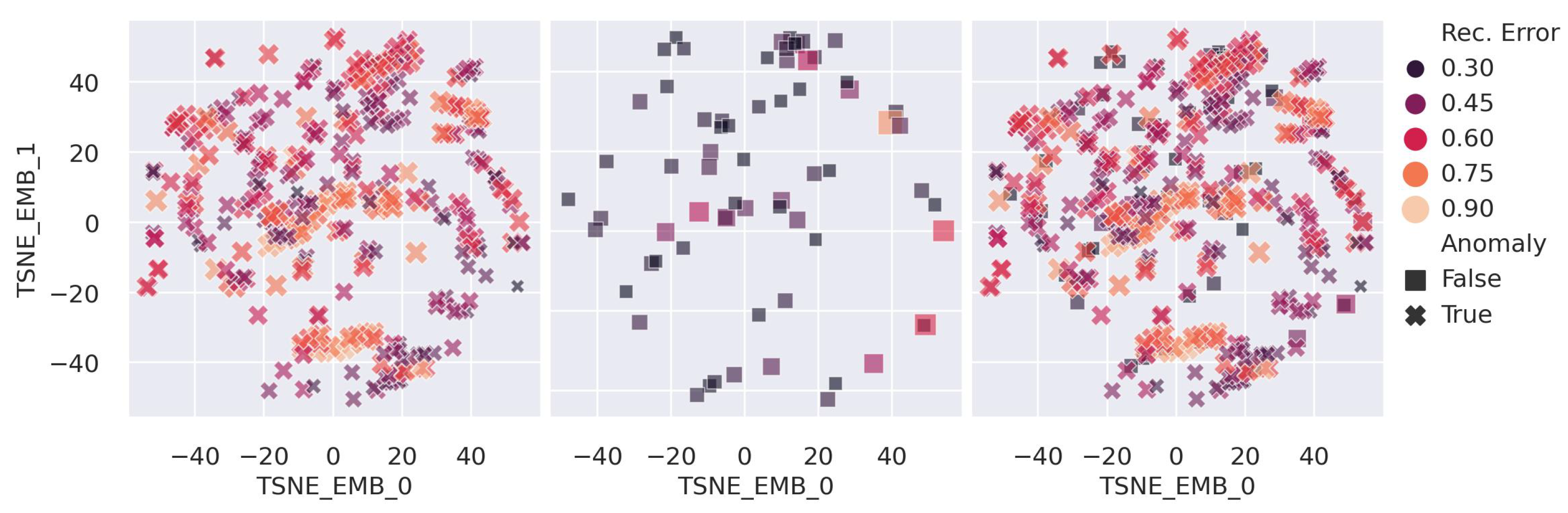
5.2. Anomaly Detection Performance
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Anomaly Detection |
| AE | Autoencoder |
| AUC | Area Under the Curve |
| CMS | Compact Muon Solenoid |
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| DQM | Data Quality Monitoring |
| ECAL | Electromagnetic Calorimeter |
| FC | Fully Connected Neural Network |
| FPR | False Positive Rate |
| GNN | Graph Neural Network |
| GraphSTAD | Graph-based ST AD model |
| HCAL | Hadron Calorimeter |
| HB, HE, HF, HO | HCAL Barrel, HCAL Endcap, HCAL Forward, and HCAL Outer subdetectors |
| HPD | Hybrid Photodiode Transducers |
| KL | Kullback–Leibler divergence |
| LHC | Large Hadron Collider |
| LR | Learning Rate |
| LS | Luminosity Section |
| LSTM | Long Short-Term Memory |
| MAE, MSE | Mean Absolute Error, Mean Squared Error |
| QIE | Charge Integrating and Encoding |
| RBX | Readout Box |
| RNN | Recurrent Neural Network |
| SiPM | Silicon Photo Multipliers |
| ST | Spatio-Temporal |
| TL | Transfer Learning |
| , , , | Digi-occupancy map, renomalized by , healthy , anomalous |
| , | Received luminosity, number of collision events |
| , , | , , and axes of the HCAL channels |
| , , | Mathematical notation of an AE model, encoder of , decoder of |
| , | AE reconstruction MSE loss score, MAE AD score |
Degradation factor of channel anomaly | |
| , | AE model of the TL source HE system, AE model of the TL target HB system |
| , | Model trained without TL, model trained with TL |
| , | TL during initialization phase, TL during training phase (frozen parameters) |
References
- Atluri, G.; Karpatne, A.; Kumar, V. Spatio-temporal data mining: A survey of problems and methods. ACM Comput. Surv. 2018, 51, 83. [Google Scholar] [CrossRef]
- Chang, Y.; Tu, Z.; Xie, W.; Luo, B.; Zhang, S.; Sui, H.; Yuan, J. Video anomaly detection with spatio-temporal dissociation. Pattern Recognit. 2022, 122, 108213. [Google Scholar] [CrossRef]
- Deng, L.; Lian, D.; Huang, Z.; Chen, E. Graph convolutional adversarial networks for spatiotemporal anomaly detection. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 2416–2428. [Google Scholar] [CrossRef]
- Tišljarić, L.; Fernandes, S.; Carić, T.; Gama, J. Spatiotemporal road traffic anomaly detection: A tensor-based approach. Appl. Sci. 2021, 11, 12017. [Google Scholar] [CrossRef]
- Fathizadan, S.; Ju, F.; Lu, Y.; Yang, Z. Deep spatio-temporal anomaly detection in laser powder bed fusion. IEEE Trans. Autom. Sci. Eng. 2023, 21, 5227–5239. [Google Scholar] [CrossRef]
- Asres, M.W.; Omlin, C.W.; Wang, L.; Yu, D.; Parygin, P.; Dittmann, J.; Karapostoli, G.; Seidel, M.; Venditti, R.; Lambrecht, L.; et al. Spatio-temporal anomaly detection with graph networks for data quality monitoring of the Hadron Calorimeter. Sensors 2023, 23, 9679. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, L.; Chen, X.; Guo, C.; Yang, B.; Kieu, T.; Huang, F.; Pedersen, T.B.; Zheng, K.; Jensen, C.S. A comparative study on unsupervised anomaly detection for time series: Experiments and analysis. arXiv 2022, arXiv:2209.04635. [Google Scholar]
- Chalapathy, R.; Chawla, S. Deep learning for anomaly detection: A survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Cook, A.A.; Mısırlı, G.; Fan, Z. Anomaly detection for IoT time-series data: A survey. IEEE Internet Things J. 2019, 7, 6481–6494. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, G. Self-supervised dam deformation anomaly detection based on temporal–spatial contrast learning. Sensors 2024, 24, 5858. [Google Scholar] [CrossRef]
- Yang, J.; Chu, H.; Guo, L.; Ge, X. A Weighted-Transfer Domain-Adaptation Network Applied to Unmanned Aerial Vehicle Fault Diagnosis. Sensors 2025, 25, 1924. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Miao, H.; Li, J.; Cao, J. Spatio-temporal knowledge transfer for urban crowd flow prediction via deep attentive adaptation networks. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4695–4705. [Google Scholar] [CrossRef]
- Yu, F.; Xiu, X.; Li, Y. A survey on deep transfer learning and beyond. Mathematics 2022, 10, 3619. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly accurate machine fault diagnosis using deep transfer learning. IEEE Trans. Ind. Inform. 2018, 15, 2446–2455. [Google Scholar] [CrossRef]
- Laptev, N.; Yu, J.; Rajagopal, R. Reconstruction and regression loss for time-series transfer learning. In Proceedings of the Special Interest Group on SIGKDD, London, UK, 19–23 August 2018; Volume 20. [Google Scholar]
- Gupta, P.; Malhotra, P.; Vig, L.; Shroff, G. Transfer learning for clinical time series analysis using recurrent neural networks. arXiv 2018, arXiv:1807.01705. [Google Scholar]
- Boullé, N.; Dallas, V.; Nakatsukasa, Y.; Samaddar, D. Classification of chaotic time series with deep learning. Phys. D Nonlinear Phenom. 2020, 403, 132261. [Google Scholar] [CrossRef]
- Wang, L.; Geng, X.; Ma, X.; Liu, F.; Yang, Q. Cross-city transfer learning for deep spatio-temporal prediction. arXiv 2018, arXiv:1802.00386. [Google Scholar]
- Hijazi, M.; Dehghanian, P.; Wang, S. Transfer learning for transient stability predictions in modern power systems under enduring topological changes. IEEE Trans. Autom. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Shao, L.; Zhu, F.; Li, X. Transfer learning for visual categorization: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 1019–1034. [Google Scholar] [CrossRef]
- Niu, S.; Liu, Y.; Wang, J.; Song, H. A decade survey of transfer learning (2010–2020). IEEE Trans. Artif. Intell. 2020, 1, 151–166. [Google Scholar] [CrossRef]
- Adama, D.A.; Lotfi, A.; Ranson, R. A survey of vision-based transfer learning in human activity recognition. Electronics 2021, 10, 2412. [Google Scholar] [CrossRef]
- Chato, L.; Regentova, E. Survey of transfer learning approaches in the machine learning of digital health sensing data. J. Pers. Med. 2023, 13, 1703. [Google Scholar] [CrossRef] [PubMed]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Sarker, M.I.; Losada-Gutiérrez, C.; Marron-Romera, M.; Fuentes-Jiménez, D.; Luengo-Sánchez, S. Semi-supervised anomaly detection in video-surveillance scenes in the wild. Sensors 2021, 21, 3993. [Google Scholar] [CrossRef] [PubMed]
- Natha, S.; Ahmed, F.; Siraj, M.; Lagari, M.; Altamimi, M.; Chandio, A.A. Deep BiLSTM attention model for spatial and temporal anomaly detection in video surveillance. Sensors 2025, 25, 251. [Google Scholar] [CrossRef]
- Guo, B.; Li, J.; Zheng, V.W.; Wang, Z.; Yu, Z. CityTransfer: Transferring inter-and intra-city knowledge for chain store site recommendation based on multi-source urban data. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2018, 1, 135. [Google Scholar] [CrossRef]
- Evans, L.; Bryant, P. LHC machine. J. Instrum. 2008, 3, S08001. [Google Scholar] [CrossRef]
- The CMS Collaboration. Development of the CMS detector for the CERN LHC Run 3. arXiv 2023, arXiv:2309.05466. [Google Scholar]
- The CMS Collaboration; Chatrchyan, S.; Hmayakyan, G.; Khachatryan, V.; Sirunyan, A.; Adam, W.; Bauer, T.; Bergauer, T.; Bergauer, H.; Dragicevic, M.; et al. The CMS experiment at the CERN LHC. J. Instrum. 2008, 3, S08004. [Google Scholar]
- Azzolini, V.; Bugelskis, D.; Hreus, T.; Maeshima, K.; Fernandez, M.J.; Norkus, A.; Fraser, P.J.; Rovere, M.; Schneider, M.A. The data quality monitoring software for the CMS experiment at the LHC: Past, present and future. EPJ Web Conf. 2019, 214, 02003. [Google Scholar] [CrossRef]
- Tuura, L.; Meyer, A.; Segoni, I.; Della Ricca, G. CMS data quality monitoring: Systems and experiences. J. Phys. Conf. Ser. 2010, 219, 072020. [Google Scholar] [CrossRef]
- De Guio, F.; The CMS Collaboration. The CMS data quality monitoring software: Experience and future prospects. J. Phys. Conf. Ser. 2014, 513, 032024. [Google Scholar] [CrossRef]
- Azzolin, V.; Andrews, M.; Cerminara, G.; Dev, N.; Jessop, C.; Marinelli, N.; Mudholkar, T.; Pierini, M.; Pol, A.; Vlimant, J.R. Improving data quality monitoring via a partnership of technologies and resources between the CMS experiment at CERN and industry. EPJ Web Conf. 2019, 214, 01007. [Google Scholar] [CrossRef][Green Version]
- Asres, M.W.; Cummings, G.; Parygin, P.; Khukhunaishvili, A.; Toms, M.; Campbell, A.; Cooper, S.I.; Yu, D.; Dittmann, J.; Omlin, C.W. Unsupervised deep variational model for multivariate sensor anomaly detection. In Proceedings of the International Conference on Progress in Informatics and Computing, Shanghai, China, 17–19 December 2021; pp. 364–371. [Google Scholar]
- Asres, M.W.; Cummings, G.; Khukhunaishvili, A.; Parygin, P.; Cooper, S.I.; Yu, D.; Dittmann, J.; Omlin, C.W. Long horizon anomaly prediction in multivariate time series with causal autoencoders. Phm Soc. Eur. Conf. 2022, 7, 21–31. [Google Scholar] [CrossRef]
- The CMS-ECAL Collaboration. Autoencoder-based Anomaly Detection System for Online Data Quality Monitoring of the CMS Electromagnetic Calorimeter. arXiv 2023, arXiv:2309.10157. [Google Scholar]
- Pol, A.A.; Azzolini, V.; Cerminara, G.; De Guio, F.; Franzoni, G.; Pierini, M.; Sirokỳ, F.; Vlimant, J.R. Anomaly detection using deep autoencoders for the assessment of the quality of the data acquired by the CMS experiment. EPJ Web Conf. 2019, 214, 06008. [Google Scholar] [CrossRef]
- Pol, A.A.; Cerminara, G.; Germain, C.; Pierini, M.; Seth, A. Detector monitoring with artificial neural networks at the CMS experiment at the CERN Large Hadron Collider. Comput. Softw. Big Sci. 2019, 3, 3. [Google Scholar] [CrossRef]
- Parra, O.J.; Pardiñas, J.G.; Pérez, L.D.P.; Janisch, M.; Klaver, S.; Lehéricy, T.; Serra, N. Human-in-the-loop reinforcement learning for data quality monitoring in particle physics experiments. arXiv 2024, arXiv:2405.15508. [Google Scholar]
- Xie, P.; Li, T.; Liu, J.; Du, S.; Yang, X.; Zhang, J. Urban flow prediction from spatiotemporal data using machine learning: A survey. Inf. Fusion 2020, 59, 1–12. [Google Scholar] [CrossRef]
- Lai, Y.; Zhu, Y.; Li, L.; Lan, Q.; Zuo, Y. STGLR: A spacecraft anomaly detection method based on spatio-temporal graph learning. Sensors 2025, 25, 310. [Google Scholar] [CrossRef]
- Strobbe, N. The upgrade of the CMS Hadron Calorimeter with Silicon photomultipliers. J. Instrum. 2017, 12, C01080. [Google Scholar] [CrossRef]
- Huber, F.; Inderka, A.; Steinhage, V. Leveraging remote sensing data for yield prediction with deep transfer learning. Sensors 2024, 24, 770. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Liu, J.; Li, M.; Sun, Y.; Shen, F. Fast sparse coding networks for anomaly detection in videos. Pattern Recognit. 2020, 107, 107515. [Google Scholar] [CrossRef]
- Hasan, M.; Choi, J.; Neumann, J.; Roy-Chowdhury, A.K.; Davis, L.S. Learning temporal regularity in video sequences. In Proceedings of the Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 733–742. [Google Scholar]
- Luo, W.; Liu, W.; Lian, D.; Tang, J.; Duan, L.; Peng, X.; Gao, S. Video anomaly detection with sparse coding inspired deep neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 1070–1084. [Google Scholar] [CrossRef] [PubMed]
- Hsu, D. Anomaly detection on graph time series. arXiv 2017, arXiv:1708.02975. [Google Scholar]
- Focardi, E. Status of the CMS detector. Phys. Procedia 2012, 37, 119–127. [Google Scholar] [CrossRef]
- Neutelings, I. CMS Coordinate System. 2023. Available online: https://tikz.net/axis3d_cms/ (accessed on 14 December 2023).
- Cheung, H.W.; The CMS Collaboration. CMS: Present status, limitations, and upgrade plans. Phys. Procedia 2012, 37, 128–137. [Google Scholar] [CrossRef][Green Version]
- Virdee, T.; The CMS Collaboration. The CMS experiment at the CERN LHC. In Proceedings of the 6th International Symposium on Particles, Strings and Cosmology, Boston, MA, USA, 22–29 March 1999.
- Wen, T.; Keyes, R. Time series anomaly detection using convolutional neural networks and transfer learning. arXiv 2019, arXiv:1905.13628. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Van Laarhoven, T. L2 regularization versus batch and weight normalization. arXiv 2017, arXiv:1706.05350. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1026–1034. [Google Scholar]
- Smith, L.N.; Topin, N. Super-convergence: Very fast training of neural networks using large learning rates. In Proceedings of the Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications, Baltimore, MD, USA, 14–18 April 2019; Volume 11006, pp. 369–386. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. JMLR 2008, 9, 2579–2605. [Google Scholar]





| Dataset | Sensor Technology | No. of Channels per RBX | No. of RBXes | Calorimeter Segmentation Ranges | Sample Size |
|---|---|---|---|---|---|
| Source (HE) | SiPM | 192 | 36 | , , depth | 20,000 |
| Target (HB) | HPD | 72 | 36 | , , depth | 7000 |
| Config. | Init Mode () | Train Mode () | ||
|---|---|---|---|---|
| Notation | Description | Notation | Description | |
| 1 | RANDOM | is initialized randomly (weights: using Kaiming uniform [58], and biases: zero) | No-TL | Complete training (fine-tuning) |
| 2 | TL-4 | is initialized randomly, except the spatial learning networks (CNN and GNN) are initialized by TL from | No-TL | Complete training (fine-tuning) |
| 3 | TL-1 | GNN of is frozen (not fine-tuned) | ||
| 4 | TL-2 | CNN of is frozen | ||
| 5 | TL-2d | CNN of is frozen | ||
| 6 | TL-3 | CNN and GNN of are frozen | ||
| 7 | TL-7 | All the spatial and temporal learning networks (CNN, GNN, and RNN) of the are initialized by TL from | TL-5 | CNN, GNN, and RNN of are frozen |
| 8 | TL-6 | CNN, GNN, and RNN of , and RNN of are frozen | ||
| w.r.t = ↓ | |||
|---|---|---|---|
| Average Score | |||
| RANDOM | No-TL | – | |
| TL-4 | No-TL | −20.7% | |
| TL-4 | TL-1 | −22.5% | |
| TL-4 | TL-2 | −26.7% | |
| TL-4 | TL-3 | −25.9% | |
| TL-4 | TL-2d | 4452.2% | |
| Best Score | |||
| RANDOM | No-TL | – | |
| TL-4 | No-TL | −16.7% | |
| TL-4 | TL-1 | −18.9% | |
| TL-4 | TL-2 | −21.6% | |
| TL-4 | TL-3 | −20.5% | |
| TL-4 | TL-2d | 4844.9% | |
| w.r.t TL-↓ | |||
|---|---|---|---|
| TL-4 | TL-2d | – | |
| TL-4 | TL-2d/[BN] | −53.0% | |
| TL-4 | TL-2d/[BN, BIAS] | −51.9% |
| w.r.t = | w.r.t = | |||
|---|---|---|---|---|
| Best Score at | ||||
| RANDOM | No-TL | – | ||
| TL-4 | No-TL | −16.9% | 0.00% | |
| TL-4 | TL-1 | −19.5% | −0.17% | |
| TL-4 | TL-2 | −29.8% | −2.23% | |
| TL-4 | TL-3 | -29.3% | −2.39% | |
| TL-7 | TL-5 | −30.3% | −8.38% | |
| TL-7 | TL-6 | −32.6% | −97.77% | |
| Best Score at | ||||
| RANDOM | No-TL | – | – | |
| TL-4 | No-TL | −16.7% | 0.00% | |
| TL-4 | TL-1 | −18.9% | −0.17% | |
| TL-4 | TL-2 | −21.6% | −2.23% | |
| TL-4 | TL-3 | −20.5% | −2.39% | |
| TL-7 | TL-5 | −20.4% | −8.38% | |
| TL-7 | TL-6 | −22.6% | −97.77% | |
| w.r.t = | |||
|---|---|---|---|
| RANDOM | No-TL | – | |
| TL-4 | No-TL | −4.0% | |
| TL-4 | TL-3 | −1.6% | |
| TL-7 | TL-5 | −8.7% | |
| TL-7 | TL-6 | −8.6% |
| Channel Anomaly Type | FPR (90%) ↓ | FPR (95%) ↓ | FPR (99%) ↓ | AUC ↑ |
|---|---|---|---|---|
| : = RANDOM and = No-TL | ||||
| Degraded () | 0.993 | |||
| Degraded () | 1.000 | |||
| Degraded () | 1.000 | |||
| Degraded () | 1.000 | |||
| Dead () | 1.000 | |||
| Noisy hot () | 1.000 | |||
| Fully hot () | 1.000 | |||
| : = TL-7 and = TL-6 | ||||
| Degraded () | 0.996 | |||
| Degraded () | 1.000 | |||
| Degraded () | 1.000 | |||
| Degraded () | 1.000 | |||
| Dead () | 1.000 | |||
| Noisy hot () | 1.000 | |||
| Fully hot () | 0.000 | 1.000 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asres, M.W.; Omlin, C.W.; Wang, L.; Yu, D.; Parygin, P.; Dittmann, J.; the CMS-HCAL Collaboration. Data Quality Monitoring for the Hadron Calorimeters Using Transfer Learning for Anomaly Detection. Sensors 2025, 25, 3475. https://doi.org/10.3390/s25113475
Asres MW, Omlin CW, Wang L, Yu D, Parygin P, Dittmann J, the CMS-HCAL Collaboration. Data Quality Monitoring for the Hadron Calorimeters Using Transfer Learning for Anomaly Detection. Sensors. 2025; 25(11):3475. https://doi.org/10.3390/s25113475
Chicago/Turabian StyleAsres, Mulugeta Weldezgina, Christian Walter Omlin, Long Wang, David Yu, Pavel Parygin, Jay Dittmann, and the CMS-HCAL Collaboration. 2025. "Data Quality Monitoring for the Hadron Calorimeters Using Transfer Learning for Anomaly Detection" Sensors 25, no. 11: 3475. https://doi.org/10.3390/s25113475
APA StyleAsres, M. W., Omlin, C. W., Wang, L., Yu, D., Parygin, P., Dittmann, J., & the CMS-HCAL Collaboration. (2025). Data Quality Monitoring for the Hadron Calorimeters Using Transfer Learning for Anomaly Detection. Sensors, 25(11), 3475. https://doi.org/10.3390/s25113475









