Abstract
This paper presents a secure control framework enhanced with an event-triggered mechanism to ensure resilient and resource-efficient operation under false data injection (FDI) attacks on sensor measurements. The proposed method integrates a Kalman filter and a neural network (NN) to construct a hybrid observer capable of detecting and compensating for malicious anomalies in sensor measurements in real time. Lyapunov-based update laws are developed for the neural network weights to ensure closed-loop system stability. To efficiently manage system resources and minimize unnecessary control actions, an event-triggered control (ETC) strategy is incorporated, updating the control input only when a predefined triggering condition is violated. A Lyapunov-based stability analysis is conducted, and linear matrix inequality (LMI) conditions are formulated to guarantee the boundedness of estimation and system errors, as well as to determine the triggering threshold used in the event-triggered mechanism. Simulation studies on a two-degree-of-freedom (2-DOF) robot manipulator validate the effectiveness of the proposed scheme in mitigating various FDI attack scenarios while reducing control redundancy and computational overhead. The results demonstrate the framework’s suitability for secure and resource-aware control in safety-critical applications.
1. Introduction
Autonomous intelligent systems, encompassing technologies such as industrial automation, autonomous vehicles, and advanced robotics, are transforming modern industries by enabling complex and high-precision operations in safety-critical environments. Among these, robot manipulators are frequently employed in domains such as industrial manufacturing [1], medical rehabilitation [2], space exploration [3], and agricultural automation [4], where precision, reliability, and autonomy are essential. Equipped with various sensors and advanced control algorithms, robot manipulators can dynamically respond to environmental changes and optimize task execution, as demonstrated in [5], significantly enhancing both operational efficiency and safety in hazardous or inaccessible environments. However, the occurrence of cyber-attacks remains a critical threat, as such attacks can compromise both the performance and safety of robot manipulators [6].
Cyber-attacks may distort sensor readings, leading to incorrect environmental interpretation, unpredictable behaviors, and potential collisions. For instance, a false data injection (FDI) attack targeting a position sensor can cause the manipulator to deviate from its intended trajectory, resulting in serious reliability degradation [7]. This threat becomes even more critical in human–robot interaction (HRI) scenarios, where the physical proximity between humans and robots increases the risk. Malicious data manipulation under FDI attacks can lead to hazardous interactions, unpredictable robotic behavior, and failures in cooperative tasks. Therefore, real-time detection and mitigation of such threats are essential to ensure safe, trustworthy, and human-centric robotic assistance in both industrial and service environments. Moreover, the implications of FDI attacks are not limited to robotic manipulators; similar risks extend across a wide range of cyber–physical systems [8], where compromised sensor data may lead to unsafe control decisions and system responses in safety-critical operations.
In response to increasing cyber-attack threats, secure control strategies have been developed to maintain system performance in the presence of cyber-attacks [9]. These strategies enable systems to compensate for detected anomalies or malicious data manipulations, ensuring continuous and accurate operation even under adversarial scenarios. A crucial aspect of such frameworks is the detection of sensor anomalies, which is typically addressed through model-based, learning-based, and hybrid approaches. Model-based methods rely on the mathematical modeling of system dynamics to detect inconsistencies by comparing real-time measurements with predicted behaviors [10,11,12]. These techniques offer low-latency response and low computational complexity, making them suitable for embedded or real-time systems. However, their performance depends heavily on the accuracy of the system model, rendering them sensitive to modeling errors and external disturbances. Conversely, learning-based methods utilize artificial intelligence and machine learning techniques, such as neural networks (NNs) and deep learning algorithms, to identify anomalies through data-driven pattern recognition [13,14,15]. While effective in capturing complex system behaviors, these approaches require large-scale training data and impose significant computational overhead, which can limit their feasibility in safety-critical systems with constrained resources. To exploit the advantages of both approaches, hybrid strategies that integrate model-based estimation with learning-based techniques have been proposed [16], achieving improved robustness against uncertainties and enhanced anomaly detection performance [17]. Beyond anomaly detection, another class of secure control strategies involves state constraints imposed by control barrier functions (CBFs); however, like most detection-based methods, these strategies are usually time-triggered [18,19].
While secure control is essential for system reliability, it must also operate efficiently under resource constraints. Traditional time-triggered control, which updates inputs periodically regardless of system behavior, often leads to redundant computation and excessive communication. To address these inefficiencies, event-triggered control (ETC) updates control actions only when a predefined condition is violated [20,21]. This selective updating reduces unnecessary transmissions, network congestion, and processor load. While conventional ETC designs neglect resilience against cyber-attacks [22,23], a growing body of research has begun to address this gap by integrating ETC mechanisms into secure control strategies [24,25,26,27,28,29,30,31]. These efforts represent important steps toward enhancing the robustness of ETC systems in adversarial environments.
The frameworks in [24,25] propose event-driven secure control triggered only upon cyber-attack detection. While practically valuable, they lack formal stability guarantees and may cause undesirable transients or degraded performance during nominal operation, especially in systems sensitive to disturbances or uncertainties.
Other ETC-based secure control strategies have focused on mitigating the impact of DoS attacks. For instance, refs. [26,27] examined ETC mechanisms under actuator-side and joint sensor–actuator DoS attacks, respectively; however, neither approach incorporates an anomaly detection mechanism. A switching-like ETC scheme is introduced in [28], where the triggering threshold adapts based on the presence or absence of acknowledgment signals as indicators of communication status. While DoS attacks typically manifest as communication losses, FDI attacks compromise data integrity without disrupting the communication flow. As a result, detection strategies relying solely on communication feedback may be ineffective, particularly against stealthy integrity attacks.
Few studies have investigated secure ETC frameworks in the presence of FDI threats. The method in [29] proposes an ETC scheme under FDI attacks modeled by Bernoulli processes, using a state-dependent triggering mechanism and recursive linear matrix inequality (LMI) conditions; however, it lacks an observer or detection mechanism, which limits its ability to distinguish intentional manipulation from model mismatch. The authors who previously investigated DoS attacks in [28] later proposed a secure observer-based ETC method for actuator-side FDI attacks in [30]. An adaptive neural network estimates the injected signal, assumed to occur only at event-triggering instants. The triggering parameters are manually selected, and weight updates are performed exclusively at those instants. While this piecewise-constant strategy improves robustness against transmission corruption, it may slow convergence and reduce estimation accuracy when events are infrequent. The scheme in [31] addresses sensor-side FDI attacks by comparing -based detection index against a fixed threshold. Although a Lyapunov-based stability proof is included, the triggering and detection thresholds are not formulated as decision variables.
To the best of our knowledge, a unified ETC framework that jointly enables real-time hybrid detection of sensor-side FDI attacks, systematic triggering threshold synthesis, and closed-loop stability guarantees under resource constraints remains largely underexplored in the current literature. Unlike conventional approaches, the proposed method introduces a unified framework that integrates a Kalman filter–neural network hybrid observer with a state-dependent event-triggered control strategy. The neural network component is governed by Lyapunov-based weight update laws, and the triggering threshold is derived within a linear matrix inequality framework to ensure both stability and communication-aware control. The proposed framework is validated through a range of FDI attack scenarios exhibiting diverse temporal characteristics, specifically designed to demonstrate its robustness across a wide spectrum of adversarial conditions.
The main contributions of this study are summarized as follows:
- (i)
- Real-time hybrid anomaly detection: A hybrid detection method is developed by combining a Kalman filter with a Lyapunov-based adaptive neural network. The update laws for the neural network weights are analytically derived to ensure that the time derivative of the unified Lyapunov function remains negative definite, thereby guaranteeing the stability of both the closed-loop system and the neural network dynamics.
- (ii)
- Resource-aware secure control: A composite control structure is designed by integrating the hybrid observer with a state-dependent event-triggered mechanism. The triggering condition is dynamically adjusted based on the estimation feedback, allowing control updates to occur only when necessary. This strategy enhances resilience while significantly reducing communication and computational overhead.
- (iii)
- Stability-guaranteed LMI-based threshold synthesis: A unified Lyapunov function is constructed to capture both estimation and triggering dynamics. Based on this formulation, LMI conditions are derived to ensure boundedness of estimation and system errors. The triggering threshold is treated as a decision variable within the LMI framework, enabling systematic optimization for both stability assurance and resource efficiency.
The remainder of the paper is organized as follows: Section 2 formulates the system dynamics and models the FDI attacks. Section 3 introduces the ETC scheme and details the controller design. Section 4 describes the attack detection framework and the design of a hybrid observer integrating a Kalman filter and a neural network. Section 5 provides a Lyapunov-based stability analysis to ensure the boundedness of estimation and system errors, as well as to determine the triggering threshold. Section 6 demonstrates the effectiveness of the proposed method through simulation results. Finally, Section 7 concludes the paper.
2. Mathematical Model
A reliable detection mechanism against cyber-attacks requires a detailed characterization of the system’s behavior. Due to the nonlinear nature of robot manipulator dynamics, direct control design is often analytically intractable. To overcome this, the nonlinear equations are linearized around an operating point, yielding a simplified model that is amenable to classical control techniques. This linear approximation not only reduces computational burden but also enables structured analysis and design procedures. It forms the basis of the proposed secure control scheme, which aims to maintain stability and performance even when sensor data integrity is compromised.
2.1. FDI Attacks Model
False data injection attacks involve manipulating sensor signals to insert misleading information into control systems. Such deception causes the system to misinterpret abnormal situations as normal, potentially leading to inappropriate control actions. Consequently, this may eventually degrade system stability and reduce overall performance [9].
The effect of the attack can be modeled as
where is a known linear function, is the signal under FDI attack, and is defined as
where denotes unknown, continuous, and bounded FDI attacks, and represents the existing noise in the measurements. For simplicity, is modeled as part of the FDI attacks [32].
To avoid detection, a well-designed FDI attack would typically avoid using very large or rapidly changing signals, as such behavior could be easily identified by anomaly detection mechanisms [33].
Assumption A1.
It is assumed that is bounded such that holds for all t, where is a known positive constant.
2.2. System Model Under FDI Attack
The two-degree-of-freedom (2-DOF) robot manipulator system comprises two rotary joints, forming the fundamental structure for precise and flexible motion control. The arm links of the manipulator are characterized by their lengths, denoted as and , and their respective masses, and . The rotational motion of the joints is described by the angles and , which define the system’s configuration. Figure 1 illustrates the physical structure of the 2-DOF robot manipulator, including its rotary joints, arm links, and their associated parameters.
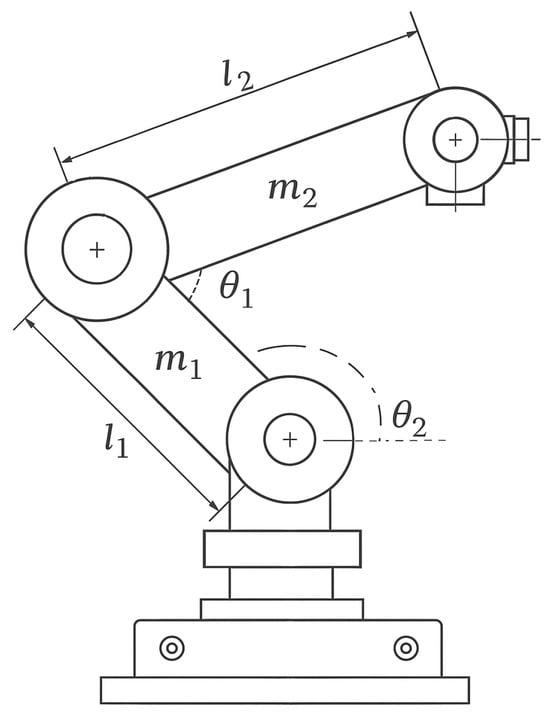
Figure 1.
The 2-DOF robot manipulator.
The dynamics of a general n-degree-of-freedom robot manipulator are mathematically formulated using the Euler–Lagrange equation [34]
In this equation, represents the joint variable vector, denotes the inertia matrix, is the Coriolis/centrifugal matrix, represents the gravity vector, includes the friction terms, and accounts for disturbances. Additionally, is the system input torque.
To facilitate the use of well-established linear control methods, which are generally more computationally efficient and easier to analyze and implement than their nonlinear counterparts, the nonlinear Euler–Lagrange model is linearized around a fixed equilibrium point. The linearization is carried out using a first-order Taylor expansion, assuming sufficiently small deviations and neglecting higher-order terms. The resulting state-space model is presented in (4), with constants and system states defined accordingly , , , .
Defining an FDI attack at the sensor introduces an additional term, , in the measurement equation, representing the influence of the attack on the system. Such an attack has the potential to destabilize the system or significantly degrade its performance [35]. The FDI attack is mathematically modeled as a function , which alters the measured feedback signals in the following manner
where represents FDI attacks that are unknown, bounded, time-varying, and continuous, directly impacting the system states.
3. Event-Triggered Control
To reduce unnecessary control updates while maintaining closed-loop stability in the presence of FDI attacks targeting sensor measurements, we propose an ETC strategy. In this framework, the control input remains constant between trigger instants and is updated only when a predefined event condition, based on the estimated state of the system, is violated. This design ensures resource efficiency while preserving performance under adversarial conditions.
Let be the time instants when an event is triggered [36]. The observer estimation error is then introduced to formulate the event-triggering criterion, defined as [37]
The observer estimation error represents the difference between the last transmitted estimate and the current observer output.
An event is triggered whenever the squared norm of the observer error surpasses the threshold defined in
which implies that the next triggering instant is determined once the inequality in (7) is violated [38]. The scalar is the design parameter that governs the trade-off between control update frequency and system performance. Rather than selecting it heuristically, this work computes by solving a linear matrix inequality derived from Lyapunov-based stability conditions, ensuring formal guarantees.
Remark 1.
The proposed event-triggering condition is designed to prevent Zeno behavior by ensuring that the time between two triggering instants is always positive. At each triggering time , the triggering error is reset to zero. If , the triggering condition is not satisfied immediately, and a positive time interval must pass before the next triggering occurs. Since is continuous, the triggering condition cannot be satisfied infinitely often in a finite time. If , the triggering condition may be violated, but this indicates that the system is in a steady state and no further control updates are needed.
The control input is designed to be updated only at the event-triggered instants according to
where K is the state feedback gain matrix, designed using the Linear Quadratic Regulator (LQR) method to ensure closed-loop stability and desired performance [39,40]. The signal represents the estimated state at the last triggering instant. The control input is held constant between triggering times using a zero-order-hold (ZOH) mechanism [36].
4. Attack Detection
In this section, a neural network-based observer framework is proposed for attack detection. A Kalman filter is first employed to estimate the system states. Given the absence of an explicit attack model and the inherently complex and uncertain nature of cyber–physical attacks, neural networks serve as powerful function approximators [41]. Thus, they are well-suited to estimate such anomalies.
4.1. Observer Design
An observer is designed to provide accurate estimations of system states, which are essential for implementing effective control strategies. Together, the linearized model, secure control framework, and state observer form a cohesive approach to addressing sensor attacks in robot manipulators, which are integral to autonomous intelligent systems operating in safety-critical environments.
Given that cyber-attacks can severely degrade control performance, reliable state estimation becomes imperative. To address this issue, an estimator based on the Kalman filter is employed to provide accurate state information under model and measurement uncertainties. The Kalman filter is a robust and widely adopted algorithm in control applications [42]. Its primary advantage lies in its capacity to fuse model-based predictions with real-time measurement data, effectively mitigating the impact of noise and uncertainty. In systems where both the process dynamics and measurement models exhibit linear behavior, the Kalman filter provides optimal state estimation in the minimum mean-square error sense [43]. In this study, it is used to refine the state prediction, ensuring the accuracy needed for both attack detection and controller execution. The mathematical representation of the estimated state dynamics is
The determination of the Kalman filter gain plays a vital role in achieving high-accuracy state estimation. The operational principle of the Kalman filter is depicted in Figure 2. According to this principle, represents the Kalman filter gain, denotes the prior covariance matrix of the state prediction error, and represents the updated covariance matrix of the state prediction error. and are the covariance matrices of the process and measurement noise, respectively. Here, k indicates the sampling instance, and represents the sampling time, with the relationship given as . At each sampling instance, the system states are iteratively updated following the algorithm presented in Figure 2, ensuring more accurate and reliable state estimation.
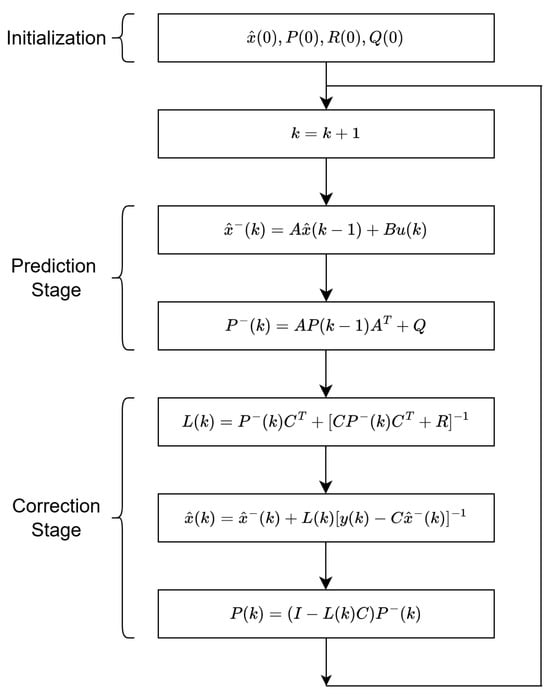
Figure 2.
Algorithm of Kalman filter.
The output estimation error is defined as
which serves as a critical input for the neural network-based observer, enabling the detection and mitigation of FDI.
4.2. Neural Network
To estimate the unknown attack signal affecting sensor measurements, a three-layer feedforward neural network is introduced. The neural network functions as a universal approximator to estimate the adversarial signal in real time [44]. However, the universal approximation theorem is guaranteed to hold only over a compact domain [45]. Since FDI attacks may occur over a non-compact time domain, a nonlinear mapping is required to project time into a compact spatial domain as proposed in [46]. Let be defined as
where is a user-defined saturation coefficient. The function can be mapped into the compact domain as
According to the universal function approximation theorem, can be represented as
Let , , and denote the number of neurons in the input, hidden, and output layers, respectively. The NN weights are given by and . The activation function is denoted by . The reconstruction error is . The input vector is constructed using previous estimates of the FDI attack and output error signals.
Note that augmenting the input vector and activation function by “1” allows us to have thresholds as the first columns of the weight matrices. Thus, any tuning of W and V then includes tuning of thresholds as well [47].
Based on (13), the output of the NN estimator is
where and are the current estimates of the ideal weights W and V. To complement the mathematical formulation, the structure of the NN is illustrated in Figure 3.
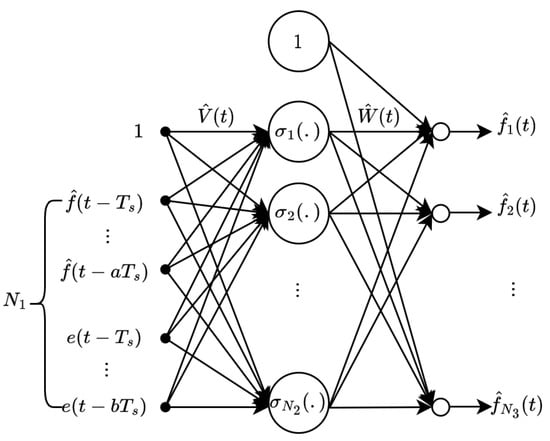
Figure 3.
The structure of the neural network.
Depicted in Figure 3, the network processes the input vector . The structure consists of two weight matrices, and , which are updated online using projection-based adaptation laws. The output nodes represent the individual components of the attack estimate vector . The NN output serves as an estimate of the unknown adversarial signal.
The mismatch between and can be approximated using a Taylor’s series approximation, which, after some algebraic manipulation, can be expressed as
where the residual term is
Here, evaluated at , and denote the outer and inner NN weight error, respectively. denotes higher-order terms and for some [48].
To minimize the estimation error defined in (16), and in accordance with the subsequent Lyapunov-based stability analysis, the update laws for the estimated weights and are designed as
where and are positive definite learning rates. To ensure that and remain bounded during adaptation, the projection operator is applied as defined in [49].
The architecture of the whole system under attack is shown in Figure 4, which summarizes the structure of the proposed event-triggered secure control system, including the hybrid observer, controller, and attack channel. The subsequent section provides the corresponding stability analysis.
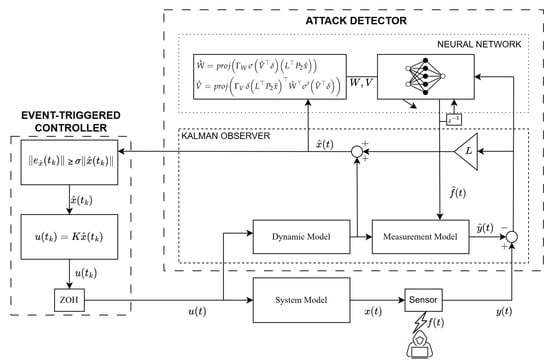
Figure 4.
The architecture of the whole system under FDI attack.
5. Stability Analysis
In this section, the stability analysis of the proposed event-triggered secure control method is presented. To ensure that the system operates robustly and reliably in the presence of sensor attacks, Lyapunov stability analysis is utilized to evaluate the system’s stability.
The following lemmas are used in the stability analysis of the closed-loop system.
Lemma 1.
Let x and y be matrices of compatible sizes. Then, the following inequality holds
Lemma 2.
The attack signal estimation error is upper-bounded by the following inequality
where denotes a positive constant [50].
Let S be defined as
where .
Remark 2.
Since and are bounded; therefore, S is bounded, i.e., , where is a known positive constant.
Theorem 1.
Proof.
A Lyapunov-based approach is used for the stability analysis of the closed-loop system. Firstly, we define observer error, which is
Then, the closed-loop system dynamics are constructed according to event-trigger-based control,
The candidate Lyapunov function is proposed as
Subsequently, the derivative of the candidate Lyapunov function is derived as
Substituting (16) into (34) and then applying (18) and (19) cancels the cross-terms. Furthermore, according to Lemma 1, an upper bound on the derivative of the candidate Lyapunov function can be defined as
To transform the stability condition into a standard LMI framework, it is necessary to derive appropriate upper bounds for the terms , and in (35). According to event condition (7), holds for all . Using Lemma 2, the upper bound for is given as follows:
The upper bound for the last term is defined as
where depends on the prediction error of system states for the observer of the and neural network attack estimation error. Substituting (36) and (37) into (35)
To manage the nonlinearity introduced by , we impose the following bound:
Accordingly, the derivative of the Lyapunov function is upper bounded as follows:
Finally, by defining the augmented state vector as
the derivative of the Lyapunov function is given by
The augmented matrix is given by
where is a symmetric matrix constructed from the cross terms and quadratic terms derived earlier. By applying the Schur complement to (43), one obtains the equivalent LMI condition given in (23). Moreover, the norm bound on is also incorporated as an additional LMI constraint. □
6. Simulation Results
Simulation studies are conducted on a 2-DOF robot manipulator with a sampling time of s. The state-space model matrices, derived from the system model defined in (4) and utilizing the parameter values provided in the literature [51], are presented as
The Kalman observer gain L and the LQR gain K are
A three-layer feedforward neural network is used to estimate the attack. The network consists of 16 input neurons, 5 hidden neurons with a hyperbolic tangent activation function, and 4 output neurons with linear activation. There is no offline training; all weight updates are performed online via Lyapunov-based adaptive update laws. To enhance the convergence rate of the estimator, which is critical for maintaining desirable closed-loop transient performance, the design parameters of the update law are selected via a genetic algorithm.
FDI attacks can manifest in different ways depending on the attacker’s strategy and the vulnerability of the system. Based on their temporal characteristics, this study considers three representative types of attacks: abrupt, incipient, and triangle-shaped. This classification enables a comprehensive assessment of the system’s resilience to both abrupt and progressively evolving FDI attacks. The system’s performance under each scenario is discussed below.
- Case 1: Abrupt Attack. Abrupt attacks involve sudden, step-like deviations that cause immediate disruption in system behavior. In this scenario, a constant bias is injected into the second state from the beginning of the simulation. The injected signal is defined as follows
- Case 2: Incipient Attack. Incipient attacks evolve slowly over time, often staying below detection thresholds and mimicking benign signal variations. The injected bias is modeled as the step response of a first-order system
- Case 3: Triangle Attack. Triangle attacks feature a linearly increasing injection followed by a linear decay, bridging the behavioral characteristics between abrupt and incipient faults. The injected signal is defined as
The actual and estimated attacks are shown in Figure 5 for all three scenarios.
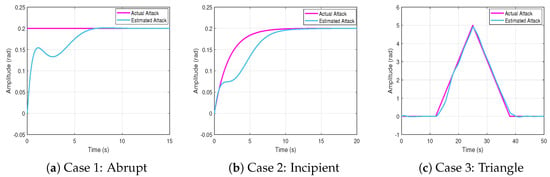
Figure 5.
Actual and estimated attacks.
The root mean square error (RMSE) between the actual and estimated attack is
where N is the total number of sampling times. The proposed neural network-based estimator effectively tracks both abrupt and gradually evolving FDI profiles. In Case 1, the estimator promptly converges to the step disturbance despite its sudden onset. In Case 2, it accurately captures the slowly increasing bias with minimal tracking delay. In Case 3, the estimator successfully follows both the rising and falling trends of the attack, demonstrating its adaptability to time-varying injection patterns. These observations are also supported by the RMSE values reported in Table 1.

Table 1.
RMSE between the estimated and actual attack signals.
To evaluate the impact of different FDI attack profiles on closed-loop performance, three representative scenarios—abrupt, incipient, and triangle-shaped—are simulated. The corresponding system responses are illustrated in Figure 6, where each plot compares three control configurations: the nominal response (ideal case without attack), the classical LQR controller (without any protective mechanism), and the proposed scheme (which integrates a hybrid estimator and an event-triggered controller). In Case 1, the classical controller exhibits a sharp deviation due to the sudden disturbance, whereas the proposed controller promptly restores the desired trajectory. In Case 2, involving a gradually increasing bias, the proposed method maintains stable tracking performance, in contrast to the classical controller, which experiences growing deviation. In Case 3, the proposed approach effectively compensates for both the rising and falling phases of the disturbance, preserving system performance and ensuring bounded behavior. These qualitative observations are quantitatively supported by the ISE values summarized in Table 2. The results demonstrate that the proposed control framework consistently achieves improved tracking accuracy by closely following the nominal output trajectory under diverse FDI attack scenarios.
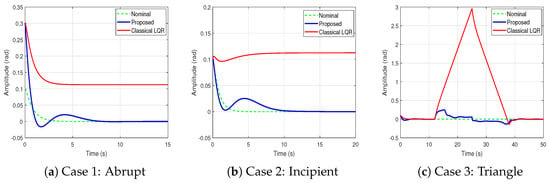
Figure 6.
Behaviour of 2nd system state under different FDI attack scenarios.

Table 2.
ISE values of controlled outputs under different FDI scenarios.
To assess the control effort associated with each method, the corresponding control signals are presented in Figure 7. Compared to the classical LQR controller, the proposed method generates smoother control actions with reduced amplitude, avoiding actuator saturation. Furthermore, Table 3 reports the control energy in terms of ISE, where the proposed scheme consistently achieves lower values, demonstrating its efficiency in minimizing control effort while preserving closed-loop performance.
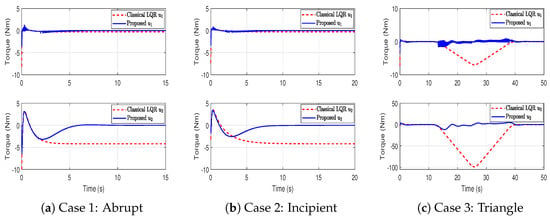
Figure 7.
Control signals of classical LQR and proposed method under different FDI attack scenarios.

Table 3.
ISE values of control signals under different FDI attack scenarios.
The event-triggering condition is designed based on the parameter , computed using the MATLAB R2018b LMI Toolbox. The resulting inter-event times for each scenario are illustrated in Figure 8, where the minimum inter-event time across all cases is 0.0010 s. The average inter-event times are 0.0369, 0.0389, and 0.0353 s for the abrupt, incipient, and triangle attack scenarios, respectively. Table 4 summarizes the number of control signal transmissions. Compared to the time-triggered approach, the proposed event-triggered scheme achieves a reduction of , , and in Cases 1–3, significantly decreasing communication load while maintaining control performance. This confirms that the proposed mechanism ensures strictly positive inter-event intervals and enables efficient resource utilization under various FDI attacks.
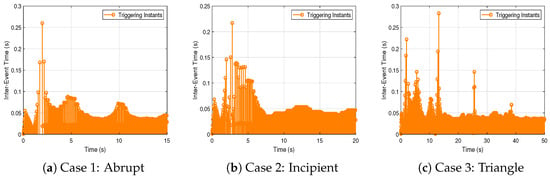
Figure 8.
Inter-event times under different FDI attack scenarios.

Table 4.
Number of control input transmissions under different FDI attack scenarios.
To evaluate the computational cost, the average CPU time per control step is calculated using built-in timing utilities provided by the simulation environment. The experiment is repeated several times to account for variability, and the average value is reported. As shown in Table 5, although the proposed method incurs slightly higher per-step computation time compared to the periodic approach, it demonstrates the potential of the framework for energy-efficient embedded implementations.

Table 5.
The total CPU time per control step.
Remark 3.
To assess the real-time feasibility of the proposed method, we measure the execution time of each control cycle in the simulation environment. The implementation is performed in MATLAB/Simulink on a desktop computer equipped with an Intel Core i7 processor (2.80 GHz, 16 GB RAM). Under a 1 ms sampling interval, the combined computation time for the observer update, neural network weight adaptation, and control signal calculation is approximately 0.2 ms per cycle. Although the control input is updated only at event-triggered instants and held constant otherwise, the computations are performed at each step. The neural network operates online using a lightweight projection-based adaptation law, without backpropagation or batch processing. Its structure is selected through offline optimization using a genetic algorithm and remains fixed during execution. These properties suggest that the proposed method is compatible with real-time implementation on embedded platforms equipped with sufficient processing capabilities, such as those based on high-end microcontrollers or FPGA-integrated systems.
7. Conclusions
This study presents an event-triggered secure control framework to address false data injection attacks targeting sensor measurements in robotic manipulators. Unlike conventional secure control strategies that rely on continuous monitoring and frequent control updates, the proposed method integrates a state-dependent event-triggered mechanism that selectively updates the control input only when necessary, significantly reducing communication and computational overhead. A hybrid observer, combining a model-based Kalman filter with a learning-based neural network, is designed to compensate for malicious sensor anomalies in real time. In addition, a Lyapunov-based update law is designed for the neural network weights to preserve closed-loop stability. The stability of the overall closed-loop system is analytically guaranteed through a Lyapunov-based analysis, supported by linear matrix inequality conditions that ensure the boundedness of estimation and system errors and provide a triggering threshold for the event-triggered mechanism.
Simulation results on a two-degree-of-freedom robot manipulator validate the effectiveness of the proposed secure control framework against three representative false data injection attack scenarios: abrupt, incipient, and triangle-shaped. In all cases, the proposed method successfully detects the injected attacks and restores the nominal system trajectory. The root mean square error between the actual and estimated attack is in the abrupt case, in the incipient case and in the triangle-shaped case. Moreover, the control signal transmissions are reduced by , , and , respectively, demonstrating the effectiveness of the event-triggered mechanism. These results confirm that the proposed framework achieves robust fault estimation and efficient control, making it suitable for resource-constrained embedded systems exposed to adversarial threats.
Beyond industrial robotics, the proposed framework can be applied to a broader range of cyber–physical systems such as autonomous vehicles, aerospace systems, and medical robotics, where secure operation and computational efficiency are essential. Many of these systems can be described by Euler–Lagrange dynamics or similar mechanical modeling approaches, which makes them suitable for applying linear control and estimation methods based on local approximations. The method developed in this study combines hybrid state estimation with neural-network-based compensation and event-triggered feedback. It relies on general principles from control theory, including observer design and Lyapunov-based stability analysis. This opens the door to adapting the same structure for a wider class of systems where real-time performance, robustness against sensor attacks, and model-based estimation are critical requirements.
Author Contributions
Conceptualization, L.U. and J.D.; methodology, L.U. and J.D.; formal analysis, N.K.K.; investigation, N.K.K.; writing—original draft preparation, N.K.K.; writing—review and editing, L.U. and J.D.; supervision, L.U. and J.D.; visualization, N.K.K.; numerical analysis, N.K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 2-DOF | Two-degree-of-freedom |
| CBFs | Control barrier functions |
| DoS | Denial of service |
| ETC | Event-triggered control |
| FDI | False data injection |
| HRI | Human–robot interaction |
| ISE | Integral square error |
| LMI | Linear matrix inequality |
| LQR | Linear quadratic regulator |
| NN | Neural network |
| RMSE | Root mean square error |
| UUB | Uniform ultimate bounded |
| ZOH | Zero-order hold |
References
- Alhama Blanco, P.J.; Abu-Dakka, F.J.; Abderrahim, M. Practical Use of Robot Manipulators as Intelligent Manufacturing Systems. Sensors 2018, 18, 2877. [Google Scholar] [CrossRef] [PubMed]
- Chellal, A.A.; Lima, J.; Gonçalves, J.; Fernandes, F.P.; Pacheco, F.; Monteiro, F.; Brito, T.; Soares, S. Robot-Assisted Rehabilitation Architecture Supported by a Distributed Data Acquisition System. Sensors 2022, 22, 9532. [Google Scholar] [CrossRef] [PubMed]
- Kuck, E.; Sands, T. Space Robot Sensor Noise Amelioration Using Trajectory Shaping. Sensors 2024, 24, 666. [Google Scholar] [CrossRef] [PubMed]
- Seo, D.; Oh, I.S. Gripping Success Metric for Robotic Fruit Harvesting. Sensors 2025, 25, 181. [Google Scholar] [CrossRef]
- Zabalza, J.; Fei, Z.; Wong, C.; Yan, Y.; Mineo, C.; Yang, E.; Rodden, T.; Mehnen, J.; Pham, Q.C.; Ren, J. Smart Sensing and Adaptive Reasoning for Enabling Industrial Robots with Interactive Human-Robot Capabilities in Dynamic Environments—A Case Study. Sensors 2019, 19, 1354. [Google Scholar] [CrossRef]
- Ahmad Yousef, K.M.; AlMajali, A.; Ghalyon, S.A.; Dweik, W.; Mohd, B.J. Analyzing Cyber-Physical Threats on Robotic Platforms. Sensors 2018, 18, 1643. [Google Scholar] [CrossRef]
- Dong, Y.; Gupta, N.; Chopra, N. False Data Injection Attacks in Bilateral Teleoperation Systems. IEEE Trans. Control Syst. Technol. 2020, 28, 1168–1176. [Google Scholar] [CrossRef]
- Ahmed, M.; Pathan, A.S.K. False data injection attack (FDIA): An overview and new metrics for fair evaluation of its countermeasure. Complex Adapt. Syst. Model. 2020, 8, 4. [Google Scholar] [CrossRef]
- Xing, W.; Shen, J. Security Control of Cyber–Physical Systems under Cyber Attacks: A Survey. Sensors 2024, 24, 3815. [Google Scholar] [CrossRef]
- Lee, C. Observability Decomposition-Based Decentralized Kalman Filter and Its Application to Resilient State Estimation under Sensor Attacks. Sensors 2022, 22, 6909. [Google Scholar] [CrossRef]
- El Mrabet, Z.; Arjoune, Y.; El Ghazi, H.; Abou Al Majd, B.; Kaabouch, N. Primary User Emulation Attacks: A Detection Technique Based on Kalman Filter. J. Sens. Actuator Netw. 2018, 7, 26. [Google Scholar] [CrossRef]
- Barzegari, Y.; Zarei, J.; Razavi-Far, R.; Saif, M.; Palade, V. Resilient Consensus Control Design for DC Microgrids against False Data Injection Attacks Using a Distributed Bank of Sliding Mode Observers. Sensors 2022, 22, 2644. [Google Scholar] [CrossRef] [PubMed]
- Inayat, U.; Zia, M.F.; Mahmood, S.; Khalid, H.M.; Benbouzid, M. Learning-Based Methods for Cyber Attacks Detection in IoT Systems: A Survey on Methods, Analysis, and Future Prospects. Electronics 2022, 11, 1502. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, S.; Ma, W.; Qu, J. Research on Attack Detection of Cyber Physical Systems Based on Improved Support Vector Machine. Mathematics 2022, 10, 2713. [Google Scholar] [CrossRef]
- Alaoui, R.L.; Nfaoui, E.H. Deep Learning for Vulnerability and Attack Detection on Web Applications: A Systematic Literature Review. Future Internet 2022, 14, 118. [Google Scholar] [CrossRef]
- Abbaspour, A.; Mokhtari, S.; Sargolzaei, A.; Yen, K.K. A Survey on Active Fault-Tolerant Control Systems. Electronics 2020, 9, 513. [Google Scholar] [CrossRef]
- Talebi, H.; Khorasani, K.; Tafazoli, S. A recurrent neural-network-based sensor and actuator fault detection and isolation for nonlinear systems with application to the satellite’s attitude control subsystem. IEEE Trans. Neural Netw. 2009, 20, 45–60. [Google Scholar] [CrossRef]
- Qin, C.; Qiao, X.; Wang, J.; Zhang, D.; Hou, Y.; Hu, S. Barrier-Critic Adaptive Robust Control of Nonzero-Sum Differential Games for Uncertain Nonlinear Systems With State Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 50–63. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Y.; Meng, L.; Yan, J.; Qin, C. Adaptive critic design for safety-optimal FTC of unknown nonlinear systems with asymmetric constrained-input. ISA Trans. 2024, 155, 309–318. [Google Scholar] [CrossRef]
- Tabuada, P. Event-triggered real-time scheduling of stabilizing control tasks. IEEE Trans. Autom. Control 2007, 52, 1680–1685. [Google Scholar] [CrossRef]
- Heemels, W.; Johansson, K.; Tabuada, P. An introduction to event-triggered and self-triggered control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3270–3285. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, G. Event-driven observer-based output feedback control for linear systems. Automatica 2014, 50, 1852–1859. [Google Scholar] [CrossRef]
- Tallapragada, P.; Chopra, N. Event-triggered dynamic output feedback control for LTI systems. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 6597–6602. [Google Scholar] [CrossRef]
- Sahoo, S.; Dragicevic, T.; Blaabjerg, F. An Event-Driven Resilient Control Strategy for DC Microgrids. IEEE Trans. Power Electron. 2020, 35, 13714–13724. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, R.; He, X. New Approaches to Detection and Secure Control for Cyber-physical Systems Against False Data Injection Attacks. Int. J. Control Autom. Syst. 2025, 23, 332–345. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, G. Secure cooperative event-triggered control of linear multiagent systems under DoS Attacks. IEEE Trans. Control Syst. Technol. 2020, 28, 741–752. [Google Scholar] [CrossRef]
- Lu, W.; Yin, X.; Fu, Y.; Gao, Z. Observer-Based Event-Triggered Predictive Control for Networked Control Systems under DoS Attacks. Sensors 2020, 20, 6866. [Google Scholar] [CrossRef]
- Yang, M.; Zhai, J. Observer-Based Switching-Like Event-Triggered Control of Nonlinear Networked Systems Against DoS Attacks. IEEE Trans. Control Netw. Syst. 2022, 9, 1375–1384. [Google Scholar] [CrossRef]
- Li, X.M.; Zhou, Q.; Li, P.; Li, H.; Lu, R. Event-Triggered Consensus Control for Multi-Agent Systems Against False Data-Injection Attacks. IEEE Trans. Cybern. 2020, 50, 1856–1866. [Google Scholar] [CrossRef]
- Yang, M.; Zhai, J. Observer-based dynamic event-triggered secure control for nonlinear networked control systems with false data injection attacks. Inf. Sci. 2023, 644, 119262. [Google Scholar] [CrossRef]
- Li, J.; Li, X.M.; Cheng, Z.; Ren, H.; Li, H. Event-based secure control for cyber-physical systems against false data injection attacks. Inf. Sci. 2024, 679, 121093. [Google Scholar] [CrossRef]
- Sargolzaei, A. A Lyapunov-based control design for centralised networked control systems under false-data-injection attacks. Int. J. Syst. Sci. 2024, 55, 2759–2770. [Google Scholar] [CrossRef]
- Hu, J.; Yang, X.; Yang, L.X. A Framework for Detecting False Data Injection Attacks in Large-Scale Wireless Sensor Networks. Sensors 2024, 24, 1643. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhao, H.; Li, T. Adaptive Super-Twisting Tracking for Uncertain Robot Manipulators Based on the Event-Triggered Algorithm. Sensors 2025, 25, 1616. [Google Scholar] [CrossRef] [PubMed]
- Pang, Z.H.; Liu, G.P.; Zhou, D.; Hou, F.; Sun, D. Two-Channel False Data Injection Attacks Against Output Tracking Control of Networked Systems. IEEE Trans. Ind. Electron. 2016, 63, 3242–3251. [Google Scholar] [CrossRef]
- Jinhui, Z.; Danyang, Z.; Daokuan, W. Observer-based control for linear system with event-triggered sensor. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 5747–5752. [Google Scholar]
- Acho, L. Event-Driven Observer-Based Smart-Sensors for Output Feedback Control of Linear Systems. Sensors 2017, 17, 2028. [Google Scholar] [CrossRef]
- Chen, X.; Hao, F. Observer-based event-triggered control for certain and uncertain linear systems. IMA J. Math. Control Inf. 2013, 30, 527–542. [Google Scholar] [CrossRef]
- Fortuna, L.; Frasca, M. Optimal and Robust Control: Advanced Topics with MATLAB®; CRC Press: Boca Raton, FL, USA, 2012; pp. 1–231. [Google Scholar] [CrossRef]
- Dul, F.; Lichota, P.; Rusowicz, A. Generalized Linear Quadratic Control for a Full Tracking Problem in Aviation. Sensors 2020, 20, 2955. [Google Scholar] [CrossRef]
- Lewis, F.L.; Jagannathan, S.; Yesildirak, A. Neural Network Control of Robot Manipulators and Nonlinear Systems; Taylor & Francis: London, UK, 1999. [Google Scholar]
- Valade, A.; Acco, P.; Grabolosa, P.; Fourniols, J.Y. A Study about Kalman Filters Applied to Embedded Sensors. Sensors 2017, 17, 2810. [Google Scholar] [CrossRef]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering: Theory and Practice with MATLAB; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lewis, F. Neural network control of robot manipulators. IEEE Expert 1996, 11, 64–75. [Google Scholar] [CrossRef]
- Cotter, N. The Stone-Weierstrass theorem and its application to neural networks. IEEE Trans. Neural Netw. 1990, 1, 290–295. [Google Scholar] [CrossRef]
- Chakraborty, I.; Mehta, S.S.; Doucette, E.; Dixon, W.E. Control of an input delayed uncertain nonlinear system with adaptive delay estimation. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1779–1784. [Google Scholar] [CrossRef]
- Patre, P.M.; MacKunis, W.; Kaiser, K.; Dixon, W.E. Asymptotic Tracking for Uncertain Dynamic Systems Via a Multilayer Neural Network Feedforward and RISE Feedback Control Structure. IEEE Trans. Autom. Control 2008, 53, 2180–2185. [Google Scholar] [CrossRef]
- Sargolzaei, A. A Secure Control Design for Networked Control System with Nonlinear Dynamics under False-Data-Injection Attacks. In Proceedings of the 2021 American Control Conference (ACC), Online, 25–28 May 2021; pp. 2693–2699. [Google Scholar] [CrossRef]
- Krstic, M.; Kokotovic, P.V.; Kanellakopoulos, I. Nonlinear and Adaptive Control Design; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Abbaspour, A.; Sargolzaei, A.; Forouzannezhad, P.; Yen, K.K.; Sarwat, A.I. Resilient Control Design for Load Frequency Control System under False Data Injection Attacks. IEEE Trans. Ind. Electron. 2020, 67, 7951–7962. [Google Scholar] [CrossRef]
- Mustafa, A.M.; Al-Saif, A. Modeling, simulation and control of 2-R robot. Glob. J. Res. Eng.-GJRE-H 2014, 14, 45–60. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).