An Elastic Fine-Tuning Dual Recurrent Framework for Non-Rigid Point Cloud Registration
Abstract
1. Introduction
- (1)
- We present that a point cloud non-rigid transform can comprise some rigid transforms with different weights.
- (2)
- We achieve fine-tuning incremental changes between successive rigid transformations, which increases the coherence and edge smoothness from rigid to non-rigid transformations.
- (3)
- We propose a local spatial consistency metric loss function to compute similarities between the transformed neighborhoods of corresponding points, which makes the rigid incremental transformations sufficiently small.
- (4)
- Extensive experiments have been conducted on various datasets for the point cloud non-rigid and rigid registration, which shows that the method proposed in this paper has SOTA performance.
2. Related Work
3. Problem Formulation
4. Methodology
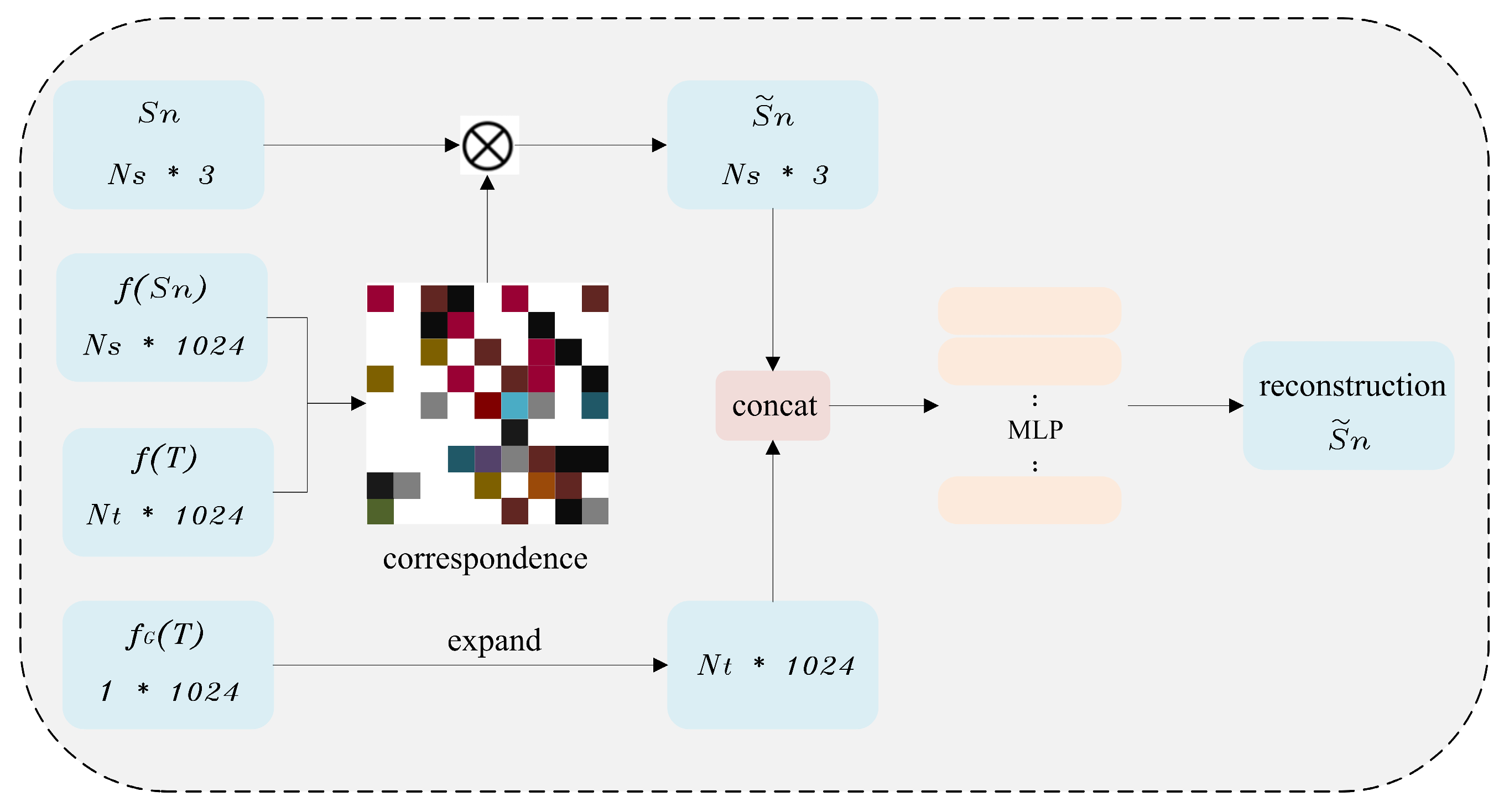
4.1. Feature Extraction
4.2. Approximation Transformation Module
| Algorithm 1 Inner-layer computation | |
| 1 | input: point cloud feature , point cloud feature , Jacobi matrix of |
| 2 | output: the n-th stage point cloud , weight vector |
| 3 | begin |
| 4 | attention compute as ’ |
| 5 | compute with , , and |
| 6 | for > threshold value |
| 7 | update |
| 8 | and compute with , , and |
| 9 | end for |
| 10 | obtain incremental transformation |
| 11 | compute with incremental transformation and |
| 12 | attention compute as ’ |
| 13 | update to form new weight vector |
| 14 | end |
4.3. Loss Function Constraints
5. Experimentation and Analysis
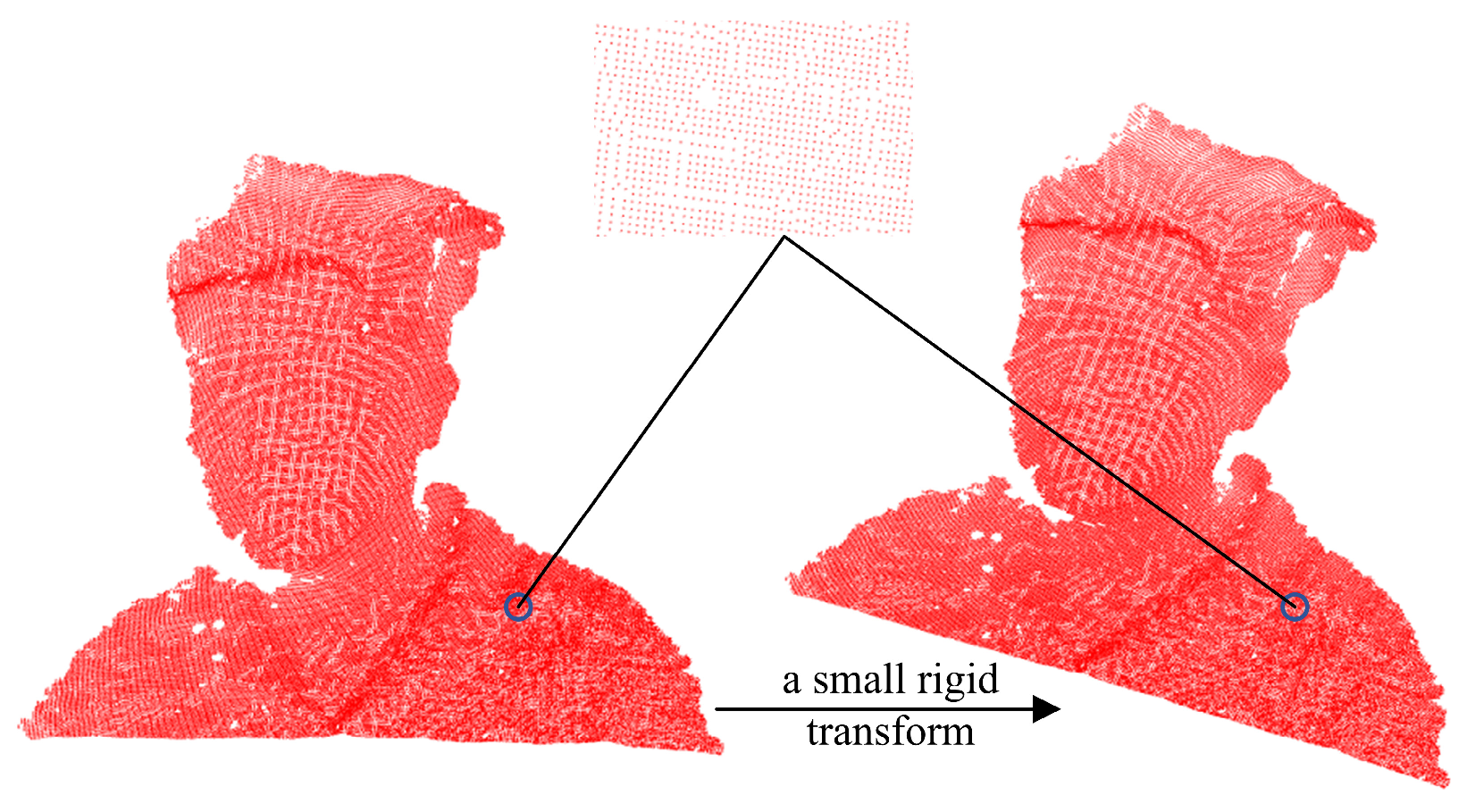
5.1. Dataset Processing
5.2. Experiment Evaluation
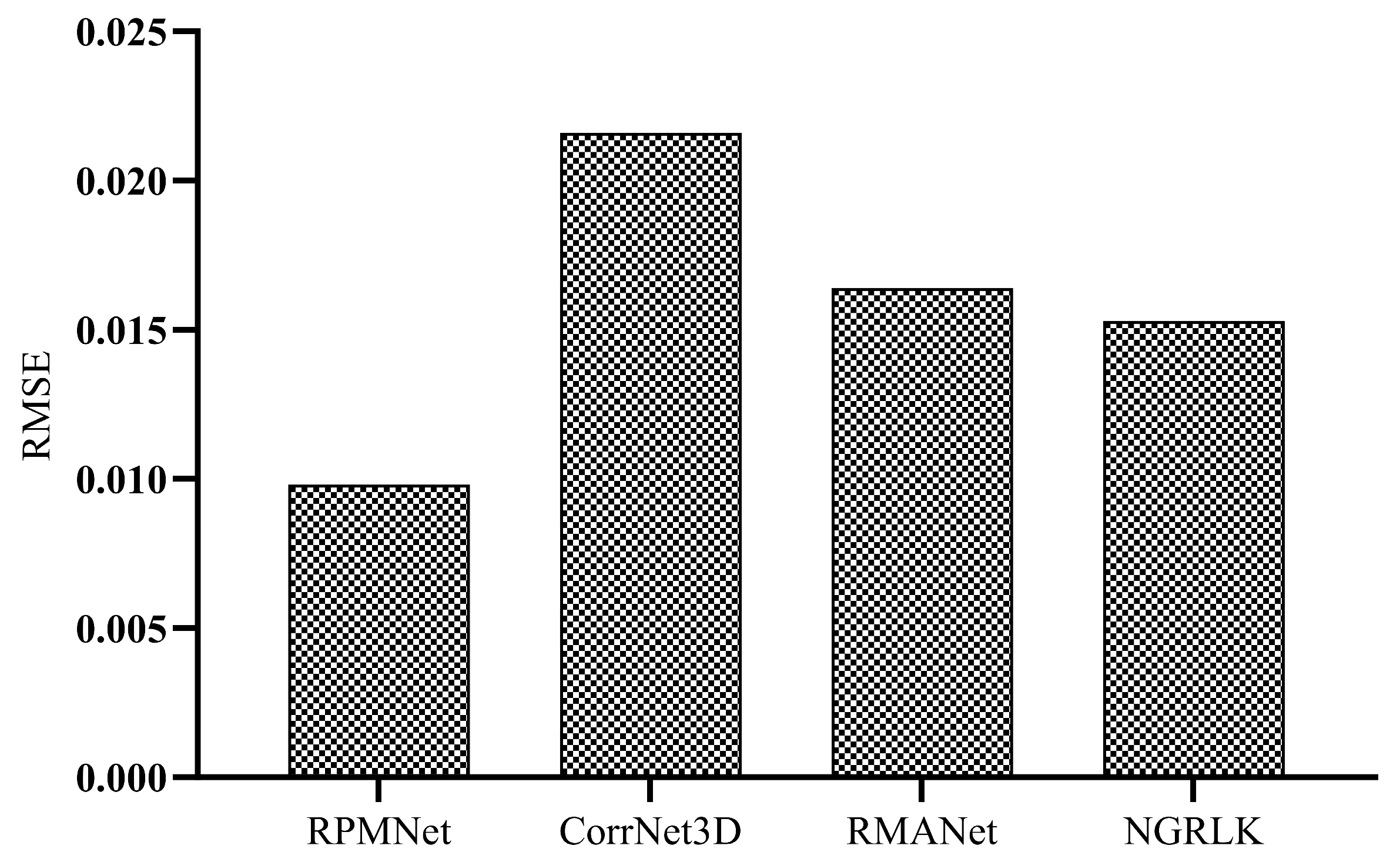
5.3. Non-Rigid Experiment
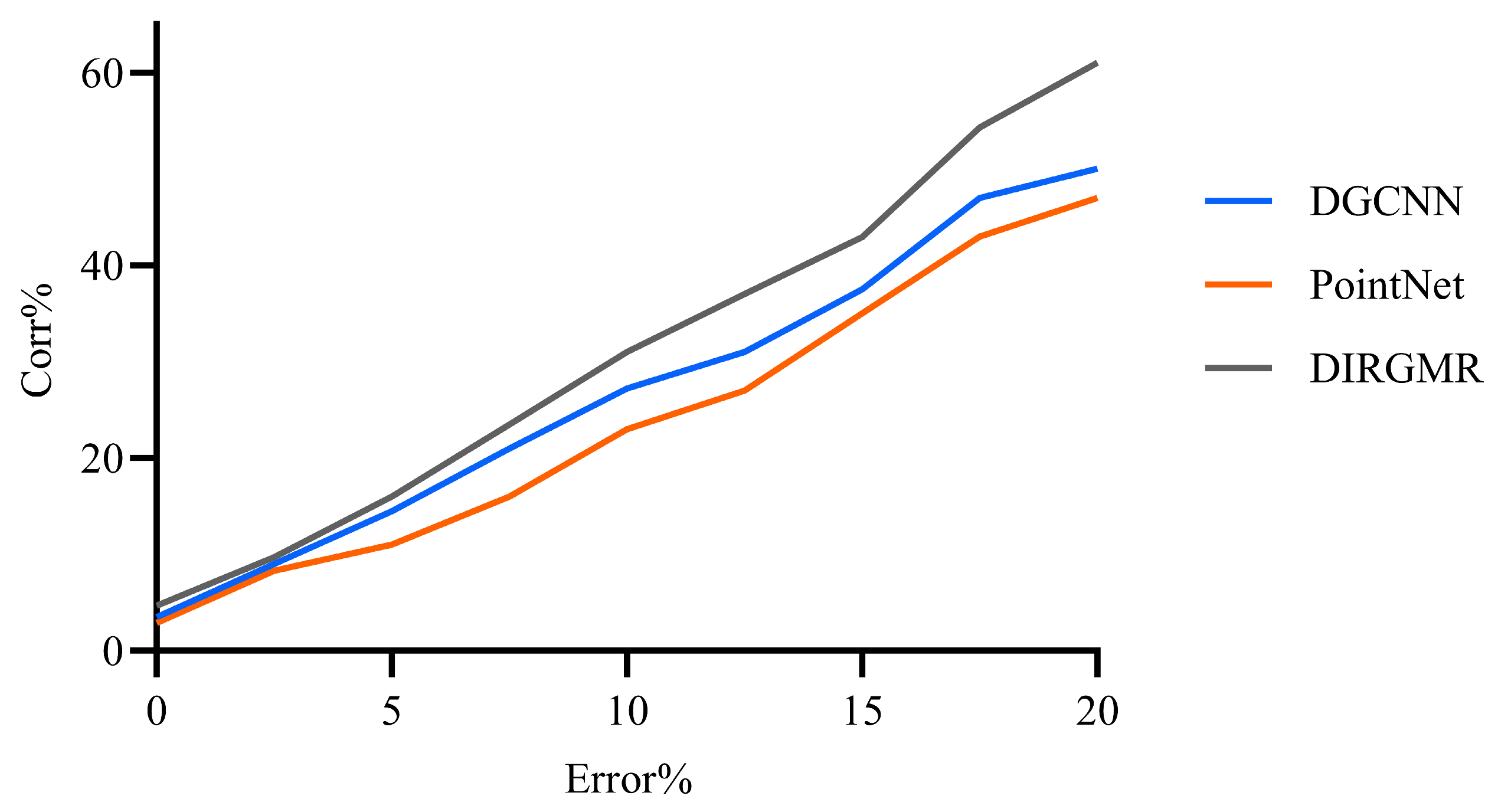
5.4. Rigid Experiment
5.5. Ablation Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Chen, Y.; Li, J. Remote sensing image registration based on dual-channel neural network and robust point set registration algorithm. In Proceedings of the 2020 5th International Conference on Intelligent Informatics and Biomedical Sciences (ICIIBMS), Okinawa, Japan, 18–20 November 2020; pp. 208–215. [Google Scholar]
- Yoo, H.; Choi, A.; Mun, J.H. Acquisition of point cloud in CT image space to improve accuracy of surface registration: Application to neurosurgical navigation system. J. Mech. Sci. Technol. 2020, 34, 2667–2677. [Google Scholar] [CrossRef]
- Lu, W.; Zhou, Y.; Wan, G.; Hou, S.; Song, S. L3-net: Towards learning based lidar localization for autonomous driving. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 6382–6391. [Google Scholar]
- Wang, M.; Yue, G.; Xiong, J.; Tian, S. Intelligent Point Cloud Processing, Sensing, and Understanding. Sensors 2024, 24, 283. [Google Scholar] [CrossRef]
- Li, Y.; Harada, T. Lepard: Learning partial point cloud matching in rigid and deformable scenes. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 5544–5554. [Google Scholar]
- Feng, W.; Zhang, J.; Cai, H.; Xu, H.; Hou, J.; Bao, H. Recurrent Multi-view Alignment Network for Unsupervised Surface Registration. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10292–10302. [Google Scholar]
- Zeng, Y.; Qian, Y.; Zhu, Z.; Hou, J.; Yuan, H.; He, Y. CorrNet3D: Unsupervised End-to-end Learning of Dense Correspondence for 3D Point Clouds. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 6048–6057. [Google Scholar]
- Wang, M.; Tian, S. A Brief Introduction to Intelligent Point Cloud Processing, Sensing, and Understanding: Part II. Sensors 2025, 25, 1310. [Google Scholar] [CrossRef]
- Newcombe, R.A.; Fox, D.; Seitz, S.M. DynamicFusion: Reconstruction and tracking of non-rigid scenes in real-time. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 343–352. [Google Scholar]
- Xu, L.; Su, Z.; Han, L.; Yu, T.; Liu, Y.; Fang, L. UnstructuredFusion: Realtime 4D Geometry and Texture Reconstruction Using Commercial RGBD Cameras. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2508–2522. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Deng, B.; Xu, W.; Zhang, J. Quasi-Newton Solver for Robust Non-Rigid Registration. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7597–7606. [Google Scholar]
- Myronenko, A.; Song, X.; Carreira-Perpinan, M. Non-rigid point set registration: Coherent Point Drift. In Advances in Neural Information Processing Systems 19; MIT Press: Cambridge, MA, USA, 2007; pp. 1009–1016. [Google Scholar]
- Anguelov, D.; Srinivasan, P.; Pang, H.C.; Koller, D.; Thrun, S.; Davis, J. The correlated correspondence algorithm for unsupervised registration of nonrigid surfaces. In Advances in Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada, 2004; pp. 33–40. [Google Scholar]
- Sahillioğlu, Y. A Genetic Isometric Shape Correspondence Algorithm with Adaptive Sampling. ACM Trans. Graph. (TOG) 2018, 37, 1–14. [Google Scholar] [CrossRef]
- Ovsjanikov, M.; Merigot, Q.; Memoli, F.; Guibas, L. One Point Isometric Matching with the Heat Kernel. Comput. Graph. Forum 2010, 29, 1555–1564. [Google Scholar] [CrossRef]
- Huang, Q.-X.; Adams, B.; Wicke, M.; Guibas, L.J. Non-rigid registration under isometric deformations. Comput. Graph. Forum 2008, 27, 1449–1457. [Google Scholar] [CrossRef]
- Rodola, E.; Bronstein, A.M.; Albarelli, A.; Bergamasco, F.; Torsello, A. A game-theoretic approach to deformable shape matching. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 182–189. [Google Scholar]
- Rampini, A.; Tallini, I.; Ovsjanikov, M.; Bronstein, A.M.; Rodolà, E. Correspondence-Free Region Localization for Partial Shape Similarity via Hamiltonian Spectrum Alignment. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Quebec City, QC, Canada, 16–19 September 2019; pp. 37–46. [Google Scholar]
- Attaiki, S.; Pai, G.; Ovsjanikov, M. DPFM: Deep Partial Functional Maps. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 175–185. [Google Scholar]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A Skinned Multi-Person Linear Model. Acm Trans. Graph. 2015, 34, 248:1–248:16. [Google Scholar] [CrossRef]
- Groueix, T.; Fisher, M.; Kim, V.G.; Russell, B.C.; Aubry, M. 3D-CODED: 3D Correspondences by Deep Deformation. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Volume 11206, pp. 235–251. [Google Scholar]
- Wang, S.; Geiger, A.; Tang, S. Locally Aware Piecewise Transformation Fields for 3D Human Mesh Registration. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 7635–7644. [Google Scholar]
- Wang, L.; Chen, J.; Li, X.; Fang, Y. Non-Rigid Point Set Registration Networks. arXiv 2019, arXiv:1904.01428. [Google Scholar]
- Wang, L.; Li, X.; Chen, J.; Fang, Y. Coherent Point Drift Networks: Unsupervised Learning of Non-Rigid Point Set Registration. arXiv 2019, arXiv:1906.03039. [Google Scholar]
- Halimi, O.; Litany, O.; Rodola, E.; Bronstein, A.M.; Kimmel, R. Unsupervised Learning of Dense Shape Correspondence. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4365–4374. [Google Scholar]
- Bozic, A.; Zollhofer, M.; Theobalt, C.; Nießner, M. DeepDeform: Learning Non-Rigid RGB-D Reconstruction With Semi-Supervised Data. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7000–7010. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Zhou, W.; Lu, J.; Yue, W. A New Semantic Segmentation Method of Point Cloud Based on PointNet and VoxelNet. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 803–808. [Google Scholar]
- Zhao, K.; Lu, H.; Li, Y. PointNetX: Part Segmentation Based on PointNet Promotion. Commun. Comput. Inf. Sci. 2023, 1732, 65–76. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. PPFNet: Global Context Aware Local Features for Robust 3D Point Matching. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 195–205. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. PPF-FoldNet: Unsupervised Learning of Rotation Invariant 3D Local Descriptors. In European onference on Computer Vision; Springer: Munich, Germany, 2018; Volume 1808.10322, pp. 1–19. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. PointNetLK: Robust & Efficient Point Cloud Registration Using PointNet. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7156–7165. [Google Scholar]
- Sarode, V.; Li, X.; Goforth, H.; Aoki, Y.; Srivatsan, R.A.; Lucey, S.; Choset, H. Pcrnet: Point cloud registration network using pointnet encoding. arXiv 2019, arXiv:1908.07906. [Google Scholar]
- Sharp, N.; Attaiki, S.; Crane, K.; Ovsjanikov, M. DiffusionNet: Discretization Agnostic Learning on Surfaces. ACM Trans. Graph. (TOG) 2020, 41, 1–16. [Google Scholar] [CrossRef]
- Shimada, S.; Golyanik, V.; Tretschk, E.; Stricker, D.; Theobalt, C. DispVoxNets: Non-Rigid Point Set Alignment with Supervised Learning Proxies. In Proceedings of the 2019 International Conference on 3D Vision (3DV), Québec City, QC, Canada, 16–19 September 2019; pp. 27–36. [Google Scholar]
- Trappolini, G.; Cosmo, L.; Moschella, L.; Marin, R.; Melzi, S.; Rodolà, E. Shape registration in the time of transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 5731–5744. [Google Scholar]
- Boscaini, D.; Masci, J.; Rodolà, E.; Bronstein, M. Learning shape correspondence with anisotropic convolutional neural networks. In 30th Conference on Neural Information Processing Systems (NIPS 2016); MIT Press: Barcelona, Spain, 2016; Volume 29, pp. 1–9. [Google Scholar]
- Wang, L.; Zhou, N.; Huang, H.; Wang, J.; Li, X.; Fang, Y. GP-Aligner: Unsupervised Groupwise Nonrigid Point Set Registration Based on Optimizable Group Latent Descriptor. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Baker, S.; Matthews, I. Lucas-Kanade 20 Years On: A Unifying Framework. Int. J. Comput. Vis. 2004, 56, 221–255. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph CNN for learning on point clouds. ACM Trans. Graph. (TOG) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Yuan, M.; Li, X. Point cloud registration method for indoor depth sensor acquisition system based on dual graph computation with irregular shape factors. IET Image Process. 2024, 18, 2161–2178. [Google Scholar] [CrossRef]
- Vakalopoulou, M.; Chassagnon, G.; Bus, N.; Marini, R.; Zacharaki, E.I.; Revel, M.P.; Paragios, N. Atlasnet: Multi-atlas non-linear deep networks for medical image segmentation. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2018: 21st International Conference, Granada, Spain, 16–20 September 2018; Springer: Granada, Spain, 2018; pp. 658–666. [Google Scholar]
- Puy, G.; Boulch, A.; Marlet, R. Flot: Scene flow on point clouds guided by optimal transport. In European Conference on Computer Vision; Springer: Glasgow, UK, 2020; pp. 527–544. [Google Scholar]
- Yuan, M.; Li, X.; Xu, J.; Jia, C.; Li, X. 3D foot scanning using multiple RealSense cameras. Multimed. Tools Appl. 2021, 80, 22773–22793. [Google Scholar] [CrossRef]
- Liu, X.; Qi, C.R.; Guibas, L.J. Flownet3d: Learning scene flow in 3d point clouds. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 529–537. [Google Scholar]
- Yew, Z.J.; Lee, G.H. RPM-Net: Robust Point Matching Using Learned Features. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11821–11830. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 14. [Google Scholar]








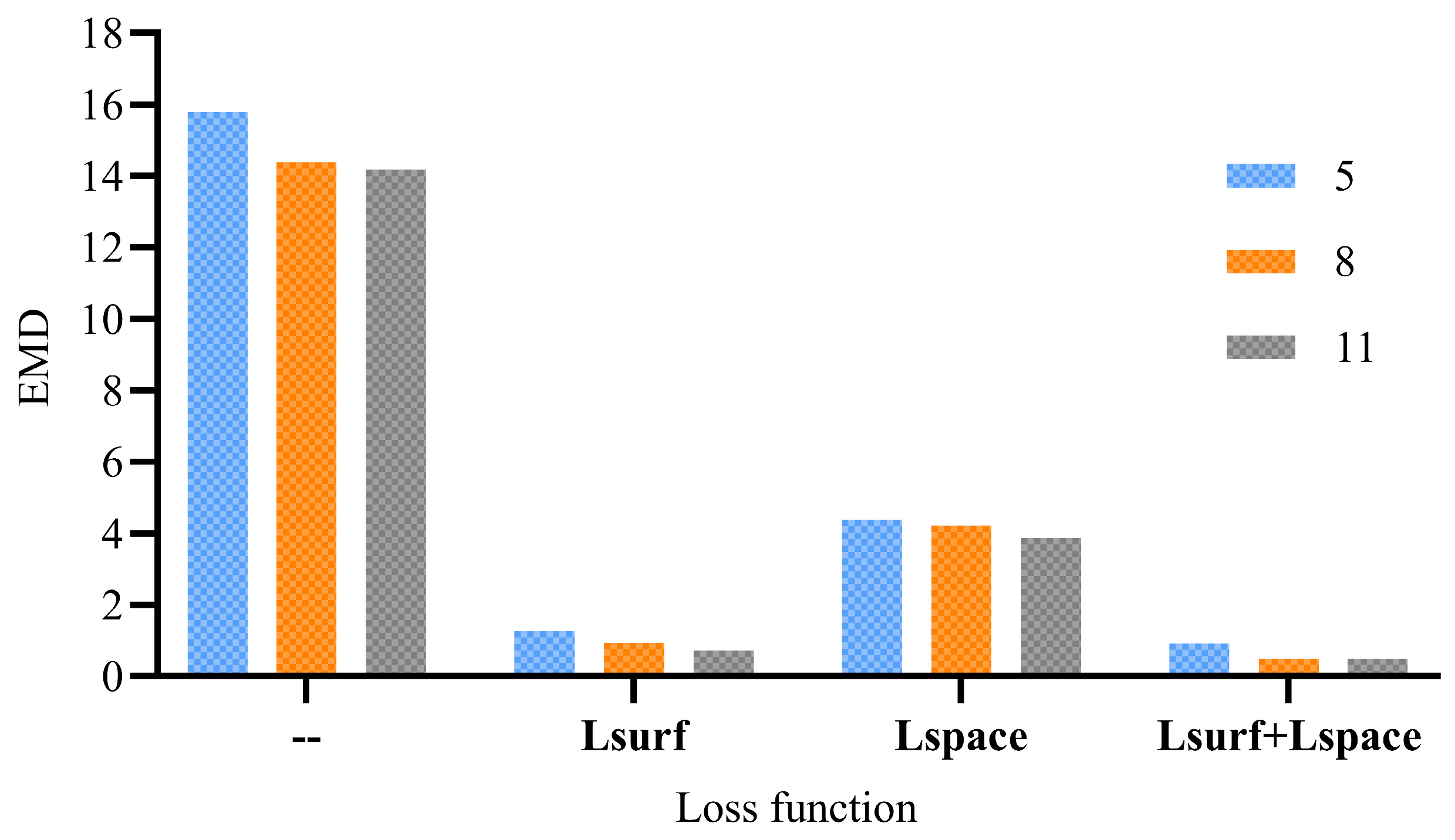
| Loss | Recurrent Number | EMD |
|---|---|---|
| - | 5 | 15.79 |
| - | 8 | 14.37 |
| - | 11 | 14.16 |
| 5 | 1.26 | |
| 5 | 4.37 | |
| 5 | 0.924 | |
| 8 | 0.943 | |
| 8 | 4.21 | |
| 8 | 0.505 | |
| 11 | 0.732 | |
| 11 | 3.879 | |
| 11 | 0.503 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, M.; Li, X.; Tan, H. An Elastic Fine-Tuning Dual Recurrent Framework for Non-Rigid Point Cloud Registration. Sensors 2025, 25, 3525. https://doi.org/10.3390/s25113525
Yuan M, Li X, Tan H. An Elastic Fine-Tuning Dual Recurrent Framework for Non-Rigid Point Cloud Registration. Sensors. 2025; 25(11):3525. https://doi.org/10.3390/s25113525
Chicago/Turabian StyleYuan, Munan, Xiru Li, and Haibao Tan. 2025. "An Elastic Fine-Tuning Dual Recurrent Framework for Non-Rigid Point Cloud Registration" Sensors 25, no. 11: 3525. https://doi.org/10.3390/s25113525
APA StyleYuan, M., Li, X., & Tan, H. (2025). An Elastic Fine-Tuning Dual Recurrent Framework for Non-Rigid Point Cloud Registration. Sensors, 25(11), 3525. https://doi.org/10.3390/s25113525