1. Introduction
Multitarget tracking is to jointly detect and track the number of targets and their individual trajectories of multiple mobile targets. The number of targets is time-varying, i.e., new targets can appear and existing targets can disappear. The sensor’s measurements suffer from missed detection, false alarms, and uncertain associations between targets and measurements. Multitarget tracking is a fundamental topic in many engineering fields, including traffic control [
1], remote sensing [
2], and computer vision [
3,
4].
Various methods have been developed to perform the multitarget tracking. A popular class is the random finite set (RFS)-based recursive Bayesian filtering methods, which are mainly composed of two types: unlabeled and labeled methods. The unlabeled RFS-based methods include the probability hypothesis density (PHD) filter [
5], the cardinalized PHD (CPHD) filter [
6], and the multi-Bernoulli (MB) filter [
7]. Compared to the unlabeled methods, the labeled RFS-based methods not only track the target states but also incorporate the target labels into the target states. The labeled RFS-based methods include the generalized labeled multi-Bernoulli (GLMB) filter [
8] and the labeled multi-Bernoulli (LMB) filter [
9,
10].
The availability of low-cost sensors has employed multiple sensors to cooperatively perform the tracking tasks. A local estimate is first computed with the measurements of each sensor. Then, the global estimate is generated by fusing all local estimates. The most commonly used fusion method is the generalized covariance intersection (GCI) fusion [
11], also called as exponential mixture density [
12]. The global estimate produced by GCI fusion is actually the one that minimized a weighted average of Kullback–Leibler divergence (KLD) from all local estimates to itself [
13,
14]. It can be interpreted as the one that leads to minimum cross-entropy from the information-theoretic viewpoint. Using the GCI fusion rule, many algorithms have been proposed for different multisensor multitarget tracking scenarios, e.g., the sensors have different fields of view [
15,
16], sensor fusion with event-triggered communication [
17,
18,
19], and so on. For the event-triggered communication in [
17,
18,
19], each sensor evaluates the KLD between the current local density and the last transmitted one and selectively sends the information that is worth transmitting, i.e., the KLD exceeds a threshold.
During these works, it is assumed that the sensor networks are secure and trusted all the time. Unfortunately, the sensor networks, such as the networked radar system [
20] and the intelligent transportation networks [
21], are vulnerable to unforeseen breaches in security. Due to the open communication between sensors, the data may not be transmitted with proper security protections. It is of great importance to accurately and quickly detect the adversarial attacks.
Among various types of adversarial attacks, false data injection (FDI) attacks [
22,
23] are a major concern. The FDI attacks are known as specific deception attacks or integrity attacks. With a successful FDI attack, an adversary can gain access to the communication and modify the transmitted data between sensors, which can manipulate the estimated values of the state variables and disrupt the system’s operation.
How to detect and defend against FDI attacks has attracted much research attention. For single-target tracking in [
24], the KLDs between local posteriors are used to partition the sensors into secure and insecure sensors. In [
25], the relative entropy was utilized as a stealthiness metric to detect whether the data transmitted through the wireless network are attacked. In [
26], the authors investigate the security of distributed filtering under false data injection attacks, and a new protection strategy is proposed. In [
27], the authors investigate a distributed secure estimation problem for a nonlinear stochastic system subject to a false data injection attack. In [
28], the authors apply sequential attack strategies to wireless mesh networks and conduct a comparative analysis with synchronous strategies. In these studies, the existence of the system state is known and time-invariant, so the dimension of system state is known and time-invariant. This is different from the multitarget tracking problem, where the targets may appear or disappear, i.e., the existence of system state is not known and time-varying, so the dimension of the system state is not known and time-varying. It is necessary to design the FDI detection method that is suitable for the multitarget tracking.
In this paper, we address multisensor multitarget tracking following a Bayesian filtering perspective where the sensor network may be compromised by FDI attacks. The transmitted data between sensors may be modified by the adversary. We propose a multisensor, multitarget tracking algorithm that can detect the possible FDI attacks over the network and provide robust and accurate tracking performance. More specifically, a local estimate is first generated from the measurements of each sensor based on the LMB filter. Then, a detection method for FDI attacks is derived with an information-theoretic criterion, where the KLD between LMB densities is utilized as a metric to quantify the similarity/difference of two local estimates. If the KLD between a local estimate and the reference estimate exceeds a given threshold, the local estimate is decided to be compromised by FDI attacks. Finally, the global estimate is obtained by minimizing the weighted sum of information gains from all secure local estimates to itself. An efficient Gaussian implementation of the proposed algorithm is also presented for the linear Gaussian state evolution and measurement model.
The contributions of this paper can be summarized as follows: (1) a detection method for FDI attacks is derived based on the KLD between LMB densities, and the statistical characteristics of the KLD are analyzed when the measurements are secure or compromised by FDI attacks, from which the value of the threshold is selected; (2) a set of suitable weight parameters are selected for the information fusion of LMB densities.
The rest of this paper is organized as follows.
Section 2 describes the system model and the FDI attacks for multisensor multitarget tracking.
Section 3 presents the proposed multisensor multitarget tracking algorithm that can detect and defend against the FDI attacks. Extensive numerical experiments are provided in
Section 4. The paper is concluded in
Section 5.
2. Problem Formulation and Background
In this section, we describe the state evolution model, measurement model, and FDI attacks for the multisensor multitarget tracking problem. This section also briefly recalls the labeled RFS and LMB filters.
2.1. Target State and Evolution Model
Suppose that there are multiple targets in the surveillance area at the time . The state vector of each target is defined as , where denotes the position and denotes the velocity of the target. The state could be extended to incorporate more variables if it is required. Both the number of targets and the state of each target are not known and time-variant.
Each target at a time
may continue to exist or disappear at the next time
. We denote the surviving probability that the target with state
will continue to exist at the next time as
. If the target
continues to exist, its state evolves according to the nearly constant velocity model [
29] as
where the transition matrix
is given by
with the
n × n identity matrix
, the time interval
, and the Kronecker product
. The term
is the additive Gaussian process noise with zero mean and covariance.
with the process noise intensity
. Accordingly, the single-target transition density is given by
Other motion models can also be used in the state space framework. The multiple targets move independently in the surveillance area.
In addition, a set of new targets are born in the surveillance area at each time step. The number of new targets is distributed according to a discrete probability distribution, and the state of each new target is distributed according to a spatial density over the surveillance area.
2.2. Sensor Network and Measurement Model
We consider a set of sensors , which are geographically dispersed in the surveillance area. Each sensor has sensing, communication, and processing capabilities.
For each target
at time
, the
nth sensor detects the target with probability
, so the probability of the missed detection is
. If the target
is detected by the
nth sensor, the measurement is governed by the single-target measurement model.
where the measurement matrix is
, and
is the Gaussian measurement noise with zero mean and covariance
. Other measurement models can also be used in the state space framework.
Moreover, the nth sensor may detect a set of false alarms in the surveillance area. It is usually assumed that the number of false alarms is distributed according to a discrete Poisson distribution, and each false alarm is generated according to a spatial density over the surveillance area.
At each time , the sensors transmit their measurements to the first sensor. The first sensor recursively estimates the multitarget states based on the measurements from all sensors up to time .
2.3. FDI Attacks
The sensors
transmit their measurements to the first sensor through some wired or wireless transmission. Generally, the sensors, such as the networked radar system [
20] and the intelligent transportation networks [
21], are spatially deployed in a monitoring region. The data may not be transmitted with proper security protections because of the broadcast nature. The wired or wireless connections between the
nth sensor and the first sensor can be maliciously compromised.
If one measurement
from the
nth sensor arrives at the first sensor, the received measurement may be compromised by FDI attacks. The attacker hijacks the data packets from the communication channel and injects data packets that are intentionally inaccurate [
20]. The compromised measurement under the FDI attack is modified as [
20].
where
is the FDI data injected by the attacker. A successful FDI attack can cause the state estimation to generate erroneous values. Since the FDI attack does not undermine the integrity of the data, it is stealthy (e.g., fools the popular
detector) and difficult to be detected. It is important to protect the security of the transmitted data and detect/defend the FDI attacks in the networks.
2.4. Labeled RFS and LMB Filter
In order to distinguish individual targets, a distinct label
is augmented to each target
[
8], where
denotes the single-target state space. The target with a label is denoted as
. Let
be the projection
. The space of all labels for targets born at time
is denoted by
. In the RFS formulation, the state of multiple targets with labels at time
can be modeled as a labeled RFS.
where each target
takes values in the state space
. Then,
is the set of labels of the RFS
. Each element in
has distinct label, i.e.,
(the sets
and
have the same cardinality). Similarly, the measurement set from the
nth sensor can also be described as a RFS
where each measurement
takes values in a single-target measurement space
.
An LMB density can be completely specified by the parameter set [
9].
where
is the existence probability of the target with label
, and
is its spatial density. The multitarget density of LMB RFS with the parameter set
is given by [
9].
where
if
and 0 otherwise, which is the distinct label indicator, and
in which
is a set of labels.
The single-sensor LMB filter estimates the multitarget states using the measurements from one sensor. For notation simplicity, we temporarily remove the index of in (8), and use the notation to denote the measurements from any one sensor.
At times
, we denote the LMB prior density by
The newly born targets at time
is also modeled as an LMB density.
Under the Bayes framework, the LMB filter recursively estimates the multitarget states with the LMB densities, including two steps: prediction and update.
The predicted multi-target density is an LMB density with the parameters [
9].
where
, and
where
is the surviving probability and
is the transition probability of the labeled target
, and the inner product notation is defined as
.
With the measurement
from any one sensor, the updated multitarget density is approximated as an LMB density with the parameters [
9].
where
and
is the space of mapping
such that
if and only if
(whose elements represent track-to-measurement association hypotheses)
denotes the set of all subsets of
,
if
and 0 otherwise,
is the detection probability, and
is the single-target likelihood function of the measurement
corresponding to the labeled target
.
3. LMB-Based Multitarget Tracking Against FDI Attacks
We derive a detection method for FDI attacks based on the KLD between LMB densities. The secure local estimates are then fused into a global estimate.
3.1. Basic Construction
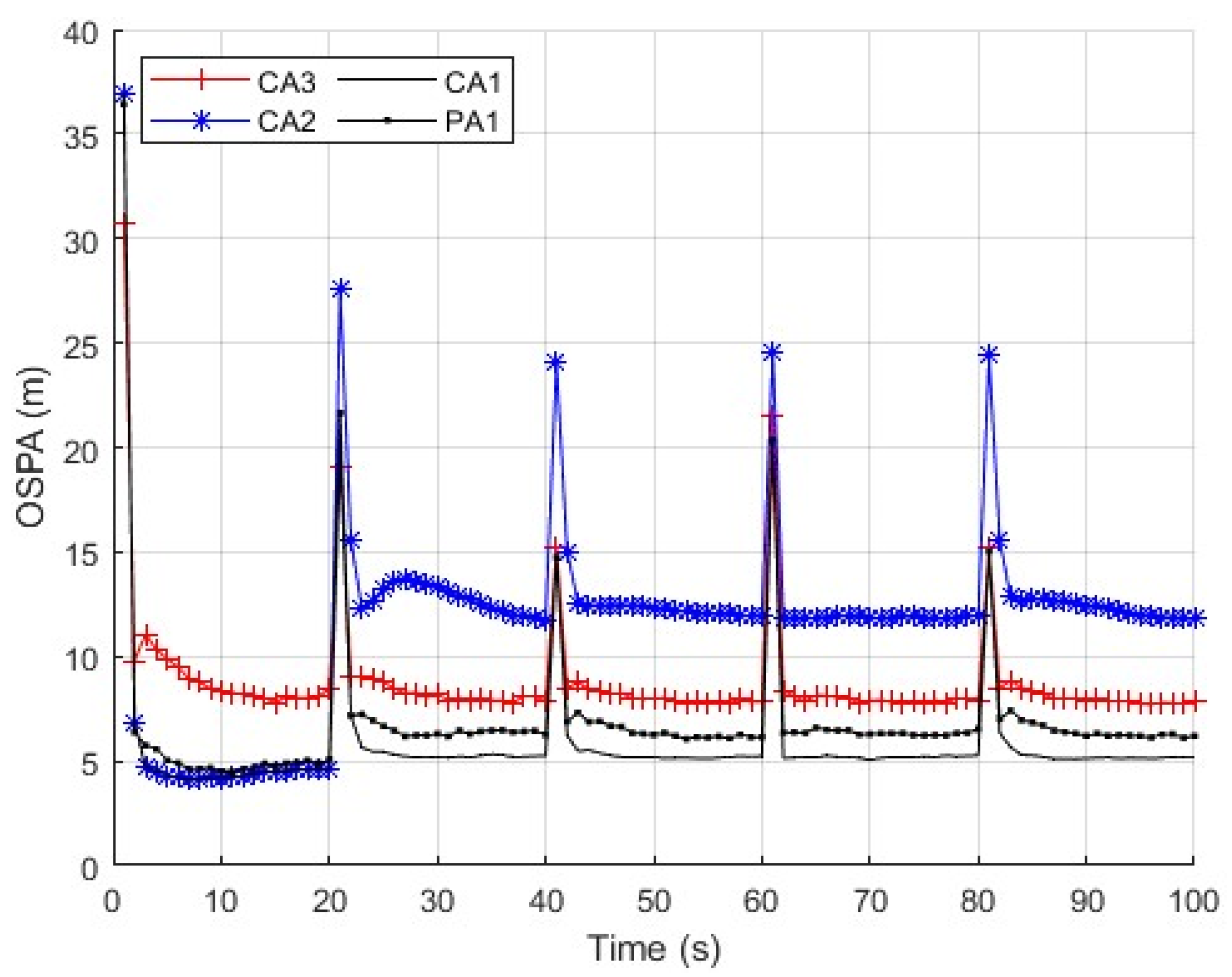
The sensors transmit their measurements to the first sensor, then the first sensor estimates the multitarget states based on the measurements of all sensors. The estimation process includes three steps: (1) the first sensor computes a local estimate based on each sensor’s measurements with the LMB filter; (2) the first sensor detects the local estimates that are comprised by FDI attacks; (3) the first sensor fuses all secure local estimates into a global estimate.
At time
, we denote the LMB prior density at the first sensor as that in (13). With the prior density and the LMB born density in (14), the first sensor computes the local estimate from the
nth sensor’s measurements, and we denote the parameter set as
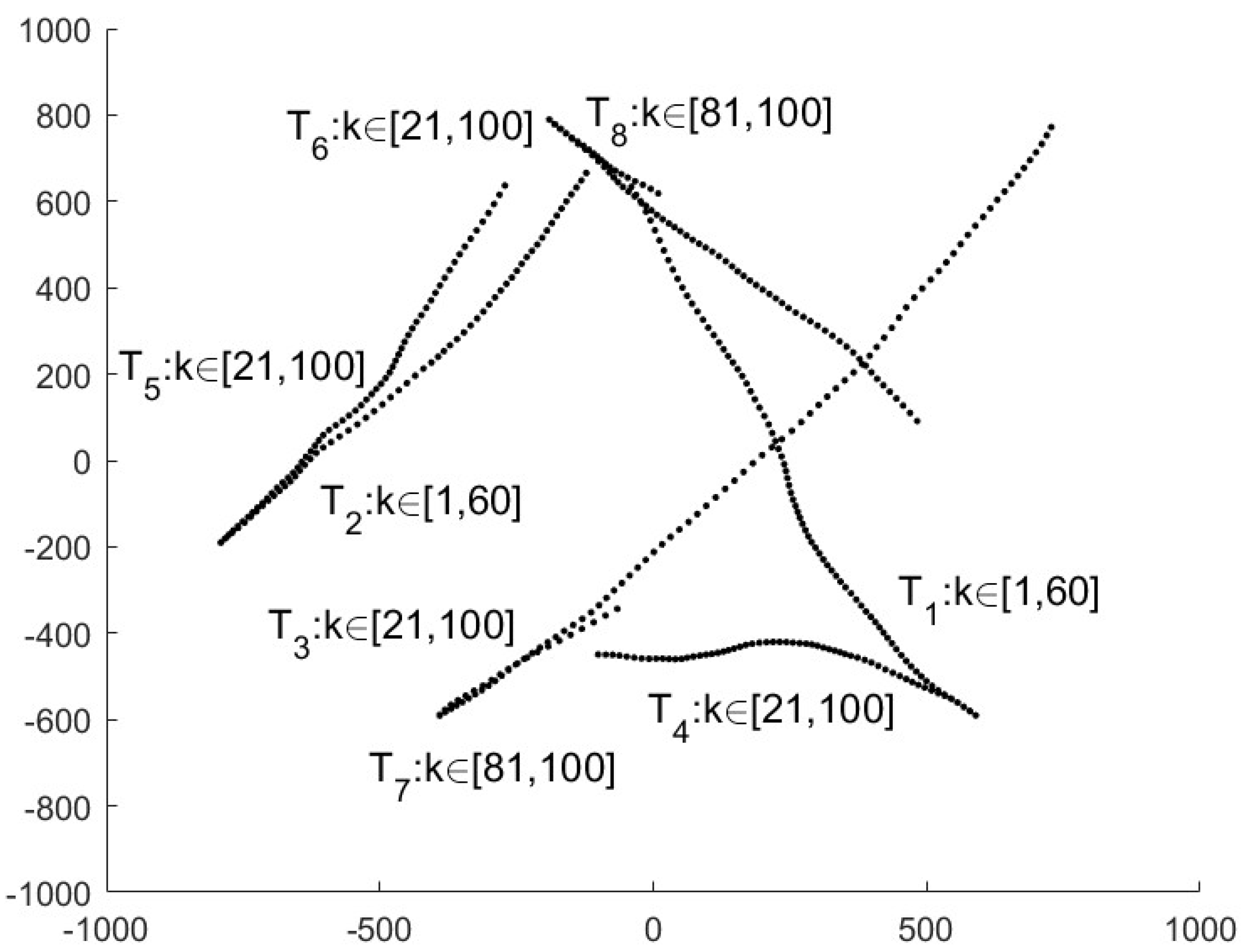
The corresponding LMB density with the form in (10) is denoted as . Since all local estimates are computed from the same prior density and born density, the label set is the same for all local estimates, and the labels corresponding to the same target in different set are also the same, i.e., there is no label mismatching problem.
Since the wired or wireless connections between the nth sensor and the first sensor may be maliciously compromised by FDI attacks, the compromised measurements will deteriorate the local estimates. It is necessary to detect the attacked sensor as well as the corresponding local estimates before the fusion process. In particular, since the first sensor directly has its measurements, it is not necessary to be transmitted over the wired or wireless connections, so it is assumed that the measurements of the first sensor are secure all the time.
For notation simplicity, we remove the index in and because all operations are executed at time in the rest of this section.
3.2. KLD-Based Detection of FDI Attacks
Because the measurements from the first sensor cannot be compromised by FDI attacks all the time, the local LMB density will be secure all the time. We consider as the reference density and utilize some metric for the discrepancy between each density () and the reference density to detect the possible FDI attacks. We introduce a binary variable for the nth sensor such that if the measurements from the nth sensor are compromised by FDI attacks, and otherwise.
There are many ways to quantify the discrepancy of two densities. The KLD is a competitive alternative in many probabilistic detection problems. The KLD of two probabilistic densities
and
is defined as
where
, and
if and only if
. The KLD quantifies how close a density is to a reference density. The KLD admits an elegant interpretation from an information-theoretic viewpoint, i.e., it represents the information gain achieved when the density
is revised into the density
[
30].
The concept of the KLD can be extended to the multitarget RFS density with the set integral. If
and
are two RFS densities, the discrepancy between
and
can be measured by the KLD.
where the integral
is a set integral defined by
The KLD is not symmetric, i.e.,
in general. The
J divergence [
31] symmetrizes the KLD as
where
is usually called forward KLD and
is reverse KLD [
32].
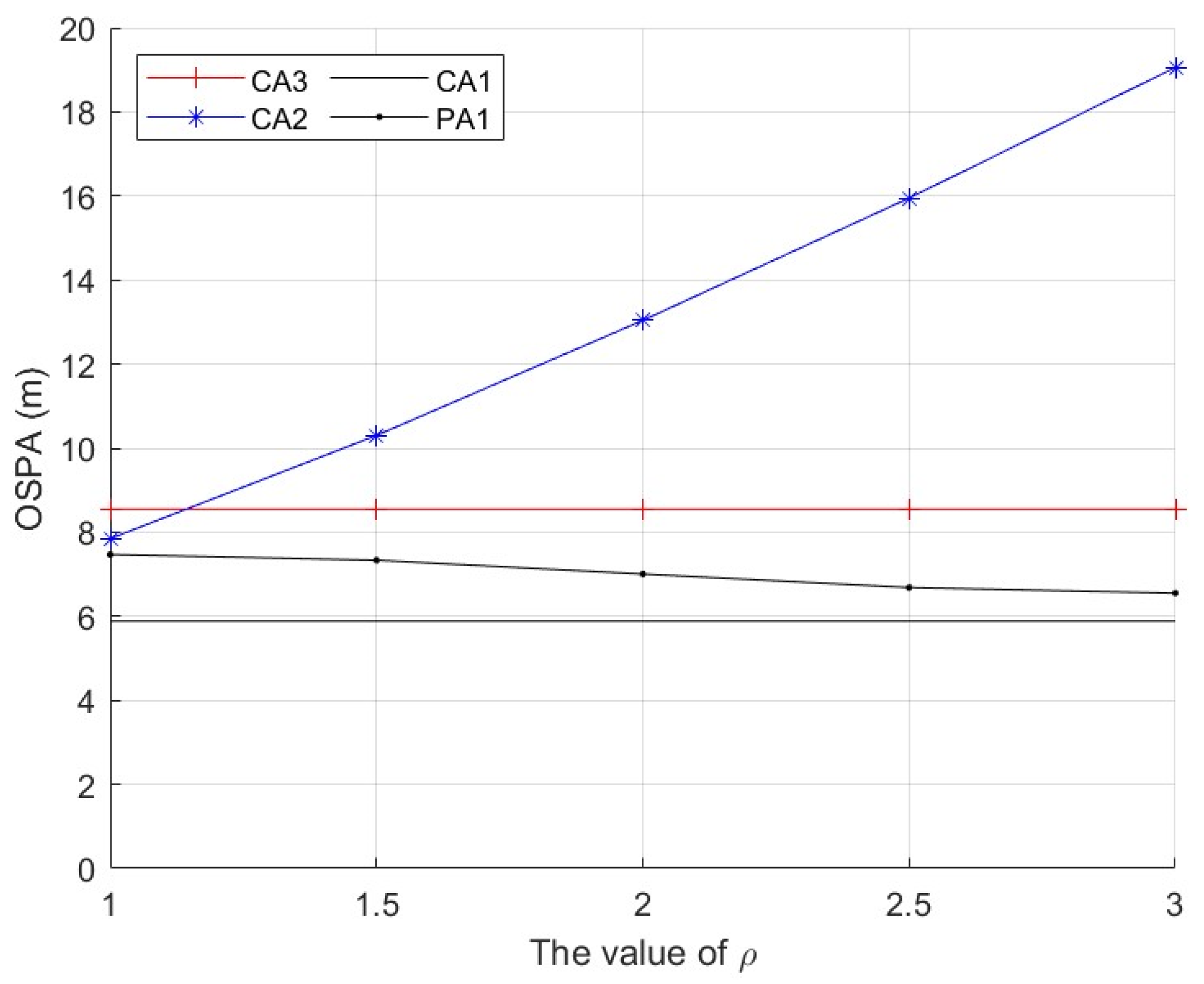
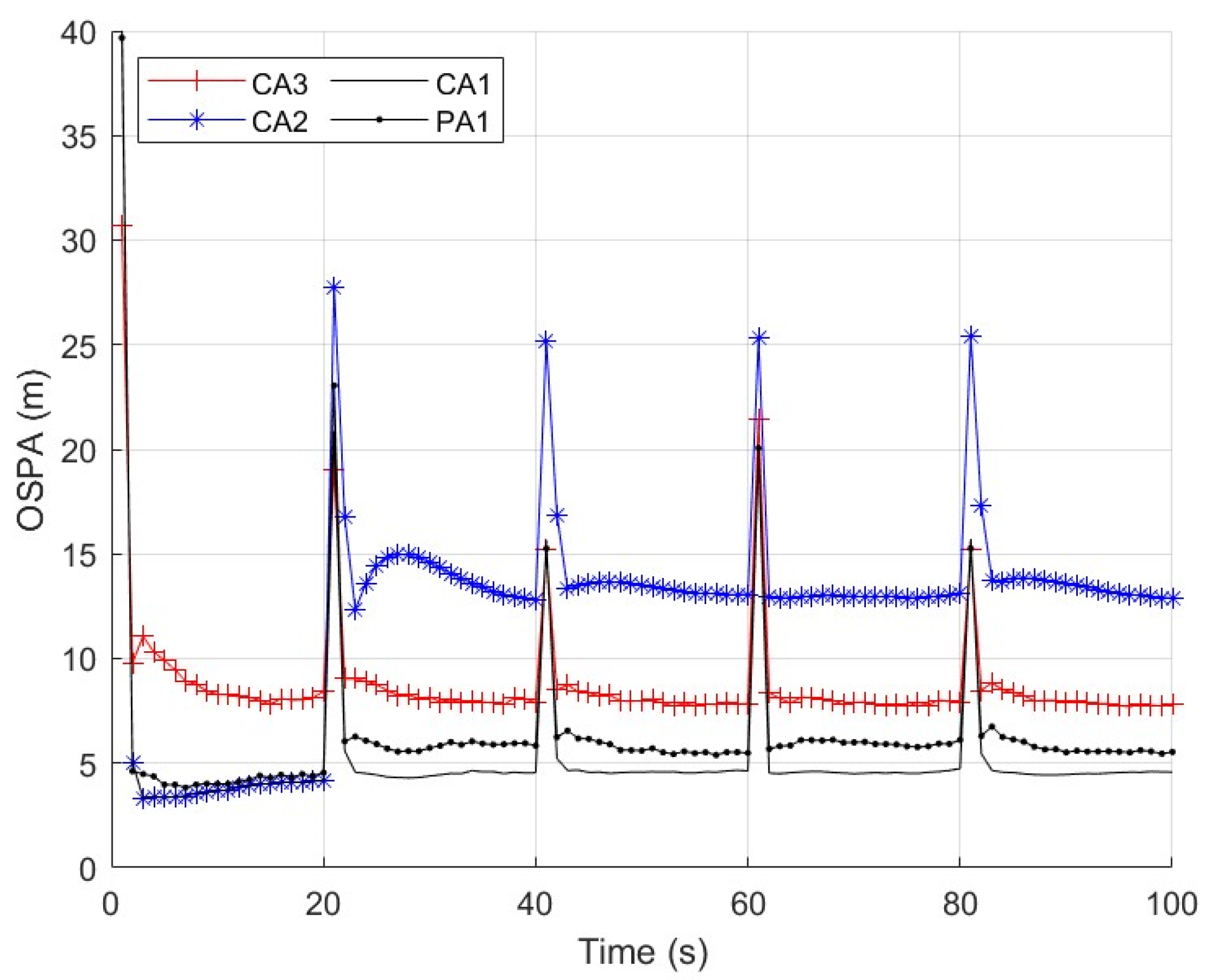
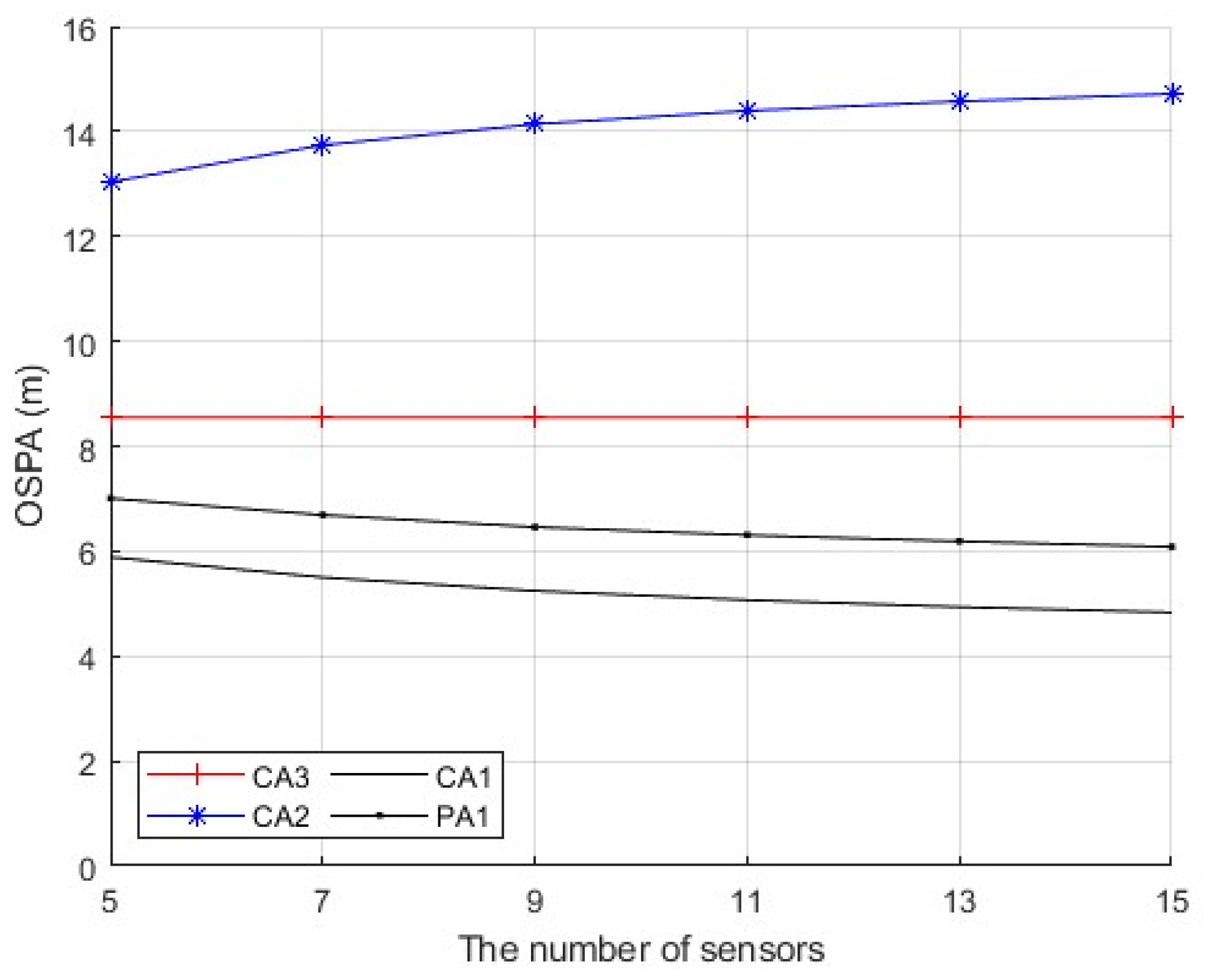
By considering the discrepancy metric in (29), the following detection method for FDI attacks is adopted as
where the scalar
τ is a design parameter that is tuned so as to achieve a desired performance. We will discuss the choice of
τ in
Section 4.2.
Substituting the LMB density
with the parameter set
into the KLD (27) and using the definition of set integral, it can be proved that [
33]
where
Because all local estimates are computed from the same prior density and born density, there is no label mismatching problem, i.e., the term with label in the local density describes the same target as the term with label in the local density . The KLD can be computed in a label-wise manner.
3.3. Information Fusion
We denote the index set of secure local estimates after the detection of FDI attacks as
The local estimates in are not considered to be compromised by FDI attacks. In order to combine all local estimates in into a global estimate, the first sensor carries out the information fusion step. The goal of the fusion step is to compute the global density that encapsulates all the information provided by the local densities in which can provide better estimation performance.
From a view of information theory, the fusion of the local densities
in
is to find the density that has minimum divergence gain from all densities
in
with respect to a suitable metric. The global density can be obtained by minimizing the weighted sum of the information gains from all local densities in
to itself as [
13].
where
denotes the information gain from the density
to the density
, and the non-negative weights
reflect the relative information confidence of
in comparison with the rest terms, which satisfies
. The KLD
between
and
is one of the popularly adopted metrics for the information gain.
It can be shown that the fusion density computed by the rule (35) with the KLD is given by [
34].
The rule in (36) is also called the GCI fusion rule. It provides a weighted geometric mean in the form of an exponential mixture of the local densities.
Because all local densities
in
are LMB densities with the parameters
, one can check that the global density
in (35) is also an LMB density with the parameters [
33].
Since the same target is described with the same label in the different parameter sets , the fusion step can be performed in a label-wise manner.
3.4. Implementation Issues
Each term of the LMB density in (14) of the newly born targets is commonly modeled as a Gaussian density.
where the model parameters
and
indicate the highest local concentrations of spontaneous birth, which can represent, for example, the airports where the target is mostly likely to appear [
35].
The computation of
in (32) is direct. In order to develop a computationally feasible implementation of
in (33), we approximate the spatial density
as a Gaussian density.
This result can be obtained by the commonly used Gaussian mixture implementation of the LMB filter and suitable pruning/merging operations. Because each term in describes only one target with the existence probability and the spatial density , the Gaussian approximation has enough accuracy.
Substituting the Gaussian form of
into (33), it will have
where
denotes the dimension of the variable
, and
means the trace of the matrix
.
Moreover, substituting the Gaussian form of
into (38), it will have
and
in (37) and (38) has the form
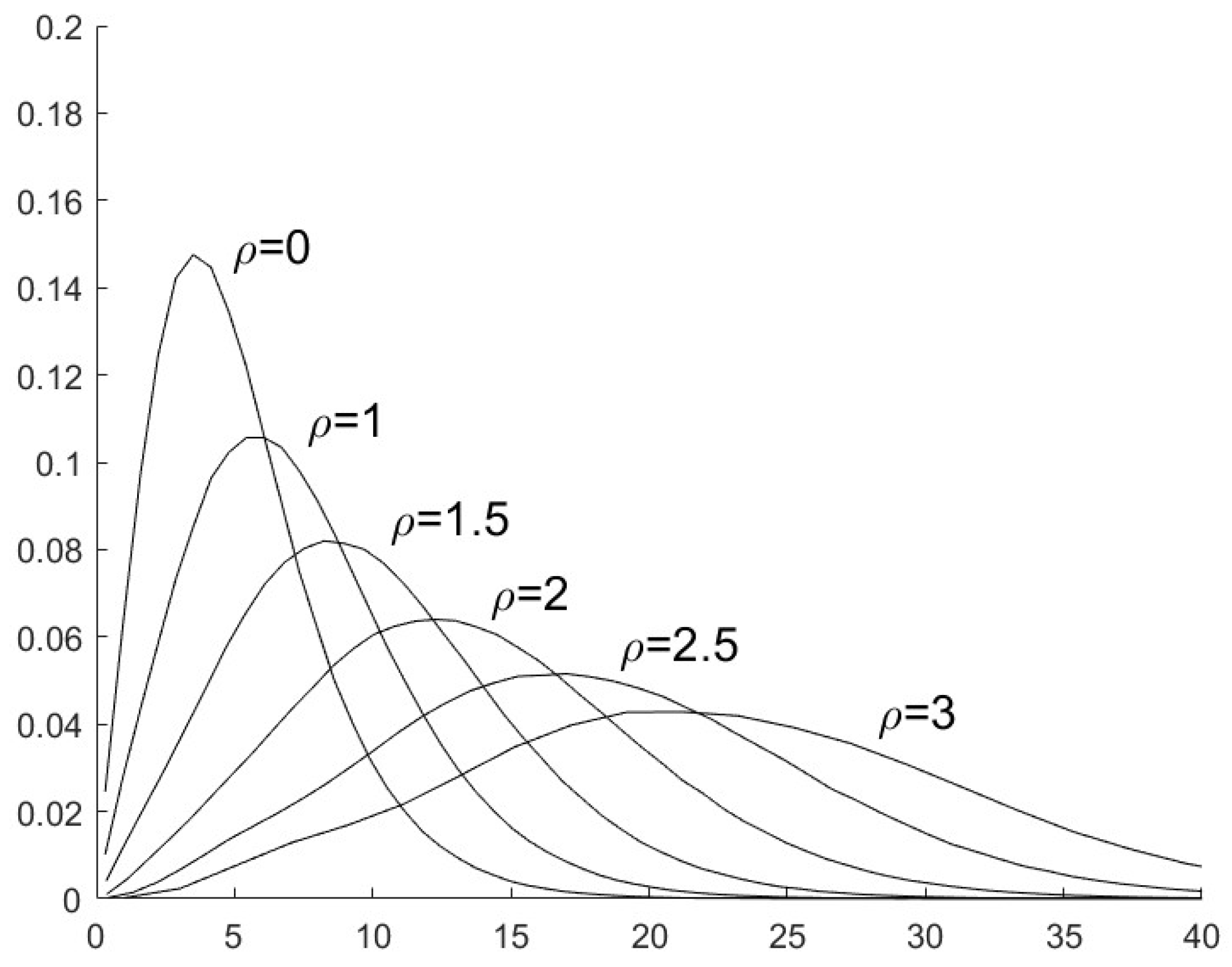
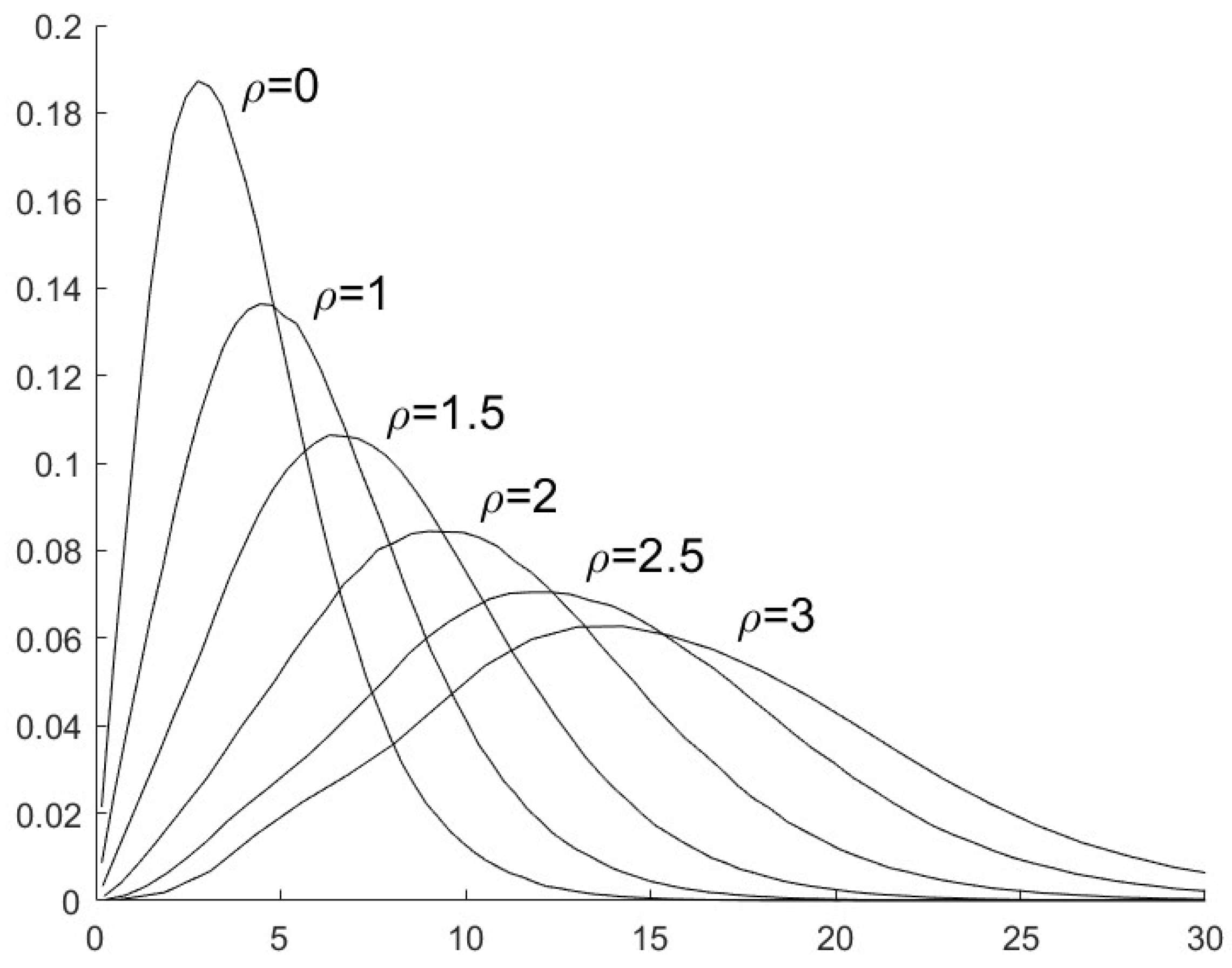
If the n sensor is not compromised by FDI attacks, the value of will be closely approximate to the value of , both of which are the existence probability of the same target with label . Similarly, the value of is also closely approximate to with the assumptions of the shared prior and the uniform Kalman gains. So the values of in (32) and in (41) are much smaller than the value of in (41). The main part of will be decided by the quadratic form . The distribution of the quadratic form can be approximated with a general distribution.
3.5. Choice of Weighting Parameters
Substituting (31) into the weighted sum of the information gains (35), it will be
where the same weight
is used for all
. We revise the information gains as
i.e., the different weight
is used for different
.
From the fused covariance
in (43), the optimality in the mean square error sense is as follows [
36]
For each
, a suboptimal solution is then given by
The suboptimal solution is calculated for each track .
The proposed algorithm is summarized in Algorithm 1. The computational burden at the first sensor mainly includes two parts: (1) The first sensor computes the KLDs
in (31) for each
with
in (32) and
in (41); (2) The first sensor computes the fused parameters
in (43) and
in (44).
| Algorithm 1: Multisensor Multitarget Tracking Against FDI Attacks |
Input: The prior density .
Output: The posterior density . |
1. The first sensor receives the measurements in (8) from the nth sensor ().
2. The first sensor computes the predicted density in (15).
3. For each measurement
, the first sensor computes the local updated density in (25) with (19) and (20), where is approximated as a Gaussian density in (40).
4. The first sensor detects the FDI attacks with (30), where is computed with (31)–(33) and (41).
5. The first sensor computes the fused density with (37), (38), and (42)–(45). |